边坡稳定备受关注,其本身构造复杂,且影响因素众多[1-3],边坡实际上是个复杂的运行体,其健康状态、滑坡风险分析是重要的系统课题。为直接有效地了解边坡状态,对其实施安全监测意义重大。由于位移与边坡的稳定性具有综合性和直接关联性,已成为边坡稳定状态及滑坡预测的最主要监测项目[2,4-5]。对边坡实测位移的分析也成为学者们研究的重点,并取得了一些成果,目前主要包括规律描述,建立监测模型等方面,但对如何利用实测信息动态定量地识别边坡的健康状态、直观地预测事故的发生率等还研究有限。作为运行系统而言,如果发生滑坡等灾害,实际上是边坡机体失效,丧失了应有的健康状态。监测表明:滑坡的发生存在发展历程,在此时段内,边坡的健康状态正发生恶化,换言之,其正常工作性能在下降,事故发生概率在增大,如果及时有效地定量识别该过程,提供实时直观的分析及预测,将极大提高滑坡危害预防能力、实现边坡状态有效健康管理。鉴于此,本文结合先进的故障预测与健康管理方法(PHM),研究基于实测信息的边坡PHM系统框架,由于PHM技术在边坡工程中的研究应用尚处起步阶段,本文以位移为代表对其状态进行故障分析,预测事故发生率。
PHM是先进的系统管理方法,主要思路是利用传感器采集系统的各类信息,以合理的推理算法评估系统健康状态,对系统故障尽早予以监测并进行有效预测,同时依据各类数据信息,提供合适的维护保障措施以实现系统的视情维修[6-8]。PHM首先在部分发达国家飞行器等军事领域得以应用[9],而后由于其先进性及显著效果逐步得到推广,本世纪研究开发了航天器集成健康管理、飞机状态监测、海军的综合状态评估等诸多系统,并积极引入、应用到民用领域[10-12],显示出巨大的发展潜力和应用前景。相对而言,国内PHM的应用相对较晚,较多尚属方案论证和框架研究。可喜的是,随着近年来对该方法认知的深入,PHM应用研究领域正在逐步扩展并取得阶段成果[7-8,13-14]。
对运行的系统而言,其健康状态的退化是一个发展过程,由正常逐渐下降,直至发生故障、功能失效,PHM注重运行系统状态的变化和识别,注重故障的预测,实现系统视情维修。对于边坡工程,从稳定到滑坡等灾害发生正是这样的变化历程,而边坡的安全监测是以监测设备获取反映边坡状态的数据信息为手段,其目的是通过监测分析对边坡进行适时加固治理,预防及减少灾害,所以将PHM引入到边坡监测分析具有很高的相容性及重大实用价值。本文结合PHM与边坡监测的特点,研究构建边坡PHM技术路线,并以位移为代表,研究基于实测位移的故障率动态识别及预测方法。
1 PHM理论及边坡PHM技术路线
PHM技术的实现本质是通过对信息的采集分析、对系统当前状态的描述以及对下一时段状态和故障的预测,以提高对系统健康状态的掌握,并采取相应措施提高系统可靠性和安全性。根据研究对象不同,PHM体系有不同构成及特点,总体上包括以下模块:数据采集、数据处理、状态监测、健康评估、故障预测及决策支持。依据分析对象的不同,数据采集项目及状态指标有所不同,评价体系存在一定差异,同样,故障形式多样化,决策支持视情而异。
PHM是一种系统主动性保障策略,可以更有效地实现系统状态监测和故障预测,使系统的运行管理方式发生转变,更有效地开展视情维修。系统维修可分为事后维修、计划维修和视情维修,相比另两种维修机制,视情维修有显著特点和优势。事后维修是指系统在发生故障后对其进行修复,此时故障甚至事故已发生;计划维修是按计划定期对系统进行维修,不考虑系统工作状态是否良好,不考虑实际应用中的突发因素;视情维修则是根据系统的工作状态对需要维修的系统进行维护和调整,是一种预测维修体制。PHM关注系统状态监测、故障预测,所以可以提供视情维修的技术依据,这对于很多系统或工程都十分重要。对边坡工程而言,事后维修加固处理往往意味着灾害已发生,而定期加固处理针对性不强,由于需要大量人力物力而经常受到限制。如果能发现状态的恶化,动态预测故障,则能及时进行有针对性的处理应对,避免或降低灾害损失,基于PHM建立边坡故障预测与健康管理体系符合该目的。依据PHM基本思想,借鉴该理论应用实践,建立边坡安全监测PHM系统框架如图1所示。

图1 边坡监测PHM系统框架
Fig.1 Framework of PHM monitoring system for slope
由图1可知:边坡PHM系统的运行可以融入多种信息手段和分析方法,鉴于边坡PHM研究尚属起步,所以在当前阶段应循序渐进加以研究。
边坡PHM系统预测故障、有效决策等目标的实现需要及时掌握边坡状态,而安全监测正是获得边坡实际状态信息的最直接方法,所以本文重点结合监测信息,以位移为代表开展故障预测研究。如前文所述,不同分析对象有着不同的状态指标,位移是反映边坡动态的一项重要综合指标,是预测滑坡的主要依据,在监测实践中,位移也是获得实时连续测值最好的项目,信息采集能力已可满足PHM分析的基础要求,而基于PHM和实测值实现位移动态故障预测是当前研究重点之一。
2 位移故障率识别
故障预测是PHM系统的重点内容,故障预测技术与各领域特点密切相关,采用合理的故障预测方法是PHM研究的关键技术。对故障诊断和预测方法的分类较多,通常包括[15-16]:损伤标尺方法、性能状态检测方法(也称为基于故障预兆监控及推理方法)以及基于使用环境信息的预测方法,还有学者强调数据融合及综合诊断预测思想。而数理统计、神经网络、可靠度分析等数学方法都可能成为故障诊断和预测的有效工具,应根据分析对象具体情况予以应用。
边坡位移作为监测的主要项目,如今已能实现实时采集、远程传输,可以持续获得较长的监测序列[2],这些数据中包含了边坡位移发展动态以及是否存在失稳可能的重要信息。失稳前的边坡位移通常会有一个不断增大的过程,当位移量达到一定程度时出现滑坡等破坏,这个过程实际上是边坡稳定性能在逐渐退化,所以将位移作为退化量。退化量是指能够反映系统健康状态退化程度的指标[17],可通过监测信息获得,可见现场实测的边坡位移具备所需条件和特质。基于性能退化的故障预测基本思想是以性能退化数据建立样本在某个时刻的可靠度,记特征量X的性能退化数据序列为x(t)={x(1),x(2),…,x(m)},其中m代表总的监测时间。如果x(t)大于或等于阈值[x],代表故障发生。给定系统的失效阈值[x]后,定义系统在 t 时刻的可靠度即为:
R(t)=P{x(t)<[x]}
(1)
对不同领域、不同退化量,可靠度有多种算法。对于临滑期的边坡而言,位移是重要而直观的判断指标,在工程实践中常采用位移或位移速率阈值来判别,部分技术标准[18-19]已有相应内容。以位移为例,基本思想是:设发生滑坡的位移量阈值为[u],当
u(t)≥[u]
(2)
认为故障发生,其中u(t)为t时刻实际位移,通过监测可以实时获得。这与基于性能退化的故障分析思想是一致的。
在临近发生滑坡期间,实测位移曲线表现出来的是位移量增大,逐渐接近[u]。当边坡位移远小于阈值时,其安全储备较大,故障发生率较小,由于实测位移是边坡状态的真实反映,而且已具备较高的精度和准确度,鉴于此,定义基于安全监测的位移t时刻故障率(FR)为实际位移量相对位移阈值的占比,记为pFR(t),算式如式(3):
(3)
相应定义位移安全储备度(RSD)为位移阈值与实际位移差相对位移阈值的占比,记为PRSD(t):
(4)
显然,分析时段是指u(t)≤[u]期间,所以位移故障率取值范围[0,1],可依据实测的位移序列绘出对应时间曲线,直观掌握各时刻的故障率pFR(t),有效进行故障率的动态识别。
如前所述,基于安全监测工作可以获得边坡的实际位移序列,其准确性和实时性目前已有保障,这也是采用式(3)、式(4)的有利基础。而位移阈值确定方式因具体情况有所不同,PHM故障识别时可以根据国家或部门技术标准的要求加以采用;当不能直接给出确切阈值时,可以根据实测位移,采用滑坡预测方法加以计算。本文根据边坡临滑期的特点,发挥实测位移序列信息优势,以斋藤迪孝模型预测滑坡时间tr,并建立监测模型预测tr时的位移u(tr),以式(3)、式(4)计算pFR(t)、PRSD(t),实现边坡位移故障动态预测。要说明的是:在一些故障预测实践中,是根据已确定的阈值再确定对应的时间,继而获得剩余寿命估计,本文针对没有既定阈值的复杂情况采用上述方法,可以利用监测信息获得系统剩余时间以及退化量的界限值。
3 位移及故障率预测
斋藤迪孝法适用于临滑坡短、中期的趋势预报,是一种影响力较大、有代表性的预测方法,被众多学者、DZ/T 0221—2006《崩塌、滑坡、泥石流监测规范》[20]加以应用。日本学者斋藤迪孝通过对滑坡模型的试验研究指出:滑坡破坏时间与稳定蠕变状态下的应变速率成反比,如式(5)表示:
(5)
式中:tr为滑坡破坏时间;![]() 为稳定蠕变阶段的应变速率。
为稳定蠕变阶段的应变速率。
斋藤迪孝假定加速蠕变段曲线为圆弧,认为应变速率与离破坏所余时间(tr-t)成反比,即认为距离最终破坏时间越短,应变速率越快,有以下模型[20]:
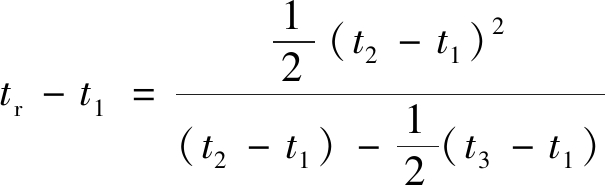
(6)
式中:t1、t2、t3是加速蠕变曲线上的3个时间段,它们之间发生的应变相等。
边坡监测中可获得边坡位移时间序列,应用斋藤模型时,可以在加速蠕变的位移-时间曲线上取3点,相邻点间相对位移量相等,3点对应的时间为t1、t2、t3,代入式(6)求得滑动破坏时间tr[21]。
对尚未滑坡的工程进行故障预测,tr对应的是将来某个时刻,该时刻的实际位移尚属未知。为此,利用已获得的实测位移序列建立预测模型,计算滑坡破坏tr时刻边坡的位移量,即该时刻的位移阈值。为获得该位移阈值,本文采用BP神经网络模型,利用实测位移作为样本加以训练,进而向后预测直至tr时刻的位移量,既可以获得后期位移变化序列,同时又获得位移阈值。
PHM以信息采集为基础,智能算法是其预测、识别的重要工具。人工神经网络经过多年研究,已经在众多领域得以应用,尤其在模式识别、人工智能、控制工程、优化计算等领域发展迅速,也是PHM系统采用的一种主要方法,本文借鉴边坡、坝工监测分析经验,以反向传播神经网络(BP网络)为工具,依据实测序列,结合斋藤迪孝法预测滑坡临界位移。
BP网络是应用广泛、成熟可靠的算法。该算法从输入层到中间层(隐层)再到输出层,依次计算各单元输出,然后从输出层向输入层反向计算,逐层调整隐层与输出层之间的权值、以及输入层与隐层之间的权值,当计算值与实际输出值精度满足要求(或学习次数足够)时,完成训练过程[2,22]。在PHM系统中,由于采集的信息种类较多,类别不同,为消除各类信息的量纲及变化范围差异带来的精度影响,建议对计算样本进行归一化处理,转换为统一变化范围的无量纲序列,然后投入神经网络计算,输出的结果再反向回归其原有量纲及大小。归一化可采用式(7)进行:
(7)
式中:![]() 为归一化前后的样本值;xmax、xmin为该样本序列的最大、最小值;K1、K2为可以控制归一化后序列的变化范围的参数,当它们分别取1、0时,变换后的序列所有值属于[0,1]。
为归一化前后的样本值;xmax、xmin为该样本序列的最大、最小值;K1、K2为可以控制归一化后序列的变化范围的参数,当它们分别取1、0时,变换后的序列所有值属于[0,1]。
在以往神经网络监测模型实践中,存在两种情况[2]:一是当影响因素信息完整、作用关系明确可以将其放置于输入层;另一种情况是作用因素不够明确,或影响因素监测信息完整性不足,这时对时间序列效用量采用时效因子作为输入层。本文以后者为例,为预测滑坡破坏时间tr时的临界位移,以时效因子作为输入层。由于位移与时间关系的复杂性,根据级数展开思想,取时间的多个幂次方作为输入层因子[2],由实测位移和时间因子形成训练样本,投入模型进行训练,当精度达到要求后,以所得模型进行预测。此时将tr代入输入层因子,模型计算输出,即得到对应的临界位移u(tr),也就是故障预测的位移阈值,根据式(3)、(4)即可获得边坡位移故障率及安全储备度。
4 应用案例
某边坡有崩塌历史,在坡内埋设固定测斜仪进行位移监测。2016年3月下旬开始,测斜孔顶部测点发生明显位移变化,并向坡外加速发展。采用斋藤迪孝法,从实测数据中获得2016年3月20日、4月7日、4月17日3个监测时间,相邻时间点之间的实测相对位移量相等,都为4 mm。由于式(2)与各时间点的间距有关,与t1起始值无关,不妨以2016年3月20日为相对起始日,对应t1=1 d,则4月7日对应t2=19 d,4月17日对应t3=29 d。代入式(2)计算得到tr=41.5 d,即从2016年3月20日开始的第41.5天为预测的滑动破坏时间。
以2016年3月20日—4月17日实测位移数据为输出层训练样本,取时间的1~3次幂形成输入层3个单元,位移为输出层,采用前文方法对样本进行归一化后投入BP网络计算,建立位移预测模型。训练结果表明:所建模型准确把握了位移大小及趋势规律,且有效地排除了采集误差的干扰,效果理想。故基于训练所得模型向后预测,得到tr=41.5 d时的位移,即临界位移u(tr),为15.89 mm。
以u(tr)位移量阈值为[u],根据位移u(t)可计算各时刻的位移故障率及安全储备度,本例边坡对应即为:
(8)
(9)
式中位移单位为毫米。
可以根据以上两式代入实测值得出直观位移故障率曲线。另外,由于已建立BP网络预测模型,模型过滤了部分误差噪音,规律更为清晰,所以也可根据模型结果绘制故障率曲线,同时利用其预测功能得到后期位移预测序列,预测将来各时刻的位移故障率,一并在图形中展现,便于了解后期边坡位移故障率及安全储备。如图2所示,图中4条曲线中,波动较大的是根据2016年3月20—4月17日实测值计算的位移故障率和安全储备度。另两条光滑曲线是根据BP模型结果得到的位移故障率和安全储备度,其中4月17日之前采用的是位移训练结果,之后是预测值。
可见,图2清晰展示了位移故障率和安全储备度发展历程,便于实际应用,而且利用预测模型实现故障率和安全储备度的后期预测,有利于边坡治理、预警决策。
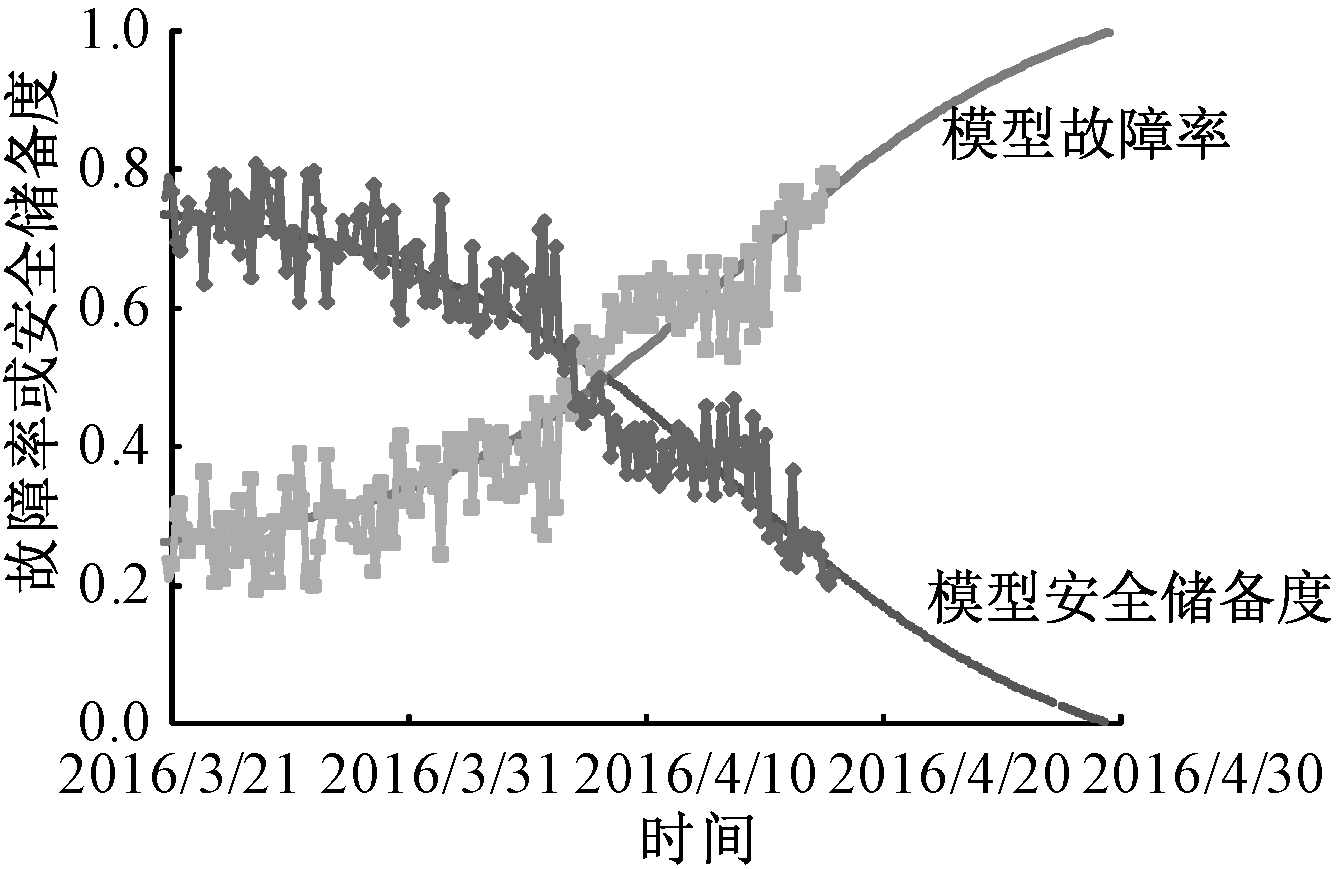
![]() — 故障率;
— 故障率; ![]() — 安全储备度。
— 安全储备度。
图2 位移故障率及安全储备度动态曲线
Fig.2 Time curves of displacement FR and RSD
该边坡后期现场监测得到tr时刻实际位移为15.91 mm,而边坡出现了局部崩塌,与预测情况相符。为防止边坡后期继续崩塌,相关部门对边坡开展了维护治理。
5 结束语
边坡安全关系重大,通过现场监测可以实时获得反映边坡状态的真实信息,将先进的PHM方法应用到边坡治理,挖掘监测数据信息,对边坡系统进行故障预测,可以有效掌握边坡发生滑坡灾害的可能性,从而指导视情加固、及时预警。本文基于故障预测与健康管理方法,构建了边坡安全监测PHM系统框架,提出了以安全监测信息为依据的边坡PHM技术路线;以位移为例,给出了位移故障率和安全储备度算式;以斋藤迪孝法计算临滑时间,以实测位移建立神经网络模型,结合斋藤迪孝法预测临界位移;进而获得边坡位移故障率、安全储备度计算式,并绘制曲线,进行位移故障率定量预测,有利于掌握边坡安全状态,根据故障率程度进行相应预警。文中以实例说明应用过程,分析结果与工程实际情况相符。
本文以安全监测为基础,提出位移故障率及安全储备度概念,并综合斋藤迪孝法和神经网络监测模型对其进行有效预测,是结合边坡特色对边坡PHM系统的初步探讨。由于PHM在边坡工程中的研究尚在起步阶段,本文在PHM系统框架内仅以位移为代表进行故障率、安全储备度预测研究,采用的方法、路线可为后期工作提供借鉴,在相关监测信息具备时,其他效应量也可进行相应研究,并探索其他算法的合理应用,以期逐步完善边坡PHM系统。
[1] 朱继良,黄润秋,张诗媛,等.某大型水电站高位边坡开挖的变形响应研究[J].岩土工程学报,2010,32(5):784-791.
[2] 黄铭. 数学模型与工程安全监测[M]. 上海:上海交通大学出版社,2008.
[3] 杨强,潘元伟,程立,等. 蓄水期边坡及地基变形对高拱坝的影响[J]. 岩土力学与工程学报,2015,34(增刊2):375-382.
[4] 黄铭,刘俊.降雨影响下高边坡渗压神经网络监测模型[J].上海交通大学学报, 2013,47(10):1548-1551.
[5] 黄铭,刘俊,葛修润. 边坡开挖期实测位移的分解与合成预测[J].岩石力学与工程学报, 2003,22(8):1320-1323.
[6] JOUIN M, GOURIVEAU R, HISSEL D. Prognostics and Health Management of PEMFC: State of the Art and Remaining Challenges[J].International Journal of Hydrogen Energy, 2013, 38(35):15307-17317.
[7] 蓝祝光,黄铭. 基于实测信息的海堤PHM系统框架及关键技术研究[J].水土保持通报, 2017, 37(3):307-313.
[8] 蓝祝光,黄铭.海堤故障预测和健康管理系统的多目标维修决策优化模型[J].工业建筑,2019,49(1):123-129.
[9] 莫固良,汪慧云,李兴旺,等. 飞机健康监测与预测系统的发展及展望[J].振动测试与诊断,2013, 33(6):925-930,1089.
[10] KHAN H, AL-GAYEM Q, RICHARDSON A M. A Housekeeping Prognostic Health Management Framework for Microfluidic Systems[J]. IEEE Transactions on Device and Materials Reliability,2017,17(2): 438-449.
[11] ALEXANDRU P, JAKUB G P, BAGETTI J M, et al. Prognostics and Health Monitoring of Electronic System: A Review[C]//18th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, EuroSimE 2017. Dresden, Germany: Institute of Electrical and Electronics Engineers Inc, 2017: 1-11
[12] MEHDI B, KAMAL M, MOHAMMED L, et al. Critical Components Selection for a Prognostics and Health Management System Design: An Application to an Overhead Contact System[C]//2016 Annual Conference of the Prognostics and Health Management Society, PHM 2016. Denver Co., United States: Prognostics and Health Management Society, 2016:93-100.
[13] 黄赞武. 轨道电路故障预测与健康管理关键技术研究[D].北京:北京交通大学, 2013.
[14] LAN Z G, HUANG M. Health Assessment Model and Maintenance Decision Model for Seawall PHM System[J]. Arabian Journal for Science and Engineering, 2019,44(10):8377-8387.
[15] 曾声奎.故障预测与健康管理(PHM)技术的现状与发展[J].航空学报,2005,26(5):627-632.
[16] 金赛赛,黄考利,连光耀,等. 面向PHM的复杂装备系统故障预测技术研究[J].信息技术, 2013(12):200-202.
[17] 冯添乐,江永丰. 基于支持向量回归机的可靠度预测模型[J],计算机与数字工程,2011,39(2):29-32.
[18] 中华人民共和国住房和城乡建设部.建筑基坑工程监测技术规范:GB 50497—2009 [S].北京:中国建筑工业出版社,2009.
[19] 中华人民共和国水利部.水利水电工程边坡设计规范:SL 386—2007 [S].北京:中国水利水电出版社, 2007.
[20] 中华人民共和国国土资源部.崩塌、滑坡、泥石流监测规范:DZ/T 0221—2006 [S]. 北京:中国标准出版社,2006.
[21] 贺可强,陈为公,张朋. 蠕滑型边坡动态稳定性系数实时监测及其位移预警判据研究[J]. 岩石力学与工程学报,2016,35(7):1377-1385.
[22] 陆迎寿,黄铭,蓝祝光.人工神经网络在海堤非稳定渗流参数反演中的应用[J].南水北调与水利科技, 2015,13(6):1147-1150.