含细粒砂土在工程中较为常见，如在海堤修筑工程中所用填筑材料采用黏性土较为合适[1-2]，但许多沿海地区禁止开山取土作为海堤填筑材料，从其他地区取土又要考虑高额运输成本，为了合理利用本地资源，工程上会将海沙海泥混合使用[3]；又如填海造陆工程中会将开采的河床或海床上的淤泥排放到陆地后，排除淤泥中的水分，使之具有可利用价值，为了使淤泥达到要求的承载能力以及考虑合理利用土料，常将附近地区的弃土料、海沙等混合进淤泥中[4-5]。这些混合沙土在承受上部车辆、波浪、地震等作用时，土的动力特性是需要关注的问题。
当细颗粒土中含少量砂土时，土通常不易液化[6-7]。而砂土中掺杂细粒土，砂土的抗液化强度可能会下降。Lee等的试验[8-9]表明含细粒砂土会发生液化现象。Perlea等的试验[10]表明：当黏粒含量低于15%时，随着黏粒含量的增加，砂土抗液化强度降低；当黏粒含量大于20%时，随着黏粒含量的增加，砂土抗液化强度又逐渐增加。文献[11-14]的研究均得出了相似的结论，且砂土的动强度最低点对应的黏粒含量范围为10%～30%。
现有研究中对含细粒砂土的动力特性研究采用的加载应力路径主要是动三轴或动扭剪试验应力路径，其动应力均是在一个方向上变换，而在实际工程中所受的荷载形式复杂，如海洋建构物地基长期经受波浪周期往复荷载的作用,其应力路径与常规的动三轴或动扭剪不同，目前对于这种复杂应力路径下含细粒砂土动力特性的研究尚存不足。
本研究采用空心圆柱扭剪仪，对含细粒饱和砂土进行动力特性试验，主要研究波浪荷载作用下孔隙水压、动强度、动模量、阻尼比等动力特性，分析应力路径、细粒含量、相对密实度、循环应力比等因素对其动力特性的影响。
1 试验介绍
1.1 试验设备
试验采用的英国GDS空心圆柱扭剪仪(HCA)，可以独立控制内外围压、轴力以及扭矩四个参数和平面条件下主应力轴旋转问题对应的四个参数：大、中、小主应力以及大或小主应力轴旋转角度，形成映射关系，实现波浪荷载等复杂应力路径。
1.2 应力加载路径实现方法
Ishihara等的研究[15]表明波浪荷载的特性如图1、2所示。
图1 波浪荷载下土体单元的应力状态
Fig.1 Stress state of soil element under wave load
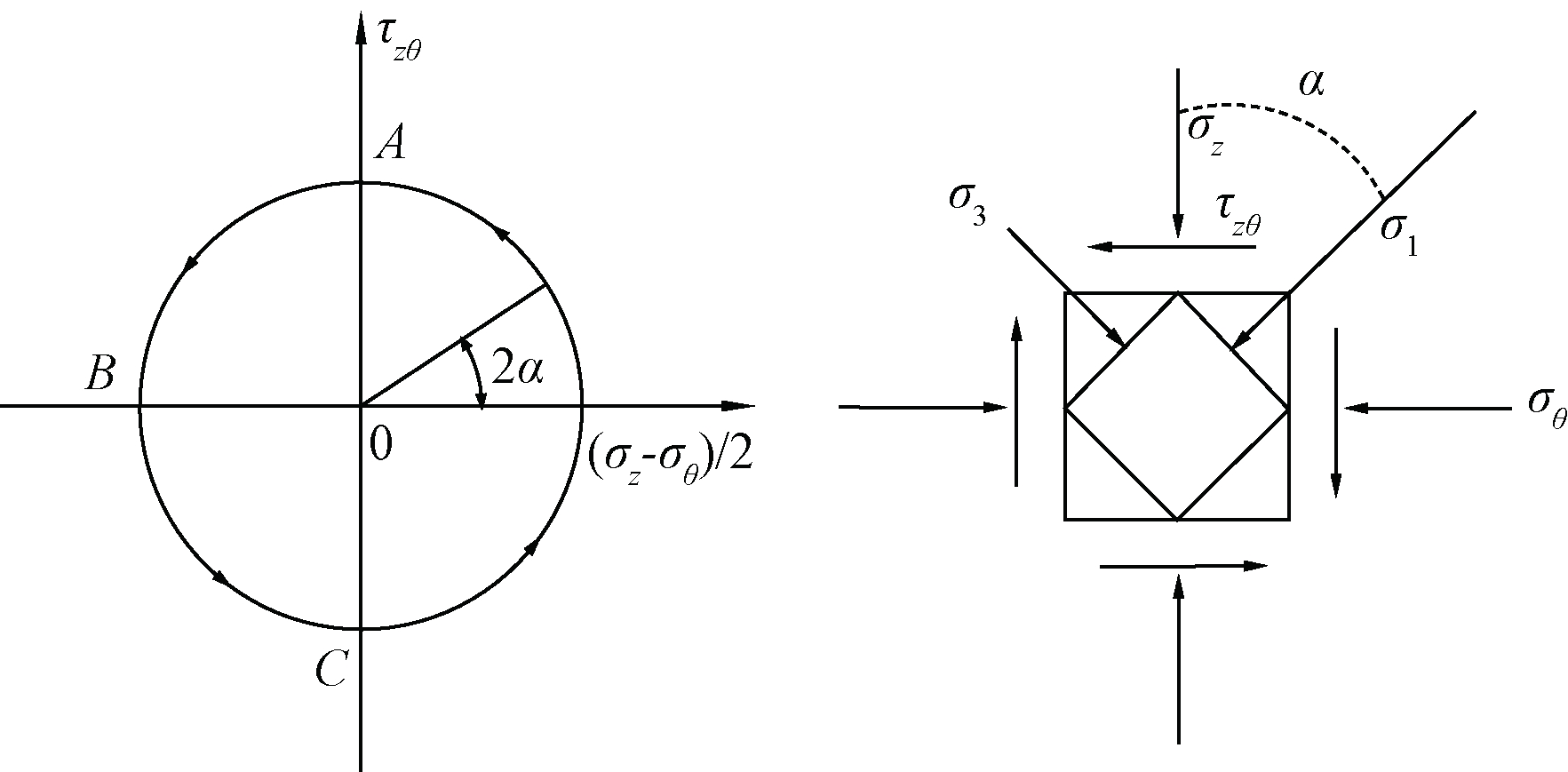
图2 波浪荷载的圆耦合应力路径
Fig.2 The circular coupling stress path of wave load
在波浪荷载作用下，土体单元会受到循环荷载作用。当土单元遇到波峰作用的瞬间，土单元受到正的竖向压力，如图1、2中的A点；当遇到波高为0的瞬时，土单元受到纯水平剪力，如图1、2中的B点；而遇到波谷作用的时刻，会受到负的竖向压力，如图1、2中的C点。如果土体所受剪应力τzθ和正应力偏差(σz-σθ)/2幅值相等，那么土体应力路径为圆形，本文简称“圆耦合应力路径”。试验中通过HCA实测的“圆耦合应力路径”如图3所示。
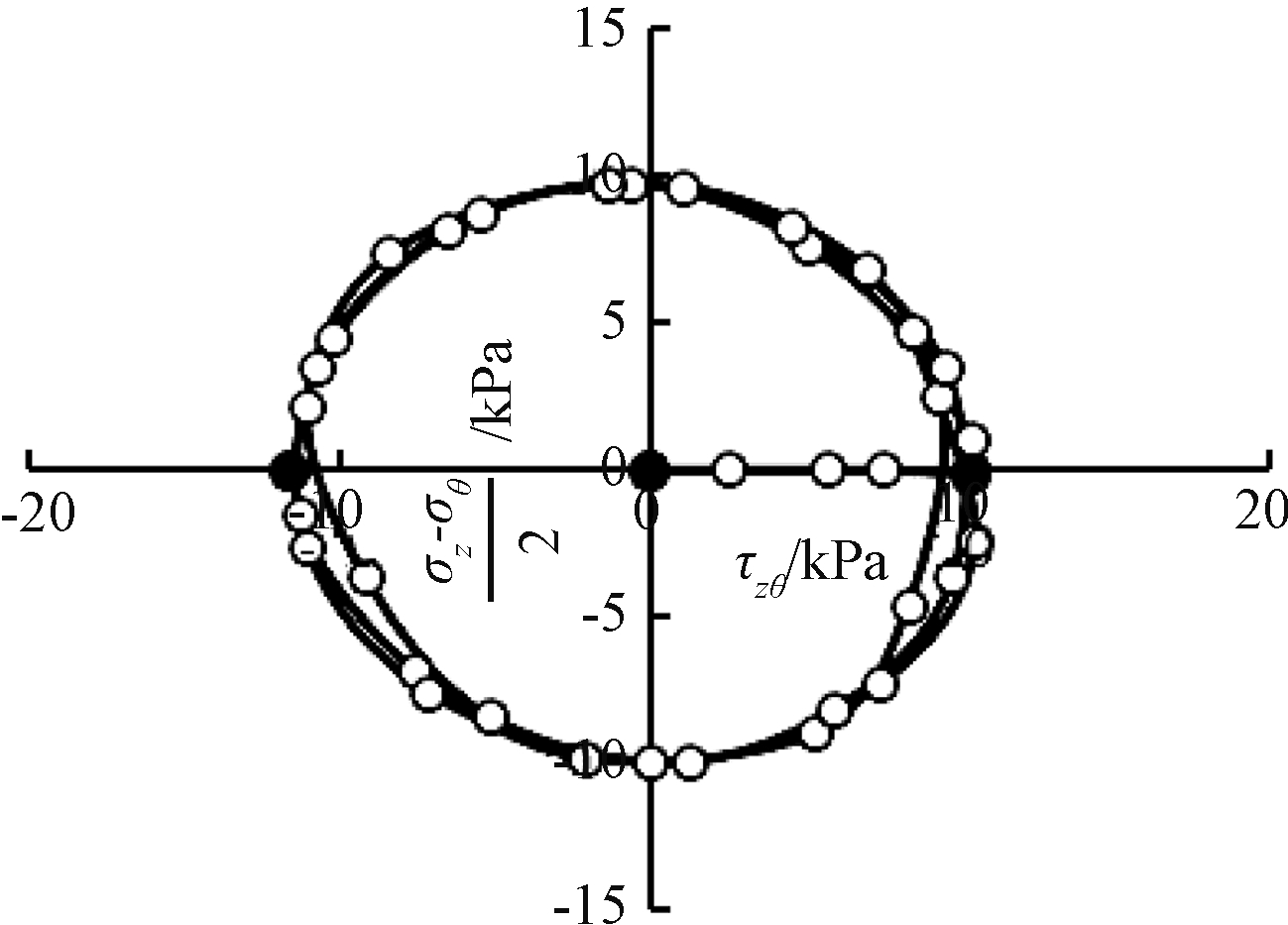
图3 实测“圆耦合应力路径”
Fig.3 Measured circular stress path
1.3 试验材料
1.3.1 土样性质
试验所用砂为福建标准砂，其基本物理参数见表1，级配曲线如图4所示。
表1 福建标准砂基本物理参数
Table 1 Basic physical parameters of Fujian standard sand
相对密度Gs最大孔隙比emax最小孔隙比emin不均匀系数Cu曲率系数Cc2.690.690.404.670.38
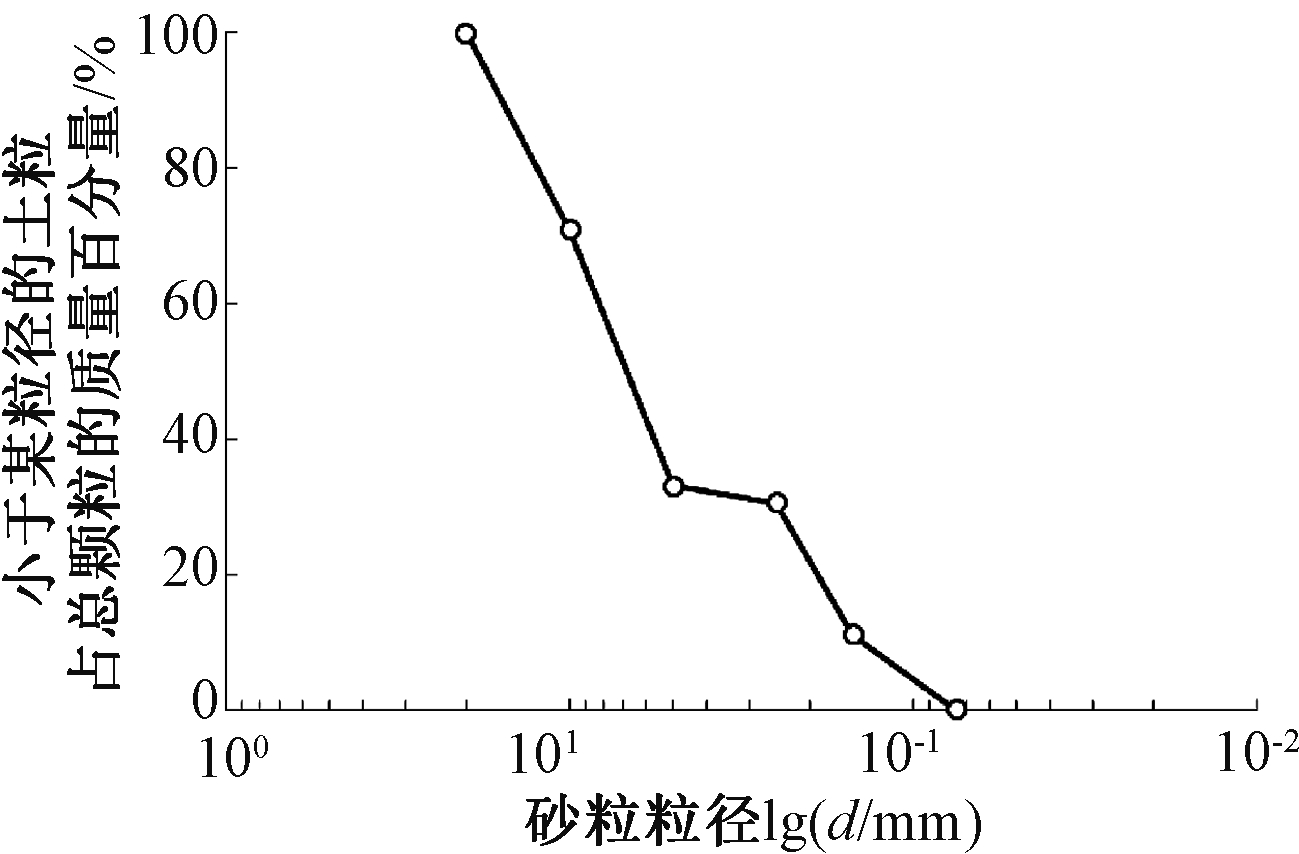
图4 福建标准砂级配曲线
Fig.4 Grading curve of Fujian standard sand
试验中所掺细粒取自太湖湖底，土体经烘干、研磨，再过网筛，得到粒径小于0.075 mm的细颗粒。其基本物理参数见表2，级配曲线如图5所示。
表2 细粒土基本物理参数
Table 2 Basic physical parameters of fine-grained soil
相对密度Gs液限wL/%塑限wp/%粉粒含量/%黏粒含量/%2.7646.825.262.537.5
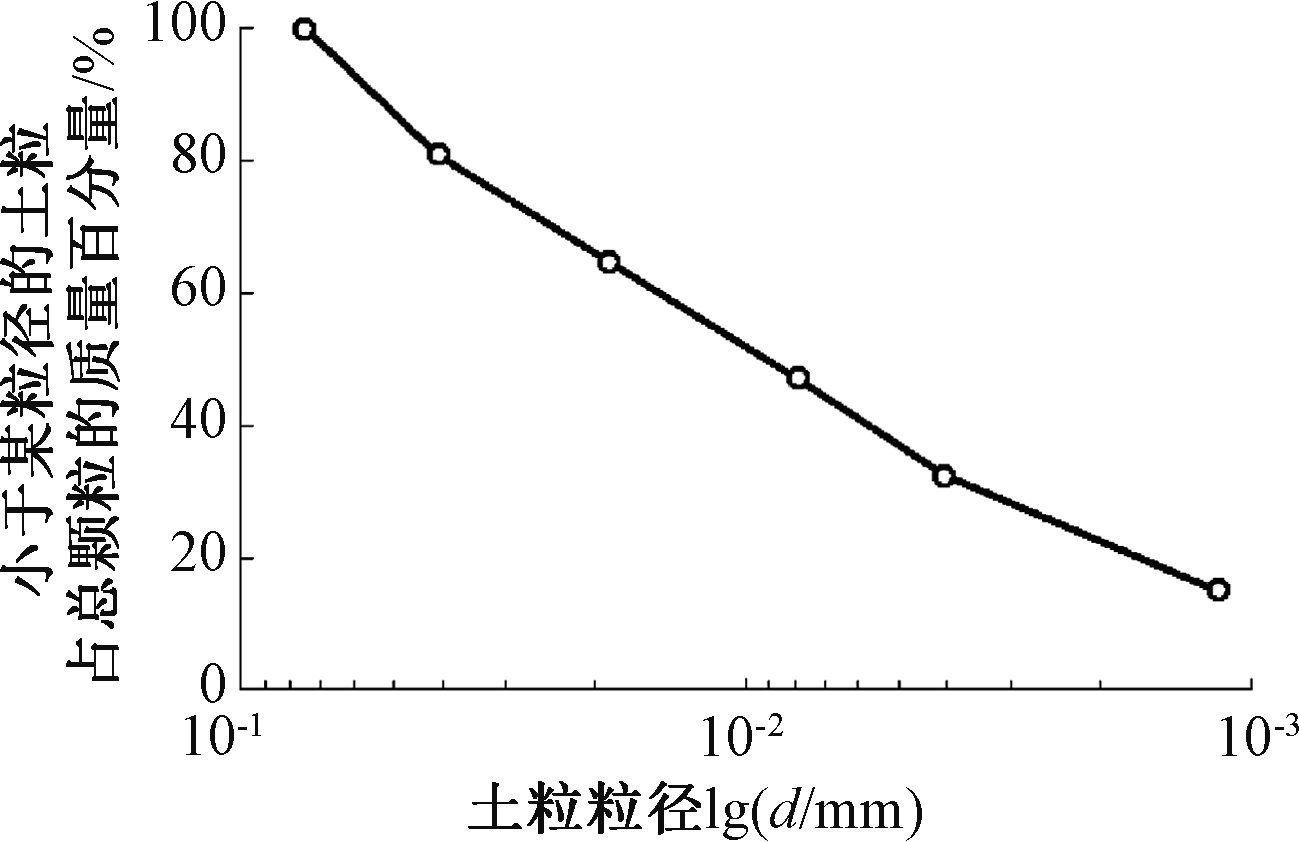
图5 细粒土级配曲线
Fig.5 Grading curve of fine grained soil
1.3.2 试样制备
试样采用空心圆柱体, 外径为100 mm、内径为60 mm、高为200 mm。用落砂法制备试样，将干砂分成10等份，每份通过长口漏斗均匀的落入空心圆柱模具，同时旋转模具，保持长口漏斗距砂土顶面恒定的5 cm距离，之后每层刮毛，再用橡胶锤侧击。
1.3.3 试样饱和及固结
为增大空心圆柱试样的饱和度，采用二氧化碳加反压饱和。先自下而上通入二氧化碳，将试样中的空气顶出，接着通入蒸馏水，排出二氧化碳，然后施加反压使残留的二氧化碳溶解于水。当等向固结孔隙水压力系数B大于0.98时，视为饱和。
试样饱和后，施加相同的内、外围压，将试样等向固结到预置有效应力状态。固结时间设置为12 h，固结完成后保持2 h，当反压体积变化率小于60 mm3/h时，判定固结排水完成。
1.4 试验方案
1.4.1 动强度试验方案
针对松砂和中密砂，考虑了不同循环应力比和细粒含量的影响，进行“圆耦合应力路径”下的动强度试验。为对比起见，设置了动三轴和动扭剪试验，具体的试验方案如表3所示，其中A代表动三轴试验，T代表动扭剪试验，C代表“圆耦合应力路径”试验。试样中所含细粒干质量占整个试样干质量的百分比称为细粒含量(FC)。循环应力比的表达式如下：
(1)
式中：σampl为循环应力幅值；
为有效围压。
所有方案均在固结后不排水条件下进行，围压为600 kPa，反压为500 kPa，初始有效应力为100 kPa，荷载的振动频率为0.1 Hz，液化破坏标准为超静孔隙水压达到围压的95%时，认为已经液化。
1.4.2 动力变形特性试验方案
动力变形特性试验方案如表4所示，加载方式为应力控制方式，试验振动频率为0.1 Hz，采用分级加载的方式，每级荷载循环6次，共8级，各级循环应力比依次为0.01、0.03、0.05、0.06、0.07、0.08、0.09、0.10。
2 试验结果及分析
2.1 超静孔隙水压力发展规律
2.1.1 细粒含量对孔压发展规律的影响
图6、7分别给出了“圆耦合应力路径”下CSR为0.1时中密砂(Dr=0.6)和松砂(Dr=0.3)在不同细粒含量作用下的超静孔隙水压力发展曲线。
表3 动力试验方案
Table 3 Dynamics test plan
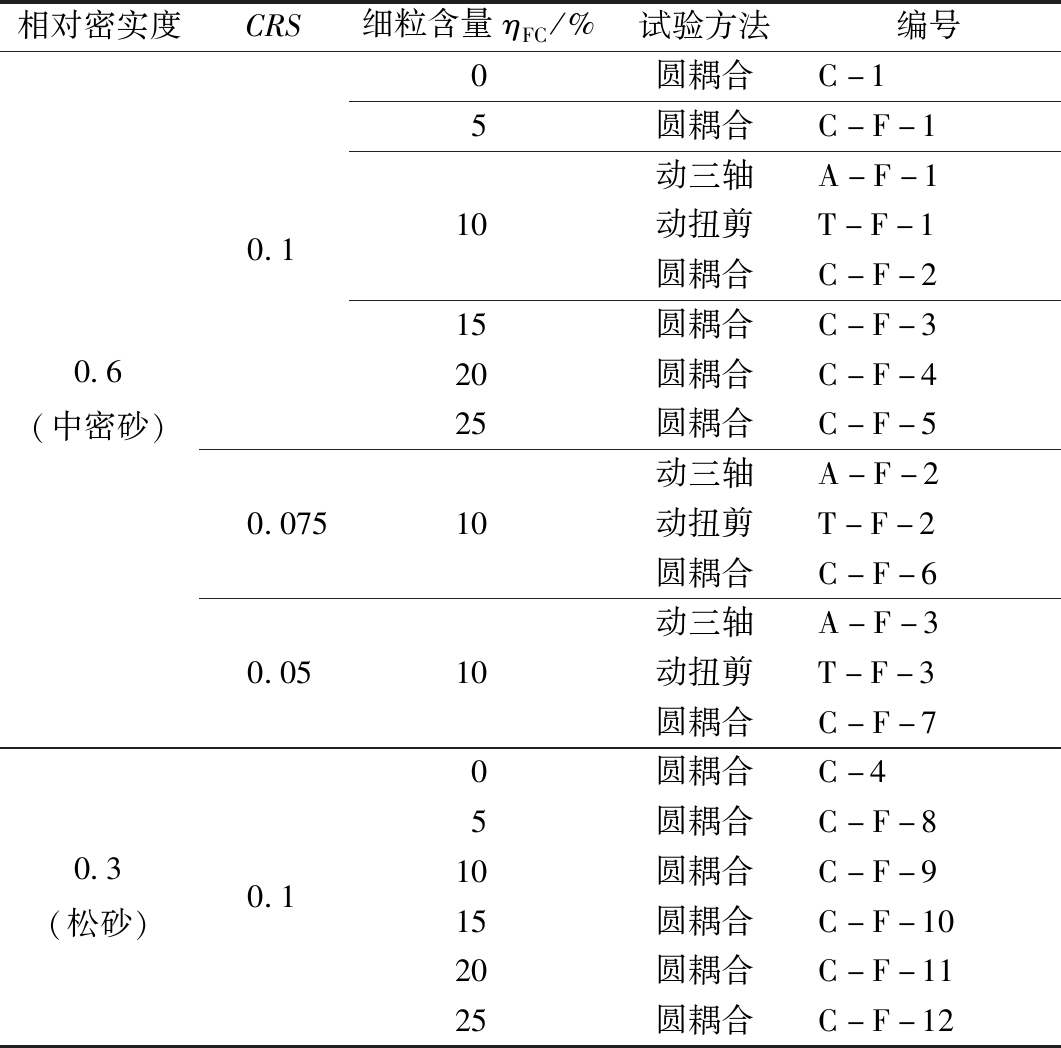
相对密实度CRS细粒含量ηFC/%试验方法编号0.6(中密砂)0.3(松砂)0.10.0750.050.1051015202510100510152025圆耦合C-1圆耦合C-F-1动三轴A-F-1动扭剪T-F-1圆耦合C-F-2圆耦合C-F-3圆耦合C-F-4圆耦合C-F-5动三轴A-F-2动扭剪T-F-2圆耦合C-F-6动三轴A-F-3动扭剪T-F-3圆耦合C-F-7圆耦合C-4圆耦合C-F-8圆耦合C-F-9圆耦合C-F-10圆耦合C-F-11圆耦合C-F-12
表4 动力变形特性试验方案
Table 4 Dynamic deformation test scheme
试样编号围压/kPa细粒含量ηFC/%C-E-11000C-E-210010C-E-32000C-E-420010
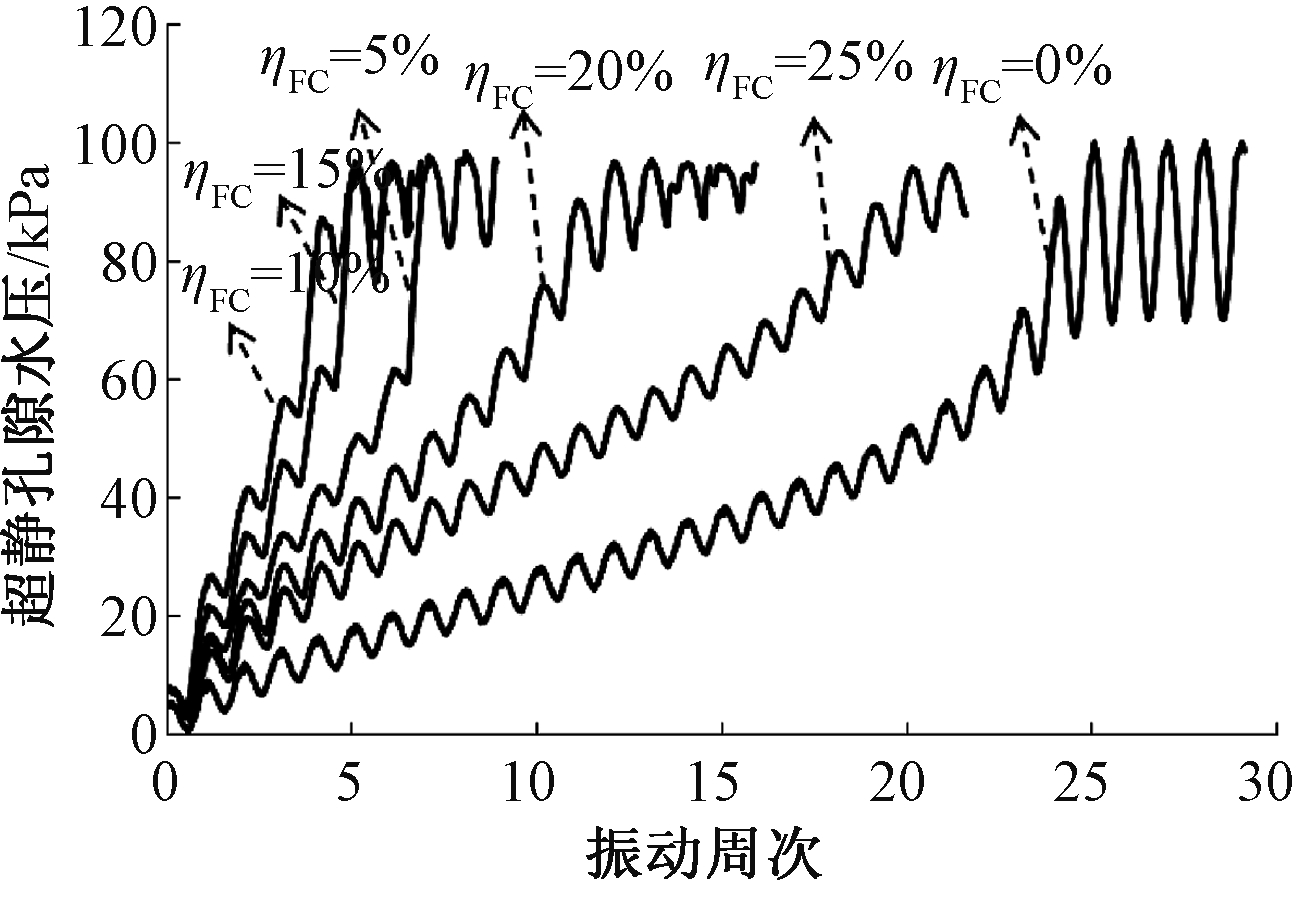
图6 不同细粒含量中密砂超静孔隙水压发展曲线
Fig.6 Excess pore water pressures development curve of medium sand with different fine grained contents
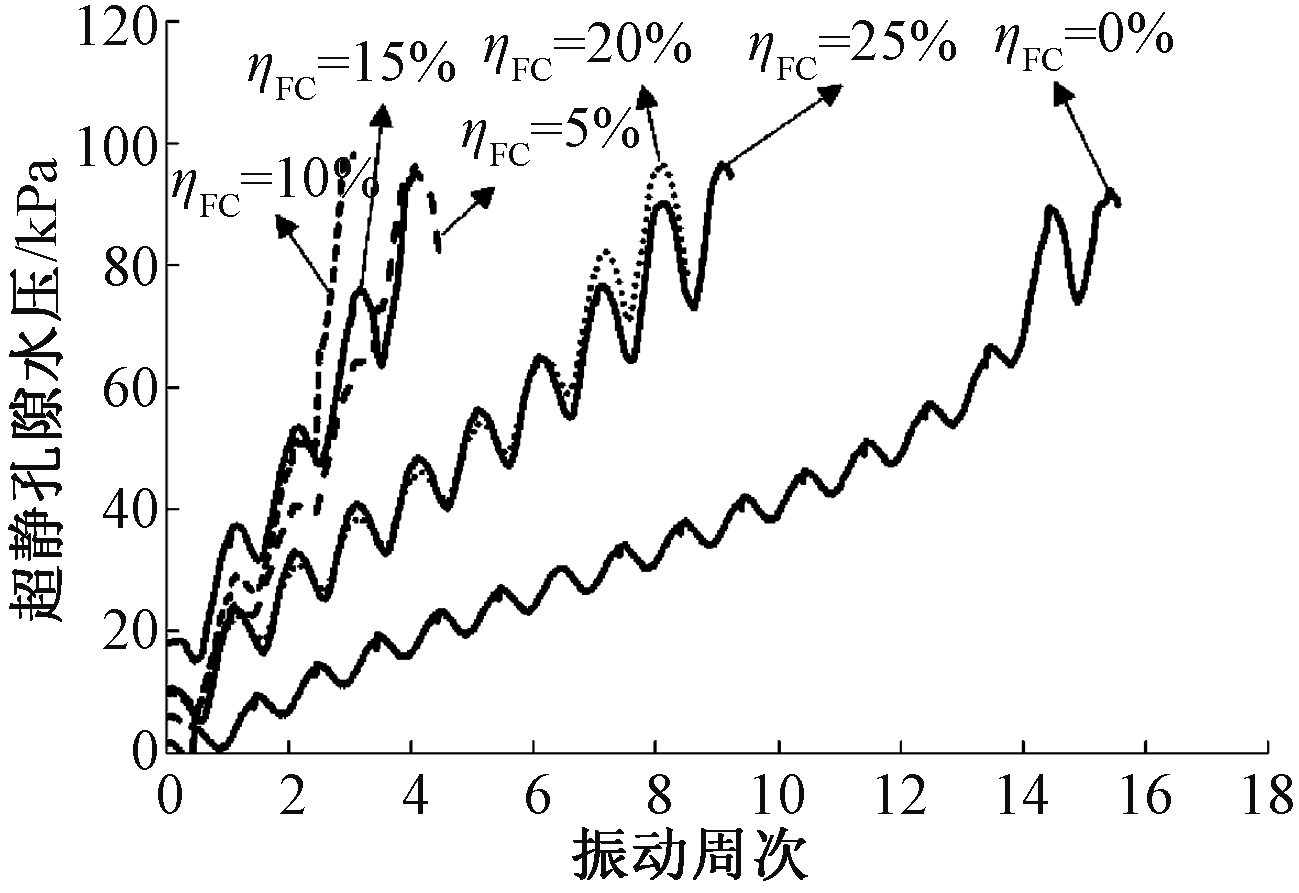
图7 不同细粒含量的松砂超静孔隙水压发展曲线
Fig.7 Excess pore water pressures development curve of loose sands with different fine grained contents
从图6、7可见:无论是中密砂还是松砂，随着振动周次的增加，超静孔隙水压力不断增大，最终达到初始液化水平。当细粒含量小于10%时，随着细粒含量的增大，孔压发展变快；当细粒含量大于10%时，随细粒含量的增大，超静孔隙水压力发展变慢。纯砂的液化循环周次最大，中密砂为26周，松砂为16周；细粒含量为10%的砂土液化循环周次最小，中密砂为5周，松砂为3周。
为清晰起见，将细粒含量与所对应的液化循环周次示于图8和表5。从图8可见：细粒含量对液化循环周次的影响存在一个阈值，小于阈值时，液化循环周次随着细粒含量的增大而降低，并在阈值时降到最低；细粒含量大于阈值后，液化循环周次随着细粒含量的增大而增大，试验的阈值为10%。同时，相同细粒含量情况下，松砂的液化循环周次要低于中密砂，并且细粒含量对液化循环周次的影响在中密砂中更明显。
— 中砂； 
- 松砂。
图8 不同相对密实度含细粒砂土与液化周次关系曲线(循环应力比为0.1)
Fig.8 Fine grained content and liquefaction cycle relation curves with different relative densities(CSR was 0.1)
表5 循环应力比为0.1的含细粒砂圆耦合试验液化循环周次
Table 5 Liquefaction cycles of sands with fine grains in circular coupled test when CSR was 0.1
ηFC/%0510152025中密砂268561321松砂 16535910
2.1.2 应力路径对超静孔隙水压发展规律的影响
图9～11分别比较了细粒含量为10%时不同循环应力比和不同应力路径作用下中密砂的超静孔隙水压发展曲线。
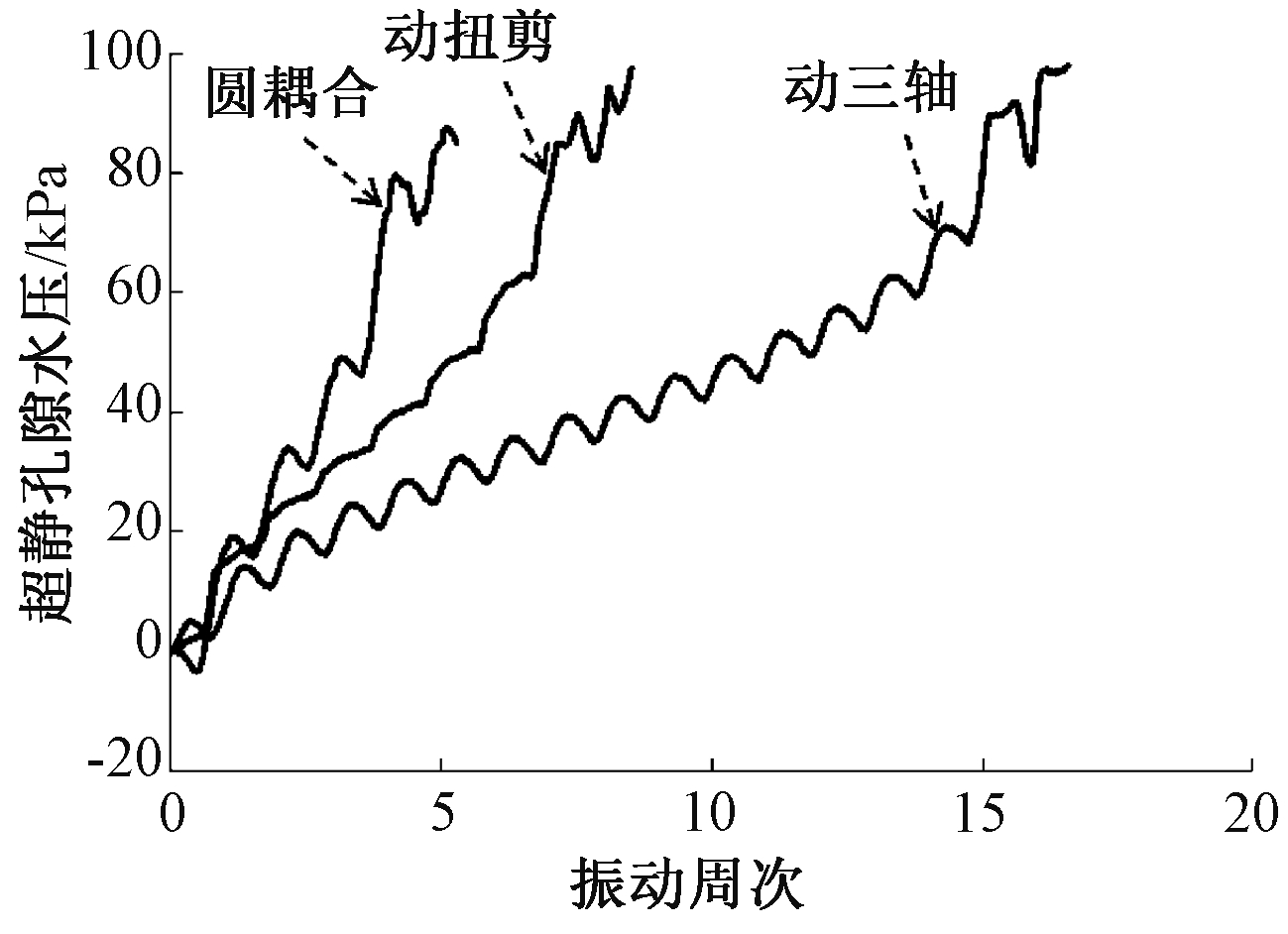
图9 不同试验方法下循环应力比为0.1时，细粒含量为10%的中密砂的超静孔隙水压变化
Fig.9 Excess pore water pressures of medium sand with 10% fine grained content under different test methods when CSR was 0.1
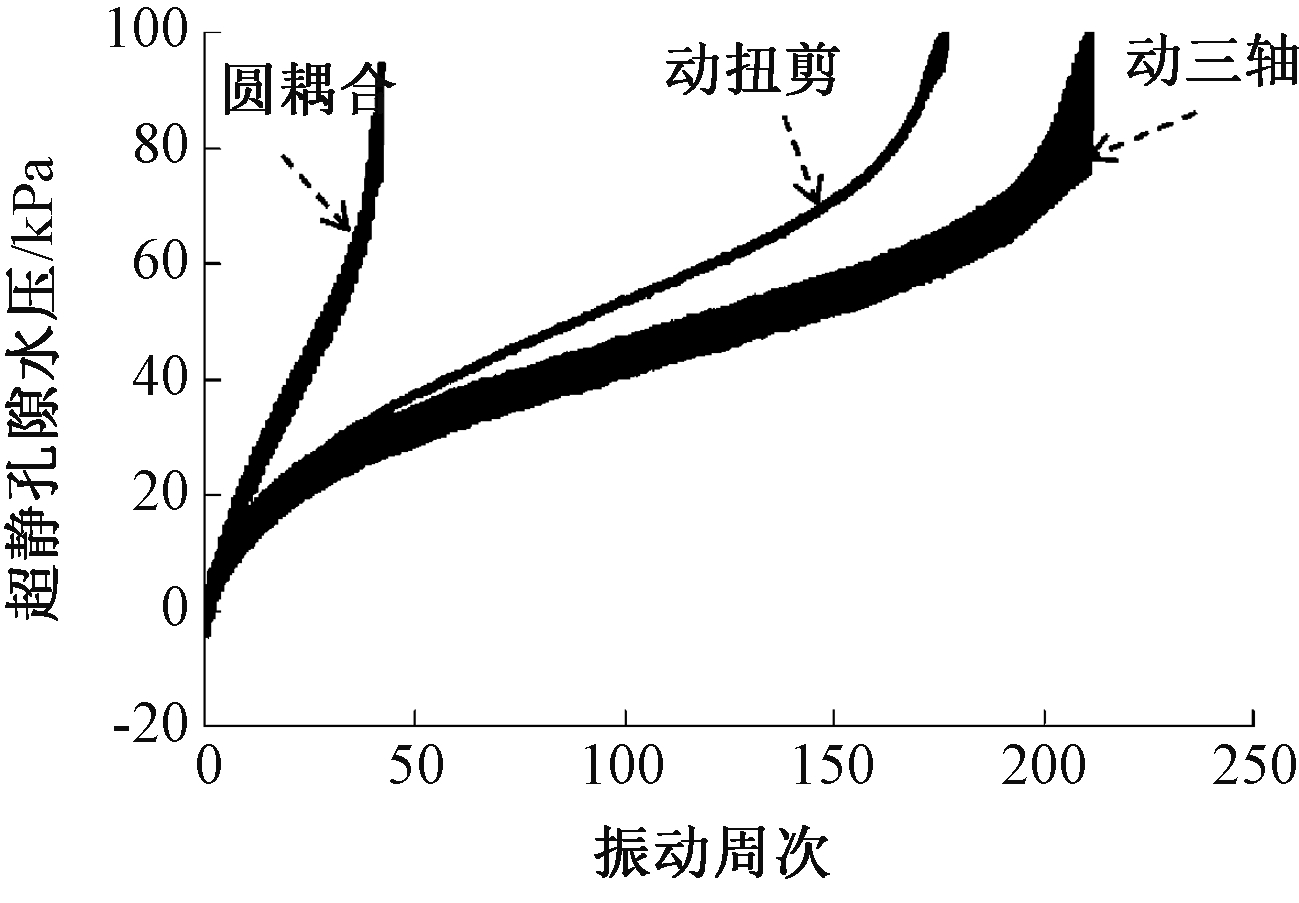
图10 不同试验方法下循环应力比为0.075时，细粒含量量为10%的中密砂超静孔隙水压变化
Fig.10 Excess pore water pressures of medium sand with 10% fine grained content under different test methods when CSR was 0.075
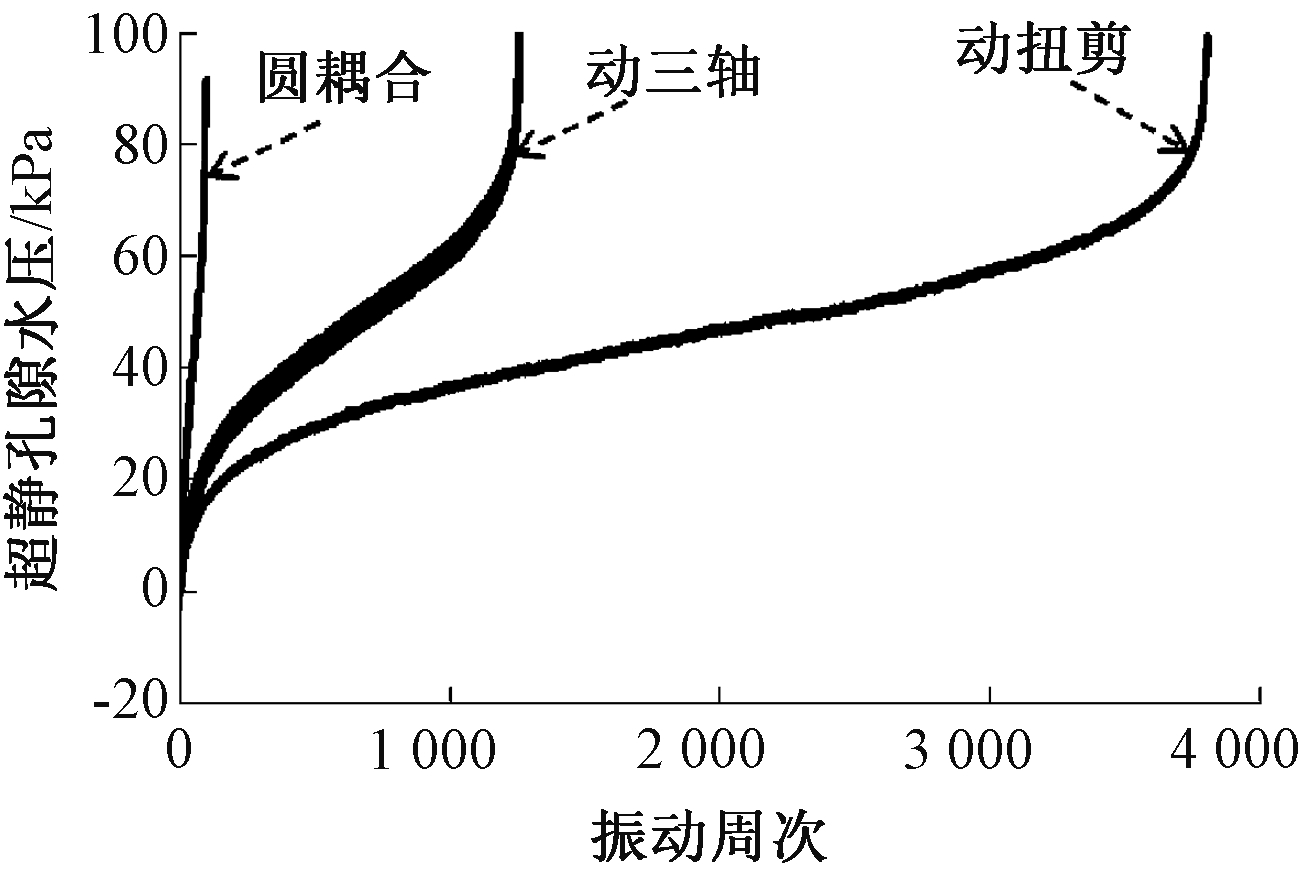
图11 不同试验方法下循环应力比为0.05时，细粒含量为10%的中密砂在超静孔隙水压变化
Fig.11 Excess pore water pressures of sand with 10% fine grained medium under different test methods when CSR was 0.05
从图9～11可见：“圆耦合应力路径”下，初期超静孔隙水压随振动周次近似线性增长，接近破坏时，超静孔隙水压陡然增大达到初始液化水平;而动三轴和动扭剪应力试验路径的超静孔隙水压发展曲线可以分为三个阶段，初期超静孔隙水压增长速度较快，当达到某一周次后超静孔隙水压相对稳定地平缓增加；接近破坏时，超静孔隙水压又迅速增大。细粒含量为0.1时，“圆耦合应力路径”的振动液化循环周次为5周，动扭剪液化周次为9周，动三轴液化循环周次为17周；循环应力比为0.075时，“圆耦合应力路径”的振动液化循环周次为42周，动扭剪液化循环周次为176周，动三轴液化循环周次为211周；循环应力比为0.05时，“圆耦合应力路径”的振动液化循环周次为91周，动扭剪液化循环周次为3 805周，动三轴液化循环周次为1 258周。不同循环应力比下，“圆耦合应力路径”的振动液化循环周次均最小。对比不同循环应力比情况下的超静孔隙水压发展曲线可知：随着循环应力比为的减小，应力路径的影响不断增大，在循环应力比为0.05时，应力路径影响尤其突出。可见掺细粒砂土在相同循环应力比条件下，圆耦合强度低于动三轴和动扭剪试验强度，在波浪荷载作用下砂土更容易液化。这可能是因为“圆耦合应力路径”加载试验中，尽管偏应力保持不变，主应力轴的旋转也会引起塑性应变的积累，所以相同细粒含量的砂土，“圆耦合应力路径”对超静孔隙水压发展曲线影响较大。
2.1.3 应力路径对动强度的影响
将一定的振动循环周次条件下，土样达到液化需要的循环应力比对应的动应力幅值的二分之一定义为土体动强度。根据试验结果，将上面细粒含量为10%的砂土试验振动液化周次与不同循环应力比整理、拟合作图12。
动三轴；
动钮剪；
圆耦合； ---动三轴拟合； -----动扭剪拟合； ……圆耦合拟合。
图12 细粒含量为10%的砂土的动强度曲线
Fig.12 Dynamic strength curve of sand with 10% fine grains
从图12见：在Dr=0.6的中密砂试验中，相同循环应力比条件下，“圆耦合应力路径”的液化循环周次最低，循环应力比小于0.075时，动扭剪液化循环周次最高，动三轴次之；循环应力比大于0.075时，动三轴液化循环周次最高，动扭剪次之。在相同的应力路径条件下，所有试验的结果都表明:随着循环应力比的增大，液化循环周次逐渐降低，试样强度降低，应力路径的影响逐渐明显，且循环应力比与液化循环周次的关系符合以下关系：
(2)
式中：c和d为拟合参数。
图12中可以看出：相同应力路径时，循环应力比越大，液化循环周次越低；相同循环应力比时，“圆耦合应力路径”的液化周次最少。
2.2 不同细粒含量孔压归一化及拟合
为了便于应用，张建民等建议使用式(3)[16]对所得含细粒中密砂(Dr=0.6)超静孔隙水压发展曲线进行拟合：
(3)
式中：u为超静孔隙水压力；uf为试样初始液化时的极限超静孔隙水压力；N为振动周次；Nf为试样初始液化时的振动周次；θ为超静孔隙水压拟合参数，调节θ大小可以实现不同的超静孔隙水压曲线。
通过拟合分析发现：细粒含量为0%、5%、10%、15%时的孔压发展曲线可用一条曲线拟合，拟合参数θ=0.4，见图13。细粒含量为20%、25%时的中密砂孔压曲线拟合结果如图14所示，拟合参数θ=0.7。
细粒含量为0%；
细粒含量为5%；
细粒含量为10%； 
细粒含量为15%;----拟合曲线。
图13 循环应力比为0.1时，细粒含量不大于15%的中密砂超静孔隙水压拟合
Fig.13 Fitting excess pore water pressure curve of sand when CSR was 0.1 and FC was not more than 15%
细粒含量为20%；细粒含量为25%; ----拟合曲线。
图14 循环应力比为0.1时，细颗粒含量为20%和25%的中密砂超静孔隙水压拟合曲线
Fig.14 Fitting excess pore pressure water curve of sand when CSR was 0.1 and FC was 20% and 25%
含细粒中密砂圆耦合试验中，细粒含量在0%、5%、10%、15%时，随振动周次比的增加，超静孔隙水压比先缓慢增长，接着增长速度逐渐加快，可以使用一条拟合曲线进行拟合，即拟合参数θ为一个定值，拟合曲线类似抛物线；细粒含量在20%、25%时，随振动周次比的增加，超静孔隙水压比增长速度由快变慢再变快，出现明显拐点，拟合参数θ增大，拟合曲线呈现S型。
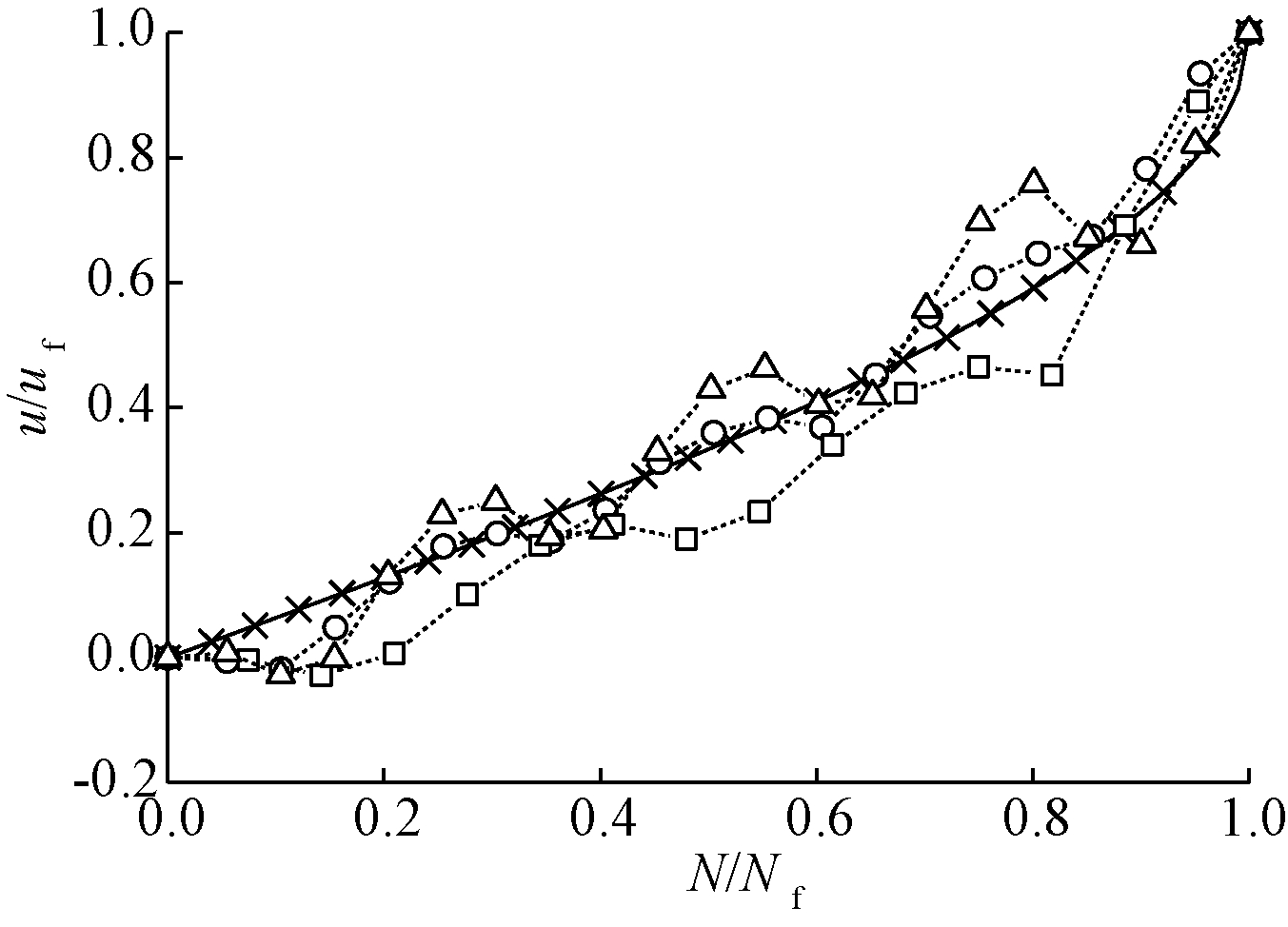
使用式(3)对所得到的含细粒松砂(Dr=0.3)超静孔隙水压发展曲线进行拟合，通过拟合分析，发现细粒含量在0%、 5%、10%、15%时的超静孔隙水压发展曲线可用一条曲线拟合，拟合参数θ=0.5，见图15所示。图16为细粒含量为20%、25%时的松砂超静孔隙水压归一化拟合曲线，拟合参数θ=0.7。
… 细粒含量为0%； 
… 细粒含量为5%； 
… 细粒含量为10%； 
… 细粒含量为15%； 
拟合曲线。
图15 循环应力比为0.1时，细粒含量不大于15%的松砂超静孔隙水压曲线拟合
Fig.15 Fitting excess pore water pressure curve of loose sand when CSR was 0.1 and FC was not more than 15%
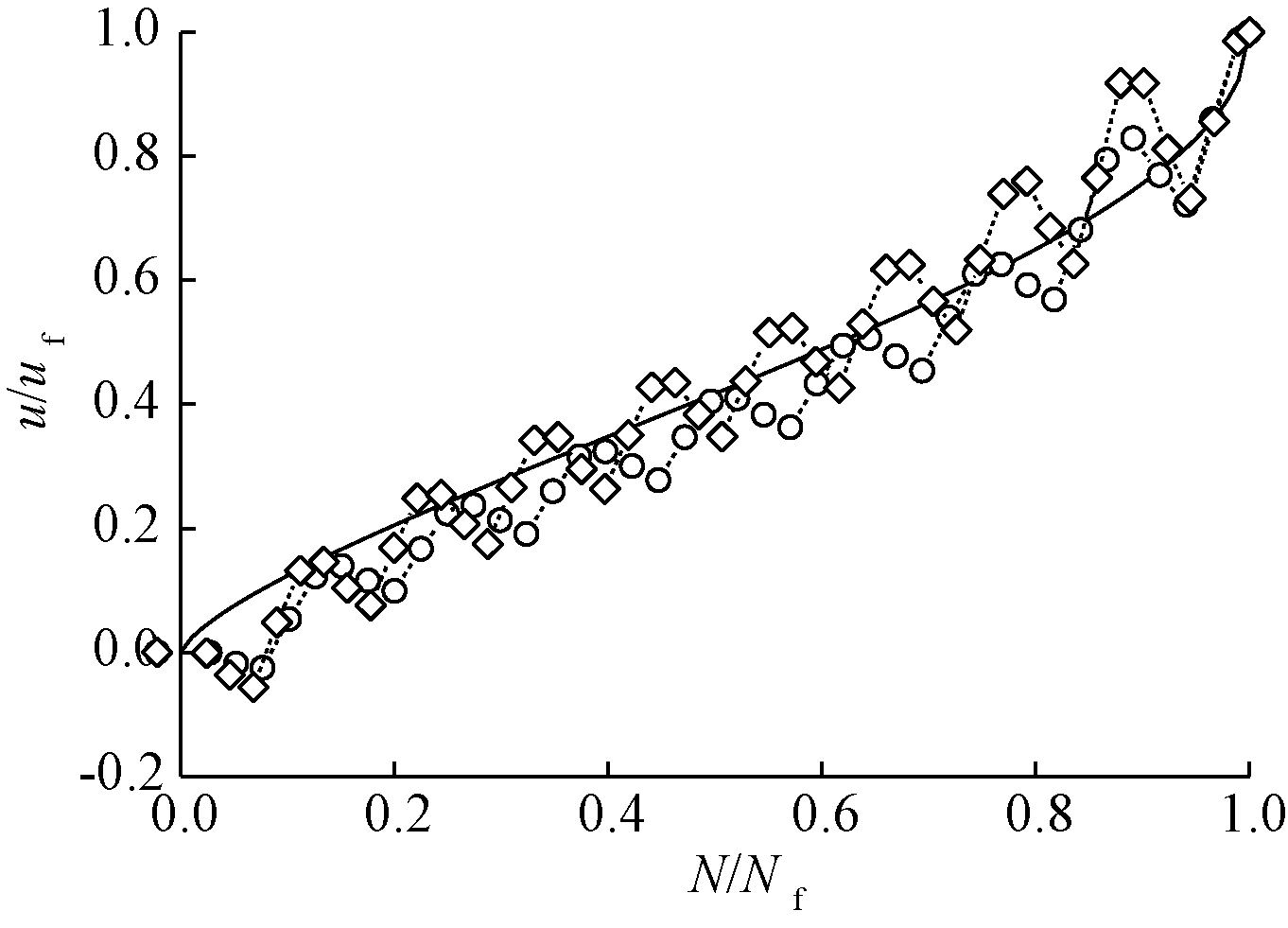
… 细粒含量为20%； 
… 细粒含量为25%; 拟合曲线。
图16 循环应力比0.1时，细粒含量为20%和25%的松砂孔压曲线拟合
Fig.16 Fitting excess pore water pressure curve of loose sand when CSR was 0.1 and FC was 20% or 25%
松砂也呈现出与中密砂相似的规律，在含细粒松砂圆耦合试验中，细粒含量小于15%时，拟合参数θ保持不变，拟合曲线类似抛物线，随振动循环周次比的增加，曲线先平缓增加后逐渐变陡；细粒含量为20%、25%时，拟合参数θ增大，拟合曲线呈S型，随振动循环周次比增加，曲线先陡后平缓接着再逐渐变陡。将拟合得到的拟合参数θ汇总于表6。
表6 循环应力比为0.1的含细粒砂圆耦合试验超静孔隙水压拟合参数θ
Table 6 Fitting excess pore water pressure parameter θ for circular coupling test with different fine grained when CSR was 0.1
含细粒砂不同细粒含量/%0510152025中密砂(Dr=0.6)0.40.40.40.40.70.7松砂(Dr=0.3)0.50.50.50.50.70.7
拟合参数θ越大，曲线就越靠近S型曲线，文献[17-24]表明：黏土的超静孔隙水压发展规律大部分类似S型曲线，而砂土的超静孔隙水压发展规律大多类似抛物线。所以，当θ值越大时，土样性质就越靠近黏土的超静孔隙水压发展规律。结合松砂和中密砂的圆耦合超静孔隙水压拟合结果可见：掺细粒砂土在细粒含量不大于15%时θ值较小，含细粒砂土孔压性质类似纯砂孔压发展规律，而细粒含量大于15%时，拟合参数θ增大，含细粒砂土超静孔隙水压随着细粒含量的增大表现出与黏土超静孔隙水压趋近的形态。
2.3 含细粒饱和砂土的动力变形特性
2.3.1 动模量
1)剪切模量。按表4所做四组试验得到的剪切模量如图17所示。可见，相同应变的时候，初始有效围压越大，对应的剪切模量越大；细粒含量越大，对应的剪切模量越小。
细粒含量为0%，有效围压为100 kPa; 细粒含量为0%，有效围压为200 kPa; 细粒含量为10%，有效围压为100 kPa; 细粒含量为10%，有效围压为200 kPa。
图17 剪切模量-剪应变关系
Fig.17 Shear modulus-shear strain relation
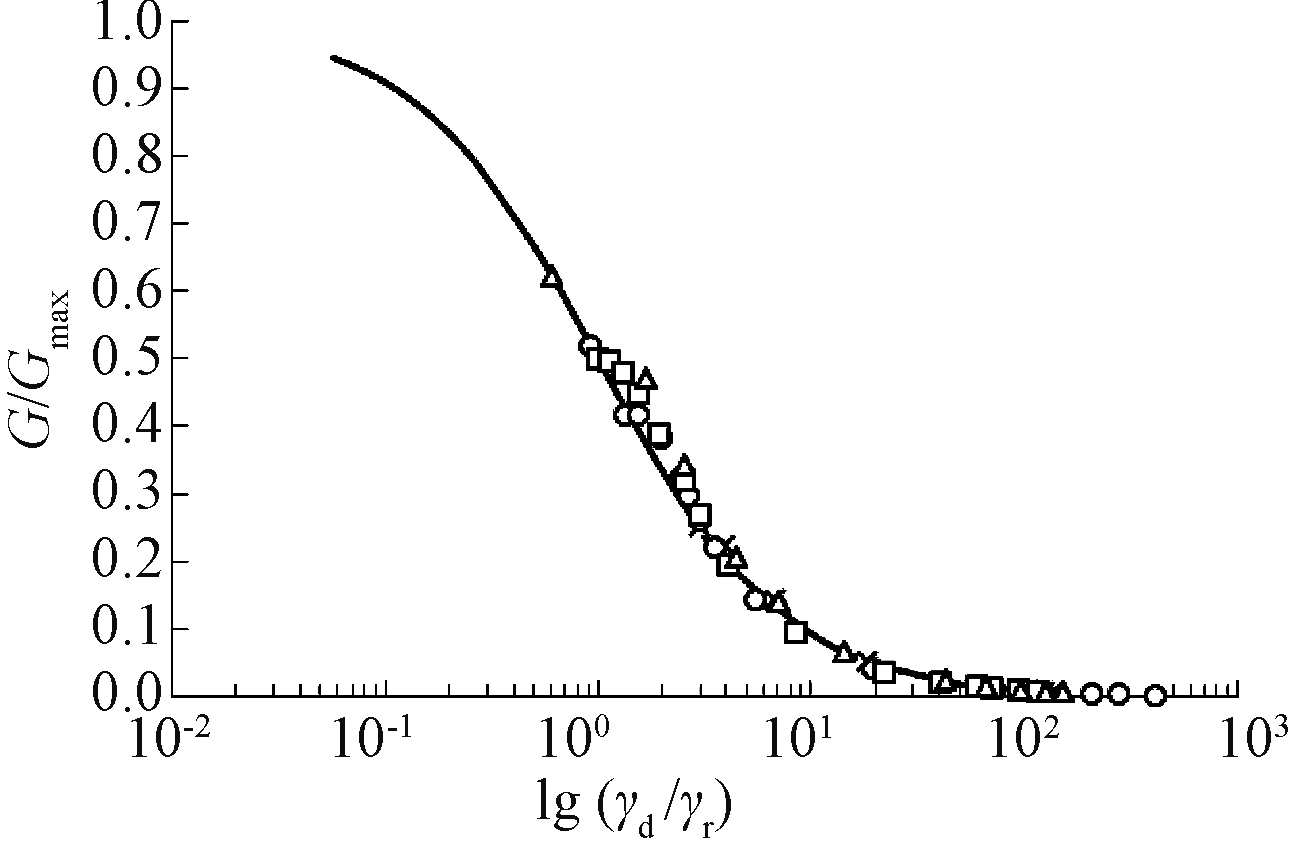
图18给出了剪切模量的归一化曲线，使用以下双曲线模型[25]进行拟合：
(4)
其中最大剪切模量Gmax为1/G-γd坐标系中纵坐标截距的倒数，γr为参考剪应变，取0.017。
从图18可见：双曲线模型可以很好地拟合剪切模量归一化曲线，说明细粒含量和初始有效围压对剪切模量归一化曲线基本没有影响。
细粒含量为0%，有效围压为100 kPa; 细粒含量为10%，有效围压为100 kPa; 细粒含量为0%，有效围压为200 kPa; 细粒含量为10%，有效围压为200 kPa；拟合曲线。
图18 G/Gmax-γd/γr关系曲线
Fig.18 G/Gmax-γd/γr relational curve
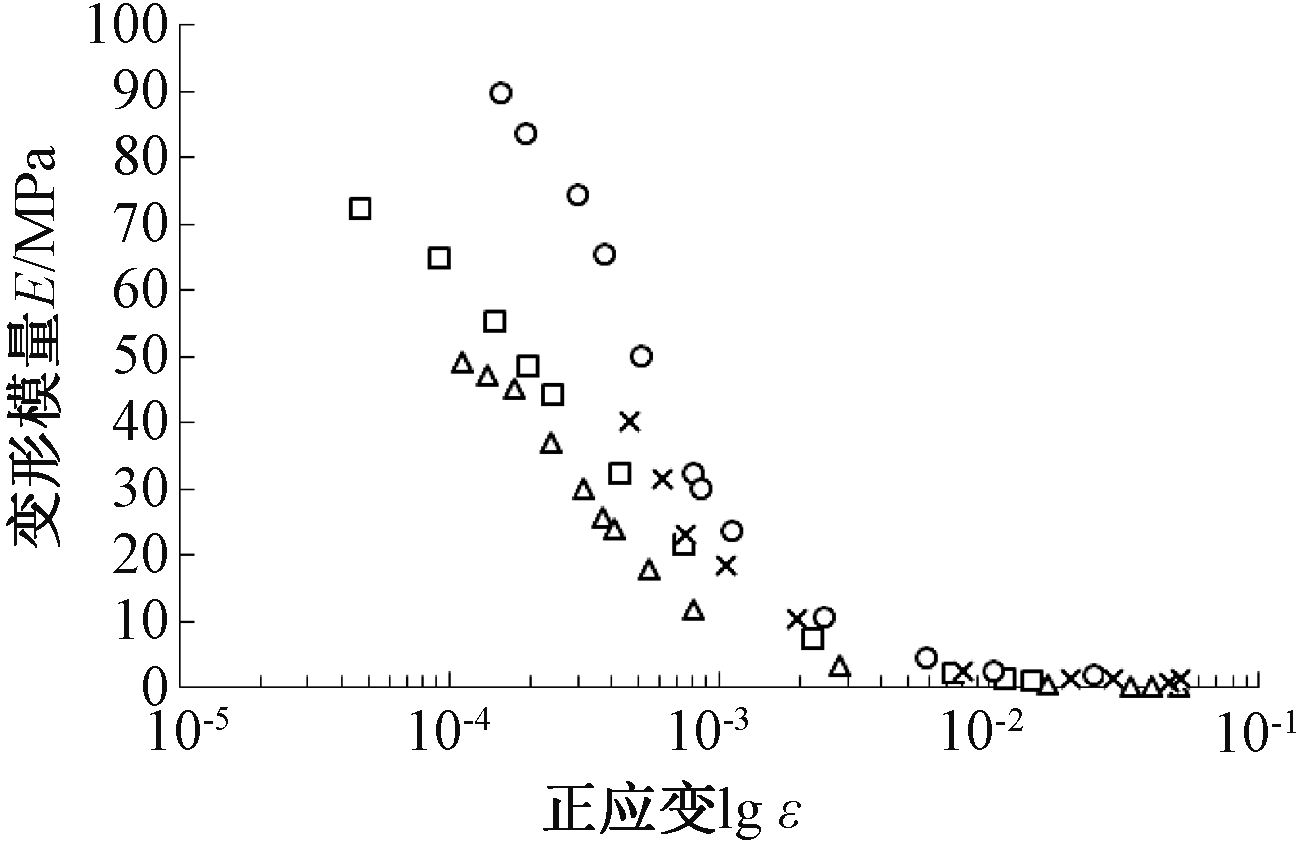
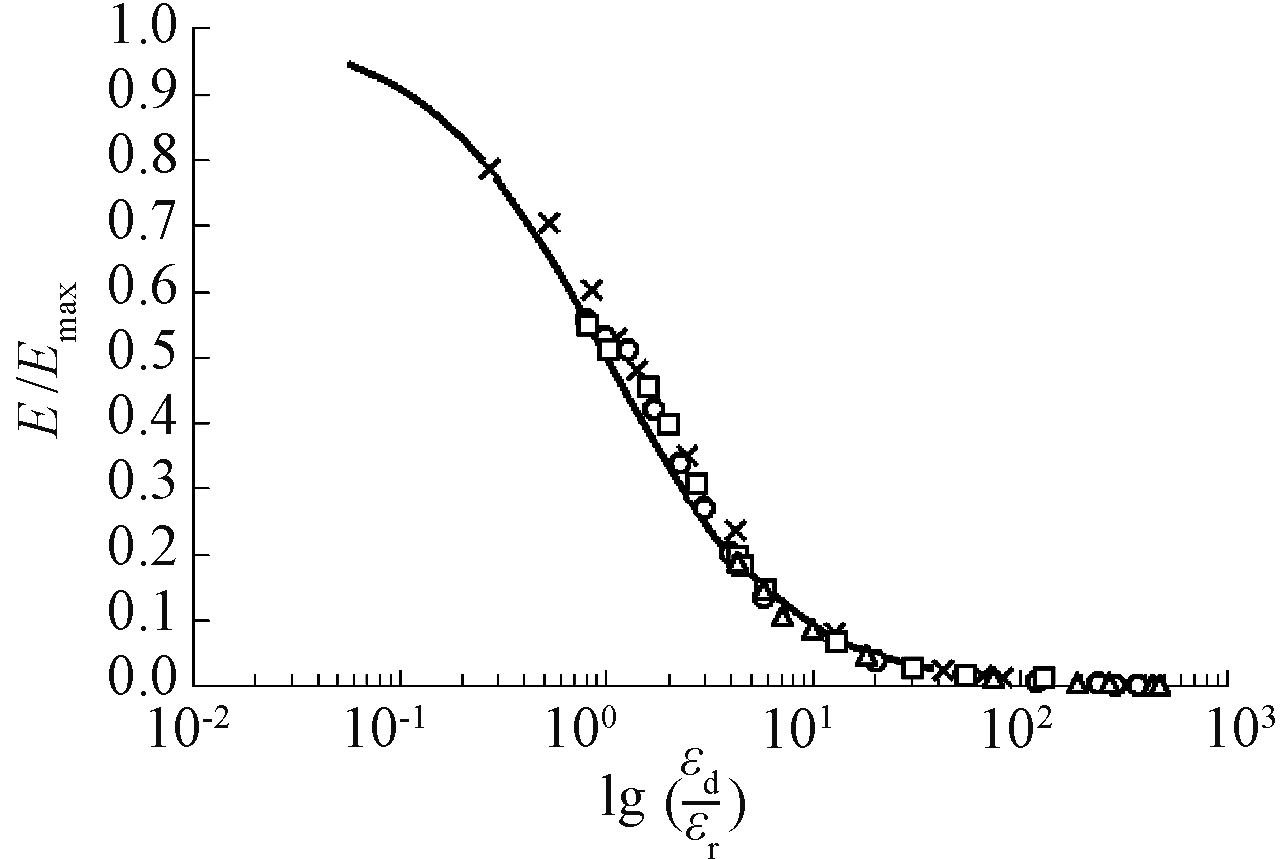
2)变形模量。表4中四组试验的变形模量及归一化曲线如图19、20所示。从图19可见：变形模量规律与剪切模量类似，相同应变的时候，有效围压越大，对应的变形模量越大；细粒含量越大，对应的变形模量越小。从图20可见：采用与式(4)类似形式的双曲线模型可很好地拟合变形模量归一化曲线，其中εr=0.021，同时说明，细粒含量和初始有效围压对变形模量归一化曲线基本没有造成影响。
细粒含量为0%，有效围压为100 kPa; 细粒含量为0%，有效围压为200 kPa; 细粒含量为10%，有效围压为100 kPa; 细粒含量为10%，有效围压为200 kPa。
图19 变形模量与正应变关系
Fig.19 The relation of deformation modulus and normal strain
拟合曲线； 细粒含量为0%，有效围压为100 kPa; 细粒含量为10%，有效围压为100 kPa; 细粒含量为0%，有效围压为200 kPa; 细粒含量为10%，有效围压为200 kPa。
图20 E/Emax-εd/εr关系曲线
Fig.20 E/Emax-εd/εr relation curve
细粒含量为0%，有效围压为100 kPa; 细粒含量为10%，有效围压为100 kPa; 细粒含量为0%，有效围压为200 kPa; 细粒含量为10%，有效围压为200 kPa。
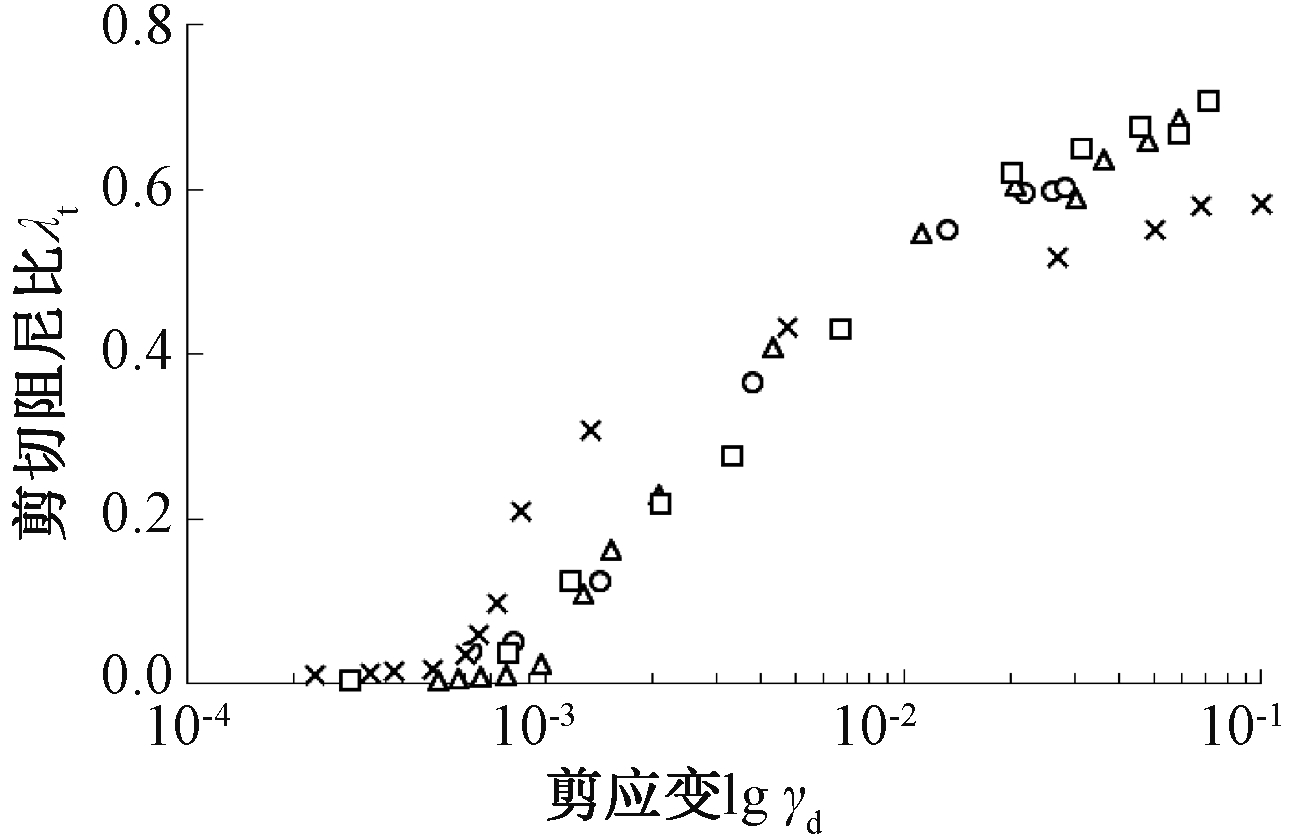
图21 剪切阻尼比-剪应变关系
Fig.21 The relation of shear damping ratio and shear strain
2.3.2 阻尼比
土体动模量和阻尼比之间存在一定关系[26]，如式(5)：
λ=λmax(1-G/Gmax)ω
(5)
式中：λ为阻尼比；λmax为最大阻尼比；Gmax为最大剪切模量；ω为拟合参数，改变拟合参数可以调整曲线。
1)剪切阻尼比。从图21所示的剪切阻尼比随剪应变变化曲线可见：剪应变在10-3之前，剪切阻尼比变化较小；过了10-2之后，剪切阻尼比随着剪应变的增大而急速增大。各最大剪切阻尼比在5.9×10-3～7.1×10-3，由于主应力轴旋转引起了显著的塑性变形，所以比常规动三轴或扭剪中的阻尼比大一些。
为进一步研究有效围压和细粒含量对剪切阻尼比的影响，用以上得到的最大剪切阻尼比对剪切阻尼比进行归一化，并用式(5)进行拟合，如图22所示，拟合参数ω见表8。
C-E-1实际剪切阻尼比； C-E-2实际剪切阻尼比； C-E-3实际剪切阻尼比； C-E-4实际剪切阻尼比； C-E-1剪切阻尼比拟合； ……C-E-2剪切阻尼比拟合； ----C-E-3剪切阻尼比拟合； ---·C-E-4剪切阻尼比拟合。
图22 λt/λmax-γd关系
Fig.22 The relationa-curves of λt/λmax and γd
表8 剪切阻尼比拟合参数ω
Table 8 Fitting parameter ω of shear damping ratio
试件C-E-1C-E-2C-E-3C-E-4拟合参数ω1075.54
从图22可见：围压越大，试样归一化剪切阻尼比越小；细粒含量为0%的归一化剪切阻尼比受有效围压的影响较小；而细粒含量为10%的归一化剪切阻尼比受有效围压的影响较大，可见含细粒砂土的归一化剪切阻尼比受有效围压的影响要大于纯砂。
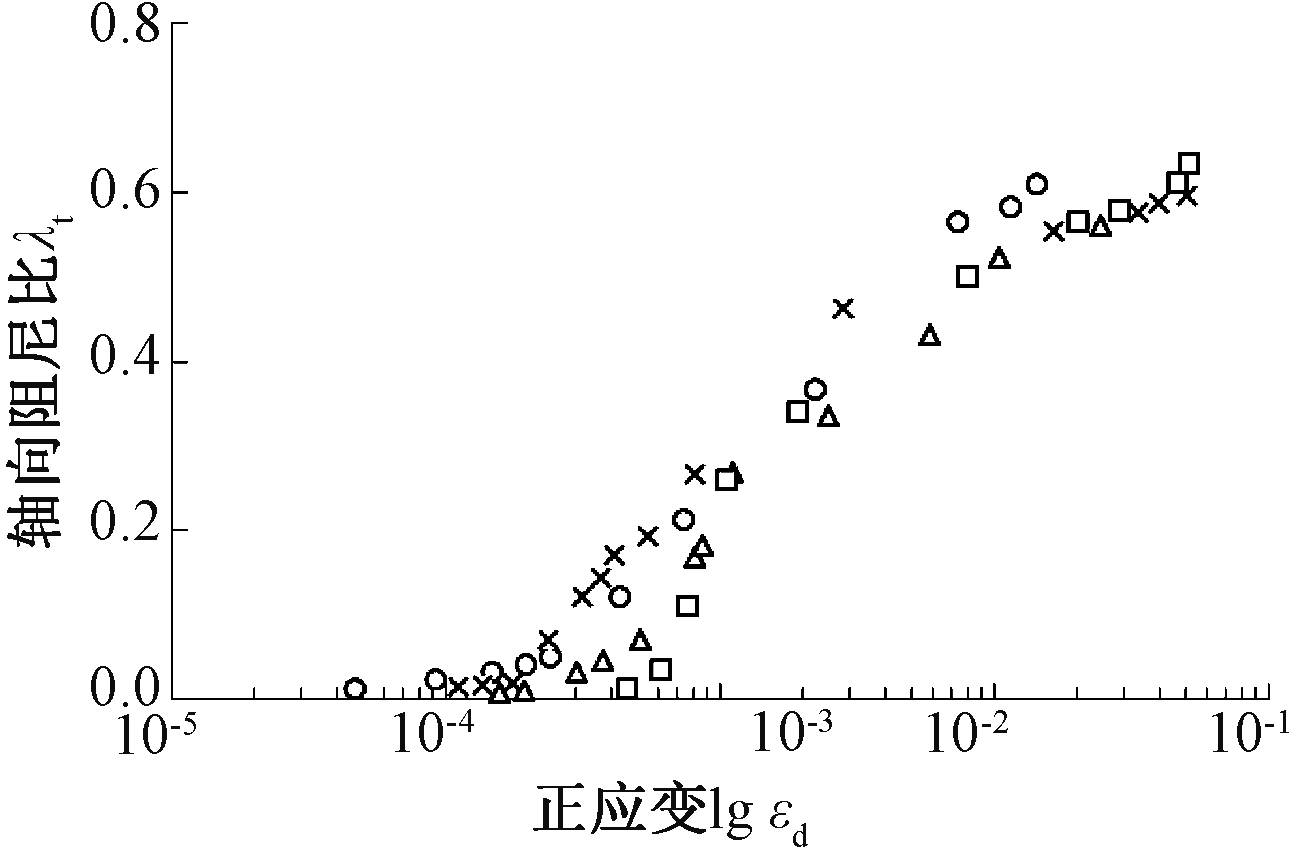
2)轴向阻尼比。从图23所示的轴向阻尼比随轴向应变变化曲线可见轴向应变在5×10-4之前，轴向阻尼比变化较小；过了5×10-4后，轴向阻尼比随着轴向应变的增大而急速增大。所有试样最大阻尼比在5.8×10-3～6.5×10-3。
细粒含量为0%，有效围压为100 kPa; 细粒含量为10%，有效围压为100 kPa; 细粒含量为0%，有效围压为200 kPa; 细粒含量为10%，有效围压为200 kPa。
图23 轴向阻尼比-轴向应变关系
Fig.23 The relation of axial damping ratio and axial strain
为进一步研究有效围压和细粒含量对轴向阻尼比的影响，用以上得到的最大轴向阻尼比对轴向阻尼比进行归一化，并进行拟合，见图24，拟合参数ω见表9。
C-E-1实际轴向阻尼比； C-E-2实际轴向阻尼比； C-E-3实际轴向阻尼比； C-E-4实际轴向阻尼比； C-E-1轴向阻尼比拟合； ……C-E-2轴向阻尼比拟合； ----C-E-3轴向阻尼比拟合； ---·C-E-4轴向阻尼比拟合。
图24 λa/λmax-εd关系
Fig.24 The relation of λa/λmax and εd
表9 轴向阻尼比拟合参数ω
Table 9 Fitting parameters of axial damping ratio
试件C-E-1C-E-2C-E-3C-E-4拟合参数ω35611
可见，有效围压越大，试样归一化轴向阻尼比越小；细粒含量为0%的归一化轴向阻尼比受有效围压的影响较小；而细粒含量为10%的归一化轴向阻尼比受有效围压的影响较大，含细粒砂土的归一化轴向阻尼比受有效围压的影响要大于纯砂。
3 结束语
采用空心圆柱扭剪仪，对含细粒饱和砂土进行了动力特性试验研究，主要结论如下：
1)波浪荷载(圆耦合)作用下，砂土的液化循环周次明显小于动三轴和动扭剪。
2)波浪荷载作用下，随着细粒含量的增大，含细粒饱和砂土的液化周次先减小后增加，细粒含量在10%左右最低。
3)细粒含量较小时，含细粒砂土超静孔隙水压发展规律类似纯砂，当细粒含量达到15%以上时，逐渐呈现出类似黏土的规律。
4)细粒含量、有效围压对模量归一化曲线无影响；掺杂细粒后砂土的阻尼比归一化曲线受围压影响比较明显，初始有效围压越大，阻尼比越小。
[1] MOHAMMAD L N, PUPPALA A J, ALAVILLI P. Effect of Strain Measurements on Resilient Modulus of Sands[C]//Procoedings of the Dynamic Geotechnique Testing Ⅱ. Philadelphia, USA:ASTM, 1994.
[2] 中华人民共和国住房和城乡建设部.海堤工程设计规范:GB/T 50154—2014[S].北京：中国计划出版社，2014.
[3] 张福海,陈庆,张晓阳,等.海砂-海泥混合料作为海堤填料的可行性试验研究[J].岩土工程学报,2017,39(增刊1):182-186.
[4] 刘莹,王清,肖树芳.不同地区吹填土基本性质对比研究[J].岩土工程技术, 2003(4):197-200.
[5] 陈义军,胡士兵.浅析吹填施工技术在造地工程中的应用[J].广东水利水电, 2015(2):48-51.
[6] 衡朝阳,何满潮,裘以惠.含黏粒砂土抗液化性能的试验研究[J].工程地质学报, 2001,9(4):339-344.
[7] 陈国兴,胡庆兴,刘雪珠.关于砂土液化判别的若干意见[C]//全国土动力学学术会议论文集.2002:141-151.
[8] LEE K L. Cyclic Stress Conditions Causing Liquefaction of Sand.[J]. ASCE, Journal of Soil Mechanics and Foundtion, 1967, 93(1)：47-70.
[9] LEE K L， FITTON J. Factors Affecting the Cyclic Loading Strength of Soil[C]//Proceedings of the Vibration Effects of Earthquakes on Soils & Foundations. 1969: 71-95.
[10] PERLEA V G,KOESTER J P,PRAKASH K S.How Liquefiable are Cohesive Soils[C]//Proceedings of the second International Conference on Earthquake Geotechnical Engineering. 1999:611-618.
[11] GHAHREMANI M, GHALANDARZADEH A. Effect of Plastic Fines on Cyclic Resistance of Sands[C]//Geoshanghai International Conference. 2006:406-412.
[12] 刘雪珠,陈国兴.黏粒含量对南京粉细砂液化影响的试验研究[J].地震工程与工程振动,2003,23(3):150-155.
[13] 潘剑锋,刘喜康,王力,等.粗细粒混合土液化特性研究综述[J].四川水利,2010(6):41-43.
[14] 褚峰,邵生俊,陈存礼.饱和淤泥质砂土动力变形及动强度特性试验研究[J].岩石力学与工程学报,2014,33(增刊1):3299-3305.
[15] ISHIHARA K,TOWHATA I.Sand Response to Cyclic Rotation of Principal Stress Directions as Induced by Wave Loads[J].Soils and Foundations, 1983, 23(4): 11-26.
[16] 张建民,谢定义.饱和砂土振动孔隙水压力增长的实用算法[J].水利学报,1991(8):45-51.
[17] 沈扬,陶明安,王鑫,等.交通荷载引发主应力轴旋转下软黏土变形与强度特性试验研究[J].岩土力学,2016,37(6):1569-1578.
[18] 王炳辉,陈国兴.循环荷载下饱和南京细砂的孔压增量模型[J].岩土工程学报,2011,33(2):188-194.
[19] 刘功勋,栾茂田.双向耦合循环剪切条件下超固结饱和海洋黏土孔压与强度特性研究[J].岩土力学,2011,32(增刊2):215-221.
[20] 曹洋. 波浪作用下原状软黏土动力特性与微观结构关系试验研究[D].杭州：浙江大学,2013.
[21] 雷华阳,娄金峰,许英刚,等.天津黏土地基动载模式下的孔压发展规律[J].中国港湾建设,2018,38(2):24-29.
[22] 魏新江,张涛,丁智,等.地铁荷载下不同固结度软黏土的孔压试验模型[J].岩土力学,2014,35(10):2761-2768,2874.
[23] 邓海峰,刘振纹,祁磊,等.波浪作用下饱和砂土孔压发展规律试验研究[J].水利与建筑工程学报,2017,15(3):45-48,59.
[24] 潘坤,杨仲轩.不规则动荷载作用下砂土孔压特性试验研究[J].岩土工程学报,2017,39(增刊1):79-84.
[25] HARDIN B O, DRNEVICH V P. Shear Modulus and Damping in Soils: Design Equations and Curves[J]. ASCE, Journal of Soil Mechanics & Foundations, 1972, 98(7):667-692.
[26] 孙静.岩土动剪切模量阻尼试验及应用研究 [D].北京：中国地震局工程力学研究所, 2004.