钢筋混凝土板是现代建筑和桥梁的常用构件,对其承载力研究[1]始于美国学者Tallbot;影响板柱结构的承载力因素主要为有效高度、板厚、配筋率,钢筋强度、加载情况等。之后一些研究者相继提出半理论半经验的计算式。由于钢筋混凝土板冲切破坏的复杂性,目前还没有一套完整的理论基础来准确解释其冲切破坏机理[2-4]。通过对比不同国家和地区的抗冲切承载力计算式[5-7],发现各个国家对冲切破坏影响因素的种类和大小有着不同看法。其中最显著的分歧在于是否考虑配筋率对冲切承载力的影响。
提高纵向配筋率可以有效提高钢筋混凝土板极限承载力[8]。对于板柱增强节点来说,提高纵筋配筋率、暗梁加密区箍筋间距及弯起钢筋截面积均可影响节点的受力性能[9-10]。对于冲跨比的影响近年来也有学者提出相关研究[11],而目前国内实施的GB 50010—2010《混凝土结构设计规范》[12],并未考虑配筋率对抗冲切承载力的影响。基于上述文献[8-11]的分析,本文在试验和数值模拟的基础上,探讨不同配筋率对钢筋混凝土桥面板的冲切承载力和破坏形态的影响,针对现行板冲切承载力计算式的不足,对其进行适当修改,得到考虑配筋率影响的抗冲切强度承载力计算式。
1 试验概况
本试验共制作两块钢筋混凝土板试件,编号分别为RC-0.72和RC-0.50;RC代表钢筋混凝土板;0.72与0.50代表配筋率分别为0.72%、0.5%。试件尺寸如表1所示,加载方式为100 mm×100 mm的方板中置加载,约束条件为四边支承,间距为1 300 mm,有效高度均为115 mm;加载形式和构件配筋如图1、2所示。
表1 板试件信息
Table 1 Slab specimen information
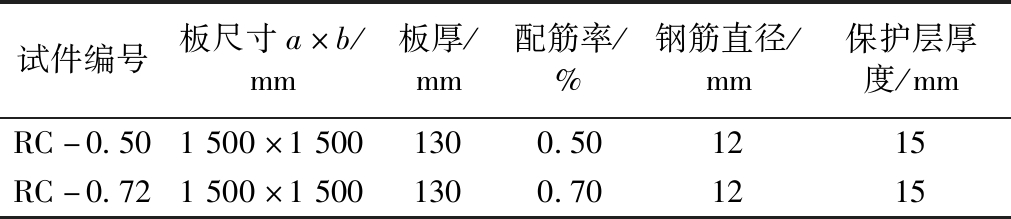
试件编号板尺寸a×b/mm板厚/mm配筋率/%钢筋直径/mm保护层厚度/mmRC-0.501500×15001300.501215RC-0.721500×15001300.701215

图1 试验加载装置
Fig.1 Test loading device
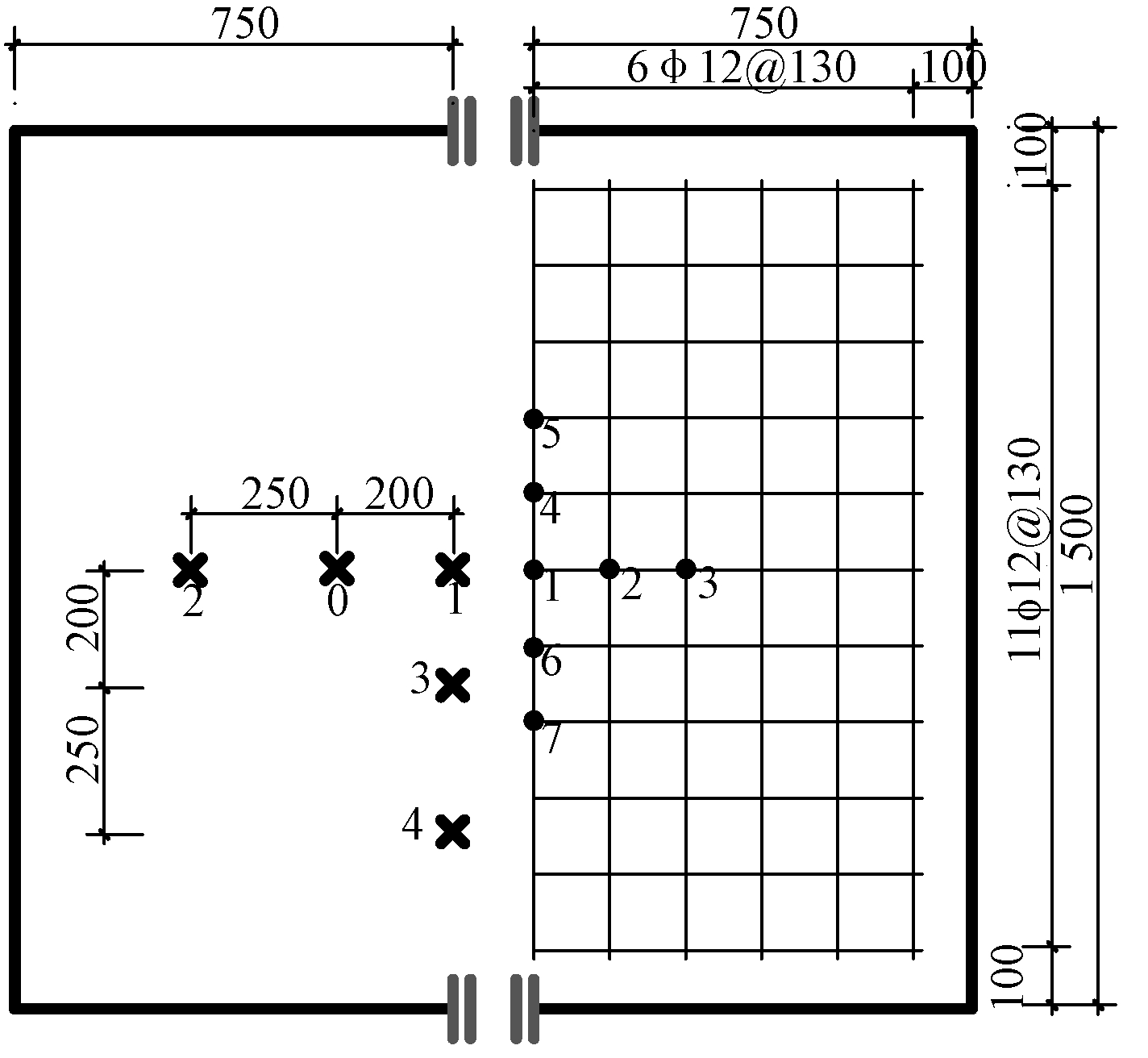
图2 板试件尺寸及钢筋布置
Fig.2 Dimensions of slab specimens and arrangement of reinforcing bars
钢筋为型号HRB400级的螺纹钢筋,实测屈服强度为535 MPa;板底双向配筋。混凝土采用强度等级为C30的商品混凝土,实测第28天的标准立方体抗压强度为37.8 MPa;弹性模量为32.07 GPa;劈裂抗拉强度为3.93 MPa;配合比如表2所示。
表2 商品混凝土的配合比
Table 2 Mix proportion of commercial concrete kg/m3
石子砂粉煤灰水泥水减水剂1035750903001757.2
2 试验结果及分析
从开始加载到试件破坏过程中,首先在加载板中心处出现第一条十字形裂纹;随荷载增加板底裂纹逐渐向四周扩散,不断增多加宽,最终试件发生破坏。由破坏状态可以看出:RC-0.50板的板底对角线附近出现几条较宽裂纹,且钢筋发生屈服,出现塑性铰,由此可知其破坏形式为弯曲破坏。而RC-0.72板的板底裂纹相对密集,且出现较大冲切破坏锥,局部钢筋屈服,既有冲切破坏的特征也有弯曲破坏的现象,钢筋发生剪切破坏的同时也部分出现塑性铰,因此其破坏形式为弯冲破坏。
从破坏后的板底裂纹分布(图3)可以看出:相同直径,配筋率高钢筋密,受力分布均匀,裂缝密但宽度窄,几乎遍布整块板底,可能是因为当配筋率较大时,钢筋与混凝土通过黏结作用所分担的力就越均匀,混凝土受力也会增加。配筋率较小时裂纹分布相对集中,且主要分布在加载板作用区域周围,板底边界处只存在几条较宽的主裂纹。对于板顶的破坏状态,由图4可知:两块试件板顶均无肉眼可见的明显裂纹,只有在加载板位置发生与加载面积同大小的区域塌陷。

a—RC-0.50; b—RC-0.72。
图3 破坏后板底裂纹分布
Fig.3 Distribution of cracks at the bottom of the slab after failure
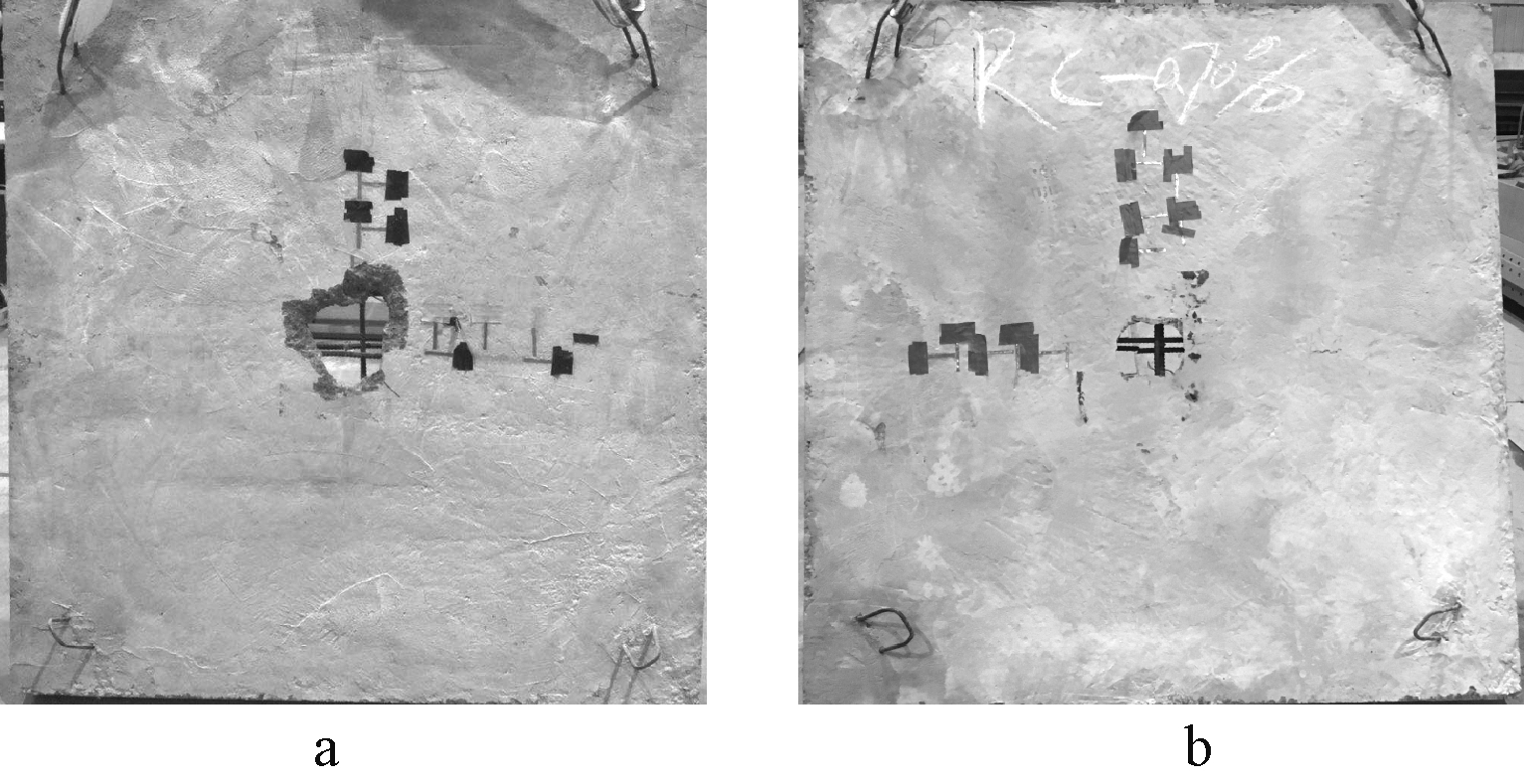
a—RC-0.50; b—RC-0.72。
图4 板破坏状态
Fig.4 Failure mode of slabs
3 试验结果与数值模拟对比
采用ABAQUS有限元软件,建立板模型。混凝土采用软件自带的塑性损伤模型来模拟,其本构采用GB 50010—2010[12]提供的混凝土本构模型,混凝土峰值应变采用欧洲标准;钢筋本构为理想弹塑性模型。混凝土采用C3D8R单元模拟,钢筋采用T3D2单元模拟;加载方式为位移加载,约束条件为四边支承。
钢筋和混凝土之间的黏结作用采用嵌入(Embedded)的方式来模拟,不考虑钢筋和混凝土的黏结滑移。
3.1 板底受拉损伤云图
图5为RC-0.50的板底受拉损伤云图,从图中可以看出:在损伤开始阶段裂纹主要集中在加载板正下方及板对角线附近,裂纹分布呈X形;随荷载的增加,钢筋屈服,板底中心区域损伤越来越严重,且板周边也逐渐出现损伤裂纹,最终板底布满损伤裂纹并发生破坏,破坏时板底裂纹呈“X饱满型”。
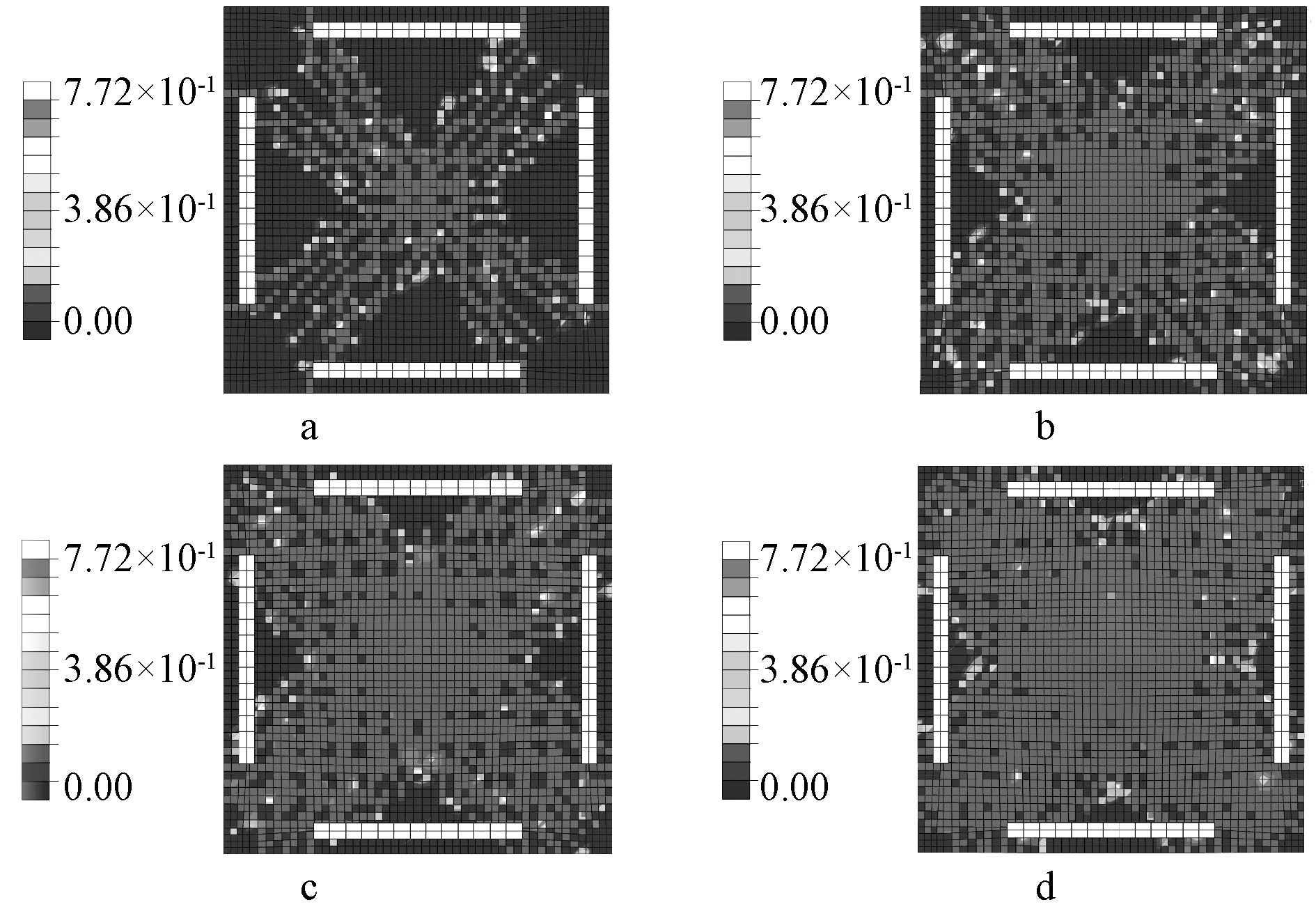
a—初始状态; b—发展状态1; c—发展装态2; d—最终状态。
图5 板底受拉损伤云图
Fig.5 Tensile damage nephogram of the bottom of the slab
3.2 板顶受拉损伤云图
图6为试件RC-0.50的板顶受拉损伤云图,从图中可以看出在变形初期板顶损伤主要集中在加载板周围;随着变形增加板顶受拉裂纹持续扩展,在达到极限状态时板顶四周区域的损伤也随之出现,最终板顶出现类似正方形的损伤且与试验现象符合较好。

a—初始状态; b—最终状态。
图6 板顶受拉损伤云图
Fig.6 Tensile damage nephogram of the top of slab
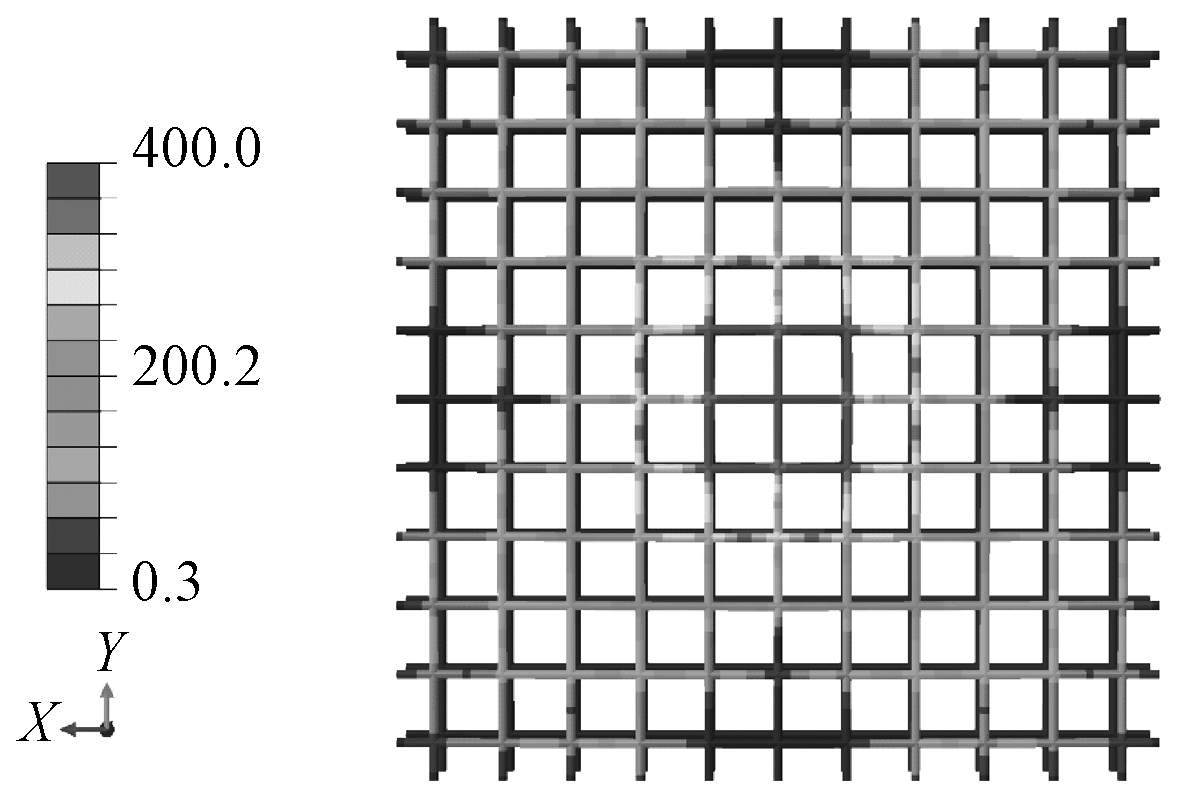
图7 试件RC-0.72板底钢筋应力分布 MPa
Fig.7 Stress distribution of the steel bar at the bottom of specimen RC-0.72
3.3 板底钢筋应力
图7为试件RC-0.72的板底钢筋应力分布云图,由图可知,在板底中心周围钢筋已经屈服,由板底中心向四周钢筋应力逐渐减小。在达到承载力极限时,板底钢筋在加载板正下方周围达到屈服。由于数值模拟并未考虑钢筋和混凝土的黏结滑移,且数值模拟不可能完全模拟钢筋和混凝土在实际工作中的相互作用,故并未出现塑性铰。
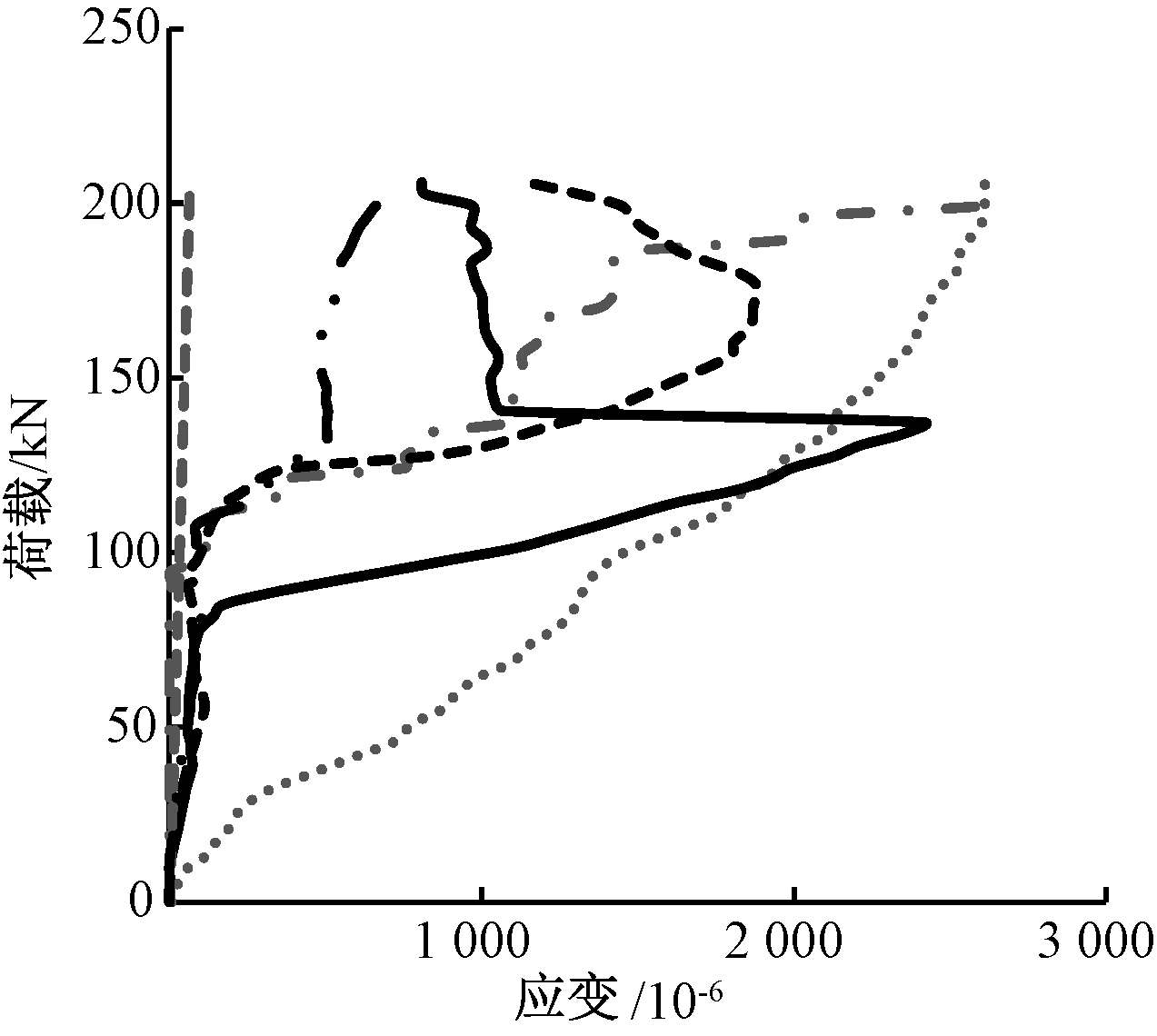
……模拟1点; ![]() 试验1点; -·-模拟2点; ----试验2点; -----模拟3点; -··试验3点。
试验1点; -·-模拟2点; ----试验2点; -----模拟3点; -··试验3点。
图8 RC-0.72板底钢筋荷载-应变曲线
Fig.8 Load-strain curves of the steel bar at the bottom of specimen RC-0.72
图8为试件RC-0.72板底钢筋网测点应变与对应模拟点荷载-应变曲线对比,在相同荷载下,越靠近加载板处,钢筋应变越大,相应应力同样越大,与数值模拟板底钢筋网应力分布一致。试验中板底钢筋测点出现应变退回现象,是由钢筋和混凝土的黏结滑移造成;由于数值模拟并未考虑黏结滑移,因此未出现应变回退。综上所述,虽模拟结果与试验曲线存在一定偏差,但是总体趋势与试验结果相一致。试件RC-0.50的板底钢筋应力分布与试件RC-0.72相似,不再赘述。
3.4 极限承载力
极限承载力试验与数值结果见表3。由试验结果可知:试件RC-0.50和RC-0.72的承载力分别为170.4,205.8 kN,模拟结果分别为176.6,195.5 kN;试验值与模拟结果的相对误差分别为-3.6%和5.0%。
表3 模拟结果与试验值对比
Table 3 Comparison of simulation results and experimental values
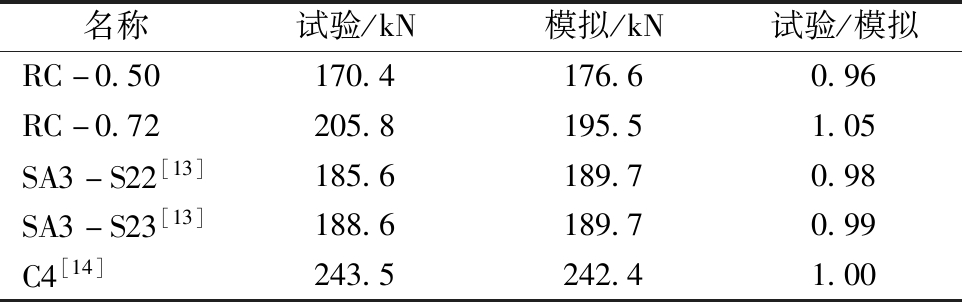
名称试验/kN模拟/kN试验/模拟RC-0.50170.4176.60.96RC-0.72205.8195.51.05SA3-S22[13]185.6189.70.98SA3-S23[13]188.6189.70.99C4[14]243.5242.41.00
图9对比了两块试件数值计算与试验荷载-位移曲线,在加载初期弹性段,由于数值模拟的简化,试件弹性段数值模拟结果大于试验值。但随着荷载增加,试件进入塑性段后,数值模拟曲线与试验曲线较为接近。

a—试件RC-0.50; b—试件RC-0.72。![]() 试验; ---模拟。
试验; ---模拟。
图9 试验荷载-位移曲线与数值模拟对比
Fig.9 Comparison of test load-displacement curves and numerical simulation of specimens
由于本试验并未加入配筋率大于0.95%的试件,为使对比结果更具说服力,引用文献[13-14]试件编号为SA3-S22、SA3-S23及C4的试验数据进行比对(表3),其中试件C4为冲切破坏,图10为试件C4荷载-位移曲线。对比几块试件试验极限承载力与数值模拟结果,分别相差-2.2%、0.58%和0.45%,符合较好。试件参数见表4。
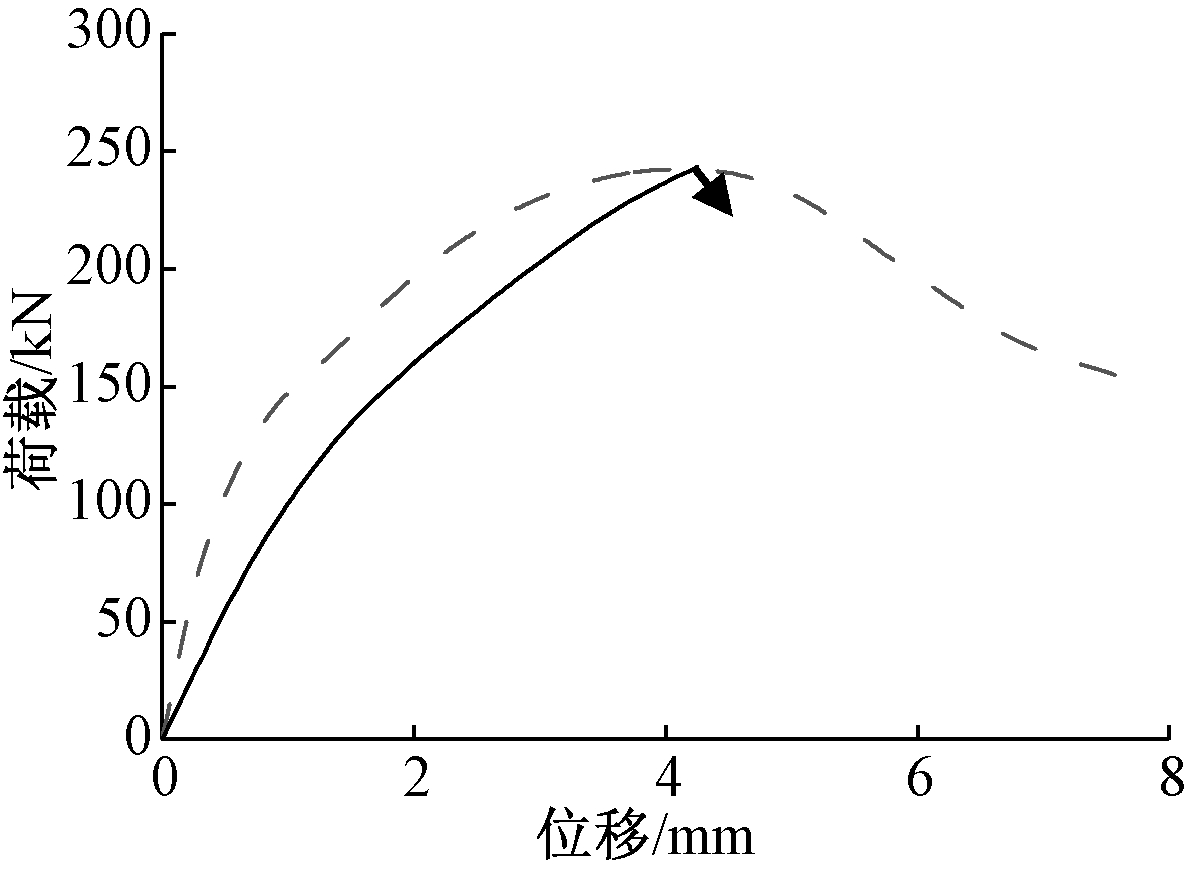
---C4模拟; ![]() C4试验。
C4试验。
图10 文献[14]试验荷载-位移曲线与数值模拟对比
Fig.10 Comparison of test load-displacement curves and numerical simulation from reference[14]
表4 文献[13-14]试件参数
Table 4 Document[13-14] specimen parameters
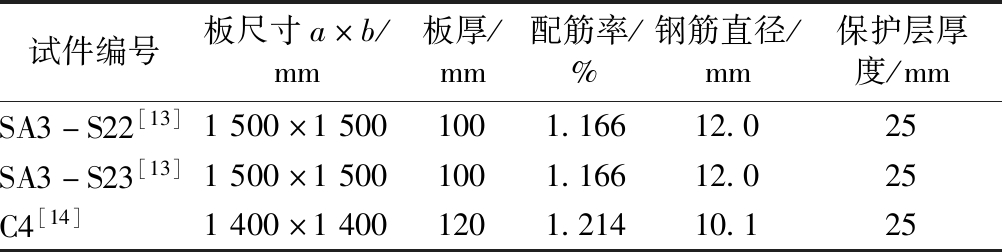
试件编号板尺寸a×b/mm板厚/mm配筋率/%钢筋直径/mm保护层厚度/mmSA3-S22[13]1500×15001001.16612.025SA3-S23[13]1500×15001001.16612.025C4[14]1400×14001201.21410.125
从上述对比可知,数值模拟裂纹分布和试验现象相对比较吻合,因此本文的数值模型是合理可靠的。
4 数值模拟结果及分析
在以上分析的基础上,以RC-0.50为标准试件建立数值计算模型,应用ABAQUS有限元软件设置配筋率分别为0.2%、0.43%、0.57%、0.72%、0.95%、1.24%、1.7%和2.2%的钢筋混凝土桥面板,分析其极限承载力变化趋势和破坏形式。
文献[15]定义了弯曲破坏和冲切破坏的主要特征,即四个阶段,分别为弹性阶段;钢筋屈服阶段;塑性铰形成阶段,此阶段钢筋屈服并且形成塑性铰;最后发生破坏,此阶段主要特征为荷载不再增加,并且荷载-位移曲线大致呈水平直线。弯曲破坏大多发生在荷载-位移曲线的第四阶段;而冲切破坏大多发生在第三阶段,且冲切破坏属于脆性破坏。
由图11可知:在加载初期板处于弹性阶段,此时位移-荷载曲线几乎为直线,随着荷载增加板逐渐进入塑性状态,钢筋屈服,混凝土裂纹不断增多加宽,最终达到极限承载力,发生破坏。本文位移-荷载曲线数值模拟结果的基本符合上述四阶段。

-··-0.20%; -·-0.43%; --0.50%; -·-·0.72%; ---0.95%; -----1.24%; ……1.70%; ![]() 2.20%。
2.20%。
图11 不同配筋率下的荷载-位移曲线
Fig.11 Load-displacement curves under different longitudinal reinforcement ratios
从图11中还可看出:提高配筋率对钢筋混凝土板极限承载力提升明显。
图12为配筋率-极限荷载曲线。可知:配筋率为0.2%~1.24%时钢筋混凝土的极限荷载的增长倍数为2.13;1.24%~2.2%时增长倍数为1.07。由此可知,当配筋率较小时,适当增加配率筋对承载力会有明显的提升,配筋率较大时,增加配筋率对承载力提升速率趋于平缓。钢筋混凝土桥面板极限荷载与配筋率的大致关系为幂函数形式。
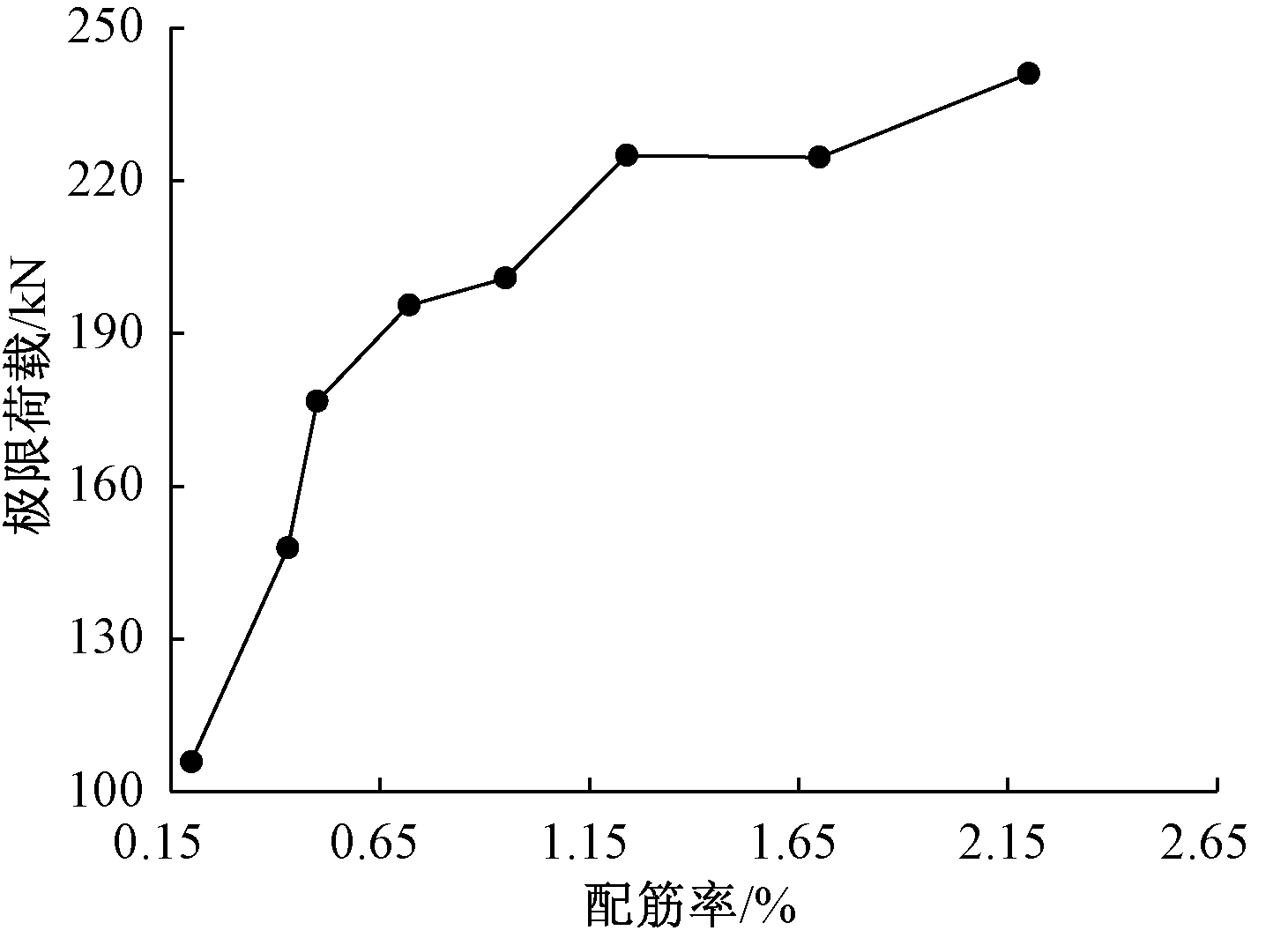
图12 配筋率-极限荷载曲线
Fig.12 Relationship between load and reinforcement ratio
配筋率不仅影响极限承载力,对钢筋混凝土板的破坏形式也有影响。当配筋率大于0.95%时发生冲切破坏,小于0.72%时发生弯曲破坏。当配筋率在0.72%~0.95%时,其破坏既有弯曲破坏特征,同时也有冲切破坏特征,属于弯冲破坏,且破坏时的极限位移介于弯曲破坏与冲切破坏极限位移之间。
文献[14]中无抗冲切筋钢筋混凝土板试件33块,其中配筋率大于0.95%的试件共有21块;在配筋率大于0.95%的试件中,发生冲切破坏有12块,占比57.2%,发生弯曲破坏有9块,占比42.8%。这表明当钢筋混凝土板在配筋率大于0.95%时,发生冲切破坏的概率较大,这与数值模拟结果基本相似。所有试件中弯曲破坏试件共21块,平均配筋率为0.89%;冲切破坏试件共12块,平均配筋为1.41%,说明配筋越大的钢筋混凝土板发生冲切破坏的概率也就越大。试件中配筋率小于0.72%的试件共7块,全部发生弯曲破坏,说明配筋率较小时,试件更易发生弯曲破坏,亦与本文结论相符。
5 各国标准计算式对比
不同国家标准对冲切承载力计算式所考虑的影响因素有所不同,在抗冲切承载力计算式建立方面,中国和美国标准体系较为相似,与欧洲标准相差较大,其主要原因在于各标准计算式所考虑影响因素及比重有所不同,详见表5。目前大多数标准的计算方法主要基于试验建立;在未配置抗冲切筋时,美国和中国标准中抗冲切破坏承载力计算式主要考虑混凝土强度、加载板大小和位置、板厚等影响因素,并未考虑配筋率的影响,欧洲标准所考虑因素相对全面合理。具体的计算式如表6所示。
表5 各国标准计算式主要影响因素汇总
Table 5 Summary of main influencing factors of national normative formulas

标准加载板有效高度配筋率混凝土强度抗拉抗压GB50010—2010○○×○×ACI318-14○○××○EN1992-1-1∶2004○○○×○
表6 各国标准公式汇总
Table 6 Summary of formulas from national standards

中国标准[12](GB50010—2010)美国标准[16](ACI318-14)欧洲标准[17](EN1992-1-1∶2004)Fl≤0.7βhftηumh0Vu≤0.75VcVr=0.141+200/h0()(100ρfck)1/3>Vminη=minη1=0.4+1.2βs;η2=0.5+αsh04umìîíïïïïüþýïïïïVc=min0.0832+4βc()λf′cb0h0;0.083αsdb0+2()λf′cb0h0;0.333λf′cb0h0ìîíïïïïïüþýïïïïïVmin=0.035[1+(200/h0)0.5]3/2(fck)1/2
注:βh为截面高度影响系数; ft为混凝土的抗拉强度标准值; um为临界截面的周长; αs为加载板位置影响系数; βs为加载板形状影响系数; h0为截面有效高度; ![]() 为混凝土圆柱体抗压强度;对于普通混凝土取λ=1; Vr为名义剪应力;ρ为配筋率; fck为混凝土圆柱体抗压强度标准值。
为混凝土圆柱体抗压强度;对于普通混凝土取λ=1; Vr为名义剪应力;ρ为配筋率; fck为混凝土圆柱体抗压强度标准值。
5.1 算式修正
对钢筋混凝土板承载力的研究方法,目前主要有塑性铰线法,极限平衡法和概率统计法三种。塑性铰线法主要适用于弯曲破坏的计算,由于冲切破坏的复杂性,目前主要采用后两种方法来研究其极限承载力,且目前大多数的国家标准中冲切承载力计算式都是基于概率统计法建立的。
根据以上分析,本文受冲切承载力计算式的回归模型主要基于GB 50010—2010所建立,考虑了板厚尺寸效应、混凝土轴心抗拉强度、加载板位置和形状、截面有效高度、临界截面周长和配筋率等影响因素。假设受冲切承载力计算式有如下关系:
Fu=λβhftηumh0ρα
(1)
式中:λ和α为计算相关系数,由试验数据经回归分析确定;η为加载板位置影响系数;其他参数物理意义见表6。
为计算配筋率对冲切承载力的影响,首先假设:
Y=βhftηumh0
(2)
式中相关参数取值均取GB 50010—2010所规定。则:
Fu=λYρα
(3)
通过分析可知λ=3.5,α=1/3。由此可知,考虑了配筋率影响的冲切承载力计算式为:
Fu=3.5βhftηumh0ρ1/3
(4)
5.2 可靠度分析
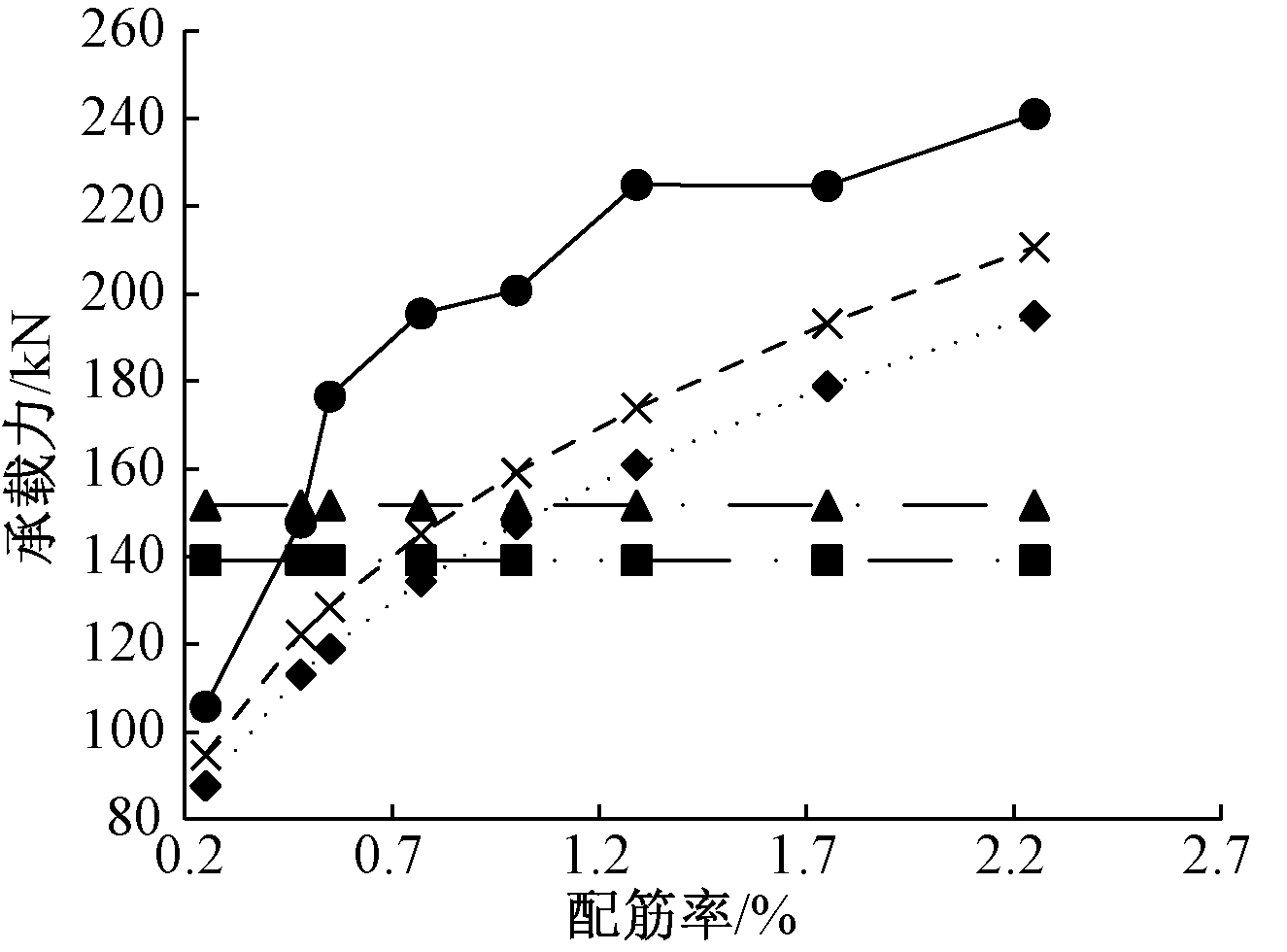
对比各计算式值与本文数值模拟结果,见图13。可以发现本文计算式结果与变化趋势与欧洲标准较为接近。由于中国标准与美国标准算式并未考虑配筋率的影响,因此在图中为水平直线,且中国标准计算值相对较小。
![]() … 本文算式;
… 本文算式; ![]() — GB 50010—2010; -
— GB 50010—2010; -![]() -- EN 1992-1-1∶ 2004;
-- EN 1992-1-1∶ 2004; ![]() ·- ACI 318-14;
·- ACI 318-14; ![]() — 模拟值。
— 模拟值。
图13 各国标准推荐算式计算结果与本方法计算结果对比
Fig.13 Comparison of calculation results from national standards and the paper
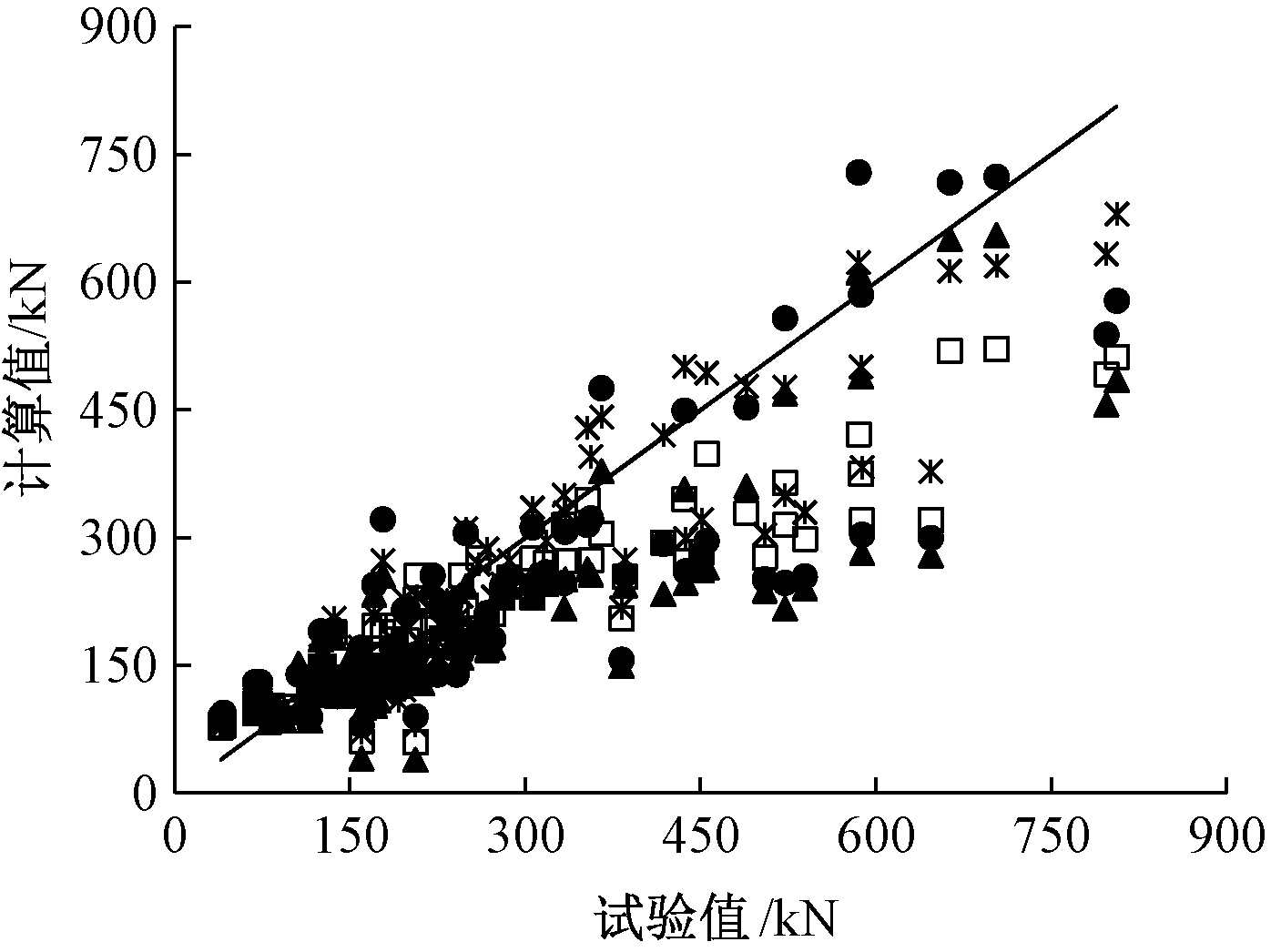
为验证本文计算式的可靠性,综合本文数值模拟数据与国内外研究者[13-14,18-21]的72块钢筋混凝土板试验数据进行对比研究,结果见表7。
![]() 本文算式;
本文算式;![]() GB 50010—2010;
GB 50010—2010;![]() EN 1992-1-1∶ 2004;
EN 1992-1-1∶ 2004;![]() ACI 318-14;
ACI 318-14; ![]() 试验值。
试验值。
图14 各国标准推荐算式计算结果与试验值对比
Fig.14 Comparison between calculated values and test values of each formula
表7 各算式计算值与试验值对比
Table 7 Comparison between calculated values and test values of each formula
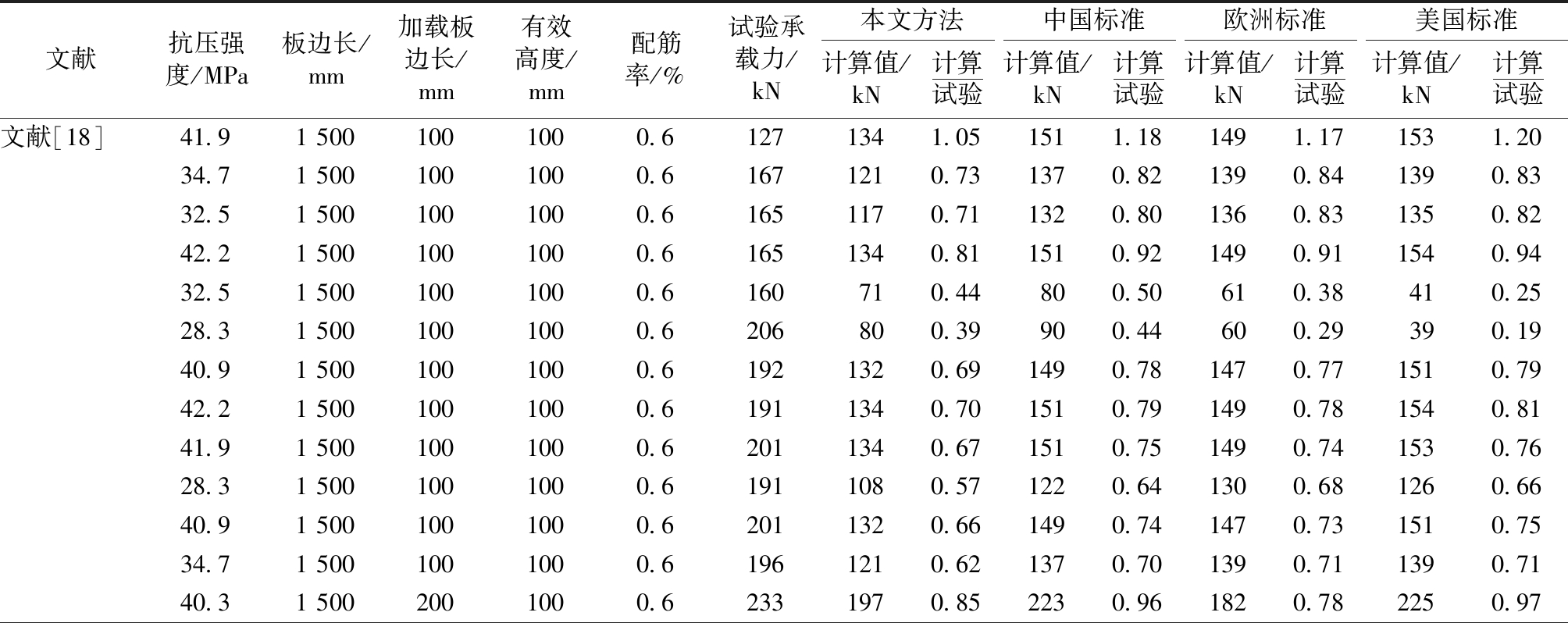
文献抗压强度/MPa板边长/mm加载板边长/mm有效高度/mm配筋率/%试验承载力/kN本文方法中国标准欧洲标准美国标准计算值/kN计算试验计算值/kN计算试验计算值/kN计算试验计算值/kN计算试验文献[18]41.915001001000.61271341.051511.181491.171531.2034.715001001000.61671210.731370.821390.841390.8332.515001001000.61651170.711320.801360.831350.8242.215001001000.61651340.811510.921490.911540.9432.515001001000.6160710.44800.50610.38410.2528.315001001000.6206800.39900.44600.29390.1940.915001001000.61921320.691490.781470.771510.7942.215001001000.61911340.701510.791490.781540.8141.915001001000.62011340.671510.751490.741530.7628.315001001000.61911080.571220.641300.681260.6640.915001001000.62011320.661490.741470.731510.7534.715001001000.61961210.621370.701390.711390.7140.315002001000.62331970.852230.961820.782250.97
续表7
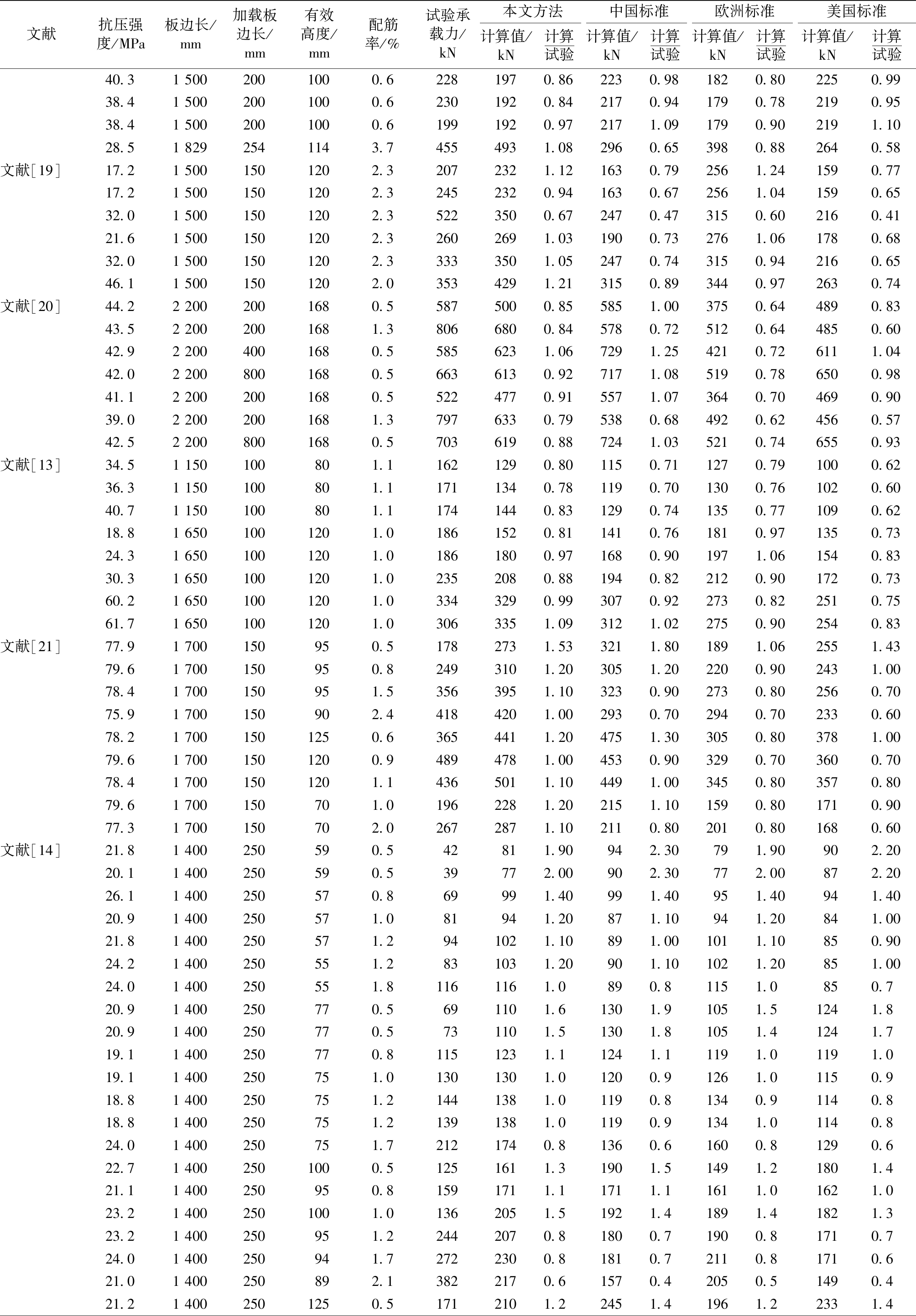
文献抗压强度/MPa板边长/mm加载板边长/mm有效高度/mm配筋率/%试验承载力/kN本文方法中国标准欧洲标准美国标准计算值/kN计算试验计算值/kN计算试验计算值/kN计算试验计算值/kN计算试验40.315002001000.62281970.862230.981820.802250.9938.415002001000.62301920.842170.941790.782190.9538.415002001000.61991920.972171.091790.902191.1028.518292541143.74554931.082960.653980.882640.58文献[19]17.215001501202.32072321.121630.792561.241590.7717.215001501202.32452320.941630.672561.041590.6532.015001501202.35223500.672470.473150.602160.4121.615001501202.32602691.031900.732761.061780.6832.015001501202.33333501.052470.743150.942160.6546.115001501202.03534291.213150.893440.972630.74文献[20]44.222002001680.55875000.855851.003750.644890.8343.522002001681.38066800.845780.725120.644850.6042.922004001680.55856231.067291.254210.726111.0442.022008001680.56636130.927171.085190.786500.9841.122002001680.55224770.915571.073640.704690.9039.022002001681.37976330.795380.684920.624560.5742.522008001680.57036190.887241.035210.746550.93文献[13]34.51150100801.11621290.801150.711270.791000.6236.31150100801.11711340.781190.701300.761020.6040.71150100801.11741440.831290.741350.771090.6218.816501001201.01861520.811410.761810.971350.7324.316501001201.01861800.971680.901971.061540.8330.316501001201.02352080.881940.822120.901720.7360.216501001201.03343290.993070.922730.822510.7561.716501001201.03063351.093121.022750.902540.83文献[21]77.91700150950.51782731.533211.801891.062551.4379.61700150950.82493101.203051.202200.902431.0078.41700150951.53563951.103230.902730.802560.7075.91700150902.44184201.002930.702940.702330.6078.217001501250.63654411.204751.303050.803781.0079.617001501200.94894781.004530.903290.703600.7078.417001501201.14365011.104491.003450.803570.8079.61700150701.01962281.202151.101590.801710.9077.31700150702.02672871.102110.802010.801680.60文献[14]21.81400250590.542811.90942.30791.90902.2020.11400250590.539772.00902.30772.00872.2026.11400250570.869991.40991.40951.40941.4020.91400250571.081941.20871.10941.20841.0021.81400250571.2941021.10891.001011.10850.9024.21400250551.2831031.20901.101021.20851.0024.01400250551.81161161.0890.81151.0850.720.91400250770.5691101.61301.91051.51241.820.91400250770.5731101.51301.81051.41241.719.11400250770.81151231.11241.11191.01191.019.11400250751.01301301.01200.91261.01150.918.81400250751.21441381.01190.81340.91140.818.81400250751.21391381.01190.91341.01140.824.01400250751.72121740.81360.61600.81290.622.714002501000.51251611.31901.51491.21801.421.11400250950.81591711.11711.11611.01621.023.214002501001.01362051.51921.41891.41821.323.21400250951.22442070.81800.71900.81710.724.01400250941.72722300.81810.72110.81710.621.01400250892.13822170.61570.42050.51490.421.214002501250.51712101.22451.41961.22331.4
续表7

文献抗压强度/MPa板边长/mm加载板边长/mm有效高度/mm配筋率/%试验承载力/kN本文方法中国标准欧洲标准美国标准计算值/kN计算试验计算值/kN计算试验计算值/kN计算试验计算值/kN计算试验22.114002501270.52212181.02551.22020.92431.121.214002501250.83062460.82450.82300.82330.821.214002501250.82802460.92450.92300.82330.822.214002501271.03852740.72570.72540.72440.622.114002501271.02862731.02550.92530.92430.823.714002501251.24372990.72600.62730.62460.623.514002501251.23182960.92590.82710.92450.827.914002501231.24513210.72790.62830.62620.624.014002501211.45053040.62510.52770.52370.524.614002501211.75393300.62540.52980.62400.435.314002501191.65883820.73030.53200.52820.533.114002501211.66473770.63000.53200.52790.4本文数值30.0150015001150.2106880.81391.3950.91521.4模拟30.0150015001150.431481130.81390.91220.81521.030.0150015001150.51771190.71390.81290.71520.930.0150015001150.721961340.71390.71450.71520.830.0150015001150.952011470.71390.71590.81520.830.0150015001151.242251610.71390.61740.81520.730.0150015001151.72251790.81390.61930.91520.730.0150015001152.22411950.81390.62110.91520.6标准差0.290.360.290.37平均值0.940.920.870.86变异系数/%30.3039.5033.5043.20
由图14可知,本文计算值与试验结果相对离散性较小,而欧洲标准计算相对偏于安全,GB 50010—2010和美国标准计算值总体偏于安全,但离散性较大,这可能与未考虑配筋影响有关。由表7对比结果标准差和变异系数可印证以上论述。综合比对分析,认为本文提出冲切承载力计算式总体与试验结果比较接近,离散性也较GB 50010—2010更小,总体偏于安全。
6 结束语
本文基于试验和数值模拟结果,研究不同配筋率对桥面板承载性能和破坏状态的影响,最终得出:
1)配筋率对桥面板弹性阶段承载力影响较小,当配筋率在0.2%~1.24%时对承载力影响较大,配筋率为1.24%~2.2%时影响趋于平缓。
2)对于破坏形态,当配筋率低于0.72%时钢筋混凝土板有较大概率发生弯曲破坏,大于0.95%时发生冲切破坏的概率较大。
3)通过试验和数值模拟结果,基于现行标准GB 50010—2010计算式,通过线性回归的方法推导出考虑配筋率的冲切承载力计算式。对比各国标准以及试验结果发现,本文计算式结果接近欧洲标准,且更接近试验值。
[1] TALBOT A N. Reinforced Concrete Wall Footings and Column Footings[D].Champaign-Urbana: University of Illinois at Urbana-Champaign, 1925.
[2] 蔡健, 林凡. 基于双剪强度理论的混凝土板极限冲切承载力计算方法[J]. 工程力学, 2006, 23(6):110-113.
[3] 严宗达. 用双剪强度理论解混凝土板冲切的轴对称问题[J]. 工程力学, 1996, 13(1):1-7.
[4] 郭晓林, 刘广义, 曹声远. 钢筋混凝土板冲切破坏机理的试验研究及冲切承载力计算[J]. 哈尔滨建筑工程学院学报, 1993(6):74-80.
[5] 魏巍巍, 贡金鑫, 田磊. 钢筋混凝土板受冲切承载力对比分析[J]. 建筑科学与工程学报, 2010, 27(4):44-56.
[6] 周朝阳, 连晓庄. 欧洲规范EC2抗冲切设计方法评介[J]. 建筑结构, 2000(10):34-37.
[7] 刘立渠. 国内外规范关于钢筋混凝土板冲切承载力的比较研究[J]. 建筑结构, 2007(7):46-50.
[8] 陈建伟, 边瑾靓, 王宁. 考虑不同配筋率影响的板柱节点抗冲切性能分析[J]. 地震工程学报, 2016, 38(4):525-532.
[9] 庞瑞, 党隆基, 倪红梅. 空心楼盖板柱增强节点抗冲切性能数值分析[J]. 工业建筑, 2017,47(2):76-81.
[10] 周朝阳. 配置抗冲切钢筋的混凝土板柱连接的破坏形态与承载力分析[J]. 建筑结构学报, 1997, 18(6):26-31.
[11] 孙健婕, 杨秋宁, 毛明杰. 冲跨比对钢筋混凝土板冲切强度的影响[J]. 工业建筑, 2018,48(2):84-88.
[12] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S]. 北京:中国建筑工业出版社,2010.
[13] 角田与史雄, 井藤昭夫, 藤田嘉夫. 鉄筋コンクリートスラブの押抜きせん断耐力に関する実験的研究[J]. 土木学会論文報告集, 1974, 229: 105-115.
[14] 李定国, 舒兆发, 余志武. 无抗冲切钢筋的钢筋混凝土板柱连接冲切强度的试验研究[J]. 湖南大学学报(自然科学版), 1986, 13(3):26-39.
[15] 楼板及基础冲切强度专题组. 钢筋砼板和基础冲切强度的试验研究[J]. 建筑结构学报, 1987, 8(4):12-22.
[16] ACI Committee. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary on Building Code Requirements for Structural Concrete (ACI 318R-14)[S]. Farmington Hills, MI: American Concrete Institute, 2014.
[17] CEN. Eurocode 2: Design of Concrete Structures - Part 1: General Rules and Rules for Buildings:EN 1992-1-1∶2004[S]. Brussels: European Committee for Standardization, 2004.
[18] 杨秋宁, 毛明杰, 张文博. 钢筋混凝土桥面板保护层厚度对冲切强度的影响[J]. 科技导报, 2014, 32(36):93-97.
[19] 韩菊红, 丁自强. 钢筋砼四边支承矩形板抗冲切性能试验研究[J]. 建筑结构学报, 1994, 15(6):38-46.
[20] 刘立渠. 钢筋混凝土板抗冲切的有限元计算研究[J]. 建筑科学, 2007, 23(1):5-9.
[21] MARZOUK H, HUSSEIN A. Experimental Investigation on the Behavior of High-Strength Concrete Slabs[J]. ACI Structural Journal, 1991, 88(6): 701-713.