0 前 言
叠合楼板是一种由工厂预制的混凝土底板和工地现浇钢筋混凝土层叠合而成的装配整体式楼板结构。由于其既具有工厂化、标准化、装配化的特点,又具有较好的整体性,在目前国内推广的装配式混凝土结构中得到广泛应用[1-5]。
现有相关技术标准中对双向受力叠合楼板间的连接方式均建议采用预留200~300 mm宽现浇带形式[6-7],如图1a所示,同时要求预制混凝土底板侧面需留出“胡子筋”,如图2所示。这种四面出筋的叠合楼板不但在工厂生产时需根据出筋间距加工不同的定型模具,钢筋按模具上的开孔逐根放置,标准化程度低。更主要的是在工程现场需要支设后浇带模板及支撑,如图3所示,并且“胡子筋”在安装时钢筋碰撞情况比较严重,影响现场施工效率。

a—整体式接缝; b—密拼式接缝。
图1 双向受力叠合楼板
Fig.1 Bidirectional composite floor slabs

图2 侧面留“胡子筋”的双向板
Fig.2 Outstretched steel bar on the side of slab

图3 后浇带现场支模
Fig.3 Field formwork of post-casting zone
为克服上述问题,JGJ 1—2014《装配式混凝土结构技术规程》[6]中也给出了双向板密拼连接的构造形式,如图1b所示。为保证连接部位楼板的有效高度,JGJ 1—2014中对叠合现浇层厚度提出了更高的要求(不小于100 mm及1.5倍底板高度),从而导致楼板综合造价较高,影响了四边不出筋叠合楼板的推广使用。不少学者对拼缝处采用附加钢筋形式的密拼叠合楼板进行的试验研究[8-10]表明:叠合楼板的板底裂缝开展和挠度变形具有明显双向受力特征。钱永梅等通过试验[11]和有限元分析[12]充分证明了分离式接缝的叠合板存在双向受力效应。Ye等的研究[13]表明:拼缝处钢筋的布置可以控制叠合板表面裂缝的发展,提高构件的承载力和延性。Jeong等的研究[14]也证明了整个叠加板的承载能力取决于拼缝处的构造设计。恽燕春等通过试验[15]指出:桁架钢筋到拼缝的距离对密拼叠合楼板承载力影响较大,距离越小,密拼叠合楼板承载力及刚度越大,受力裂缝分布比较均匀,预制和现浇结合面整体性越好。
可见,密拼楼板可以实现承载力基本等同现浇,但需要额外增加现浇层厚度,且同时加密拼缝两边的桁架钢筋间距。为了继续利用四边不出筋叠合底板的优势,同时不增加现浇层厚度及加密桁架钢筋间距,本文提出了一种新型密接拼缝的方式。通过试验及有限元分析,研究叠合板拼缝的受力性能,包括破坏机理、承载力、刚度、裂缝分布等,并重点研究环型封闭连接钢筋对叠合板性能的影响。利用有限元计算的精细化分析,深入研究连接部位处钢筋与混凝土之间的传力机理,为双向受力叠合楼板新型密拼连接的设计提供借鉴。
1 新型连接构造
1.1 凹槽设计
为了增加接缝处楼板的有效高度,在预制底板边设置垂直于板缝的凹槽。凹槽间隔设置于两根受力钢筋之间,宽度为钢筋间距-50 mm;凹槽深度为底板厚度-30 mm,即凹槽部位的底板厚度为30 mm。凹槽的内部放置搭接钢筋,因此凹槽长度由搭接钢筋长度控制。通常情况下,搭接钢筋长度需满足la,一般不小于300 mm,从而使得凹槽长度较长,制作、运输、施工中容易造成凹槽底部30 mm薄板损坏。
1.2 封闭环形连接
为减小凹槽长度,提出了封闭环形连接钢筋替代传统的直线搭接钢筋。封闭环形钢筋自成独立闭环系统,其锚固破坏承载力并非由钢筋表面握裹力控制,而是由其所包围的混凝土脱离体与周边混凝土之间的抗剪承载力控制,因此大大缩短了钢筋锚固长度。为方便现场摆放,同时也为提高拼缝连接强度和刚度,将封闭连接钢筋设计成“人”字三脚架形式,所用钢筋与板底纵筋相同,即连接钢筋用钢量是板底纵筋的两倍。
为进一步提高封闭环形连接围合区混凝土与周边混凝土之间的连接强度,预制底板内的纵向分布钢筋在板端向上弯折,且伸出预制板面。这一构造同时也进一步增强了预制底板与现浇叠合层之间的结合性能。新型密拼连接构造如图4所示。
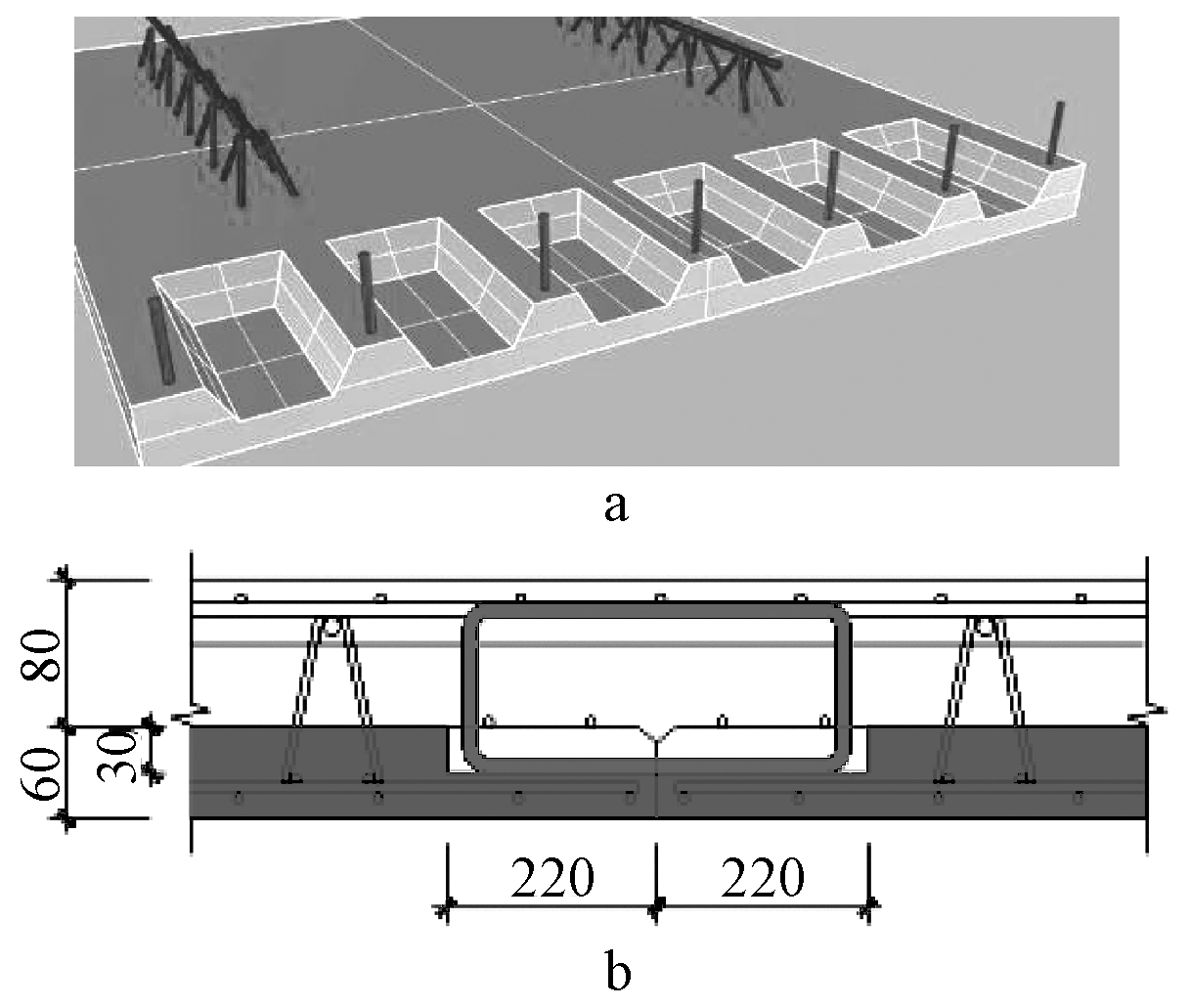
a—凹槽设计; b—封闭环形连接。
图4 密拼叠合楼板新型连接构造
Fig.4 New connection of composite floor slabs without gap
2 静力加载试验
2.1 试件设计及制作
为研究上述密拼连接节点的力学性能,进行相同条件下现浇楼板和密拼叠合板的静力加载试验,试件分组详见表1,装配试件长3 000 mm,宽度为780 mm,钢筋等级HRB400,混凝土强度等级为C30。密拼叠合板的预制底板厚60 mm,现浇层厚80 mm,拼接端设四个凹槽,凹槽长200 mm,宽110 mm,深30 mm,如图5所示。除连接处构造外,现浇试件尺寸及配筋均与装配试件相同。
表1 试验楼板试件参数
Table 1 Parameters of floor slab specimens
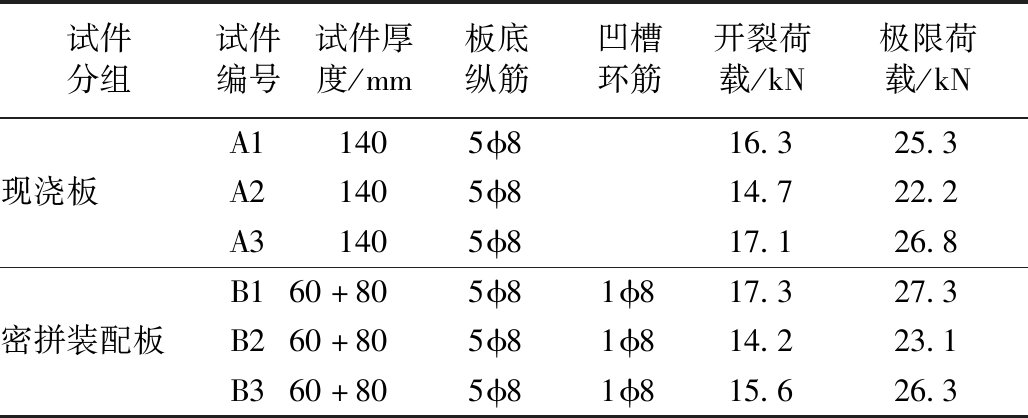
试件分组试件编号试件厚度/mm板底纵筋凹槽环筋开裂荷载/kN极限荷载/kNA11405ϕ816.325.3现浇板A21405ϕ814.722.2A31405ϕ817.126.8B160+805ϕ81ϕ817.327.3密拼装配板B260+805ϕ81ϕ814.223.1B360+805ϕ81ϕ815.626.3

a—试件板条加工; b—连接拼缝。
图5 叠合板加工制作
Fig.5 Manufacturing of composite floor slab
2.2 材料性能
装配试件混凝土分两次浇筑完成,先浇筑预制底板,一周后浇筑上部叠合层。现浇试件在浇筑装配试件叠合层时浇筑。每次浇筑混凝土时预留3个150 mm×150 mm×150 mm的立方体试块,试验进行当天混凝土试块已经养护28 d,实测其抗压强度,得到混凝土立方体抗压强度平均值为35.3 MPa。板内纵筋、搭接钢筋均采用HPB300钢筋,钢筋屈服强度约为350 MPa。
2.3 加载方案及测量
楼板静力加载如图6所示,楼板两端为简支约束,板上设置一分配梁,进行三分点对称加载,以实现跨中纯弯段、板纯弯段长度900 mm。支座和加载位置设置垫块避免局部应力集中。系统实现单调静力加载,荷载传感器控制加载值,百分表位移测点布置于跨中部,试验数据通过计算机全自动采集。
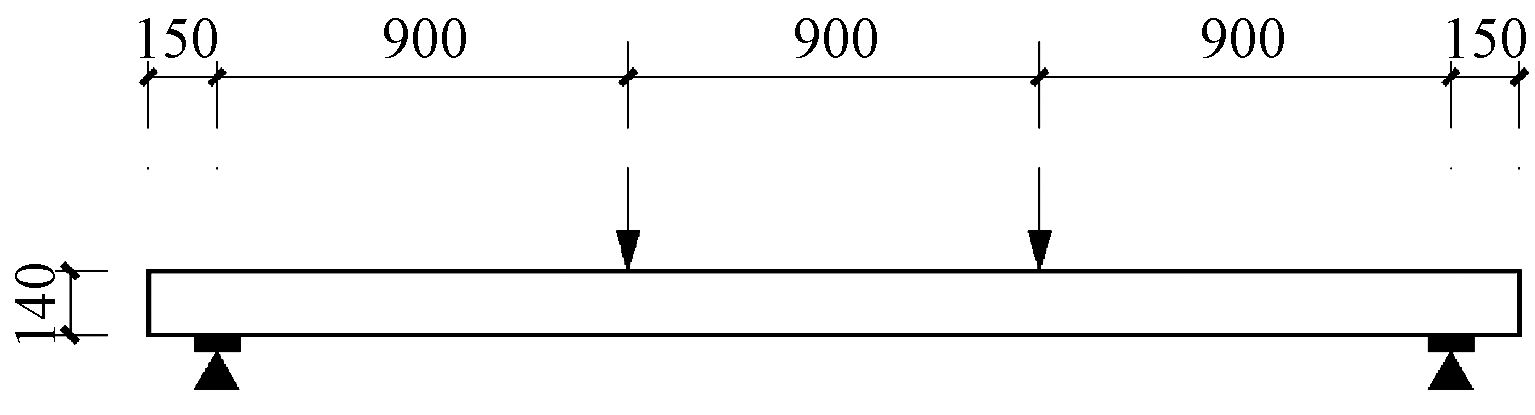
图6 试验加载示意
Fig.6 Test loading diagram
2.4 试验现象
现浇试件在加载至8 kN时,板底部开始出现第1条裂缝;加载至10 kN时,板底部出现第2条裂缝;加载至15 kN时,肉眼能观察到的裂缝已达到5条,且第2条裂缝为主裂缝,已经贯穿整个板底,最大裂缝宽度达到1.5 mm。此时,跨中挠度已达到2 mm。当加载至25 kN时,加载已无法维持,挠度和裂缝宽度不断变大,试件最终丧失承载能力。装配试件的破坏模式基本与现浇试件相同,加载至6 kN时拼缝处被拉开,首先出现肉眼可见细微裂缝;加载至15 kN时,板底陆续出现第2、3条裂缝,但拼缝处的第1条裂缝并未继续开展;加载至23 kN时,肉眼能观察到的裂缝数量已达6条,最大主裂缝并非为拼缝处,而是靠近加荷位置的一条裂缝,最大裂缝宽度为2 mm,此时跨中挠度达到2 mm。当加载至27 kN时,载荷已无法维持,构件挠度和板底裂缝不断变大,试件最终丧失承载能力。楼板的开裂荷载和极限荷载详见表1,板侧和板底裂缝分布情况如图7所示。

a—现浇板; b—装配板; c—现场照片。
图7 裂缝形态
Fig.7 Cracks patterns
3 有限元分析
3.1 模型参数
由上述试验现象可见,在楼板静力加载过程中,随着荷载施加,板底受拉区混凝土开裂,混凝土开裂后刚度迅速退化,拉应力主要由钢筋承担。混凝土开裂刚度退化是一个高度非线性过程,为准确模拟楼板受拉过程中混凝土的非线性,采用ABAQUS通用有限元软件,基于混凝土塑性损伤模型,见图8,对试验楼板混凝土和钢筋精细化分离式建模,进行楼板受荷过程受力变形特性分析。混凝土采用C3D8R实体单元,钢筋采用T3D8杆单元双折线强化模型。
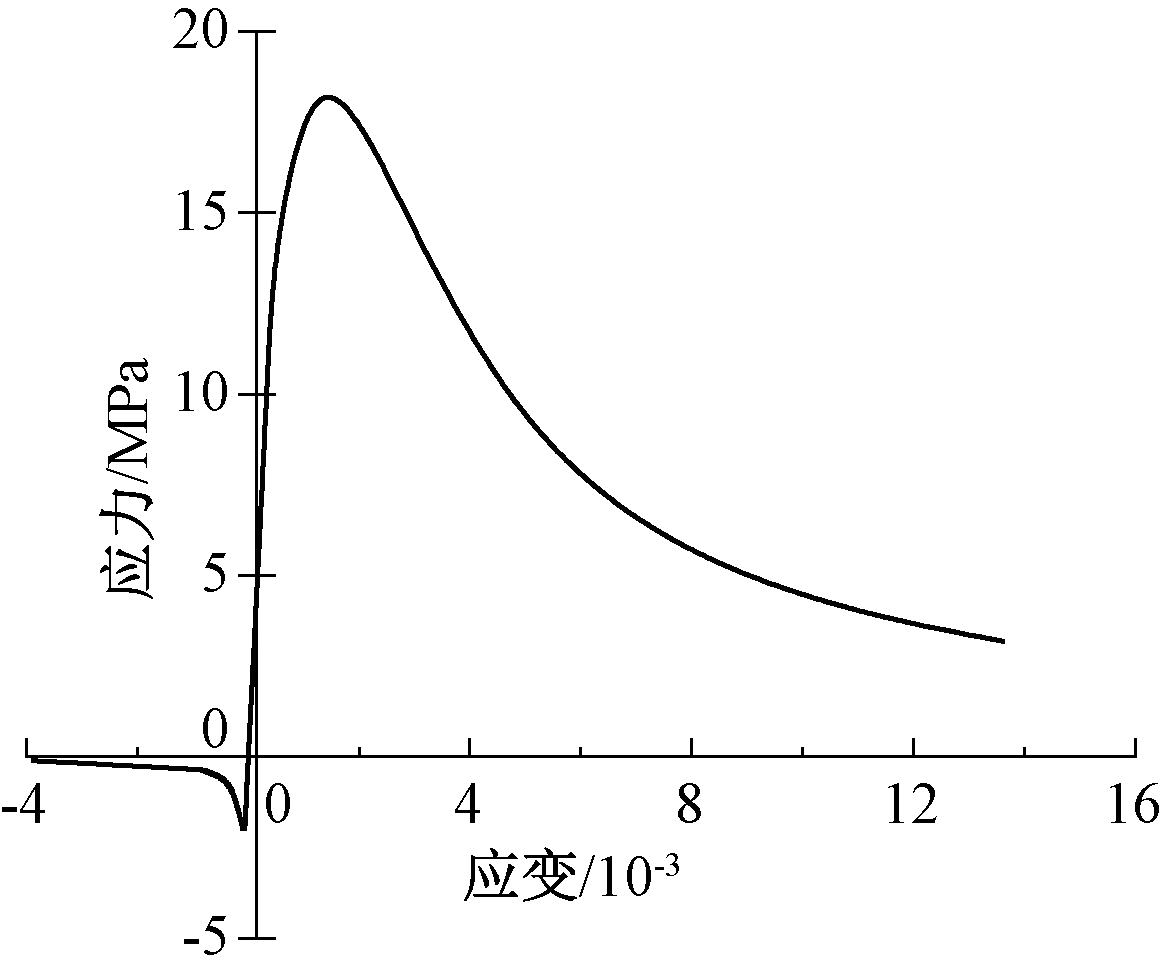
图8 典型混凝土应力-应变关系曲线
Fig.8 Typical stress-strain curve of concrete
混凝土叠合板叠合面抗剪性能通过自然振捣、抹光和拉毛等方式能保证叠合面抗弯和抗剪承载力充分发挥而不发生沿叠合面的剪切破坏;并且混凝土和钢筋具有良好的握裹力,因此混凝土和钢筋采用Embedded接触,假定钢筋与混凝土共同变形,不发生滑移变形,拉裂破坏均发生在混凝土内部。有限元模型荷载施加位置及支座处设置刚性垫块,避免集中力引起应力集中,模型网格尺寸约25 mm,如图9所示。模型左侧支座中心位置约束竖向及水平向位移,右侧支座中心位置仅约束竖向位移,达到简支约束边界条件。
图9 有限元模型示意
Fig.9 Schematic diagram of the finite element model
3.2 承载力与刚度分析
装配叠合板与现浇板的荷载-挠度曲线如图10所示,图中同时给出了有限元数值计算曲线。从图中可以看出:数值计算与试验结果吻合较好。各试件开裂前变形均呈线性,挠度很小且差别不大,开裂后挠度增长趋势有了较明显的差别。有限元加载过程中,当构件挠度为2 mm时,楼板受拉区混凝土开裂,荷载-挠度曲线有较为显著的拐点。荷载达到15 kN附近,各试件曲线斜率开始降低,结合试验现象可知:原因为在此荷载下楼板表面混凝土开裂导致楼板刚度下降。荷载达到25 kN后,各试件位移增长迅速,说明板内钢筋开始进入屈服。从试验曲线可看出,装配试件的初始刚度较现浇试件略大,且开裂荷载也略大于现浇试件,主裂缝并非发生在密拼缝处,从承载力和刚度角度上看可以认为与现浇楼板等同。主要原因在于拼缝处实配钢筋量大于预制板底钢筋,且有效板厚与现浇板基本相同。
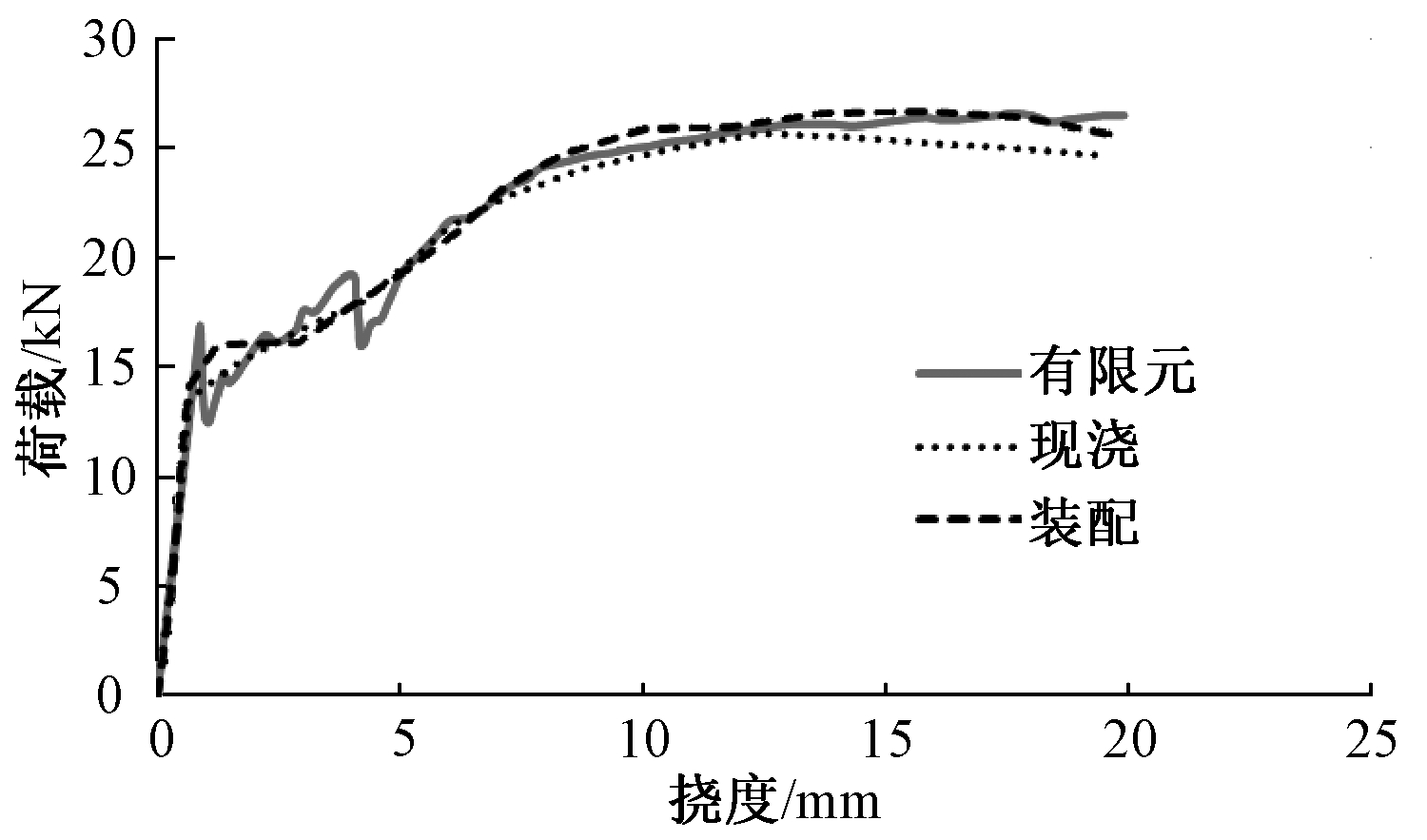
图10 荷载-挠度曲线
Fig.10 The load-deflection curves
3.3 钢筋应力分析
为进一步分析新型连接节点受力过程中混凝土及钢筋的受力变形特性,提取钢筋应力进一步分析。装配式叠合楼板及现浇楼板对应跨中位移20 mm时,楼板受拉区钢筋应力如图11所示。现浇板三分点加载范围对应纯弯段纵向受力钢筋应力较为均匀,纵向钢筋应力已达到屈服强度300 MPa;装配式叠合板在拼缝位置纵向受力钢筋断开, 8根封闭环形搭接钢筋在拼缝处的应力约为160 MPa,预制板内5根受拉钢筋在搭接区域外的应力值已达到屈服强度,拼缝处拉应力通过封闭环形钢筋有效传递至预制板纵向受拉钢筋。
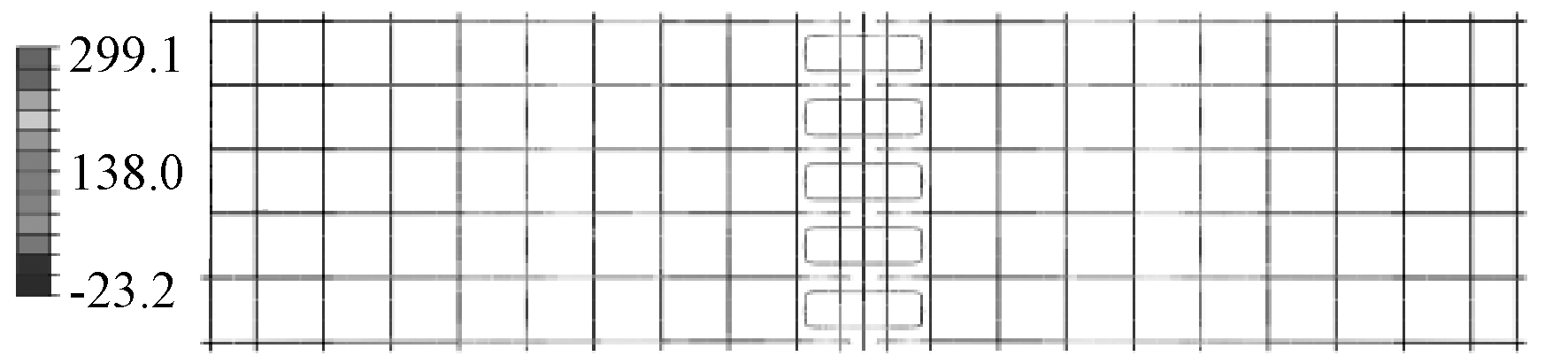
图11 钢筋应力云图 MPa
Fig.11 Reinforcement stress contour
3.4 混凝土应力分析
有限元分析中混凝土采用塑性损伤模型进行模拟,通过混凝土刚度退化来描述混凝土开裂后工作性能。楼板跨中位移发展至20 mm时,装配式叠合板与现浇板受拉区混凝土损伤因子分布如图12所示,三分点加载纯弯段区域混凝土开裂损伤刚度退化显著,损伤因子在0.9以上,表明受拉区混凝土开裂后基本退出工作。装配式叠合板与现浇板的混凝土损伤因子分布基本一致。

a—装配式叠合板; b—现浇板。
图12 混凝土损伤因子分布
Fig.12 Damage factor distribution of concrete
环形搭接钢筋和预制板内纵向钢筋之间的内力依靠图13中阴影部分混凝土的抗剪承载力传递,此部分混凝土的抗剪承载力为:
Fv=nfvA/2
(1)
式中:n为抗剪面数量,此处为8;fv为混凝土抗剪强度,此处取3.55 MPa;A为阴影部分面积,此处为20 000 mm2。
由式(1)计算得核心区混凝土抗剪承载力为284 kN。而5根HPB300钢筋的抗拉承载力为75 kN,远小于混凝土抗剪承载力,因此试件不会发生封闭环形钢筋连接核心区混凝土剪切破坏,故只能在连接区域外发生和现浇楼板相同的钢筋受拉屈服,即该连接节点的承载力大于构件强度。

图13 传力混凝土核心区
Fig.13 Concrete core for transferring load
4 结束语
提出了一种双向受力叠合楼板新型密拼连接技术,通过对不带拼缝的现浇楼板和新型装配楼板试件的静载试验,观察两者从裂缝开始出现到破坏的全过程,并对试件在各级荷载下的挠度、抗弯承载力的变化进行分析,结合数值模拟,得到以下结论:
1)采用在预制底板开槽后放置连接钢筋的措施,有效增加了拼缝部位楼板的有效高度,使得叠合板刚度得到提高,挠度有所减小,达到设计预期。
2)封闭环形连接钢筋有效缩短了开槽长度,同时增强了拼缝处钢筋的配筋率,使得连接部位刚度和强度得以提高,裂缝不再最先出现在拼缝处,且拼缝处也非最终塑性铰位置,实现了等同现浇的初衷。
3)通过有限元数值模拟,进一步揭示了拼缝位置封闭环形钢筋与混凝土的传力机制,新型连接技术通过封闭环形钢筋与预制板内弯折纵筋形成环扣连接,数值计算与试验结果吻合较好,封闭环形钢筋与纵筋的搭接长度显著小于传统的直线钢筋搭接长度。
[1] 颜锋,高杰,田春雨,等.带接缝的混凝土叠合楼板足尺试验研究[J].建筑结构,2016,46(10):56-60.
[2] 叶献国, 华和贵, 徐天爽, 等. 叠合板拼接构造的试验研究[J]. 工业建筑, 2010, 40(1): 59-63.
[3] 刘运林, 丁克伟, 叶献国,等. 叠合板增强型拼缝传力性能的试验研究[J]. 工业建筑, 2014, 44(5): 43-46.
[4] 崔士起, 刘传卿, 刘文政,等. 分离式接缝叠合板垂直接缝方向抗弯刚度的试验及计算方法研究[J]. 建筑结构学报, 2018, 39(9): 75-84.
[5] 蔡斌, 李波, 赵良龙. 钢筋混凝土叠合板受剪承载力可靠度分析[J]. 混凝土, 2017, 337(11): 166-172.
[6] 中华人民共和国住房和城乡建设部.装配式混凝土结构技术规程: JGJ 1—2014[S]. 北京: 中国建筑工业出版社, 2014.
[7] 中华人民共和国住房和城乡建设部.装配式混凝土结构连接节点构造: G310-1~2[S]. 北京: 中国计划出版社, 2015.
[8] 翟伟, 张伟林, 沈小璞. 拼接叠合楼板抗弯性能研究[J]. 安徽建筑大学学报, 2015, 23(1): 6-12.
[9] 王宏. 叠合式楼板钢筋应变的试验研究与分析[D].合肥:安徽建筑大学,2014.
[10] 姜海锋. 叠合式双向板抗裂性的试验[D]. 合肥: 安徽建筑大学, 2014: 26-27.
[11] 钱永梅, 邹超英, 尹新生.混凝土单向薄板叠合矩形板的双向受力效应试验研究[J]. 哈尔滨建筑大学学报, 2002, 35(3): 30-34.
[12] 钱永梅, 邹超英, 尹新生. 混凝土单向薄板叠合成矩形板的双向受力性能分析[J]. 哈尔滨建筑大学学报, 2002, 35 (1): 38-42.
[13] YE X G, YANG K N, CHONG X. Experimental Study on Properties of Side Joint Between Superimposed Slabs with Lattice Steel Bars[J]. Advanced Materials Research, 2014, 638: 109-114.
[14] JEONG Y J. Simplified Model to Predictpartial Interactive Structural Performance of Steel-Concrete Composite Slabs[J]. Journal of Construction Research, 2007, 64(2): 238-246.
[15] 恽燕春, 陈鹏, 王柏生, 等. 密拼叠合楼板受力性能研究[J].施工技术, 2018, 47(12): 75-79.