0 前 言
碳纤维增强复材(CFRP)具有轻质、高强、耐腐蚀性等优点,近年来CFRP加固技术在工程中得到了越来越广泛的应用。经CFRP加固后构件的承载力、刚度、抗疲劳性能等均得到了明显的提高,但通过粘贴普通的无预应力CFRP材料加固存在材料强度利用率低、加固后构件的正常使用状态性能改善小等弊端[1-3]。而采用预应力CFRP加固后的构件的承载能力、抗裂度、刚度、疲劳性能以及材料的利用率得到了明显提高;但加固后的构件延性明显降低,构件破坏形式发生改变,主要为混凝土压碎破坏、CFRP与构件之间的黏结滑移破坏以及CFRP被拉断等形式[4-9]。上述破坏形式在破坏前均无承载力迅速降低的明显征兆,属于脆性破坏。这就使得预应力CFRP加固在推广应用上受到了限制。
针对以上问题,课题组提出基于预警理论的预应力CFRP加固抗弯构件的设计方法[10],其设计理念为:对加固构件附加构件预警保险丝,在设计中保险丝的断裂点根据正常使用阶段构件的安全储备的最大值即为正常使用阶段的最大承载力确定,并通过控制保险丝的张拉控制应力,使得当构件的安全储备指标低于设计目标值时保险丝达到其抗拉强度极限点(断裂),发出明显的预警信号,方便工程维护人员及时发现并采取对策。该设计方法将加固材料分为预警部分和承载部分,均使用CFRP板材料,预警部分的CFRP即为保险丝。CFRP板在梁底的布置情况如图1所示,根据对预警部分和承载部分的CFRP板的面积和初始预应力进行分配,使得当荷载达到构件的预警点时保险丝断裂并与梁体发生剥离而发出预警信号,并且保证在保险丝断裂后构件通过部分CFRP板可以继续承载。
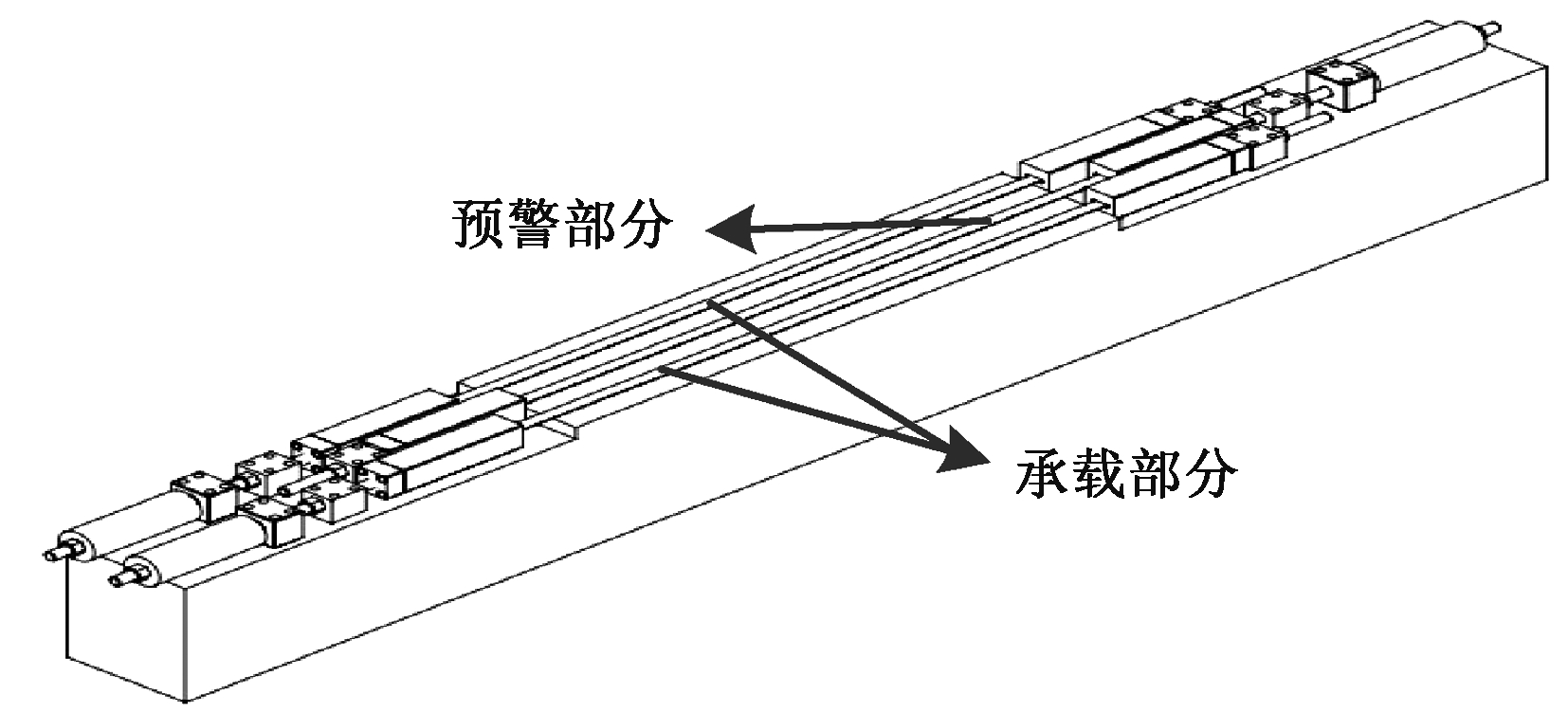
图1 梁底CFRP板分布示意
Fig.1 Schematic diagram of CFRP sheet distribution at the bottom of beam
1 试验研究
1.1 试件制作
为验证该方法的可行性与正确性,设计了4根矩形截面的混凝土梁,试件设计参数如表1所示,LA-0为未加固对比梁,LA-1、LA-2、LA-3为加固梁。试件截面尺寸为200 mm×300 mm,全长2 300 mm,净跨2 100 mm。弯剪段和纯弯段长度均为700 mm,底部受拉纵筋和上部架立筋均采用HRB400级钢筋2 16,配筋率为0.335%;箍筋采用HRB335级钢筋
16,配筋率为0.335%;箍筋采用HRB335级钢筋![]() 10@150 mm,保险丝面积为12 mm2,试件具体几何尺寸及配筋如图2所示。
10@150 mm,保险丝面积为12 mm2,试件具体几何尺寸及配筋如图2所示。
表1 试件设计参数
Table 1 Specimen design parameters
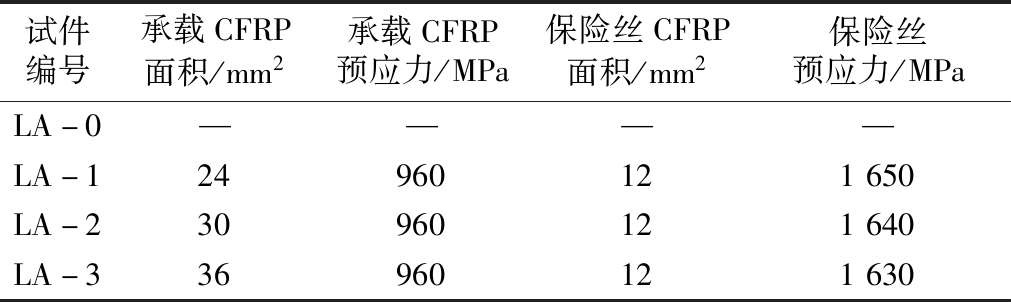
试件编号承载CFRP面积/mm2承载CFRP预应力/MPa保险丝CFRP面积/mm2保险丝预应力/MPaLA-0————LA-124960121650LA-230960121640LA-336960121630
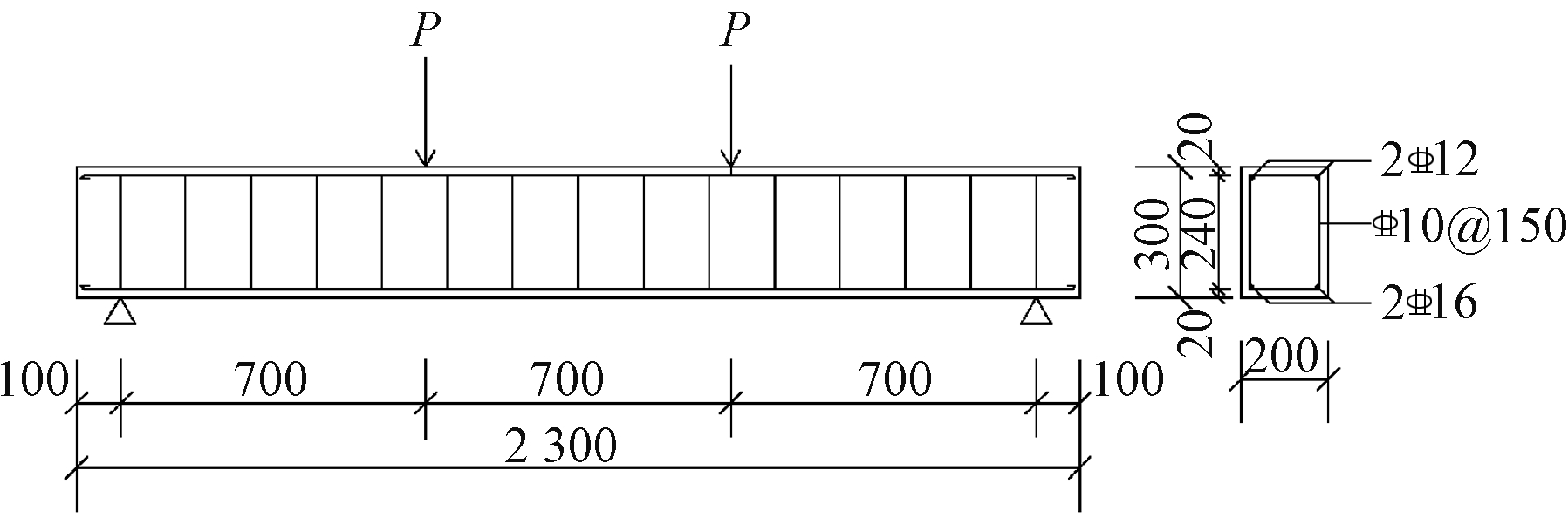
图2 试件配筋mm
Fig.2 Reinforcement of specimen
1.2 材料性能
试验混凝土强度等级为C50,实测立方体抗压强度为50.1 MPa。受拉筋实测屈服强度为430 MPa,抗拉强度为586 MPa。CFRP板力学性能见表2。
表2 CFRP板材料的力学性能
Table 2 Mechanical properties of CFRP sheet material

检测项目抗拉强度标准值/MPa受拉弹性模量/GPa伸长率/%层间剪切强度/MPa标准要求条形板强度Ⅰ级≥2400≥160≥1.6≥50检验结果24181691.6861
1.3 施工工艺及测点布置
该加固设计方法与传统的预应力CFRP加固方法在施工阶段并没有太大的差别,即通过打孔植筋、锚具安装、CFRP板张拉、涂抹胶层以及胶层养护等步骤来完成,保险丝的断裂点通过计算后由施加预应力大小来控制。
为测量构件的承载力、裂缝、挠度等,分别在混凝土、钢筋、碳纤维板上粘贴电阻应变片,在试件的跨中、加载点以及支座处均布置位移计以测量梁体变形和支座沉降。具体的测点布置如图3所示。

图3 测点布置 mm
Fig.3 Arrangement of measuring points
1.4 试验分析
1.4.1 试验现象
所有试验梁在试验前期均经历了弹性阶段及带裂缝工作阶段,由于预应力碳纤维板的存在,故3根加固梁的开裂荷载均有明显的提高,开裂后裂缝发展的速度,裂缝的宽度、高度均有下降;当荷载达到保险丝断裂点时,保险丝发生断裂,发出明显的断裂声,与梁底发生剥离垂落,如图4所示。

图4 保险丝断裂发出预警信号
Fig.4 Fuse fracture warning signal
保险丝断裂后退出工作,将荷载卸载到钢筋以及碳纤维板上,承载力仍可继续提升。继续增加荷载,裂缝宽度继续增大,高度不再增加,承载部分的碳纤维板被拉断并发出巨大声响,梁顶混凝土被压碎、梁体挠度迅速增大,承载能力迅速降低,试件破坏。
1.4.2 试验结果分析
试验结果如表3所示,由表3可以看出与未加固梁相比较,加固梁的特征承载力明显提高了,但相应的挠度明显减小,延性系数降低明显,不能满足文献[11]中规定延性系数μ不小于3.0的要求。
表3 试验结果
Table 3 Test results
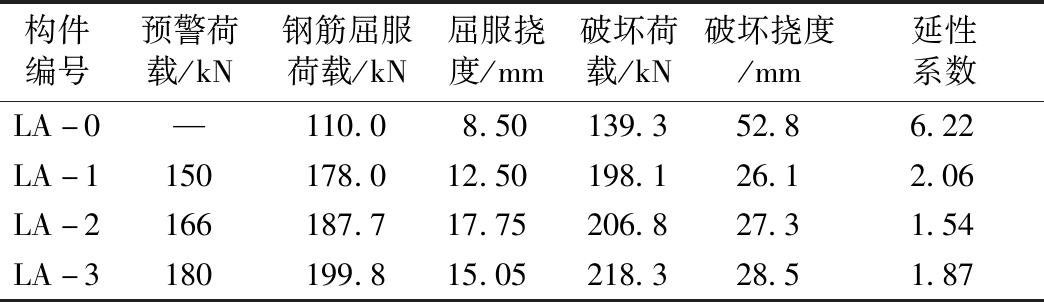
构件编号预警荷载/kN钢筋屈服荷载/kN屈服挠度/mm破坏荷载/kN破坏挠度/mm延性系数LA-0—110.08.50139.352.86.22LA-1150178.012.50198.126.12.06LA-2166187.717.75206.827.31.54LA-3180199.815.05218.328.51.87
尽管加固后构件的承载力有很大幅度的提升,但是由于不能满足传统的钢筋混凝土结构或钢结构在设计中的延性要求,严重影响其工程应用。
2 安全储备指标分析
实际上结构或构件的安全储备是指从设计状态点到极限破坏状态的承载力和变形两个方面的“安全富余程度”。由于传统的钢筋混凝土结构或钢结构在屈服后承载力增长很少,所以在屈服后仅仅考虑变形延性;但是采用高强弹性材料进行加固的构件在钢筋屈服后承载力还有较大地增长,仅仅因为其变形延性系数低就认为其安全储备不足是不全面的。
2.1 安全储备组成
如图5所示,安全储备由基本安全储备和附加安全储备两部分组成,基本安全储备是针对可预见性荷载以及材料的变异性提供的安全储备,即保证结构构件在正常使用阶段的受力不超过屈服荷载。附加安全储备是针对超出预见或不可预见的偶然荷载,即结构构件在屈服后应该具备的必要的附加安全储备[12]。
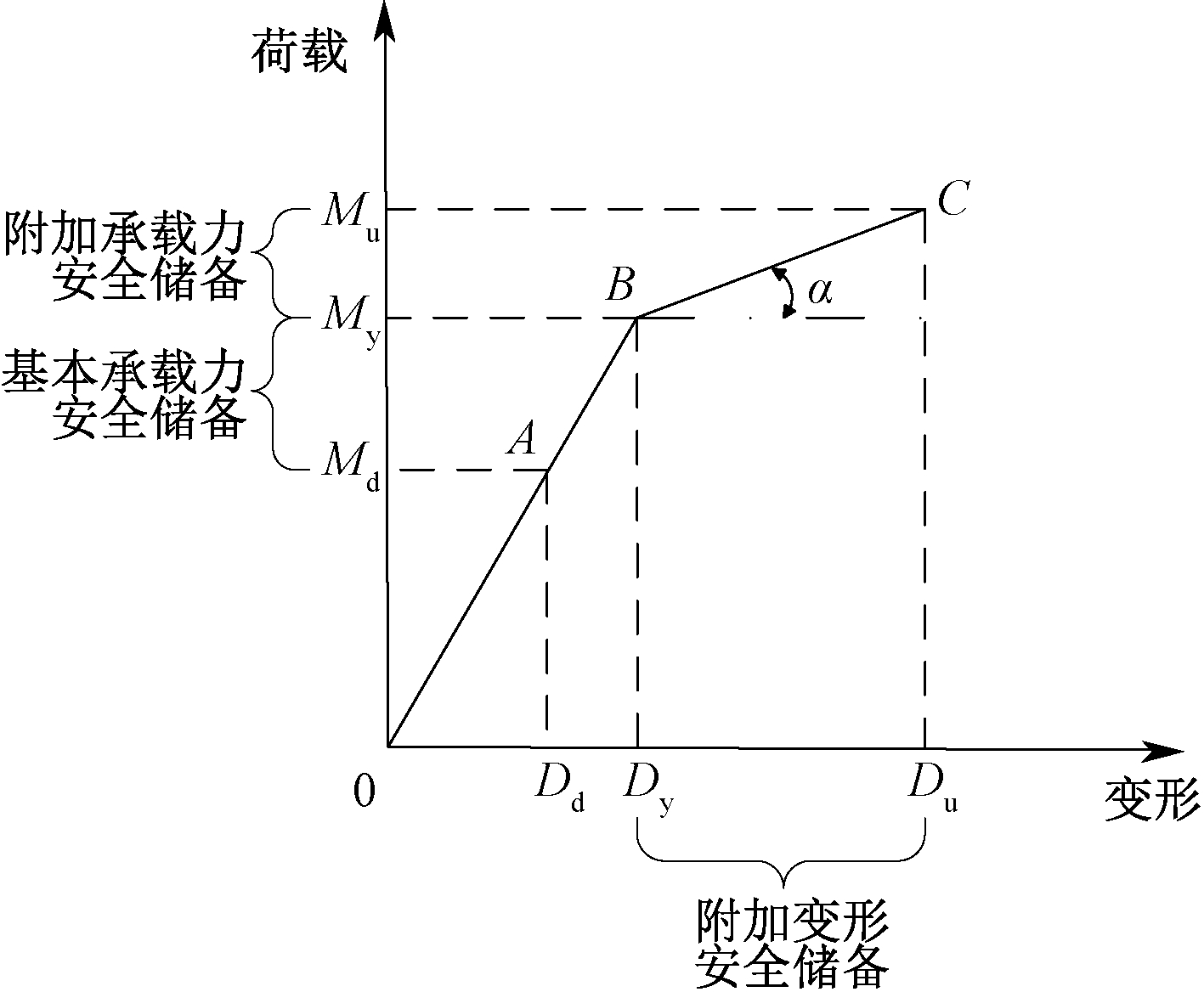
图5 安全储备组成
Fig.5 Safety reserve composition
本文提出的加固设计理论安全储备组成如图6所示。其中D点为设计的保险丝断裂预警点。合理选择构件的预警点,可以使加固构件的基本安全储备指标和附加安全储备指标均符合相应的要求。
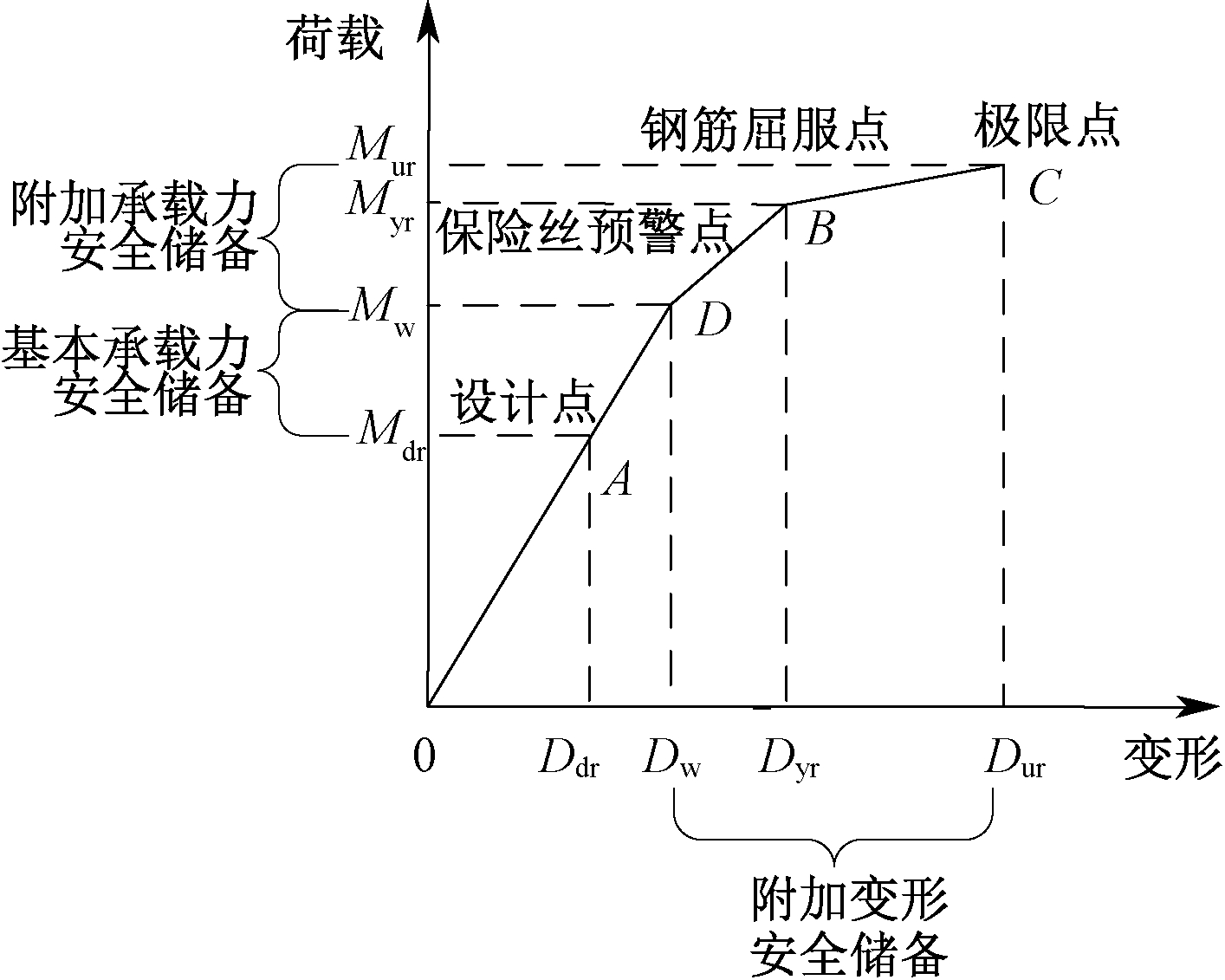
图6 附加预警保险丝的强化弹塑性模型安全储备
Fig.6 Safety reserve of the enhanced elastoplastic model with additional warning fuse
2.2 延性评价指标
由于延性系数已经不能全面地评价不同受力特征的结构构件的安全储备,所以本文采用的安全储备指标评价系数为叶列平等[12]提出的基本安全储备指标K0和等效安全储备指标Keq,其满足结构构件安全储备的取值范围为:K0≥1.5,Keq≥2.1。
K0=Fy/Fd
(1a)
(1b)
式中:KE和KD分别为变形能力储存指标和变形能储存指标;Fy和Fd分别为屈服承载力和设计承载力。
3 构件屈服点的定义方法
随着新材料的出现与应用,传统方法确定构件屈服点已不再适用,而屈服点是工程结构设计及安全储备指标的重要参考点。准确的屈服点是安全储备评价的前提,现阶段对于构件屈服点的定义尚没有一个统一的方法,国内外学者提出了各自的方法[13-15],主要有传统定义方法、作图法、最远法。
为确定基于预警理论的加固构件合理准确的屈服点,准确评价加固构件的安全储备,验证加固后构件的安全储备并不会降低,故在试验基础上利用以上方法做了讨论分析,并对加固构件的屈服点做出了合理定义。
3.1 传统方法
传统方法通常以主要材料的屈服点定义为构件的屈服点。各试件的荷载-挠度曲线以及钢筋屈服点如图7所示。
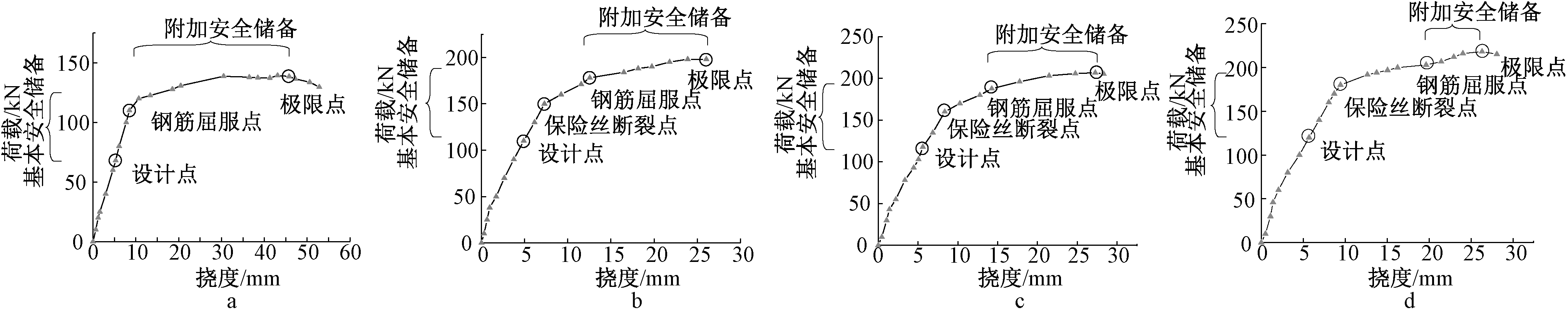
a—LA0; b—LA1; c—LA2; d—LA3。
图7 传统定义构件屈服点
Fig.7 Traditionally defined component yield points
为了评价传统方法定义构件屈服点是否合理,采用的安全储备评价指标为K0、Keq。在试验的基础上计算每根梁的K0、Keq,结果见表4。
表4 构件安全储备评价指标(传统方法)
Table 4 Evaluation indexes of component safety reserve(traditional method)
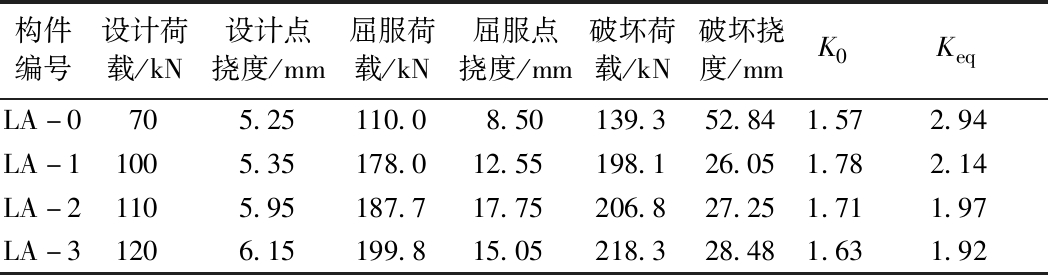
构件编号设计荷载/kN设计点挠度/mm屈服荷载/kN屈服点挠度/mm破坏荷载/kN破坏挠度/mmK0KeqLA-0705.25110.08.50139.352.841.572.94LA-11005.35178.012.55198.126.051.782.14LA-21105.95187.717.75206.827.251.711.97LA-31206.15199.815.05218.328.481.631.92
由表4可以分析:对于4根试验梁通过传统方法确定的构件屈服点经过计算,其K0为1.57、1.78、1.71、1.63,均能满足正常使用阶段对于构件安全储备的需求。未加固梁LA-0的Keq为2.94,满足要求。但是3根加固梁中只有LA-1满足要求,LA-2、LA-3的等效安全储备指标Keq均不足2.1,不满足工程要求。
出现这种情况的原因即构件的屈服点定义不准确,正常使用阶段的安全储备明显增大,但附加安全储备却明显降低。传统的定义方法不再适用。
3.2 作图法
本文选用的作图[16]法为现阶段使用最多的一种方法,图8为利用作图法确定的构件屈服点,其过程为:过荷载-挠度曲线原点做曲线切线OA,过峰值点E做水平线AE,两条直线相较于点A,过A点做X轴的垂线AB与曲线相交于点B,连接OB并延长与水平线相交于点C,过点C做X轴的垂线与曲线相交于D,交点D即定义为作图法确定的构件的屈服点。
利用作图法确定构件屈服点后,根据确定的构件屈服点的荷载以及挠度值,计算了各个试验梁的K0、Keq,结果见表5。
表5 构件安全储备评价指标(作图法)
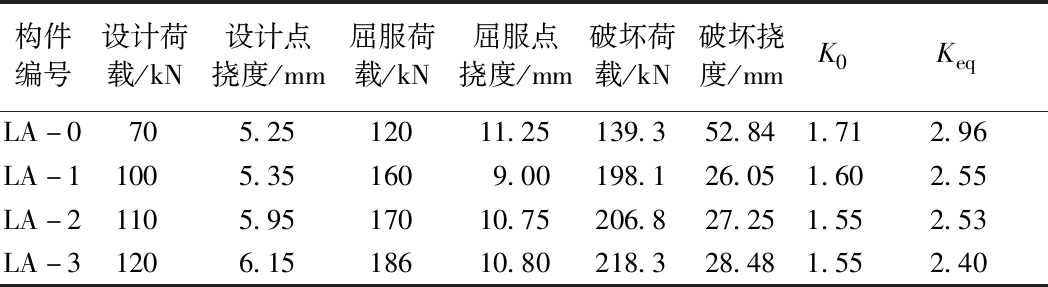
Table 5 Evaluation indexes of component safety reserve(graphic method)
构件编号设计荷载/kN设计点挠度/mm屈服荷载/kN屈服点挠度/mm破坏荷载/kN破坏挠度/mmK0KeqLA-0705.2512011.25139.352.841.712.96LA-11005.351609.00198.126.051.602.55LA-21105.9517010.75206.827.251.552.53LA-31206.1518610.80218.328.481.552.40
由上表可以分析,4根试验梁的K0为1.71、1.60、1.55、1.55,均能满足正常使用阶段对于构件安全储备的需求,Keq为2.96、2.55、2.53、2.40,均能满足承载力极限状态对构件安全储备的需求。
综上分析,利用作图法确定的构件屈服点经计算其K0、Keq均满足要求,说明通过作图法确定构件屈服点的方法与传统方法相比较更为合理。但该方法对于初始刚度依赖性较大,所以利用作图法确定构件屈服点对荷载-变形曲线的准确性有较高的要求,初始刚度的较小差别会造成屈服点较大误差。
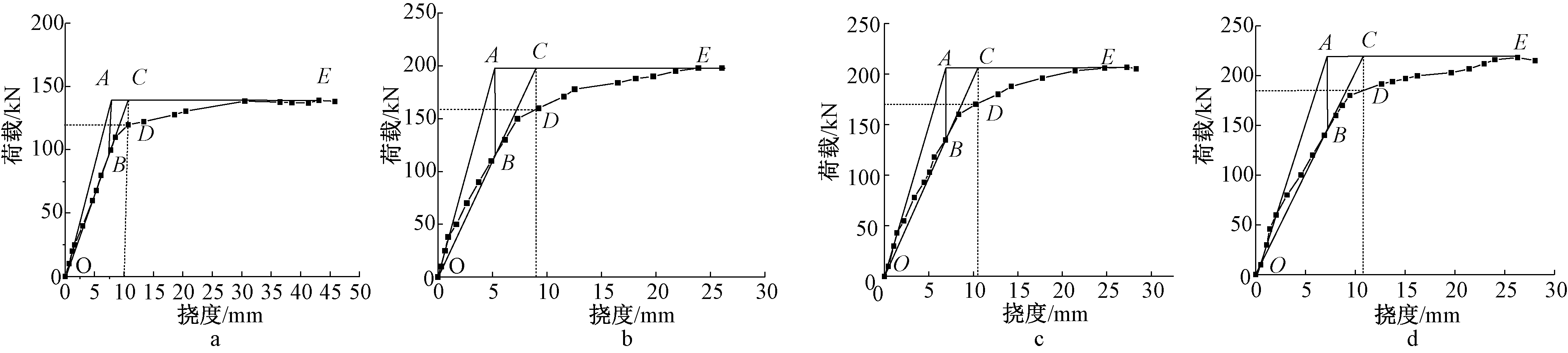
a—LA0; b—LA1; c—LA2; d—LA3。
图8 作图法定义构件屈服点
Fig.8 Graphic method for defining the yield points of components
3.3 最远法
最早提出最远法[17]的是冯鹏,在荷载-挠度曲线上找到距离原点和峰值点最远的点即为构件屈服点。图9为最远法定义构件屈服点示意,其过程为:在荷载-挠度曲线上以原点和峰值点的连线为基线,做该基线的平行线并与曲线相切,切点即为构件屈服点,但要求两条平行线之间的距离不能太小,当有多个切点时以最大值点为构件屈服点。
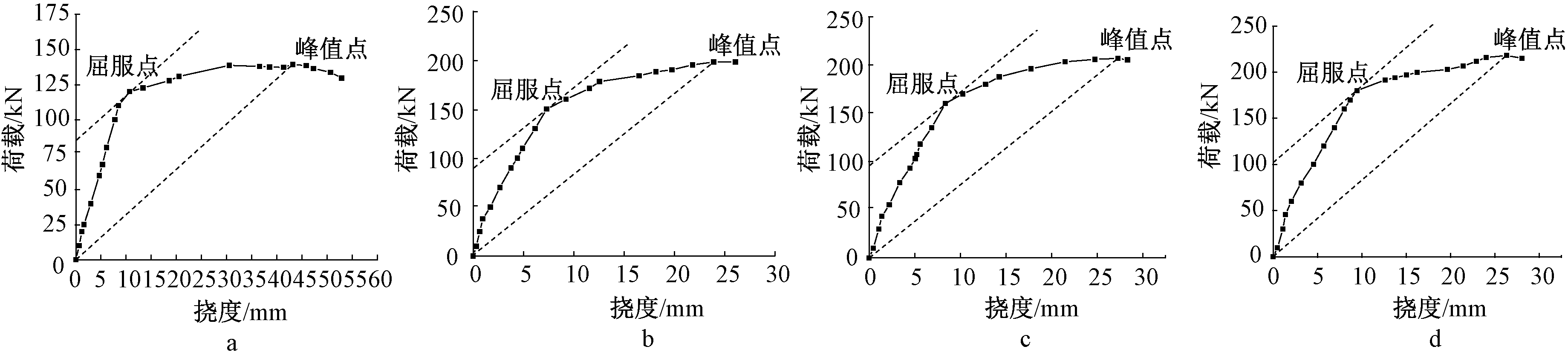
a—LA-0; b—LA-1; c—LA-2; d—LA-3。
图9 最远法定义构件屈服点
Fig.9 Farthest law for defineing component yield points
利用最远法确定了构件屈服点,根据确定的构件屈服点的荷载值以及挠度值,计算了各个试验梁的K0、Keq,结果见表6。
表6 构件安全储备评价指标(最远法)
Table 6 Evaluation indexes of component safety reserve(farthest method)
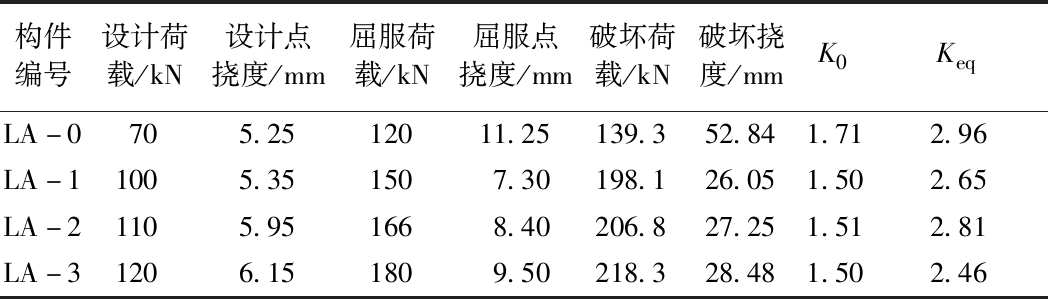
构件编号设计荷载/kN设计点挠度/mm屈服荷载/kN屈服点挠度/mm破坏荷载/kN破坏挠度/mmK0KeqLA-0705.2512011.25139.352.841.712.96LA-11005.351507.30198.126.051.502.65LA-21105.951668.40206.827.251.512.81LA-31206.151809.50218.328.481.502.46
由上表可以分析,对于四根试验梁的K0为1.71、1.50、1.51、1.50,均能满足正常使用阶段对构件安全储备的需求。等效安全储备指标值Keq为2.96、2.65、2.81、2.46,均能满足承载力极限状态对构件安全储备的需求。
综上分析,利用最远法确定的构件屈服点经计算其K0、Keq均满足要求,说明通过最远法确定构件屈服点的方法与传统方法相比较更为合理。
3.4 预警理论抗弯加固构件屈服点定义
为准确定义基于预警理论的抗弯加固构件屈服点,将以上3种方法确定的构件屈服点与预警点做对比,结果见表7。
表7 构件屈服点
Table 7 Component yield points kN

构件编号传统方法作图法最远法预警点LA-0110.0120120—LA-1178.0160150150LA-2187.7170166166LA-3199.8186180180
由表7分析可得,利用作图法确定的构件屈服点与预警点有较小的差别,但与最远法确定的构件屈服点相吻,这是由于在保险丝断裂后,构件承载力的提高程度以及刚度有所下降,构件的荷载-挠度曲线有明显的转折点,导致了预警点为距离原点与峰值点连线的最远点,即为最远点确定的构件的屈服点。故将基于预警理论的预应力CFRP加固的预警点定义为构件的屈服点。
预警点对于加固构件具有明显的物理意义,即弹性与塑性的分界点。预警点即为人为设定的构件正常使用的上限,在偶然荷载或罕遇荷载情况下构件的承载力以及变形安全储备能够满足构件安全性的要求。
对预应力CFRP加固构件增设预警点后能够解决加固构件破坏前无明显预兆问题,重新定义构件屈服点后以K0、Keq代替传统的延性系数来评价构件的安全储备更加准确,且经过加固后构件的挠度、裂缝的宽度以及碳纤维板的耐腐蚀性均能够满足工程上对于构件适用性以及耐久性的使用要求,这将有助于预应力CFRP在加固领域的推广与应用。
4 结束语
通过试验与理论分析,可以得到以下结论:
1)针对于预应力CFRP板加固后构件破坏形式发生改变,破坏前无明显预兆,提出了基于预警理论的预应力CFRP加固设计方法,该方法可在安全储备低于设计值时通过保险丝的断裂发出预警信号。
2)针对延性系数不能准确评价安全储备的问题,建议了用基本承载力安全储备指标K0、等效安全储备指标Keq代替延性系数,且在该评价指标的计算下,本文提出的加固设计方法的安全储备均满足要求。
3)通过作图法与最远法确定加固构件的屈服点即为预警点,经K0、Keq评价后加固构件安全储备满足要求。
[1] KOJIMA T, TAKAGI N, HAMADA Y, et al. Flexural Strengthening of Bridge by Using Tensioned Carbon Fiber Reinforced Polymer Plate[C]//Proceedings of the International Conference on FRP Composite in Civil Engineering. HongKong: 2001:1077-1084.
[2] 周仕刚,高永飞.CFRP加固初始受载钢筋砼梁弯曲性能的试验研究[J].玻璃钢/复合材料,2003(1):3-6.
[3] 贺学军,周朝阳,徐玲.内嵌CFRP板条加固混凝土梁的抗弯性能试验研究[J].土木工程学报,2008(12):14-20.
[4] ALI A, ABDALLA J, HAWILEH R, et al. CFRP Mechanical Anchorage for Externally Strengthened RC Beams Under Flexure [J]. Physics Procedia, 2014, 55(55):10-16.
[5] HEFFERMAN P J, ERKI M A. Fatigue Behavior of Reinforced Concrete Beams Strengthened with Carbon Fiber Reinforced Plastic Laminates[J]. Journal of Composites for Constructions,ASCE,2004,8(2):132-140
[6] 肖凯东,沈兆坤,李典豪.预应力CFRP板加固技术在桥梁工程中的应用[J].公路交通科技(应用技术版),2015,11(7):17-19.
[7] 彭晖,尚守平,金勇俊,等.预应力碳纤维板加固受弯构件的试验研究[J].工程力学,2008(5):142-151.
[8] 郭蓉,杜力峰,郭娇,等.碳纤维板加固钢筋混凝土梁的受弯性能[J].土木建筑与环境工程,2017,39(6):61-67.
[9] 郭蓉,彭志会,郭娇,等.有黏结预应力CFRP板加固RC梁抗弯疲劳试验与理论分析[J].公路交通科技,2018,35(7):50-57,85.
[10] 郭蓉, 王明浩, 彭志会,等. 基于预警丝理念的预应力CFRP抗弯加固设计部分[J].玻璃钢/复合材料,2019(11):18-23.
[11] 沈蒲生. 高层建筑结构疑难释义[M].北京:中国建筑工业出版社, 2011
[12] 叶列平,冯鹏,林旭川,等.配置FRP的结构构件的安全储备指标及分析[J].土木工程学报,2009,42(9):21-31.
[13] PARK R. State of the Art Report Ductility Evaluation from Laboratory and Analytical Testing[C]∥Proceedings of Ninth World Conference on Earthquake Engineering. Tokyo, Kyoto, Japan: 1988: 605-616.
[14] CEN. Eurocode: Design of Steel Structures: Part 1-8[S]. Brussels: European Committee for Standardization, 2002.
[15] HUANG M S, LIU Y H, SHENG D C. Simulation of Yielding and Stress-Stain Behavior of Shanghai Soft Clay[J]. Computers and Geotechnics, 2011, 38(3): 341-353.
[16] 过镇海, 时旭东. 钢筋混凝土原理和分析[M]. 北京:清华大学出版社, 2003.
[17] 冯鹏,强翰霖,叶列平.材料、构件、结构的“屈服点”定义与讨论[J].工程力学,2017,34(3):36-46.