20世纪90年代初， Li教授团队基于对合成纤维与水泥基材料的相互作用机理研究，建立了纤维增强水泥基复合材料的微观断裂力学模型[1]，从理论上探索出了具有应变硬化特性的纤维增强水泥基复合材料的设计方法，并在实验室成功研制出了该类材料[2]，将其命名为工程水泥基复合材料(Engineered Cementitious Composite，简称ECC)。我国新制定的建材行业标准JC/T 2461—2018《高延性纤维增强水泥基复合材料力学性能试验方法》根据该材料的组成和特性，将其命名为高延性纤维增强水泥基复合材料[3]。ECC是以纤维作为增强增韧组分，以水泥、矿物掺料、超细骨料和外加剂为基体原材料，经加水搅拌、成型、养护制得的一种复合材料。其最大的特点是在拉伸荷载下呈现出应变硬化和多缝开裂的延性特征(图1)，极限延伸率高达1%～7%，而普通混凝土的延伸率仅为0.01%～0.03%。
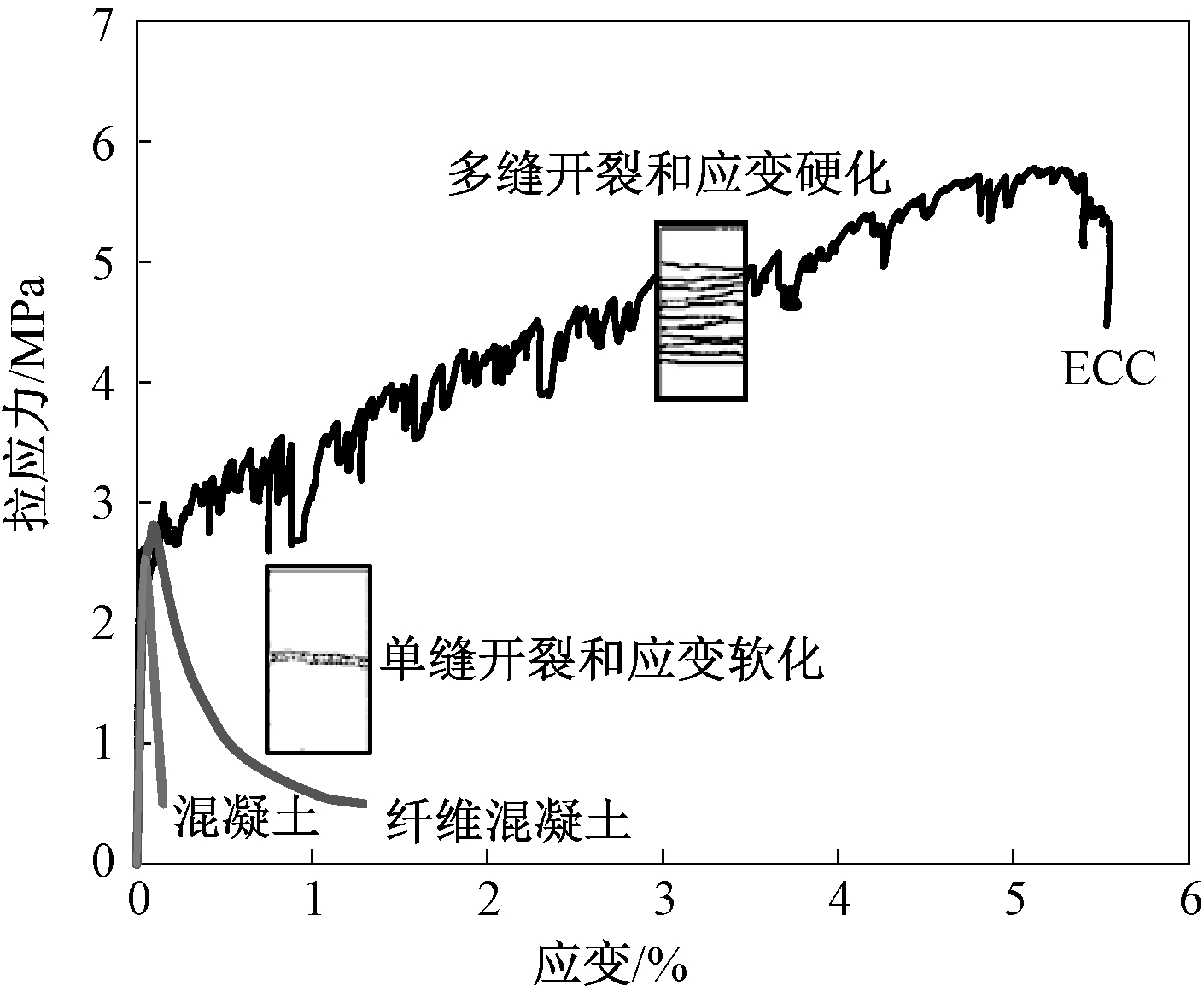
图1 普通混凝土、纤维混凝土和ECC的拉伸应力-应变曲线
Fig.1 Tensile stress versus strain curves of ordinary concrete, fiber reinforced concrete and ECC
美国密歇根大学[4-5]、新加坡国立大学[6-7]、德国德累斯顿工业大学[8]和澳大利亚国防学院[9]的科研人员研究发现:ECC抗冲击性能明显优于普通混凝土和纤维混凝土。在落锤冲击试验中，ECC板迎击面的侵彻深度远远小于钢筋混凝土板和钢纤维混凝土板[6]。此外，普通钢筋混凝土板在2次冲击后，底面混凝土严重破坏，部分保护层剥离；而ECC板在经受20次冲击后，底面仅呈现出多而细密的裂缝，ECC板相对完好，未破坏[7]。
现有的ECC主要以聚乙烯(PE)纤维[10]、聚乙烯醇(PVA)纤维[11-14]和聚丙烯(PP)纤维[15]等合成纤维为增强增韧组分，这些合成纤维耐高温性能差。为解决ECC高温延性失效问题，需使用耐高温性能优异的纤维(如玄武岩纤维)作为增强增韧材料，宋嵩[16]将玄武岩纤维添加到水泥基材料中，通过一定配比并进行静态力学性能试验，得到其呈现多缝开裂、拉伸应变硬化、极限拉伸应变大于0.5%等特征的玄武岩纤维增强高延性水泥基复合材料。本研究在其静态力学研究的基础上，利用φ50 mm变截面SHPB试验装置对不同玄武岩纤维掺量的BFRCC进行动态冲击压缩试验，获取其动力性能，为其在抗爆抗冲击领域的应用垫定理论基础。
1 试验材料及方法
1.1 试验原材料及配合比
试验原材料包括鸭牌铝酸盐水泥(CAC)、硅灰(SF)、粉煤灰(FA)、山西晋投玄武岩纤维、聚羧酸减水剂和水。水泥、粉煤灰和硅灰的化学成分如表1所示；玄武岩纤维性能参数如表2所示。
表1 主要原材料化学成分(质量)
Table 1 Chemical constituents of CAC,FA and SF %
成分二氧化硅氧化铝氧化铁氧化钙氧化镁三氧化硫烧失量铝酸盐水泥7.9550.332.3832.62.03—0.57粉煤灰48.6337.373.783.051.6084.003.61硅灰87.281.090.750.871.761.474.74
表2 玄武岩纤维性能参数
Table 2 Properties of basalt fibers
密度/(g·cm-3)抗拉强度/MPa弹性模量/GPa断裂伸长率/%长度/mm直径/μm2.695223085.82.851214.1
试验材料配合比如表3所示。试件制作时，将全部胶凝材料(CAC、SF、FA)混合均匀倒入搅拌锅中，加入减水剂、水，低速搅拌1 min，高速搅拌2 min，使浆体流动度达到要求。然后均匀加入玄武岩纤维，搅拌2 min，将浆体倒入模具。待浆体倒入模具后，将模具放到振动台振动2 min振实抹平。每组配合比制作成尺寸为100 mm×40 mm×40 mm的试样，24 h后拆模，进行标准养护28 d，取出试样采取钻芯取样法，将试样做成φ50 mm×25 mm的适用于SHPB试验的试样，并磨平处理，两端面平行度不大于0.05 mm。
表3 材料配合比
Table 3 Material mix proportion
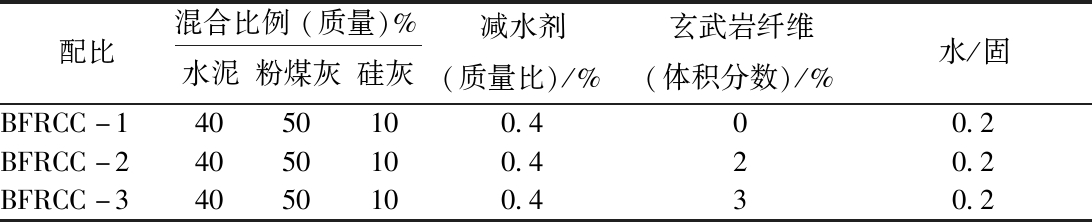
配比混合比例(质量)%水泥粉煤灰硅灰减水剂(质量比)/%玄武岩纤维(体积分数)/%水/固BFRCC-14050100.400.2BFRCC-24050100.420.2BFRCC-34050100.430.2
1.2 SHPB试验
采用φ50 mm直锥变截面SHPB试验装置，其试验原理如图2所示。对3种不同纤维掺量的试样每种进行4个应变率的冲击压缩试验，通过调节弹速和波形整形器控制入射波来实现不同应变率(表4)的加载，图3为同一类型试样在4个应变率下的典型的入射波、反射波和透射波。
图2 直锥变截面SHPB装置
Fig.2 SHPB device with straight cone and variable cross section
表4 不同试验应变率设置
Table 4 Strain rate settings for different tests
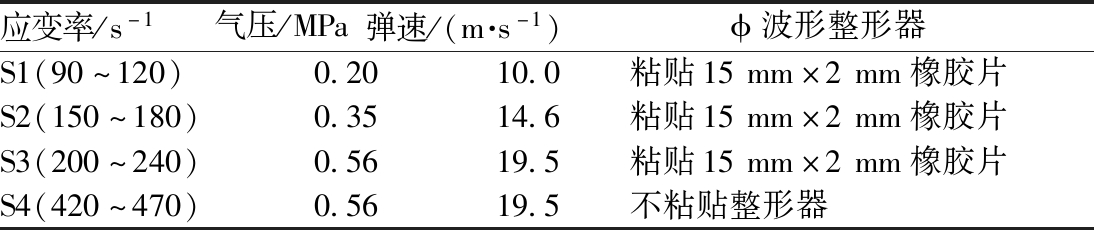
应变率/s-1气压/MPa弹速/(m·s-1)ϕ波形整形器S1(90～120)0.2010.0粘贴15mm×2mm橡胶片S2(150～180)0.3514.6粘贴15mm×2mm橡胶片S3(200～240)0.5619.5粘贴15mm×2mm橡胶片S4(420～470)0.5619.5不粘贴整形器
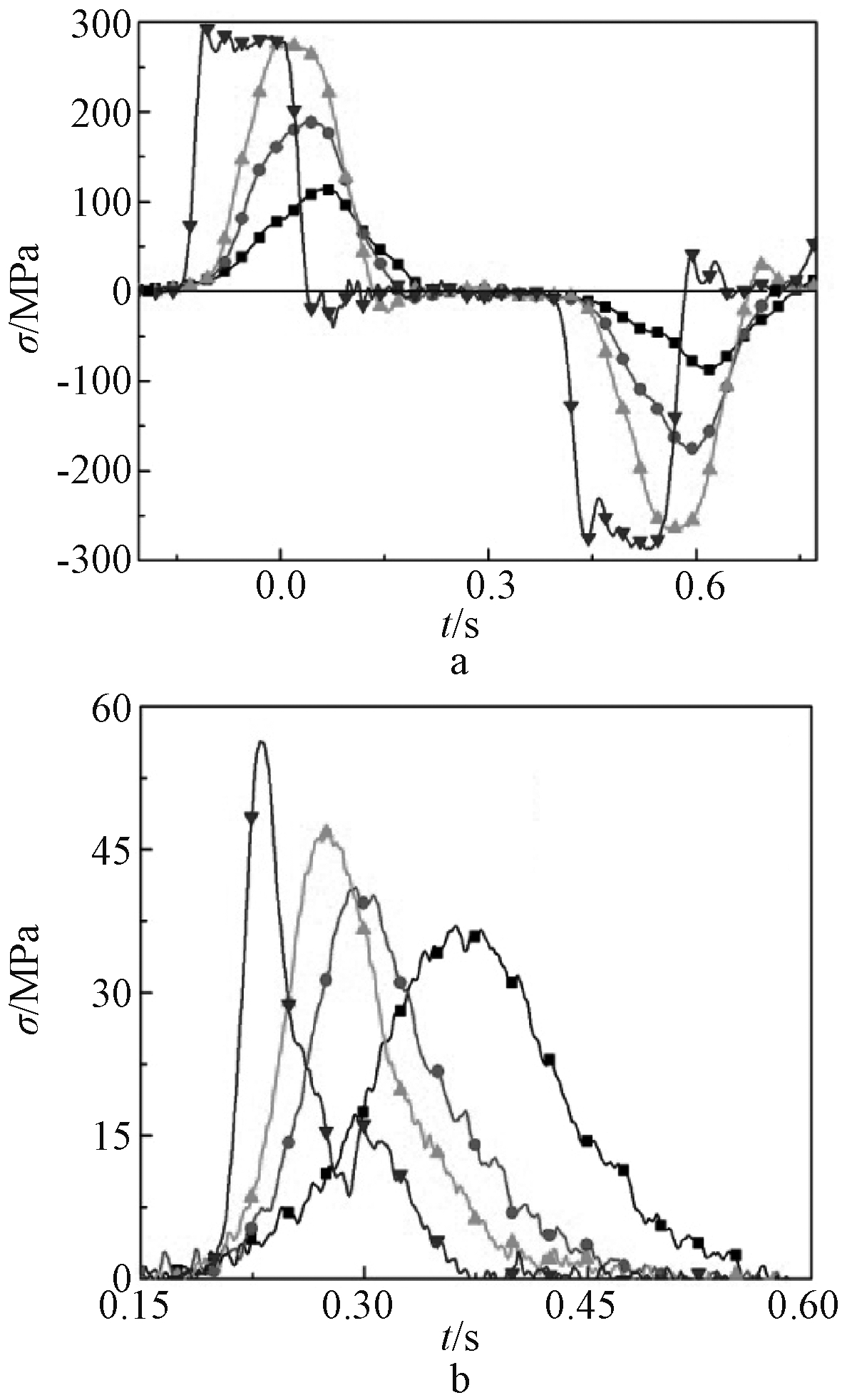
a—入射波和反射波; b—透射波。
— S1(90～120)； 
— S2(150～180)；
— S3(200～240)； 
— S4(420～470)。
图3 典型的4种应变率入射波、反射波、透射波
Fig.3 Incident,reflected and transmitted waves at typical four strain rates
采用经典两波法得到试样特定应变率下的应力-应变曲线，如式(1)所示：
(1a)
(1b)
(1c)
其中 εS(t)=εi(t)-εt(t)
式中：C0、E、A0分别为压杆的弹性波波速、弹性模量、横截面面积；AS、lS为试件的横截面面积和长度；εi、εr、εt分别为λ射波、反射波和透射波引起的应变，
为试件受冲击时产生的应力、应变和应变率。
2 试验结果和讨论
2.1 BFRCC试件破坏形态
3种纤维掺量的试件在4种应变率下呈现不同的破坏形态，图4为纤维掺量为3%时的典型破坏形态，总体呈现出边裂、多条裂缝开裂、碎成小块至粉碎的破坏形态，从受力薄弱截面开始破坏直至分区域整体抵抗冲击荷载的影响。其在准静态荷载作用下，裂纹会从最薄弱截面开始产生，进而逐渐扩展形成多条主裂纹，最后达到破坏的状态。随着动态荷载的增大，其应变率迅速增大，导致材料变形时间极短，裂纹来不及扩展进而达到破坏的状态。
2.2 BFRCC的应力-应变曲线
不同纤维掺量的BFRCC在不同应变率下的应力-应变曲线如图5所示，总结该应力-应变曲线得到BFRCC在动态压缩作用下具有以下特征：1)BFRCC 动态抗压强度随应变率的增加而逐渐增大；2)BFRCC应力-应变曲线加载段呈非线性变化，包含初始弹性段、平台段、压实段，且随着应变率的增加平台段逐渐减小，同时压实段斜率随应变率的增加而增加；3)BFRCC应力-应变曲线卸载段存在转折点，在转折点之后存在波动的应力平台，随着应变率的提高卸载段应力平台时间增长，应变增大显著。
BFRCC在受力变形过程中，首先是线弹性阶段，在荷载达到一定数值时，应力-应变曲线出现平台段，而后继续增加，达到峰值应力；随着应变率增加，BFRCC的动态抗压强度增强，峰值应变增大；在达到峰值应力后，进入卸载段进一步压缩，玄武岩纤维与水泥基材料基体同时受力，纤维起到明显的桥接作用，因此出现较长的应力平台，并通过试验得到:随着玄武岩纤维掺量的增大，应力-应变曲线的卸载段应力平台增长，应力下降减慢。
2.3 动态抗压强度与应变率的关系
不同纤维掺量试件动态抗压强度呈现出应变率敏感性的特点。为分析不同玄武岩纤维掺量的BFRCC试件在不同应变率下的变化趋势，将各组试件在4应变率下的有效动态抗压强度汇总至图6。从图6可以发现：随着应变率的变化，不同纤维掺量试件的动态抗压强度上升趋势有所不同：1)随着应变率的上升，3种纤维掺量的试件动态抗压强度均呈现上升的趋势；2)在应变率小于200 s-1时，3种纤维掺量的试件动态抗压强度相差不大；在应变率大于200 s-1时，纤维掺量3%时的试件动态抗压强度增大较多，说明纤维在高应变率时对动态抗压强度的增强起到了一定的作用；3)动态抗压强度的增长率随着应变率的增加呈现先增大后减小的趋势，应变率200 s-1为临界点，3种纤维掺量的动态抗压强度增长率在应变率大于200 s-1时增大较多。
图4 四种应变率下BFRCC典型破坏形态(纤维掺量3%)
Fig.4 Typical failure modes of BFRCC at four strain rates(fiber content 3%)
a—S1; b—S2; c—S3; d—S4。
图5 不同玄武岩纤维掺量的BFRCC的应力-应变曲线
Fig.5 Stress-strain curves of BFRCC with different basalt fiber content
— 0%； 
— 2%； 
— 3%。
图6 3种纤维掺量4种应变率下动态峰值应力
Fig.6 Dynamic peak stress diagrams with three fiber contents and four strain rates
2.4 BFRCC吸能性能分析
由于BFRCC-3属于高延性材料，其压缩强度虽然较低，但其在荷载作用下变形呈现多缝开裂，增大了承载面积，塑性变形能力较强。由文献[17]可知，试件碎块的动能占总吸收能量比值会随着加载速率的增加而增加，且当弹速小于20 m/s时，其比值小于15%。在BFRCC试件动态压缩试验中，弹速最大为19.69 m/s，小于20 m/s，因此可以断定大于或等于85%吸收能量是用于试件裂纹的扩展，或高应变率下试件的破碎。
由图5所示不同纤维掺量的BFRCC在不同应变率下的应力-应变曲线可以看到：加载段是纤维增强水泥基材料压缩变形直至产生初始破坏形态所吸收的能量，卸载段才是玄武岩纤维为控制塑性变形发挥其吸能效果的阶段。借鉴钢纤维混凝土压缩韧度指数来分析BFRCC韧度指数θ，如式(2)所示：
(2)
式中：Wmax为总应变能密度；W0.85fdc表示应力值为0.85fdc所对应的应变能密度，该值反映的是基体弹性变形吸能；fdc表示不同应力率的抗压强度。
通过该计算，可以有效消除材料强度对吸能性能的影响，则θ越大表示BFRCC的卸载段吸收能量越多。
2.4.1 BFRCC能量吸收
材料冲击破坏的原动力是能量[18-20]。根据能量守恒原理，计算试件SHPB试验冲击过程中BFRCC的吸收能量公式为：
Ws(t)=Wi(t)-Wr(t)-Wt(t)
(3a)
(3b)
(3c)
(3d)
式中：Wi(t)为入射能；Wr(t)为反射能；Wt(t)为透射能。
在SHPB动态压缩试验中，试件吸收的能量主要转化为3部分:试件裂纹扩展所需能量、试件碎块的动能和其他能量(比如热能等)。为判断不同纤维掺量BFRCC试件在不同应变率下吸收能量的能力，根据BFRCC试件冲击压缩试验结果，计算不同纤维掺量的BFRCC试件在不同的应变率下能量吸收时程曲线，如图7所示。
从图7可以看到:不同纤维掺量的试件在试验中均具有应变率效应，即随应变率的增加能量吸收显著提高。在冲击荷载作用下，加载速率提高的结果就是荷载作用时间缩短，试件的应变率也相应增大。由BFRCC试件在不同应变率下的破坏形态(图4)可以看到，试件裂纹呈现逐渐增多的现象，而裂纹产生所需的能量远大于裂纹扩展所需的能量。因此，在相近应变率下由试件的破坏形态得知，3%纤维掺量裂纹较2%纤维掺量裂纹多，2%纤维掺量试件裂纹较0%掺量裂纹多。
2.4.2 BFRCC韧度指数与应变率的关系
不同玄武岩纤维掺量水泥基复合材料θ与应变率的变化关系，如图8所示。
由图8看到:其基本呈现线性变化,运用方程式(4)拟合其关系为：
a—0%; b—2%; c—3%。
图7 不同应变率下BFRCC试件能量吸收时程曲线
Fig.7 Energy absorption time-history curves of BFRCC specimens at different strain rates
0%； 
0%拟合曲线；
2%； ---- 2%拟合曲线；
3%； …… 3%拟合曲线。
图8 BFRCC韧度指数-应变率曲线
Fig.8 Tougthness index versus strain rate curves of BFRCC
(4)
式中：A,B为拟合参数，
为动态应变率。对玄武岩纤维掺量为0%、2%、3%的试件在4种不同应变率下的韧度系数进行线性拟合，得到的拟合式分别为：
(5)
(6)
(7)
3条拟合曲线的平均相关系数分别为0.983、0.996、0.982。 对比不同纤维掺量试件的韧度指数，得到：1)θ值随着应变率的增大而增大；2)随着玄武岩纤维掺量的增加，相近应变率时，纤维掺量越高θ值越大，即随着玄武岩纤维掺量的增加BFRCC的吸能性能逐渐提高；3)3种不同纤维掺量水泥基材料韧度指数随应变率均呈现线性关系，2%、3%掺量的BFRCC韧度指数随着应变率增加速率高于0%掺量，说明增大玄武岩纤维的掺量能有效提升BFRCC的韧度和吸能性能。
2.4.3 BFRCC韧度指数与应力率的关系
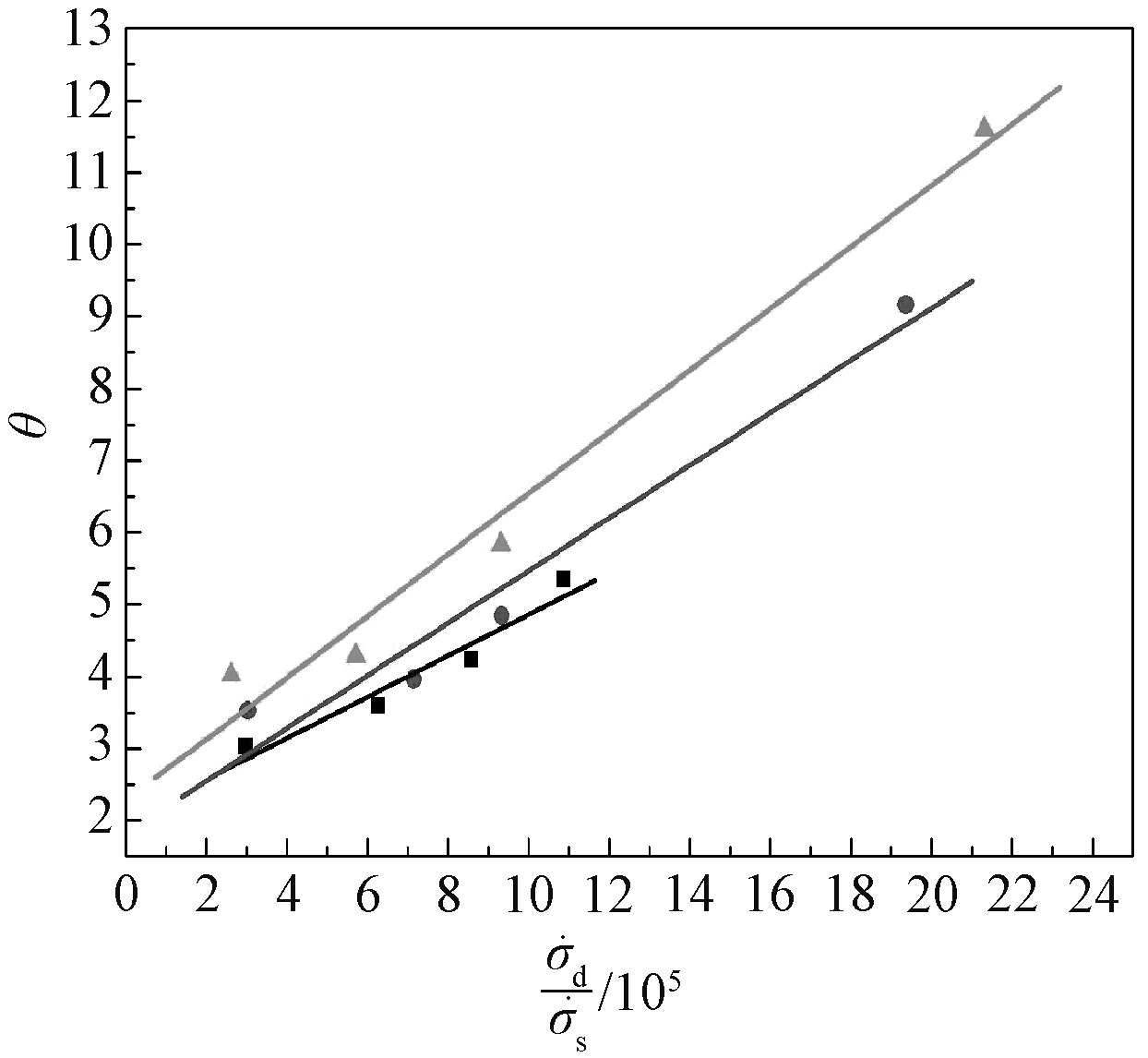
不同玄武岩纤维掺量水泥基复合材料θ与应力率的变化关系，如图9所示。
0%； 0%拟合曲线； 2%； ---- 2%拟合曲线； 3%； …… 3%拟合曲线。
图9 BFRCC韧度指数-应力率曲线
Fig.9 Tougthness index versus stress rate curves of BFRCC
由图9看到:其基本呈现线性变化,运用方程式(8)拟合其关系为：
(8)
式中:α,β为拟合参数;
为fdc所对应的应力率;
为准静态应力率，根据静态试验其值为2×10-4 GPa/s。对玄武岩纤维掺量为0%、2%、3%时韧度指数随应力率变化的曲线进行拟合，得到拟合式分别为：
(9)
(10)
(11)
3条拟合曲线的平均相关系数分别为0.972、0.980、0.989。 对比不同纤维掺量试件的韧度指数，得到：1)θ值随着应力率的增大而增大；2)相同的应力率纤维掺量越高则θ值越大，即随着玄武岩纤维掺量的增加BFRCC的吸能性能逐渐提高；3)随着应力率的增加3种掺量水泥基材料均呈现线性关系，但2%、3%掺量的BFRCC韧度指数随着应力率增加速率较接近，且都高于0%掺量，说明增大玄武岩纤维的掺量能有效提升BFRCC的韧度和吸能性能。
3 结束语
1)玄武岩纤维增强水泥基复合材料(BFRCC)具有明显的应变率效应，即3种不同纤维掺量试件的动态抗压强度均随着应变率的增大而增大，峰值应力具有应变率敏感特点。
2)由应力-应变曲线得到，玄武岩纤维体积掺量增大,BFRCC试件的塑性变形能力增强，达到动态压缩峰值应力后延性增加明显，即能量吸收能力增强。
3)同一应变率下不同的能量吸收能力从大到小依次为3%纤维掺量、2%纤维掺量、0%纤维掺量；不同应变率下相同纤维掺量的能量吸收呈现应变率效应，即随着应变率的增大能量吸收能力增强。
4)定义了表征BFRCC吸能性能的韧度指数，分析了韧度指数与应变率、应力率的关系。在相同或相近应变率或应力率下，韧度指数均随纤维掺量的增加呈现增加的趋势。在不同应变率或应力率下，韧度指数呈现应变率、应力率敏感性的特点，即随着应变率、应力率的增加而增大。随纤维掺量增加，韧度指数随应变率增长趋势与随应力率增长趋势均增大。
[1] LI V C, LEUNG C K Y. Steady State and Multiple Cracking of Short Random Fiber Composites [J]. ASCE J. Eng. Mech., 1992, 188(11): 2246-2264.
[2] MAALEJ M, LI V C. Flexural/Tensile Strength Ratio in Engineered Cementitious Composites [J]. J. Mater. Civ. Eng., ASCE ，1994, 6(4): 513-528.
[3] 中华人民共和国工业和信息化部.高延性纤维增强水泥基复合材料力学性能试验方法：JC/T 2461—2018[S]. 北京：建材工业出版社，2018.
[4] YANG E H, LI V C. Rate Dependence in Engineered Cementitious Composites [C]//In RILEM Workshop on HPFRCC in Structural Applications. Honululu, Hawaii： 2005： 83-92.
[5] YANG E H, LI V C. Tailoring Engineered Cementitious Composites for Impact Resistance [J]. Cem. Concr. Res., 2012, 42(8): 1066-1071.
[6] MAALEJ M, QUEK S T, ZHANG J. Behaviour of Hybrid-Fiber Engineered Cementitious Composites Subjected to Dynamic Tensile Loading and Projectile Impact [J]. ASCE J. Mater. Civ. Eng., 2005, 17(2): 143-152.
[7] ZHANG J, MAALEJ M, QUEK S T. Performance of Hybrid-Fibre ECC Blast/Shelter Panels Subjected to Drop Weight Impact [J]. J. Mater. Civ. Eng., ASCE ， 2007, 19(10): 855-863.
[8] MECHTCHERINE V, MILLON O M, BUTTLE M, et al. Mechanical Behaviour of Strain Hardening Cement-Based Composites Under Impact Loading [J]. Cem. Concr. Comp. 2011, 33(1): 1-11.
[9] SOEK T, ZHANG Y X, ZHANG L C. Impact Resistance of Hybrid-Fiber Engineered Cementitious Composite Panels [J]. Comp. Struct., 2013, 104: 320-330.
[10] LI V C, MISHRA D K, WU H C. Matrix Design for Pseudo-Strain-Hardening Fibre Reinforced Cementitious Composites [J]. Mater. Struct., 1995, 28(10): 586-595.
[11] LI V C, WANG S, WU C. Tensile Strain-Hardening Behaviour of Polyvinyl Alcohol Engineered Cementitious Composite (PVA-ECC) [J]. ACI Mater. J., 2001, 98(6): 483-492.
[12] ZHOU J, QIAN S Z, BELTRAN M G S, et al. Development of Engineered Cementitious Composites with Limestone Powder and Blast Furnace Slag [J]. Mater. Struct., 2010, 43(6): 803-814.
[13] 高淑玲, 徐世烺. PVA纤维增强水泥基复合材料拉伸特性试验研究[J].大连理工大学学报, 2007, 47(2): 233-239.
[14] 张君, 公成旭, 居贤春. 高韧性低收缩纤维增强水泥基复合材料特性及应用[J].水利学报, 2011 (12): 1452-1461.
[15] PAKRAVAN H R, JAMSHIDI M, LATIFI M. Study on Fiber Hybridization Effect of Engineered Cementitious Composites with Low-and High-Modulus Polymeric Fibers [J]. Constr. Build. Mater., 2016, 112: 739-746.
[16] 宋嵩. 玄武岩纤维增强高延性水泥基复合材料常温与高温力学性能研究[D].天津：河北工业大学，2019.
[17] ZHANG Z X，KOU S Q，JIANG L G，et al. Effects of Loading Rate on Rock Fracture： Fracture Characteristics and Energy Partitioning[J].International Journal of Rock Mechanics and Mining Sciences，2000，37(5)：745-762.
[18] 赵光明, 马文伟, 孟祥瑞. 动载作用下岩石类材料破坏模式及能量特性[J]. 岩土力学, 2015, 36(12): 3598-3605.
[19] FERROG, CARPINTERIA. Effect of Specimen Size on the Dissipated Energy Density in Compression[J]. Journal of Applied Mechanics, 2008, 75(4): 699-703.
[20] 梁昌玉, 李晓, 吴树仁. 中低应变率加载条件下花岗岩尺寸效应的能量特征研究[J]. 岩土力学, 2016, 37(12):3472-3480.