方钢管混凝土组合柱截面形式灵活,具有承载力高,延性好的优点。其单肢柱可以包裹在墙体内部,避免室内角部出现凸角,在钢结构住宅发展中具有较好的应用前景。但方钢管混凝土组合柱钢管的抗火设计是工程应用中亟需解决的主要问题之一。
国内外对钢管混凝土柱耐火性能的研究已经取得了一定成果。文献[1-8]介绍了由火灾试验得到的混凝土类型及截面形式、尺寸等对钢管混凝土柱耐火性能的影响;Sakumoto等研究[9]表明使用耐火钢可提高钢管混凝土柱的耐火性能;Lu等研究了填充自密实混凝土的钢管混凝土的耐火性能[10];韩林海等通过大量耐火试验,探究了影响钢管混凝土柱耐火极限的关键因素[11-13]。对于采用新型防火保护措施的方钢管混凝土组合柱,相关耐火性能研究较少。
本研究通过建立新型防火保护措施下方钢管混凝土组合柱温度场及耐火性能的有限元分析模型,在经试验结果验证模型合理性的基础上,分析组合柱截面形式、荷载比、长细比、保护层厚度等参数对方钢管混凝土组合柱耐火极限的影响,为此类构件的抗火设计提供参考。
1 有限元模型建立
1.1 温度场模型
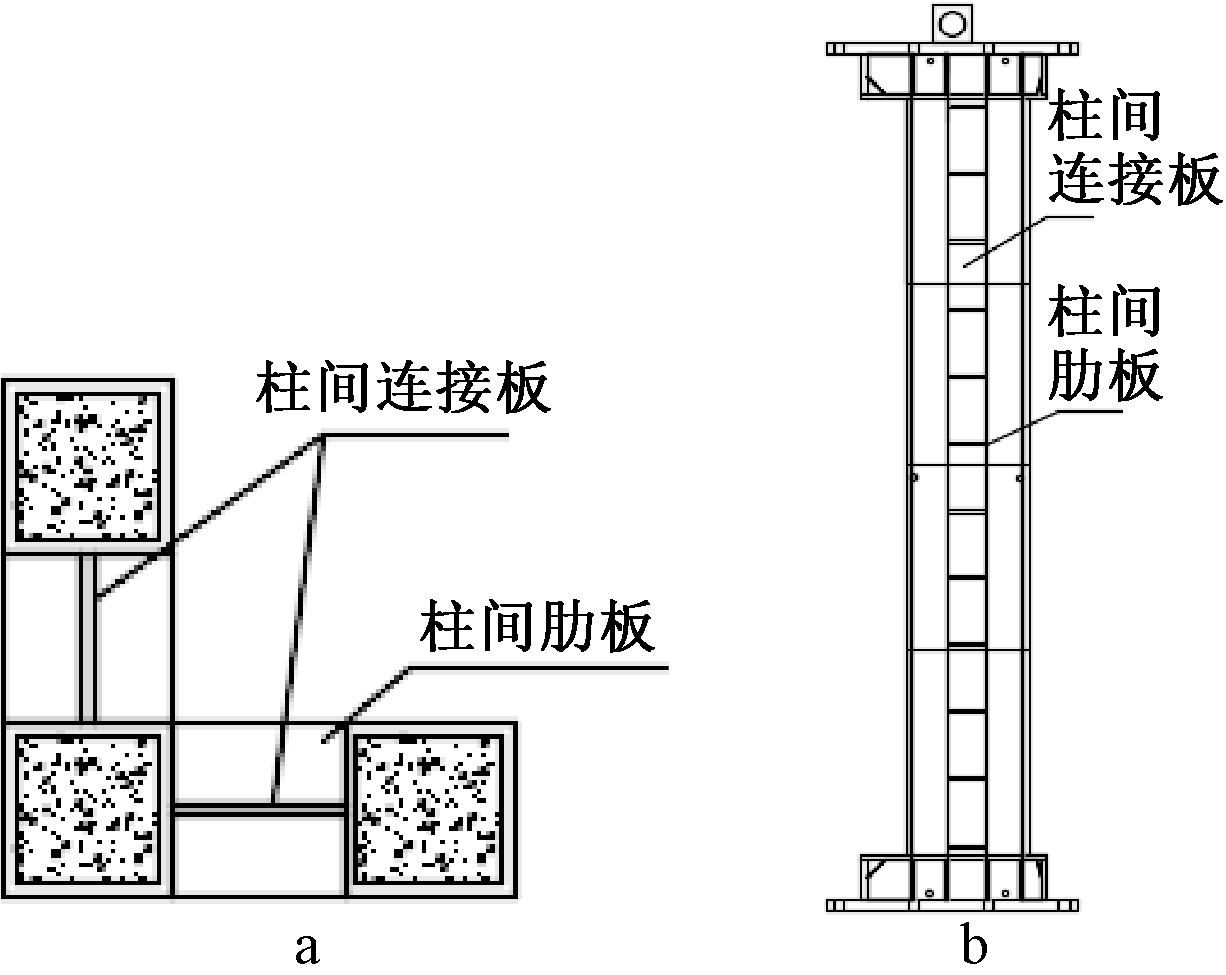
a—组合柱横截面;b—组合柱立面。
图1 组合柱构件构造示意
Fig.1 Schematic diagram of concrete composite columns
为研究方钢管混凝土组合柱的耐火性能并计算其耐火极限,须确定其截面的温度场分布,图1为组合柱构件构造示意。采用ABAQUS对普通钢管混凝土柱和有防火保护的L形方钢管混凝土组合柱在标准升温曲线ISO 834下的温度场进行建模分析。
1.1.1 材料的热工参数
钢材和混凝土的热工参数采用Lie提出的模型[14],本文分析的防火保护层材料及其热工参数如表1所示。
表1 防火保护材料热工性能
Table 1 Thermal performance of fire protection materials

防火保护层材料密度/(kg·m-3)导热系数/(W·m-1·℃-1)比热容/(J·kg-1·℃-1)厚涂型防火涂料4000.1161047蒸压轻质混凝土板6000.1701700
1.1.2 温度场模型建立
取对流系数25 W/(m2·K),钢管表面综合辐射系数0.5,防火板表面综合辐射系数0.8。忽略钢管与混凝土之间、防火保护层与钢管之间的接触热阻,采用约束“tie”来保证两者之间热量完全传递。模型单元采用结构化网格划分方法,钢管及保护层采用4结点线性热传递壳单元DS4,混凝土则采用8结点线性热传递实体单元DC3D8。
1.2 耐火性能分析有限元模型
1.2.1 高温下的力学分析模型
钢材采用Lie提出的高温下钢材应力-应变关系与热膨胀模型[14],混凝土采用时旭东[15]在试验基础上回归得到的混凝土瞬态热应变计算式。
(1a)
f(T,0.001) εs>εp
(1b)
其中 εp=4×10-6fy0。
式中:fy为钢材的屈服强度,MPa;fy0为室温下钢材的屈服强度,MPa。
1.2.2 模型建立
利用ABAQUS进行顺序热力耦合分析,钢材采用理想弹塑性模型,满足von Mises屈服准则,混凝土采用塑性损伤模型。钢管与混凝土之间法向采用硬接触,切向采用库仑摩擦。对钢管混凝土,韩林海建议摩擦系数μ可取0.2~0.6[16],考虑高温作用,本文取界面摩擦系数为0.3。端板与混凝土之间采用硬接触。两侧端板边界条件设置为铰接。钢材采用SR4单元,混凝土采用C3D8R单元。
2 与文献[14,17-18]试验结果对比
2.1 温度场对比
为验证本文所建立温度场模型的合理性及准确性,选取文献[14]中试件C09和SQ01及文献[17]中部分钢管混凝土柱试件S-2及文献[18]中L形方钢管混凝土组合柱耐火试验的试验结果进行验证,试件参数见表2,试件截面温度测点布置见图2,测点温度与时间关系曲线计算值与试验值的比较结果如图3~5所示。
表2 文献[14,17]中试件信息
Table 2 Information of reference[14,17]

编号D×T×L/mmfy/MPafcu/MPaN/kNna/mmtcr/minC09186.3×6.35×381035028.61500.13080SQ01152.4×6.35×381035043.53760.26066S-2350×7.7×381028417.827000.72511140
注:D为圆形截面直径或方形截面边长;t为钢管厚度;L为柱长;fy为钢材屈服强度;fcu为28 d混凝土立方体抗压强度;N为柱端的轴心压力;n为轴压比;a为防火保护层厚度;tcr为试件实测耐火极限。
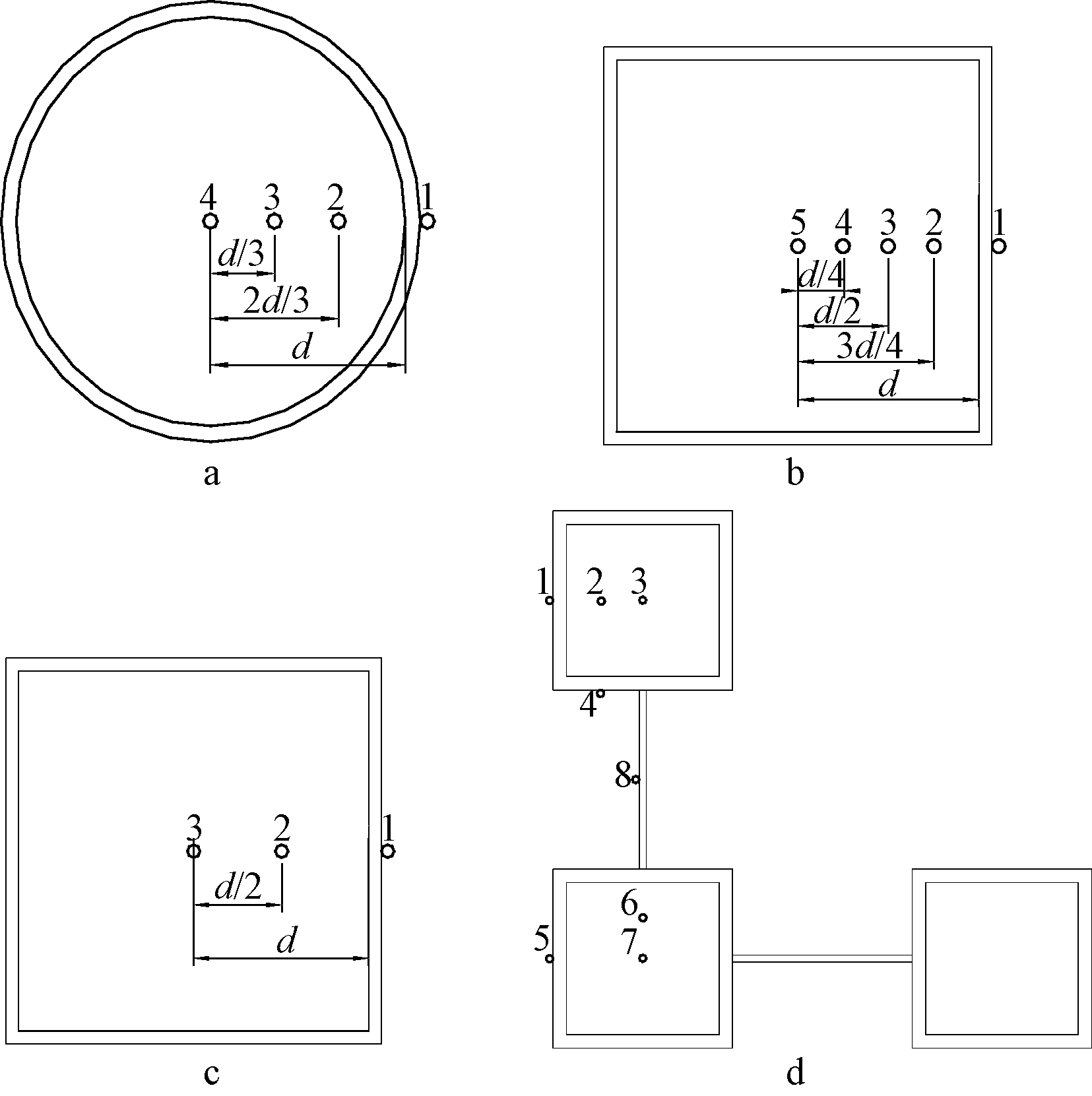
a—C09测点;b—SQ01测点;c—S-2测点;d—文献[18]试件测点。
图2 试件截面温度测点布置
Fig.2 Specimen section temperature measurement point layout
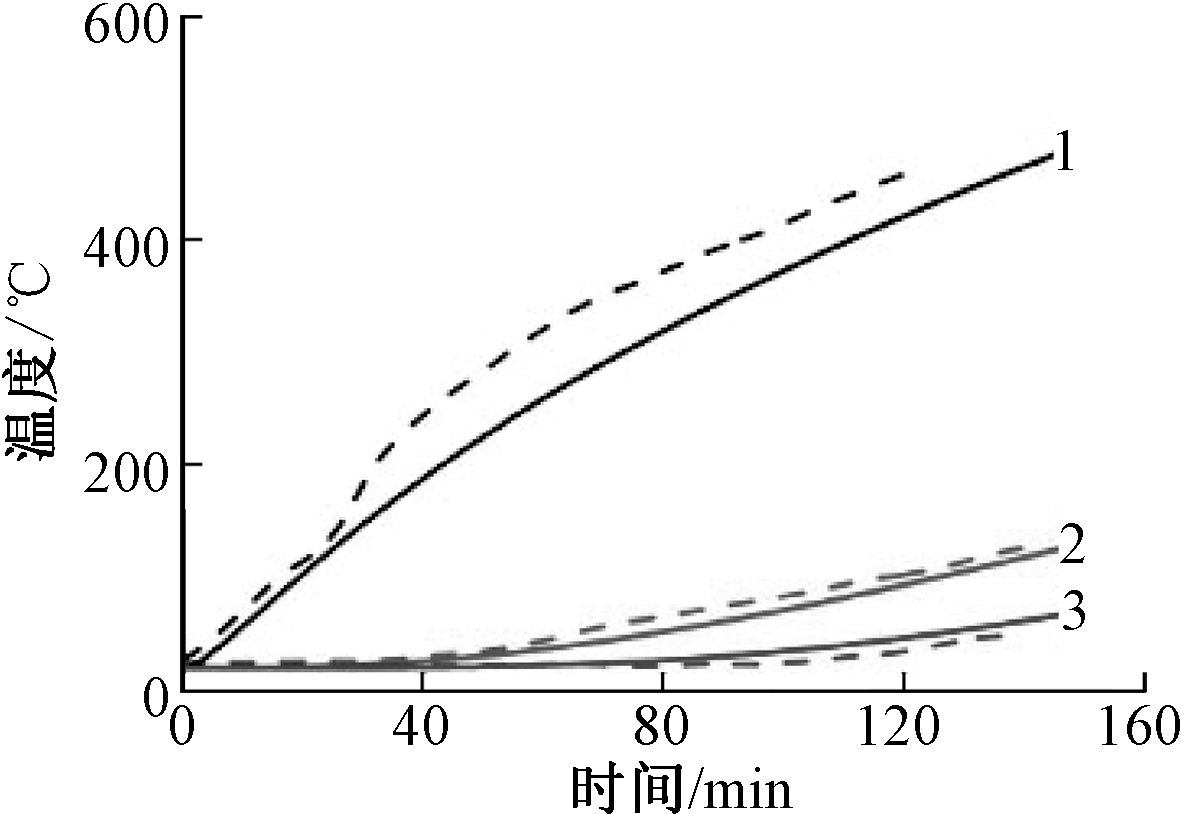
由图3~5可知:有限元计算结果能较好地反映实测截面温度的变化趋势;有限元计算结果与试验结果吻合良好,参数选取合理,温度场模型具有可靠性。试件S-2及文献[18]试件由于防火保护层存在拼缝及试验中出现破损等情况,导致试验值较计算值偏高。
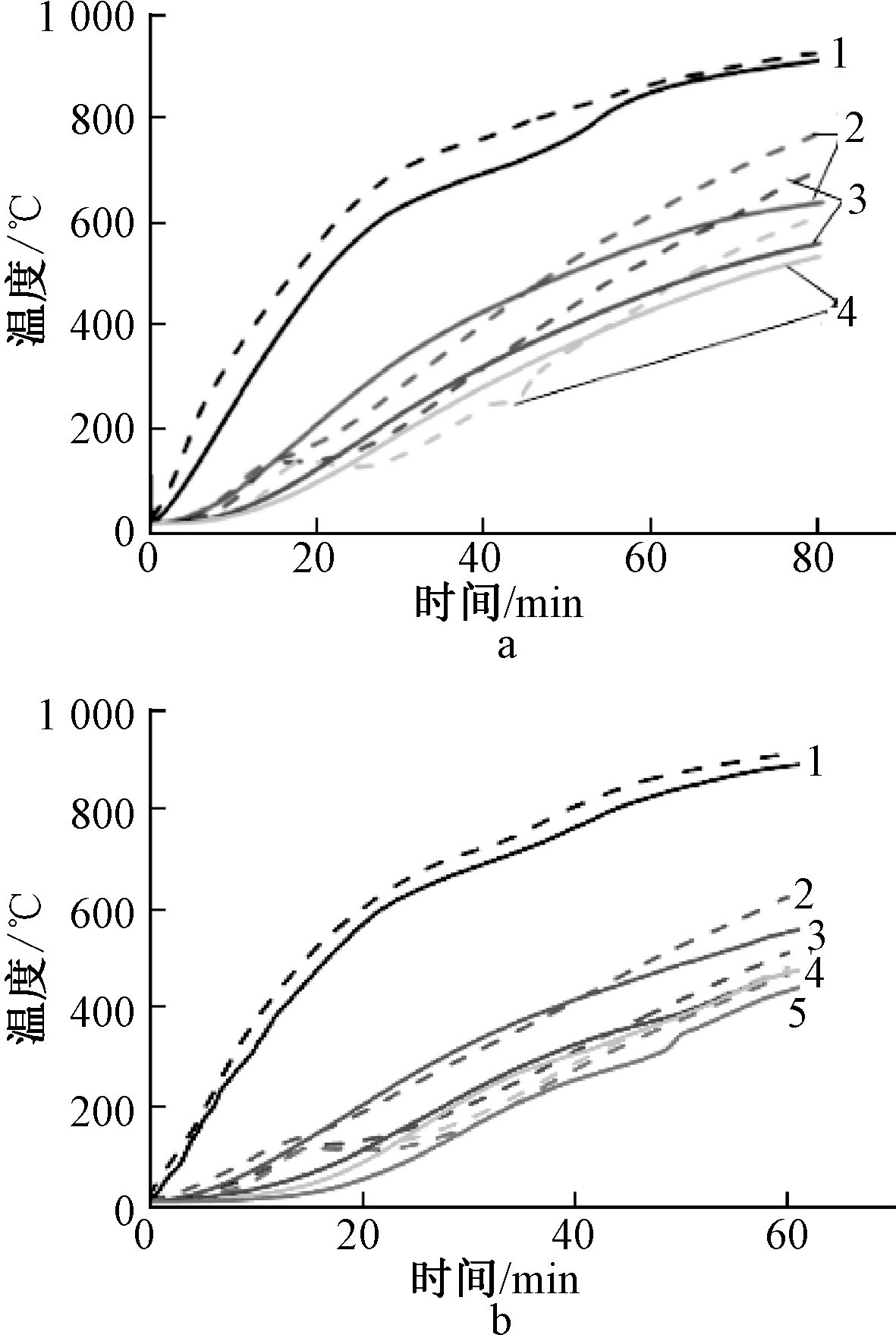
a—试件C09;b—试件SQ01。
----试验值;![]() 计算值。
计算值。
注:1~5为测点编号。
图3 文献[14]试件温度场结果对比
Fig.3 Comparison of temperature field results of the specimen[14]
----试验值;![]() 计算值。
计算值。
注:1~3为测点编号。
图4 文献[17]试件S-2温度场结果对比
Fig.4 Comparison of temperature field results of the specimen S-2[17]
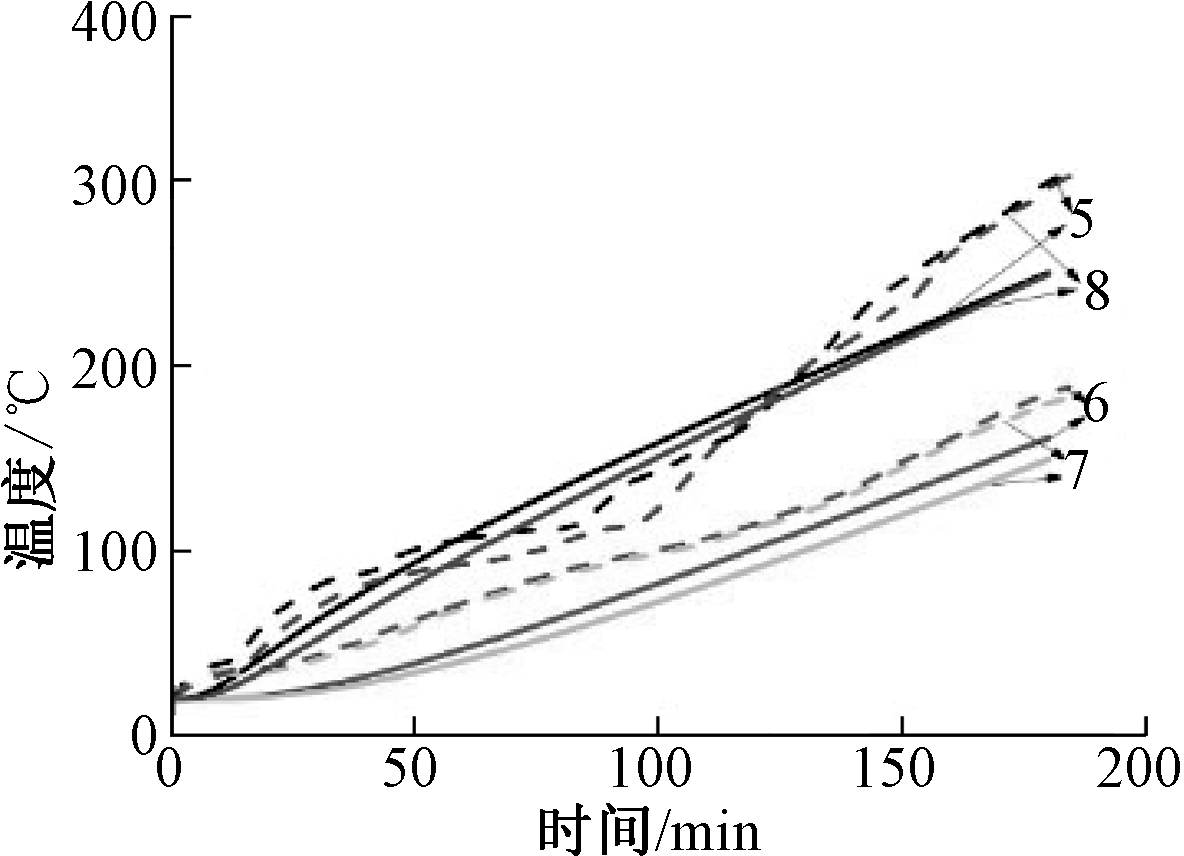
----试验值;![]() 计算值。
计算值。
注:5~8为测点编号。
图5 文献[18]试件温度场结果对比
Fig.5 Comparison of temperature field results of the specimen[18]
2.2 耐火性能对比
为验证耐火性能分析模型的正确性,选取4根钢管混凝土柱的耐火极限进行计算,分别得到其轴向位移Δ-时间t变化关系曲线,对比结果如图6~8所示。

a—C09;b—SQ01。
----试验值;![]() 计算值。
计算值。
图6 文献[14]试验轴向位移(Δ)-时间(t)变化关系曲线
Fig.6 Relationship between axial displacement (Δ) and time (t) of the test[14]

----试验值;![]() 计算值。
计算值。
图7 文献[17](试件S-2)试验轴向位移(Δ)-时间(t)变化关系曲线
Fig.7 Relationship between axial displacement (Δ) and time (t) of the test[17] (specimen S-2)

----试验值;![]() 计算值。
计算值。
图8 文献[18]试验轴向位移(Δ)-时间(t)变化关系曲线
Fig.8 Relationship between axial displacement (Δ) and time (t) of the test[18]
由图6可知:对于无防火保护的钢管混凝土柱,有限元计算结果合理反映了试件先膨胀再压缩的变形规律。在升温初期,柱膨胀变形的计算值较试验值略小,原因在于试验过程中对炉温的控制无法完全按照既定的标准升温曲线进行升温,文献[1]表明试验中实际炉温要比标准升温曲线高,从而导致膨胀变形的试验值偏大。
由图7可知:采用有限元计算试件的耐火极限,对于C09、SQ01两根无防火保护的试件,其耐火极限的计算值和实测值基本一致。对于有防火保护的试件S-2和文献[18]试件,其耐火极限计算值较试验值偏大,原因在于进行有限元分析时,无法模拟出实际试验过程中防火涂料保护层在高温作用下发生的裂缝、剥落等损伤,有限元计算出的耐火极限值偏大。
由图8可知:对于文献[18]中的L形方钢管混凝土组合柱试件,在3 h后的轴向变形极小,仅为0.65 mm。同时,有限元计算得到的压缩变形量也较小,轴向位移与实测值基本吻合。由于试验条件限制,该试验进行至3 h后终止,故其后位移情况仅为有限元模拟结果。
所选取文献[14,17-18]试件耐火极限计算值与试验值的对比情况汇总见表3。可知,有限元分析方法具有一定的可靠性与合理性,对无防火保护的钢管混凝土柱,耐火极限计算误差较小,最大误差为3.1%;而对于有防火保护的钢管混凝土柱,其耐火极限计算值比实测值偏大9%左右,两者都在工程应用允许的合理误差范围之内。
3 与本文试验结果对比
为了进一步验证所建立有限元模型对于有防火采用上述有限元模型对3个试件的温度场进行计算,其中SJ-2与SJ-3的防火保护方式相同,温度场计算模型相同。有限元计算值与部分测点试验对比结果如图10所示。对SJ-1~SJ-3试件的耐火极限进行计算,得到位移-时间变化关系曲线如图11所示。由图10、11可见,数值模拟值分析反映的温度变化趋势及组合柱变形特点与试验值基本吻合, 数值分析模型具有可靠性。
表3 耐火极限对比结果
Table 3 Comparison of fire resistance limits min

耐火极限试件C09[14]试件SQ01[14]文献[17]试件文献[18]试件计算值8264184184试验值8062169169
保护的方钢管混凝土组合柱的适用性。本文设计制作了3根方钢管混凝土组合柱试件并进行耐火性能试验,将试验结果与有限元计算值作对比分析。试件设计参数见表4,其中:t为防火保护层厚度,L为柱高度,e为荷载偏心距,NF为试验荷载,n为轴压比。试件外钢管采用Q235级钢材,由标准拉伸试验确定钢材的力学性能指标如表5所示。核心混凝土的强度等级为C40,第28天立方体抗压强度为71.86 MPa。
试验通过预埋在混凝土内和固定在柱壁的12个热电偶记录试件不同部位的温度变化,图9为热电偶布置示意。通过固定在柱顶端加载板上的位移计记录试验过程中柱的轴向压缩及膨胀变形。利用液压装置对柱施加恒定轴向荷载,最大竖向加载能力为10 000 kN。试验在达到GB 50016—2014《建筑设计防火规范》[19]要求的3 h耐火极限后终止。
表4 试件概况
Table 4 General situation of specimen

序号试件编号防火保护材料t/mmL/mme/mmNF/kNn1SJ-1纤维增强硅酸钙板153750040000.77纤维增强硅酸钙板153750040000.772SJ-2纤维增强硅酸钙板153750040000.77硅酸铝纤维毯203750040000.773SJ-3纤维增强硅酸钙板153750048000.91硅酸铝纤维毯203750048000.91
表5 钢材的力学性能
Table 5 Mechanical properties of steel MPa

钢构件类型弹性模量屈服强度极限抗拉强度方钢管2.64×105247.5452.5连接板1.95×105296.0428.0
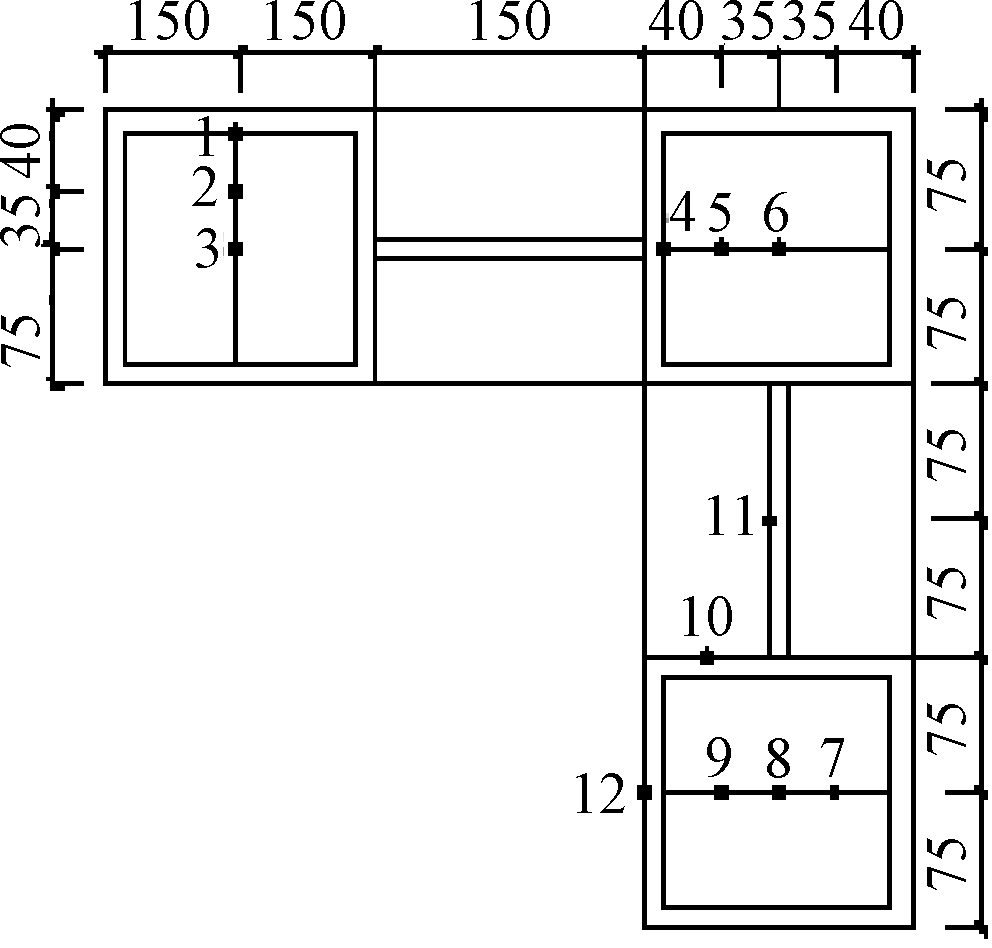
图9 热电偶布置示意
Fig.9 Schematic diagram of thermocouple arrangement
4 耐火极限影响因素分析
采用本文建立的模型探讨截面形式、荷载比、长细比、保护层厚度及材料强度等因素对组合柱耐火极限的影响规律。选择典型柱构件为无防火保护组合柱,柱长3 650 mm,单肢柱截面150 mm×150 mm×6 mm,柱间连接板150 mm×6 mm,柱间肋板150 mm×65 mm×6 mm,钢管采用Q345钢材,混凝土强度等级为C40。

a—SJ-1混凝土测点;b—SJ-1柱壁测点;c—SJ-2混凝土测点;d—SJ-2柱壁测点。
----试验值;![]() 计算值。
计算值。
图10 试验温度场部分测点结果对比(图中数字为测点编号)
Fig.10 Comparison of the results of some test points in the test temperature field (the numbers in the figure are the measuring points)
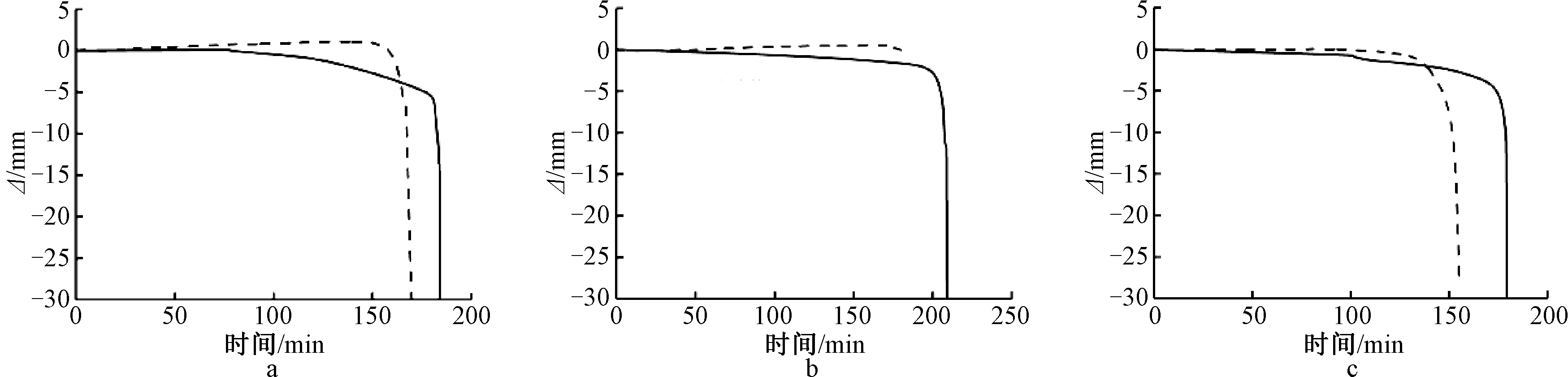
a—SJ-1;b—SJ-2;c—SJ-3。
----试验值;![]() 计算值。
计算值。
图11 试验轴向位移-时间关系
Fig.11 Relationship between axial displacement and time
4.1 截面形式
在实际工程中,方钢管混凝土组合柱可采用L形、T形、十字形及加长柱肢(两单肢边柱长为200 mm)的截面形式,保持其他基本参数不变,模拟分析不同截面形式柱的耐火极限结果如图12所示。由图可知,L形、T形和十字形截面的耐火极限相差较小,主要原因是混凝土截面较小,吸热作用较弱,且高温下柱间连接板及肋板强度退化,减弱各单肢柱间协同作用。对于端柱加长的L形组合柱,其耐火极限明显提高,说明混凝土的截面面积对耐火极限有较大影响。

图12 截面形式对耐火极限的影响
Fig.12 Effect of cross section on fire resistance
4.2 轴压比
火灾轴压比对耐火极限的影响模拟分析结果如图13所示。由图可知,火灾轴压比对耐火极限有很大影响,随着轴压比增大,组合柱的耐火极限减小。当轴压比较小时(n<0.5),轴压比对耐火极限影响较为显著;当轴压比较大时(n≥0.5),耐火极限随轴压比增大变化趋势较为平缓。
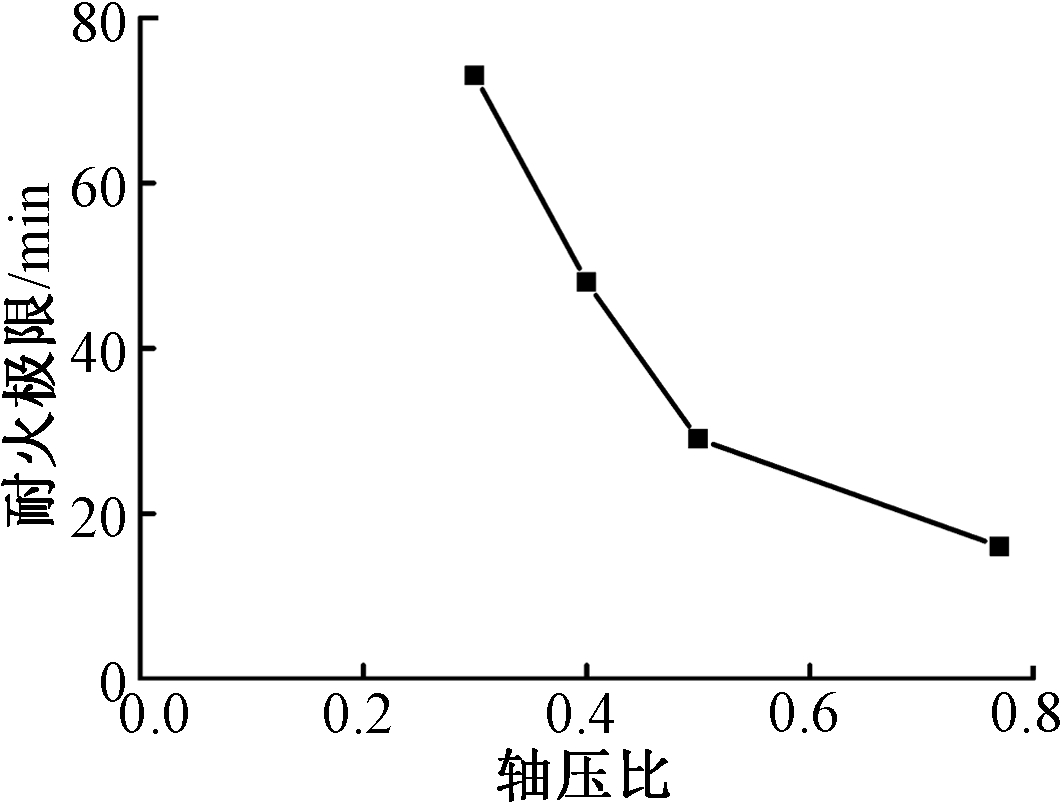
图13 轴压比n对耐火极限的影响
Fig.13 Effect of axial compression ratio n on fire resistance
4.3 长细比
对于柱肢间间距相等的L形方钢管混凝土组合柱,截面为单轴对称,经计算可确定,截面主轴分别为:对称轴x-x轴及与之垂直的y-y轴,如图14所示。对典型试件的长细比进行计算,得到λx=33.11,λy=20.73,分别调整柱长计算得到不同长细比的耐火极限,模拟分析结果如图15所示。由图可见,长细比对耐火极限有很大影响,随着长细比增大,组合柱耐火极限减小。其中,长细比对弱轴的影响较强轴更大,当λ<30时,耐火极限下降速度较快。
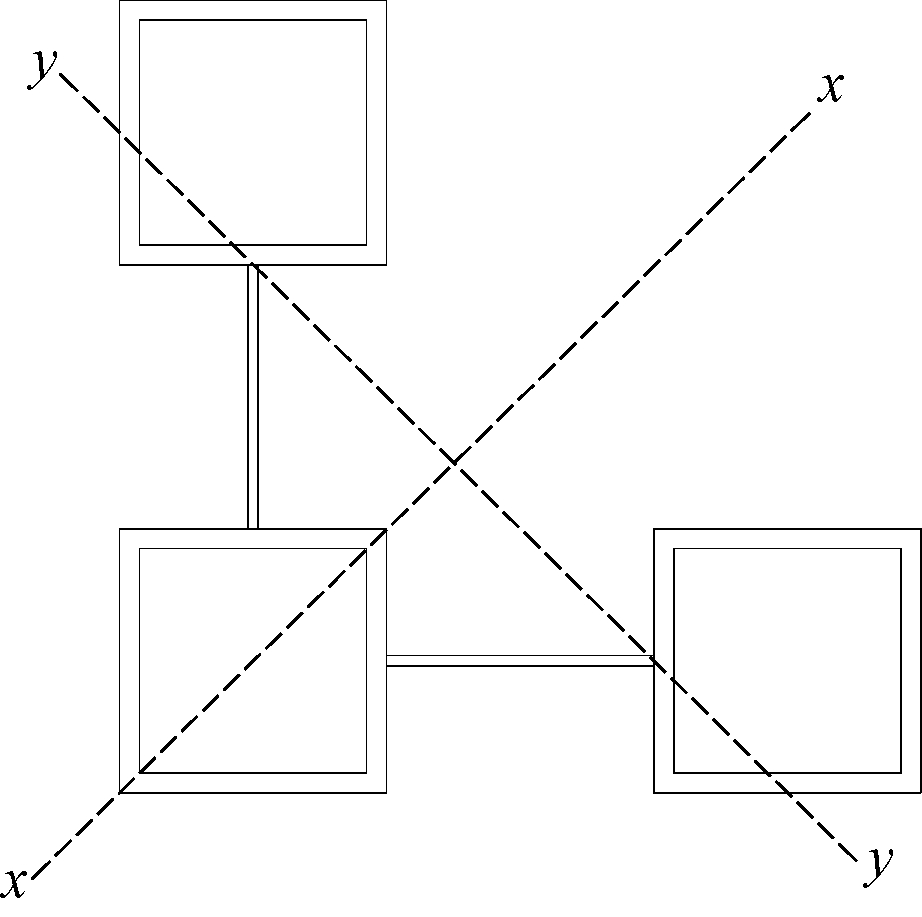
图14 L形方钢管混凝土组合柱截面
Fig.14 Cross section of L shape concrete-filled square steel tubular columns
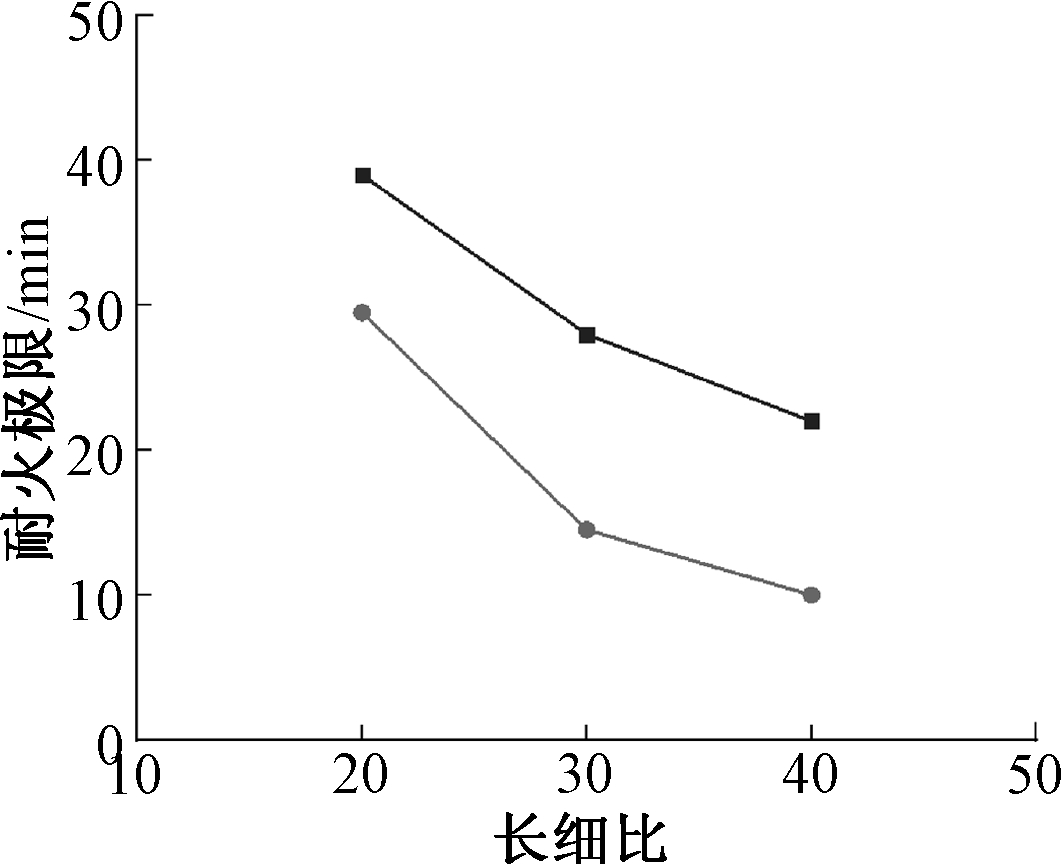
![]() — 对强轴的影响;
— 对强轴的影响;![]() — 对弱轴的影响。
— 对弱轴的影响。
图15 长细比λ对耐火极限的影响
Fig.15 Effect of slenderness ratio lambda on fire resistance
4.4 保护层厚度影响
采用有限元模型计算防火保护层蒸压轻质混凝土板(ALC板)厚度对耐火极限的影响,模拟分析结果如图16所示。由图可见,在有效荷载作用下,组合柱的耐火极限随着ALC板厚度的增加而逐渐提高,当板厚大于30 mm时,耐火极限提高较为显著;板厚约为40 mm时,组合柱耐火极限达到180 min,可满足柱构件耐火等级一级的要求。
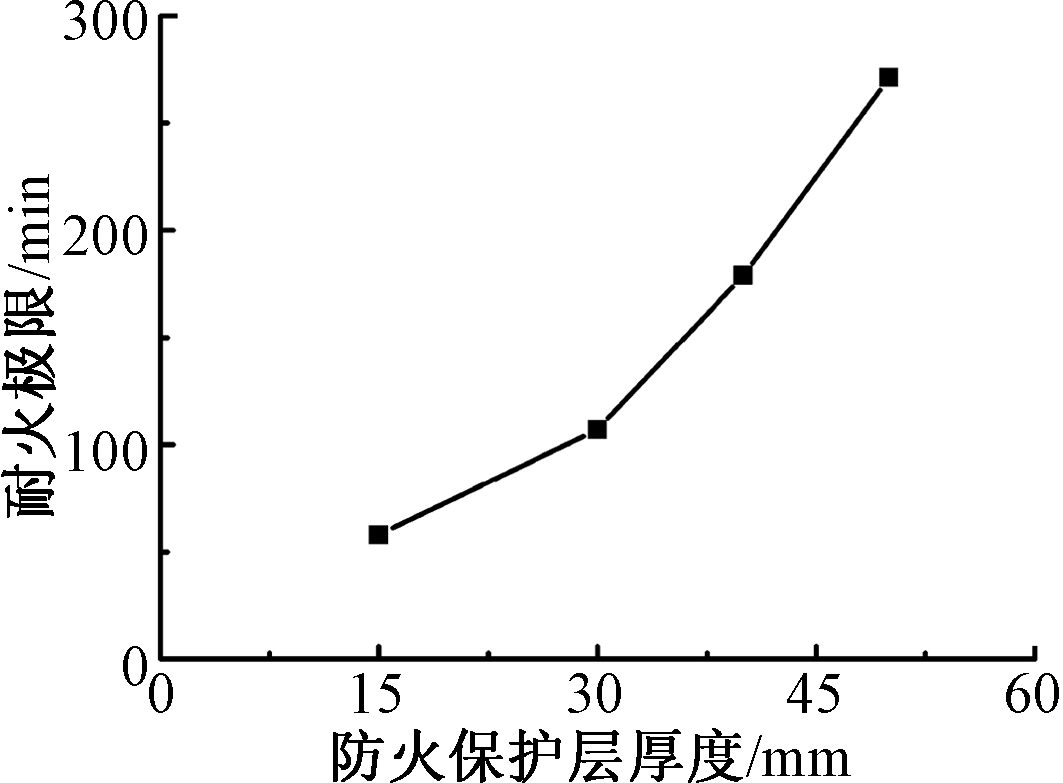
图16 保护层厚度对耐火极限的影响
Fig.16 Influence of thickness of protective layer on fire resistance
4.5 材料强度影响
分别计算不同钢材屈服强度和混凝土抗压强度对耐火极限的影响,模拟分析结果如图17所示。由图可见,钢材屈服强度和混凝土抗压强度对组合柱耐火极限影响较小。随着钢材强度增加,耐火极限略有降低;随着混凝土强度增加,耐火极限略有增加,总体趋于平稳。
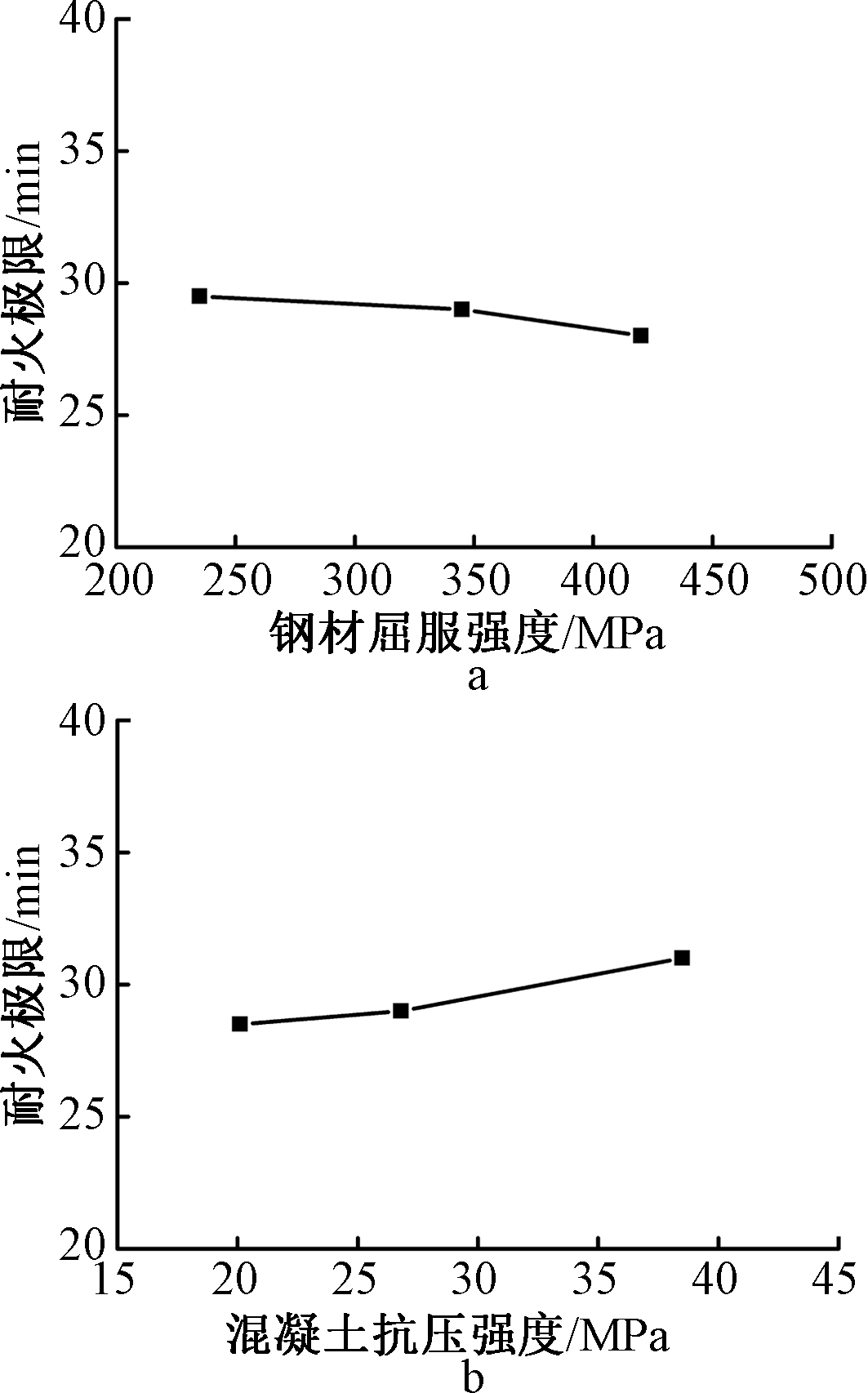
a—钢材强度影响;b—混凝土强度影响。
图17 材料强度对耐火极限的影响
Fig.17 Effect of material strength on fire resistance
5 结束语
1)采用有限元方法得到的普通钢管混凝土柱及方钢管混凝土组合柱的温度场和耐火极限的计算值与试验值吻合良好,有限元模型可靠,可以用于有防火保护层的方钢管混凝土组合柱耐火性能的分析模拟。
2)混凝土截面面积是影响组合柱耐火性能的重要因素。核心混凝土截面面积越大,混凝土内部温度越低,构件耐火极限越高。
3)组合柱的耐火极限随着轴压比增大而减小。轴压比小于0.5时,对耐火极限影响更为显著。长细比对弱轴的影响较强轴更大,λ<30时,耐火极限下降速度较快。
4)外包防火材料能有效地降低组合柱温度,避免各单柱四面受火,使连接板、肋板在较低温度状态下发挥连接作用。组合柱自身钢材及混凝土材料强度对其耐火性能影响较小。
[1] LIE T T, CHABOT M. Experimental Studies on the Fire Resistance of Hollow Steel Columns Filled with Plain Concrete: No.611[R]. Canada, Ottawa Ont: NRC-CNRC Internal Report, 1992.
[2] CHABOT M, LIE T T. Experimental Studies on the Fire Resistance of Hollow Steel Columns Filled with Bar-Reinforced Concrete: No.628[R]. Canada, Ottawa Ont: NRC-CNRC Internal Report, 1992.
[3] LIE T T, DENHAM E M A. Factors Affecting the Fire Resistance of Circular Hollow Steel Columns Filled with Bar-Reinforced Concrete: No.651[R].Canada, Ottawa Ont: NRC-CNRC Internet Report, 1993.
[4] KODUR V K R, LIE T T. Experimental Studies on the Fire Resistance of Circular Hollow Steel Columns Filled with Steel-Fire-Reinforced Concrete: No.691[R]. Canada, Ottawa Ont: NRC-CNRC Internet Report, 1995.
[5] KODUR V K R, LIE T T. Experimental Studies on the Fire Resistance of Square Hollow Steel Columns Filled with Steel-Fire-Reinforced Concrete: No.662[R]. Canada, Ottawa Ont: NRC-CNRC Internet Report, 1996.
[6] LIE T T, CARGON S E. Fire Resistance of Hollow Steel Columns Filled with Siliceous Aggregate Concrete: Test Results: No.573[R]. Canada, Ottawa Ont: NRC-CVRC Internal Report, 1988.
[7] KODUR V K R, LATOUR J C. Experimental Studies on the Fire Resistance of Hollow Steel Columns Filled with High-Strength Concrete: No.215[R]. Canada, Ottawa Ont: NRC-CNRC Research Report, 2005.
[8] KODUR V K R. Solutions for Enhancing the Fire Endurance of HSS Columns Filled with High-Strength Concrete[J]. AISC Engineering Journal, 2006, 43(1): 1-7.
[9] SAKUMOTO Y, OKADA T, YOSHIDA M, et al. Fire Resistance of Concrete-Filled, Fire-Resistant Steel-Tube Columns[J]. Journal of Materials in Civil Engineering, 1994, 6(2): 169-184.
[10] LU H, ZHAO X L, HAN L H. Fire Behavior of High Strength Self-Consolidating Concrete Filled Steel Tubular Stub Columns[J]. Journal of Constructional Steel Research, 2009, 65(10): 1995-2010.
[11] HAN L H, ZHAO X L, YANG Y F, et al. Experimental Study and Calculation of Fire Resistance of Concrete-Filled Hollow Steel Columns[J]. Journal of Structural Engineering, 2003, 129(3): 346-356.
[12] 韩林海, 贺军利. 钢管混凝土柱耐火性的试验研究[J]. 土木工程学报, 2000, 33(3):31-35.
[13] 韩林海,徐蕾. 带保护层方钢管混凝土柱耐火极限的试验研究[J]. 土木工程学报, 2000(6):63-69.
[14] LIE T T. Fire Resistance of Circular Steel Columns Filled with Bar-Reinforced Concrete[J]. Journal of Structural Engineering, ASCE, 1994, 120(5): 1489-1509.
[15] 时旭东. 高温下钢筋混凝土杆系结构试验研究和非线性有限元分析[D]. 北京:清华大学, 1992.
[16] 韩林海. 钢管混凝土结构:理论与实践[M]. 北京:科学出版社, 2007.
[17] 徐蕾. 方钢管混凝土柱耐火性能及抗火设计方法研究[D]. 哈尔滨: 哈尔滨工业大学,2002.
[18] 赵炳震. 方钢管混凝土组合异形柱框架-支撑结构体系力学性能研究[D]. 天津: 天津大学, 2017.
[19] 中华人民共和国住房和城乡建设部.建筑设计防火规范:GB 50016—2014[S].北京:中国计划出版社,2015.