0 前 言
钢-混凝土组合空腹夹层板(简称“组合空腹夹层板”)是一种适用于大跨度建筑的轻型网格板。该类楼板体系具有节材、轻质、高强、美观等优点,目前已在我国多个省份有工程应用。如图1a所示,钢-混凝土组合空腹夹层板由上、下两层交叉钢肋网格通过方管剪力键刚性连接形成双层网格受力体系,其上覆盖混凝土面层,形成协同受力的整体体系。与传统井字格楼板不同,该类结构将井字网格板肋的腹腔材料抽空以减轻结构质量,提高材料的利用效率。
目前有关“组合空腹夹层板”的研究主要集中在对其整体受力性能的研究[1-4],剪力键作为“组合空腹夹层板”关键受力构件,其受力性能的优劣直接关系到整体受力体系的可靠性。故方管剪力键的受力性能一直是业内工程师关心的问题。陈强研究了剪力键节点域加劲板对“组合空腹夹层板”的整体挠度、网格内力的影响[5]。刘卓群通过建立精细化的“组合空腹夹层板”数值模型,研究了混凝土板对剪力键和钢肋的影响,得到了合理的混凝土板厚度取值[6-7]。黄勇对未设置加劲板的钢管-混凝土组合剪力键的受力性能进行了试验研究和数值分析[8]。
图1展示了组合空腹夹层板、空腹钢梁以及剪力键之间的关系(黑色粗箭头为作用在结构上的等效外荷载,虚线箭头为构件截面产生的内力)。在针对杆件层面的受力分析时,通常将空腹夹层板的面荷载等效为集中荷载,空腹钢梁可看作双向正交的基本受力单元,上、下弦杆通过方管剪力键连接后将等效集中荷载的作用转化成上、下弦杆的轴力和剪力。方管剪力键主要承受由于上下弦杆的轴力差引起的剪力(如图1c所示)。由此可见,剪力键抗侧刚度的强弱对空腹钢梁上下弦杆的协同受力起着关键的作用。
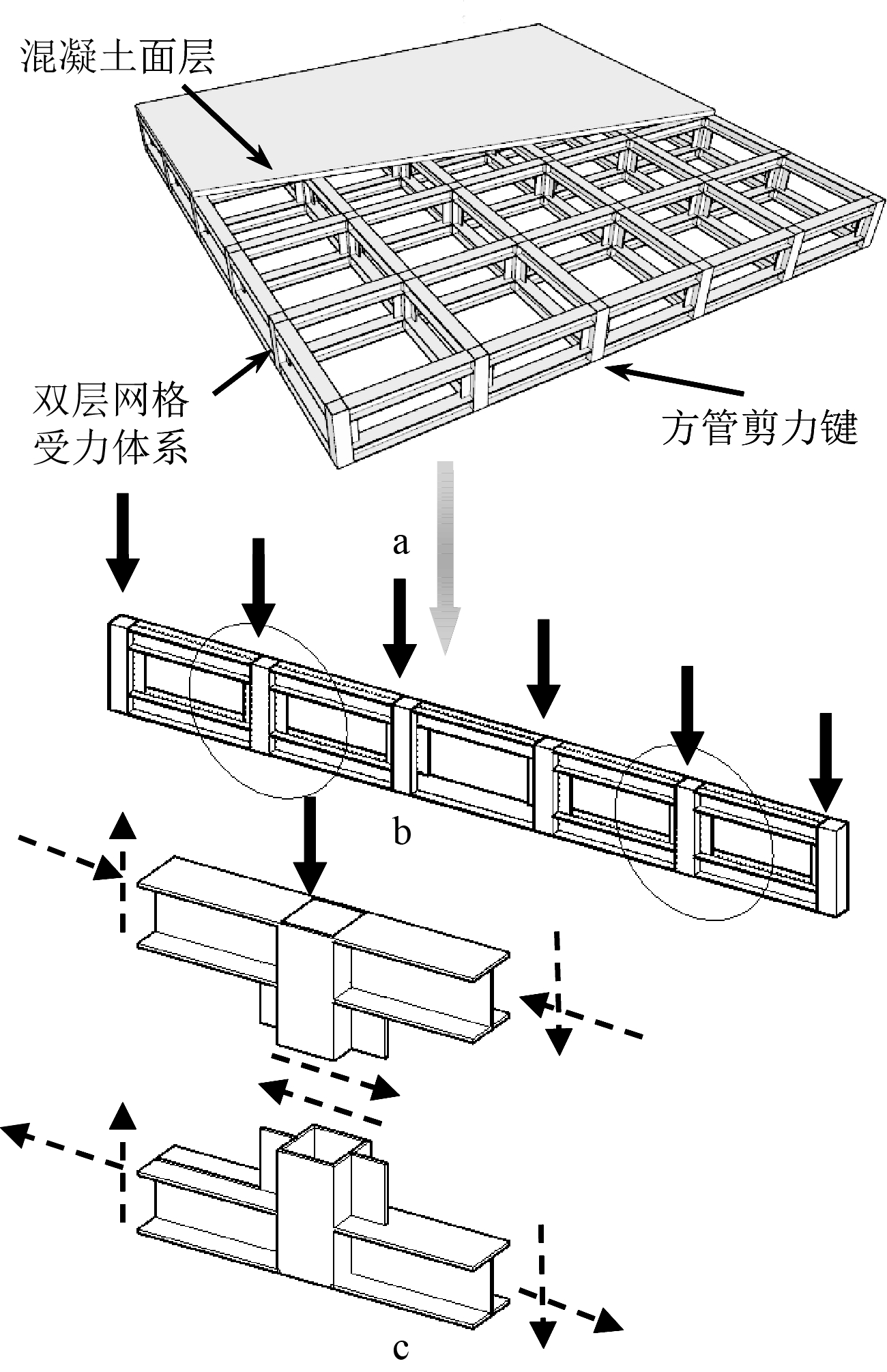
a—钢-混凝土组合空腹夹层板; b—剪力键式空腹钢梁; c—方管剪力键。
图1 钢-混凝土组合空腹夹层板构造
Fig.1 Construction of steel-concrete composite open-web sandwich plate
工程实践中,通常采用在钢管外壁贴焊加劲板以提高剪力键的抗侧刚度。如何考虑加劲板对剪力键的增强作用,是将剪力键进行精细化设计必须考虑的问题。为了研究加劲板对方管剪力键承载能力的影响,刘卓群建立了带外置加劲板的剪力键全壳单元数值模型,做了参数化分析并给出了设计建议[9]。白志强则对连接T形钢肋的方管剪力键的受力性能做了试验研究[10]。
在工程实践中,为了改善构件受力,增强网格尤其是边网格的承载能力,通常用H形钢肋代替T形钢肋,这相当于对组合空腹夹层板腹杆四周补强。这种改进措施在增加边网格承载能力的同时,又可兼顾管线安装,可谓一举两得。然而,与连接T形钢肋的区别是,连接H形钢肋的方管剪力键,构件连接区域的应力集中区域发生了变化,剪力键由于侧壁约束增强,抗侧刚度也发生了变化。加劲板对连接H形钢肋时剪力键的受力影响具体如何尚未研究清楚。针对此问题,本文以某工程案例为参考,制作了两个尺寸完全相同的足尺试件(一个未设置加劲板,另一个设置加劲板),通过单调加载进行破坏性对比试验,对H形钢肋与方钢管剪力键的连接区域的受力状态和应力集中现象进行对比研究,并在试验的基础上借助有限元模拟进一步进行参数化分析,以期得到有价值的设计建议。
1 试验方案
1.1 试件制作及尺寸
为了便于描述,无加劲板的试件命名为ST-0;带加劲板的试件命名为ST-1。制作试件时,为了更好地模拟实际工程中混凝土楼板对上钢肋上翼缘的约束边界,将试件倒置,且用4个直径为80 mm的地脚螺栓结合4个刚性垫块将试件固定在实验室地槽上,如图2所示。

a—ST-0; b—ST-1。
图2 试件加载过程
Fig.2 Loading procedure of specimens
贴地钢板厚度为15 mm,同时设置4块三角加劲板,以确保贴地钢板具有足够的平面外刚度。方管剪力键总高度为840 mm,方管截面尺寸为200 mm,厚度为6 mm;剪力键上、下两端钢肋均为H150×200×10×10,但为了便于试件制作,下钢肋下翼缘与底板合二为一;加劲板尺寸为-440×120×10;作动器与弦杆端板螺栓连接,加载的水平力模拟实际工程中剪力键受到的剪切力。以试件ST-1为例,说明加载示意如图3所示。
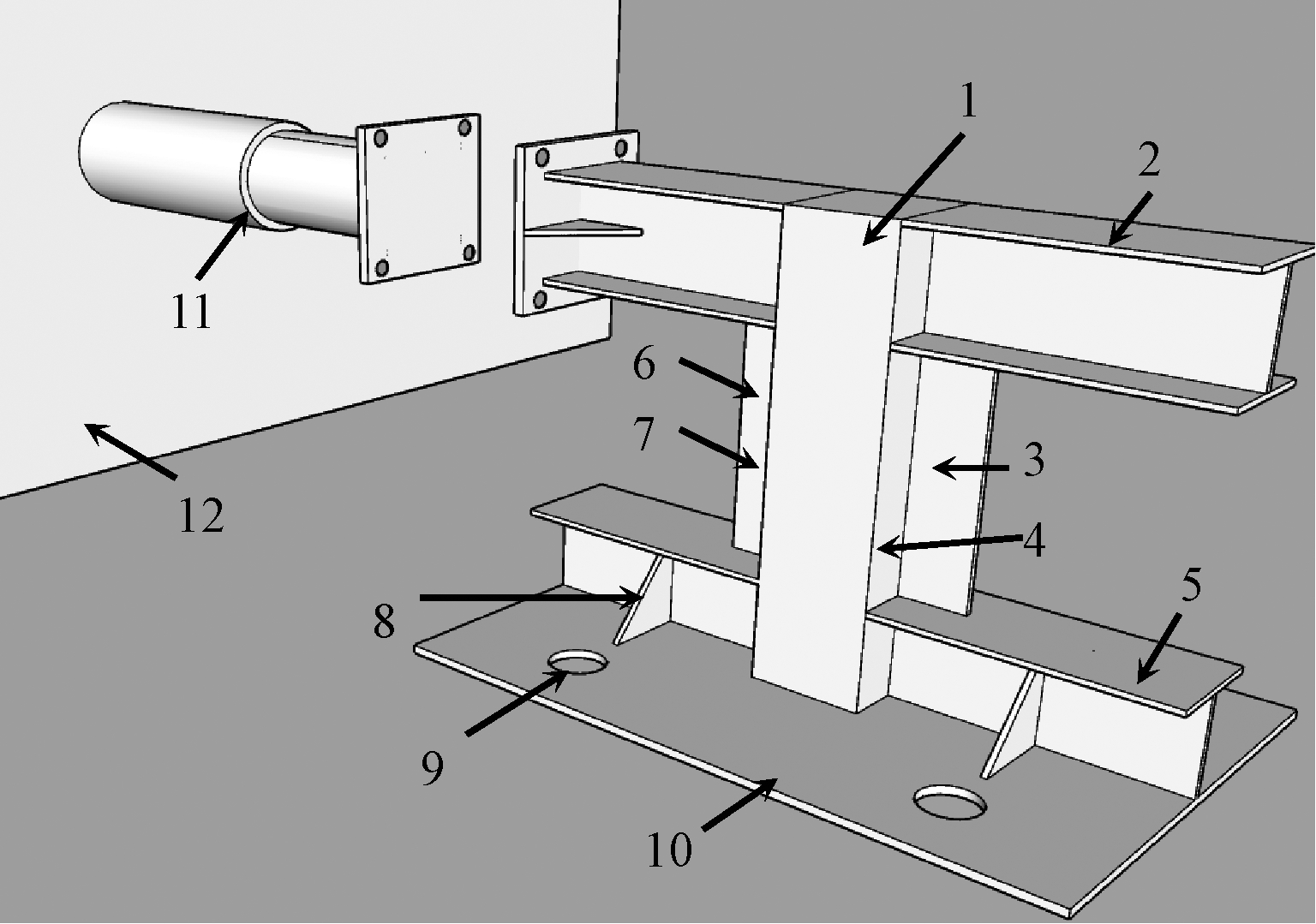
1—方管剪力键;2—上钢肋;3—背力面加劲板;4—背力面;5—下钢肋;6—迎力面加劲板;7—迎力面;8—三角加劲板;9—地脚螺栓孔;10—贴地钢板;11—水平加载装置(作动器);12—反力墙。
图3 ST-1试件加载方案
Fig.3 Loading scheme for specimen ST-1

a—迎力面测点布置;b—背力面测点布置。
注:1~6为应变测点;D1、D2为位移测点,D3为底板侧移监测点。
图4 ST-1剪力键应变测点和位移测点布置
Fig.4 The arrangement of shear connector ST-1 strain and displacement measuring points
1.2 试验测点布置
通过有限元初步模拟的应力状态,在易出现应力集中的区域设置应变监测点。为统一测点定位,所有应变测点距离所在板件边缘约20 mm;位移测点设置3个,D1、D2号位移测点设置在净空高度处,D3号测点设置在底板对称轴端部,D1测点和D2测点位移的平均值减去D3号测点位移,即为剪力键在净空处的实测侧移。图4为ST-1试件的测点布置情况。需要说明的是,由于ST-0试件没有加劲板,故没有5、6测点,其余测点的位置完全相同。
1.3 试验设备及加载方案
加载设备采用长春科新试验仪器有限公司生产的600 kN作动器;应变测试设备为秦皇岛信恒科技有限公司生产的CM-1J-32型数字静态应变仪;位移测试设备为秦皇岛协力仪器有限公司生产的XL2116B型位移测量仪,位移传感器量程为50 mm。
采用混合加载方式。在构件弹性受力阶段,先采用力加载。即安装就位后,先给试件一个初加载(0.5 kN),用于消除地脚螺栓与地梁之间的安装间隙,第一级荷载加载至5 kN后采集数据,之后每增加5 kN采集一次数据;当试件接近屈服荷载时,改为位移加载,侧移每增加20%的屈服位移时,采集一次数据,直至试件出现明显的屈曲或者破坏。
2 试验数据分析
2.1 加劲板对侧移曲线的影响
由图5可以看出:两种曲线均具有明显的非线性变形特点。但设置加劲板的试件ST-1的曲线倾角明显大于ST-0试件。说明加劲板对方管剪力键的抗侧刚度增强作用是非常显著的。ST-1试件当侧移达到6 mm时,其承载力可达到200 kN以上,几乎是未设置加劲板的ST-0极限承载力的2倍。
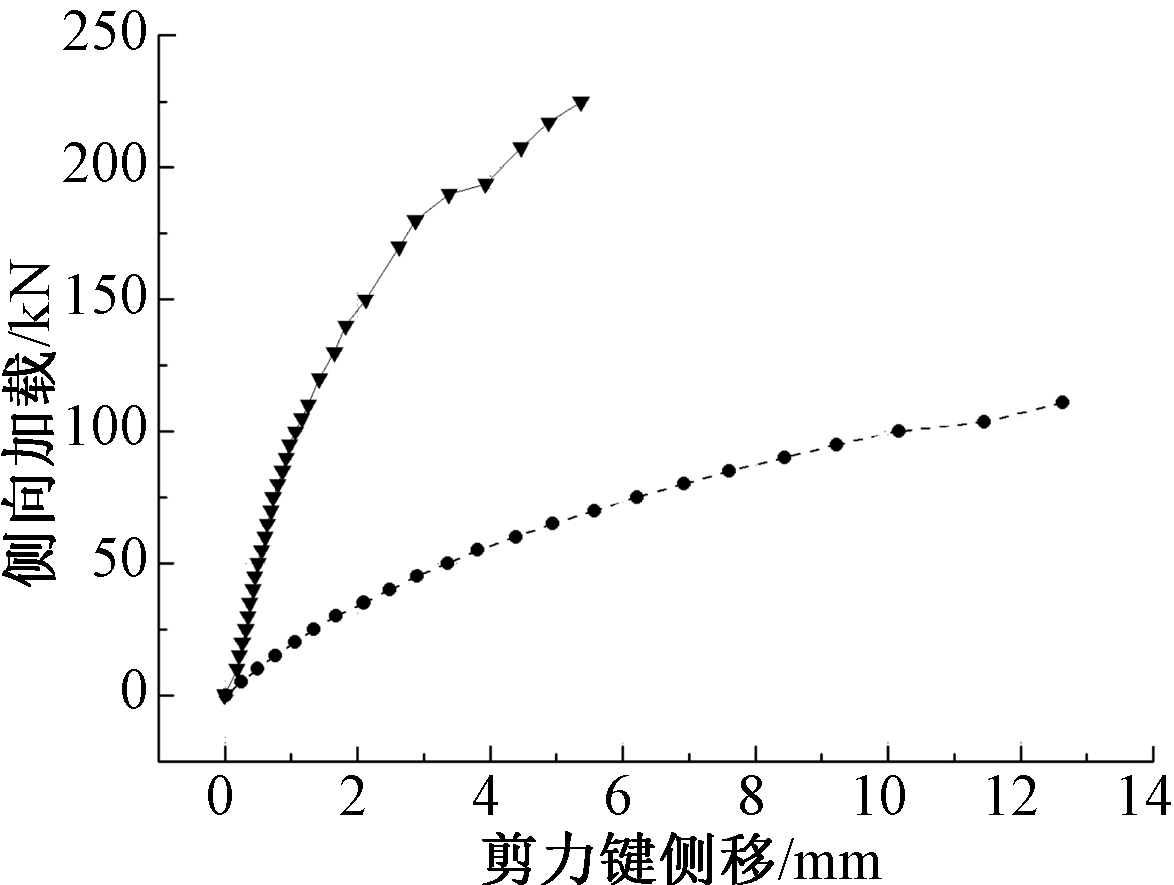
![]() — ST-1;
— ST-1;![]() — ST-0。
— ST-0。
图5 两试件的荷载-侧移曲线对比
Fig.5 Comparison of loading-lateral displacement curves of two specimens
2.2 加劲板对剪力瞬时抗侧刚度的影响
为了进一步研究剪力键在加载过程中抗侧刚度的变化,假设共加载n级荷载至试件发生破坏,引入瞬时刚度的概念:
ki=(Pi+1-Pi)/(di+1-di)
i=1,2,3,…,n-1 (1)
式中:ki为加载至第i级荷载时方管剪力键的瞬时抗侧刚度,kN/m;Pi为第i级荷载,kN;Pi+1为第i+1级荷载,kN;di为第i级荷载对应的侧移,m;di+1为第i+1级荷载对应的侧移,m。
通过图6可以看出,随着各级加载的递增,两种试件的瞬时抗侧刚度整体分布呈下降趋势。在0~100 kN的加荷范围内,ST-0试件的刚度近似呈直线下降趋势,从25 kN/m左右递减至5 kN/m,瞬时刚度分布有轻微离散现象;而ST-1试件由于设置了加劲板,其瞬时抗侧刚度分布尽管具有明显的离散性,但多数都在50 kN/m以上。在相同的承载水平下,加劲板对剪力键瞬时抗侧刚度的提高作用稳定在2倍以上。
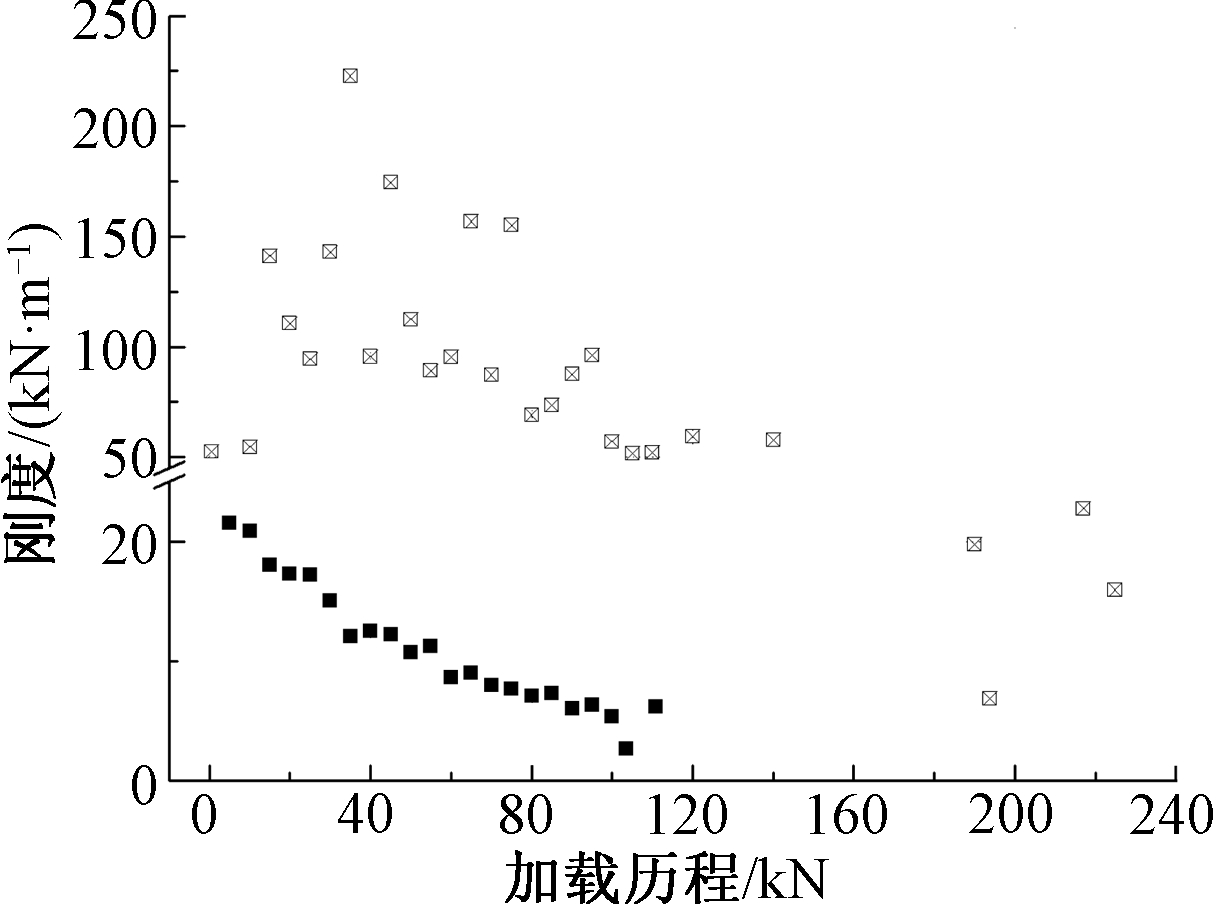
![]() — ST-0;
— ST-0;![]() — ST-1。
— ST-1。
图6 两种试件在加载过程中的瞬时刚度分布
Fig.6 The instantaneous stiffness distribution of two specimens in loading process
2.3 H形钢肋与剪力键连接区域的应变分布状态
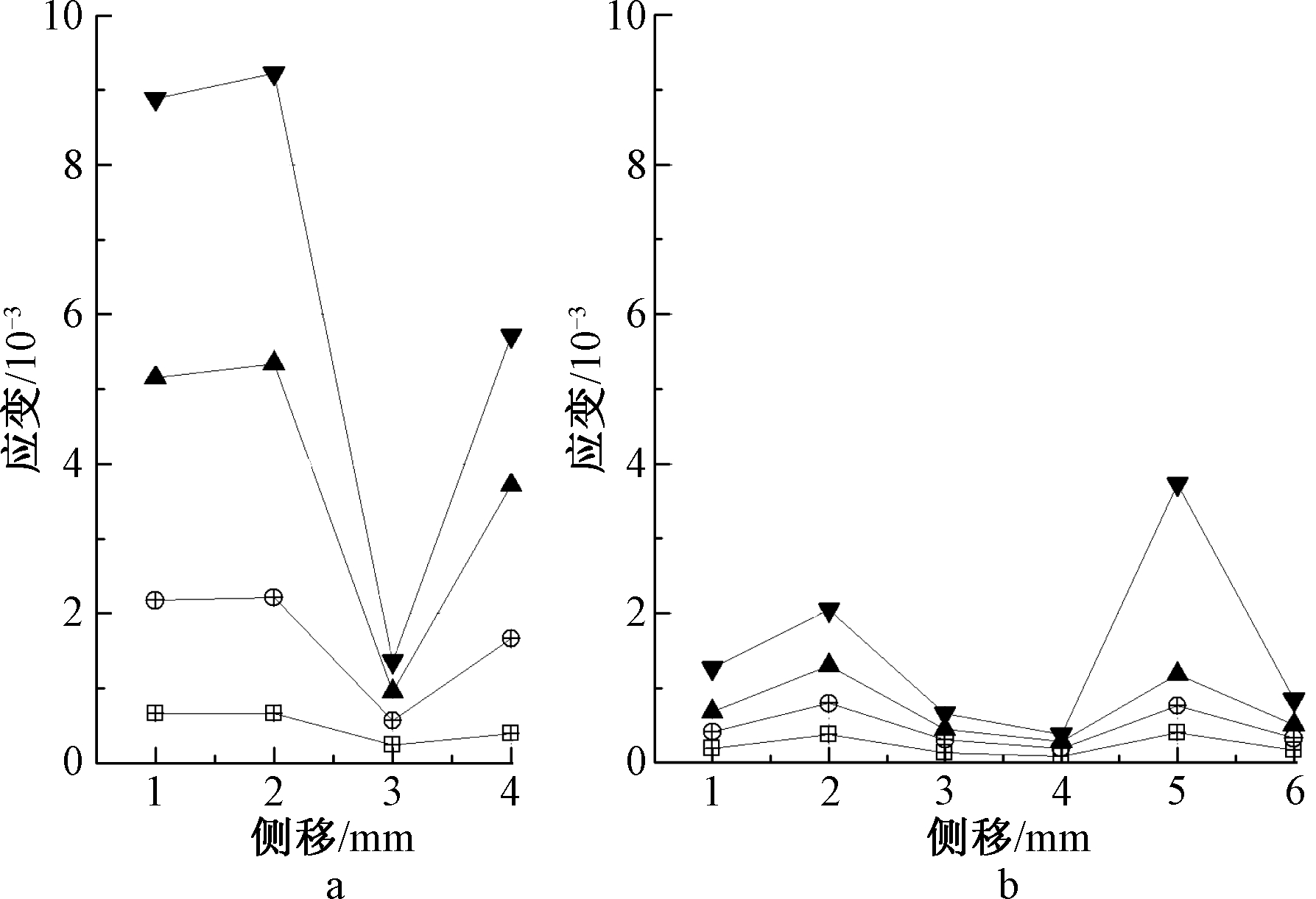
a—ST-0;b—ST-1。![]() — 25 kN;
— 25 kN;![]() — 55 kN;
— 55 kN;![]() — 85 kN;
— 85 kN;![]() — 120 kN。
— 120 kN。
图7 两种试件的应变分布
Fig.7 Comparison in strain distribution between two specimens
图7为两种试件的应变测点在相同加载水平下的应变测值。比较可知,带加劲板的试件ST-1在各级荷载下测点的应变均明显小于试件ST-0对应的各点应变。表明:加劲板能够明显降低测点的应变程度,改善剪力键端部构件连接区域的应力集中现象,延缓材料的破坏过程,对充分发挥剪力键的材料性能具有重要的意义。
3 试验数据与有限元对比分析
3.1 试验现象对比
两种试件在受力过程中,迎力面由于材料以受拉应力为主,试验现象不明显,仅有少许焊缝浮渣崩落,但焊缝整体保持完好;背力面受压凹曲现象较为明显,加劲板出现面外失稳后退出工作,如图8所示。两种试件的数值模拟破坏模式与试验现象较为吻合。
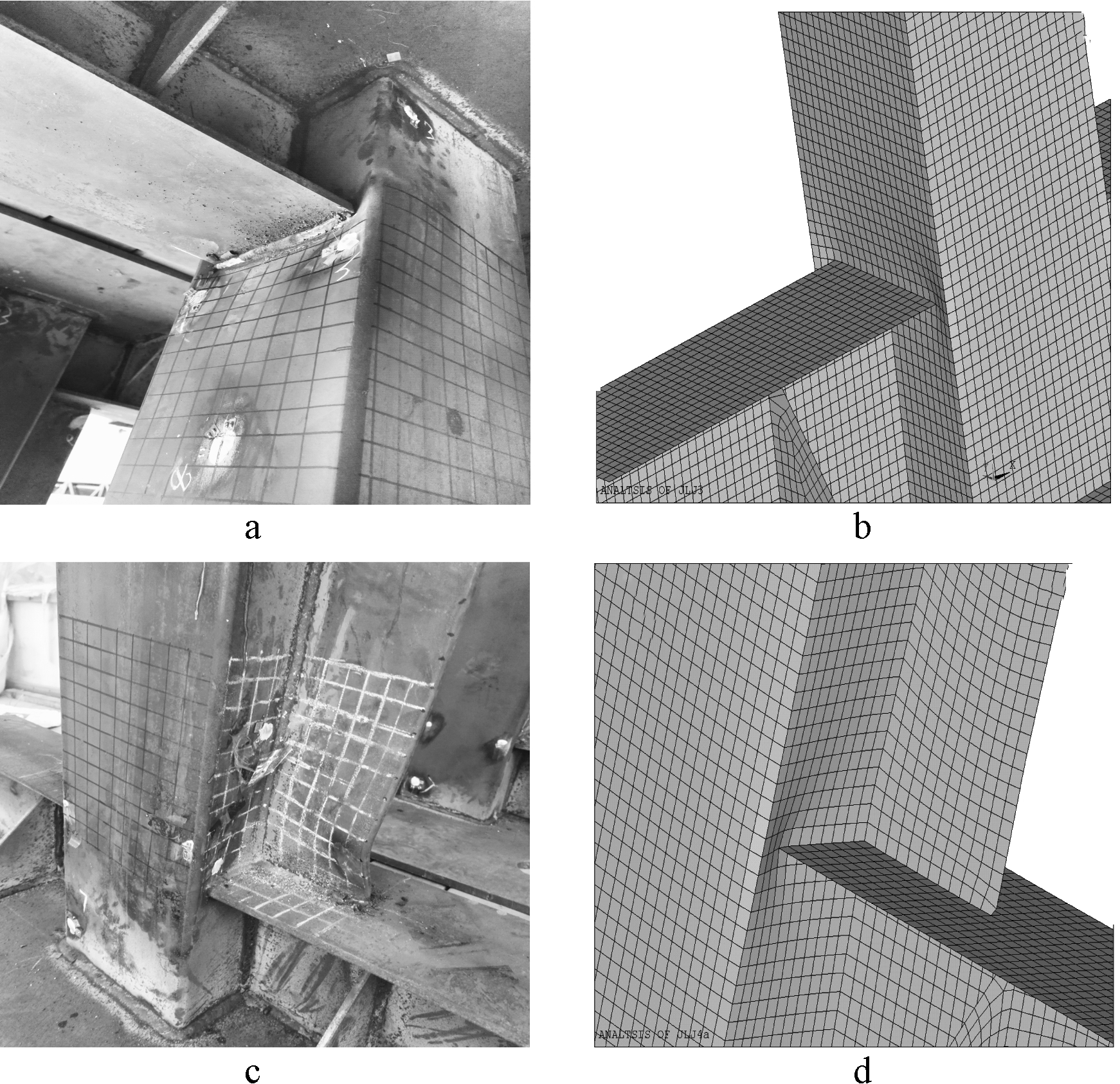
a—ST-0试验现象;b—ST-0数值模拟;c—ST-1试验现象;d—ST-1数值模拟。
图8 两试件的试验与数值模拟对比
Fig.8 Comparison of test phenomenon and numerical simulation between two specimens
3.2 位移及刚度比较
从试验与数值模拟的荷载-侧移曲线(图9、图10)来看,两种曲线趋势基本一致,说明本文的数值模拟方案能够反映实际构件的受力特点和变形规律。
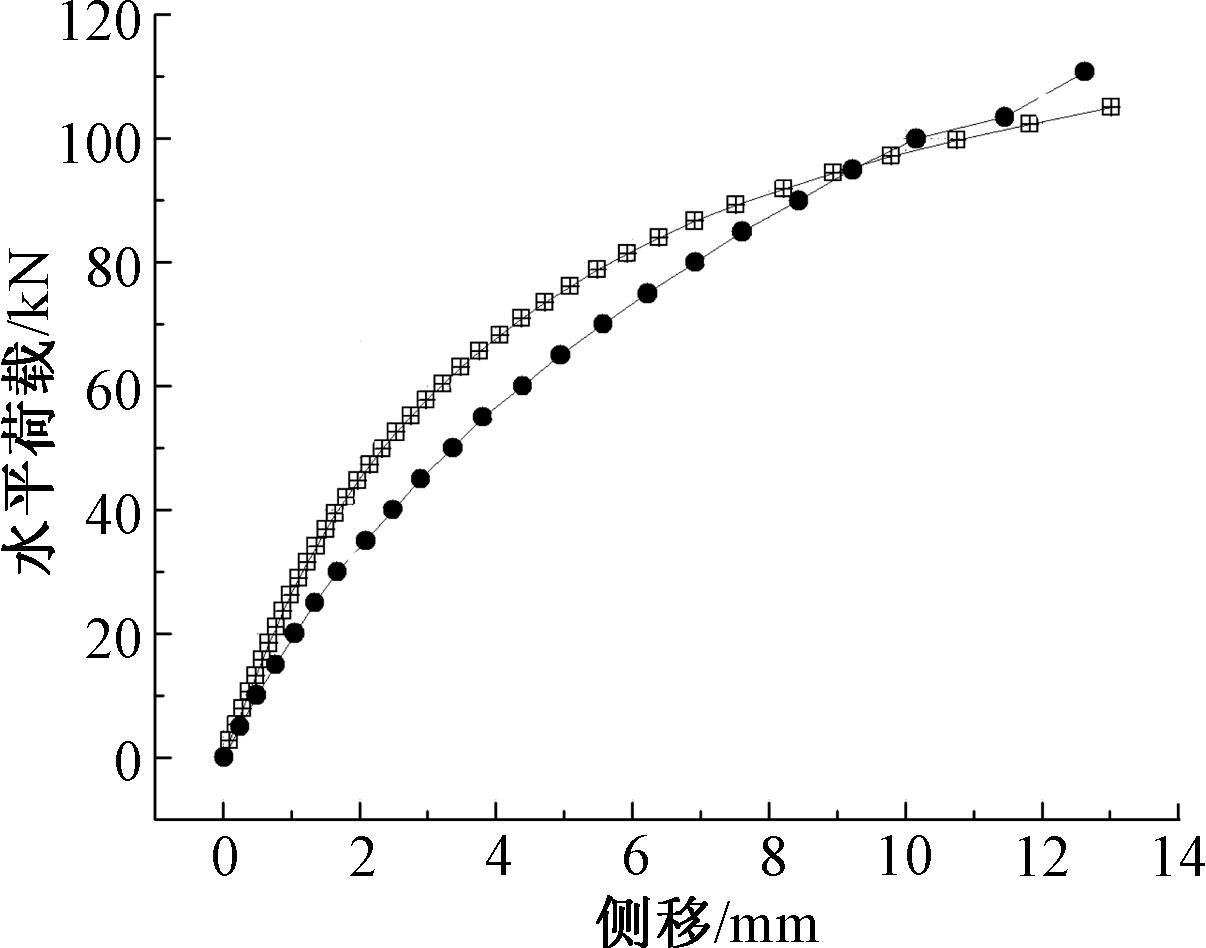
![]() — 数值;
— 数值;![]() — 试验。
— 试验。
图9 ST-0 荷载-侧移曲线
Fig.9 The loading-lateral displacement curves of ST-0
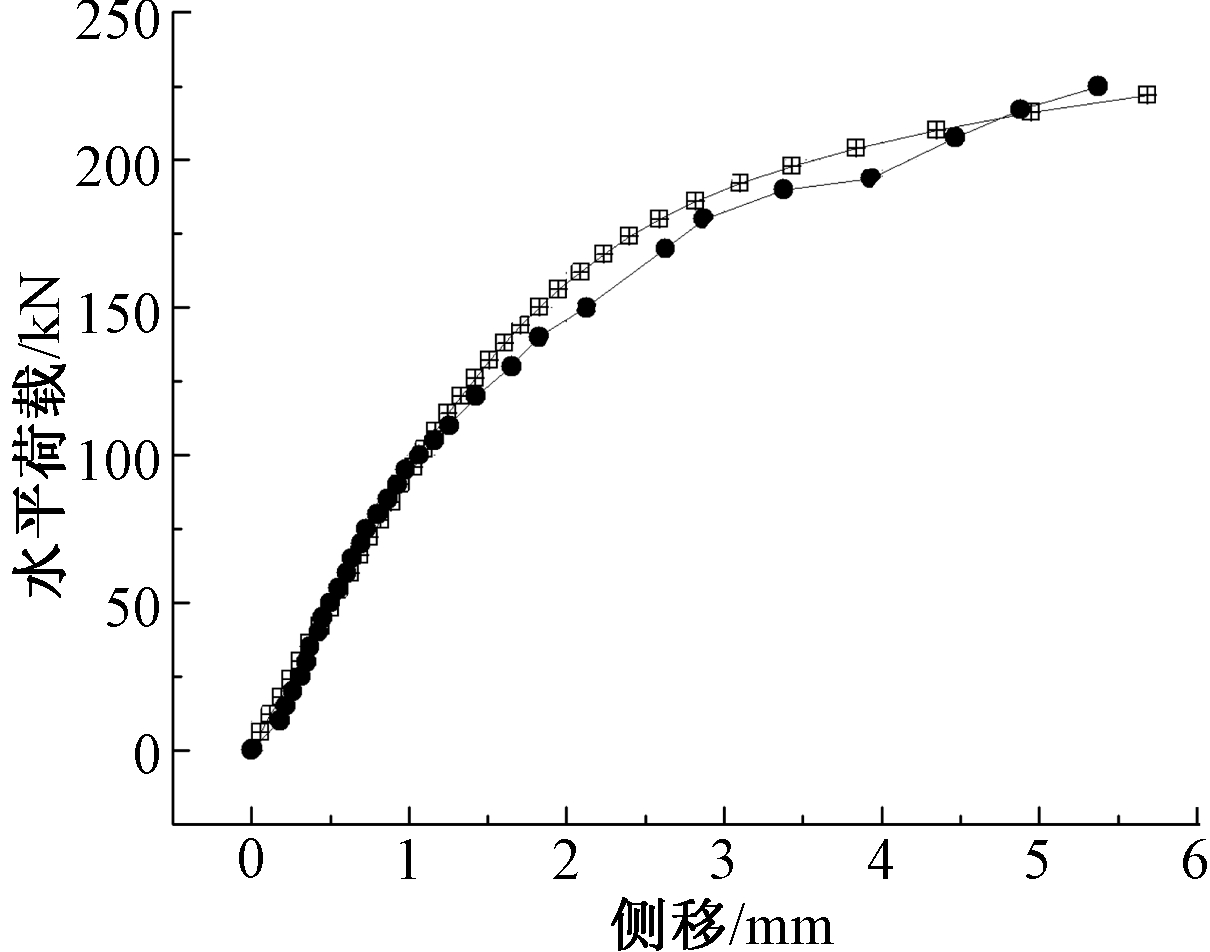
![]() — 数值;
— 数值;![]() — 试验。
— 试验。
图10 ST-1 荷载-侧移曲线
Fig.10 The loading-lateral displacement curves of ST-1
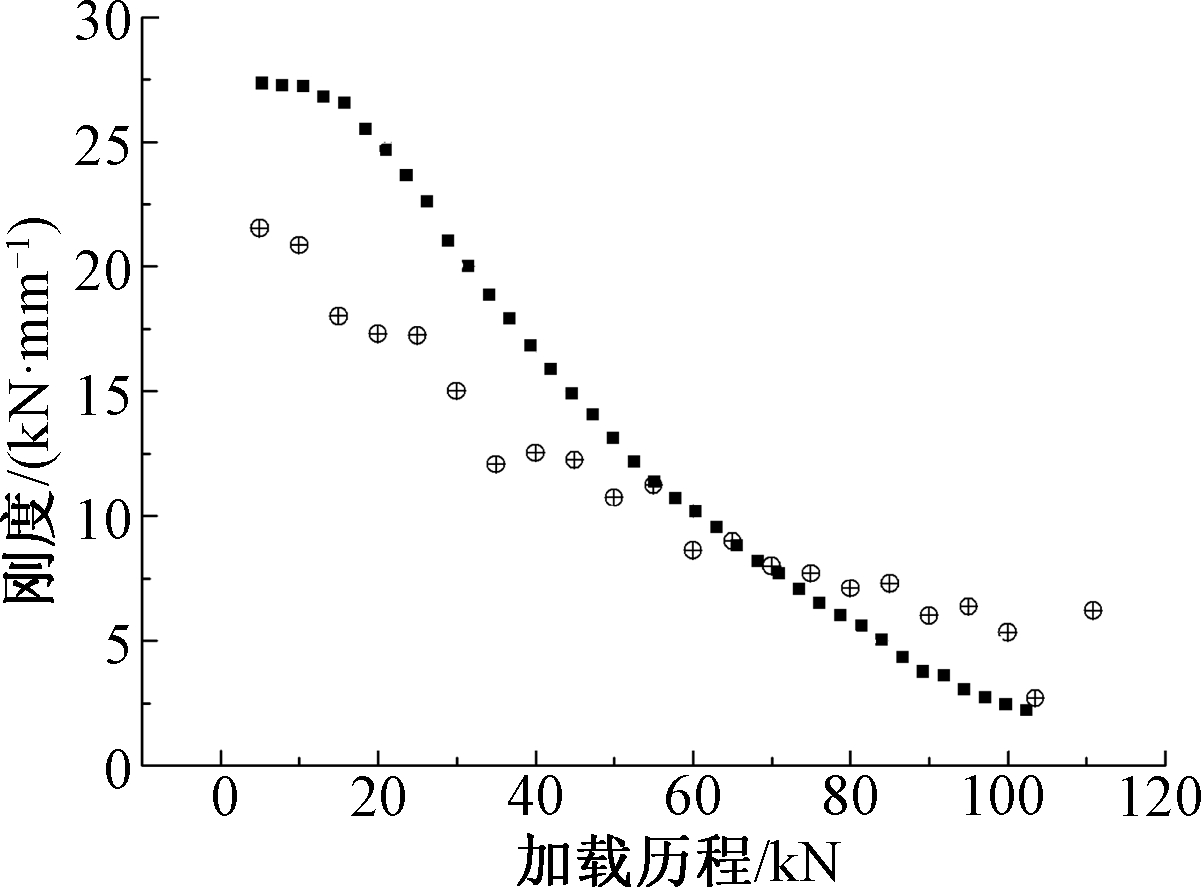
为了进一步比较试验模型和数值模型对剪力键在加载过程中抗侧刚度的变化趋势,现将各级加载下的瞬时抗侧刚度分布情况绘于图11。
![]() 有限元法;
有限元法;![]() 试验方法。
试验方法。
图11 ST-0 瞬时抗侧刚度分布
Fig.11 The instantaneous stiffness distribution of ST-0
从图11可以看出:试件刚度的实测结果与数值分析结果有差别。其原因:一是在于板件材性的随机性,本文数值模拟采用GB 50017—2017《钢结构设计标准》规定的材性指标,与实际试件存在一定的差异;二是瞬时抗侧刚度在计算过程中,由于每一级的荷载、位移读数存在随机性,系统误差使得瞬时抗侧刚度的分布存在一定的跳跃性。但总体来看,两种方法的瞬时抗侧刚度分布总体趋势一致。无论是数值方法还是试验方法,无加劲板剪力键的抗侧刚度随着加载进程均逐渐减小,这意味着无加劲板时,方管剪力键几乎没有弹性变形阶段;有限元模型的初始刚度明显大于试件的初始刚度,但后期试件模型的残余刚度稍大于数值模拟的结果。
由图12可知,带加劲板剪力键的瞬时抗侧刚度分布情况总体趋势仍然一致。两种方法的瞬时抗侧刚度分布状态均可按加载历程分为两个阶段:第一阶段为0~100 kN时,此阶段瞬时抗侧刚度几乎维持在80 kN/m以上,试验数据离散性较大,从统计意义上来讲,与数值方法所得结果一致,此阶段可认为方管剪力键处在完全弾性工作阶段;第二阶段为从100 kN加载至构件失效,此阶段瞬时抗侧刚度随着加载逐渐降低,可认为是弹塑性工作阶段。由此可见,加劲板的设置使得方钢管剪力键具有明显的弹性工作阶段和弹塑性工作阶段。

![]() 有限元法;
有限元法;![]() 试验方法。
试验方法。
图12 ST-1 瞬时刚度分布
Fig.12 The instantaneous stiffness distribution of ST-1
3.3 应变分布对比
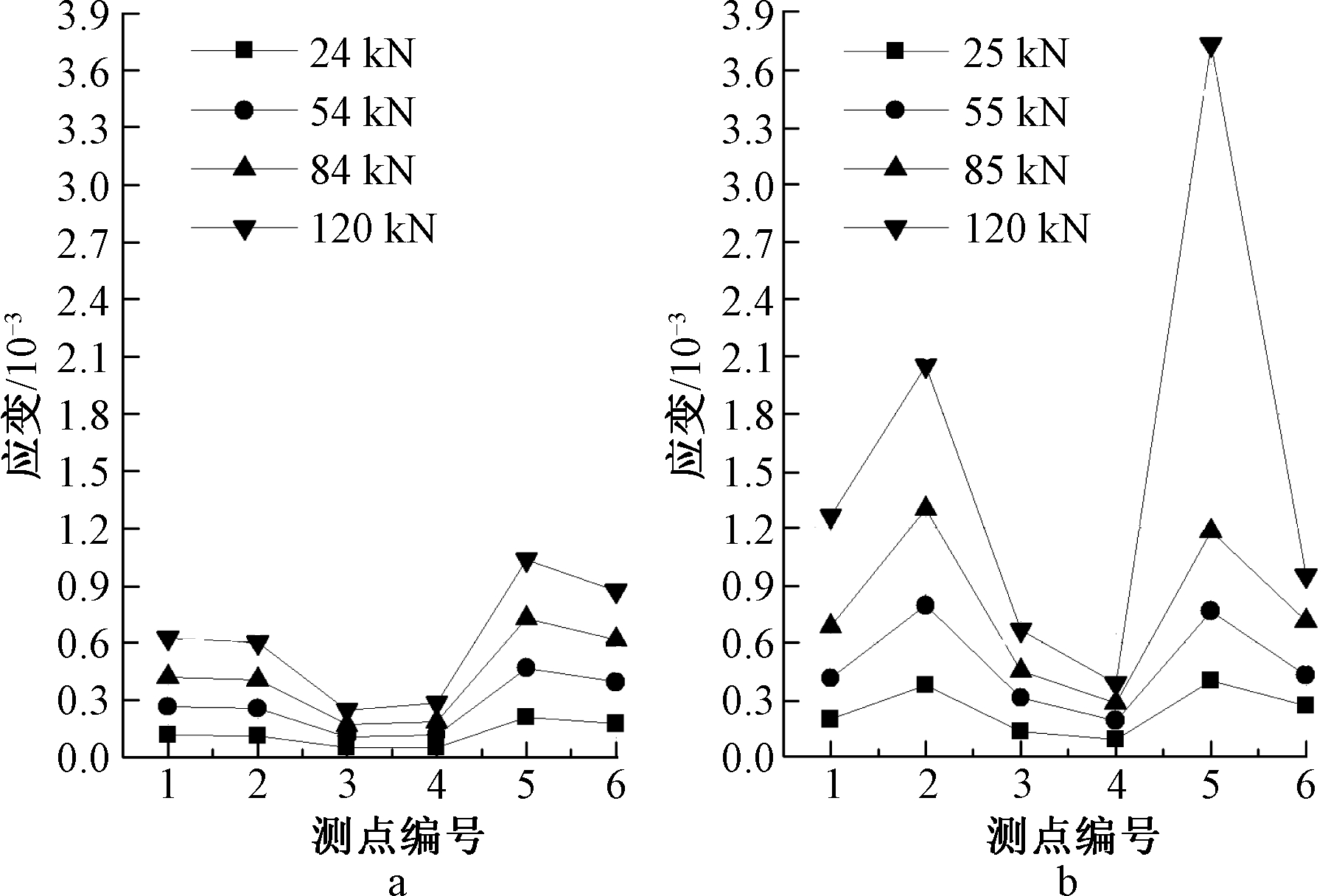
图13 ST-1 数值模拟与试验结果对比
Fig.13 Comparison between finite element analysis and test results of ST-1
以ST-1试件为例,对比了四级荷载下相同测点的应变情况。需要说明的是,根据试验极限承载状态,数值模型施加的总荷载值为240 kN,数值模型在取得40个荷载步时,能较好地兼顾计算效率和收敛性。每一级荷载按6 kN递增,故近似选择了24,54,84,120 kN时的数值模拟结果分别与试验时加载到25,55,85,120 kN时的试验结果做近似对比。由图13可知:数值模拟结果总体上小于试验结果,尤其是加载至120 kN时,测点5应变试验值是对应数值模拟值的近3倍。可能的原因是:由于应力集中区域的应力梯度很大,试验测点选点的位置稍有偏差,使得实测数据偏差很大。但从总体对比来看,数值模拟结果和试验数据结果均表明:测点1、测点2、测点5及测点6是应变程度较大的点,总体应变分布规律两者是一致的。
4 有限元分析
4.1 建模参数
数值建模时,考虑到试件均由钢板拼焊而成,采用Shell 181模拟钢板;由于试件均由规则的矩形钢板组成,采用映射网格划分方式划分网格;程序非线性分析时,采用完全的牛顿-拉普森方法;考虑到参数化批量分析时的计算量和计算收敛性,同时兼顾计算精度,经过多次试算,每个网格控制在20 mm时能取得较满意的计算结果;将贴地钢板的4个地脚螺栓孔附近的节点自由度全部约束住,以模拟试件贴地钢板在地脚螺栓和刚性垫块的挤压约束作用。限制加载端板竖直方向的自由度,以模拟作动器的水平加载作用;网格划分及边界约束如图14所示。假定试件材料为理想弹塑性,采用双线性随动强化模型,钢材弹性模量E为206 000 MPa,材料屈服后的弹性模量近似按0.01E取值,以近似模拟材料的理想塑性流动,泊松比取0.3。

图14 数值模型的边界约束与网格划分
Fig.14 Boundary constraints and meshing of the numerical model
钢材屈服强度按GB 50017—2017《钢结构设计标准》取235 MPa,泊松比为0.3,采用双线性随动强化模型。
为了研究加劲板尺寸对剪力键受力的影响,基于参数化建模分析,假定在方管剪力键尺寸不变的情况下,仅改变加劲板的宽度和厚度,考察加劲板宽度和厚度变化对连接区域受力性能的影响程度。建模参数如表1所示。
表1 加劲板宽度和厚度取值
Table 1 The widths and thickness of stiffening plates mm

剪力键编号加劲板宽度加劲板厚度SC-00-00(ST-0)——SC-06-106010SC-12-10(ST-1)12010SC-18-1018010SC-24-1024010SC-12-061206SC-12-081208SC-12-10(ST-1)12010SC-12-1212012SC-12-1412014
4.2 加劲板宽度对剪力键的影响
4.2.1 刚度影响分析
瞬时抗侧刚度在加载过程中数值保持稳定,意味着构件连接区域的受力仍然处于弹性阶段。由图15中四级加劲板宽度下的瞬时抗侧刚度分布趋势可知,加劲板宽度对刚度的提高作用非常显著,且4种构件均表现出明显的刚度稳定阶段(弹性受力阶段)和刚度下降阶段(弹塑性受力阶段)。加劲板宽度由60 mm增至120 mm时,弹性受力阶段过程明显延长,继续增加加劲板宽度,弹性受力阶段的延长已不明显。

图15 加劲板宽度对瞬时刚度分布的影响
Fig.15 Effect of stiffening plate width on instantaneous stiffness distribution
4.2.2 Mises应力比较
由图16可知:除了测点3外,其余测点应力均随着加劲板宽度的增加呈现减小趋势;当宽度由60 mm变至120 mm时,剪力键背力面的测点1、2的应力下降最为明显,继续增加宽度,该两点应力降低幅度则不太明显;测点3处于钢管角部与贴地钢板交汇处,应力状态复杂,随着加载进程,该测点应力出现反复变化;但总体上,测点5应力始终起控制作用。
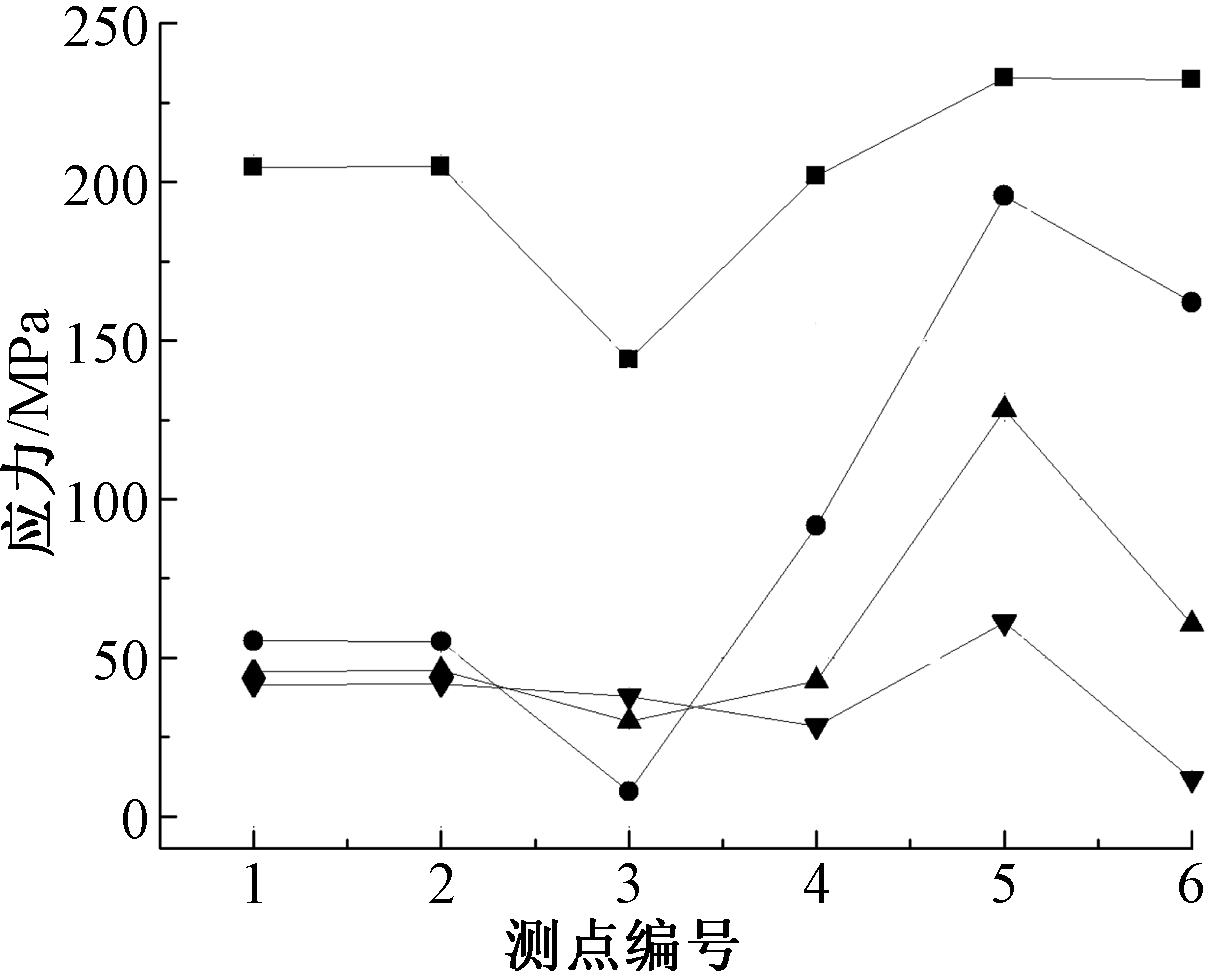
![]() — 60 mm;
— 60 mm;![]() — 120 mm;
— 120 mm;![]() — 180 mm;
— 180 mm;![]() — 240 mm。
— 240 mm。
图16 加劲板宽度Mises应力分布的影响
Fig.16 The Mises stress distribution at different stiffening plate widths
4.3 加劲板厚度对剪力键的影响
4.3.1 刚度影响分析
由图17可知,各级厚度下瞬时刚度分布仍然呈现出如4.2.1节所述的两阶段,且厚度增加能提高构件刚度,但其影响不如宽度的明显。
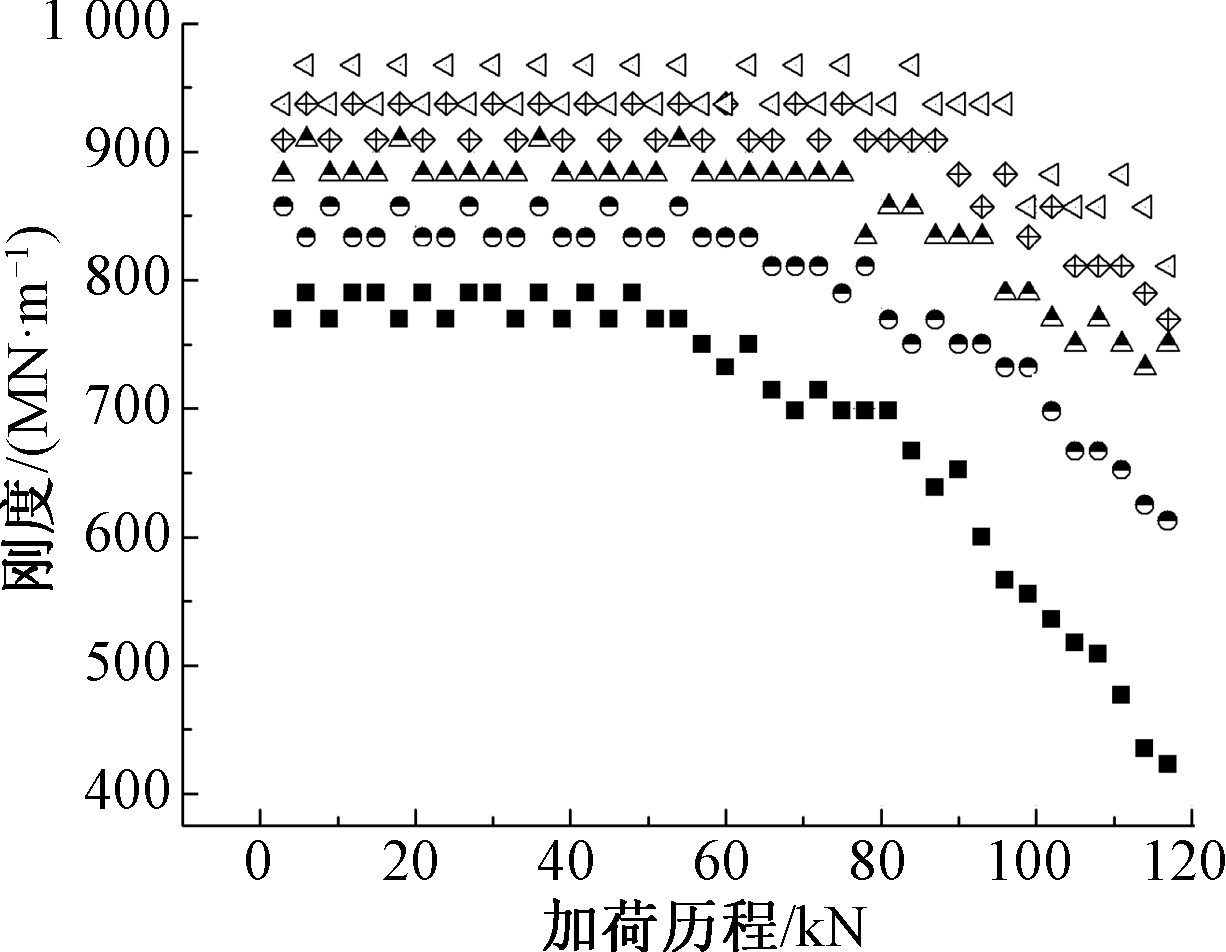
![]() 6 mm;
6 mm;![]() 8 mm;
8 mm;![]() 10 mm;
10 mm;![]() 12 mm;
12 mm;![]() 14 mm。
14 mm。
图17 加劲板厚度对瞬时刚度分布的影响
Fig.17 Effect of stiffening plate thickness on instantaneous stiffness distribution
4.3.2 Mises应力比较
由图18可知:除了测点3外,厚度的增加对其他各测点Mises应力具有较为明显的减弱作用,测点5应力状态仍然起着控制作用。
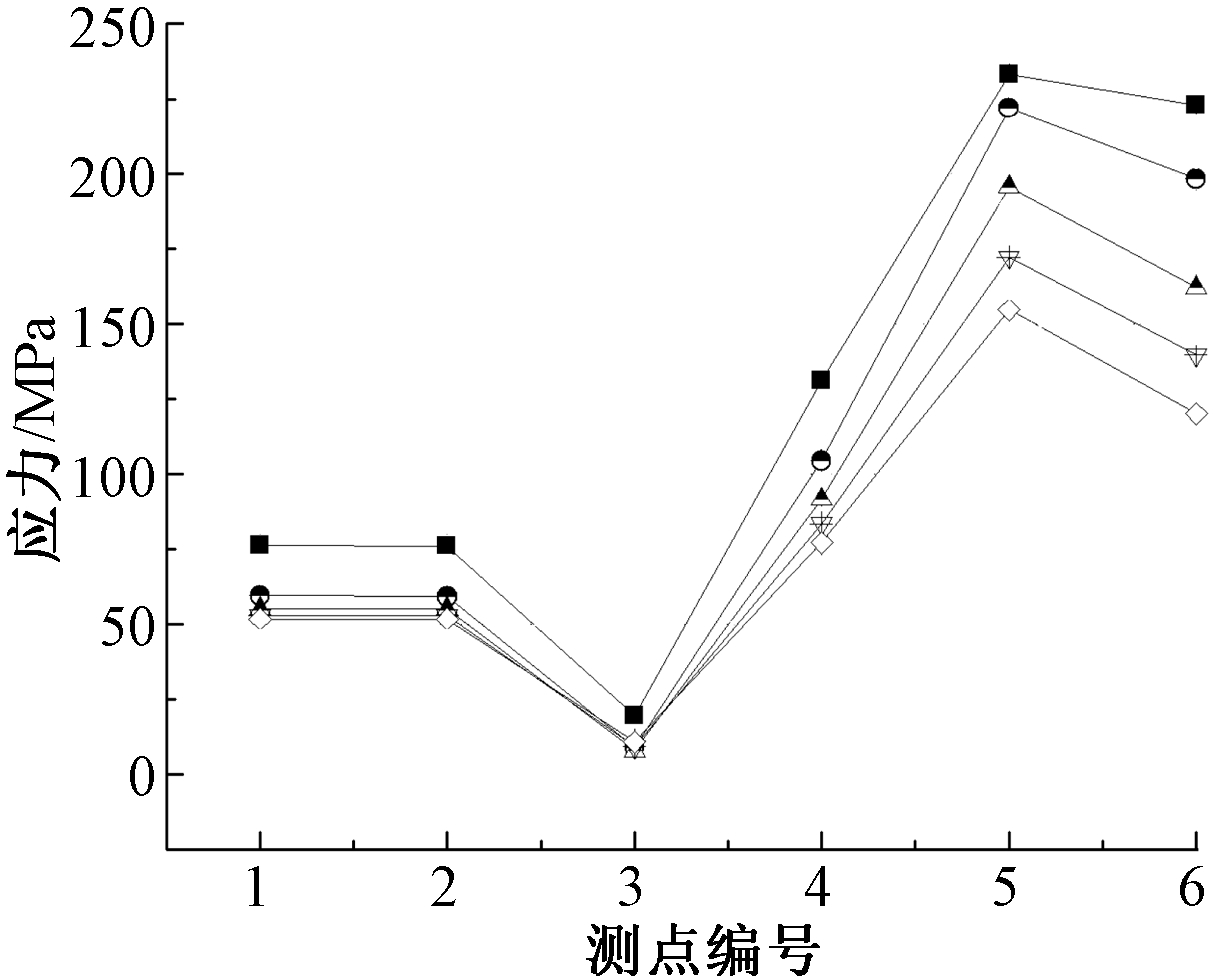
![]() — 6 mm;
— 6 mm;![]() — 8 mm;
— 8 mm;![]() — 10 mm;
— 10 mm;![]() — 2 mm;
— 2 mm;![]() — 14 mm。
— 14 mm。
图18 加劲板厚度对Mises应力分布的影响
Fig.18 The Mises stress distribution at different stiffening plate thicknesses
5 结束语
本文重点研究了加劲板对方管剪力键构件连接区域的应力、应变状态和抗侧刚度的影响,总结如下:
1)加劲板对方管剪力键节点区域的受力具有明显的改善作用。设置加劲板能够使构件受力具有明显的弹性工作阶段和弹塑性工作阶段。在构件抗震设计时建议考虑加劲板的改善作用。
2)增加加劲板的宽度和厚度均可以提高构件的刚度和承载能力,且增加宽度时的改善效果要优于增加厚度的改善效果。
3)采用本文的数值模拟方案能够较好地模拟剪力键连接区域的受力和变形。
4)工程设计中,应合理考虑加劲板的有利作用降低构件应力水平,充分发挥材料性能、节约钢材。
[1] 白志强,魏艳辉,卢亚琴,等. 钢-混凝土组合空腹夹层板基本频率的参数分析[J].空间结构,2018,24(4): 68-73.
[2] 姜岚, 马克俭, 张华刚,等. 协同式空腹夹层板动力特性分析及舒适度研究[J].地震工程与工程振动,2017,37(6):122-131.
[3] 孙涛, 马克俭, 刘宪庆,等. 钢空腹夹层板结构等效剪切刚度分析[J]. 空间结构, 2017, 23(2):54-59.
[4] LUAN H, MA K, QIN Y, et al. Investigation of the Structural Behavior of an Innovative Steel Open-Web Floor System[J]. International Journal of Steel Structures, 2017, 17(4):1365-1378.
[5] 陈强,肖建春,马克俭,等.剪力键节点域对钢空腹夹层板静力特征的影响分析[J].广西大学学报(自然科学版),2018,43(1):41-49.
[6] 刘卓群, 马克俭, 肖建春,等. 混凝土板对钢空腹夹层板楼盖静力性能影响分析[J]. 广西大学学报(自然科学版), 2016(1):1-10.
[7] 刘卓群, 肖建春, 陈靖,等. 钢-混凝土组合空腹夹层板关键部位力学特性分析[J]. 贵州大学学报(自然科学版), 2015(3):119-122.
[8] 黄勇, 陈伟刚, 段莉. 钢管混凝土短柱(剪力键)受剪性能试验研究[J]. 建筑结构学报, 2011, 32(12):178-185.
[9] 刘卓群, 马克俭, 肖建春,等. 加劲板对钢空腹夹层板剪力键节点静力特性影响分析[J]. 建筑钢结构进展, 2017, 19(2):29-37.
[10] 白志强,刘晓东,邢栋,等.连接T形钢肋方钢管剪力键的静力性能试验[J].工业建筑,2018,48(10): 159-164.