空间网格结构在建筑结构中通常用来实现大跨度,其具有传力机制明确、施工速度快、造型美观等优点[1]。螺栓球节点具有受力简单明确、易于设计加工、装配误差容忍度好的特点,是目前我国运用最为广泛的一种装配式节点形式。为克服传统钢制空间网格结构在海洋岛礁、温泉湖泊、化工厂等特殊性环境下的腐蚀问题,课题组提出采用纤维增强树脂基复合材料(FRP)拉挤型材为杆件,高强铝合金为节点的FRP-铝合金空间桁架结构[2]。其节点采用螺栓球节点形式,考虑到承载螺栓为关键受力部件,拟采用高强铝合金或高强不锈钢材料。
由于节点处允许杆件与节点之间的相对转动,故一直以来,人们通常把螺栓球节点作为铰接点来处理,认为不具有抗弯能力,不能应用在承受弯矩的结构中。但实际上,理论研究和工程实践证明:螺栓球节点并不是理想的铰接点,而是具有一定转动刚度、介于刚节点和铰接点之间的一种半刚性节点。半刚性节点的概念起先来源于钢框架结构领域,早在1936年,英国标准就引入了以半刚性连接框架分析为基础的连接设计方法[3],对于框架结构的节点刚度,国外学者提出了许多分类方法,到目前为止趋于成熟,在欧洲钢结构设计标准[4](EC3)中也有详细规定。但对于空间网格结构节点刚度的分类,国内外研究较少。Wang等指出:EC3的节点刚度分类标准不适用于空间格构节点[5]。2011年,Fan等考虑节点刚度对网格结构整体性能的影响程度,并将节点抗弯刚度与杆件线刚度之比作为节点刚度系数,建立了新的节点分类体系[6]。
关于半刚性节点受弯性能,国内外学者进行了大量的试验研究、数值模拟和理论分析,其中试验研究最为基础,也最为直观。See[7]和Fathelbab[8]分别对螺栓球节点在弯矩荷载下的试验进行研究,得到了该节点的弯矩-转角曲线及套筒松动对节点转动刚度的影响规律。范峰等进一步开展了螺栓球节点压弯联合作用下的试验研究,同时建立了考虑轴压力及螺栓预紧力的半刚性节点精细化数值分析模型,得到了节点在压弯荷载联合作用下的节点转动刚度及极限承载力[9-10]。Chenaghlou进一步对螺栓球节点进行了弯矩荷载和不同轴力荷载作用下试验研究,研究表明轴力会降低螺栓球节点的极限承载力[11-12]。Fan等对碗式节点在弯矩作用和压弯联合作用下的试验进行了研究[9],并应用ANSYS进一步对碗式节点进行了数值模拟[13],研究了螺栓直径、垫片尺寸、螺栓预紧力、以及压弯应力比等不同参数对碗式节点抗转动性能的影响,拟合出了碗式节点弯矩-转角曲线预测算式。上述研究均是针对钢质节点,目前对采用铝合金及不锈钢材料的螺栓球节点抗弯性能的试验研究还鲜见报道。
本课题须对铝合金-不锈钢螺栓球节点抗弯性能展开研究。根据螺栓材料、套筒承压面积的不同,设计制备4组不同螺栓球节点,对其进行节点抗弯性能试验,得到其破坏模式、初始抗弯刚度、抗弯承载力等节点性能指标,并考察螺栓材料、套筒承压面积对节点抗弯性能的影响。根据半刚性节点分类标准,对铝合金及不锈钢螺栓球节点在FRP空间格构结构中使用进行性能分类,为结构计算提供参考。
1 试 验
1.1 材料性能试验
1.1.1 试验概况
为了解7075-T6铝合金和S51740高强不锈钢的基本力学性能,进行标准拉伸材性试验。每种材料取3个相同的标准试件,直径为8 mm,标距40 mm,分别由南京华明金属材料有限公司和上海亚螺精密紧固技术有限公司提供,具体尺寸和试件实物如图1所示。图中,L0为原始标距;Lc为平行长度;R为过渡半径;b0为试件直径。
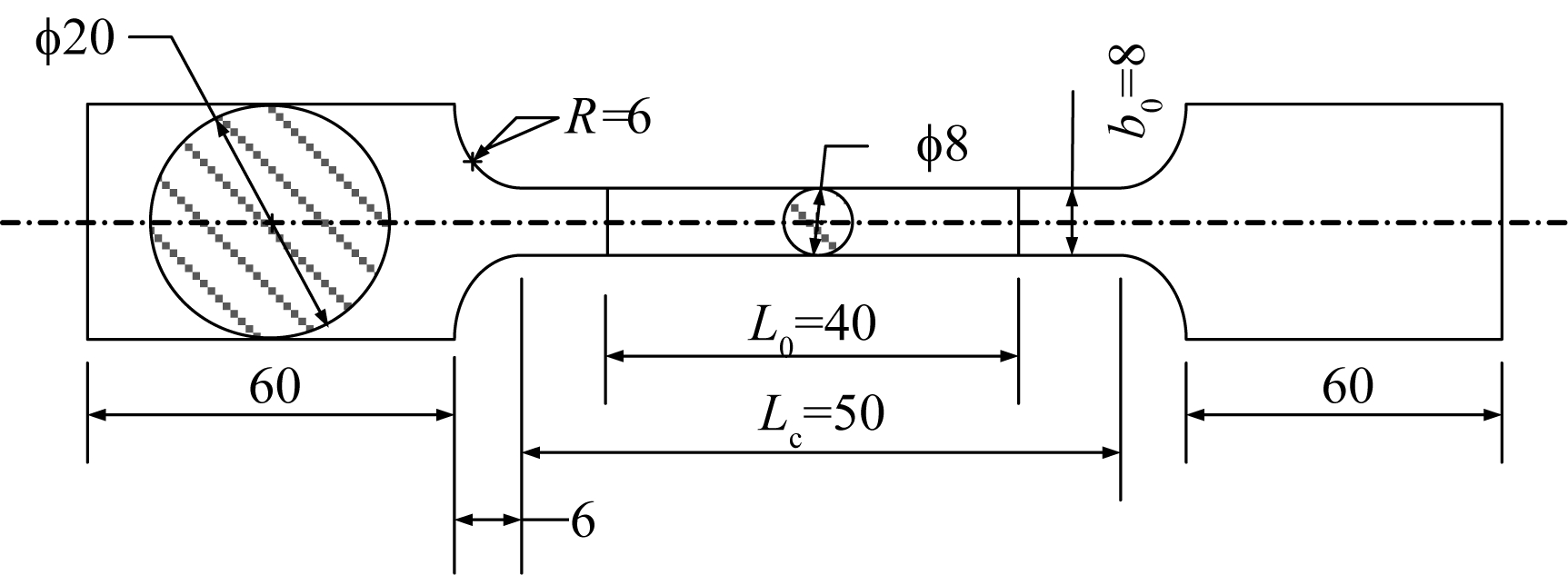
图1 铝合金-不锈钢材料标准试件及其几何尺寸
Fig.1 Standard specimen of aluminum alloy-stainless steel and sample size
试件几何尺寸及加载符合GB/T 16865—2013《变形铝、镁及其合金加工制品拉伸试验用试样及方法》[14]和GB/T 228.1—2010《金属材料 拉伸试验第1部分:室温试验方法》[15]中的规定。试验在100 kN试验机上进行,采取位移控制,加载速率0.05 mm/s,直至试件被拉断。用EIR LE-05电子引伸计(激光引伸计)测量变形。
1.1.2 试验结果
试验过程中,7075-T6铝合金试件拉断前无明显颈缩现象发生,拉断比较突然,伴随有较为低沉的响声;S51740高强不锈钢试件拉断前有明显的颈缩现象发生,响声比较清脆。试件破坏形态如图2所示。

a—铝合金标准试件破坏; b—不锈钢标准试件破坏。
图2 拉断后的试件
Fig.2 Specimens after tensile test
通过试验得出了两种材料的弹性模量、名义屈服强度、抗拉强度、断后伸长率等力学性能,见表1。
表1 材性参数
Table 1 Material mechanics property parameters
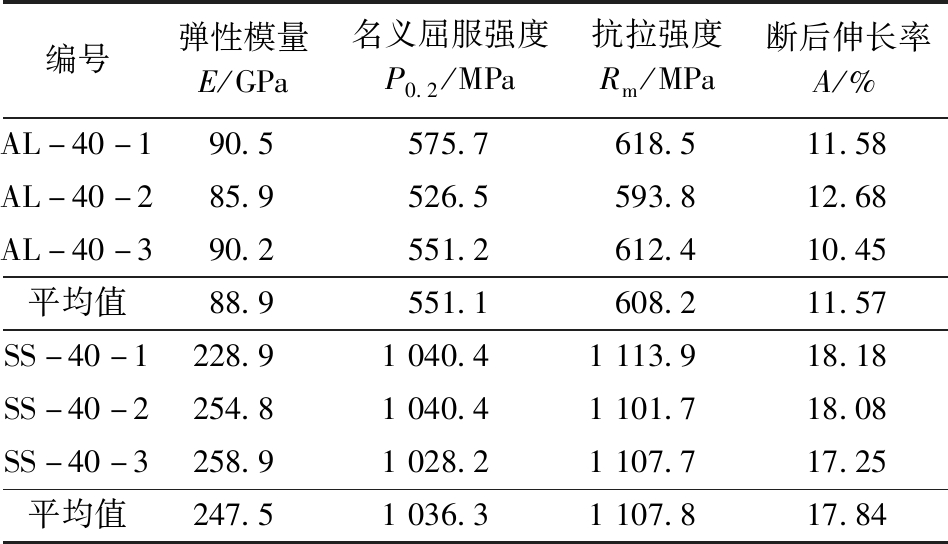
编号弹性模量E/GPa名义屈服强度P0.2/MPa抗拉强度Rm/MPa断后伸长率A/%AL-40-190.5575.7618.511.58AL-40-285.9526.5593.812.68AL-40-390.2551.2612.410.45平均值88.9551.1608.211.57SS-40-1228.91040.41113.918.18SS-40-2254.81040.41101.718.08SS-40-3258.91028.21107.717.25平均值247.51036.31107.817.84

a—7075-T6铝合金; b—S51740高强不锈钢。
图3 两种材料标准试件应力-应变曲线
Fig.3 Stress-strain curves of two standard specimens
7075-T6铝合金和S51740高强不锈钢试样的应力-应变曲线见图3。可知,各曲线差异性不大,故认为试验结果合理可靠。由表1可知,S51740高强不锈钢的抗拉强度约为7075-T6铝合金的2倍,弹性模量约为7075-T6铝合金的3倍,且在断裂前有明显的颈缩现象,断后伸长率是7075-T6铝合金的1.54倍,具有较好的韧性。两种高强螺栓材料的材性特点将对节点抗弯性能带来显著影响。
1.2 抗弯性能试验
半刚性节点连接的主要问题是转动变形,而弯矩与转角之间的关系即为节点刚度。在受力分析过程中,可用弯矩-转角特性曲线进行表述。
1.2.1 试件设计
试验采用7075-T6铝合金和S51740高强不锈钢两种不同材质的高强螺栓,分别搭配两种不同截面积的套筒,共计4个试件,编号见表2。节点由铝合金球体、套筒、封板、螺栓组成。其中,螺栓材料分别为S51740高强不锈钢和7075-T6铝合金,其余部件采用2A12-T4高强铝合金。封板设置外螺纹,与钢管外套筒内螺纹形成螺纹对[2]。各部件的具体尺寸标注如图4所示,取值详见表3。
表2 试件编号
Table 2 Specimen number

序号试件编号螺栓材料 套筒1AL-S17075-T6铝合金小套筒2AL-S27075-T6铝合金大套筒3SS-S1S51740高强不锈钢小套筒4SS-S2S51740高强不锈钢大套筒
1.2.2 试验设置及量测方案
试验在南京航空航天大学土木工程试验中心进行,采用SYB-2双向千斤顶加载,节点位移采用量程为200 mm、精度为0.01 mm的电子位移计测量,安装位置如图5所示。为了提高量测位移的精度,在钢管的上表面(位移计的正下方)粘贴了方形钢板,如图6所示。试验段包括铝合金球体、套筒、封板和螺栓,为确保试验对象是螺栓球节点,减少试验中两端杆件对试验结果的影响,尽量做大两端杆件的刚度,所以选用304不锈钢钢管,其内径60 mm,壁厚10 mm,长度670 mm。钢管两端焊接T型钢板,直接搭放在支座上(图7),故该试件可以看作是简支梁承受跨中集中荷载。

图4 螺栓球几何标注
Fig.4 Geometric annotation of bolted-ball
表3 螺栓球几何尺寸
Table 3 Size of the bolted-ball
mm
RDt1h1h2l1l2l3l4s1s2d504010421622442530323720

注:L=670 mm,L1=L4=200 mm,L2=L3=150 mm。
图5 位移计布置
Fig.5 Arrangements of displacement meters

图6 螺栓球节点现场试验布置
Fig.6 Field test arrangement of bolt-ball joint
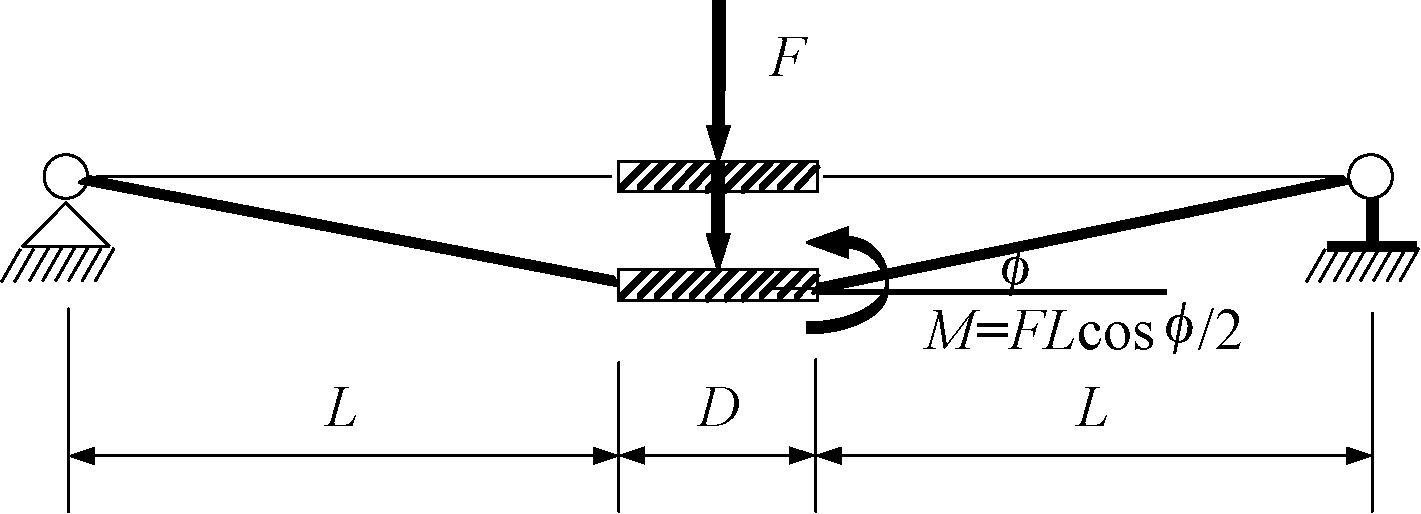
图7 计算简图
Fig.7 Computing model
节点的真实转角不便于直接测量,但钢管的转角可以作为节点的名义转角也能反映真实的节点转动情况,所以布置6个电子位移计,通过所测位移来计算节点的转角。记图5中左侧钢管上3个位移计测得的位移分别为Δ1、Δ2、Δ3,则可以计算出转角φ12=|Δ1-Δ2|/L1,φ23= |Δ2-Δ3|/L2,同理可得右侧钢管的转角φ45= |Δ4-Δ5|/L3,φ56= |Δ5-Δ6|/L4,用两侧钢管转角的平均值φ作为节点的名义转角,其计算见式(1)。
(1)
试件两端简支,在球上端施加竖直向下的压力。在此压力作用下,球与套筒连接处产生弯矩,弯矩可由压力传感器测得的荷载结合弯剪段长度推算得到,计算简图如图7所示,从而可绘出其弯矩-转角曲线。
节点承受的弯矩值为:
(2)
式中:F为施加的垂直压力;φ为两侧钢管夹角的平均值,计算见式(1);L为杆件长度。
2 试验结果及讨论
2.1 破坏模式
2.1.1 AL-S1、AL-S2试件
加载AL-S1和AL-S2试件时,随着集中力的缓慢增加,试件均出现较为明显的挠曲变形,继续加载,套筒中和轴以上部分与球和锥头相互挤紧,而中和轴以下部分,接触面相互脱开。当锥头与套筒接触面处的弯矩达到0.99 kN·m时,AL-S1试件的螺栓发生脆性断裂;而对于AL-S2试件,当锥头与套筒接触面处的弯矩达到1.34 kN·m时,螺栓发生脆性断裂。螺栓断裂声音清脆,断裂位置均位于螺栓第一螺纹根部,其余螺纹保持完好(图8a、8b),表明在弯矩作用下,节点的最薄弱部件为螺栓;试验中套筒均未见明显变形,表明节点破坏由铝合金螺栓承载能力控制。

a—AL-S1螺栓断裂; b—AL-S2螺栓断裂; c—SS-S1螺栓和套筒; d—SS-S2螺栓和套筒。
图8 试验后照片
Fig.8 Pictures after experiment
2.1.2 SS-S1、SS-S2试件
加载SS-S1和SS-S2试件时,随着集中力的增加,试件均出现明显的挠曲变形,当锥头与套筒接触面处的弯矩分别达到1.26 kN·m和1.48 kN·m时,两个试件的中和轴以下接触面分别脱开,套筒中和轴以上部分均出现压缩变形,随着弯矩的继续增大,变形也继续增大,当弯矩分别增大到2.14,2.52 kN·m时,开始卸载,节点弹性变形恢复,保留塑性残余变形。调整位移计并加上垫块后进行二次加载,此时荷载值已不再增长,表明节点处已产生塑性铰。整个过程中套筒均未出现裂缝,但出现了较大的压缩变形。拆下螺栓后,两个试件的螺栓均发生了明显弯曲变形(图8c、8d),且SS-S2试件的螺栓变形明显小于SS-S1试件的螺栓变形,说明增大套筒面积能够分担螺栓所受弯矩,并提高节点的抗弯承载能力。
2.2 弯矩-转角曲线
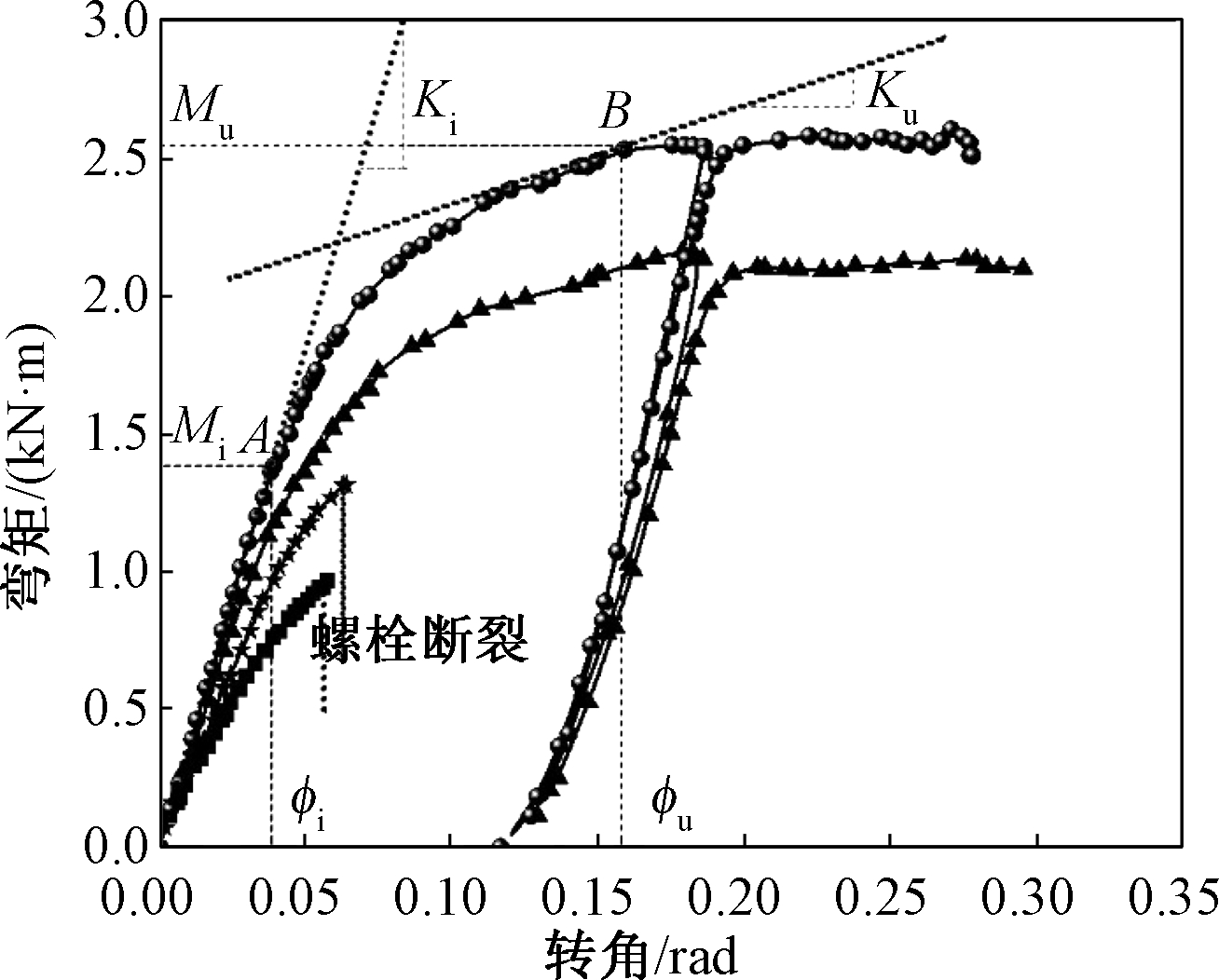
绘制实测的弯矩-转角曲线如图9所示。可知,螺栓球节点具有一定的抗弯刚度,其弯矩-转角曲线表现出了明显的非线性特征。可知:
![]() — AL-S1;
— AL-S1;![]() — AL-S2;
— AL-S2;![]() — AL-S3;
— AL-S3;![]() — AL-S4。
— AL-S4。
注:Ki为节点的初始刚度;Mi为弹性抗弯承载力[13],与曲线弹性阶段的最高点A对应;Mu为节点的最大抗弯承载力,对应于B点,而B点的弯曲刚度值Ku=Ki/10。
图9 弯矩-转角曲线
Fig.9 Moment rotation curves
1)初始阶段,4组螺栓球节点弯矩-转角曲线的变化规律基本类似。随着弯矩的增大,转角呈直线形上升,可以判断此阶段为弹性阶段。
2)对于高强铝合金螺栓球节点试件,小套筒试件和大套筒试件的弯矩分别达到0.99,1.34 kN·m之后,发生脆性断裂,节点破坏。实际上此时节点受弯性能并没有得到充分发挥,螺栓承载能力不足使得节点过早失效。将试件中的小套筒更换为大套筒,即套筒截面积提高52%时,极限承载力提高了35.35%。
3)对于高强不锈钢螺栓球节点试件,小套筒试件和套筒试件弯矩分别上升到1.14,1.43 kN·m后,弯矩增长趋势减缓,而转角急剧增大,此时节点试件处于塑性状态。当弯矩分别为2.14,2.54 kN·m时,达到极限。即套筒截面积提高52%时,极限承载力提高了18.69%。进行二次加载,其曲线基本与卸载曲线吻合。
Ki和Ku值见表4。由表4可知:随着套筒面积的增加,节点初始刚度随之增加。当套筒截面积提高52%时,高强铝合金螺栓试件和高强不锈钢螺栓试件的初始刚度分别提高12.14%、14.57%;对于同一套筒,节点的初始刚度与高强螺栓的材料性质有关,但与材料的弹性模量并非成正比例关系。
表4 初始刚度Ki及弯曲刚度Ku的值
Table 4 Computation of the Ki and Ku kN·m/rad
参数AL-S1AL-S2SS-S1SS-S2Ki22.6625.4131.1735.71Ku2.272.543.123.57
2.3 节点分类判定
范峰等将节点抗弯刚度与杆件线刚度之比作为节点刚度系数α[6],建立了新的节点分类体系,其分类如表5所示。
表5 基于节点刚度系数α的空间结构节点分类
Table 5 Joint classification of the spatial structure based on the determination coefficient α

分类节点刚度系数α刚性节点α≥5半刚性节点5>α>0.05铰接节点α≤0.05
注:节点刚度系数![]() 其中,
其中,![]() 表示结构中连接节点的杆件刚度,E表示杆件的弹性模量,I表示杆件的转动惯量,L0表示杆件的长度,K表示节点的初始抗弯刚度。
表示结构中连接节点的杆件刚度,E表示杆件的弹性模量,I表示杆件的转动惯量,L0表示杆件的长度,K表示节点的初始抗弯刚度。
该节点用在FRP-铝合金网格结构中,根据前期课题组的设计[2],FRP杆件可根据不同条件使用玻璃纤维(GFPR)、碳纤维(CFRP)或混杂纤维(HFRP),其对应弹性模量E的取值不同,以外径D为60 mm、内径d为48 mm、杆件长度L0为1 000 mm的圆管为例,分别计算节点刚度系数α的值,见表6。
表6 节点刚度系数α的值
Table 6 Computation of the determination coefficient α

纤维类别E/GPaα1α2α3α4CFRP1200.500.560.690.79HFRP700.860.971.191.36GFRP481.251.411.731.98
注:α1为不同种类复合材料网架结构中AL-S1节点的节点刚度系数;α2为AL-S2节点的节点刚度系数;α3为SS-S1节点的节点刚度系数;α4为SS-S2节点的节点刚度系数。
可见,FRP-铝合金螺栓球节点可作为半刚性节点考虑,在结构设计计算中需要考虑节点抗弯性能对结构性能的影响。
3 结束语
1)通过试验研究,验证了FRP-铝合金螺栓球节点具有一定的弯曲刚度,是介于刚接和铰接之间的一种半刚性节点。
2)对于高强铝合金螺栓,由于延性相对较差,在承受弯矩时,容易发生脆性断裂,在螺栓球节点上使用时,不能充分发挥节点抗弯性能。通过增加套筒截面积可以提高弯矩极限承载能力,对于M20的螺栓,套筒截面积提高52%时,极限承载力提高35.35%、初始刚度提高12.14%。
3)对于高强不锈钢螺栓试件组,卸载后的二次加载曲线基本上与初次加载曲线吻合,说明在初次加载期间,节点已经达到塑性阶段,且其抗弯承载能力较好。同样,套筒截面积的增加能提高抗弯承载能力和初始刚度。对于M20的螺栓,当套筒截面积提高52%时,抗弯承载力提高18.69%、初始刚度提高14.57%。
[1] 董石麟,罗尧治,赵阳. 大跨度空间结构的工程实践与学科发展[J].空间结构,2005,11(4):4-11
[2] 李峰,朱锐杰,张冬冬.高强铝合金螺栓球节点轴向受力性能与初始刚度计算模型[J]. 建筑结构学报,2018(增刊2):103-111.
[3] 冯东海. 半刚接钢框架的有限元整体分析及其影响[D].兰州:兰州理工大学, 2007:2-3.
[4] European Committee for Setandardization. Eurocode 3.Design of Steel Structures. Part1.1: General Rules and Rules for Buildings, European Prestandard:ENV 1993-1-1[S]. British: the National Annex, 1992.
[5] WANG W,CHEN Y Y. Modelling and Classification of Tubular Joint Rigidity and Its Effect on the Global Response of CHS Lattice Girders[J].Structural Engineering and Mechanics,2005,21(6): 1-22.
[6] FAN F,MA H H,CAO Z G,et al. A New Classification System for the Joints Used in Lattice Shells[J]. Thin-Walled Structures,2011,49:1544-1553.
[7] SEE T. Large Displacement Elastic Buckling Space Structures[D]. Cambridge: University of Cambridge,1983.
[8] FATHELBAB F A. The Effect of Joints on the Stability of Shallow Single Layer Lattice Domes[D]. Cambridge:University of Cambridge, 1987.
[9] FAN F,MA H H,CHEN G B, et al. Experimental Study of Semi-Rigid Joint Systems Subjected to Bending with and Without Axial Force [J]. Journal of Constructional Steel Research, 2012, 68: 126-137.
[10] 范峰,马会环,沈世钊.半刚性螺栓球节点受力性能理论与试验研究[J]. 工程力学,2009,26(12):92-99.
[11] CHENAGHLOU M R, NOOSHIN H. Axial Force-Bending Moment Interaction in a Jointing System Part I: (Experimental Study)[J]. Journal of Constructional Steel Research, 2015, 113: 261-276.
[12] CHENAGHLOU M R, NOOSHIN H. Axial Force-Bending Moment Interaction in a Jointing System Part Ⅱ: (Analytical Study)[J]. Journal of Constructional Steel Research, 2015, 113: 277-285.
[13] MA H H, FAN F, CHEN G B, et al. Numerical Analyses of Semi-Rigid Joints Subjected to Bending with and Without Axial Force [J]. Journal of Constructional Steel Research, 2013, 90: 13-28.
[14] 中国国家标准化管理委员会.变形铝、镁及其合金加工制品拉伸试验用试样及方法:GB/T 16865—2013[S].北京:中国标准出版社,2013.
[15] 中国国家标准化管理委员会.金属材料 拉伸试验 第1部分:室温试验方法:GB/T 228.1—2010[S].北京:中国标准出版社,2010.