近年来，随着我国经济的飞速发展、科学技术的进步、施工工艺的不断完善，在大跨空间结构的建设方面取得了较显著的成就。大跨空间结构外形美观、结构新颖，被越来越多的公共设施所采用，大跨空间结构的发展也成为了衡量一个国家建筑行业发展水平的一项重要指标[1-2]。随着轻质高强材料的使用，建筑跨度越来越大，结构自振周期增长、阻尼较小，风敏感性较强，风荷载成为主要控制荷载，风对结构造成的破坏频发。1995年，佐治亚穹顶在暴风雨的袭击下破坏[3]，1996年，15号强台风正面袭击广东省湛江市，湛江市体育馆5 000 m2的屋面被吹走了2/3；2002年，苏州新建的尚未投入使用的体育场部分屋顶被强风掀去[4]。工程结构的服役环境存在不同程度的腐蚀性[5]，在长期的自然环境侵蚀以及使用功能的双重作用下，由于钢材自身的特性，网架极易出现老化、锈蚀以及疲劳现象，严重影响结构的安全性[6]。当风流经屋面时，在屋面产生强大吸力的同时会引起屋面的剧烈振动，对使用了一定年限、构件产生锈蚀的结构更易造成严重破坏，目前亟需对既有在役大跨屋盖结构的风致响应及响应控制进行研究。
本文对带挑檐大跨屋盖的刚性结构模型进行风洞试验，利用实测风压对屋盖风振响应进行数值模拟，并对增设黏弹性阻尼器的屋盖结构的减振效果进行分析。
1 试验简介
1.1 试验模型和测点布置
试验模型的原型结构屋盖平面尺寸为60.5 m×36.5 m，其中挑檐的悬挑长度为5.5 m，屋面高度为15 m。屋盖采用正四角锥网架结构，网架高度为2.1 m，采用上弦节点支撑方式，分格为3 m×3 m，上弦节点数为345个。材料选用钢材Q345B，强度设计值为305 MPa，密度为7 850 kg/m3，弹性模量为2.06×105 MPa。钢构件选用φ60×3.5、φ114×4、φ159×8三种型号。使用3D3S软件进行屋盖结构设计，风向角示意见图1。
图1 风向角示意
Fig.1 Schematic diagram of wind direction angle
风洞试验采用刚性结构模型，模型缩尺比取1∶100。试验模型的屋面测点与节点分布如图2所示，其中实心圆为上弦节点，空心圆为风压测点。
图2 节点与测点分布
Fig.2 Arrangement of nodes and pressure measuring points
风洞模型试验在0°～360°范围内每隔10°取一个风向角，并加测45°、135°、225°、315°风向角，共测得40个风向角的风压数据。
1.2 风场模拟
风洞模型试验在北京交通大学风洞实验室进行，试验模型结构位于城市郊区地带，参考GB 50009—2012《建筑结构荷载规范》[7],地貌类型为B类，粗糙度系数α=0.15。
由于空气的流动会受到地面上的各种粗糙元的摩擦作用，这种摩擦作用会随高度的增加而减弱，依据GB 50009—2012，大气边界层中的风速剖面以式(1)表示：
U(Z)=Ub(Z/Zb)α
(1)
式中：U(Z)为离地面Z处的平均风速；Z为计算高度；Ub为离地面高度Zb处、50年重现期、10 min的平均风速；Zb为参考高度，GB 50009—2012通常取Zb=10 m；α为地貌粗糙度指数。
风洞试验的风场布置与试验模型见图3。通过调整尖劈、挡板和粗糙元来模拟B类风场，试验风场最大阻塞率为2%，满足阻塞率小于5%的试验要求。
图3 风场与试验模型
Fig.3 Wind field and test model
试验前先测量模型试验区的风速以及湍流度，以获得模型处风速和湍流度随高度的变化曲线，以及模型高度15 cm处风速谱图，如图4和图5所示。可以看到，模拟的风速剖面和湍流度剖面与我国GB 50009—2012的B类风场吻合较好。
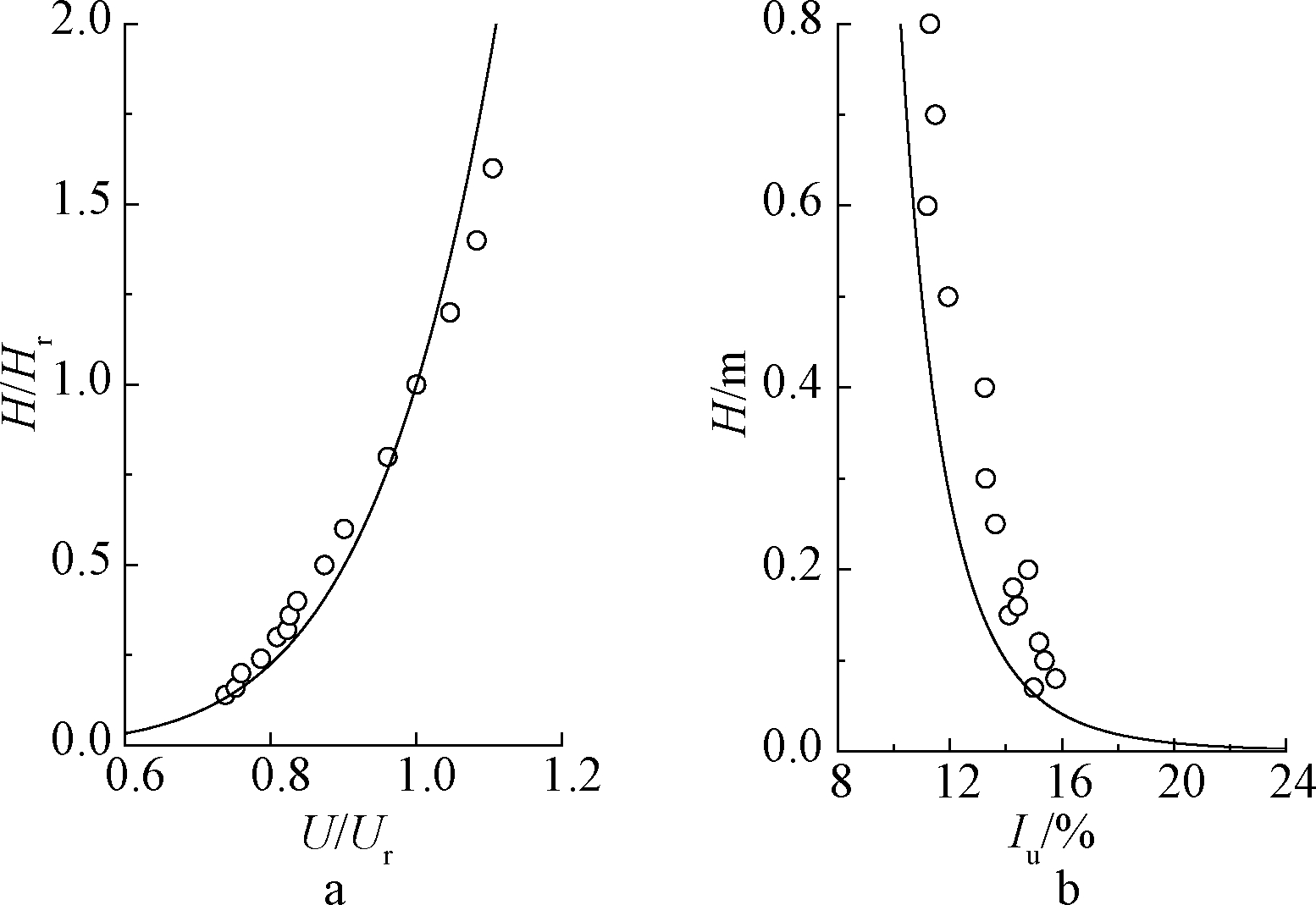
a—平均风速剖面； b—湍流度剖面。
试验值； ----GB 50009—2012计算值。
图4 B类地貌风剖面及湍流度剖面
Fig.4 B geomorphological wind profile and turbulence profile
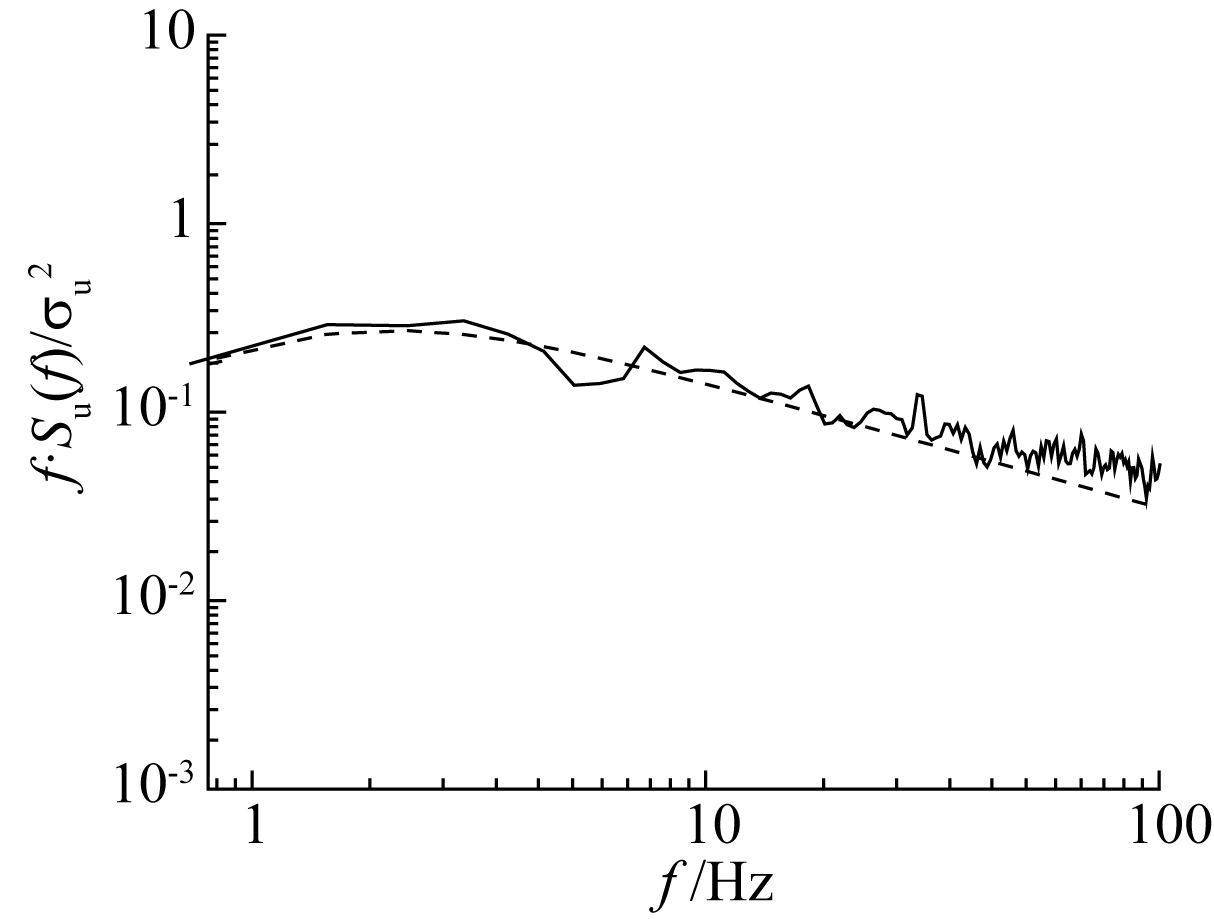
试验风速谱；
Karman谱。
图5 模型高度15 cm处脉动风速谱
Fig.5 The fluctuating wind speed spectrum at the height of 15 cm of the model
1.3 试验数据处理
1.3.1 节点风压时程的获取
采样频率为313 Hz，时长172 s，参考文献[8]对试验数据进行修正，以排除信号畸变影响。取风压力的风压系数为正，风吸力的风压系数为负。试验模型屋盖表面测点i的风压力用压力系数来表示。压力系数计算如下:
(2)
式中：CPi(t)为t时刻测点i的压力系数；Pi(t)为t时刻作用在测点i的风压力；P0和P∞分别为距地面高度15 cm处的总压与静压。
对风洞试验获得的各测点风压系数时程数据，通过本征正交分解(POD)法进行插值，利用MATLAB编程计算，可得屋面各节点处的风压系数时程。
1.3.2 时间相似比的处理
该结构所在区域为B类风场，50年重现期、10 m高度处的基本风压ω0为0.5 kPa，相对应的基本风速
风洞试验参考点选在模型高度为15 cm处，该高度与原型结构高度15 m处相对应，根据式(1)可计算得到原结构15 m处相应的50年重现期的平均风速为30.1 m/s，风洞试验参考点风速为7 m/s，于是风速相似比Cv=7/30.1=1/4.3，模型几何相似比CL=1/100，由相似原理可得到时间比例尺为CT=CL/Cv=(1/100)·(1/4.3)-1=1/23.3，即风洞试验所得荷载时程曲线的时间坐标放大23.3倍，为原型结构承受风荷载时程的时间坐标。
1.3.3 风荷载及其分布
基于风洞试验所得的各节点风压系数时程，通过式(3)可得作用于原型结构屋盖对应节点的风荷载合力时程。
(3)
式中：Cpi(t)为风压系数时程，由风洞试验得到；ρ为空气密度；Ai为节点的承载面积；U为原型结构15 m高度处对应的风速。
2 有限元建模
原型结构采用有限元软件ANSYS进行建模。由于大跨屋盖网架结构的风振响应主要由自身的振动引起，下部结构的振动对屋盖的响应影响较小，所以在建模及计算过程中仅考虑上部的屋盖结构，忽略下部支撑体系，约束条件简化为铰支[9]。网架杆采用Link 180单元模拟，计算模型如图6所示，前十阶振型及频率如图7所示，结构阻尼比取0.02。
图6 带悬挑大跨屋盖计算模型
Fig.6 Calculation model of long-span roof with overhanging eaves
a—f=2.65 Hz； b—f=2.90 Hz； c—f=4.14 Hz； d—f=5.08 Hz； e—f=5.09 Hz; f—f=5.12 Hz； g—f=5.13 Hz； h—f=5.30 Hz； i—f=5.49 Hz； j—f=5.66 Hz。
图7 结构前十阶振型及频率
Fig.7 First ten mode and frequency of the structure
3 最不利风向角的确定
对于结构整体而言，最不利风向角通常有以下三种情况：该风向角作用下的屋面负风压最大、正风压最大或风压梯度最大。屋盖的等效静力风荷载主要以向上的吸力为主，因此主要考虑负风压最大[10]，根据对试验数据的分析，该结构的最大负风压出现在210°风向角时。
4 结构风振响应分析
本文考虑一般设计荷载下的结构响应，根据GB 50009—2012，恒荷载取0.5 kN/m2，屋面活荷载取0.5 kN/m2。
为研究脉动风对结构的作用规律，对部分节点的位移响应进行统计分析。脉动风速时程是平稳高斯过程，所以结构的位移响应也可以看作是平稳随机过程，具体的统计分析公式如下：
(4)
式中：Xi为样本点i的样本值，具体指代节点位移响应；σ为位移响应的均方根。
由于结构初始响应不规律，剔除响应时程前期不稳定部分的样本点，对响应时程数据进行分析。典型节点统计结果见表1和表2。限于篇幅，只给出了部分典型节点的响应统计值。
表1 屋盖中部典型节点响应统计值
Table 1 Statistical response value of typical nodes in the middle of roof
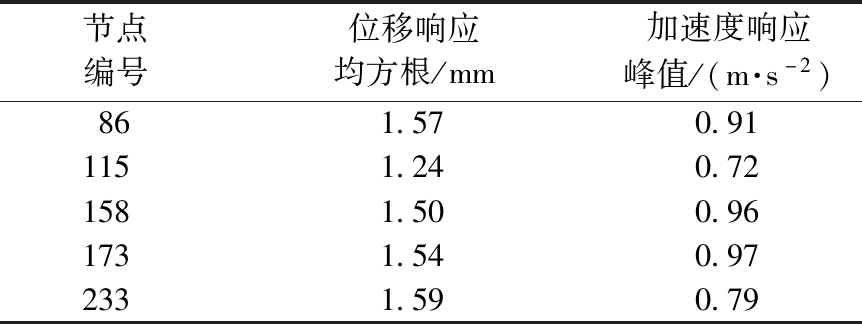
节点编号位移响应均方根/mm加速度响应峰值/(m·s-2)861.570.911151.240.721581.500.961731.540.972331.590.79
表2 屋盖挑檐部分典型节点响应统计值
Table 2 Statistical response value of typical nodes on roof eaves
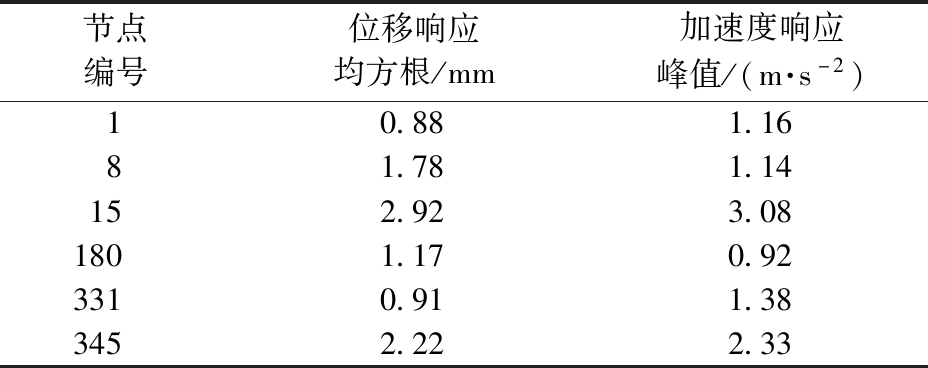
节点编号位移响应均方根/mm加速度响应峰值/(m·s-2)10.881.1681.781.14152.923.081801.170.923310.911.383452.222.33
从表1和表2可看到：屋盖中部区域，由于挑檐的存在，降低了其对风荷载作用的敏感性；位于迎风向挑檐部分的节点8、15和345受到的脉动风影响较大，其加速度响应峰值以及位移响应均方根均大于屋盖中部区域的节点，受到脉动风影响最大的为挑檐角部节点15。而位于背风向挑檐角部的331节点，加速度响应峰值以及位移响应均方根最小，风的作用较弱。下面将重点对迎风挑檐部分进行风致振动与减振分析。
5 阻尼减振分析
黏弹性阻尼器主要依靠黏弹性材料提供附加刚度和阻尼，从而减小结构的动力响应，可作为大跨度空间结构的有效减振方式[11]。
5.1 黏弹性阻尼器有限元模型及布置
黏弹性阻尼器的力学性能可由弹簧元件和阻尼元件并联来描述，力学模型如图8所示。
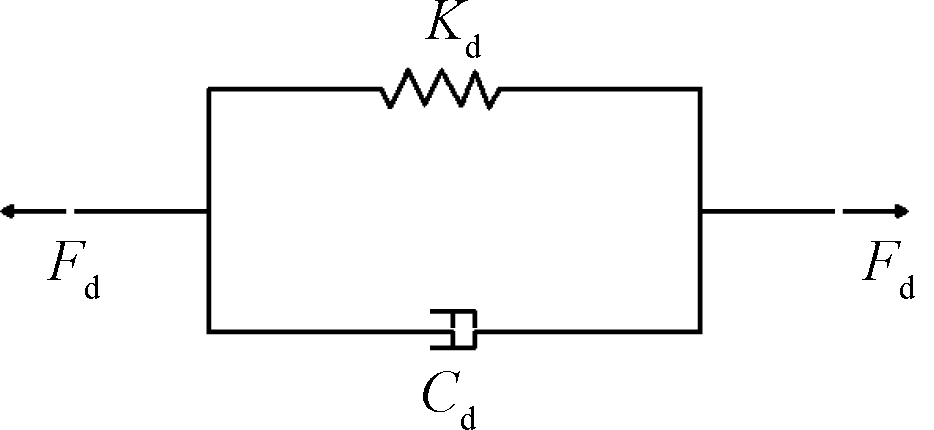
图8 黏弹性阻尼器力学模型
Fig.8 Mechanical model of viscoelastic damper
黏弹性阻尼器力-位移关系为：
(5)
式中：kd为黏弹性阻尼器的等效刚度；Cd为等效阻尼；u为阻尼器运动时内外壳体相对位移；
为阻尼器运动时内外壳体相对速度。
kd、Cd按式(6)计算：
(6a)
(6b)
式中：h为弹性层厚度；S为弹性层面积；ω为激励频率；G′、G″分别为黏弹性材料的储能剪切模量和损耗剪切模量。
时程分析阻尼器选择Combine 14单元进行模拟。由前文分析可知，挑檐角部区域风振位移响应较大，在该区域增设黏弹性阻尼器，具体布置方式如图9所示。结构风振响应减振效果采用减振系数β表示：
(7)
式中：δ0为减振前结构响应峰值;δ减振后结构响应峰值。可知，β越大表示减振效果越好。
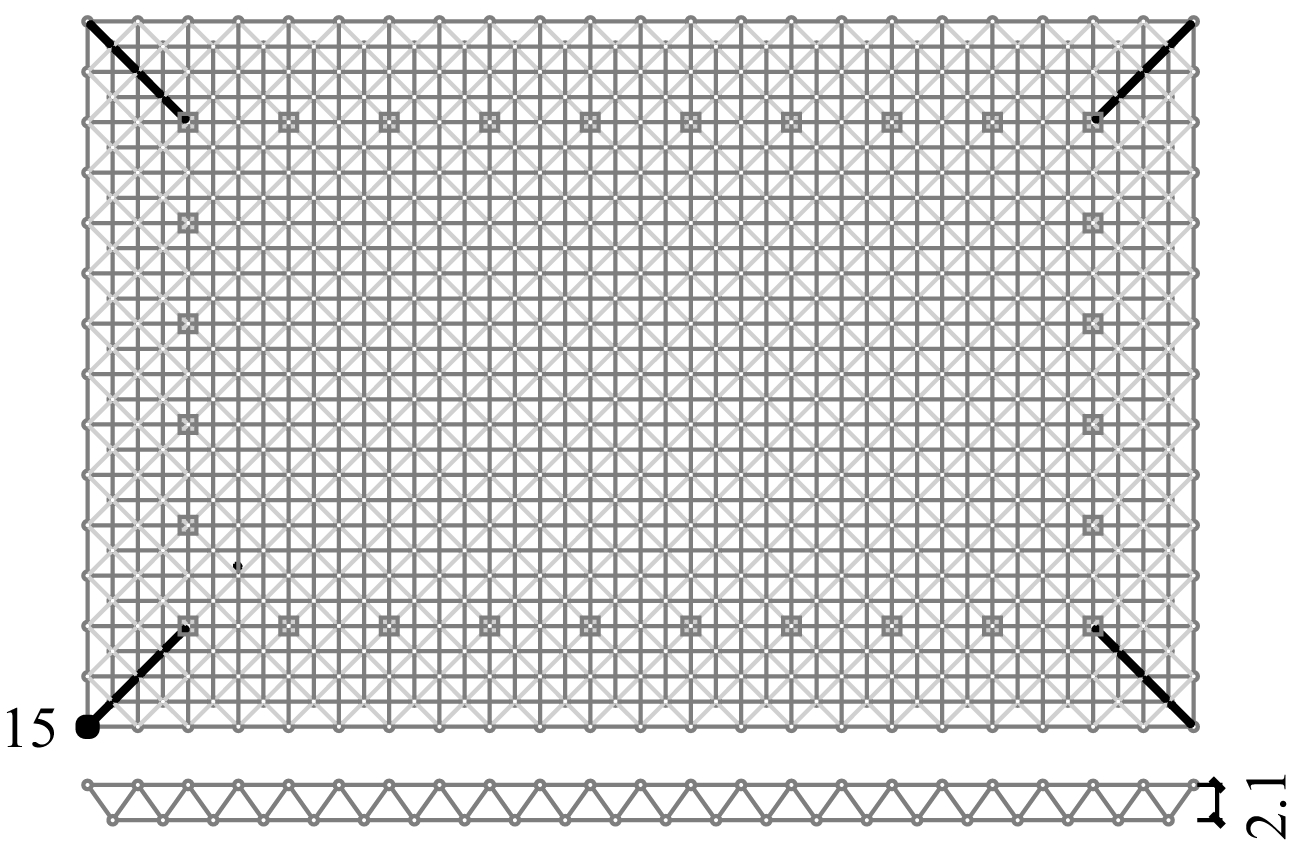
图9 阻尼器布置示意 m
Fig.9 Schematic diagram of dampers arrangement
5.2 黏弹性阻尼器对网架风振控制效果分析
5.2.1 普通网架增设阻尼器
将最不利210°风向角风压时程作用在屋盖结构上，进行风振响应分析，增设阻尼器黏滞阻尼系数为500 kN/(m·s-1)，等效刚度为2 000 kN/m。节点15处增设阻尼器前后的位移响应时程与加速度响应时程的对比分别如图10、图11所示。
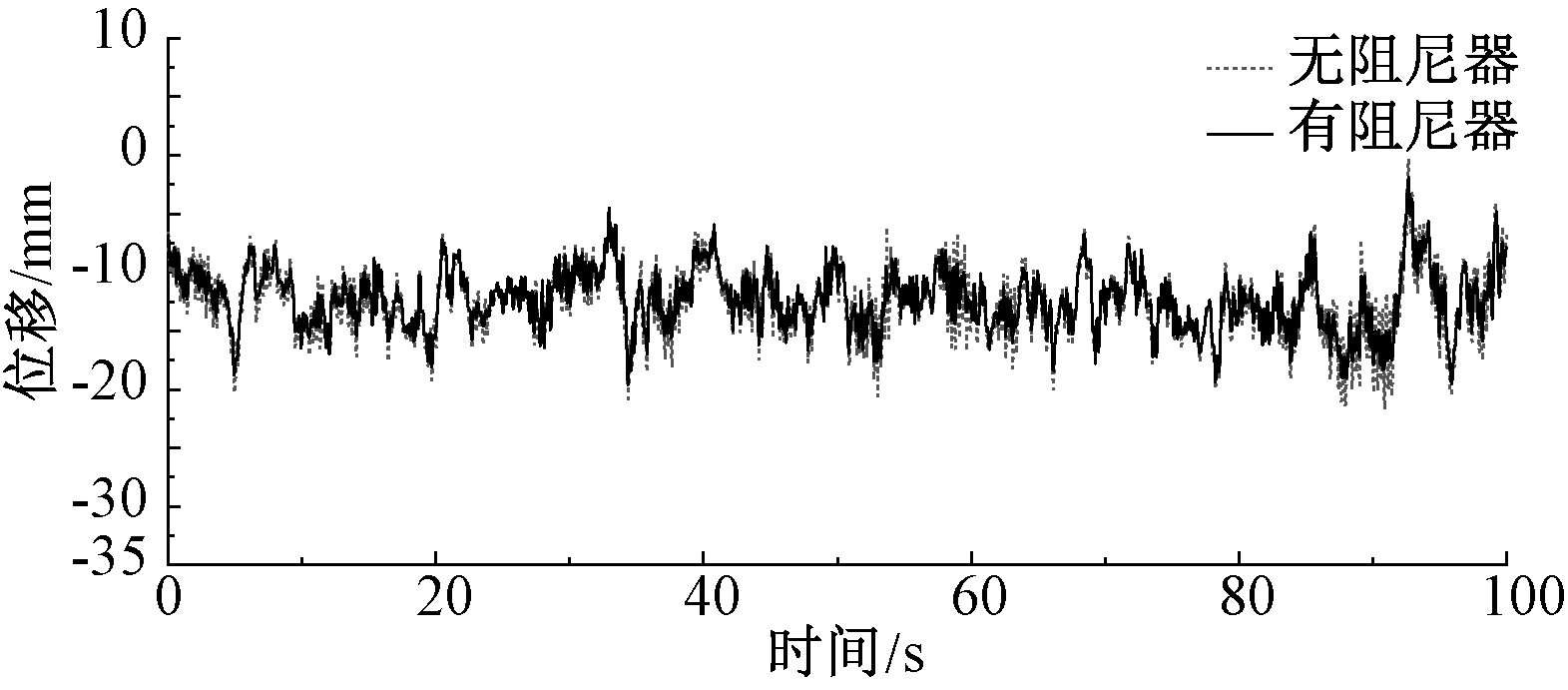
图10 节点15减振前后位移响应对比
Fig.10 Comparison of displacement responses before and after vibration reduction at node 15
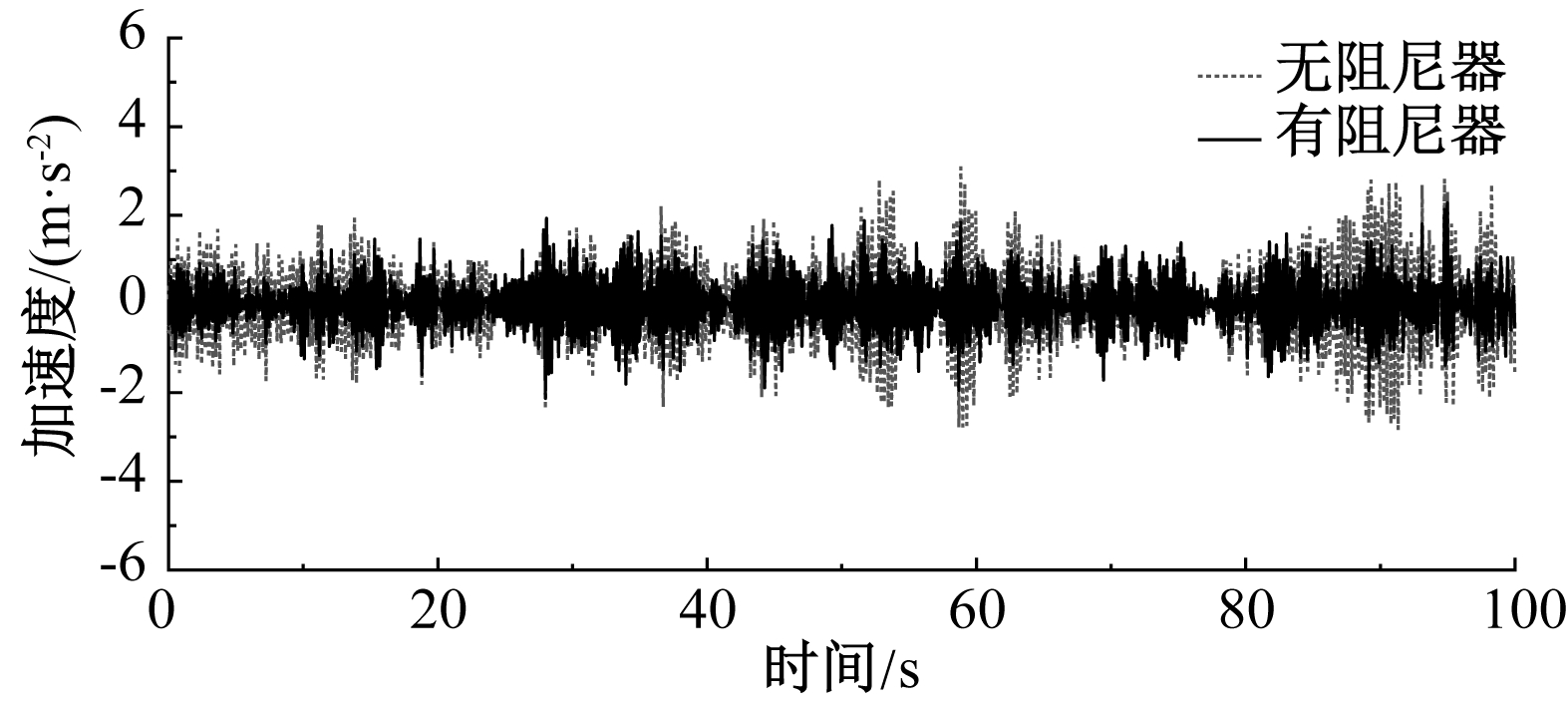
图11 节点15减振前后加速度响应对比
Fig.11 Comparison of acceleration response before and after vibration reduction at node 15
从图10和图11可以看到，增设阻尼器后，结构悬挑部位的位移响应以及加速度响应得到明显控制。将风振响应的统计值进行整理，可知，位移响应均方根值减振系数为10.3%，加速度响应峰值减振系数为26.3%，表明在悬挑部位利用黏弹性阻尼器进行风振控制可取得较好的减振效果。
5.2.2 既有锈蚀网架增设阻尼器
网架结构一般采用钢制材料，由于直接承受外界风雨的侵蚀，在使用一段时间后，容易出现锈蚀，使得结构承载力下降，出现不满足结构使用要求的情况。对既有网架结构进行调查，发现钢制构件的锈蚀深度一般在1 mm左右[12]。本文通过调整杆件截面(图12)来模拟不同锈蚀深度，截面积按式(8)计算。
(8)
式中：A为计算截面积；b为锈蚀深度；d为杆件内直径；D为杆件外直径。
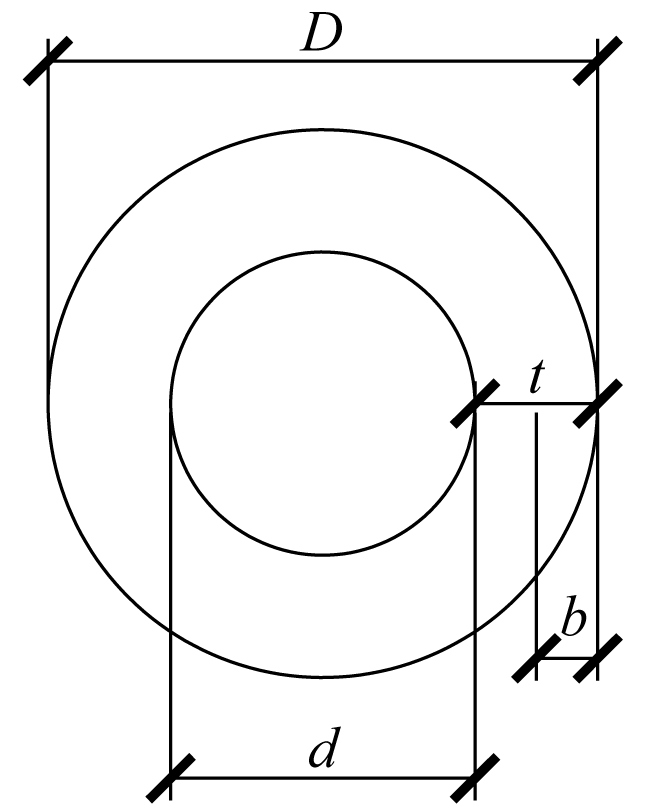
图12 杆件截面
Fig.12 Bar section
1)锈蚀对结构响应的影响。
根据文献[13]，网架腐蚀程度最严重的为上弦杆、腹杆，而下弦杆基本完好。所以对于本屋盖结构，分析网架上弦杆及腹杆(锈蚀深度达1 mm)在风荷载作用下的风振响应，图13与图14给出了锈蚀前后的风振响应对比。从图13可以看到，由于网架锈蚀造成屋盖整体刚度降低，不仅其自重作用引起的位移响应值变大，挑檐迎风前缘节点15风振位移响应亦随之增大。从图14可看到，锈蚀网架加速度响应也随之增大。
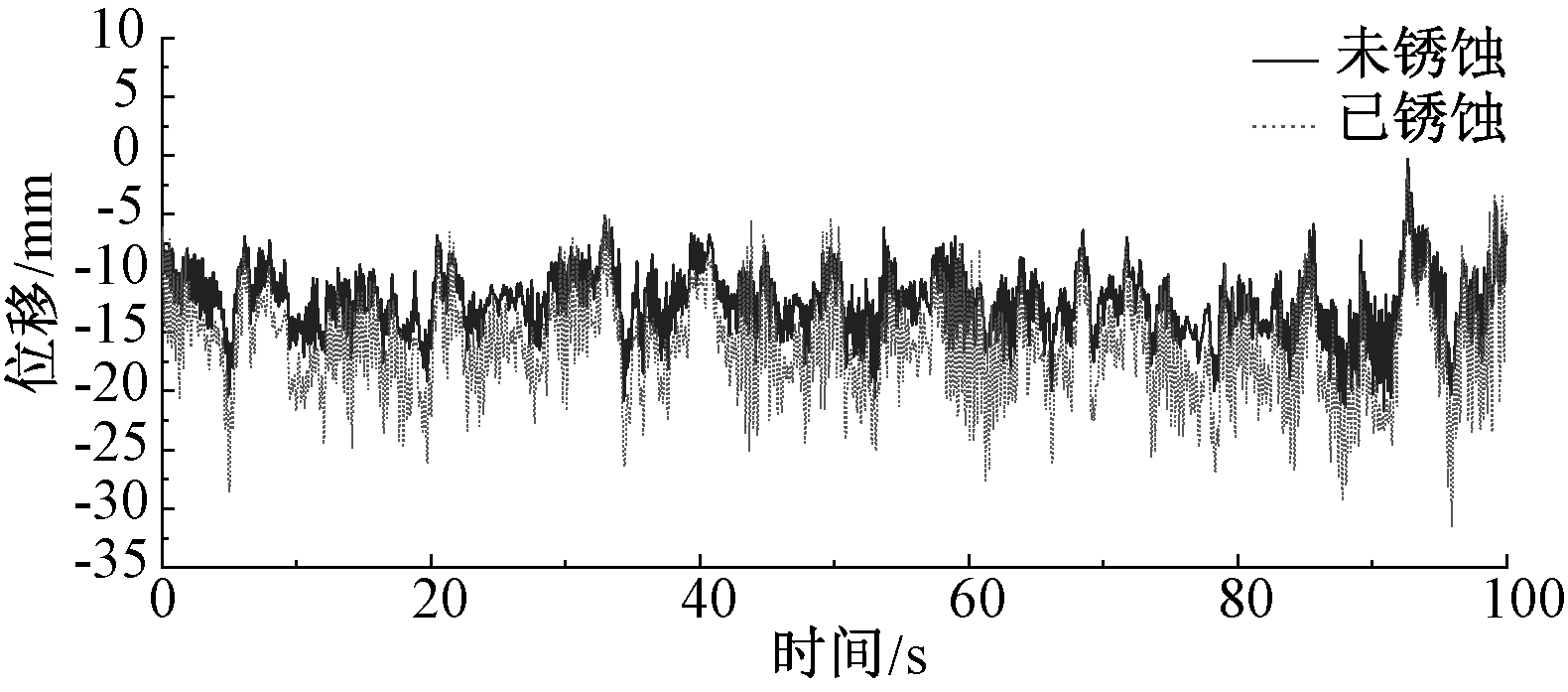
图13 结构锈蚀前后节点15位移响应对比
Fig.13 Comparison of displacement responses of structures before and after corrosion at node 15
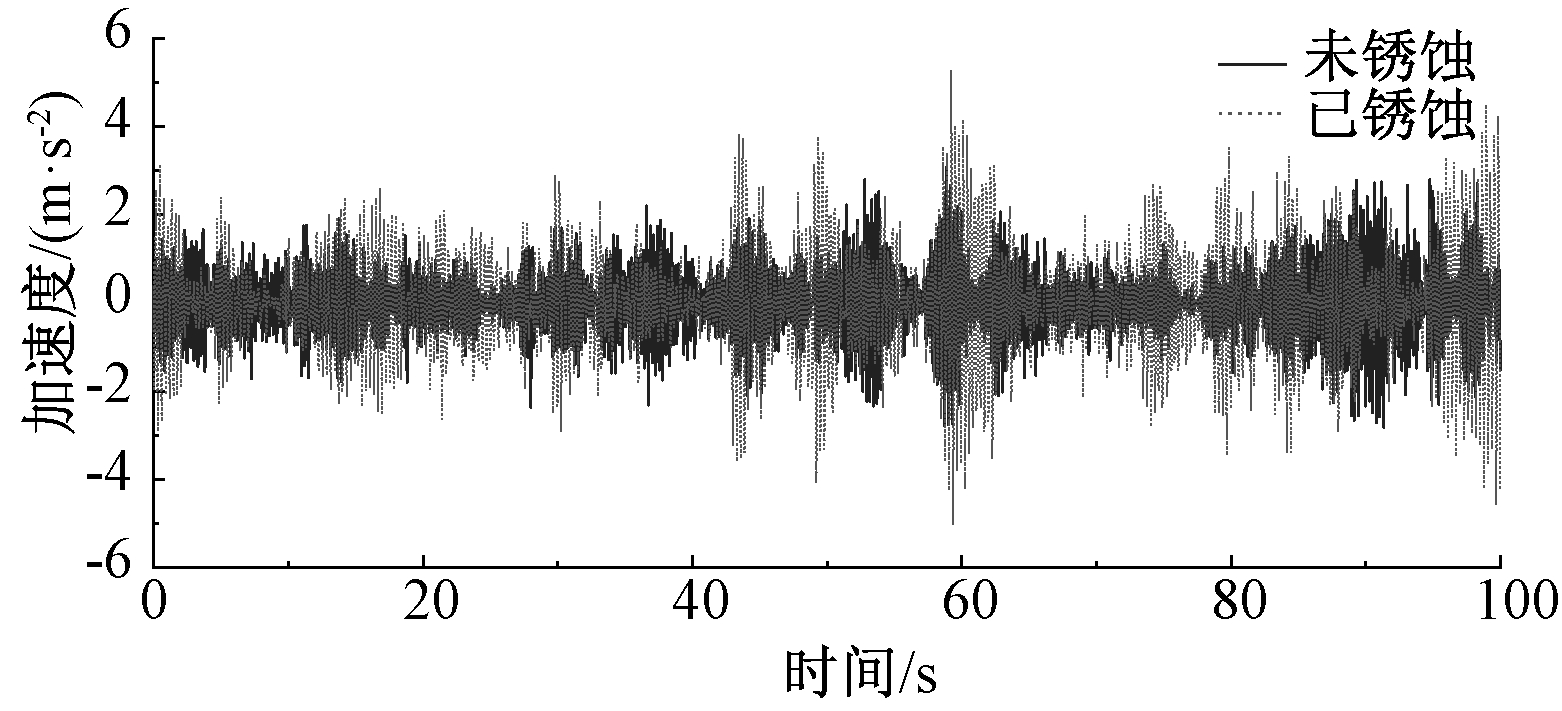
图14 结构锈蚀前后节点15加速度响应对比
Fig.14 Comparison of acceleration responses of structures before and after corrosion at node 15
2)锈蚀深度对减振效果影响。
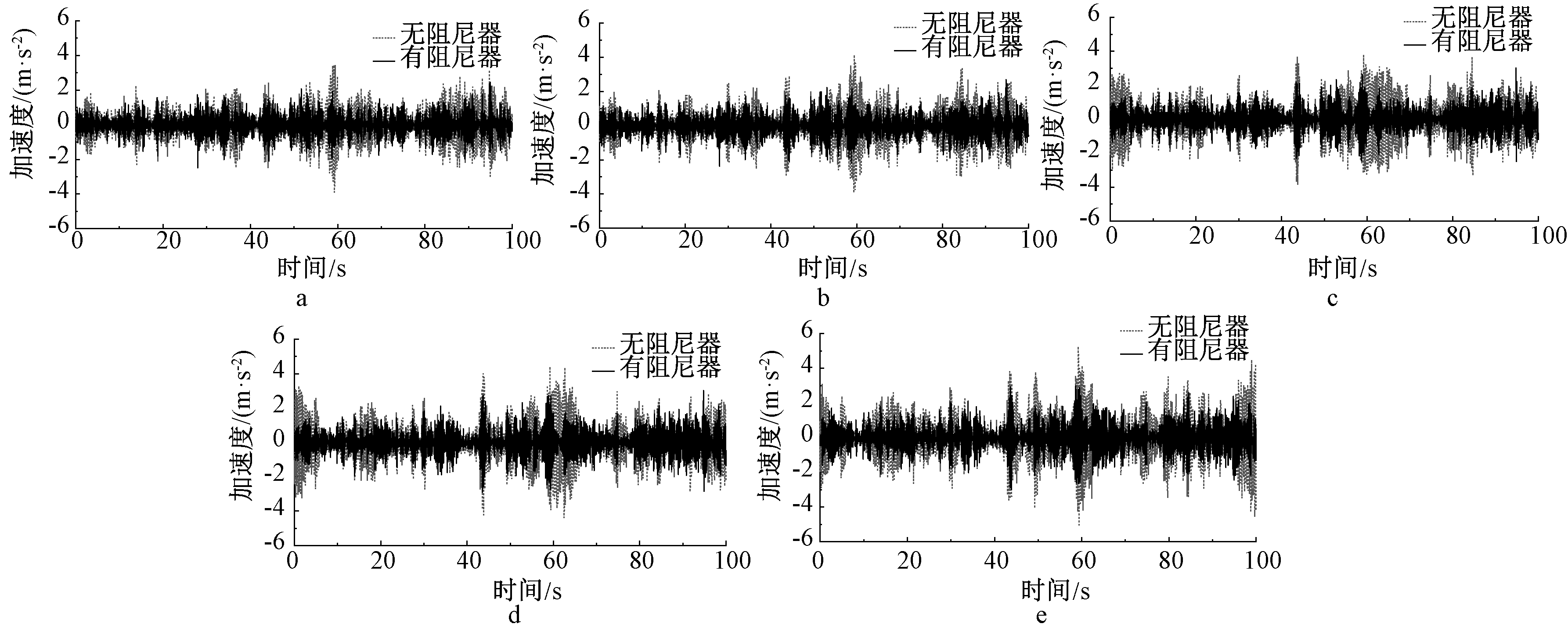
为探究黏弹性阻尼器对不同锈蚀深度既有屋盖结构的减振效果，对比分析锈蚀深度0.2，0.4，0.6，0.8，1.0 mm状态下，阻尼器控制前后的屋盖结构风振响应。图15和图16给出了不同锈蚀深度的屋盖结构的节点15设置阻尼器前后的风振响应对比。图17和图18给出了设置阻尼器前后风振响应的统计值对比。
从图15、图16中可看到，节点15的位移响应以及加速度响应随着锈蚀深度的增加而增大，设置阻尼器后风振响应得到明显控制。对图17、图18的风振响应的统计按式(7)进行整理，可知，位移响应均方根减振系数达到10.3%～21.0%，加速度响应峰值减振系数达到26.3%～39.6%。表明在既有存在锈蚀的大跨网架结构中增设黏弹性阻尼器，对风振响应可以取得良好的减振效果。
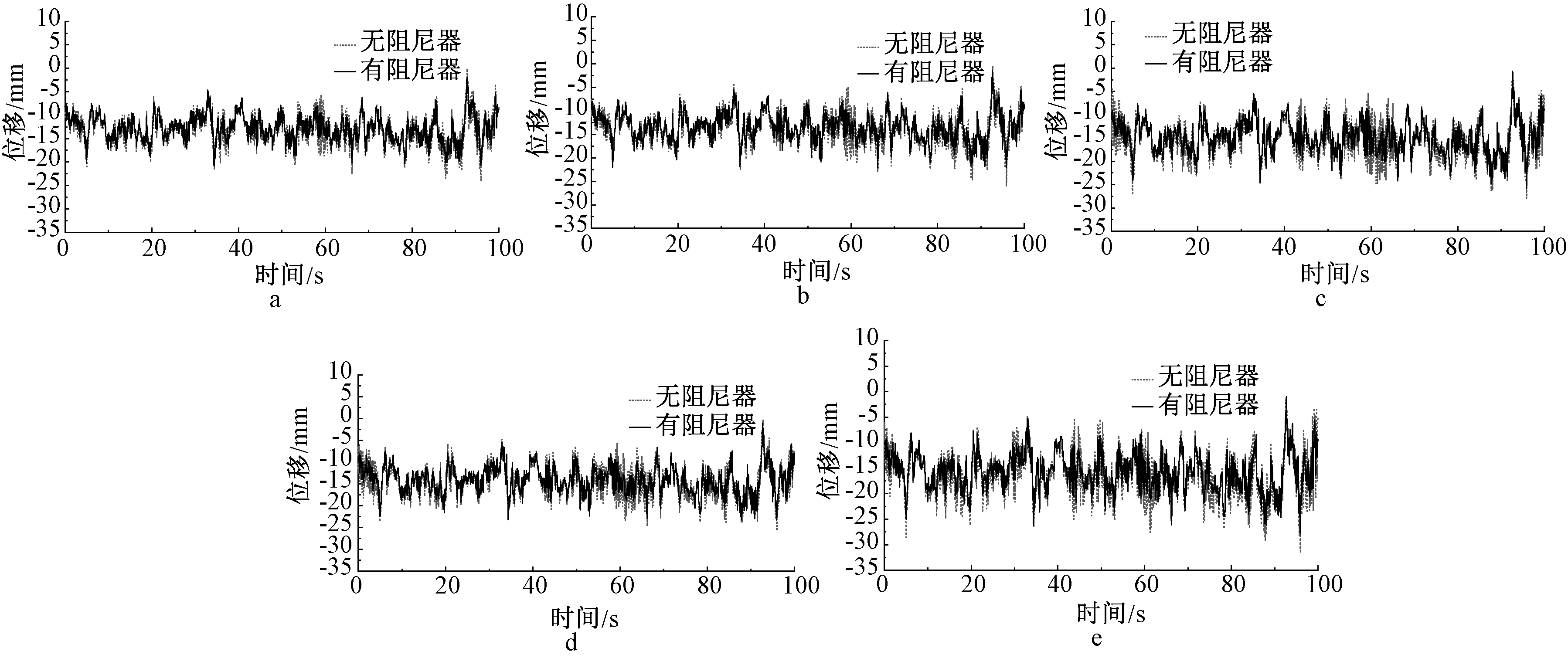
a—锈蚀深度0.2 mm； b—锈蚀深度0.4 mm； c—锈蚀深度0.6 mm； d—锈蚀深度0.8 mm； e—锈蚀深度1.0 mm。
图15 不同锈蚀深度减振前后位移响应对比
Fig.15 Comparison of displacement responses before and after vibration reduction under different corrosion depths
a—锈蚀深度0.2 mm； b—锈蚀深度0.4 mm； c—锈蚀深度0.6 mm； d—锈蚀深度0.8 mm； e—锈蚀深度1.0 mm。
图16 不同锈蚀深度减振前后加速度响应对比
Fig.16 Comparison of acceleration responses before and after vibration reduction under different corrosion depths
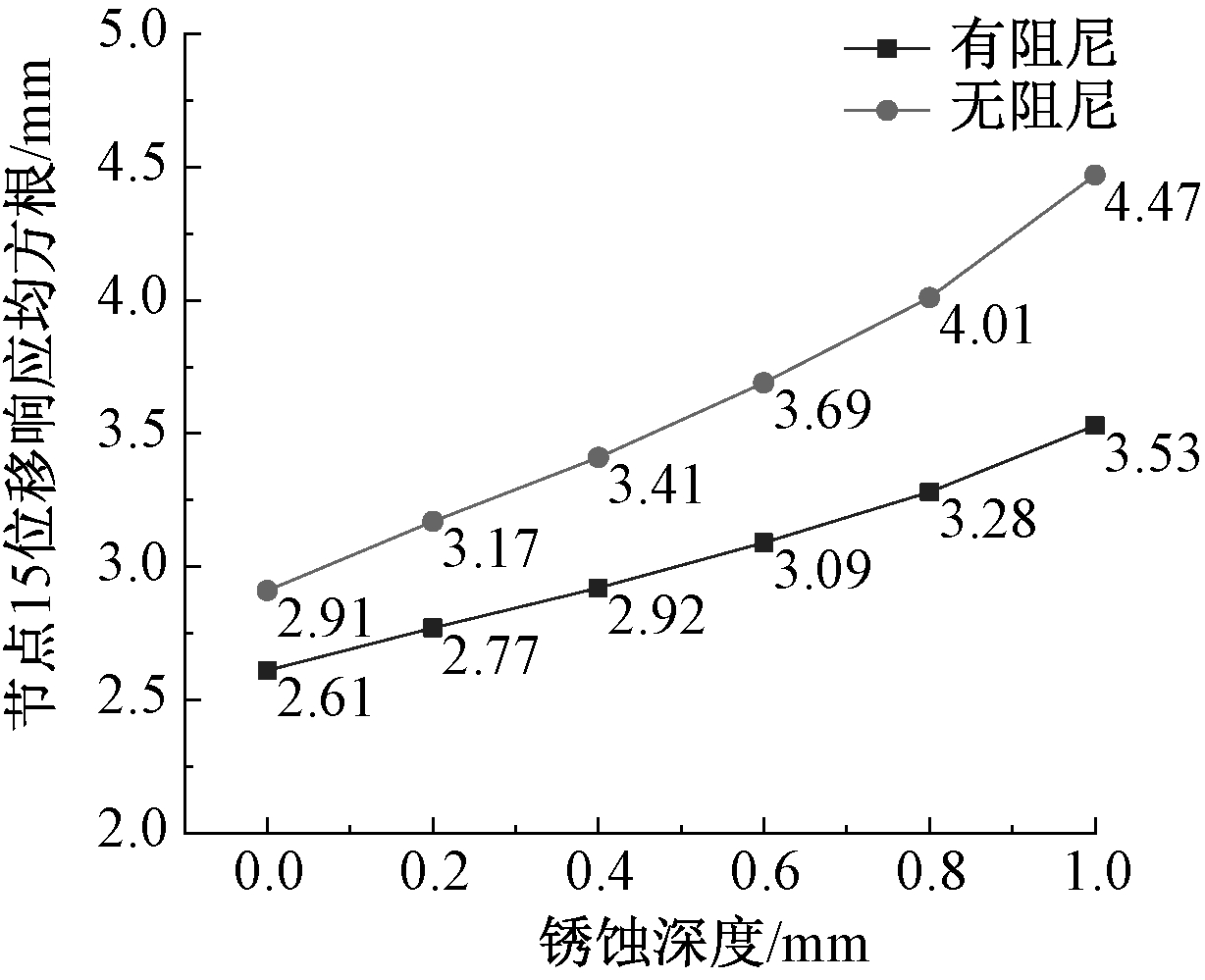
图17 位移响应均方根变化趋势
Fig.17 Changing trend of root mean square of displacement response
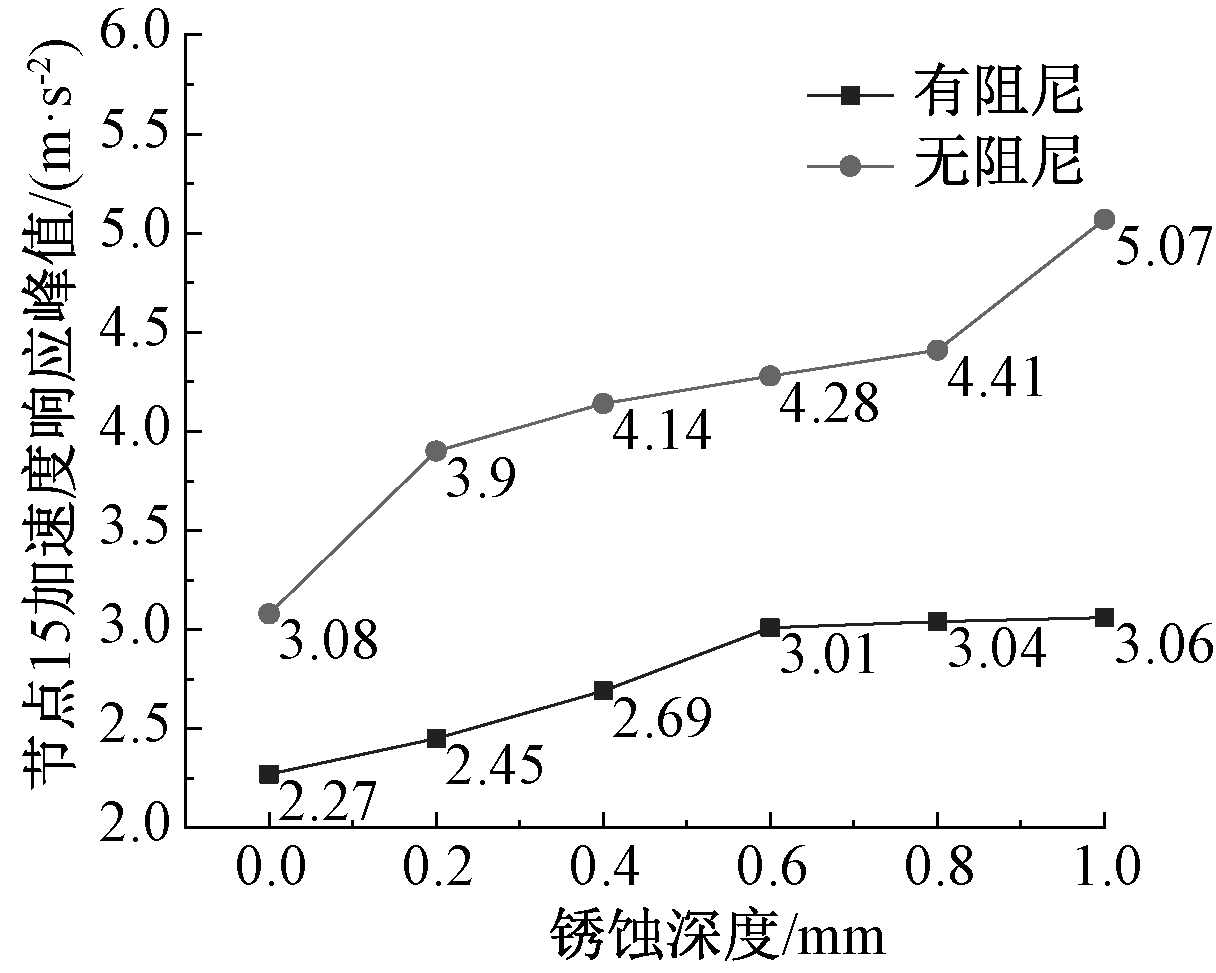
图18 加速度响应峰值变化趋势
Fig.18 Changing trend of peak acceleration response
6 结束语
对带挑檐大跨屋盖结构刚性模型进行风洞试验，利用试验数据对原型屋盖网架结构进行风振响应分析，以及加设阻尼器后的减振效果分析，得到结论如下：
1)风洞试验表明挑檐部分由于上下表面风压叠加作用，负风压较大，相对于屋盖中部区域，对风的作用较为敏感，工程中应考虑这一不利影响。
2)在挑檐角部设置黏弹性阻尼器，对大跨屋盖结构的挑檐风振响应控制效果良好。位移响应均方根减振系数为10.3%，加速度响应峰值减振系数为26.3%。
3)存在一定程度的既有锈蚀的网架结构，风致响应随锈蚀深度增加而增大。增设黏弹性阻尼器杆件对风振响应减振效果明显，锈蚀深度小于1 mm时，位移响应均方根减振系数达到10.3%～21.0%，加速度响应峰值减振系数达到26.3%～39.6%。
[1] 沈世钊. 大跨空间结构的发展回顾与展望[J]. 土木工程学报，1998(3):5-14.
[2] 项海帆. 结构风工程研究的现状和展望[J]. 振动工程学报，1997(3):12-17.
[3] KAREEM A, KIJEWSKI T. 7th US National Conference on Wind Engineering: A Summary of Papers [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 62: 81-129.
[4] 黄本才, 汪丛军. 结构抗风分析原理及应用[M]. 2版.上海： 同济大学出版社, 2008.
[5] 刘红波，刘东宇，徐杰. 天津新港船闸桥锈蚀检测与结构性能评估[J]. 天津大学学报(自然科学与工程技术版)，2015,48(增刊1):147-150.
[6] DA贝利斯，DH迪肯. 钢结构的腐蚀控制[M].2版. 丁桦,译. 北京：化学工业出版社，2005.
[7] 中华人民共和国住房和城乡建设部.建筑结构荷载规范:GB 50009—2012[S]. 北京：中国建筑工业出版社，2012.
[8] 陈波，骆盼育，杨庆山. 测压管道系统频响函数及对风效应的影响[J]. 振动与冲击，2014, 33(3):130-134.
[9] 刘娟. 大跨屋盖结构风荷载特性及抗风设计研究[D].成都： 西南交通大学，2011.
[10] 曹华兵.大跨度屋盖结构风致响应分析[D]. 南京：东南大学，2009.
[11] 苏毅. 大悬挑钢网架采用筒式粘弹性阻尼器的风振控制研究[D]. 南京：东南大学，2006.
[12] 苏萍. 既有空间网架结构加固方法研究[D]. 济南： 山东大学，2014.
[13] 武岳，王凤来，陈波，等. 某游泳馆屋盖网架结构检测及安全性评估[J].建筑结构,2008,38(12):110-112.