0 引 言
双曲面斜交网格筒[1-3]是一种由分布在圆柱面上的两族竖向直柱,其柱顶分别绕顺时针和逆时针旋转相同角度形成的新型结构体系。旋转后两方向斜柱交叉相贯,结构呈现出上下端大、中部小的双曲面形状,再在柱顶和柱底设置环梁或其他边界约束保证结构的整体性,即为图1所示典型双曲面斜交网格筒。
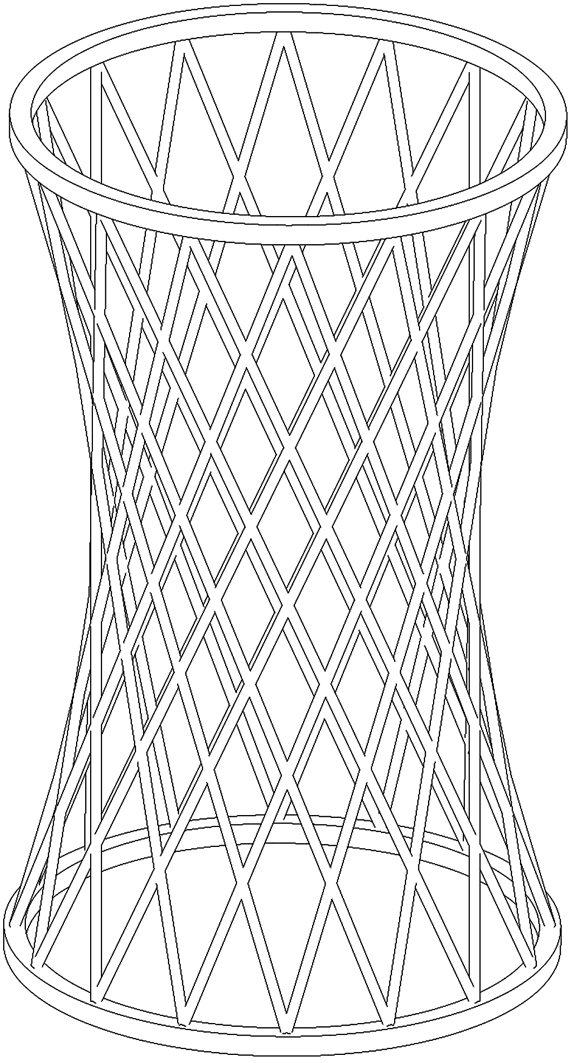
图1 双曲面斜交网格筒示意
Fig.1 Schematic diagram of hyperboloid diagrid tubes
双曲面斜交网格筒采用两方向斜柱代替了柱面网格筒中正交布置的传统横梁竖柱,使其在保持竖向承载能力的同时,具备了优秀抗侧性能;且双曲面斜交网格筒造型美观,因而受到建筑师们的青睐。由中南建筑设计有限公司设计、浙江中南建设集团钢结构有限公司承建的中国动漫博物馆项目就采用了双曲面斜交网格[4-6]。如图2所示,中国动漫博物馆结构一层以上采用钢框架-支撑-跨层桁架结构;一层为三大三小共6个网格筒,作为承重子结构支撑着上部结构。其中Y2筒体采用的就是双曲面斜交网格筒,其由分布在圆柱面上的两族竖向直柱分别绕顺时针和逆时针相对旋转60°形成,整体为上下端大、中部小的双曲面形状。筒体结构整体高9.93 m,顶部直径37 m,底部直径35 m。
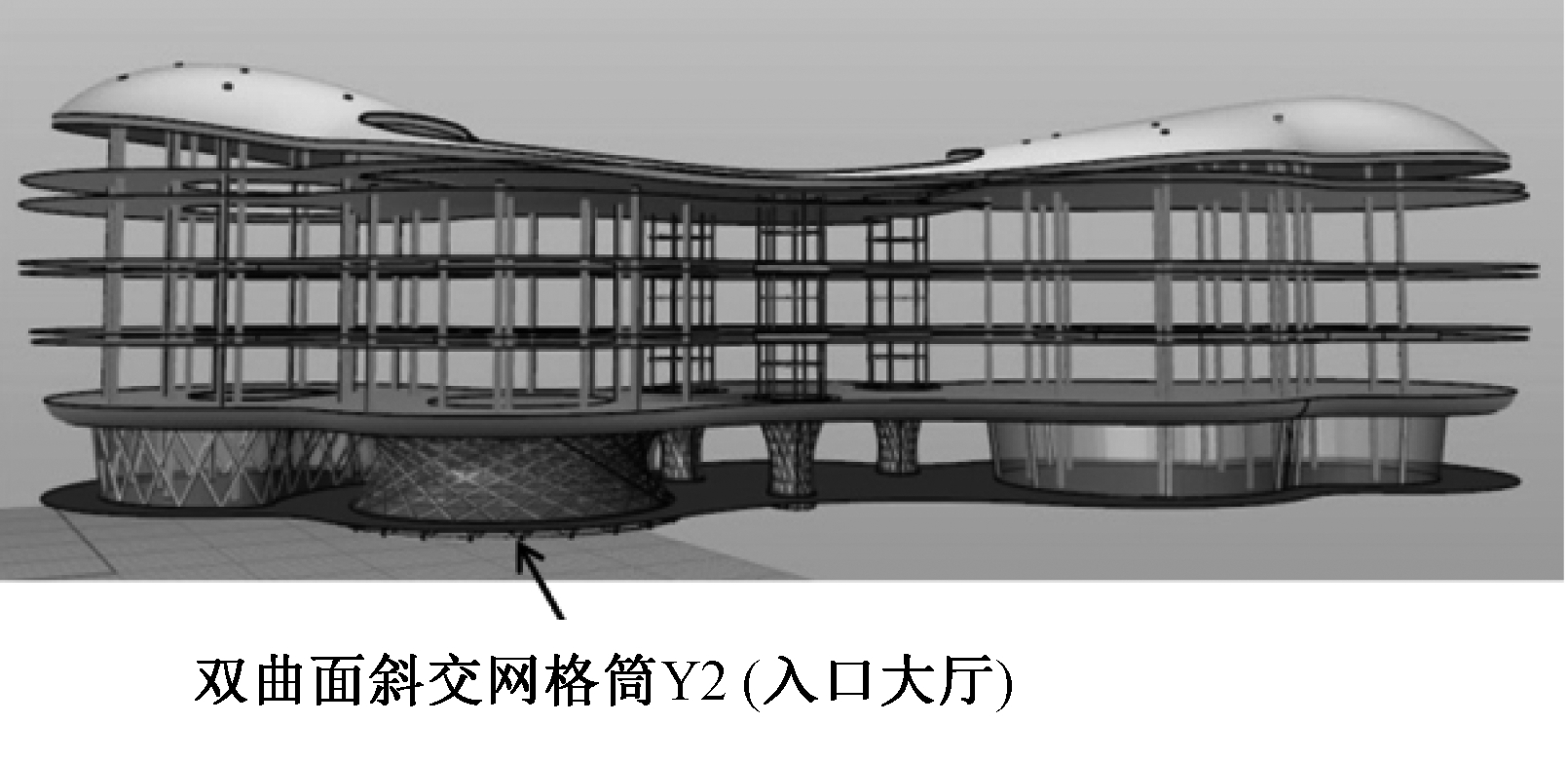
图2 中国动漫博物馆结构示意
Fig.2 Structure schematic diagram of China Comic and Animation Museum
由于建筑使用功能的要求,网格筒结构可能存在多层楼板抽空或不设置面外支撑的情况,因而容易在竖向荷载作用下发生面外群柱失稳[7-8]。双曲面斜交网格筒(Y2)不仅存在类似现象,还在筒体立面开设有一大一小两门洞,进一步降低结构的失稳荷载,因此双曲面斜交网格筒(Y2)的面外群柱失稳问题是其结构设计的关键问题之一。目前已有学者对网格筒的面外群柱稳定性能进行了理论分析[9-13],但并不成熟,且还没有针对双曲面斜交网格筒的相关试验研究。因此本文结合中国动漫博物馆工程,采用试验方法对双曲面斜交网格筒在竖向荷载下的群柱稳定性能进行试验研究。试验目的是:1)了解双曲面斜交网格筒在竖向荷载作用下的失稳破坏模式和失稳机理;2)获得双曲面斜交网格筒(Y2)在竖向荷载作用下的极限承载力,验证结构设计的安全性;3)评估设计中所提出加强方案的有效性。
考虑到Y2网格筒在顶面呈环向形式,作用有多达24个竖向集中荷载,如在每个柱顶采用独立千斤顶加载,需要采用很多加载架,不仅成本昂贵,而且试验室场地和设备的局限也使得这一多点加载方案难以实现。因此,本文将依据试验要求确定一个合理、经济的试验加载方案,实现网格筒柱顶环形多点集中加载的目的。
1 试验模型设计
在中国动漫博物馆结构设计中,双曲面斜交网格筒(Y2)每根交叉斜柱的柱顶位置均设置了橡胶隔震支座,筒体以上结构的框架柱直接落在橡胶隔震支座上。由于橡胶隔震支座的水平刚度较小,能够有效地释放上部结构对筒体施加的水平力作用,因此双曲面斜交网格筒(Y2)的试验模型仅选取至顶部环梁为止,并认为双曲面斜交网格筒(Y2)仅承受竖向荷载。
根据相似性原理以及前期的初步有限元模拟分析结果[14],在保证模型与实际结构材料、几何尺寸、荷载等尽可能相似的条件下,综合考虑实验室场地条件、试验设备的加载能力等因素,最终确定采用缩尺比例为1∶7的试验模型。缩尺后试验模型如图3所示,底部直径为5 000 mm(轴线),顶部直径为5 286 mm(轴线),筒高1 412 mm(除底部支座盘)。其中主斜柱采用单根钢管通长设置,次斜柱分段设置并与主斜柱相贯焊接。由于门洞1上部传来的竖向荷载较大,为整体结构的薄弱位置,因而在结构设计中增大了该处管件截面,称为加强斜柱。顶部环梁作为双曲面斜交网格筒(Y2)唯一的面外约束,结构设计中在顶部环梁平面内增设了12道工字形截面钢支撑以提高环梁的面内刚度。此外试验模型在底部还设置了由底部环梁和米字形内支撑组成的刚性盘,以模拟地面对柱脚的约束作用。
试验模型采用的材料和截面尺寸见表1。门框1、门框2、加强斜柱和环梁在原结构中采用Q420B钢制成,但考虑到材料的采购困难,本试验全部等效替换为Q345B钢,替换的原则为选取合适的截面尺寸,使得构件的截面面积放大420/345倍,同时不改变构件截面惯性矩。

图3 双曲面斜交网格筒(Y2)试验模型及其组成
Fig.3 Detailed diagram of the experimental model of the hyperboloid diagrid tube (Y2)
表1 试验模型构件材料与截面尺寸
Table 1 Member materials and section dimensions of the experimental model mm
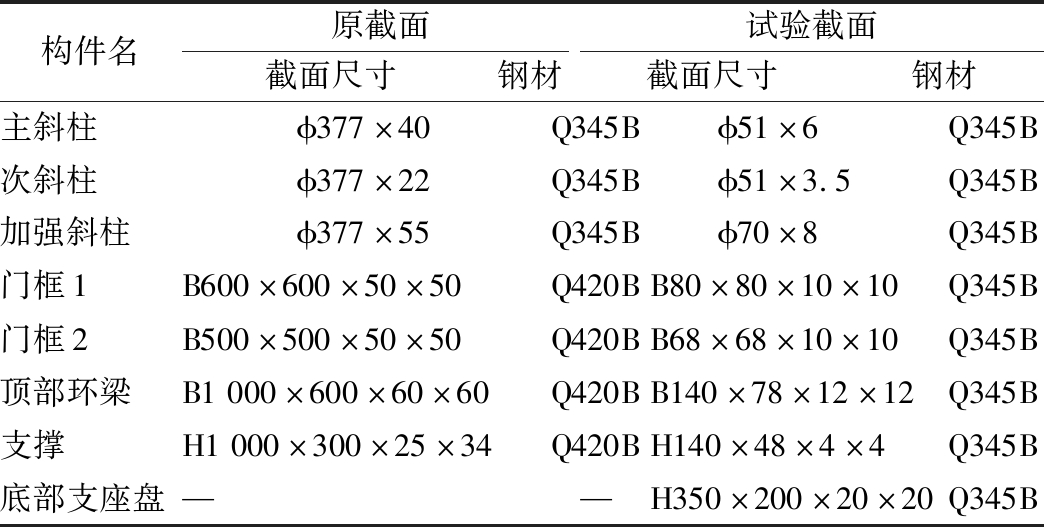
构件名原截面试验截面截面尺寸钢材截面尺寸钢材主斜柱ϕ377×40Q345Bϕ51×6Q345B次斜柱ϕ377×22Q345Bϕ51×3.5Q345B加强斜柱ϕ377×55Q345Bϕ70×8Q345B门框1B600×600×50×50Q420BB80×80×10×10Q345B门框2B500×500×50×50Q420BB68×68×10×10Q345B顶部环梁B1000×600×60×60Q420BB140×78×12×12Q345B支撑H1000×300×25×34Q420BH140×48×4×4Q345B底部支座盘——H350×200×20×20Q345B
2 网格筒环向多点竖向加载方案
在设计荷载工况1.35D(恒载)+0.98L(活载)作用下,双曲面斜交网格筒(Y2)每个柱顶受到的竖向荷载都不相同。在实际试验加载中,通过24个千斤顶在24个加载点上实现协同加载,无论加载设备准备还是加载控制都是非常困难的。因此本试验提出了等效荷载+多榀辐射张弦式荷载分配结构[15]的加载方案,使得加载问题得以解决。
等效荷载的思路在于依据筒顶实际设计荷载的分布与幅值,以其中受力较大的9个柱顶为基准,其余柱顶荷载向这9个柱顶转移合并。在实际操作中,为避免由于力过于集中造成局部破坏,又增设了两个加载点,最终形成如图4所示的9大2小共11个竖向力的等效荷载。
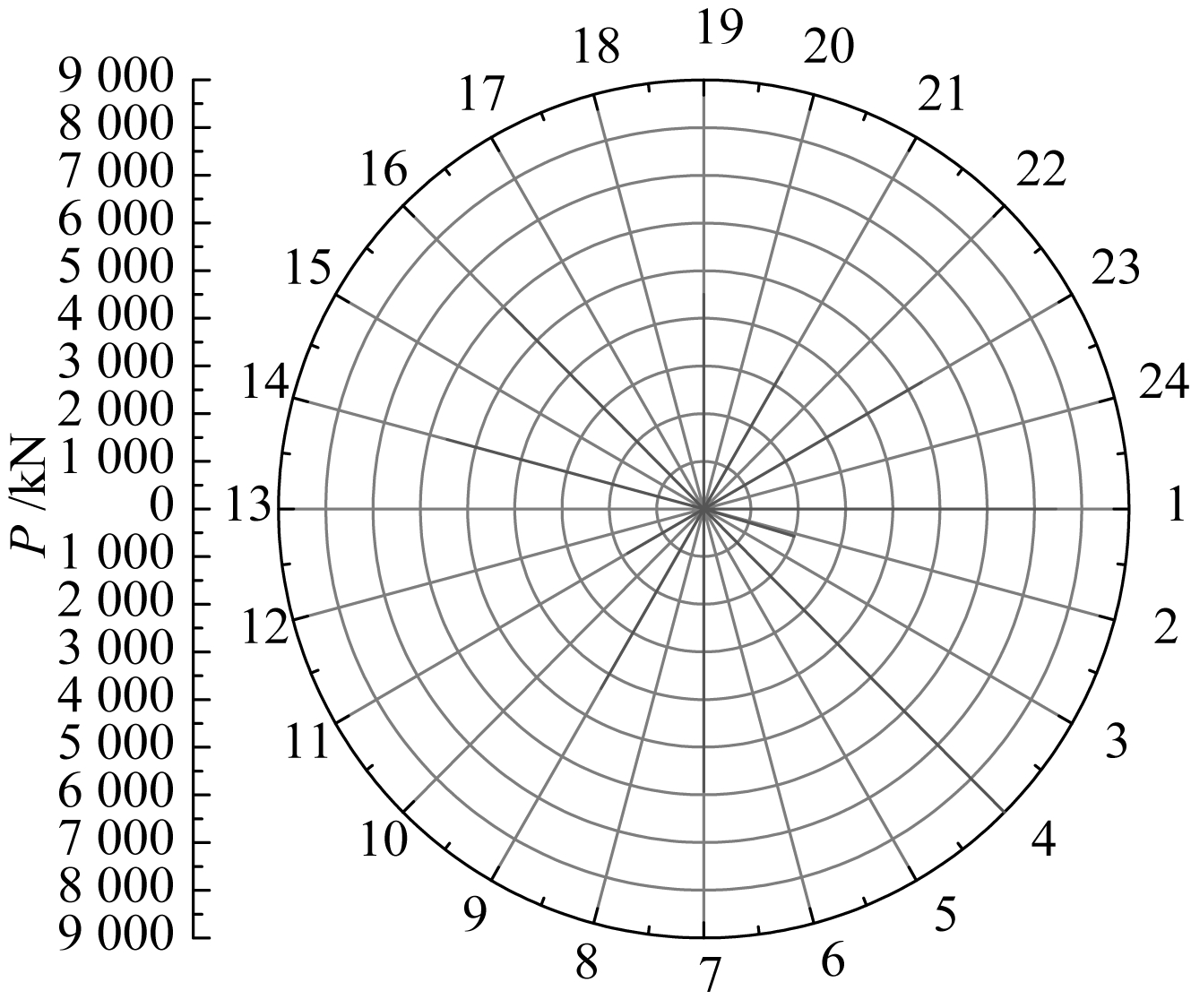
图4 网格筒柱顶等效荷载
Fig.4 Equivalent loads on the column tops of the hyperboloid diagrid tube (Y2)
等效荷载的提出减少了加载点的数量,但实际加载操作仍然困难。为此专门设计了一套多榀辐射张弦式荷载分配结构,可将作用在荷载分配结构上的竖向荷载按照所期望的比例和幅值分配至各柱顶加载点,以实现单点加载代替多点协同加载。图5所示即为本试验设计的多榀辐射张弦式荷载分配结构,其由中部的飞柱、上弦的径向梁以及下弦的拉杆组成,径向布置的张弦梁共用一个中心飞柱并在张弦梁外端通过弧形支撑连接,保证整个装置的整体性。荷载分配盘在径向梁端部还设置了短柱和卡槽,可直接架设在试验模型的顶部环梁之上。同时为使试验与实际工程更接近,在短柱和环梁的接触面设置了一层6 mm厚的橡胶垫,以模拟实际工程中钢材与橡胶隔震支座的摩擦情况,除此之外,还在卡槽挡板和试验模型顶部环梁之间预留了足够的间隙,以便荷载分配结构的短柱和试验模型环梁之间能够较容易地发生相对滑移。
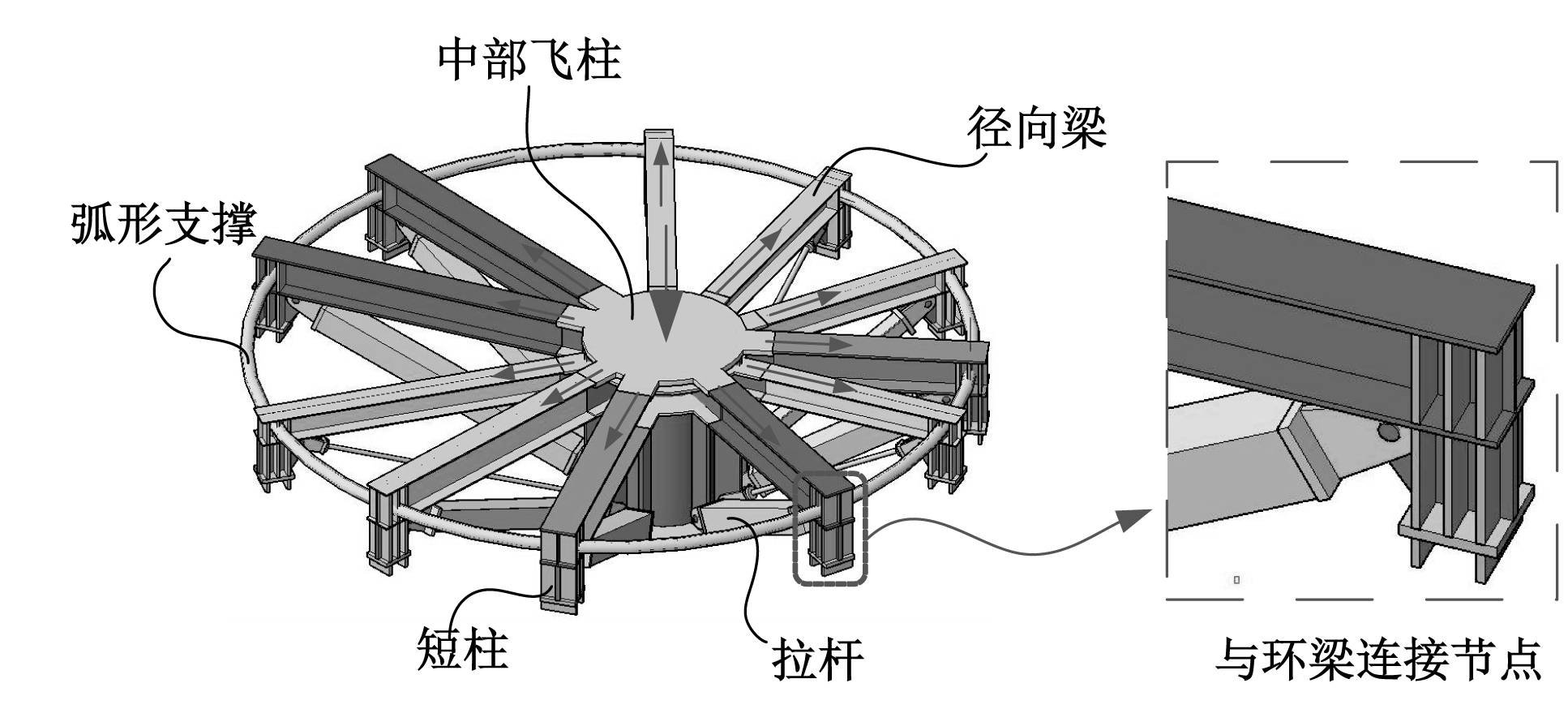
图5 多榀辐射张弦式荷载分配结构
Fig.5 Radial beam-string load distribution structure
在试验加载过程中,只需将总荷载作用在中部飞柱的中心,荷载将自动分配至各加载点,分配的比例可通过计算选择合适的中部飞柱平面位置以及各径向梁和斜向拉杆的截面积予以实现。具体设计过程可依据图6所示的简化计算模型对荷载分配结构进行初步设计,试验模型在整个荷载分配中的作用可用图6中的端部弹簧代替,加载点i的弹簧刚度ki可由在试验有限元模型中对应加载点施加单位力进行计算,所求得的加载点竖向位移的倒数即为弹簧刚度ki。通过静力平衡可以确定中部飞柱的平面位置应为各加载点竖向力的合力作用点,再根据试验模型和场地尺寸选定飞柱的高度lc,即确定了荷载分配盘的几何形状。由于变形协调,通过不同加载点的单榀张弦梁单元计算得到的中部飞柱竖向变形应为定值。给定中部飞柱竖向变形的限值,即可求得每个单榀张弦梁所需的刚度,进而可以对径向梁和拉杆的截面积进行设计。本试验中最终采用的荷载分配盘各构件尺寸见表2。

图6 荷载分配装置的简化计算模型
Fig.6 Simplified calculation model of the load distribution structure
试验加载装置如图7所示,荷载施加采用清华大学工程结构实验室的多功能空间加载装置。由于荷载分配结构的采用,本试验的加载制度得到了大大的简化,只需利用千斤顶在荷载分配盘的中心施加竖向荷载直至结构破坏或承载力下降至极限承载力的85%即可。
表2 荷载分配结构各构件的截面尺寸
Table 2 Section dimensions of the members of the
load distribution structure mm
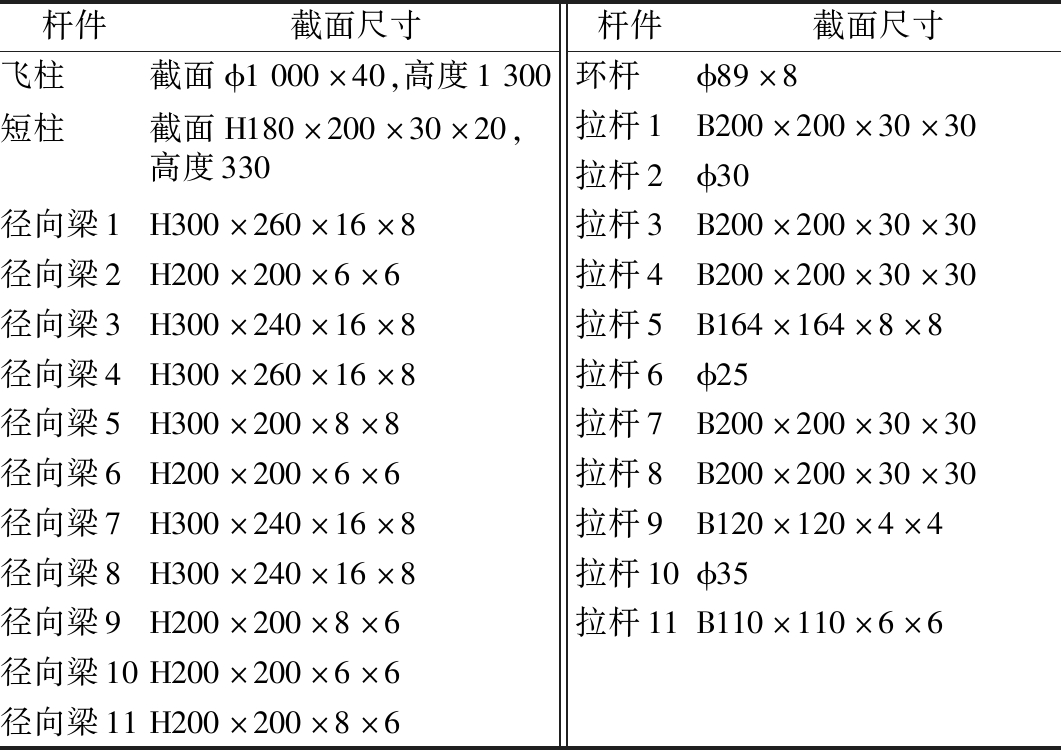
杆件截面尺寸杆件截面尺寸飞柱截面ϕ1000×40,高度1300短柱截面H180×200×30×20,高度330径向梁1H300×260×16×8径向梁2H200×200×6×6径向梁3H300×240×16×8径向梁4H300×260×16×8径向梁5H300×200×8×8径向梁6H200×200×6×6径向梁7H300×240×16×8径向梁8H300×240×16×8径向梁9H200×200×8×6径向梁10H200×200×6×6径向梁11H200×200×8×6环杆ϕ89×8拉杆1B200×200×30×30拉杆2ϕ30拉杆3B200×200×30×30拉杆4B200×200×30×30拉杆5B164×164×8×8拉杆6ϕ25拉杆7B200×200×30×30拉杆8B200×200×30×30拉杆9B120×120×4×4拉杆10ϕ35拉杆11B110×110×6×6

图7 试验加载装置
Fig.7 Test setup
3 试验结果及讨论
图8所示为试验模型所受到的总竖向荷载和各测点的柱顶竖向位移、中部面外位移之间的关系。可以发现:在加载初期(总竖向荷载Ptotal<1 900 kN),试验模型保持为弹性,各柱顶的竖向位移和柱中部的面外位移都随着荷载的增大而线性增大,直至屈服最先出现在门框1的角点(图8a中的A点)。这是因为门洞的开设截断了与门框连接的斜柱的传力路径。这也从侧面验证了设计中加强该处管件的有效性。随着荷载的继续增加,门洞1两侧的次斜柱柱脚先后屈服,且屈服区随着荷载的增加沿次斜柱开始扩展。

a—柱顶竖向位移; b—中部面外位移。
图8 总荷载-位移关系曲线
Fig.8 Total vertical load versus displacement relation curves
在屈服区沿着次斜柱发展的同时,试验模型也表现出一定的屈曲征兆。如图8b所示,自门框1屈服(图8b中B点)起,门洞1左侧测点Ⅵ的面外位移便开始停止增长,甚至随着荷载增大出现微小的负增长。随着门洞1左侧次斜柱屈服的继续发展,网格筒在该区域的刚度进一步降低,直至当总竖向荷载继续增大至4 000 kN时(图8a中D点),屈曲最先发生在门洞1左侧区域。屈曲后,门洞1左侧区域面外鼓曲的幅值和范围均迅速扩大,测点Ⅵ的荷载-位移曲线出现明显的反向,最终在门框1左侧形成如图9a所示的向外鼓曲的群柱失稳。在门洞1左侧发生屈曲之后,由于此时屈曲范围相对于整个筒体仍然较小,网格筒仍具备进行内力重分布的能力,因而可继续承载。门框1左侧由于屈曲被卸去的荷载会向两侧的邻近区域重新分配,尤其是门洞1右侧区域,最终在总竖向荷载达到4 560 kN时(图8a中E点),门洞1右侧也由于次斜柱屈服和荷载的显著增大而发生波状的面外群柱失稳,失稳变形与实测初始缺陷一致,如图9b所示。

a—门框1左侧; b—门框1右侧。
图9 试验模型的屈曲变形
Fig.9 Buckling deformation of the experimental model
至此,试验模型的薄弱区域门洞1两侧均发生了屈曲,屈曲区域占筒体结构近一半。试验模型此时已完全丧失继续承载的能力,图8a中E点对应的即是试验模型的极限承载力,为4 560 kN,其值为曲面斜交网格筒(Y2)试验模型设计荷载值(1 352 kN)的3.37倍,说明双曲面斜交网格筒(Y2)具备足够的安全储备。随后,试验模型开始进入加载的下降段(图8a中EF段),门洞1及周边区域由于屈曲,承载力随着变形的增大而降低,直至总竖向荷载降至3 860 kN时,停止试验加载。
4 结束语
双曲面斜交网格筒具有竖向受压承载力高和抗侧刚度大等良好的力学特性,在工程中主要用于承担压弯荷载作用的支承结构。本文重点介绍了中国动漫博物馆Y2斜交网格筒在竖向荷载作用下的试验加载方案,通过设置多榀辐射张弦式荷载分配结构实现单点集中竖向加载向多点竖向加载的转换,完成了斜交网格筒的加载试验研究。主要结论如下:
1)设计了一套新型的多榀辐射张弦式荷载分配结构以完成双曲面斜交网格筒(Y2)的1∶ 7缩尺模型竖向轴压稳定试验。通过调整中心飞柱的平面位置以及各榀张弦梁的刚度幅值和比例,实现了单点竖向加载代替双曲面斜交网格筒(Y2)柱顶环向分布的24个竖向集中荷载的目的。并提出了该新型多榀辐射张弦式荷载分配结构的简化计算模型和设计方法。
2)试验过程中,由于门洞的开设截断了与门框连接的斜柱的传力路径,屈服最先出现在门框1的角点。测试数据表明,门洞1所在区域受到的竖向荷载是筒体中最大的,门洞1上方测点的竖向位移也明显大于其余测点。试验验证了设计中加强该处管件的有效性。
3)试验结果反映了双曲面斜交网格筒(Y2)的破坏模式,即在门洞1两侧区域的片状面外群柱失稳。模型试验最终获得的整体稳定承载力是其设计荷载的3.37倍,说明网格筒整体稳定承载力足够,安全裕度在合理的范围内。
[1] MOON K S. Dynamic Interrelationship Between Technology and Architecture in Tall Buildings [D]. Combridge: Massachusetts Institute of Technology, 2005.
[2] MOON K S. Diagrid Structures for Complex-Shaped Tall Buildings [J]. Procedia Engineering, 2011, 14: 1343-1350.
[3] 周健, 汪大绥. 高层斜交网格结构体系的性能研究[J]. 建筑结构, 2007(5): 87-91.
[4] GUO Y L, ZHANG Y H, ZHU B L, et al. Experimental and Numerical Studies of Instability Mechanism and Load Resistance of Rhombic Grid Hyperboloid-Latticed Shells Under Vertical Load [J]. Engineering Structures, 2018, 166: 167-186.
[5] 章友浩, 朱博莉, 郭彦林, 等. 双曲面斜交网格筒中相贯节点破坏机理与试验研究[J]. 建筑结构学报,2020. Doi:org/10.14006/j.jzjgxb.2019.0156.
[6] 郭彦林, 章友浩, 童精中, 等. 一种能够提高群柱失稳荷载的杂交网格筒: CN105756195A[P].2016-07-13.
[7] 王永海. 通高区群柱的面外稳定性能与设计方法研究[D]. 北京: 清华大学, 2009.
[8] IZADI M, BARGI K. Natural Draft Steel Hyperbolic Cooling Towers: Optimization and Performance Evaluation [J]. Structural Design of Tall & Special Buildings, 2013, 2399: 713-720.
[9] 周承倜. 弹性稳定理论[M]. 成都: 四川人民出版社, 1981.
[10] TONG G S. The Stiffness and Strength Requirements for Platform-Beams in an Industrial Hall [J]. Journal of Constructional Steel Research, 1990, 16(3): 205-220.
[11] JAUNKY N, JR N F K, AMBUR D R. Formulation of an Improved Smeared Stiffener Theory for Buckling Analysis of Grid-Stiffened Composite Panels [J]. Composites Part B Engineering, 1996, 27(5): 519-526.
[12] 郭彦林, 王永海. 三层通高区群柱面外稳定性能与设计方法研究[J]. 土木工程学报, 2011, 44(8): 16-24.
[13] WANG D, ABDALLA M M. Global and Local Buckling Analysis of Grid-Stiffened Composite Panels [J]. Composite Structures, 2015, 119: 767-776.
[14] 章友浩. 网格筒结构稳定性能与设计方法研究[D]. 北京: 清华大学, 2019.
[15] 郭彦林, 章友浩, 朱博莉, 等. 一种能够实现大尺寸模型多点荷载分配的试验加载装置: CN105758658A[P].2016-07-13.