随着城市地铁线路密度的加大,地铁下穿隧道或建筑将越来越多,由于地层的沉降及管线影响,地铁隧道的施工建设难度会越来越大。随着地铁修建规模和工程难度的增加,在地铁施工方面,其方式、方法在不断更新换代,从最开始的矿山施工法到如今明挖法、浅埋暗挖法以及近年来广泛应用的盾构法。盾构法已经成为发达国家在地铁施工中运用的主要方法。新建地铁工程中,邻近既有地铁线路受新建线路施工影响存在着极大的技术困难及安全方面的风险[1-3]。
地铁的地表沉降研究在国外时间相对较早,Peck提出经验公式法[4],通过观测大批量沉降数据,最终提出地表沉降槽形状满足正态分布特点的概念。地层损失能引起地层移动,同时认为在地铁施工过程中地面沉降一般发生在不排水的情况下,因此假定为地表产生的沉降槽的体积与地层损失的体积相吻合。该方法假定为地层损失是沿着地铁新建隧道掘进方向均匀分布的,地表区域沉降的横截面方向分布的曲线形状基本满足正态分布特点。王剑晨等讨论了新建隧道施工工法、辅助施工方法、新建隧道与既有隧道的埋深、既有隧道刚度、新建隧道双洞间距、变形缝位置等因素对经验参数的影响,给出经验参数的修正公式[5]。将经验参数修正公式与Peck公式相结合,并通过工程实例验证了预测方法的有效性。张迪等以有限元为手段,分析不加固与加固两种工况下盾构下穿既有铁路桥的沉降及应力变化[6]。
目前,新建隧道下穿既有隧道相关工程研究方向主要在以下几个方面,隧道下穿施工对既有结构变形及内力的影响[7-11]、新建隧道施工控制技术[12-14]、安全风险控制[15-19]等。
1 工程概况
1.1 下穿概况
广州地铁21号线5标黄村站—世界大观站区间标段位于广州市天河区,本区间场地地貌属冲积平原线路基本沿大观南路下铺设,下穿车陂路车行隧道和人行隧道。
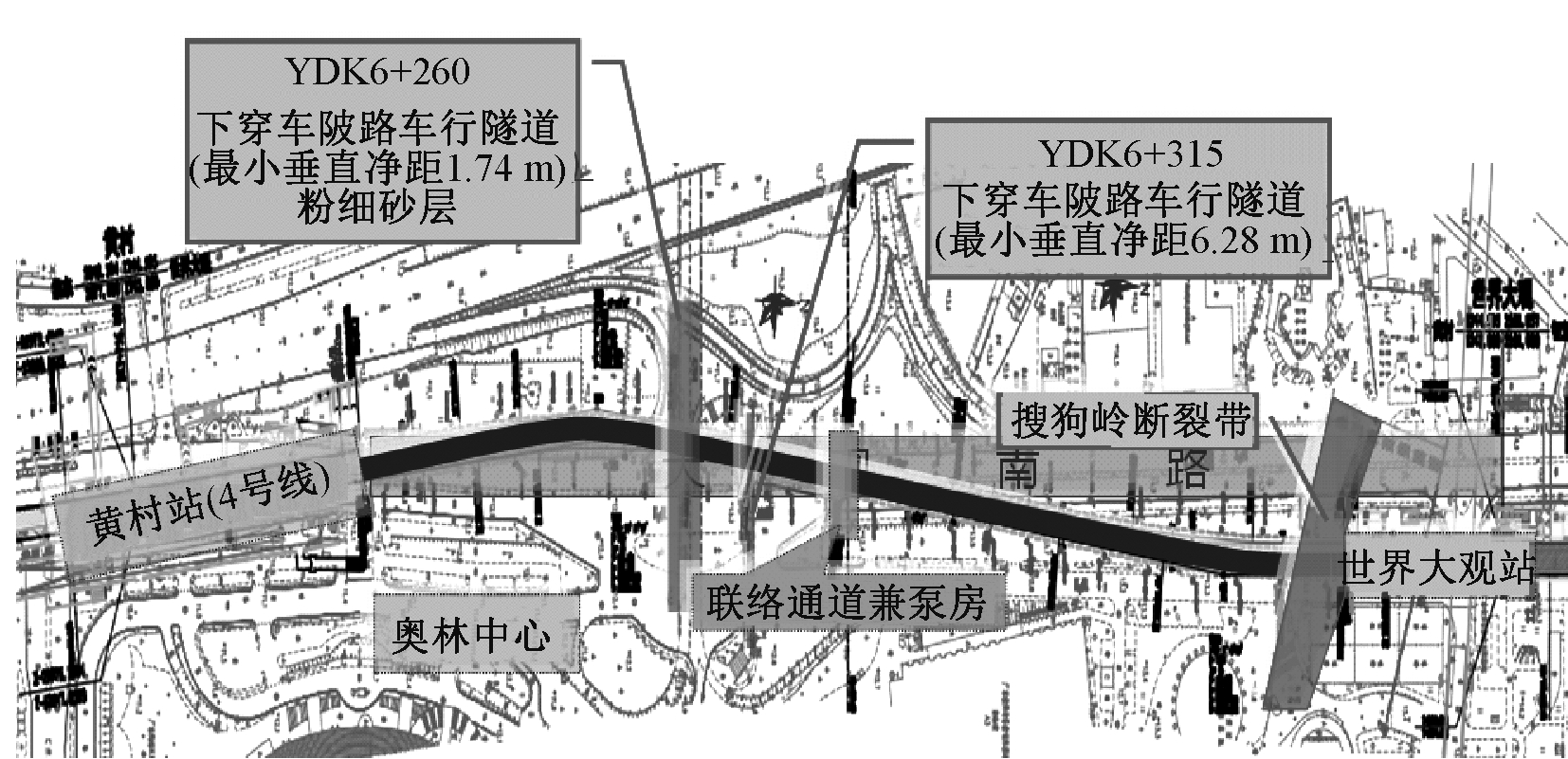
图1 黄村站—世界大观站区间平面示意
Fig.1 The schematic plan of Huangcun-Shijiedaguan subway interval
黄村站—世界大观站盾构区间在YDK6+250~YDK6+270处下穿既有车陂路车行隧道,右线盾构隧道与车陂路车行隧道底板垂直最小净距为1.98 m,左线为1.74 m(图2),且处于粉细砂地层。因此施工中对既有隧道、行车车辆的安全有很大影响。

图2 车陂路隧道横截面剖面 m
Fig.2 The cross-section drawn Chebei road tunnel
盾构法区间线路下穿地表及地下环境风险多,风险级别高,盾构掘进技术控制要求高。黄村站—世界大观站区间隧道基本位于环市大道下方,地下管线众多。盾构进洞地层较差,有较厚的砂层,盾构易发生姿态突变。盾构隧道下穿车陂路车行隧道,盾构与隧道底板距离较近。
1.2 工程地质与水文地质条件
黄村站—世界大观站盾构区间地下水位埋深-1.4~-4.0 m,隧道顶以上8.0~10.0 m;黄村站—世界大观站区间地下水类型主要有第四系孔隙水和基岩裂隙水,主要含水层为冲洪积粉细砂层③1、中粗砂层③2、砾砂层③3和卵石层③4,地层基本分布连续,局部缺失,厚度不大,砾砂③-3局部分布。砂层水一般覆盖有黏性土层,地下水略具承压性,根据抽水试验成果及地区经验,砂层为中等透水,强—中风化岩为风化裂隙水,为弱—中等透水地层。
黄村站—世界大观站盾构区间穿越地层主要为砾质黏性土、全、强、中等、微风化泥质粉砂岩地层。区间穿越地层复杂多变,均呈现地层分界起伏较大,风化深槽分布较多,上覆地层主要为第四系人工填土、冲洪积相层、河湖相沉积层及碎屑岩残积层,基岩类型主要为白系碎屑岩(砾岩、泥质粉砂岩),区间整体上软下硬或软硬不均复合地层特性明显,盾构掘进控制要求高。
2 数值模拟
2.1 数值建模
对黄村站—世界大观站区间采用盾构法左右双线错距施工,本次数值模型尺寸与实际工程按1∶1比例实施,高42.45 m,沿新建双线隧道纵向长度140 m,横向宽度92.5 m,双线隧道上覆土体厚15.45 m。
模型网格(图3)单元数135 480个,单元结点数145 101个,网格单元为退化块体和六面块体网格,对其进行反复检查后,网格模型可用。

图3 模型网格
Fig.3 Grid model diagram
模型边界条件设置,底面施加竖向约束,地表面自由无约束,其余四个方向面对其水平方向约束竖直方向自由。
2.2 计算假设
1)根据现场地质勘测资料,简化分为6个均质土层。
2)忽略地面荷载对地下在建及既有隧道沉降影响(图4)。
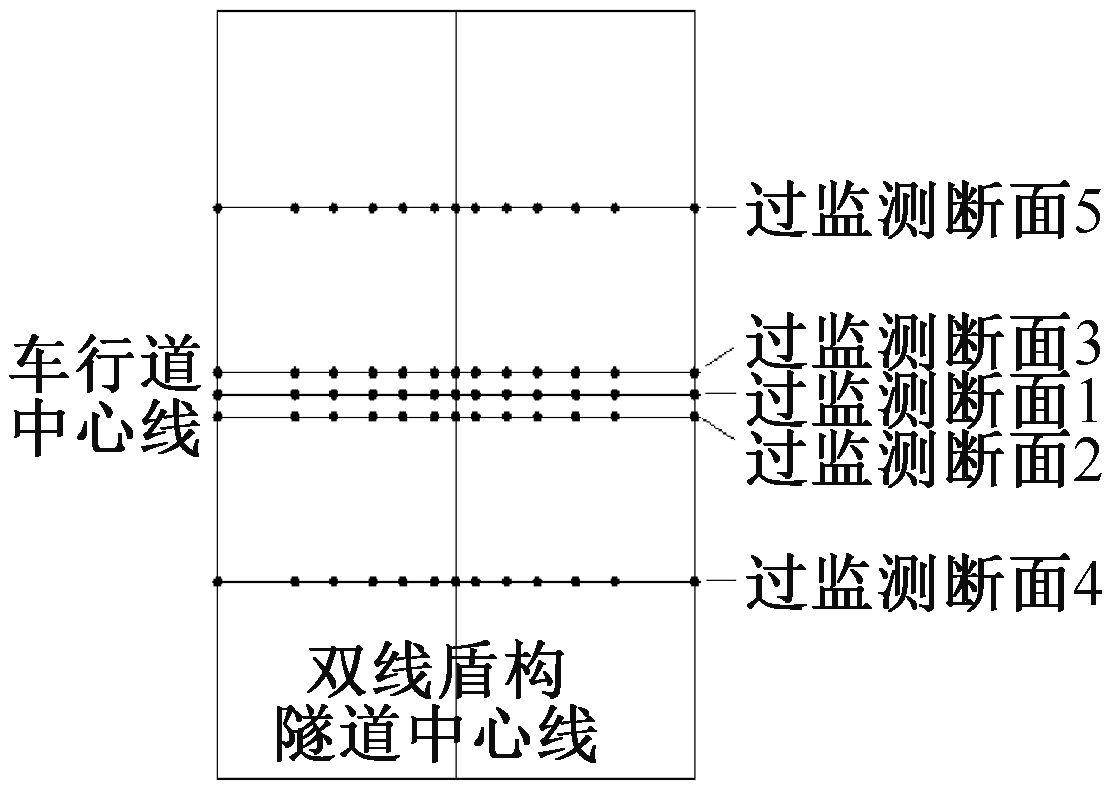
图4 模型地表沉降监测点布置
Fig.4 Arrangement of ground settlement monitoring points
3)盾构管片材料选取等级为C50高强混凝土,考虑到管片拼装方式等影响,模型中此部分强度需进行折减,折减系数为0.85。
4)盾构掌子面顶进压强为0.3 MPa。
5)数值模拟计算中,采用水土合算的方法,地下水位以下采用饱和重度。
6)在对区间隧道土体开挖施工的过程中,不考虑由于时间变化引起的地层土体下沉,地层土体的下沉仅与荷载步有关。
7)不考虑地层损失造成的影响。
2.3 力学物理参数
根据水文地质勘测数据,地表以下15 m为人工填土和黏土层,具体模型中对应参数如土层编号1和2,以下冲洪积粉细砂层3-1对应模型中的土层3,中粗砂层3-2对应土层4,砾砂层3-3和卵石层3-4分别对应土层5和6,其模型中具体地层物理参数如表1所示。
表1 地层物理参数
Table 1 Physical parameters

土层编号土质类型密度/(kg·m-3)体积模量/MPa剪切模量/MPa黏聚力/kPa内摩擦角/(°)土层1人工填土1 8003.002.22024土层2黏土层1 8303.332.545.512.5土层3粉细砂层1 91710.850.229土层4中粗砂层1 9503010035土层5砾砂层2 0803212.8034土层6卵石层2 10036.4529.66040
在实际工程中某些组合结构的弹性模量不能准确测得,因此,本文中采取等效刚度法[20]。其具体算式如下:
(1)
式中:E′为等效弹性模量,MPa;E为混凝土或喷射混凝土弹性模量,MPa;E1为超前支护结构钢管或钢筋等的弹性模量,MPa;A0为混凝土结构的截面面积,m2;A1为钢材或者钢架的截面面积,m2。
对于既有隧道与新建隧道交汇位置注浆加固土体强度是采用强化围岩强度参数的方法进行模拟,模型中浆体厚度采用等效方法模拟[21],等效公式如下:
(2)
式中:R为浆液的扩散半径,m;S为相邻两注浆孔间距,m;D为等效厚度,m。
2.4 施工过程模拟与实现
主要研究在双线盾构隧道下穿既有车行隧道过程中,周围土体及既有车行隧道变形沉降。模拟过程中需要将具体施工步骤进行必要简化:第一步,右线隧道提前盾构开挖;第二步,待盾构至规定间距后左线隧道开挖施工;第三步,右线隧道盾构至接近其下穿既有车行隧道时,要对右线在建隧道管壁内侧进行二次注浆加固周围土体,左线盾构隧道通过既有车行隧道时亦是如此;第四步,同时盾构施工至双线贯通。数值模拟黄村站—世界大观站盾构区间左右线掘进施工时,选取左右线错距为25 m的盾构掘进方案。
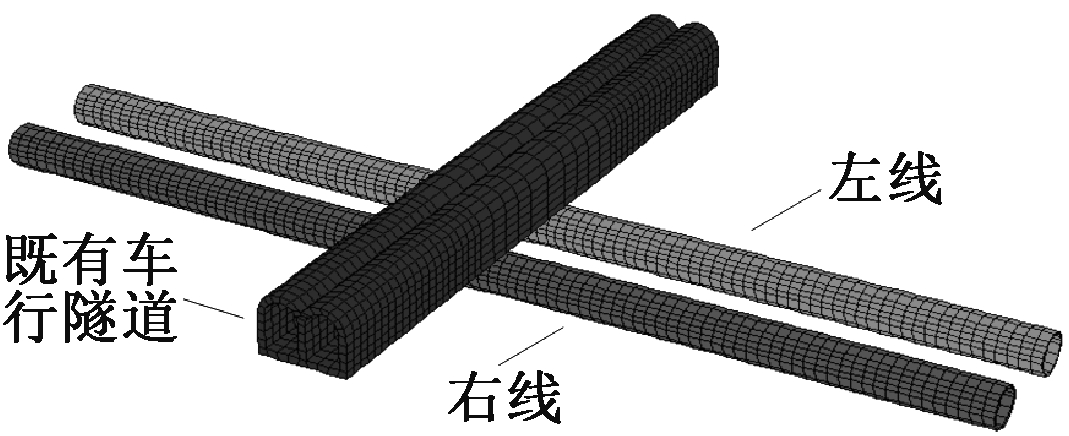
图5 双线盾构隧道与车行隧道位置关系
Fig.5 The location diagram of shield tunnel and car tunnel
该模拟采用摩尔-库仑屈服准则对开挖土体施工进行模拟分析,采用Drucker-Prager模型模拟结构的非线性特征。该模型无其他外力荷载,仅施加土体自重及盾构机施加于掌子面的0.3 MPa。模拟开挖过程是以2 m为一个开挖步,开挖土体时同时释放50%的初始应力,开挖土体采用空单元进行模拟实现,待初支撑支护后释放剩余应力。
由图6可知:既有车行隧道上方土体沉降较小,其两侧地表土体沉降相对较大。图7为既有车行隧道对称轴线切面沉降云图,图7与图8、图9对比可知,在建隧道与既有车行隧道错落交叉位置土体沉降相对较明显,沉降范围相对集中。而由图8、图9可知:土体沉降范围明显加大,土体沉降最大值同样在拱顶位置显现。

图6 双线隧道贯通后地表沉降俯视云图
Fig.6 Ground settlement clound after the double-line tunnel breaks through

图7 监测断面1截面沉降云图
Fig.7 Ground settlement clound of monitoring cross section 1

图8 监测断面2截面沉降云图
Fig.8 Ground settlement clound of monitoring cross section 2

图9 监测断面4截面沉降云图
Fig.9 Ground settlement clound of monitoring cross section 4
双线隧道盾构下穿车行隧道至贯通时车行隧道底板竖向变形曲线如图10所示:由于盾构掘进造成上部土体下沉,导致应力重分布,车行隧道所在地层下沉,盾构隧道与既有车行隧道交汇区域的车行隧道底板的竖向变形值明显加大,盾构下穿过程中对车行隧道有明显的扰动作用,并且在盾构隧道中心偏右位置沉降最大,须在此段区域进行注浆加固土体。
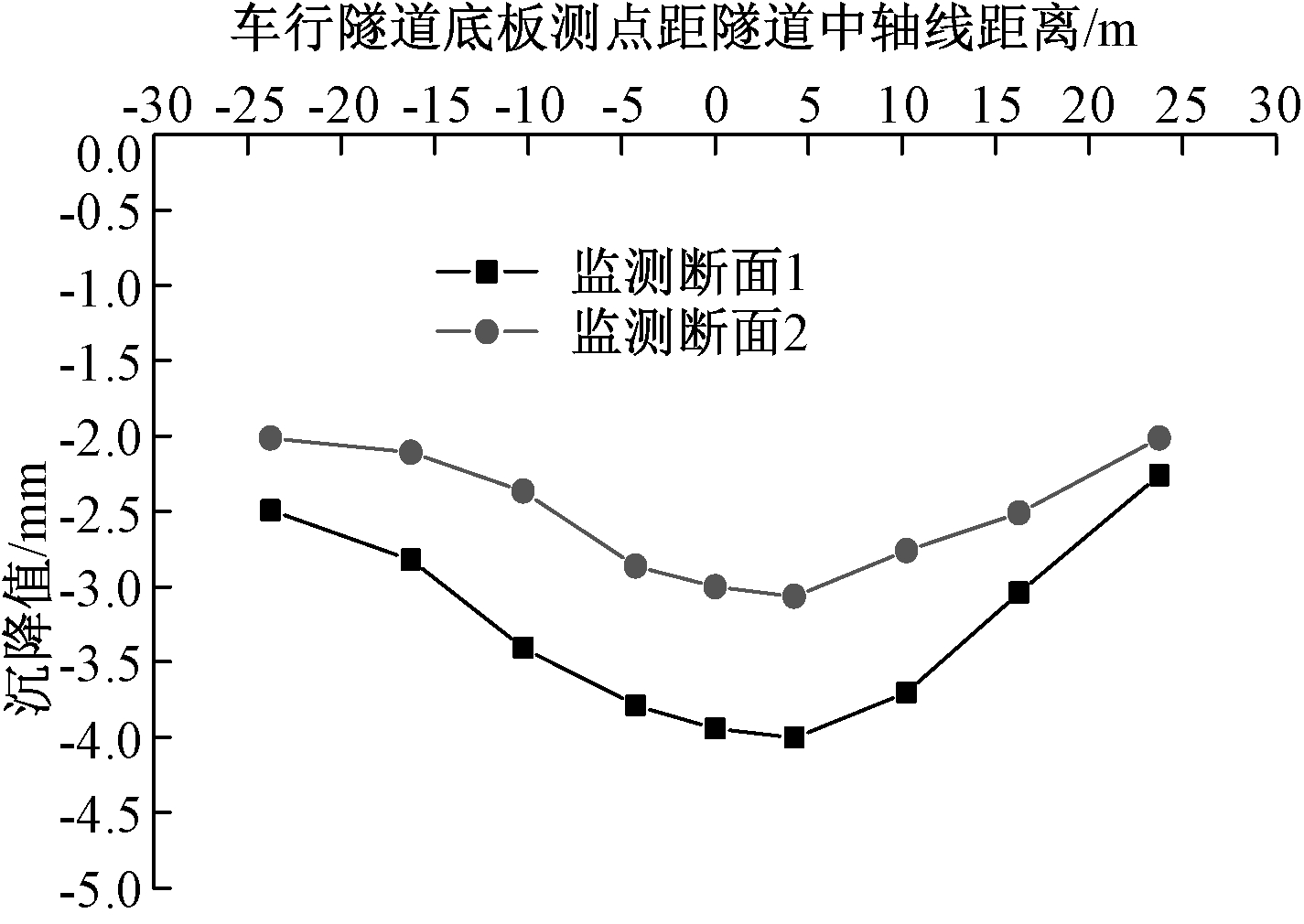
图10 车行隧道底板监测点沉降曲线
Fig.10 The subsidence curve of the car tunnel floor
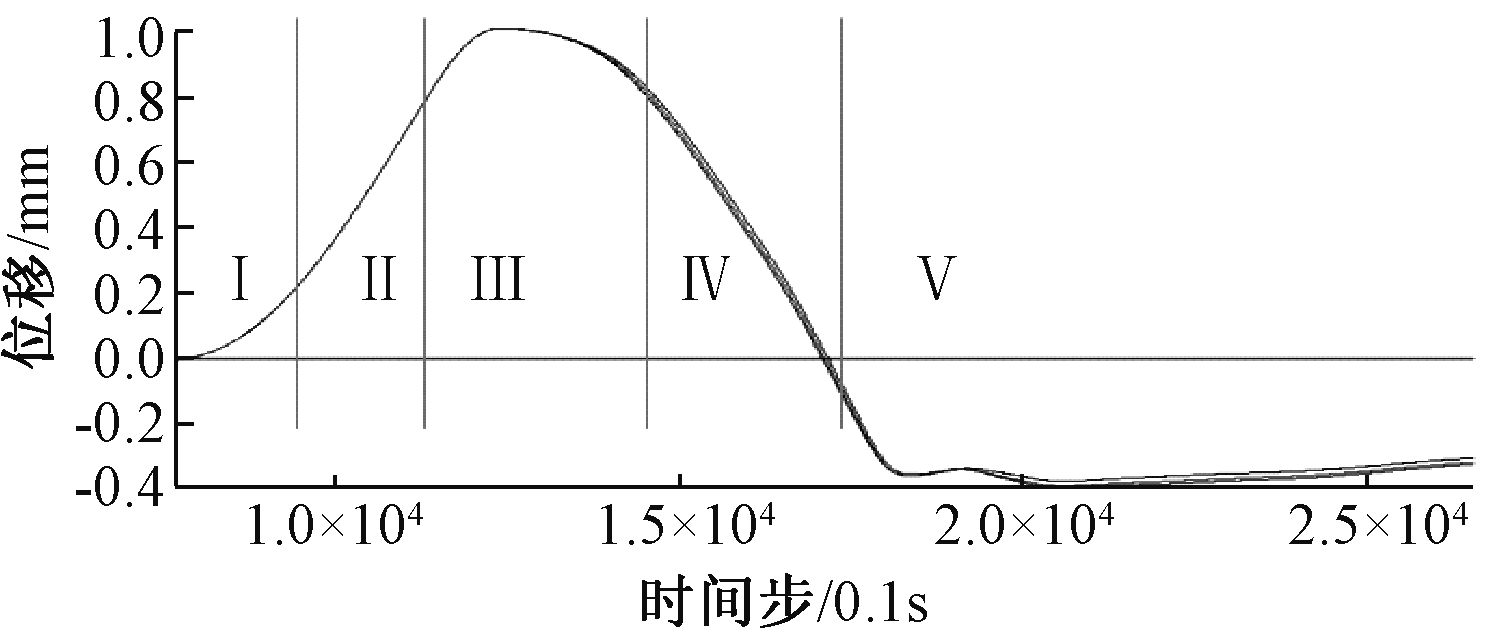
图11 车行隧道底板竖向位移随施工进度时程曲线
Fig.11 The car tunnel floor vertical displacement as the construction schedule
图11为既有车行隧道底板3个监测点的时程曲线,显示了双线盾构隧道掘进过程中对既有车行隧道底板的扰动影响。图中,区域Ⅰ为右线隧道超前左线盾构掘进25 m的时程曲线;区域Ⅱ为右线隧道盾构开挖面到达既有车行隧道下方土体的时程曲线;区域Ⅲ为右线隧道盾构开挖穿越既有车行隧道下方土体过程的时程曲线;区域Ⅳ为右线隧道盾构开挖面穿过车行隧道下方土体后的时程曲线;区域Ⅴ为左线隧道盾构穿越车行隧道下方土体过程以及贯通的时程曲线。
由图11可知:区域Ⅰ监测点竖向位移为正,由于开挖面顶进力作用,此过程车行隧道底板隆起2.15 mm;随着开挖面距离车行隧道越来越近,导致开挖面顶进力对车行隧道下方土体作用越来越明显;区域Ⅱ的车行隧道底板上隆越来越严重;待右线盾构掘进穿越车行隧道的过程中底板隆起达到最大值,如区域Ⅲ所示;随着右线盾构掘进,车行隧道整体下沉,这是由于土体压缩,其应力得到释放,如区域Ⅳ所示;当右线隧道盾构掘进时,左线隧道也同时在掘进,如区域Ⅴ所示,左线盾构穿越车行隧道的过程中车行隧道底板继续下沉;当左右线隧道盾构开挖错距25 m时,车行隧道底板沉降没有发生明显的叠加效应,待左线盾构穿越车行隧道直至最后贯通时,车行隧道底板监测点最终平均下沉3.69 mm。
3 双线盾构错距方案比选
数值模拟过程中,所选取的施工面错距分别为10,20,25 m(实际工况), 30 m和35 m。通过以上5种错距的比较分析,探究在不同施工错距的情况下,新建隧道对其下穿近邻既有车行区间隧道的沉降影响。
隧道左右线盾构错距分别为10,20,25,30,35 m时,监测断面2对应的地表沉降最大值分别为31.53,30.35,28.26,28.01,27.96 mm,同时对应的沉降槽反弯点距离分别为11.47,11.72,12.14,12.19, 12.18 m;监测断面4对应的地表沉降最大值分别为35.93,34.22,32.52,31.92,31.72 mm,同时对应的反弯点距离分别为11.71,12.01,12.47,12.51,12.59 m。随着盾构开挖错距增加,最大沉降值均减小,反弯点距离反而增加。原因是当盾构掘进错距增加时,左右线盾构施工产生的土体沉降叠加效应减弱,对地表土体的扰动相对较小,虽然左线隧道盾构掘进会对右线产生相对较长的地层扰动,但是由于右线相应区间已经完成管片安装以及同步注浆,因此对右线隧道上部土体扰动较小。综合比较发现,此区间左右线隧道盾构错距小于25 m时对地层扰动的叠加效应明显,超过25 m之后叠加效应明显减弱,最终沉降较大区域均集中在左右隧道中轴线附近。同时,结合地表最大沉降值和反弯点距离两个指标,可知,选择左右线盾构错距25 m时可行。随着开挖错距增加,软件计算步在增加。在模拟分析中,单位长度盾构掘进施工用时进行统一后,可用计算步来反映盾构施工工期。因此,随左右线隧道盾构错距增加,盾构施工工期在增加,盾构错距从25 m增加到30 m时,增加幅度较大。
4 结束语
对黄村站—世界大观站盾构区间在建地铁隧道和既有车行隧道进行数值建模和计算,并分析了双线盾构区间地表沉降规律和双线盾构隧道下穿既有车行隧道过程中土体及结构变形规律,提出可行性方案,具体得出结论如下:
1)由于开挖面顶进力作用,在右线盾构掘进穿越既有车行隧道过程中,既有车行隧道底板变形特点为先向上隆起,随着盾构的深入,隆起值也逐渐加大,当盾构开挖面穿过既有车行隧道下方土体时,由于应力释放等原因,交汇区域土体会有向下运动趋势,待盾构开挖面远离既有车行隧道后,交汇区域土体下沉。左线盾构模式引起的既有车行隧道底板沉降类似右线隧道的,当左右线隧道盾构开挖错距为25 m时,车行隧道底板沉降没有发生明显的叠加效应,待左线盾构穿越车行隧道直至最后贯通后,车行隧道底板监测点最终平均下沉3.69 mm。
2)左右线隧道盾构错距小于25 m时对地层扰动的叠加效应明显;超过25 m之后叠加效应明显减弱,最终沉降较大区域均集中在左右隧道中轴线附近。盾构错距为25 m的方案,在地表最大沉降量、反弯点距离以及工期三方面均为最佳选择,所以,综合考虑,实际施工过程中建议采用盾构掘进错距为25 m的方案。
[1] CHANG S B, MOON S J A Case Study on Instrumentations of a Large Tunnel Crossing Under the Existing Subway Structure[C]// Proceedings of the KGS 2000 Spring Conference. 2000: 56-59.
[2] SHARMA J S, HEFNY A M, ZHAO J, et al. Effect of Large Excavation on Deformation of Adjacent Mrt Tunnels [J]. Tunnelling and Underground Space Technology, 2001, 16(1): 93-98.
[3] BRENNER B, NEFF T. Design and Management for Underground Uncertainty on the Central Artery/Tunnel Project[C]// North American Tunnelling. 2000: 13-21.
[4] PECK R B. Deep Excavations and Tunnelling in Soft Ground [C]//Proc.7th Int. Conf. SMFE. Mexcio,1969:225-290.
[5] 王剑晨,张顶立,张成平,等.北京地区浅埋暗挖法下穿施工既有隧道变形特点及预测[J].岩石力学与工程学报,2014,33(5):947-956.
[6] 张迪,周庆九,卓旭阳,等.大型盾构隧道穿越铁路框架桥的影响分析[J].现代隧道技术,2013,50(6):131-138.
[7] 刘大雷.新建隧道上穿对既有隧道纵向位移的计算方法[J].安徽建筑, 2018, 24 (6):245-250.
[8] 刘军,南志领,金鑫,等.地铁工程穿越施工中热力管线变形及控制研究[J].施工技术,2017,46(增刊2):1053-1057.
[9] 黄明利,瞿晓巍,谭忠盛,等.地铁重庆北站零距离立体交叉暗挖施工力学效应分析[J].土木工程学报,2017,50(增刊2):21-27.
[10] 许有俊,葛绍英,孙超.隧道斜交下穿施工引起既有线的沉降变形分析[J].建筑技术,2017,48(11):1163-1166.
[11] 苏宗贤,何川.盾构隧道纵向变形附加内力的壳-弹簧-接触模型数值分析[J].现代隧道技术,2015,52(6):70-76.
[12] 王智高.城市地铁超近距离叠交区段盾构隧道施工技术[J].工程技术研究,2018(16):31-32.
[13] 来弘鹏,郑海伟,何秋敏,等.砂土地层盾构隧道小角度斜下穿既有隧道施工参数优化研究[J].中国公路学报,2018,31(10):130-140.
[14] 武永珍,王亚会,陆瑶.新建隧道上跨施工对既有隧道的影响及加固措施研究[J].施工技术,2017,46(增刊2):18-25.
[15] 洪文霞,钱瑾玉,贾明磊.邻近建筑物条件下青岛地铁盾构施工风险评价[J].隧道建设(中英文),2018,38(增刊2):68-74.
[16] 白海洋,王正仲.隧道下穿施工对既有线路影响研究[J].山东交通科技,2018(6):28-30.
[17] 王凯旋,王雨,康荣学,等.新建管线近距离上跨地铁车站的安全控制分析[J].中国安全科学学报,2018,28(12):89-95.
[18] 高永,孙俊.南京地铁盾构隧道纵横断面结构安全评估研究[J].都市快轨交通,2015,28(6):60-64,70.
[19] 罗有权,张黎红.隧道开挖对周边既有桩基变形影响研究[J].建筑技术, 2017,48(11):1175-1178.
[20] 李术才,朱维申,陈卫忠,等. 弹塑性大位移有限元方法在软岩隧道变形预估系统研究中的应用[J]. 岩石力学与工程学报,2002(4):466-470.
[21] 刘天宇. 超前小导管在隧道工程中的应用及数值模拟[J]. 土工基础, 2013(2): 67-70.