输电线路是重要的电力基础设施,关系到国计民生。若输电线塔混凝土基础发生均匀沉降,以导线相连的邻近输电线塔受力状态也将发生改变,预测输电线塔混凝土基础的均匀沉降可以设计预留足够长的导线,避免输电线塔沉降时通过导线拉倒邻近输电线塔。混凝土基础间的不均匀沉降会使输电线塔倾斜,倾斜超过一定限度有可能导致铁塔倾倒,使电力输送中断,尤其是一些电压等级高、输送能量大的线路,往往会引起严重的后果,根据输电线塔混凝土基础已有沉降监测数据预测将来沉降大小和不均匀沉降,可以及早采取必要的调平措施,避免铁塔倾斜过大。因此,对输电线塔基础沉降的计算和根据已有的沉降数据预测未来的沉降具有重要意义。
沉降的计算方法主要有计算机仿真和算式法。计算机仿真主要有有限元和有限差分方法;计算基础沉降最常用的算式计算法为分层总和法[1],大致流程为测试土的侧限压缩参数、计算附加应力和自重应力,之后分层计算分层应变与本分层厚度之积得到分层沉降,最后累加得到基础沉降。需要指出的是:分层总和法计算的只是主固结沉降,对于有机质成分较高的土层,尚应考虑次固结沉降的影响。
根据已有沉降数据预测未来的沉降可以用曲线拟合法,常用的有三点法[2]、双曲线法[3]、Asaoka 法[4]、泊松曲线法[5]等。姚仰平等提出了适用于高填方长期沉降的蠕变沉降实用算法[6],具有参数少、物理意义明确的特点,且可以计算给定精度下的有效预测时间范围或预测时间范围的沉降误差[7]。
本文首先通过分层总和法计算输电线塔混凝土基础的主固结沉降;根据已有监测沉降数据使用蠕变沉降实用算法、三点法、双曲线法等通过对输电线塔混凝土基础的未来沉降进行预测对比,验证蠕变沉降实用算法具有较理想的计算精度,并给出了其有效预测区间。
1 工程和地质概况
1.1 工程位置和地质概况
要计算的输电线塔位于山西省阳泉市郊区桐花树村东北约0.5 km的山坡上,杆塔G15(勘探点位置的经、纬度分别为东经113.661 638°、北纬37.914 218°)。杆塔东侧区域为铝土矿露天开采场地,开采后形成的矿坑由填土回填形成铝土矿回填场地,其南部为采煤沉陷区光伏基地汇集站,汇集站配套220 kV的输出线路经过此铝土矿回填场地,输电线路中G15杆塔位于回填场地西北侧边坡上。输电线塔型号为2B3-ZMC2,输电线塔有4个混凝土独立基础,正面和侧面根开均为7.3 m。输电线塔坐落于铝土矿回填场地上,塔下填土厚度为30 m左右,填土时间为2~5 a前,填土时未分层碾压,仅将填土压实到可承载填土运输车辆。
阳泉勘察区出露地层主要为第四系全新统填土地层,下伏第四系上更新统的灰黄、棕黄色黄土(粉土、粉质黏土)。填土主要由粉质黏土、粉土组成,土质不均匀,夹块石、漂石(母岩成分为砂岩、页岩、石灰岩、煤矸石等),含大量角砾和中粗砂,混粉土、粉质黏土。东侧回填较厚,西侧回填较薄,填土分布于整个场地,本次勘察未揭穿,未见地下水。
碾压后填土重度为18.1 kN/m3,压缩系数为0.29 MPa-1,为中压缩性土;黏聚力为57.8 kPa,内摩擦角为19.1°;渗透系数1.8×10-5cm/s。填土的侧限压缩试验e-p曲线如图 1所示。

图1 填土侧限压缩试验曲线
Fig.1 Confined compression curve of the fill
1.2 地基处理方式
输电线塔混凝土独立基础的地基为填土,填土之下为原状土。为加强地基承载力,4个独立混凝土基础下布铺了一层5 m厚的三七灰土层,分层碾压密实。由于没有对灰土取样做室内侧限压缩试验,借用文献[8]中三七灰土土性参数,其密度1.963 g/cm3,重度19.237 4 kN/m3,由侧限压缩试验结果可得到e-p之间的关系(图2)。
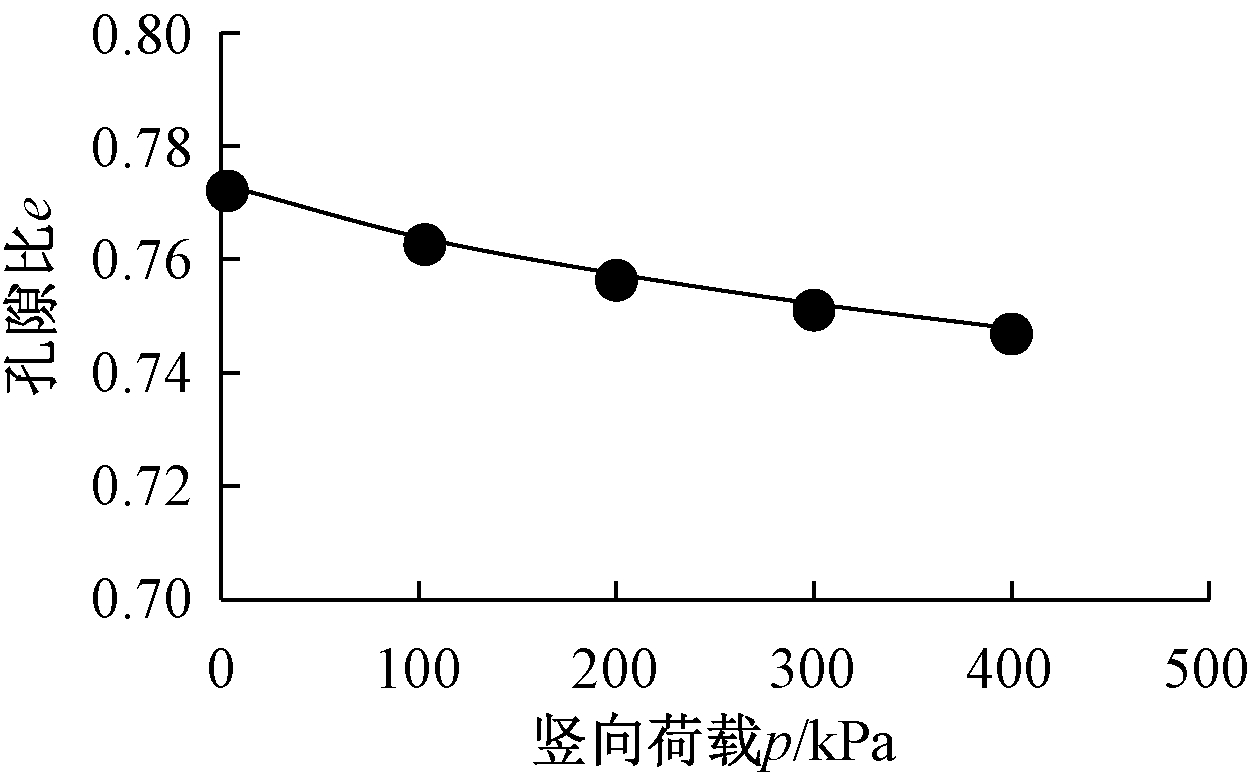
图2 三七灰土侧限压缩试验曲线
Fig.2 Confined compression curve of 37 lime soil
2 沉降监测
2.1 监测方法
沉降观测按照国家二等水准测量要求进行。各次观测中,水准点、观测点组成的观测路线为闭合路线。每次观测前均对仪器进行检校,每次观测后均对闭合差进行检查。沉降观测仪器采用美国天宝DINI03精密水准仪一台,精度指标0.3 mm/km;条码铟钢水准标尺一副。
根据GB 50026—2007《工程测量规范》[9],布设了4个沉降观测点(A、B、C、D)分别位于混凝土基础顶端,3个基准点BM1、BM2和BM3分别在沉降影响范围之外,见图3。
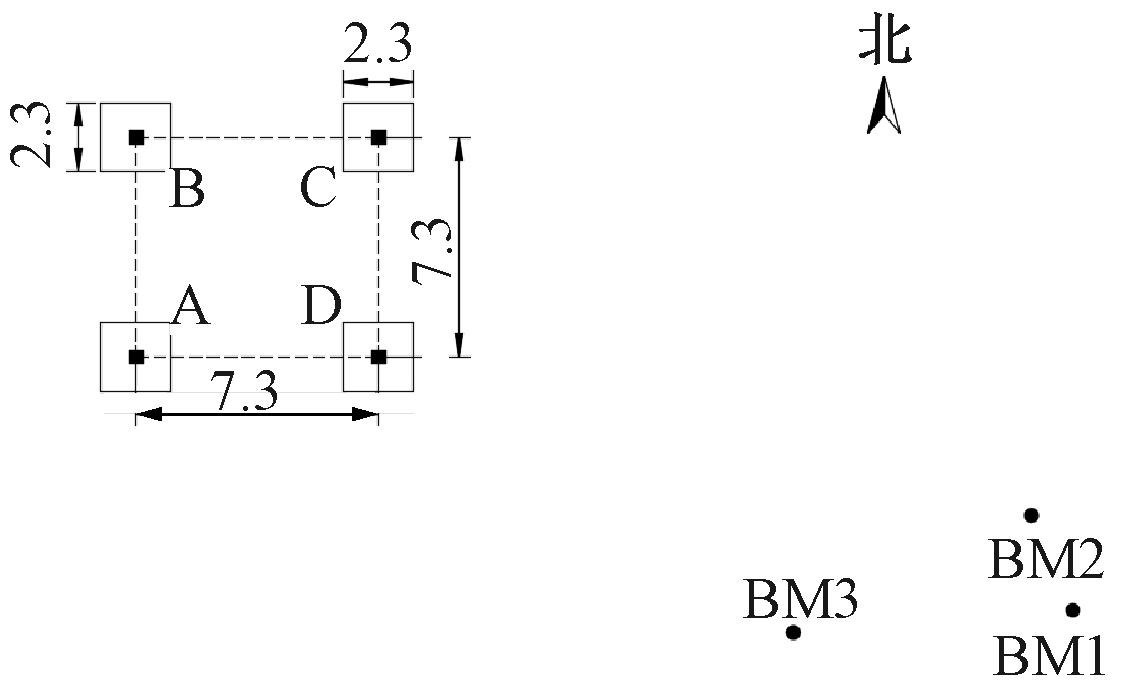
图3 G15塔基准点、沉降观测点布置 m
Fig.3 Arrangement of datum point and settlement observation points G15
2.2 监测结果
沉降监测共15次,历时324 d。由表 1可知:最大累计沉降量为B号点4.76 mm,最小累计沉降量为D号点2.53 mm。四点平均沉降量为3.56 mm,沉降变化未见异常。B、D号观测点间距离为10.32 m,沉降差为2.23 mm,两点间沉降差与距离之比为0.000 2,小于GB 50007—2011《建筑地基基础设计规范》[10]规定的地基整体倾斜变形允许值0.004。
表1 G15塔4个独立基础沉降监测数据
Table 1 Settlement monitoring data of 4 independent foundations of G15 mm
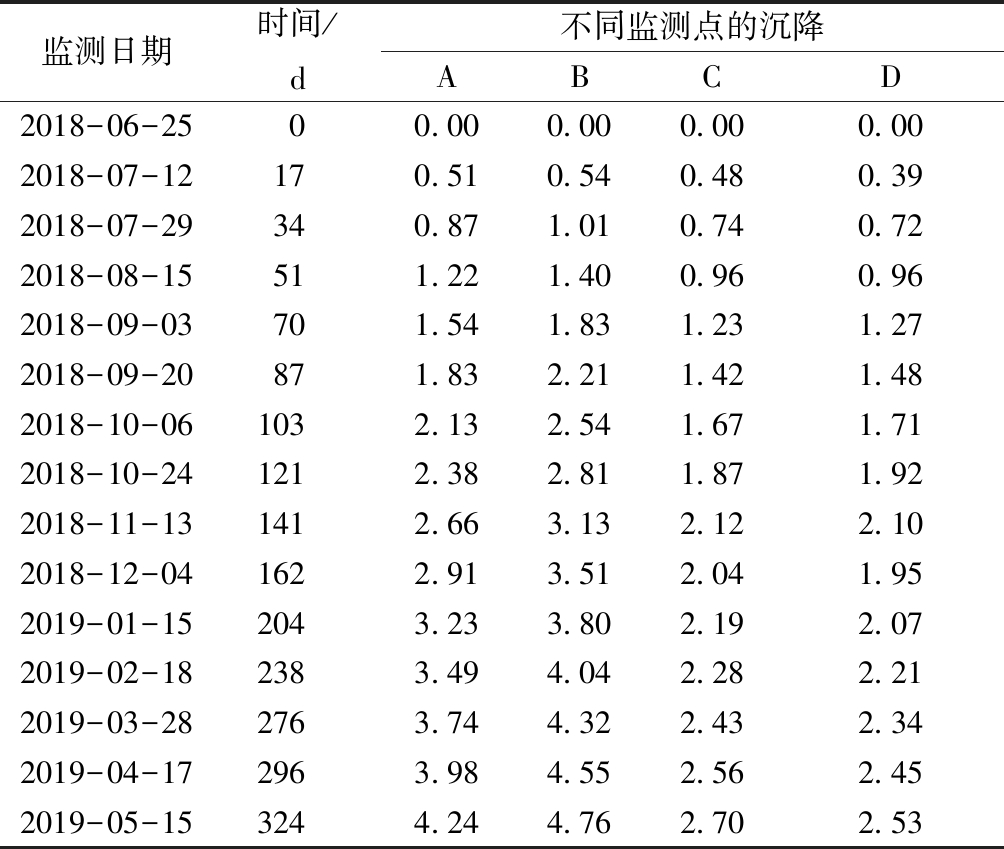
监测日期时间/d不同监测点的沉降ABCD2018-06-2500.000.000.000.002018-07-12170.510.540.480.392018-07-29340.871.010.740.722018-08-15511.221.400.960.962018-09-03701.541.831.231.272018-09-20871.832.211.421.482018-10-061032.132.541.671.712018-10-241212.382.811.871.922018-11-131412.663.132.122.102018-12-041622.913.512.041.952019-01-152043.233.802.192.072019-02-182383.494.042.282.212019-03-282763.744.322.432.342019-04-172963.984.552.562.452019-05-153244.244.762.702.53
已有监测数据的后100 d平均沉降速率为:A点0.034 mm/d,B点0.039 mm/d,C点为0.023 mm/d,D点为0.022 mm/d。JGJ 8—2016《建筑变形测量规范》[11]第5.5.5条规定:当最后100 d的沉降速率小于0.01~0.04 mm/d时可认为沉降变形进入稳定阶段。若按0.01 mm/d速率判别,则4点均未达到沉降稳定阶段。GB 50026—2007第10.5.8条规定:以0.02 mm/d作为统一的终止沉降观测的稳定指标值。可见,4个监测点的沉降都需要继续观测。
3 沉降计算和预测
3.1 分层总和法计算基础沉降
以图3中基础A为例用分层总和法计算其沉降。首先计算自重应力和附加应力。根据设计方案,基础的混凝土强度等级为C25,包括基础、垫层和地栓护帽在内混凝土总体积2.97 m3,每个混凝土基础对地基的下压力极限值(包含基础、塔身、电缆的重力以及风、坠冰等荷载)为377.6 kN。忽略基础露出地表部分体积,基础所占空间的填土重力为53.757 kN,基础最下部板为正方形,长度与宽度相等,为 2.3 m,底面积为5.29 m2,基础底面处作用荷载p0=61.22 kPa,均布荷载下矩形基础角点处任意深度z处附加应力可由式(1)求出,矩形基础任意位置下应力可由角点法求出。
分层厚度hi一般不大于基础宽度b的40%或4 m,故hi小于0.92,此处取hi=0.6 m。
(1)
其中 m=l/b;n=z/b
式中:σz为均布荷载p0作用在矩形基础上时,在基础角点下任意深度z处引起的附加应力;b为矩形基础宽度;l为矩形基础长度。
不考虑和考虑另外三个基础对该基础的应力影响,根据角点法分别得到A基础底面中心点下附加应力![]() 和
和![]() 如图4所示,随着深度的增大,基础B、C、D对基础A底面中心点下附加应力的影响逐渐增大,故在计算基础A沉降时考虑它们对A基础的应力影响,即计算基础A沉降时附加应力采用
如图4所示,随着深度的增大,基础B、C、D对基础A底面中心点下附加应力的影响逐渐增大,故在计算基础A沉降时考虑它们对A基础的应力影响,即计算基础A沉降时附加应力采用![]() 而非
而非![]()
![]()
图4 A基础底面中心点下附加应力随深度变化
Fig.4 Additional stress changed with depth at the center point of foundation A
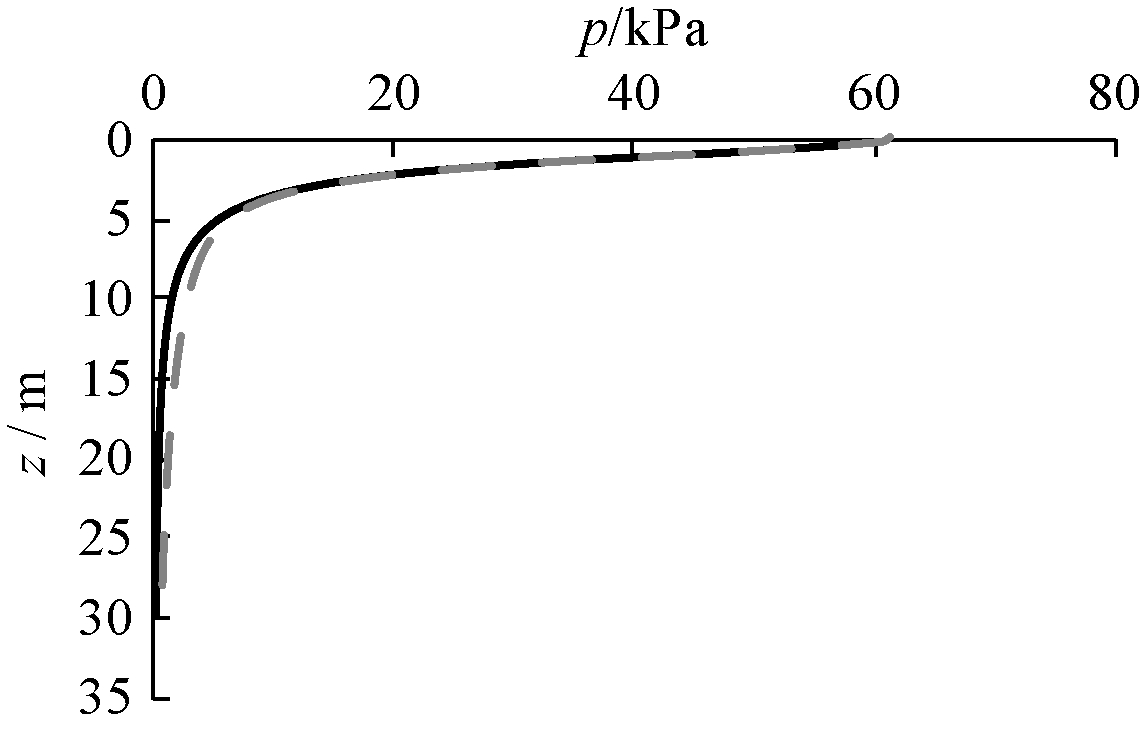
附加应力和自重应力分布如图5所示,左侧为基础底面中心点下的自重应力随深度变化,右侧为同样位置附加应力随深度变化。
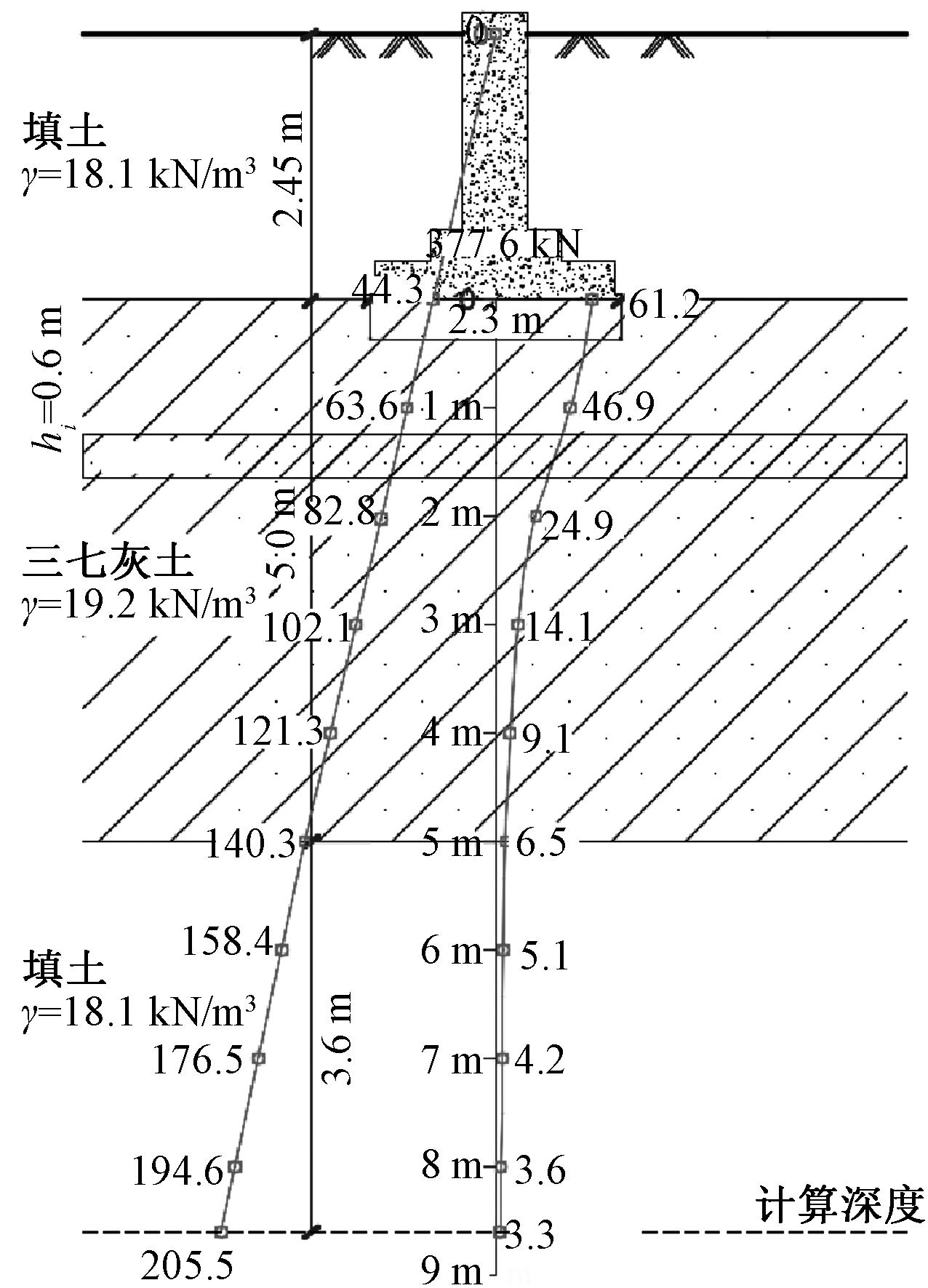
图5 基础A处自重应力和附加应力 kPa
Fig.5 The geostatic stress and additional stress below foundation A
计算结果列在表2中,其中z代表混凝土基础中心下部深度,也是计算土层厚度中心处坐标;σz1代表深度z处自重应力大小;e1为自重应力σz1时材料对应的孔隙比大小,可以根据材料的孔隙比与应力关系插值得到;Δσz为深度z处附加应力大小;σz2为深度z处自重应力和附加应力之和;e2为σz2对应的孔隙比大小,也可由插值得到;s为该分层厚度的沉降量。
若假定土层为侧限压缩,则沉降计算式为:
(2)
式中:si为第i层土层沉降;e1i为第i层土层厚度中心处自重应力对应的孔隙比;e2i为第i层土层厚度中心处自重应力和附加应力之和所对应的孔隙比;hi为计算的第i层土层厚度。
使用分层总和法计算基础沉降,除了需要知道自重应力分布、附加应力分布、孔隙比或压缩模量,还需要知道沉降计算深度,计算的深度需要满足计算深度处向上取厚度Δz(根据基础宽度b大小可知此厚度取0.6 m)的土层变形值不大于计算深度范围内所有土层总沉降的0.025。由表 2可知:计算到基础下8.6 m深度时,总沉降7.067 mm,最下层0.6 m厚度土层沉降0.168 mm,此时倍数关系为0.024,满足计算深度条件。
灰土部分总沉降量5.751 mm,填土部分总沉降量1.316 mm,基础总沉降量为所有分层沉降相加,总沉降量为7.067 mm。
3.2 蠕变沉降实用算法预测基础沉降
姚仰平等提出的蠕变沉降实用算法[6]可以根据已有沉降监测数据,预测未来沉降,并在承德机场工后沉降预测、陕西某黄土高填方地基中得到了验证[12]。蠕变沉降实用算法计算式如下:
(3)
式中:s为土体蠕变沉降量,mm;t为历时天数,d;Ct为反映填土与原地基总体蠕变速率的无量纲参数;ht为反映填方体与原地基总体蠕变刚度的无量纲
表2 分层总和法计算沉降
Table 2 Settlement calculated by layer-wise summation method
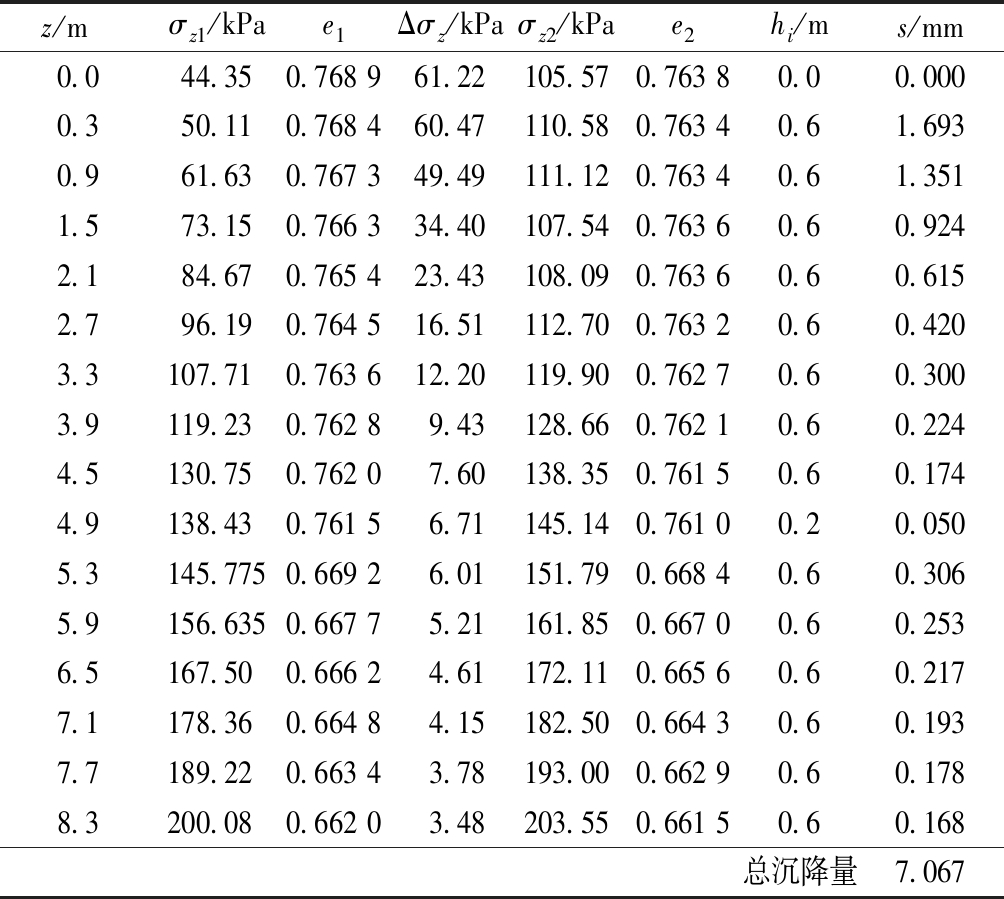
z/m σz1/kPae1Δσz/kPaσz2/kPae2hi/ms/mm0.044.350.768 961.22105.570.763 80.00.0000.350.110.768 460.47110.580.763 40.61.6930.961.630.767 349.49111.120.763 40.61.3511.573.150.766 334.40107.540.763 60.60.9242.184.670.765 423.43108.090.763 60.60.6152.796.190.764 516.51112.700.763 20.60.4203.3107.710.763 612.20119.900.762 70.60.3003.9119.230.762 89.43128.660.762 10.60.2244.5130.750.762 07.60138.350.761 50.60.1744.9138.430.761 56.71145.140.761 00.20.0505.3145.7750.669 26.01151.790.668 40.60.3065.9156.6350.667 75.21161.850.667 00.60.2536.5167.500.666 24.61172.110.665 60.60.2177.1178.360.664 84.15182.500.664 30.60.1937.7189.220.663 43.78193.000.662 90.60.1788.3200.080.662 03.48203.550.661 50.60.168总沉降量7.067
参数;t0、s0为消除量纲的单位常量,即t0=1 d,s0=1 mm。
根据沉降监测数据求解式(3)中Ct和ht时,可以采用文献[7]中方法,也可以采用拟合方法。拟合方法可以以沉降监测值或算式预测值作最小二乘为目标函数,通过遗传算法等优化算法使目标函数最小,即可求得最优的Ct和ht。因为式(3)过(0,0)点且有Ct和ht两个待求解参数,采用拟合方法时至少使用两个非零的监测值,且采用监测值越多,求解出的Ct和ht的总体预测效果越好。
为进一步验证蠕变算法的有效性,以基础A为例,同时采用三点法和双曲线法进行长期沉降预测比较。
曾国熙基于太沙基固结理论推导了地基一维固结度方程,认为蠕变沉降曲线是以最终沉降量为渐近线的指数函数,其计算式[2]:
s=s∞(1-αe-βt)
(4)
式中:s∞、α和β为计算参数;s∞为最终沉降量。三点法的缺点是可能不过零点。
双曲线法全称为双曲线配合法[3],由Sridharan等提出。该方法假设沉降与时间是简化的双曲线关系:
(5)
式中:t0、s0分别为拟合计算起始参考点的观测时间和沉降值,一般取t0、s0均为零;α、β为计算参数。
比较步骤为: 1)以A基础为例,假定只知道表 1中前238 d的监测数据,即采用0~238 d的监测数据拟合出三种算法的参数和决定系数(表3)。
表3 基础A 238 d的监测数据得到的三种算法参数
Table 3 Parameters of three algorithm obtained from 238 d monitoring data of foundation A

方法计算参数决定系数计算238 d预测324 d三点法s∞=4.638 5α=0.995 2, β=0.005 9s0=0, t0=00.999 60.998 4双曲线法α=34.183 4, β=0.140 10.999 40.999 1蠕变算法Ct=6.152 4, ht=11.894 50.999 20.999 1
2)比较0~238 d的决定系数和0~324 d的决定系数,得出沉降蠕变实用算法有较好的适用性,以前238 d的数据拟合式预测324 d内得到的数值见表4,效果见图 6。
表4 基础A前238 d监测数据预测324 d内沉降
Table 4 Prediction of settlement within 324 d by the early 238 d monitoring data of foundation A

监测日期时间/d实测沉降/mm预测数据/mm三点法双曲线法蠕变沉降实用算法2018-06-25 00 0.020.000.002018-07-12170.510.460.460.482018-07-29340.870.860.870.892018-08-15511.221.221.231.252018-09-03701.541.581.591.592018-09-20871.831.871.881.872018-10-061032.132.122.122.112018-10-241212.382.382.372.352018-11-131412.662.632.612.602018-12-041622.912.862.852.832019-01-152043.233.253.253.252019-02-182383.493.503.523.552019-03-282763.743.733.793.852019-04-172963.983.833.913.992019-05-153244.243.964.074.18
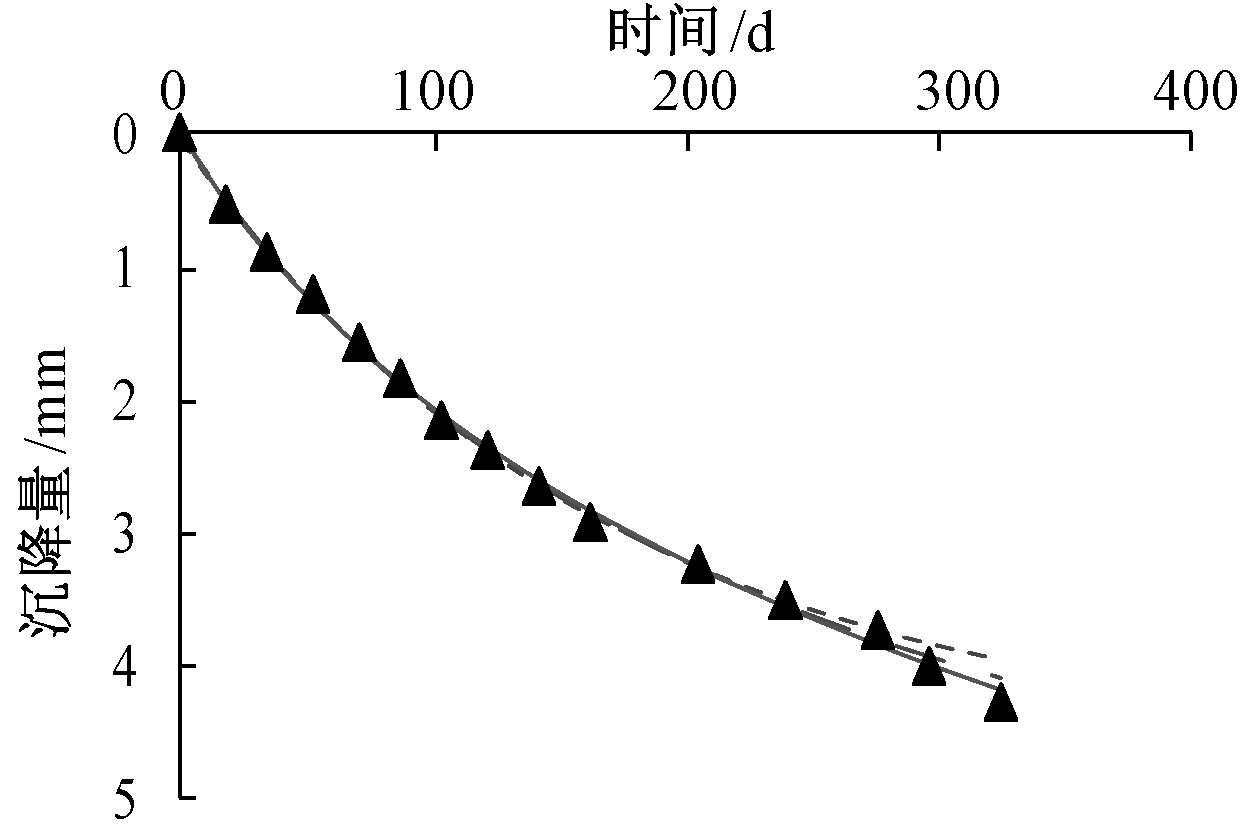
![]() 实测沉降; ----三点法; ---双曲线法;——蠕变沉降实用算法。
实测沉降; ----三点法; ---双曲线法;——蠕变沉降实用算法。
图6 三种曲线预测沉降对比
Fig.6 Comparison of predicted settlements by three formula curves
3)用蠕变沉降实用算法拟合了324 d内的沉降数值,并给出其参数和决定系数、拟合结果。
由表3中决定系数可知:三点法拟合238 d内的数据时效果最好,但用此拟合参数预测324 d内的数据效果最差。由表4、图6可知:蠕变沉降实用算法用238 d内的数据拟合的参数用于预测324 d内的数据时效果最好。
根据G15塔4个独立基础324 d内的沉降数据得到了蠕变沉降实用算法参数和对应的预测数据,见表5、表6,由决定系数和图7可见拟合效果较好。
表5 各基础前324 d监测数据得到的
蠕变沉降实用算法参数
Table 5 Practical parameters of practical creep settlement algorithm obtained by early 324 d monitoring data of each foundation

监测点计算参数决定系数AC=6.122 3, h=11.822 10.999 2BC=6.426 0, h=11.910 40.998 6CC=2.530 9, h=3.778 30.993 6DC=2.225 5, h=3.097 00.989 2
表6 各基础前324 d监测数据得到的蠕变沉降实用算法拟合数据
Table 6 Fitting data obtained by the early 324 d monitoring data of each foundation using practical creep settlement algorithm
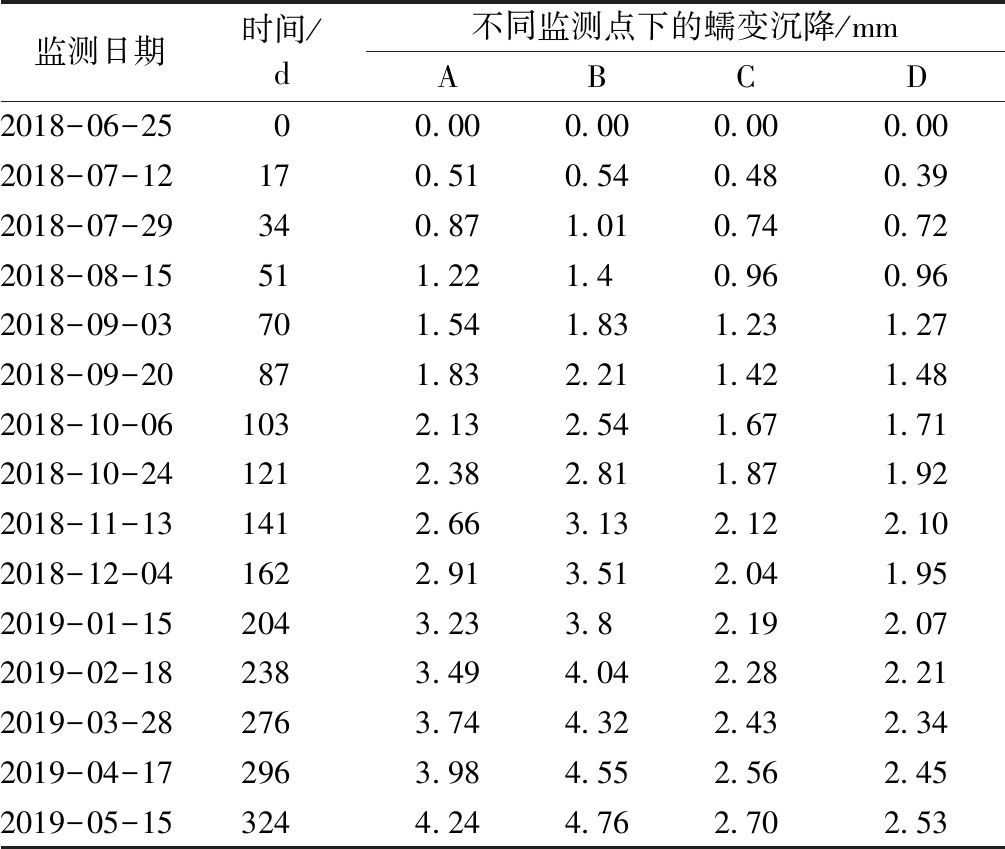
监测日期时间/d不同监测点下的蠕变沉降/mmABCD2018-06-2500.000.000.000.002018-07-12170.510.540.480.392018-07-29340.871.010.740.722018-08-15511.221.40.960.962018-09-03701.541.831.231.272018-09-20871.832.211.421.482018-10-061032.132.541.671.712018-10-241212.382.811.871.922018-11-131412.663.132.122.102018-12-041622.913.512.041.952019-01-152043.233.82.192.072019-02-182383.494.042.282.212019-03-282763.744.322.432.342019-04-172963.984.552.562.452019-05-153244.244.762.702.53
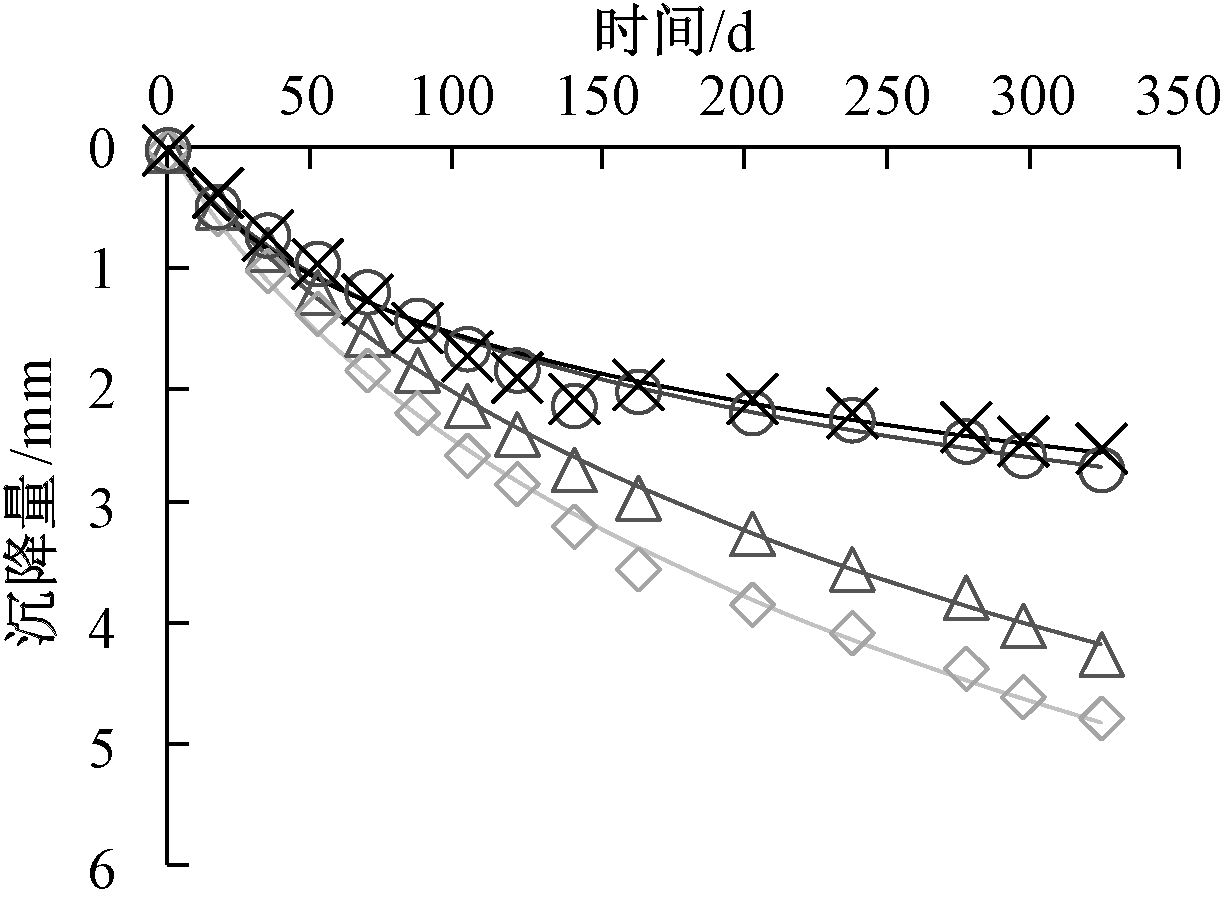
注:![]()
![]()
![]()
![]() 分别为A、B、C、D基础的沉降监测数据,曲线为依据实测值拟合的预测曲线。
分别为A、B、C、D基础的沉降监测数据,曲线为依据实测值拟合的预测曲线。
图7 蠕变沉降实用算法预测数据与监测数据对比
Fig.7 The prediction data of the practical creep settlement algorithm compared with monitoring data
3.3 蠕变沉降实用算法的有效预测区间
曲线拟合法根据已有沉降数据预测未来沉降时,普遍规律是预测时间越长,预测误差越大。蠕变沉降实用算法作为曲线拟合法的一种,也不例外,但蠕变沉降实用算法有效预测区间原理给出了在设定的预测精度下对应的预测时间[7],蠕变沉降实用算法有效预测区间原理描述如下:
蠕变沉降实用算法根据全部沉降数据中的部分数据(0~tm时间段的数据,tm被称为观测时间),用式(3)拟合后可以预测后续沉降,当预测沉降值sme与实际监测沉降值se之差即预测误差等于临界值时,见式(6a),sme对应的时间被称为有效预测时间te(te大于tm),这个临界误差值被称为误差限ε(一般取为定值),tm~te被称为0~tm数据在误差限ε时的有效预测区间。当tm取不同天数时,可以得到不同的te,这一系列的(tm,te)可以用式(6b)拟合,拟合出参数κ和n后,令tm取最后实际观测日期时,就可以计算出在误差限ε时tm对应的te了。
|sei-smei|=ε
(6a)
(6b)
式中:κ和n为拟合参数;tmi和tei分别为第i次拟合时所用的观测时间和有效预测时间;smei和sei分别为第i次计算时tei对应的预测沉降值和监测沉降值。t0=1 d,是消除量纲的单位常量。
因为式(6b)有κ和n两个未知数,故需要找到至少两个(tm,te)点拟合出κ和n,(tm,te)点越多越好,但有可能出现tm较小时,在给定较大误差限ε下于已有沉降数据中仍找不到te的现象,此时需要减小ε。由于监测沉降数据一般离散性较大,可能找出的te不随tm单调增加,故在用蠕变沉降实用算法有效预测区间前首先需要将离散的沉降数据变化平缓[13]。
因4个独立基础沉降值均不大,其中基础A、B沉降相对较大,求取基础A、B有效预测区间时设定的ε=0.2 mm在水准仪测量精度内,故仅对基础A、B求其用全部沉降数据(此时tm=324 d)对应的效预测时间。对A、B基础光滑后的沉降数据分别应用有效预测区间原理,得到一系列(tm,te)点,如图8所示,A基础数据由式(6b)拟合得到κ=3.966和n=0.470,故tm=324 d时,te=591 d;同理,由基础B数据拟合得到κ=4.378和n=0.529,故tm=324 d时,te=520 d。
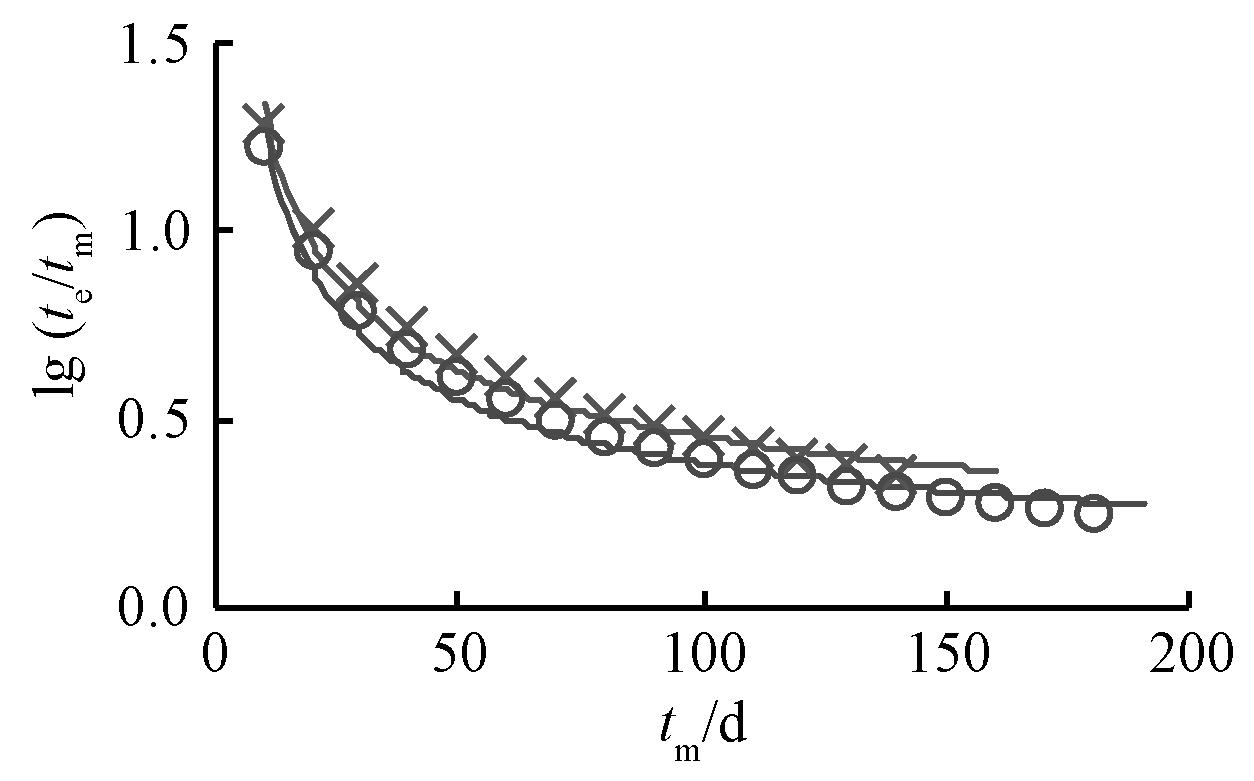
注:![]()
![]() 分别为A、B基础的沉降实测值;曲线为拟合曲线。
分别为A、B基础的沉降实测值;曲线为拟合曲线。
图8 基础A、B tm-tc关系
Fig.8 The tm-tc relationship of foudation A and B
对于基础A全部沉降监测数据,应用蠕变沉降实用算法拟合后,预测第591天时沉降5.505 mm,且误差不大于0.2 mm,对于基础B,预测第520天时沉降5.902 mm,且误差也不大于0.2 mm。按较小的第520天计算,预测A点基础沉降5.21 mm,B点沉降5.9 015 mm,C点沉降3.159 5 mm,D点沉降2.9 922 mm,四点平均总沉降量为4.315 8 mm。B、D两点之间不均匀沉降最大,倾斜0.000 3,小于倾斜变形允许值0.004。
根据表5的Ct和ht,采用式(3)对未来10 a的沉降作初步估测(认为此时沉降基本稳定),各监测点沉降随时间的变化如图 9所示。
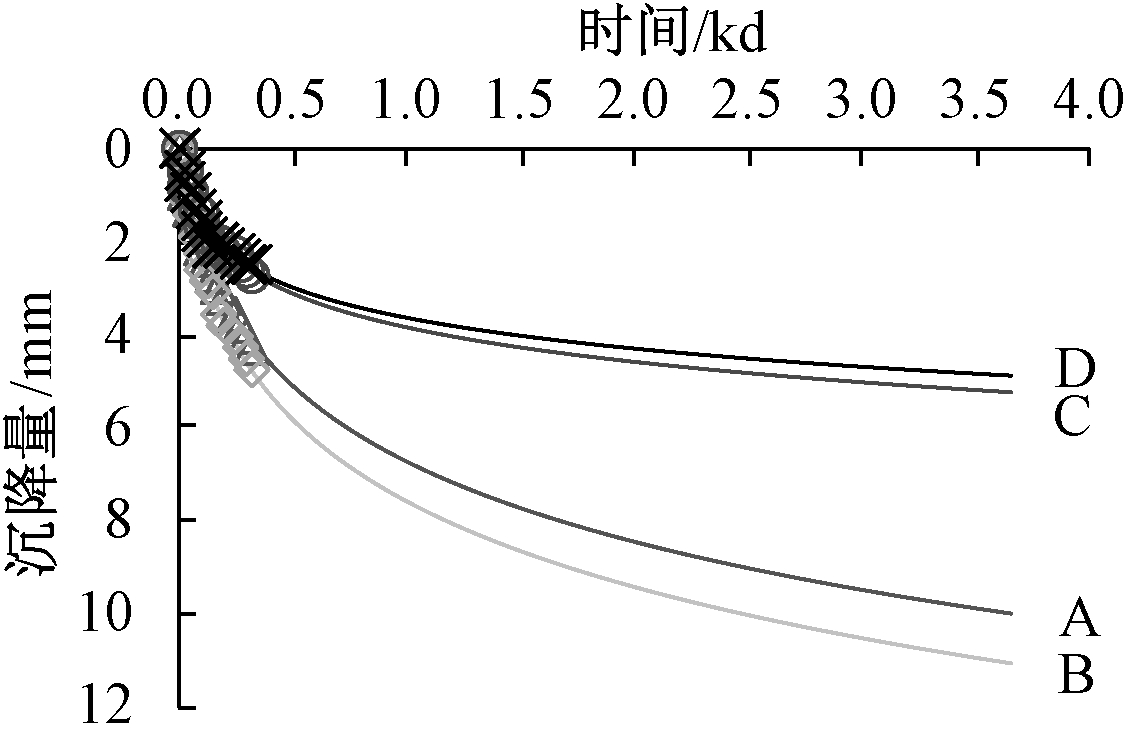
图9 10年后4个监测点的沉降预测值
Fig.9 Predicted settlement values of 4 monitoring points in the future 10 years
经10 a的沉降,A点基础沉降10.05 mm,B点沉降11.04 mm,C点沉降5.25 mm,D点沉降4.84 mm,四点平均总沉降量为7.79 mm。B、D两点之间不均匀沉降最大,倾斜0.000 6,小于倾斜变形允许值0.004。
4 结束语
1)通过对比三点法、双曲线法和蠕变沉降实用算法拟合前238 d监测数据预测全部324 d监测数据的效果(表 3),说明蠕变沉降实用算法对新近堆积填土具有较好的适用性。
2)根据已有全部沉降数据的有效预测区间,预测第520天时B、D基础不均匀沉降最大,B、D基础倾斜0.000 3,小于倾斜变形允许值0.004。
3)根据已有全部沉降数据拟合蠕变沉降实用
算法参数,并以此参数预测10 a后四个基础沉降,B、D基础不均匀沉降最大,B、D基础倾斜0.000 6,小于倾斜变形允许值0.004。
[1] 松岡元.土力学[M].罗汀,姚仰平,译.北京:中国水利水电出版社,2001.
[2] 曾国熙,杨锡令.砂井地基沉陷分析[J].浙江大学学报,1959(3):34-72.
[3] PRAKASH K,MURTHY N S, SRIDHARAN A.Rectangular Hyperbola Method of Consolidation Analysis[J].Géotechnique,1987,37(3):355-368.
[4] ASAOKA A. Observational Procedure of Settlement Prediction[J]. Soils and Foundations, 1978, 4(18): 87-101.
[5] 宰金珉, 梅国雄.全过程的沉降量预测方法研究[J]. 岩土力学,2000, 21(4): 322-32.
[6] 姚仰平,祁生钧,车力文.高填方地基工后沉降计算[J].水力发电学报,2016,35(3):1-10.
[7] 姚仰平,王珅,王乃东,等.临线堆载影响下高铁路基长期沉降预测方法[J].岩土工程学报,2019,41(4):625-630.
[8] 张世贤, 黄双华, 彭雄志. 昔格达土加筋三七灰土物理力学性质试验研究[J]. 铁道建筑, 2012(4):105-108.
[9] 中华人民共和国建设部.工程测量规范:GB 50026—2007[S].北京:中国有色金属工业协会,2008.
[10] 中华人民共和国住房和城乡建设部.建筑地基基础设计规范:GB 50007—2011[S].北京:中国建筑工业出版社,2011.
[11] 中华人民共和国住房和城乡建设部.建筑变形测量规范:JGJ 8—2017[S]. 北京:中国建筑工业出版社,2016.
[12] 姚仰平,车力文,祁生钧,等.高填方地基蠕变沉降计算方法研究[J].工业建筑,2016,46(9):25-31.
[13] 杨海星,黎浩,曹净.基于样条函数的监测数据平滑算法与Matlab实现[J].长春工程学院学报(自然科学版),2018,19(3):92-97,120.