红砂岩是红层岩石的一种,在我国的江西、湖南、广东、四川等地大量分布[1-2];红砂岩风化土则是由红砂岩经人工或自然风化、崩解后的产物,在工程建设中一般用作路基填料。大量的工程实践和试验研究表明:红砂岩风化土作为路基填料被压实后虽可获得较高的强度,但由于其水活性和崩解性,其工程性质不稳定,在循环荷载作用下容易引发一些问题[3-5]。现有很多科研工作者对红砂岩风化土的物理力学性质、静力特性以及在冲击荷载下的能量耗散、位移规律、变形特性做了大量研究并取得了一定的成果:喻泽红等通过大型直剪试验研究了压实度和土工格栅对红砂岩风化土的工程特性和影响[6];韦慧等研究了路用红砂岩碎石土在干湿循环条件下的湿化压缩变形规律[7];彭勃等研究了在静力压实下不同厚度、粗粒含量、含水率对红砂岩土变形特性、能量耗散的影响[8-11];杨建永等对路基强夯处理时红砂岩土的压实特性、作用效应、能量耗散也做了大量研究[12-14]。但当前对红砂岩风化土在循环荷载作用下的行为表征的相关研究还较少,因此研究循环荷载作用下红砂岩风化土的动强度特性具有重要意义。本试验主要利用GDS动三轴操作系统,根据选定的破坏标准,得到了试样破坏时动应力和振次,进而得到了动强度曲线,并分析其变化规律,最后通过计算得到动强度指标。
1 试验方案
1.1 试验设备和试验土样
试验采用GDS动三轴操作系统。土样均取自江西省赣州市武陵大桥附近某施工现场,所取土体均取自同一深度,土体呈红褐色,无气味,杂质较少,含水率低,易破碎。根据JTG E40—2007《公路土工试验规程》得到了红砂岩风化土的主要物理和静力学指标:干密度为1.89 g/cm3,相对密度为2.71,塑限为12.1%,液限为26.8%,黏聚力35.69 kPa,内摩擦角为20.99°。根据GB 50007—2011《地基基础设计规范》可知其为粉质黏土。制作的圆柱体重塑土试样半径为25 mm,高为100 mm,干密度为1.66 g/cm3,含水率为12%。试样制作过程中,对试样进行了饱和,先用真空饱和器将试样饱和到一定程度后,再进行反压饱和,测得孔隙水压力系数B值为0.95之后再进行下一步固结试验。
1.2 加载方案
结合工程实际情况,试验主要研究应力历史中的初始固结条件对红砂岩风化土动强度的影响规律,采用单轴加载的方式施加动荷载,加载频率为1 Hz,波形为正弦波。根据以往的研究可以发现:固结围压主要是为模拟和还原土体初始时在不同深度四周所受到的应力,针对实际情况,试验挑选了三组有代表性的围压150,200,250 kPa;固结应力比Ke主要是为还原和模拟土体初始时在不同深度时竖向和水平向平面所受的应力情况,在实际情况中,由于山坡、地面不平整以及侧压力系数和泊松比的存在,土体多处于不等向固结状态,所以试验主要考虑了等向固结(Kc=1.0)和不等向固结(Kc=1.5)两种固结比对试样变形特性的影响。试验具体的加载方案如表1所示。
表1 试验加载方案
Table 1 Test loading plan

编号围压σc/kPa固结比Kc动应力幅值σdm/kPa11501.040,50,7021501.530,40,5032001.060,70,8042001.550,60,8052501.080,90,10062501.580,90,100
1.3 破坏标准
在进行动三轴试验时,破坏标准的选取对试验结果的判定有较大的影响,根据以往的研究,常用的有如下几种破坏标准:1)应变标准。当土体为塑性指数较大、渗透性不好的黏性土、淤泥质土等,多以总应变达到某一值作为判断依据,目前使用比较多的是以轴向总应变达到5%作为破坏依据。2)孔压标准。当土体为渗透性较好的砂性土、粉土等,其在循环荷载作用下易发生液化,可将砂土液化时的孔压作为破坏标准。3)极限平衡标准。根据土力学定义的抗剪强度包络线,包络线以上为土体已破区,以下为未破坏区,落在包络线上为极限平衡状态,故由此方法判断土体是否破坏对计算结果的精确度要求较高,如果计算不精准,则会对最后结果产生较大的影响。4)屈服标准。土体在循环动力荷载作用下,土体由弹性变形发展到塑性变形,到最终的破坏,此过程中将土体形变发生突变时作为破坏依据,但对试样变形突变的判断人为影响较大,也不好准确判断。综上所述,考虑到三轴试验土样的变形规律和土样的类型,所以试验采用轴向应变为5%作为破坏标准[15]。
2 红砂岩风化土动强度特性分析
2.1 滞回曲线分析
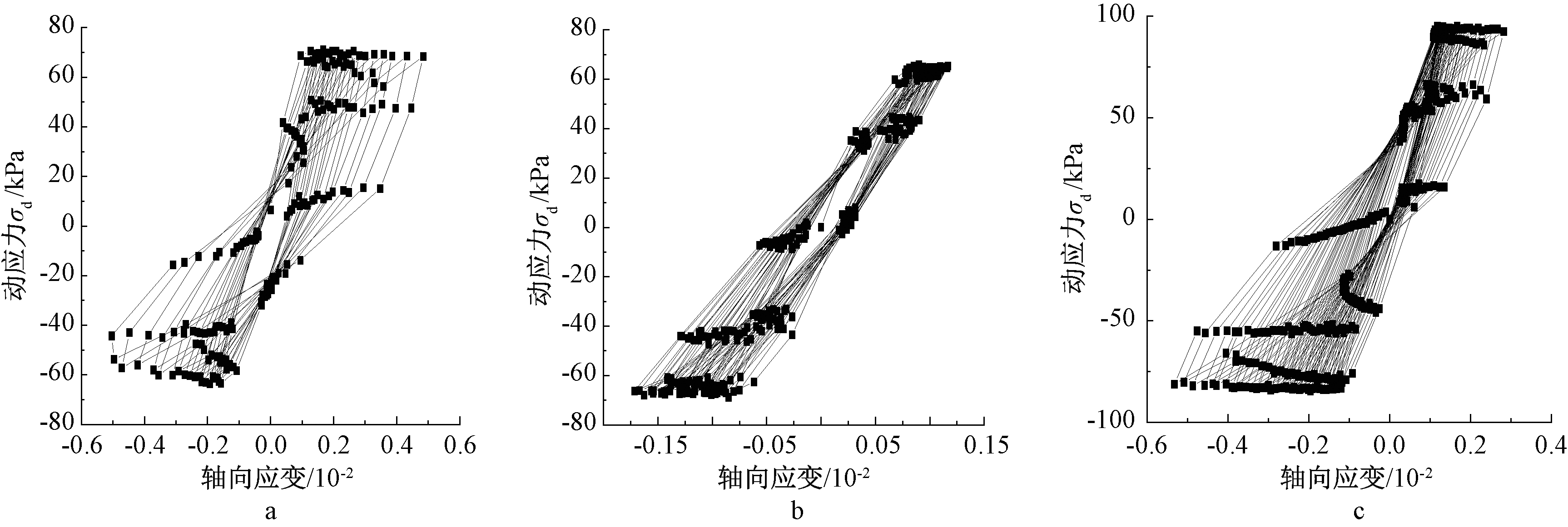
a—σc=150 kPa,σdm=70 kPa; b—σc=200 kPa,σdm=70 kPa; c—σc=250 kPa,σdm=90 kPa。
图1 等向固结条件下滞回曲线
Fig.1 Hysteresis curve under isotropic consolidation conditions
滞回曲线可以反映土体在循环动力荷载下的应力-应变关系和变形规律,是研究土体动强度的基础。根据现有的研究可以发现土体的变形一般会经历两个阶段:第一阶段为可复原的弹性变形阶段;第二阶段为不可复原的塑性变形阶段;随着塑性应变的不断累积,土体最终会发生破坏。图1为试样在Kc=1.0时的滞回曲线,从中可以看出:红砂岩风化土的滞回曲线大致呈一系列连续的封闭曲线;试验刚开始加载时,曲线分布很集中,对角斜率也较大,说明此阶段试样还有一定的抵抗变形的能力,其变形也近似为弹性变形。随着轴向应变不断累积,试样的滞回曲线慢慢向右产生了倾斜,其斜率也在不断增加,同时伴随着曲线的拉长和分散,表明由于试样进入了塑性变形阶段,其抵抗变形的能力在慢慢减弱。
图2为试样在偏压固结状态下(Kc=1.5)的滞回曲线,由于红砂岩风化土的崩解破裂性和初始固结静偏应力的剪切的作用,其滞回曲线的线型与图1时(Kc=1.0)有显著的区别,在Kc=1.5时,没有滞回圈倾斜、拉长等线型上的改变,其曲线大致呈一系列平行曲线,随着土体塑性变形的不断累积,滞回曲线的分布会慢慢变得稀疏,表明试样变形在初始的弹性变形阶段速度会较慢,试样进入塑性阶段后其变形速度会逐渐加快。
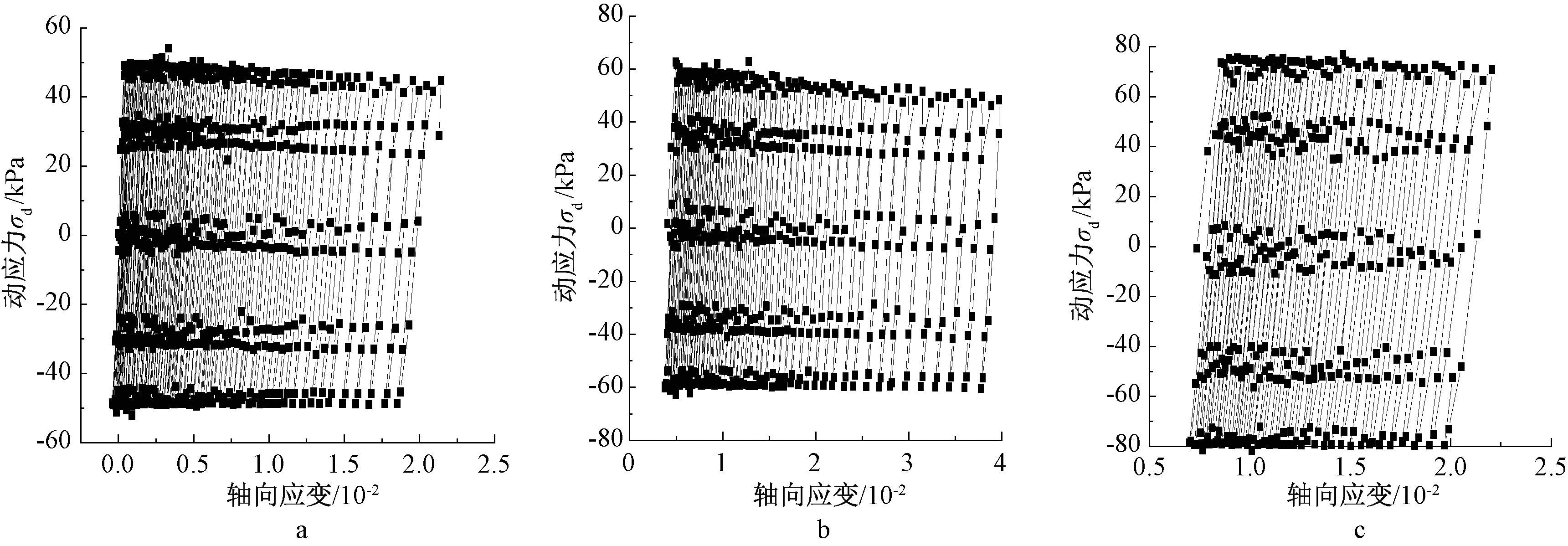
a—σc=150 kPa,σdm=50 kPa; b—σc=200 kPa,σdm=60 kPa; c—σc=250 kPa,σdm=80 kPa。
图2 不等向固结条件下(Kc=1.5)滞回曲线
Fig.2 Hysteretic curve under anisotropic consolidation(Kc=1.5)
可见,红砂岩风化土在循环动力荷载作用下的变形发展规律由于红砂岩风化土的崩解破裂性和固结静偏应力的剪切作用,等向固结条件与不等下固结条件下的变形规律有很大差异。
2.2 动强度曲线分析
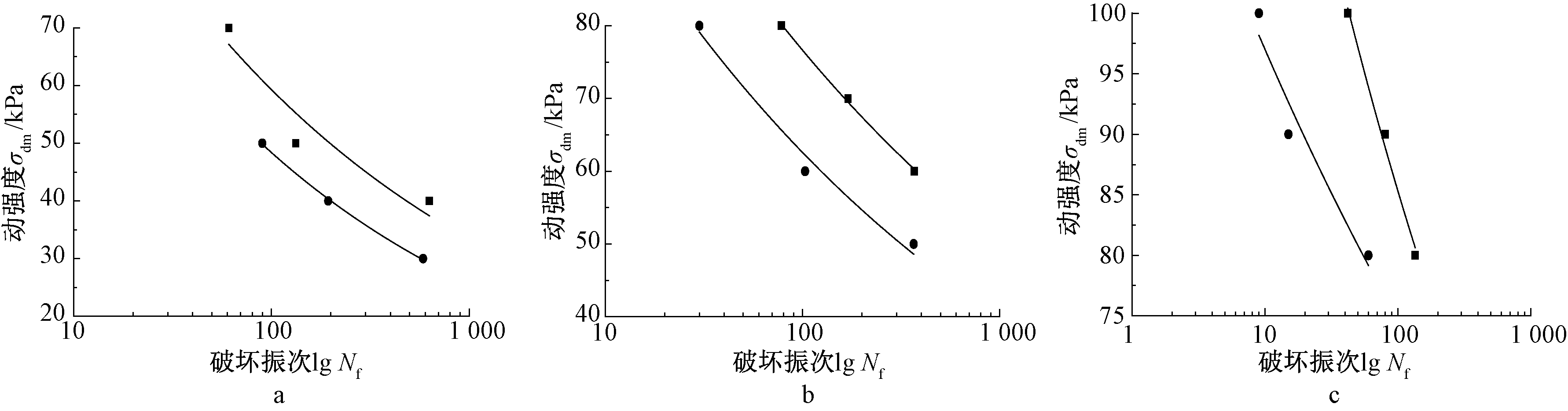
土体动强度在加载时会表现出速率效应和循环效应,根据以往的研究发现:循环振次对于土的动强度影响更大,所以本次试验主要考虑循环效应对红砂岩风化土动强度的影响。根据选定的破坏标准,取达到破坏时的振次Nf以及动强度σdm,得到了试样的动强度σdm-lg Nf 曲线,见图3、图4。

a—Kc=1.0; b—Kc=1.5。![]() σc=150 kPa;
σc=150 kPa;![]() σc=200 kPa;
σc=200 kPa;![]() σc=250 kPa。
σc=250 kPa。
图3 不同固结比下动强度曲线
Fig.3 Dynamic strength curve under different consolidation ratios
另一种形式的动强度曲线是动应力比与破坏振次关系曲线,即σdm/(2σ0)-Nf曲线,可知,当作用在土体上的动应力很小时,即使循环振次增加,土体也不会发生破坏,所以研究土体的动应力比与振次的关系具有非常重要的意义。
由图3可知:围压与土体的动强度成正比,这是因为土体在较高的围压下,孔隙率会相应地减少,大小土颗粒也会相互填充,从而形成结构性更好的骨架密实结构,而土颗粒之间的摩擦咬合增加了土体的抵抗变形的能力,所以随着围压的提高,土体动强度也会相应地增加。
相对于Kc=1.0的土样,在Kc=1.5时土体内部的初始应力会发生偏转。根据试验得到的不同围压下的红砂岩风化土的动强度曲线(图4)可以发现:试样在相同围压下,Kc=1.0时的动强度大于Kc=1.5时的动强度,表明土体在静偏应力剪切作用下,局部剪应力较大,促进了局部损伤的发展,加剧了试样的竖向崩解和软化,动强度也随之降低。
由图5可见:不同固结围压下的σdm/(2σ0)-Nf的散点图虽有一定的离散性,但基本上还是在一条曲线附近分布,说明围压对试样的动应力比以及振次的关系影响不明显。本试验中每种固结条件下都有三种动应力比,土样都在1 000个循环振次内发生了破坏,未出现增加振次,试样却没有破坏的情况,故可以认为红砂岩风化土临界动应力比较小。
2.3 动强度曲线表达式
从试验所得的动强度曲线可见:不同试验条件下的破坏振次Nf与动强度σdm基本符合幂函数关系,为了更好地运用和描述试样规律,采用式(1)的幂函数关系对曲线进行拟合,拟合结果见表2。
σdm=c(Nf)d
(1)
式中:c和d为与固结应力比、固结围压等试验条件相关的参数。
由表2可见:不同固结围压和固结应力比条件下σdm-lgNf曲线的决定系数R2全部在0.94以上,说明式(1)的幂函数模型可以很好地描述红砂岩风化土动强度曲线。
a—σc=150 kPa; b—σc=200 kPa;c—σc=250 kPa。![]() Kc=1.0;
Kc=1.0;![]() Kc=1.5。
Kc=1.5。
图4 不同围压下动强度曲线
Fig.4 Dynamic strength curves under different confining pressures
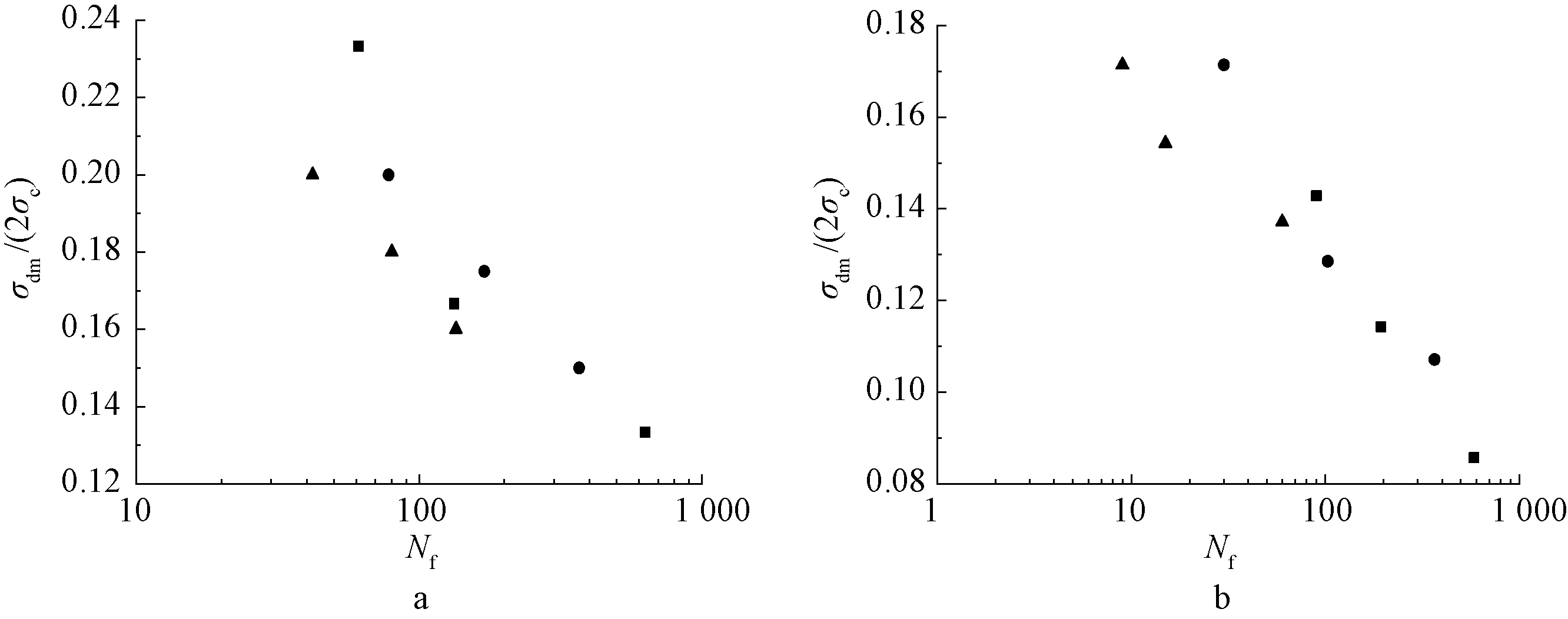
a—Kc=1.0; b—Kc=1.5。![]() σc=150 kPa;
σc=150 kPa;![]() σc=200 kPa;
σc=200 kPa;![]() σc=250 kPa。
σc=250 kPa。
图5 不同固结条件下σdm/(2σc)-Nf关系曲线
Fig.5 σdm/(2σc)-Nf curve under different consolidation conditions
2.4 动强度指标
以往的研究表明摩尔-库仑准则也可用于土动力学[16]:
τ=cd+σtan φd
(2)
式中:τ为剪应力;σ为正应力;cd为动黏聚力;φd为内摩擦角。
表2 不同固结条件下动强度曲线参数拟合结果
Table 2 Fitting results of dynamic strength curve parameters under different consolidation conditions
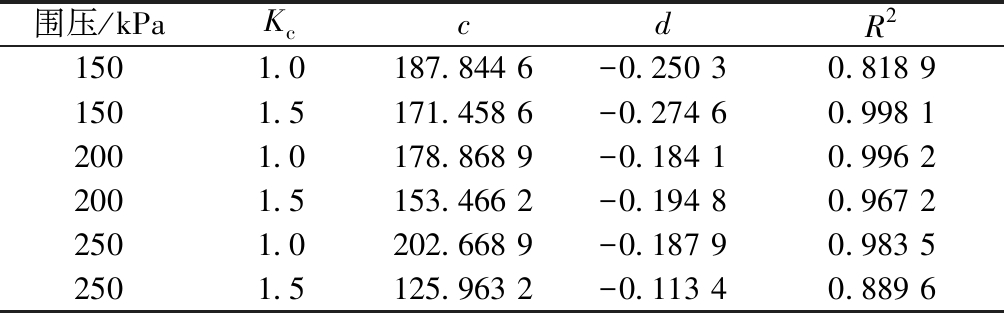
围压/kPaKccdR21501.0187.844 6-0.250 30.818 91501.5171.458 6-0.274 60.998 12001.0178.868 9-0.184 10.996 22001.5153.466 2-0.194 80.967 22501.0202.668 9-0.187 90.983 52501.5125.963 2-0.113 40.889 6
为了更准确地求得动强度指标,利用了Excel规划求解功能[17]。以等向固结为例,求得了红砂岩风化土在等向固结条件下的不同破坏振次所对应的动抗剪强度指标,如表3所示。
表3 等向固结条件下不同破坏振次的动强度指标
Table 3 Dynamic strength indices of different vibration frequencies under isotropic consolidation conditions
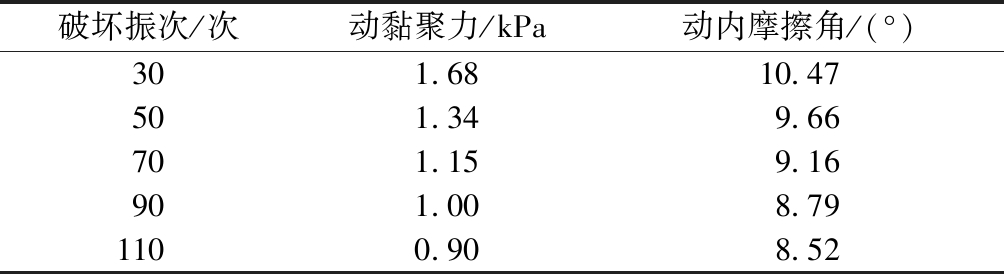
破坏振次/次动黏聚力/kPa动内摩擦角/(°)301.6810.47501.349.66701.159.16901.008.791100.908.52
由表3可见:试样的动黏聚力、动内摩擦角均随着破坏振次的增加而减小,但是减小的幅度并不是很大;在破坏振次为30次时,相比于静力作用下的黏聚力和内摩擦角,其动黏聚力同比降幅为95%,动内摩擦角同比降幅为50%,且随着破坏振次的增加,这两个指标的降幅也在进一步增大。因此,在分析计算循环荷载作用下红砂岩风化土的抗剪强度时,如果用静力状态下的强度指标(黏聚力和内摩擦角)替代动强度指标(动黏聚力和动内摩擦角)就会产生较大的误差。故在实际工程中,土体在受循环荷载时,就不能单一的只考虑静力状态下土体的强度。
3 结束语
1)循环荷载作用下,红砂岩风化土的变形发展规律在等向固结条件与不等向固结条件下有很大差异。围压的增大有助于动强度的提高,而由于红砂岩风化土的崩解破裂性和固结静偏应力的剪切作用,使红砂岩风化土在不等向固结状态下的动强度小于等向固结状态下的动强度。
2)在等向固结或不等向固结条件下,围压对红砂岩风化土动应力比与振次关系的影响不显著。试样都在1 000个循环振次内破坏,没有出现增加振次试样却未发生破坏的情况,因此红砂岩风化土的临界动应力比较小。
3)把红砂岩风化土在不同固结条件下得到的动强度σdm与破坏振次Nf曲线用幂函数进行拟合,取得了较好的拟合效果。
4)相比静力状态下的强度指标(黏聚力和内摩擦角),在循环荷载作用下红砂岩风化土的动黏聚力和动内摩擦角大幅下降,且随着破坏振次的增加,降幅进一步增大。
[1] 潘志新, 彭华. 国内外红层分布及其地貌发育的对比研究[J]. 地理科学, 2015,35 (12): 1575-1584.
[2] LIU J, ZHANG H. Water Content Influence on Properties of Red-Layers in Guangzhou Metro Line, China[C]//Advances in Materials Science and Engineering. 2017:1-12. DOI:10.1155/2017/4808909.
[3] 张剑锋,岳国生,黄春耈.红砂岩修筑浆砌石坝的岩土工程研究[J].上海地质,1989(2):1-6.
[4] 郭永春,谢强,文江泉.红层岩土水理性质工程判别准则试验研究[J].水文地质工程地质,2008(4):71-74.
[5] 朱彦鹏,马滔,杨校辉,等.基于正交设计的红砂岩改良土抗剪强度试验和回归分析[J].岩土工程学报,2018,40(增刊1):87-92.
[6] 喻泽红,魏红卫,邹银生.加筋红砂岩风化土强度和变形特性[J].岩石力学与工程学报,2005(15):2770-2779.
[7] 韦慧,曾胜,赵健,等.路用红砂岩碎石土湿化变形特性试验[J].中南大学学报(自然科学版),2015,46(6):2261-2266.
[8] 彭勃,杨建永,吴建奇,等.红砂岩填土压实厚度对压实能量消耗规律影响试验研究[J].江西理工大学学报,2015,36(3):30-35.
[9] 彭勃,杨建永,温树杰, 等.静力压实不同厚度红砂岩土变形特征试验研究[J].建筑技术,2016,47(5):433-436. DOI:10.3969/j.issn.1000-4726.2016.05.012.
[10] 彭勃,吴建奇,刘凌瀚,等.含水率对红砂岩粗粒土压实变形特征的影响[J].人民长江,2016,47(7):91-96.
[11] 彭勃,刘凌瀚,潘建平,等.粗粒含量对红砂岩土静力压实能耗规律影响[J].四川建筑科学研究,2017,43(1):55-59.
[12] 杨建永,卢凯,甘芳芳.红砂岩土在单点冲击荷载下的作用效应[J].建筑科学,2013,29(3):70-75.
[13] 杨建永,黎寒冰,艾鹏,等.红砂岩土在四点冲击荷载下的冲击试验分析[J].解放军理工大学学报(自然科学版),2015,16(6):543-547.
[14] 杨建永,曾潇,高盼盼,等.红砂岩土在低量级单点冲击荷载下的能量消耗[J].江西理工大学学报,2016,37(1):21-25.
[15] LEE K L. Cyclic Strength of a Sensitive Clay of Eastern Canada[J]. Canadian Geotechnical Journal, 1979, 16(1): 163-176.
[16] 刘保健. 随机荷载下土动力特性测试分析法[M].北京:人民交通出版社,2001.
[17] 阮波,张向京,彭意.Excel规划求解三轴试验抗剪强度指标[J].铁道科学与工程学报, 2009,6(5):57-60.