根据《世界液化天然气(LNG)报告2018》,全球LNG贸易已连续三年创记录,达到2.931亿t,为满足日益增长的能源需求和全球液化产能的不断扩大,储液罐大规模发展,其安全性能是最重要的考虑因素,地震作用易引发储罐倒塌和其他严重的次生灾害,给人类带来无法估量的影响和经济损失。邓民宪等计算了动力荷载下储液罐的罐壁轴向应力,其应力峰值大于工业设备抗震设计中采用的计算应力值[1]。相比单向地震加载,由于竖向地震的作用,锚固罐的水平位移增加,基底剪力、弯矩和罐壁轴向应力均有不同程度增加,储液罐容易进入塑性,发生不可逆的屈曲破坏[2-6]。传统的锚固储罐在地震作用下,罐壁由于竖向轴应力和环向拉应力的综合作用容易出现局部屈曲,最经典的有象足破坏和菱形破坏,且竖向地震对结构响应的放大作用不可忽视,尤其是其对罐壁应力的增加。Ozdemir得出了非锚固储液罐的基底剪力、倾覆弯矩和变形比锚固罐的小[7]。考虑到经济因素和力学性能,非锚固罐被大力提倡。
2013年,高云鹏研究了放松柱脚竖向约束的立式液化天然气球罐地震响应[8-10],结果表明:当柱脚提离后,结构的受力状态得到很大改善,应力水平降低,随后设计了一种新型的耗能柱脚阻尼器构造,使阻尼器耗能发生塑性变形而结构仍处于弹性阶段,更换柱脚阻尼器后结构可继续使用,从而实现储罐的可恢复功能。
为了讨论阻尼器的应用以及新型结构形式的可行性,采用有限元方法对带耗能柱脚阻尼器储液罐进行了水平和竖向地震作用下的动力分析,考虑了罐底提离作用,旨在实现具有可恢复功能LNG储液罐的抗震设计。
1 有限元模型
本文研究对象为带耗能柱脚阻尼器支撑式储液罐,见图1 ,相比传统柱罐,受力性能更好且无罐壁屈曲破坏形态,占地面积少,适用于各类环境。储液罐上部罐体高度为20.8 m,外径为3.2 m,壁厚为40 mm,下部支柱为工字钢,高度为1.37 m,翼缘宽度为450 mm,腹板高度为410 mm,内部为LNG。

a—储液罐; b—有限元模型。
图1 支承式储液罐
Fig.1 Supported liquid storage tank
流体力学中采用欧拉坐标系描述流体的运动,假设其在稳定状态附近做小扰动,固体为线弹性材料,将流固耦合动力学问题简化为线性问题进行探讨,有限元方程被表示为位移-压力格式。通过耦合交界面结点径向位移以保证法向力连续且不考虑切向力。求解流固耦合问题需要离散求解域并构造插值函数,则有流体的压力表达式为:
(1)
式中:mf为流体单元结点数;{pε}为流体单元结点压力向量;Ni为结点i对应的插值函数。
固体的位移表达式:
(2)
式中:ms为固体单元结点数;{aε}为固体单元结点压力向量;![]() 为结点i对应的插值函数。
为结点i对应的插值函数。
由标准波动方程和边界条件的加权余量的伽辽金提法,形成流体域方程和固体域方程,则有流固耦合系统的有限元方程为:
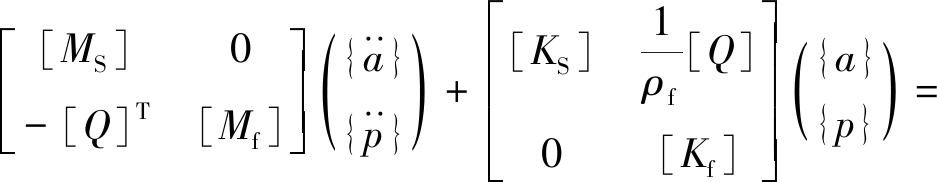
![]()
(3)
式中:{p}为流体结点压力向量;{a}为固体结点位移向量;[Q]为流固耦合矩阵;[Mf]和[Kf]分别为流体质量矩阵和刚度矩阵;[MS]和[KS]分别为固体质量矩阵和刚度矩阵;ρf为流体质量密度;{FS}为固体外荷载向量,采用有限元的离散思想可得到数值模拟解。
罐体为薄壁构件,由壳单元模拟,支柱为压弯剪构件,由梁单元模拟,阻尼器由双线性弹簧单元模拟,有限元模型见图1 。储罐与支柱为刚性连接,阻尼器与支柱为铰接并允许支柱发生竖向位移,材料参数见表1。液体与结构同时建模且独立,计算耦合交界面结点的径向位移时,必须考虑重力效应以实现液面晃动,采用规则的六面体单元并不作大变形假设。
表1 材料参数
Table 1 Material properties

材料参数密度/(kg·m-3)弹性模量/MPa泊松比屈服强度/MPa切线模量/MPa罐体7 8502×1050.32501 450支柱7 8502.06×1050.32351 240液体470256
提离罐约束柱底水平位移,采用点点接触法限制支柱负向位移并允许其提离,接触算法选用增广拉格朗日法,通过找到精确的拉格朗日乘子对罚函数修正项进行反复迭代。与罚函数的方法相比,该方法不易引起病态条件且对接触刚度的灵敏度较小,接触压力定义如下:
(4a)
(4b)
式中:un为法向位移;λi为第i步拉格朗日乘子;ε为相容性误差。式中参数皆采用默认值,接触面为标准接触。地震动选用El Centro波、Kern County波和人工波,峰值0.4g,时程曲线见图2。阻尼采用Rayleigh阻尼,阻尼比取0.02。
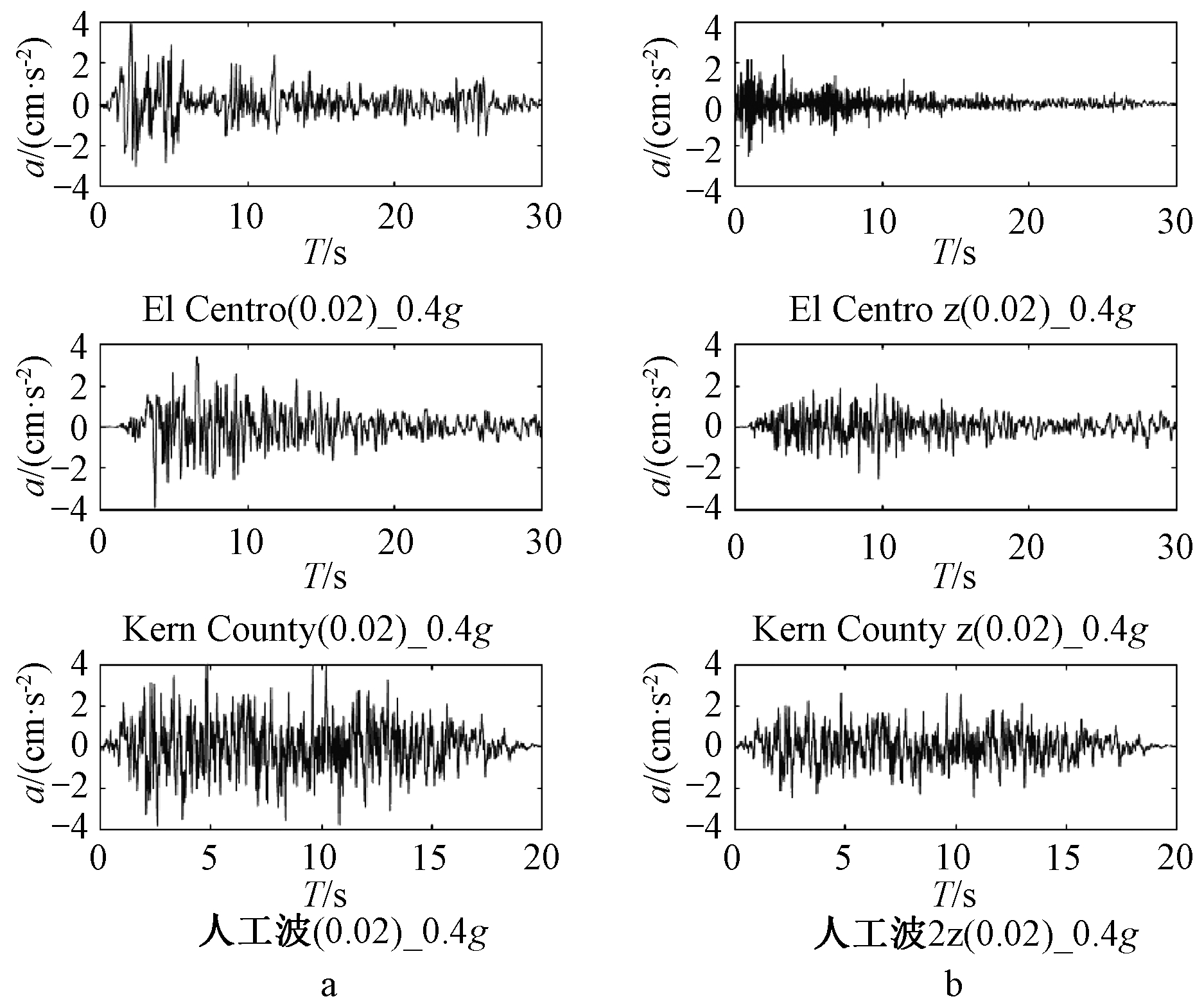
a—水平向; b—竖向。
图2 地震波时程曲线
Fig.2 Time histories of earthquake records
2 模态分析和静力分析
通过模态分析得到了80%储液容量结构的基本振动频率,见表2(L1表示液体一阶晃动模态)。可知:液体晃动为长周期振动模态,锚固罐的一阶模态为整体结构的水平振动,其罐体和液体的位移方向相反,见图3,当安装阻尼器构件之后,液体晃动频率基本保持不变,但整体结构的自振频率降低明显,对动力分析起主要贡献作用的一阶自振频率降低幅度达到85%,提离罐在地震作用下变为长周期振动。
表2 结构振动频率
Table 2 Natural frequencies of structure Hz
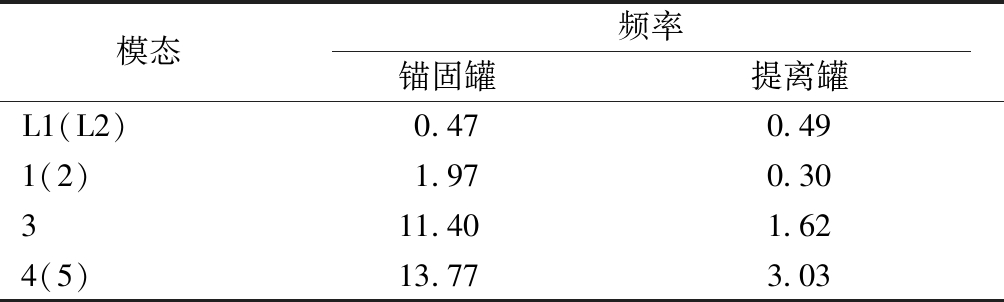
模态频率锚固罐提离罐L1(L2)0.470.491(2)1.970.30311.401.624(5)13.773.03

a—液体; b—结构。
图3 一阶振动模态
Fig.3 The 1st vibration mode of structure
图4为静力荷载下结构罐壁的等效应力和支柱轴应力图,罐壁最大应力出现在上部罐体和下部支柱的连接部位,最大值为17.5 MPa,该位置为结构的易破坏点。静载作用下支柱为纯压构件,轴应力为10 MPa。
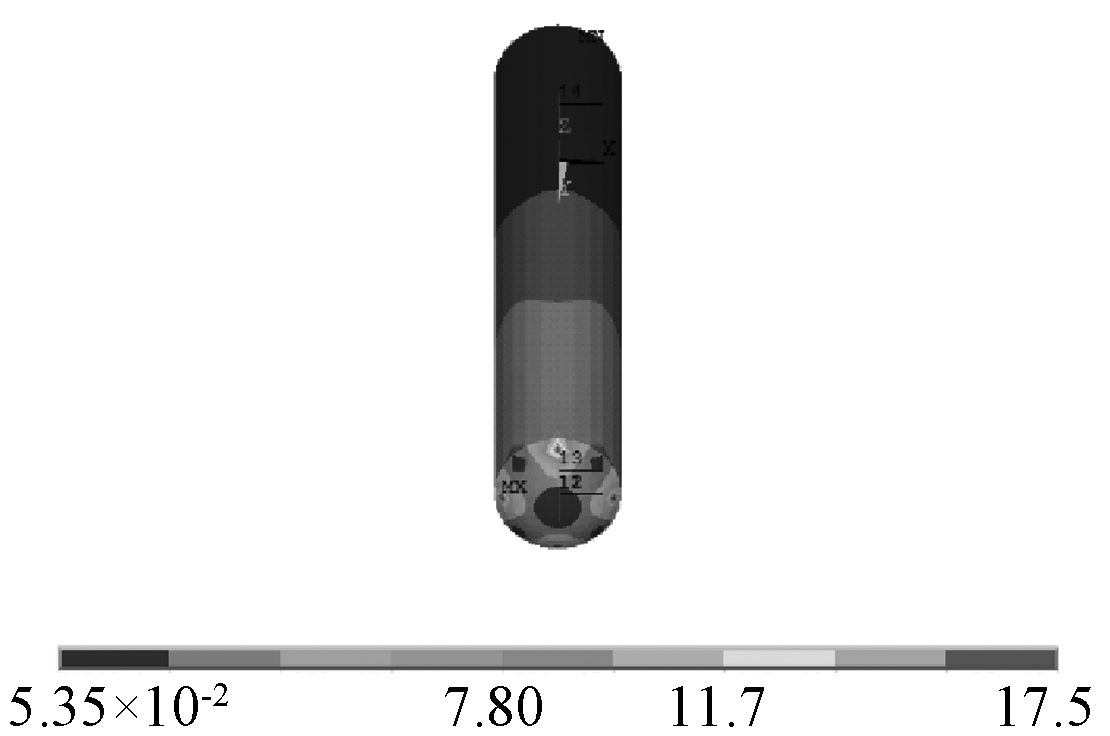
图4 罐壁等效应力 MPa
Fig.4 Equivalent stress of tank walls
3 动力响应分析
通过对软钢阻尼器的小幅横幅加载试验,高云鹏通过局部加劲肋改善了构件平面外屈曲问题[10],取得了良好的耗能性能,图5为改良后的阻尼器形式。通过计算储液罐的提离位移,根据高云鹏的设计方法[10],改变阻尼器尺寸并得出应用于本文支承式储液罐地震响应分析的柱脚耗能构件,该位移型阻尼器采用双线性模型,其屈服位移为20 mm,极限位移为80 mm,弹性阶段刚度为15×106 N/m,塑性阶段刚度为1×106 N/m,见图6。对80%储液容量的支撑式储罐进行了水平和竖向地震作用下的动力响应分析并对比了锚固罐和带耗能阻尼器提离罐的峰值响应,见表3。

图5 加劲肋软钢阻尼器
Fig.5 Stiffened hysteretic damper
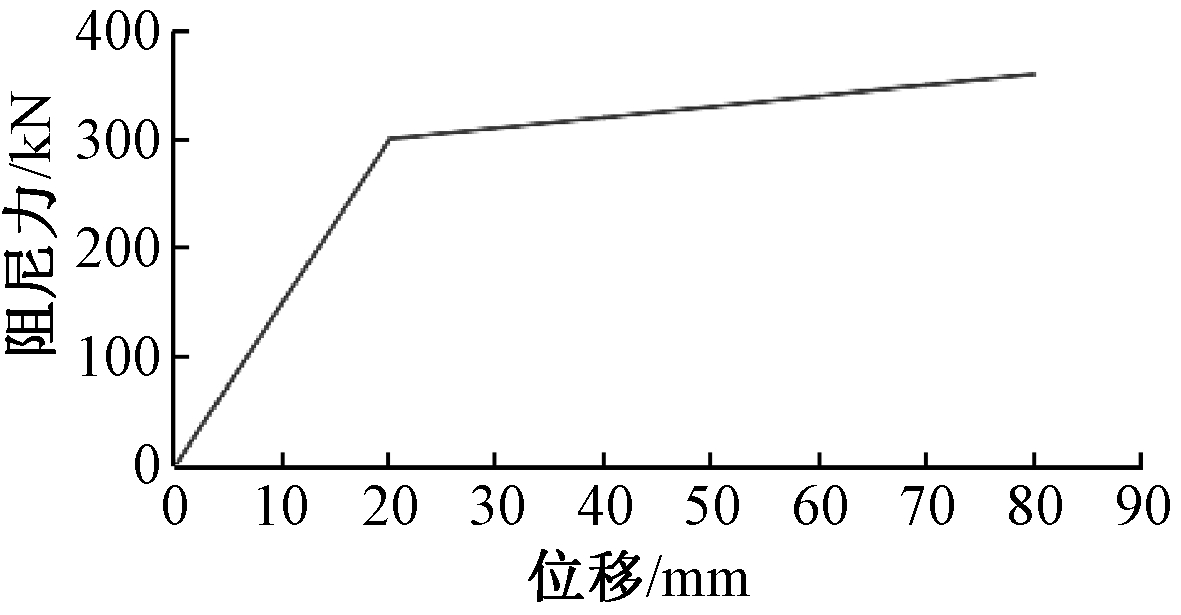
图6 阻尼器双线性模型
Fig.6 Bilinear model of damper
3.1 位移响应
以Kern County地震下储罐动力响应为例,图7为该罐顶水平位移时程曲线,锚固罐最大位移为111.1 mm,提离罐在水平和竖向地震下,罐顶水平位移由158.4 mm增加至161.7 mm。相比锚固罐,提离罐在El Centro波和人工波下,水平位移峰值分别增加了56.8%和171.4%,与单向地震相比,提离罐的位移峰值在考虑竖向地震后再放大了约2%。其次提离使结构竖向位移增加,人工波下的最大增量为22.5 mm。由此可见,储罐振动以水平运动为主且有小幅竖向振动,提离是造成位移增加的主要原因,竖向地震有一定的放大效应,结构位移的增大对提离罐是不利的,可能会引发整体倾覆,在抗震设计中应计入竖向地震的影响并设置限定值。
表3 地震作用下结构动力响应最大值
Table 3 Maximum dynamic responses of structure under earthquake
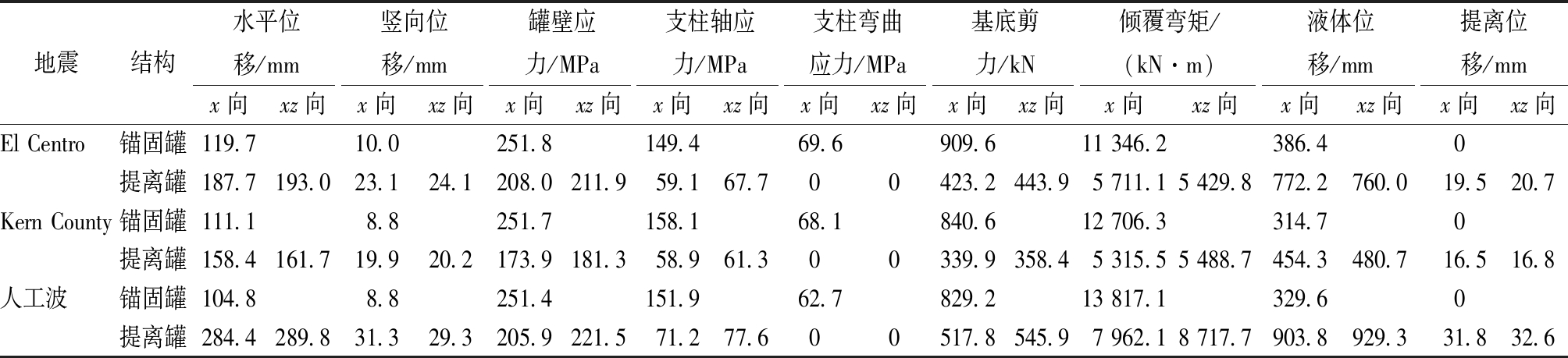
地震结构水平位移/mm竖向位移/mm罐壁应力/MPa支柱轴应力/MPa支柱弯曲应力/MPa基底剪力/kN倾覆弯矩/(kN·m)液体位移/mm提离位移/mmx向xz向x向xz向x向xz向x向xz向x向xz向x向xz向x向xz向x向xz向x向xz向El Centro锚固罐119.710.0251.8149.469.6909.611 346.2386.40提离罐187.7193.023.124.1208.0211.959.167.700423.2443.95 711.15 429.8772.2760.019.520.7Kern County锚固罐111.18.8251.7158.168.1840.612 706.3314.70提离罐158.4161.719.920.2173.9181.358.961.300339.9358.45 315.55 488.7454.3480.716.516.8人工波锚固罐104.88.8251.4151.962.7829.213 817.1329.60提离罐284.4289.831.329.3205.9221.571.277.600517.8545.97 962.18 717.7903.8929.331.832.6
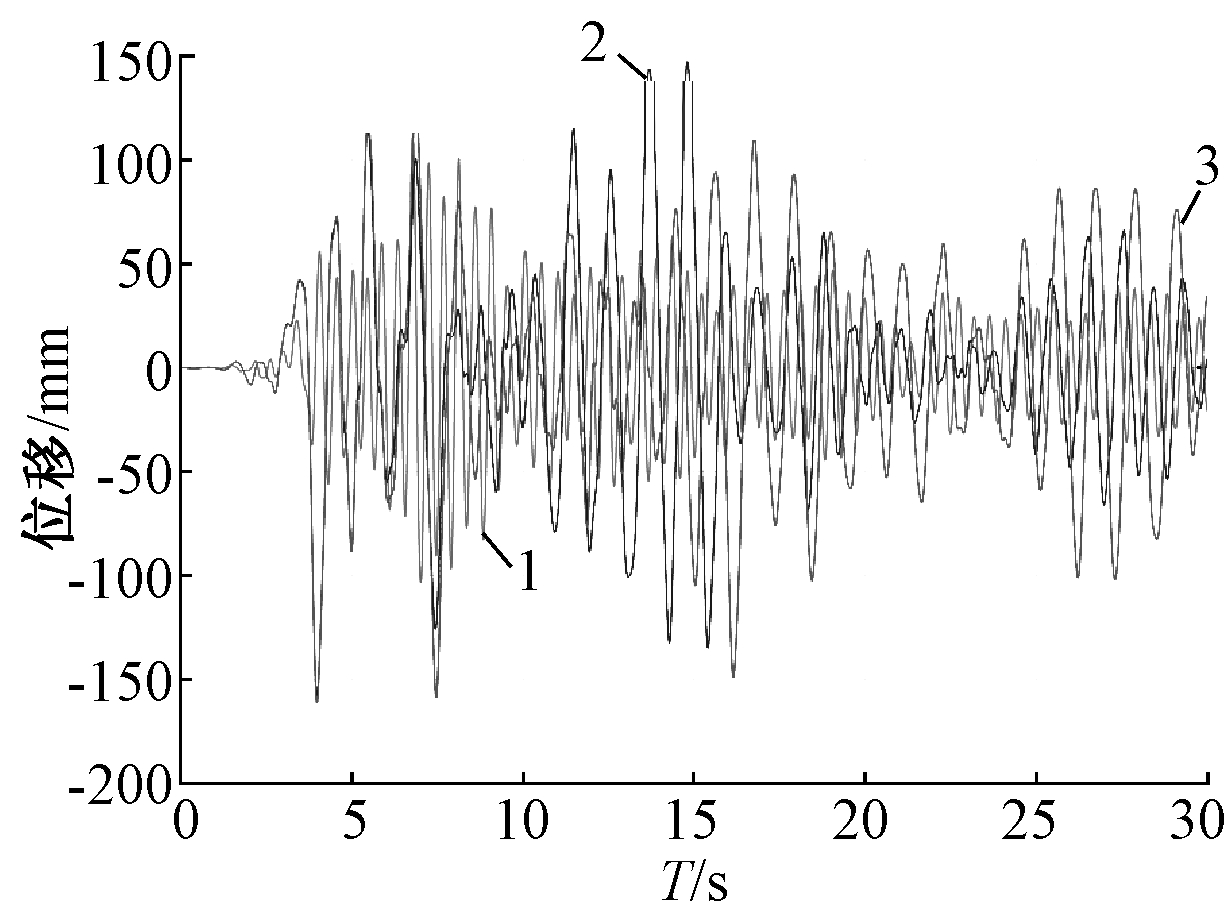
1—锚固罐; 2—提离罐x向; 3—提离罐xz向。
图7 Kern County波下水平位移
Fig.7 Horizontal displacement of tank under Kern County
对于限制水平位移但竖向自由放置的储罐,柱脚提离是其与锚固罐最大的区别,图8为平行于振动方向0°支柱的提离位移。由图8可知,储罐仅有正向位移,说明了有限元模型单向提离的有效性,虽提离位移小于阻尼器屈服位移,但竖向地震存在放大效应,增幅为1.8%。0°柱和180°柱交替发生提离,一方脱离地面时另一方产生压缩变形。El Centro波下,竖向地震作用使提离位移由19.5 mm增大至20.7 mm,阻尼器进入屈服阶段。人工波单向作用下,最大柱脚提离位移为31.8 mm,阻尼器屈服且考虑竖向荷载后有2.5%的增幅。在工程中可根据抗震设防条件设计合适的阻尼器,使其进入屈服状态而耗能。
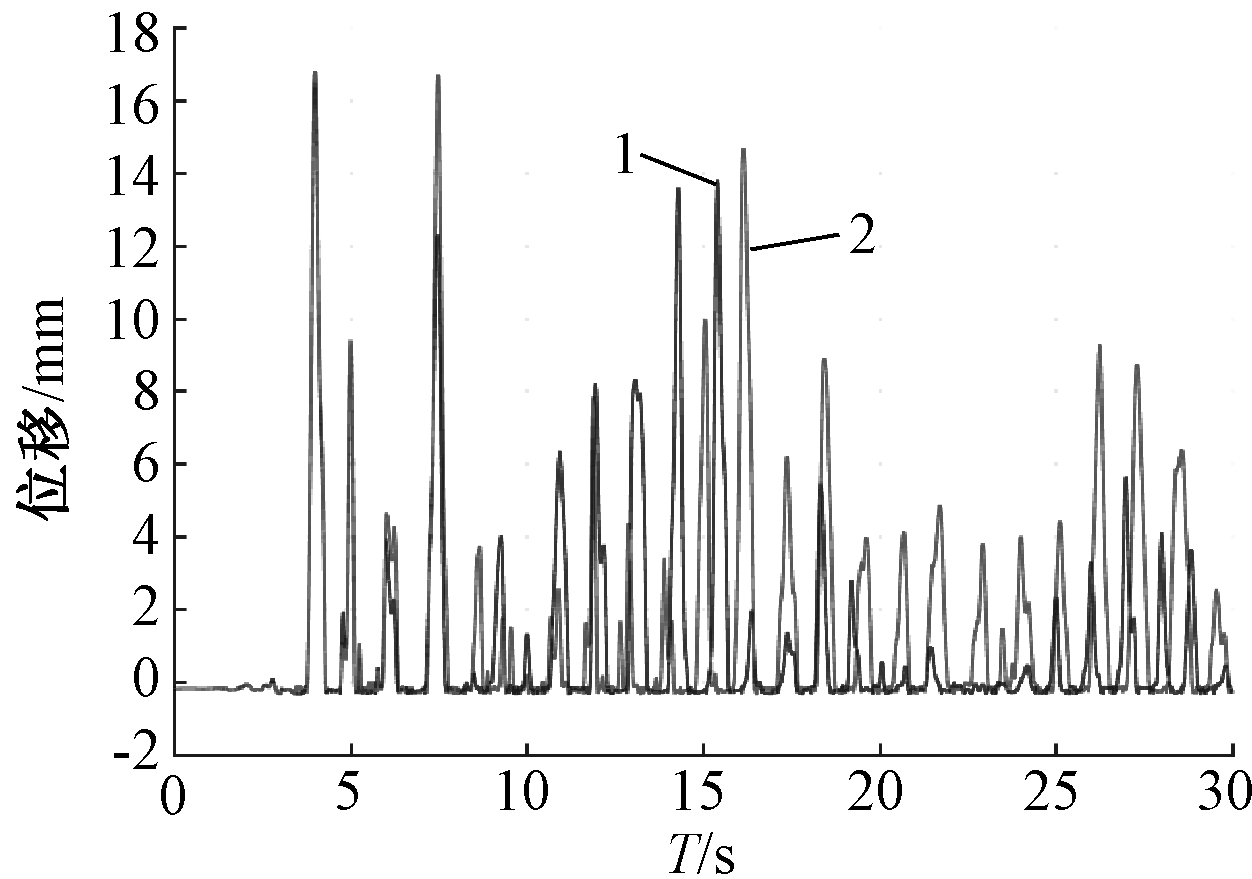
1—提离罐x向; 2—提离罐xz向。
图8 0°柱脚提离
Fig.8 Uplift of columns under El Centro record
储罐提离由倾覆弯矩大于结构自身恢复弯矩引起,液体晃动若与结构运动同步会加剧水平位移而增加结构倾覆的可能性。图9为外侧液面的晃动位移,与锚固罐相比,提离罐的液体晃动基本一致,但峰值从314.7 mm增加到454.3 mm,增幅为44.4%,竖向地震使其放大5.8%,达到480.7 mm。El Centro波下,竖向地震作用未增加峰值位移,但提离作用约使其放大2倍。人工波下,其幅值增加最显著,考虑竖向地震作用后,达到929.2 mm,增幅为181.9%。

1—锚固罐; 2—提离罐x向; 3—提离罐xz向。
图9 Kern County波下液体晃动
Fig.9 Liquid sloshing under Kern County
3.2 内力响应
支撑式储罐内部液体重量往往远大于结构本身,除了整体倾覆,最有可能发生支柱与罐壁连接处的罐壁进入塑性或者支柱的强度破坏。图10为平行于振动方向的支柱与罐壁连接处的罐壁的等效应力时程。可知:5~10 s出现应力峰值,锚固罐为251.7 MPa,超过罐体屈服强度,提离使其降低了30.9%,虽竖向地震存在4.3%的放大效应,但仍然处于较低的应力水平,没有达到强度破坏状态。El Centro波和人工波下类似,考虑竖向振动后罐壁等效应力有小幅增加。图11为支柱的轴向应力时程曲线。可以发现:提离罐支柱的轴向应力呈锯齿状,没有正值且在零轴附近出现多次跳跃,弯曲应力降低至10-3的数量级,可忽略不计,说明提离罐支柱主要承受结构和储液引起的轴向压力且弯曲应力急剧减小,不会发生屈曲;从峰值来看,人工波下最大轴应力为71.2 MPa,竖向地震使其增加了9.0%,但远小于屈服强度且比锚固罐减小了53.1%。因此,带耗能柱脚阻尼器提离罐能有效降低结构高应力区的应力水平,通过阻尼器耗能屈服使结构仍处于弹性状态而减震。
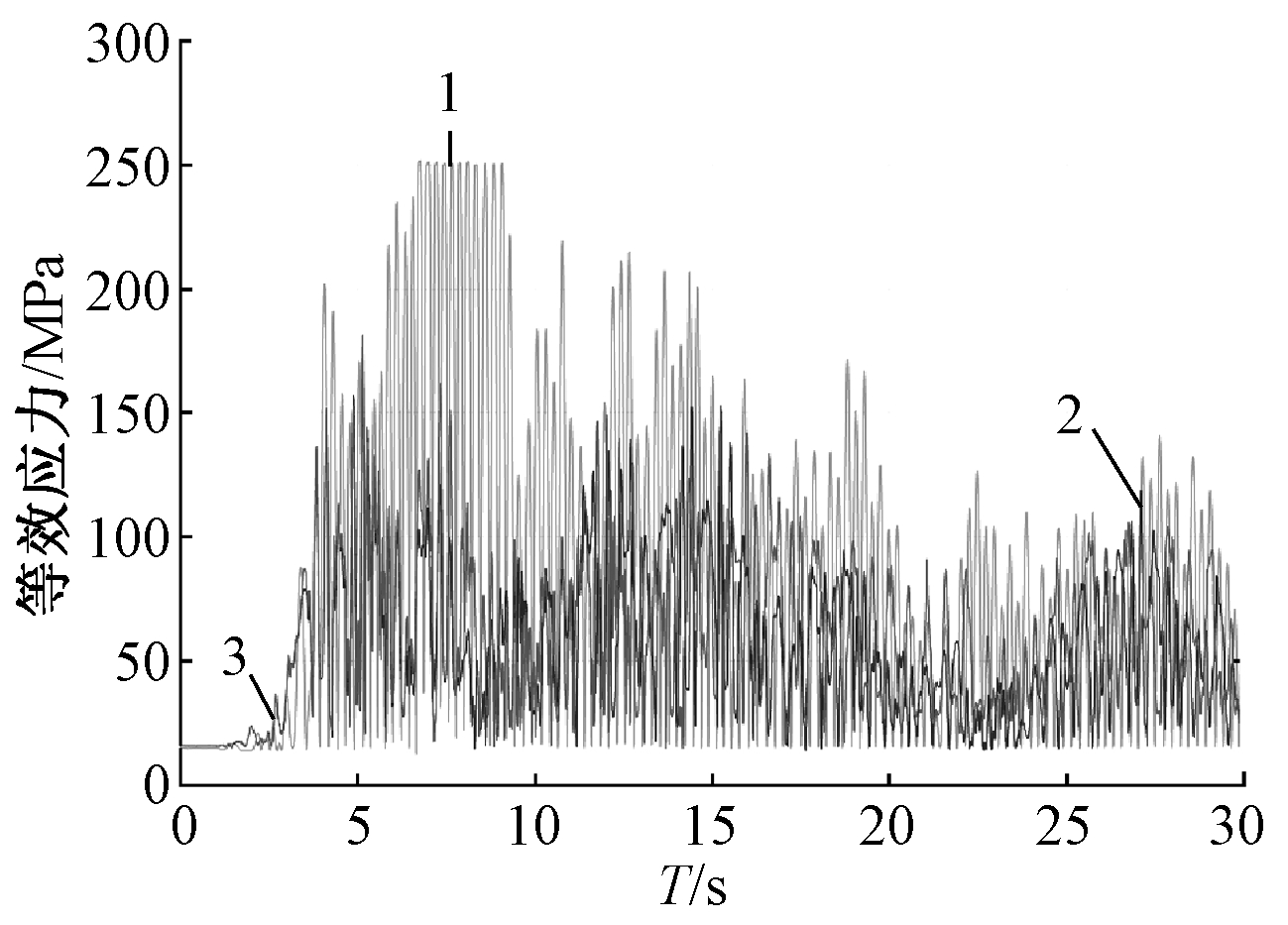
1—锚固罐; 2—提离罐x向; 3—提离罐xz向。
图10 Kern County波下罐壁等效应力
Fig.10 Equivalent stress of wall under Kern County
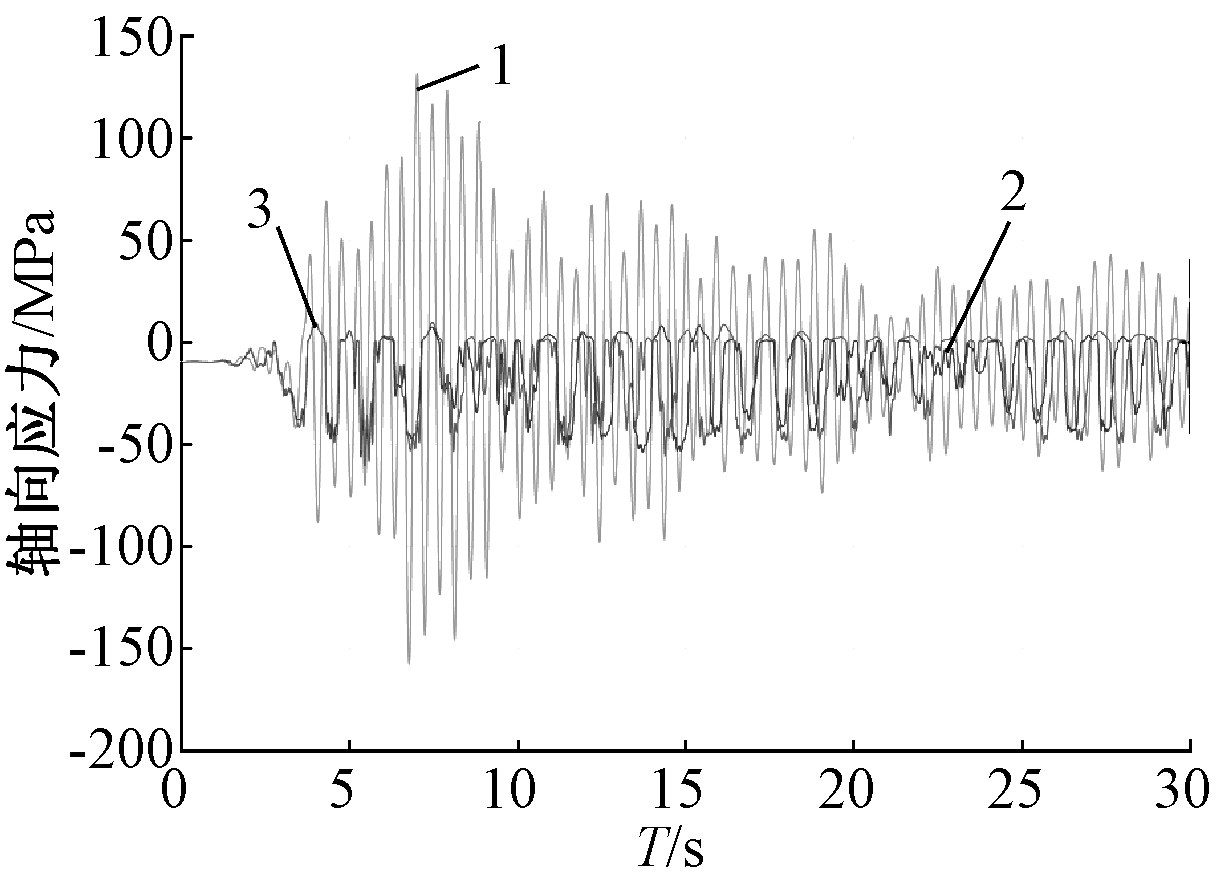
1—锚固罐; 2—提离罐x向; 3—提离罐xz向。
图11 Kern County波下支柱轴向应力
Fig.11 Axial stress of column under Kern County
图12、图13为基底剪力和倾覆弯矩时程曲线,由于竖向地震的作用,结构基底剪力和倾覆弯矩峰值分别增加到358.4 kN和5 488.7 kN·m,增幅分别为5.4%和3.3%,但相比锚固罐,峰值明显降低,达到59.6%和58.2%。El Centro波下,提离罐的剪力和倾覆弯矩峰值分别减小了53.5%和49.7%。人工波下,提离罐的剪力和倾覆弯矩峰值也分别有37.6%和42.2%的降幅,且竖向地震有放大作用。在储罐抗震设计中应考虑竖向地震的放大作用,带耗能柱脚阻尼器提离罐能有效降低结构内力。

1—锚固罐; 2—提离罐x向; 3—提离罐xz向。
图12 Kern County波下基地剪力
Fig.12 Base shear force under Kern County
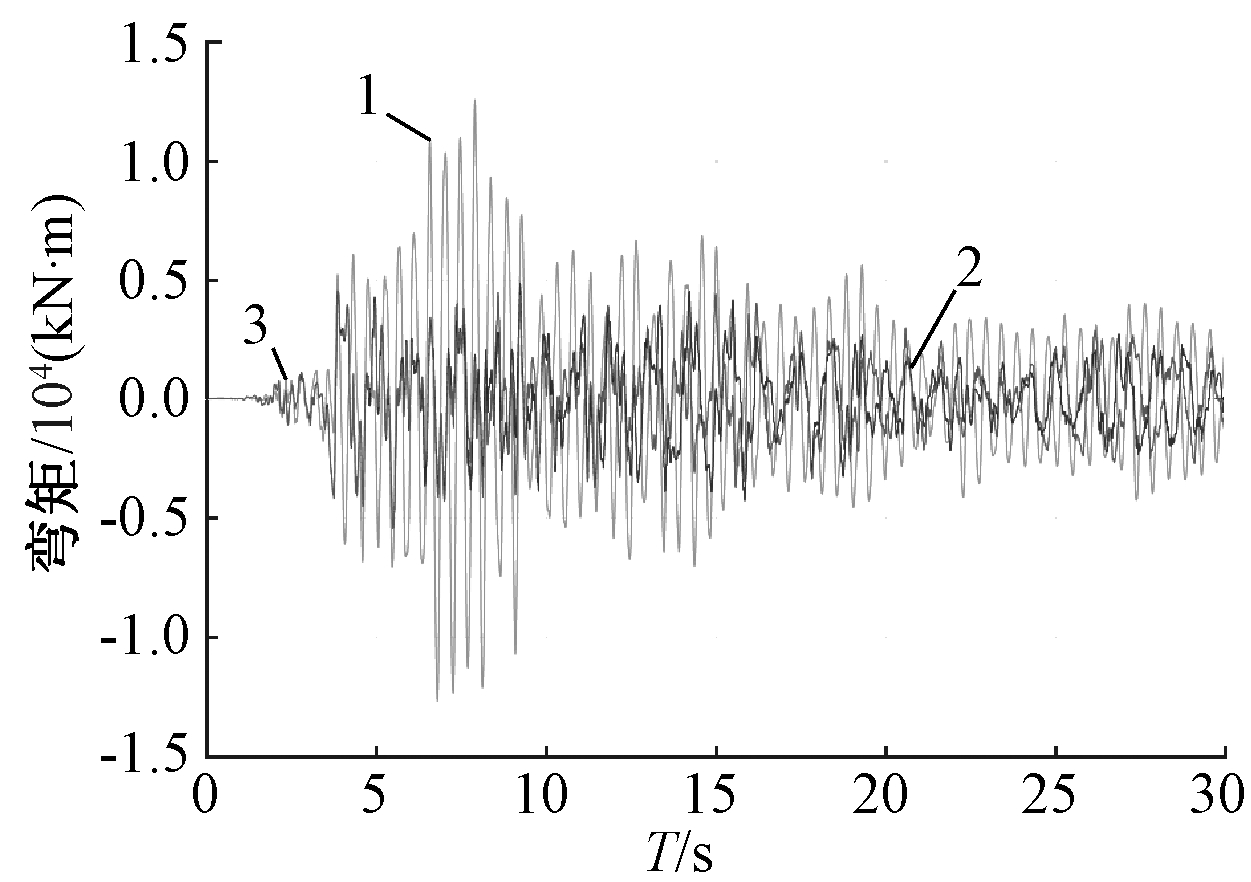
1—锚固罐; 2—提离罐x向; 3—提离罐xz向。
图13 Kern County波下倾覆弯矩
Fig.13 Overturning moment under Kern County
从上述结果可以发现,竖向荷载作用对结构的地震响应有不同程度的增加,与锚固罐相比,带耗能柱脚阻尼器的提离罐虽罐顶位移和液体晃动位移增加,但由于结构提离使阻尼器屈服耗能,有效降低了结构的应力水平、基底剪力和倾覆弯矩,且结构由塑性阶段进入弹性阶段,可实现LNG储罐的可恢复功能。
4 结束语
本文采用有限元方法建立了支撑式LNG储液罐模型,通过耦合自由度和接触方法实现了流固耦合作用和柱脚提离,进行了水平地震和水平竖向双向地震荷载下的动力分析,探讨了锚固罐和带耗能柱脚阻尼器提离罐的区别,对比了结构的地震响应。结果表明:竖向地震对结构响应有放大作用,与锚固罐相比,提离罐罐顶水平、竖向位移以及液面晃动位移均有增加,应设置位移限值,防止整体倒塌、支柱弯曲应力消失变为轴压构件;通过柱脚提离和阻尼器屈服耗能,结构应力水平明显下降,结构由塑性进入弹性阶段,柱底剪力和结构倾覆弯矩降低显著,地震后可通过更换柱脚阻尼器使结构快速恢复使用;带耗能柱脚阻尼器的新型LNG储液罐有更好的抗震性能且可实现可恢复功能。
[1] 邓民宪, 张永凯, 师俊平. 常压立式储油罐地震应力的有限元计算[J]. 地震学刊, 2000, 20(3): 18-23.
[2] 孙建刚, 王振, 王向楠, 等. 浮放储罐三维地震反应有限元分析[J]. 地震工程与工程振动, 2008, 28(6): 191-199.
[3] MIRZABOZORG H, HARIRI-ARDEBILI M A, NATEGHI A R. Seismic Behavior of Three Dimensional Concrete Rectangular Containers Including Sloshing Effects[J]. Coupled Systems Mechanics, 2012, 1(1): 79-98.
[4] GHAEMMAGHAMI A R, KIANOUSH M R. Effect of Wall Flexibility on Dynamic Response of Concrete Rectangular Liquid Storage Tanks Under Horizontal and Vertical Ground Motions [J]. Journal of Structural Engineering, 2010, 136(4): 441-451.
[5] 张如林, 程旭东, 王淮峰, 等. 竖向地震作用对储液罐地震响应的影响分析[J]. 地震工程学报, 2017, 39(4): 592-599.
[6] ALEMBAGHERI M. A New Dynamic Procedure for Evaluation of Steel Storage Tanks Under Multidirectional Seismic Excitations[J]. Ksce Journal of Civil Engineering, 2014, 18(6): 1696-1703.
[7] OZDEMIR Z, SOULI M, FAHJAN Y M. Numerical Evaluation of Nonlinear Response of Broad Cylindrical Steel Tanks Under Multidimensional Earthquake Motion[J]. Earthquake Spectra, 2012, 28(1): 217-238.
[8] 高云鹏, 赵鸣. 带减震构造的立式LNG球罐减震性能分析[J]. 特种结构, 2013, 30(5): 57-64.
[9] 高云鹏, 赵鸣, 刘磊. 液化天然气球罐耗能柱脚的研究[J]. 特种结构, 2013, 30(4): 18-22.
[10] 高云鹏, 赵鸣. 减震立式液化天然气球罐柱脚用带孔剪切钢板阻尼器性能分析[J]. 工业建筑, 2018, 48(1): 184-188.