2017年中国火电厂发电量占总发电量的70.5%,且未来长时间内火力发电都占中国电力工业的主导地位[1]。火电厂常采用的框排架结构体系存在质量、刚度不规则和不均匀等问题,地震作用时有较多的薄弱环节[2],因此,十分必要在火电厂结构中应用消能减震技术。质量调频阻尼器(TMD)作为消能减震技术在超高层、高耸及大跨结构中广泛应用于风致振动控制,考虑地震作用的复杂性,其在地震控制方面的应用需做进一步研究[3-4]。文献[5]对TMD的最佳布置位置、最优频率以及参数灵敏度进行研究分析,为TMD结构应用于地震响应控制提供了依据。文献[6]研究显示TMD能够降低单自由度结构地震响应。文献[7]进行地震模拟振动台试验研究,证明TMD加层减震模型结构有明显的减震效果。不同于传统质量调频减震结构需附加额外质量到结构上,火电厂结构中煤斗质量通常可达总结构质量的10%左右[8],能为TMD提供充足的质量比,且煤斗处于结构的较高位置,接近质量布置的最优位置[9-10],因此形成以煤斗质量作为TMD质量单元的煤斗TMD火电厂结构,目前该技术构造方式包括悬吊式和支承式[11]。文献[12]对悬吊煤斗TMD结构进行弹塑性分析,表明其对减小火电厂结构的地震响应有显著效果。文献[13]研究表明悬吊式煤斗比支承式煤斗TMD效果明显,且减震率随频率比的变化而变化。文献[14]对煤斗TMD进行较为详尽的分析,表明煤斗TMD具有显著减震效果,但未涉及同时布置多个煤斗TMD的双向地震作用研究。
对布置多个煤斗的悬吊煤斗TMD火电厂结构进行参数优化设计,为考察该参数优化方案的合理性,建立有限元模型进行时程分析;为验证悬吊煤斗TMD结构优化后的减震效果,制作钢筋混凝土模型进行振动台试验分析。
1 多自由度下TMD参数优化
电厂常规结构是将煤斗与楼层固接,而煤斗TMD结构是将煤斗与楼层采用弹性元件和阻尼元件连接。将火电厂结构简化为n层结构模型,如图1所示,煤斗设置于k层, 结构在基底地震加速度![]() 激励下系统动力方程为:
激励下系统动力方程为:
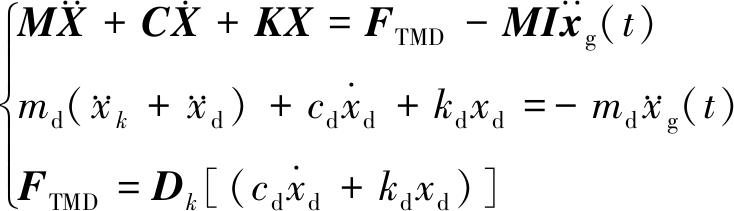
(1)
式中:M、K、C分别为结构质量、刚度和阻尼矩阵;md、kd、cd分别为煤斗的质量、弹簧刚度及阻尼;X为结构楼层相对于地面的位移向量,即![]() 分别为结构楼层相对于地面的速度、加速度向量;xd为煤斗相对于结构第k层xk的相对位移;
分别为结构楼层相对于地面的速度、加速度向量;xd为煤斗相对于结构第k层xk的相对位移;![]() 分别为煤斗相对于结构第k层的相对速度和加速度;I为单位向量;Dk=[0…0 1 0…0]T为减震煤斗的位置向量,其中第k个元素为1,其他元素为0;FTMD为减震煤斗所提供的阻尼力。
分别为煤斗相对于结构第k层的相对速度和加速度;I为单位向量;Dk=[0…0 1 0…0]T为减震煤斗的位置向量,其中第k个元素为1,其他元素为0;FTMD为减震煤斗所提供的阻尼力。
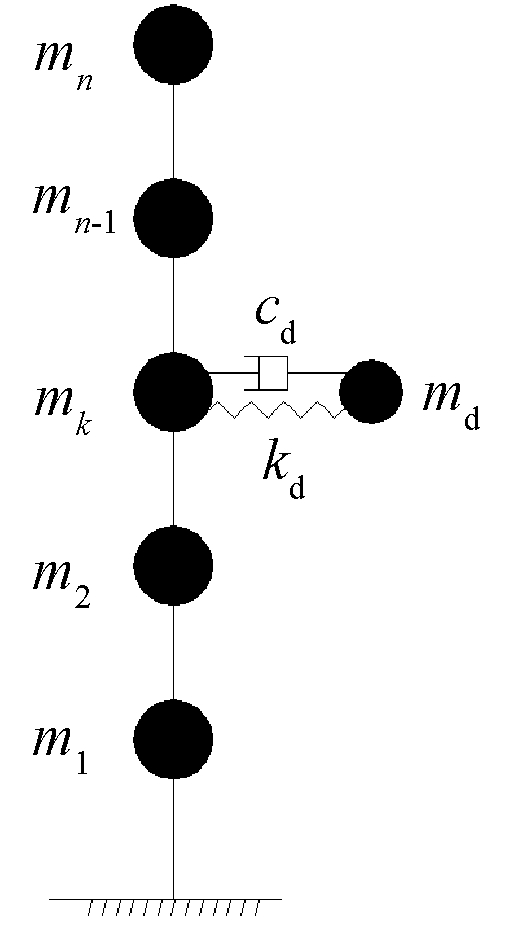
图1 多自由度体系TMD减震示意
Fig.1 Schematic diagram of MOF system TMD damping
将结构动力平衡方程进行振型分解,为得到结构第j阶振型,将X=φjqj代入式(1),其中φj,qj分别为第j阶振型向量和振型广义坐标,左端乘![]() 得:
得:
(2)
其中 ![]()
式中:φjk为φj的第k个元素,其与煤斗布置位置对应;ζn为第n阶振型的阻尼比;ωn为第n阶振型的圆频率;Mn为结构第n层的质量。
则第1阶振型为:
(3)
其中![]()
不考虑高阶振型影响,用振型坐标代换式(1)中的![]() 则可得:
则可得:
(4)
在简谐激励下![]() 其中令:
其中令:
q1=H1(ω)eiωt, xd=Hd(ω)eiωt
(5a,b)
(5c,d)
(5e,f)
将式(5)代入式(3)、式(4),可得:
(6)
式中:η1、ξ1、ω1分别为结构第1阶振型的振型参与系数、振型阻尼比以及振型圆周频率;ωd、ξd分别为煤斗TMD圆周频率和阻尼比。
得到结构位移响应的传递函数为:
(7)
假定地震波为平稳随机白噪声,地震波功率谱密度为S0,得到主结构位移响应方差:
(8)
假定ωd=λω1,λ定义为TMD系统频率比,以控制位移响应方差![]() 最小为目标函数,确定λ、ξd,即:
最小为目标函数,确定λ、ξd,即:
(9)
实际工程中火电厂煤斗通常布置多个,假定多个煤斗在地震作用下同一时刻运动方向一致,依据上述目标函数对悬吊煤斗双向减震结构的水平纵向(X向)和横向(Y向)两方向分别独立地进行参数优化。首先要确定缩尺模型的无煤斗荷载结构的X、Y两方向的主控振型,然后分别试算两方向目标函数以确认两方向频率比和阻尼比,再由各方向最优频率比得出TMD减震装置频率,从而得出弹性元件刚度,由最优阻尼比求得阻尼,最后将X、Y两方向所得刚度和阻尼分别平均并联到每个煤斗X、Y两方向上。图2所示为一个方向参数优化的具体流程,X、Y两方向分别按照该流程进行参数优化。

图2 参数优化流程
Fig.2 Parameter optimization flow chart
2 有限元模拟
2.1 模型背景
某典型火电厂主厂房结构,设计基本加速度为0.2g,基本地震烈度为8度,场地类别Ⅱ类,设计地震分组为第二组,特征周期Tg=0.40 s,抗震设计等级为一级。截取该主厂房包含煤斗层的结构,如图3所示,方框圈出部分为截取部分的模型,为7层错层结构,第4层为煤斗层,对其进行1∶12缩尺,相似系数按相似理论确定,如表1所示,缩尺后模型尺寸如图4所示。包括结构质量,试验模型总质量为13 988 kg,其中第4层的4个煤斗总质量为2 000 kg,占结构总质量的14.3%。
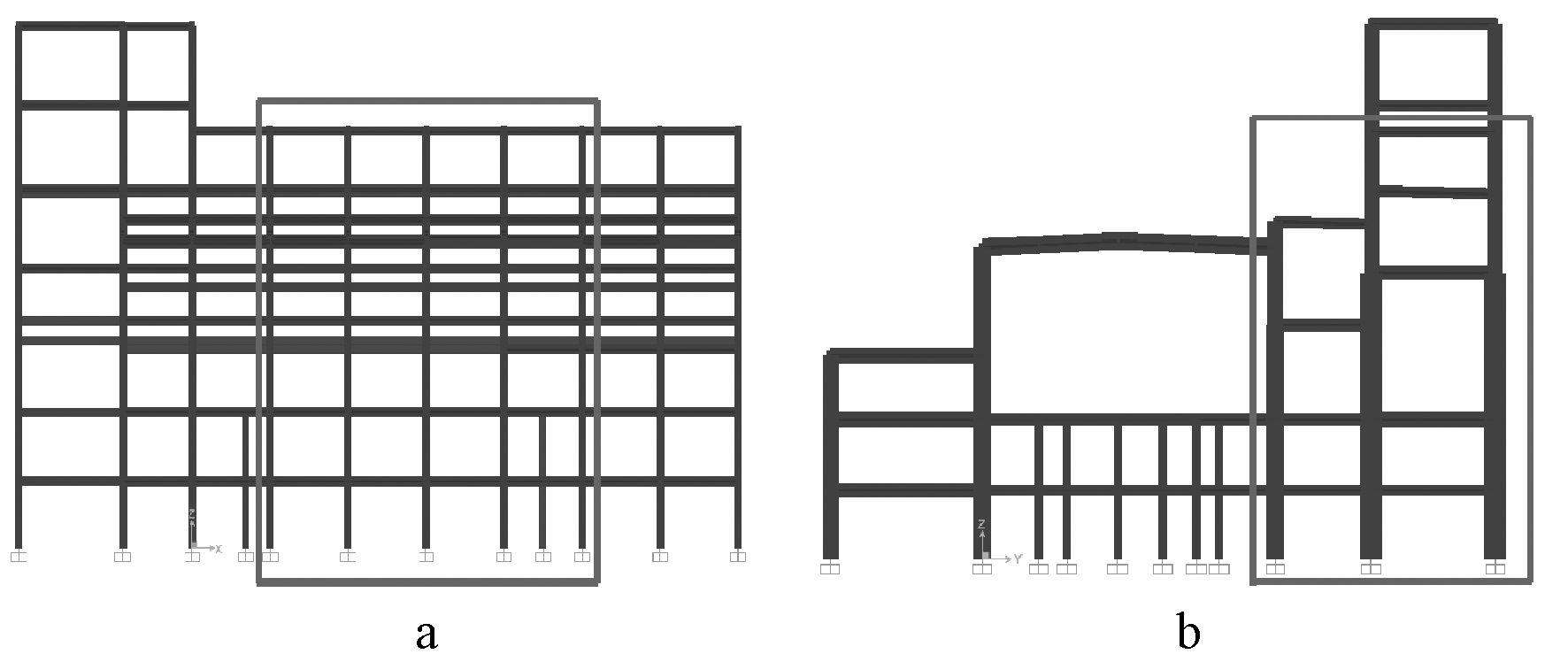
a—正视; b—侧视。
图3 模型截取示意
Fig.3 Schematic diagram of model interception
表1 相似系数
Table 1 Similarity coefficient

物理量量纲相似系数线尺寸l[L]SL=1/12弹性模量E[FL-2]SE=1等效质量密度ρe[FL4T2]Sρe=2.4时间t[T]ST=SLSρe/SE=0.13自振频率ω[T-1]Sω=1/ST=7.75加速度幅值a[LT-2]Sa=SE/(SLSρe)=5

a—正视; b—侧视; c—俯视。
图4 试验模型尺寸
Fig.4 Test model size
2.2 悬吊煤斗TMD参数优化设计
依据上述方法进行参数优化,为获取无煤斗荷载结构两方向的主控振型,通过SAP 2000建立无煤斗结构有限元模型进行模态分析,选取模型第1阶振型和第2阶振型为两方向主控振型,两振型如图5所示,TMD最优设计参数如表2所示。
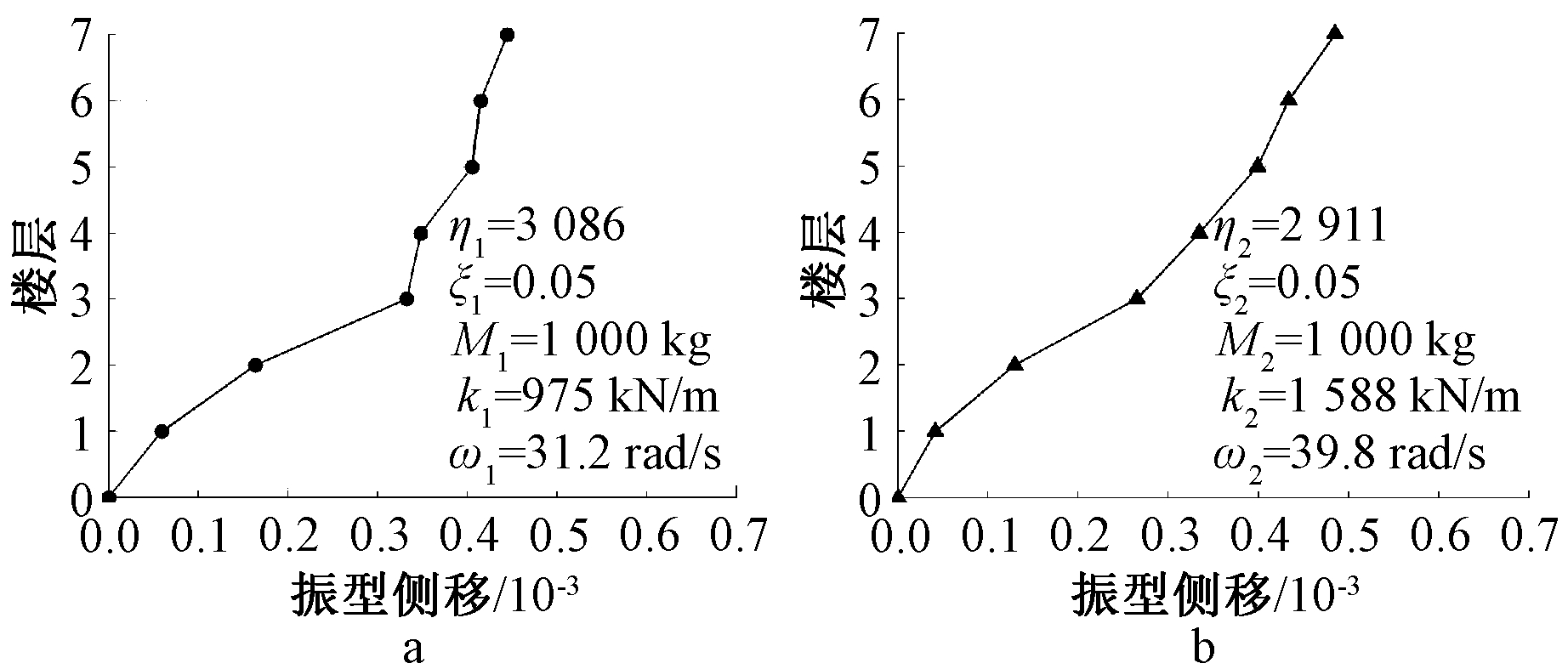
a—第1阶振型; b—第2阶振型。
图5 无煤斗结构第1、2阶振型
Fig.5 The first and second vibration modes of the coal-free bucket structure
表2 TMD最优设计参数
Table 2 Optimal design parameters of TMD

方向频率比阻尼比减震装置频率/HzX向0.710.233.5Y向0.720.224.6
2.3 悬吊煤斗TMD结构有限元模型
通过SAP 2000有限元软件建立的悬吊煤斗TMD结构有限元模型如图6所示。其中原结构模型中煤斗质量以楼面荷载的形式附加到煤斗层,而悬吊煤斗TMD结构模型中以附加质量的结点来模拟煤斗质量,节点通过Link连接单元与主结构连接,通过对Link连接单元两方向分别赋予刚度系数和阻尼系数模拟悬吊煤斗TMD装置的频率条件和阻尼条件。
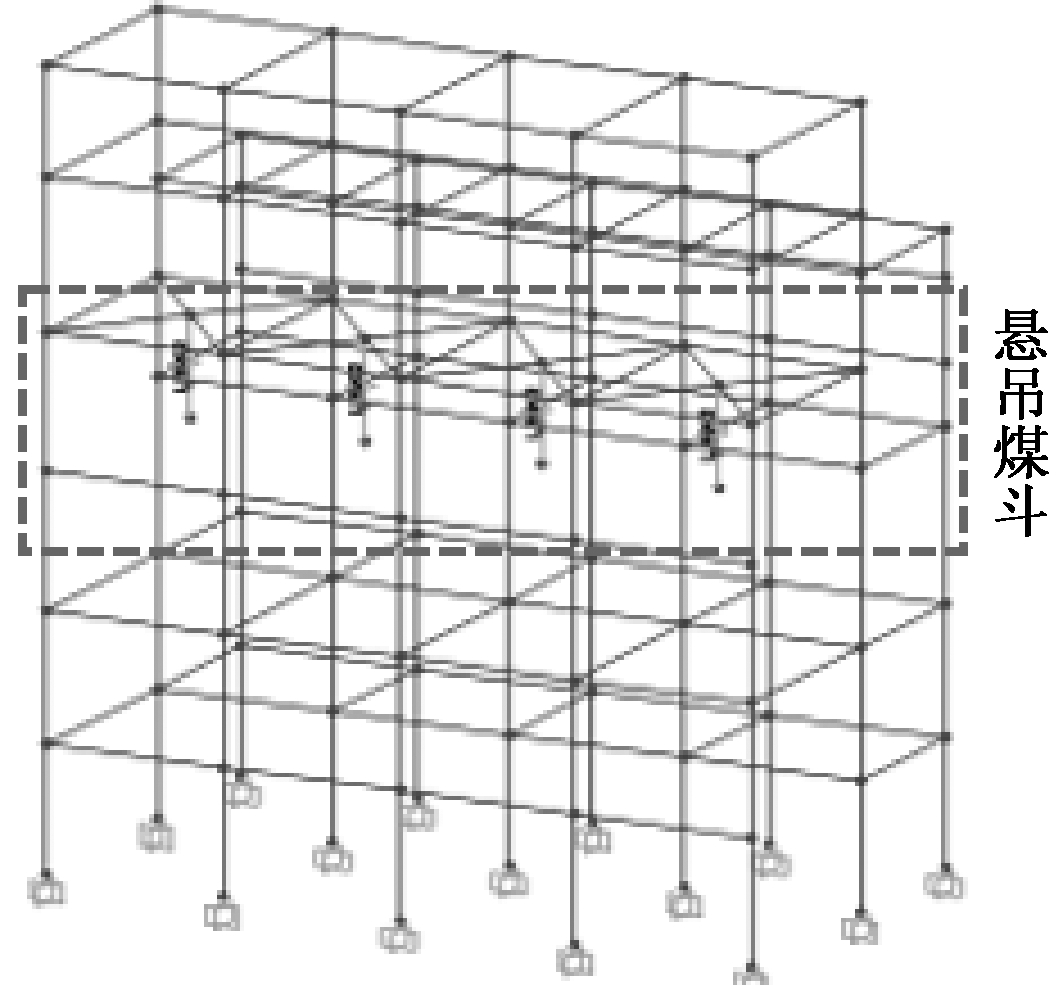
图6 悬吊煤斗TMD结构有限元模型
Fig.6 Finite element model of TMD structure of suspension coal bucket
根据GB 50011—2010《建筑抗震设计规范》要求选择地震动,包括两条天然波Saratoga-Aloha波(简称“Saratoga-A”)和Petrolia波以及一条人工波RGB波,两条天然波的相关信息见表3,地震时程记录和反应谱曲线如图7所示,可以看出两条自然波脉冲特征较RGB波更为明显,短时间达到峰值后趋于平缓,而RGB波大幅振动持续时间较长(约20 s)。模拟输入地震波时按表1相关比例系数调整。
表3 天然地震波相关信息
Table 3 Information on natural seismic waves

地震波地震年份震级Saratoga-ALom Prieta19896.9PetroliaCape Mendocino19927.3
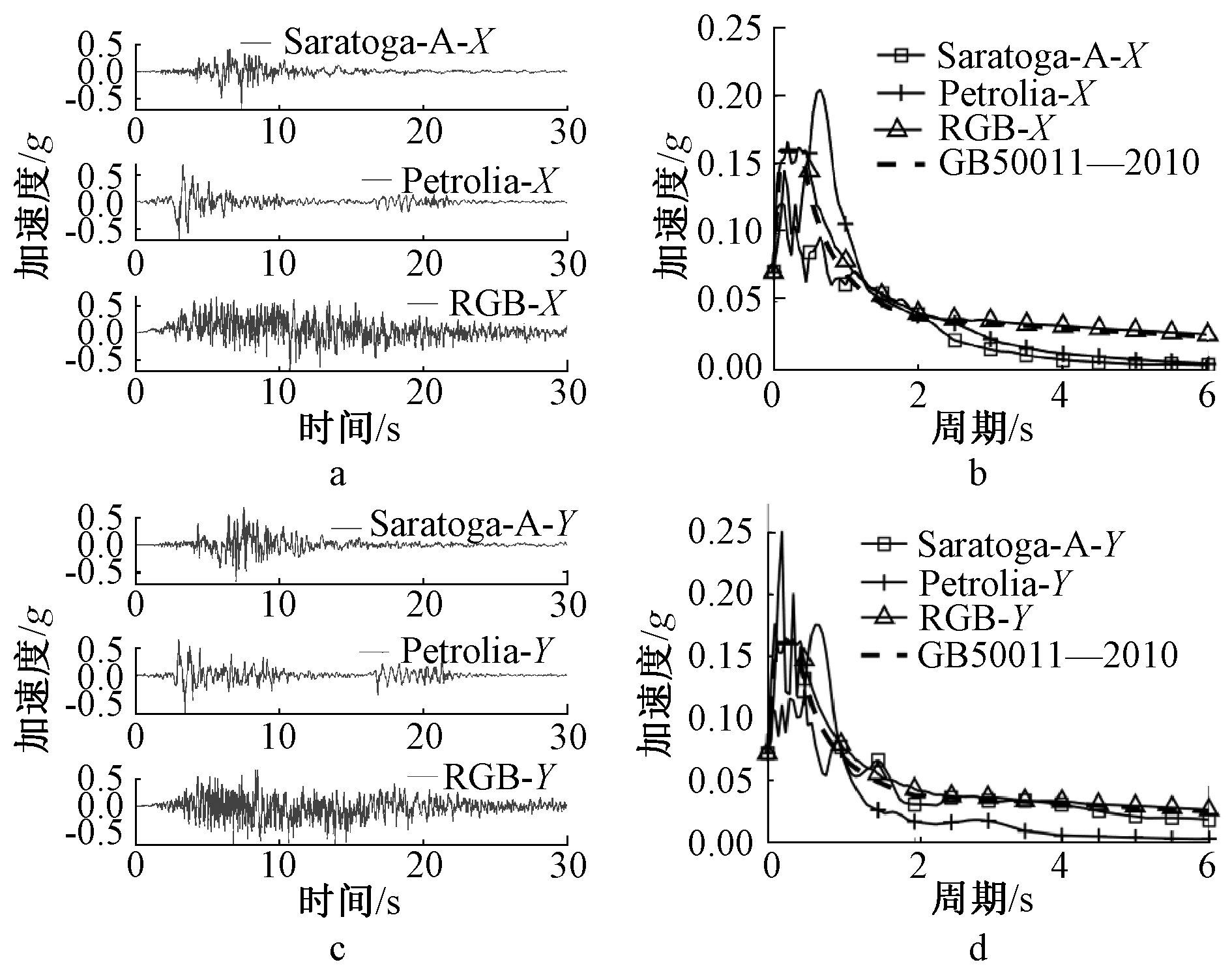
a—X向地震波时程; b—X向反应谱; c—Y向地震波时程; d—Y向反应谱。
图7 地震波时程及反应谱
Fig.7 Seismic wave time history and response spectrum
通过分析悬吊煤斗TMD结构的单个方向在单向和双向地震作用下的减震效果,考察TMD两方向的耦合作用情况。将选取的3条地震波按单向和双向输入结构模型,其中单向输入是结构的X或Y单一方向输入地震波,双向输入是结构的X和Y方向同时输入地震波。本模拟对有限元模型进行设防烈度弹性时程分析,具体输入工况如表4所示。
表4 模拟工况
Table 4 Simulated working conditions

工况地震波地震波方向输入峰值/g1Saratoga-AX1.02Saratoga-AY1.03Saratoga-AX+Y1.04PetroliaX1.05PetroliaY1.06PetroliaX+Y1.07RGBX1.08RGBY1.09RGBX+Y1.0
2.4 有限元模拟结果
3组地震波设防水准单向和双向地震作用下,悬吊煤斗TMD结构X、Y两方向层间位移峰值减震率平均值如表5所示,各层层间位移峰值减震率如图8所示,可以得出:
1)悬吊煤斗TMD结构单个方向的减震效果与单向和双向地震作用下相差较小,即TMD两方向耦合作用较小,X向减震率差值比最大为0.4%,Y向减震率差值比最大为8.5%。
2)悬吊煤斗TMD结构对不同地震波的减震效果表现出离散性,整体减震效果良好。三组地震波双向地震作用下,X向位移峰值减震率平均值47.3%,Y向位移峰值减震率平均值34.1%。
3)结构层间位移峰值减震率表现出在煤斗层(第四层)以上有下降的趋势,其中,Saratoga-A波和RGB波尤其明显。
表5 层间位移峰值减震率平均值
Table 5 Average value of peak damping rate of interstory displacement

地震波输入方向减震率平均值/%X向Y向单、双向差值/%Saratoga-AX54.0-0.2Saratoga-AY50-8.4Saratoga-AX+Y54.154.2PetroliaX41.40.0PetroliaY16.58.5PetroliaX+Y41.415.1RGBX46.70.4RGBY33.6-1.5RGBX+Y46.533.1
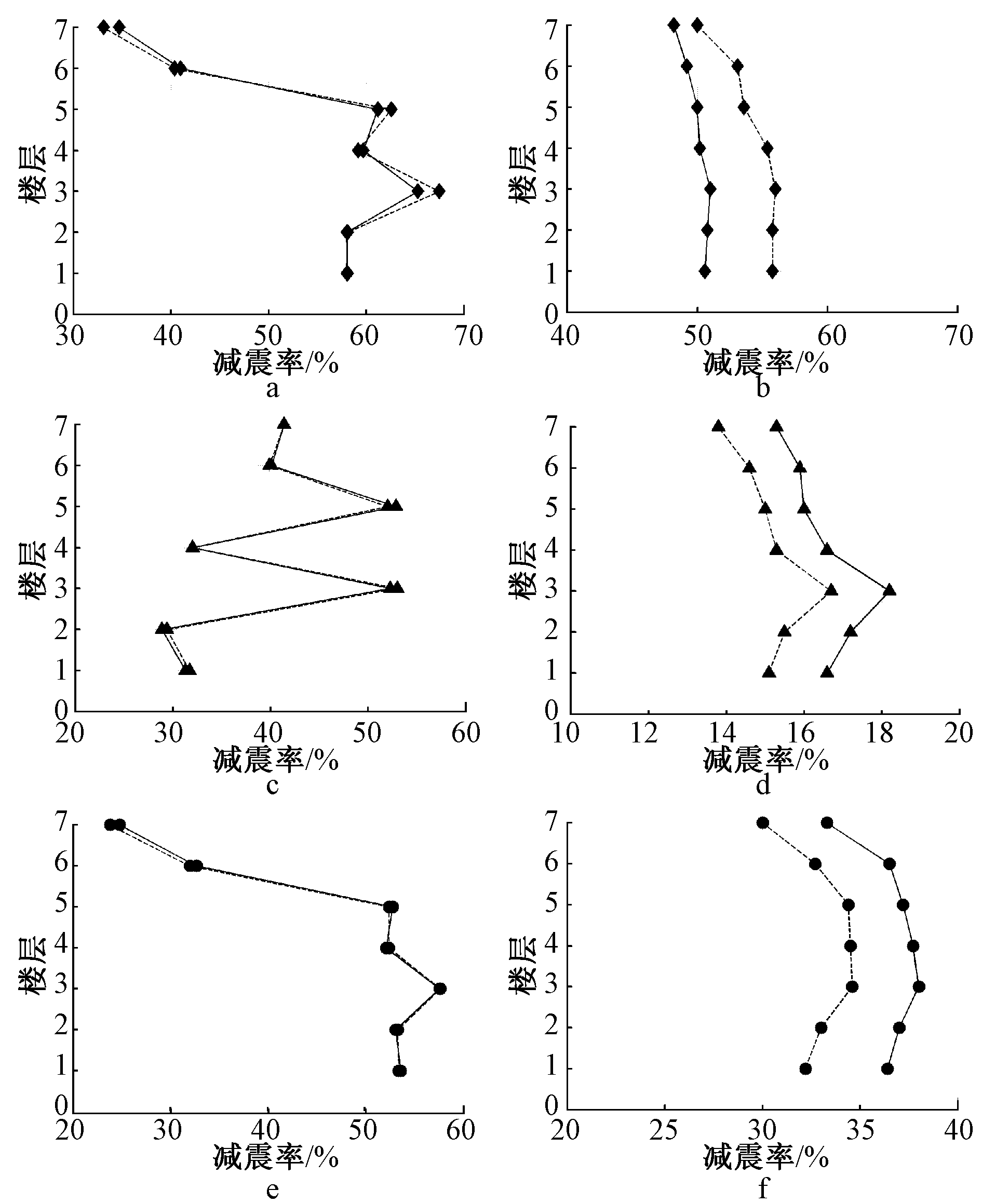
a—Saratoga-A波X向; b—Saratoga-A波Y向; c—Petrolia波X向;d—Petrolia波Y向; e—RGB波X向; f—RGB波Y向。![]() —单向Saratoga-A波; -
—单向Saratoga-A波; -![]() --双向Saratoga-A波;
--双向Saratoga-A波; ![]() —单向Petrolia; -
—单向Petrolia; -![]() --双向Petrolia波;
--双向Petrolia波;![]() —单向RGB波; -
—单向RGB波; -![]() --双向RGB波。
--双向RGB波。
图8 各层位移峰值减震率
Fig.8 Peak displacement damping rate of each layer
3 试验概况
3.1 TMD装置动力特性测试
悬吊煤斗TMD刚度由摆动吊杆和拉伸弹簧共同决定,通过设计吊杆长度和弹簧刚度满足频率比条件,阻尼由黏滞阻尼器提供,通过设计黏滞阻尼器阻尼系数实现阻尼比条件。为验证悬吊煤斗TMD参数及构造设计,截取试验模型单个煤斗结构制作钢筋混凝土模型,如图9所示。在振动台试验前进行煤斗TMD装置动力特性测试,试验采用人工激振的方式,给定煤斗初始位移使其做自由衰减运动,衰减曲线如图10所示,其中试验衰减曲线为试验测得,理论衰减曲线为所求最优设计参数条件下的衰减曲线,得出减震装置两方向频率及阻尼比如表6所示,试验测得频率和阻尼比与理论最优设计值接近,悬吊煤斗TMD装置整体设计合理。

a—悬吊煤斗TMD装置; b—阻尼器及弹簧布置。
图9 悬吊煤斗TMD装置
Fig.9 TMD device for suspended coal bucket
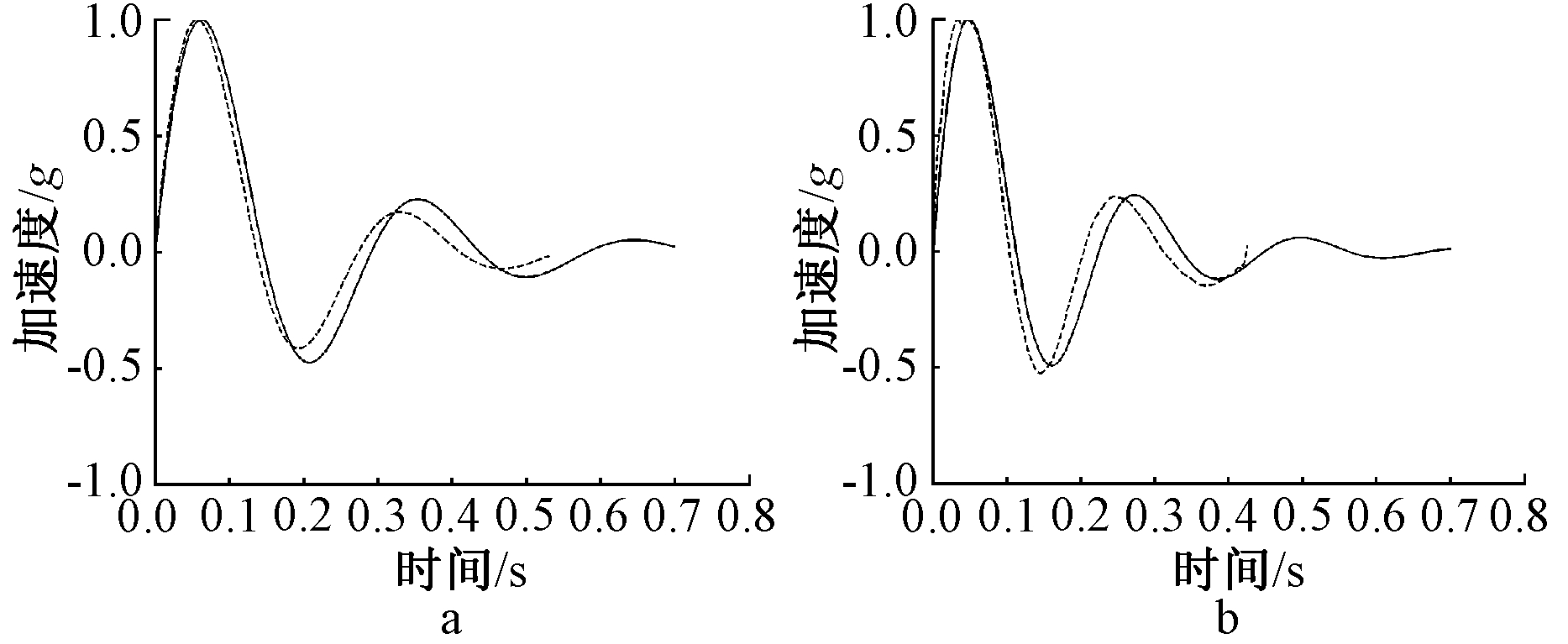
a—X向自由衰减曲线; b—Y向自由衰减曲线。
……试验衰减; ——理论衰减。
图10 减震装置自由衰减曲线
Fig.10 Free attenuation curve of damping device
表6 动力特性测试
Table 6 Dynamic characteristic test results

方向煤斗测试频率/Hz测试阻尼比/%X向3.8727.5Y向4.6920.3
3.2 振动台试验传感器布置及加载工况
振动台试验模型为钢筋混凝土结构,细石混凝土强度为C50,模型如图11所示。为验证多个悬吊煤斗在地震作用下运动方向的一致性,沿X、Y两方向对煤斗布置拉线位移计以获得煤斗沿两方向位移运动状态。为测量各层加速度,从二层起,在各楼层③轴和 轴相交处布置双向加速度传感器以测量各楼层沿X、Y方向的加速度,加速度传感器编号A-2~A-7;为测量各层层间位移,从二层起,在层间布置拉线位移计,X向拉线位移计编号为DX-2~DX-7,考虑到位移计拉线过长的不利影响,Y方向在①轴和③轴之间布置拉线位移计,Y向拉线位移计编号DY-2~DY-7。加速度传感器及拉线位移计布置位置如图12所示。为检测黏滞阻尼器在振动台试验中的工作状况,X、Y方向分别选取阻尼器连接力传感器和拉线位移计,基于测试结果给出阻尼器滞回曲线。
轴相交处布置双向加速度传感器以测量各楼层沿X、Y方向的加速度,加速度传感器编号A-2~A-7;为测量各层层间位移,从二层起,在层间布置拉线位移计,X向拉线位移计编号为DX-2~DX-7,考虑到位移计拉线过长的不利影响,Y方向在①轴和③轴之间布置拉线位移计,Y向拉线位移计编号DY-2~DY-7。加速度传感器及拉线位移计布置位置如图12所示。为检测黏滞阻尼器在振动台试验中的工作状况,X、Y方向分别选取阻尼器连接力传感器和拉线位移计,基于测试结果给出阻尼器滞回曲线。

图11 钢筋混凝土试验模型
Fig.11 Experimental model of reinforced concrete
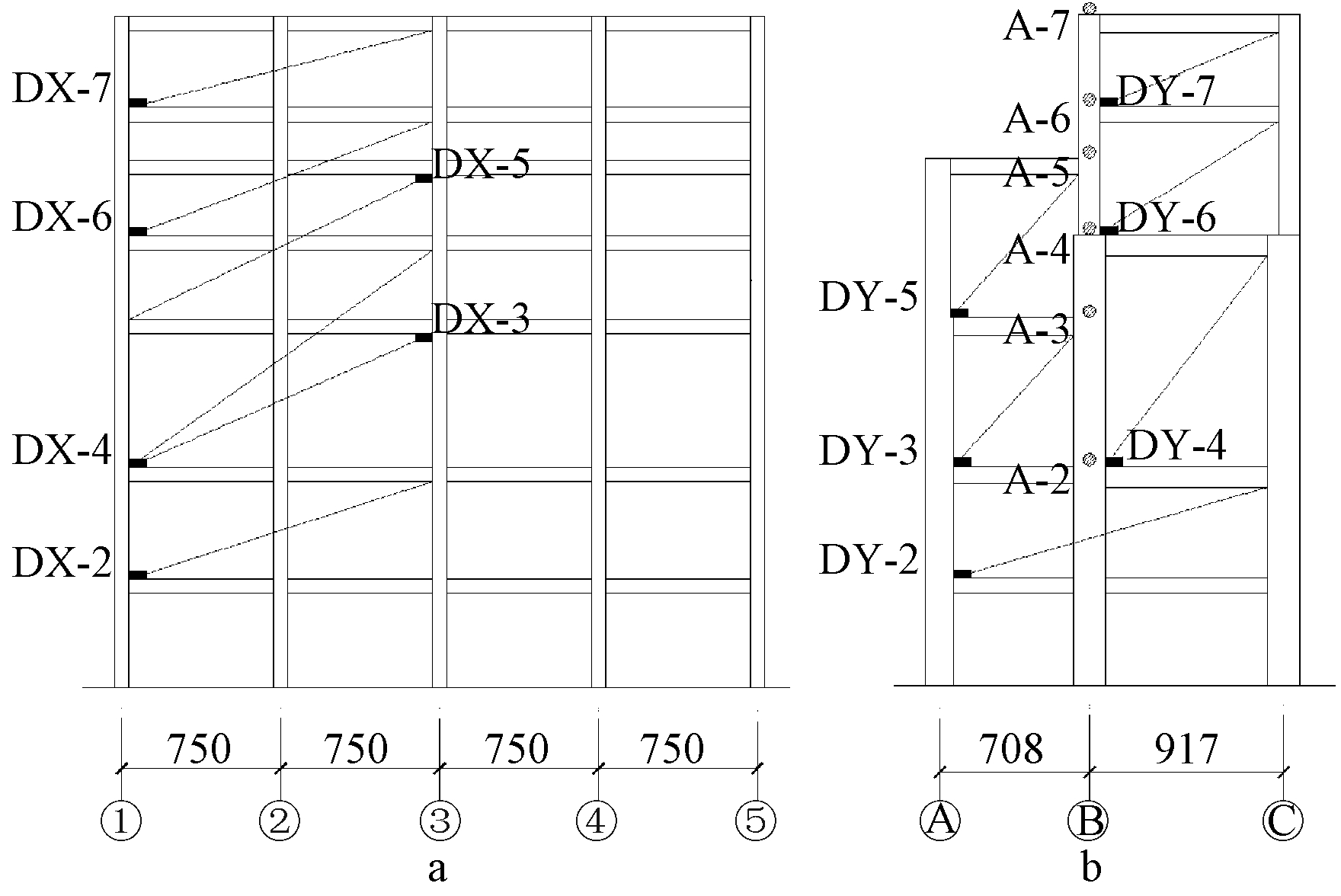
a—X向拉线位移计; b—Y向拉线位移计及双向加速度传感器。
图12 位移计和加速度传感器布置
Fig.12 Displacement meter and acceleration sensor arrangement
试验输入地震波时按表1相关比例系数调整。以验证悬吊煤斗TMD的减震效果为主要试验内容,设置了在多遇(0.07g)、设防(0.2g)以及罕遇(0.4g)地震作用下悬吊煤斗TMD结构和原结构的对比工况,其中为研究有、无阻尼对减震效果的影响,多遇地震作用下设置了有阻尼煤斗TMD、无阻尼煤斗TMD及无煤斗TMD三组对比工况,具体试验工况如表7所示。悬吊煤斗TMD结构和原结构通过悬吊或者固定煤斗质量来转换。
表7 试验工况
Table 7 Test conditions
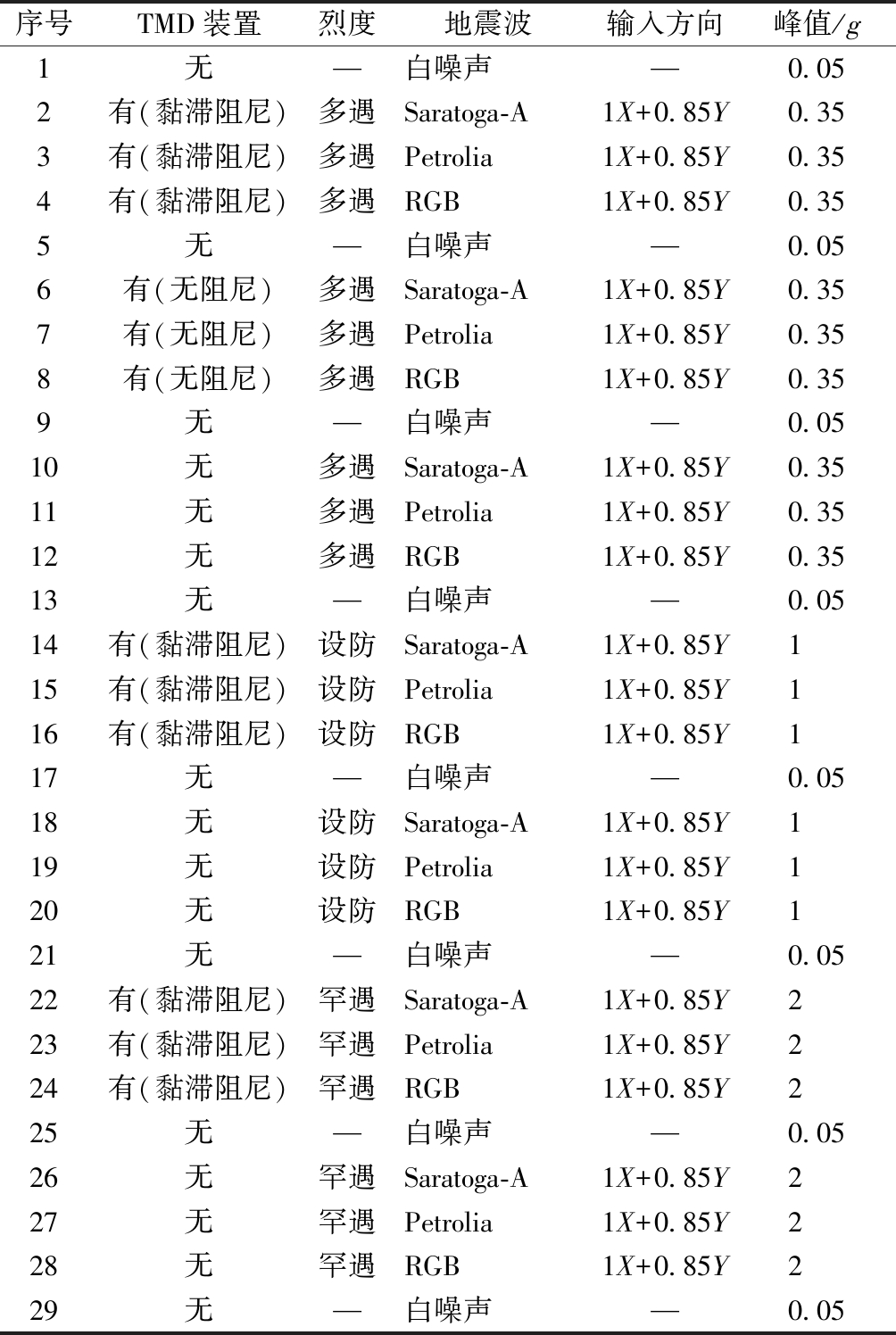
序号TMD装置烈度地震波输入方向峰值/g1无—白噪声—0.052有(黏滞阻尼)多遇Saratoga-A1X+0.85Y0.353有(黏滞阻尼)多遇Petrolia1X+0.85Y0.354有(黏滞阻尼)多遇RGB1X+0.85Y0.355无—白噪声—0.056有(无阻尼)多遇Saratoga-A1X+0.85Y0.357有(无阻尼)多遇Petrolia1X+0.85Y0.358有(无阻尼)多遇RGB1X+0.85Y0.359无—白噪声—0.0510无多遇Saratoga-A1X+0.85Y0.3511无多遇Petrolia1X+0.85Y0.3512无多遇RGB1X+0.85Y0.3513无—白噪声—0.0514有(黏滞阻尼)设防Saratoga-A1X+0.85Y115有(黏滞阻尼)设防Petrolia1X+0.85Y116有(黏滞阻尼)设防RGB1X+0.85Y117无—白噪声—0.0518无设防Saratoga-A1X+0.85Y119无设防Petrolia1X+0.85Y120无设防RGB1X+0.85Y121无—白噪声—0.0522有(黏滞阻尼)罕遇Saratoga-A1X+0.85Y223有(黏滞阻尼)罕遇Petrolia1X+0.85Y224有(黏滞阻尼)罕遇RGB1X+0.85Y225无—白噪声—0.0526无罕遇Saratoga-A1X+0.85Y227无罕遇Petrolia1X+0.85Y228无罕遇RGB1X+0.85Y229无—白噪声—0.05
4 振动台试验结果
振动台试验所测结果主要为各楼层层间位移响应值和加速度响应值,分别求得两者的峰值减震率和均方根减震率,作为悬吊煤斗TMD结构减震效果的判断依据。
4.1 悬吊煤斗运动状态
通过沿煤斗两方向布置的拉线位移计获得煤斗沿两方向的位移运动,如图13所示为两煤斗在设防烈度地震下的位移时程曲线。可以看出:煤斗在不同地震波作用下位移运动状态表现不同,但同一地震波下两个煤斗同一时刻运动方向相同,与参数优化时假定一致。
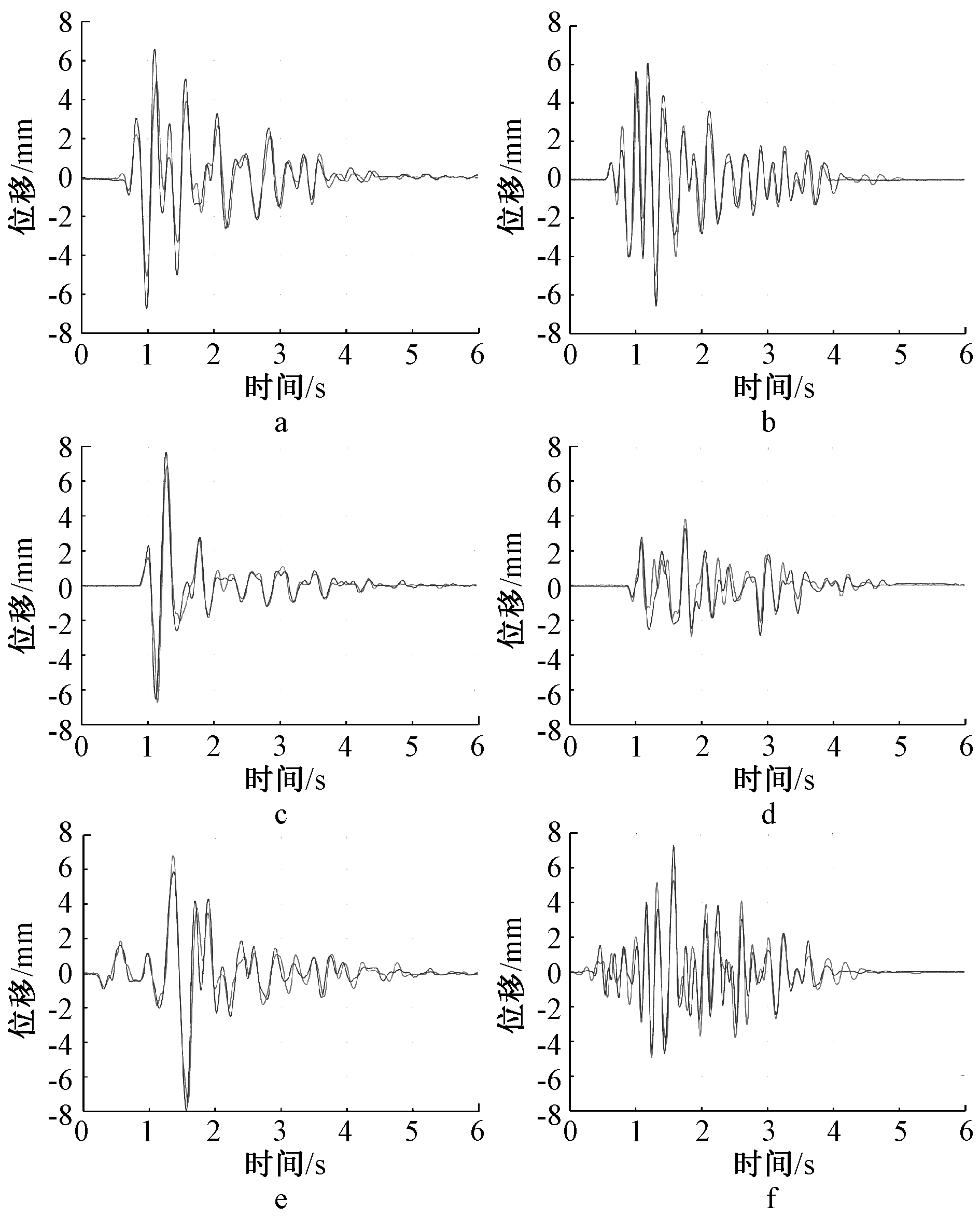
a—Saratoga-A波X向; b—Saratoga-A波Y向; c—Petrolia波X向; d—Petrolia波Y向; e—RGB波X向; f—RGB波Y向。![]() 煤斗1;
煤斗1;![]() 煤斗2。
煤斗2。
图13 两煤斗位移时程曲线
Fig.13 Displacement time-distory curves of two coal buckets
4.2 三组地震波三水准地震作用下减震效果
三水准地震作用下,3组地震波悬吊煤斗TMD结构的减震率平均值如表8所示,其中X向位移减震率如图14所示,可以得出:
1)悬吊煤斗TMD结构对不同地震波的减震效果表现出离散性。
2)悬吊煤斗TMD结构位移减震效果明显,多遇地震下Y向各层层间位移峰值减震率平均值高达26.1%,Y向均方根减震率达32%,但随着地震作用水准的增高,X、Y两方向的峰值减震率和均方根减震率都有所下降,甚至在罕遇地震3组地震波作用下Y方向的各层层间位移峰值和均方根减震率平均值出现负值,但其中RGB波各层层间位移峰值减震率平均值为16%,仍表现出较好的减震水平,X方向罕遇地震3组地震波各层层间位移峰值和均方根减震率平均值也表现较好。
3)悬吊煤斗TMD结构在多遇地震作用下对加速度有一定减震效果,X、Y向峰值减震率分别为6.0%和12.7%,随着地震作用水准的提高,X、Y两方向的加速度峰值减震率和均方根减震率都有所下降,甚至出现负控制现象,但在实际工程结构设计中往往更考虑结构层间位移的影响。
4)悬吊煤斗TMD结构显示出峰值减震率和均方根减震率在煤斗层(第四层)以上有下降的趋势,Petrolia波三水准下都较为明显。
如图15所示为悬吊煤斗TMD结构在Saratoga-A波作用下X方向结构的第3层层间位移减震效果。可以看出:悬吊煤斗TMD结构减震作用的滞后特点显著,在峰值处减震效果明显;地震作用开始时,TMD减震装置未产生相对结构的位移,未发挥减震作用,随后产生相对位移,减震作用发挥,通常相对位移幅度越大,减震装置提供的阻尼比越大,耗能能力越好。已有研究结果表明适当增大阻尼比可以提高结构减震率。
表8 三组地震波减震率均值
Table 8 Avevage value of damping rate of three groups of wave %

参数方向减震率多遇设防罕遇位移峰值X20.124.817.4Y26.18.0-11.5位移均方根X31.912.08.8Y32.08.3-4.9加速度峰值X6.0-10.6-16.9Y12.7-10.5-17.9加速度均方根X7.0-10.5-25.6Y8.6-11.4-21.2
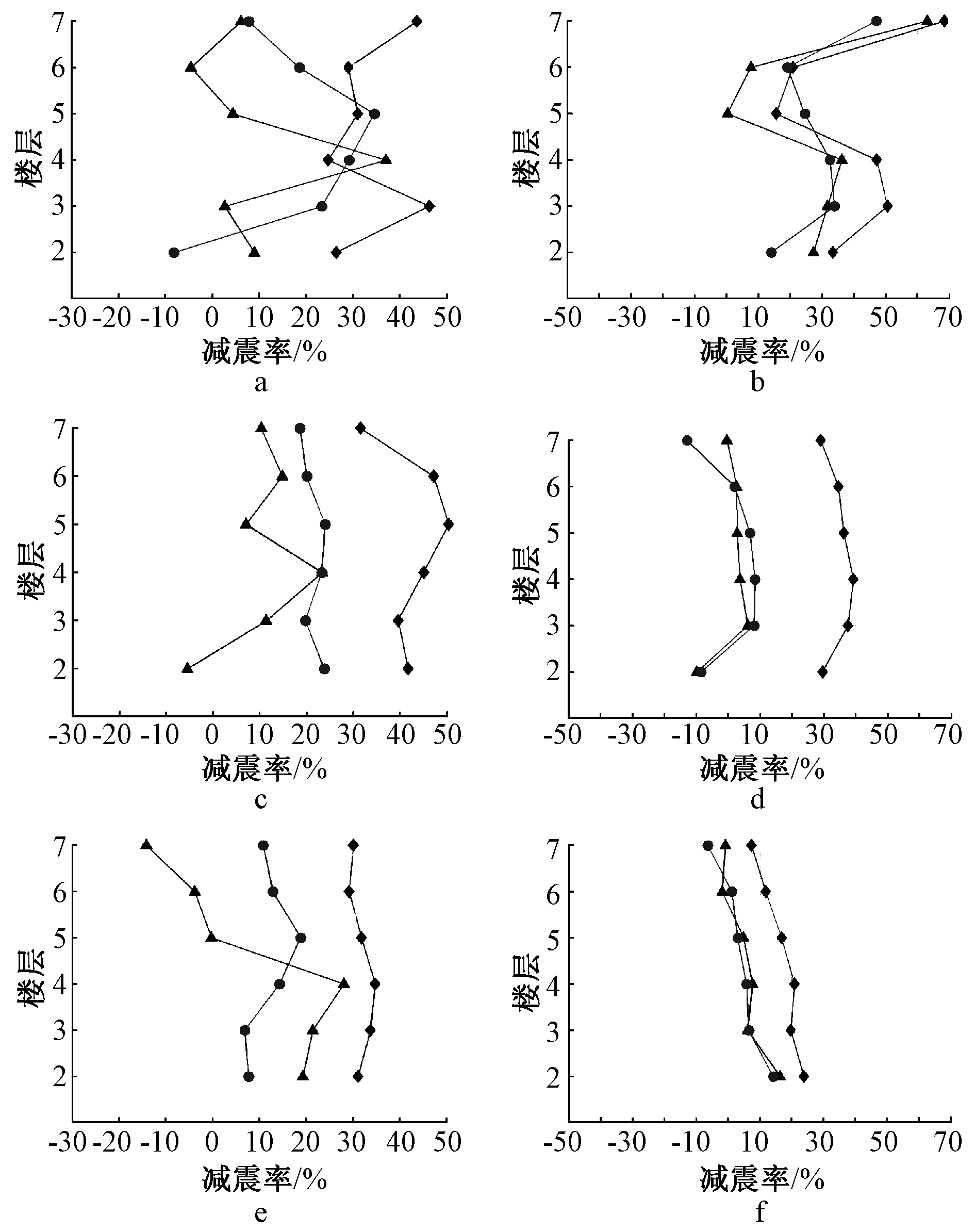
a—多遇、峰值; b—多遇、均方根; c—设防、峰值; d—设防、均方根; e—罕遇、峰值; f—罕遇、均方根。![]() —黏滞阻尼Saratoga-A波;
—黏滞阻尼Saratoga-A波; ![]() —Petrolia波;
—Petrolia波; ![]() —RGB波。
—RGB波。
图14 三组地震波X向位移减震率
Fig.14 Damping rate of X-direction displacement of three sets of waves

a—设防减震; b—罕遇减震。
——悬吊煤斗减震; ……无减震。
图15 Saratoga-A波第3层层间位移减震效果
Fig.15 Interlayer displacement damping effect of the third layer of saratoga-A
4.3 多遇地震有阻尼和无阻尼TMD结构减震
多遇地震作用下,3组地震波有阻尼和无阻尼悬吊煤斗TMD结构的位移及加速度减震率平均值如表9所示,其中两种减震结构Y向位移减震率对比如图16所示,可以得出:
表9 三组地震有无阻尼减震率
Table 9 Damped and undamped damping rate of three groups of waves
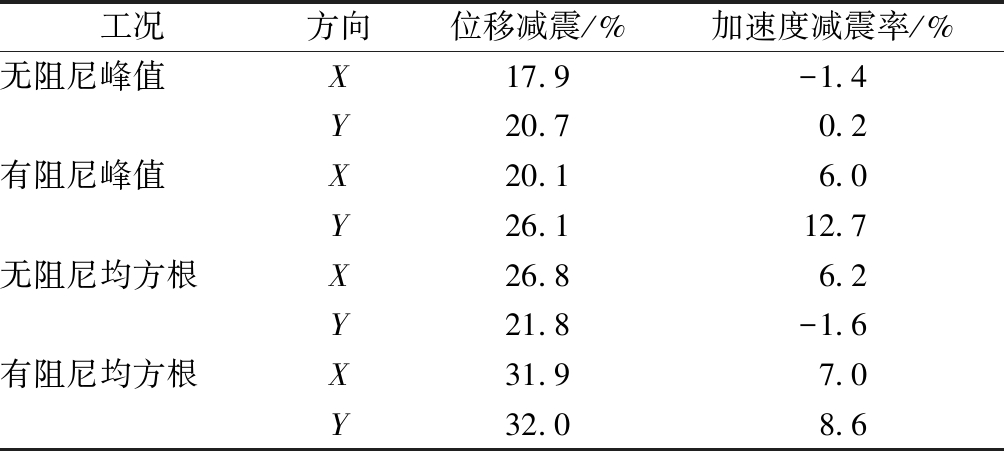
工况方向位移减震/%加速度减震率/%无阻尼峰值X17.9-1.4Y20.70.2有阻尼峰值X20.16.0Y26.112.7无阻尼均方根X26.86.2Y21.8-1.6有阻尼均方根X31.97.0Y32.08.6
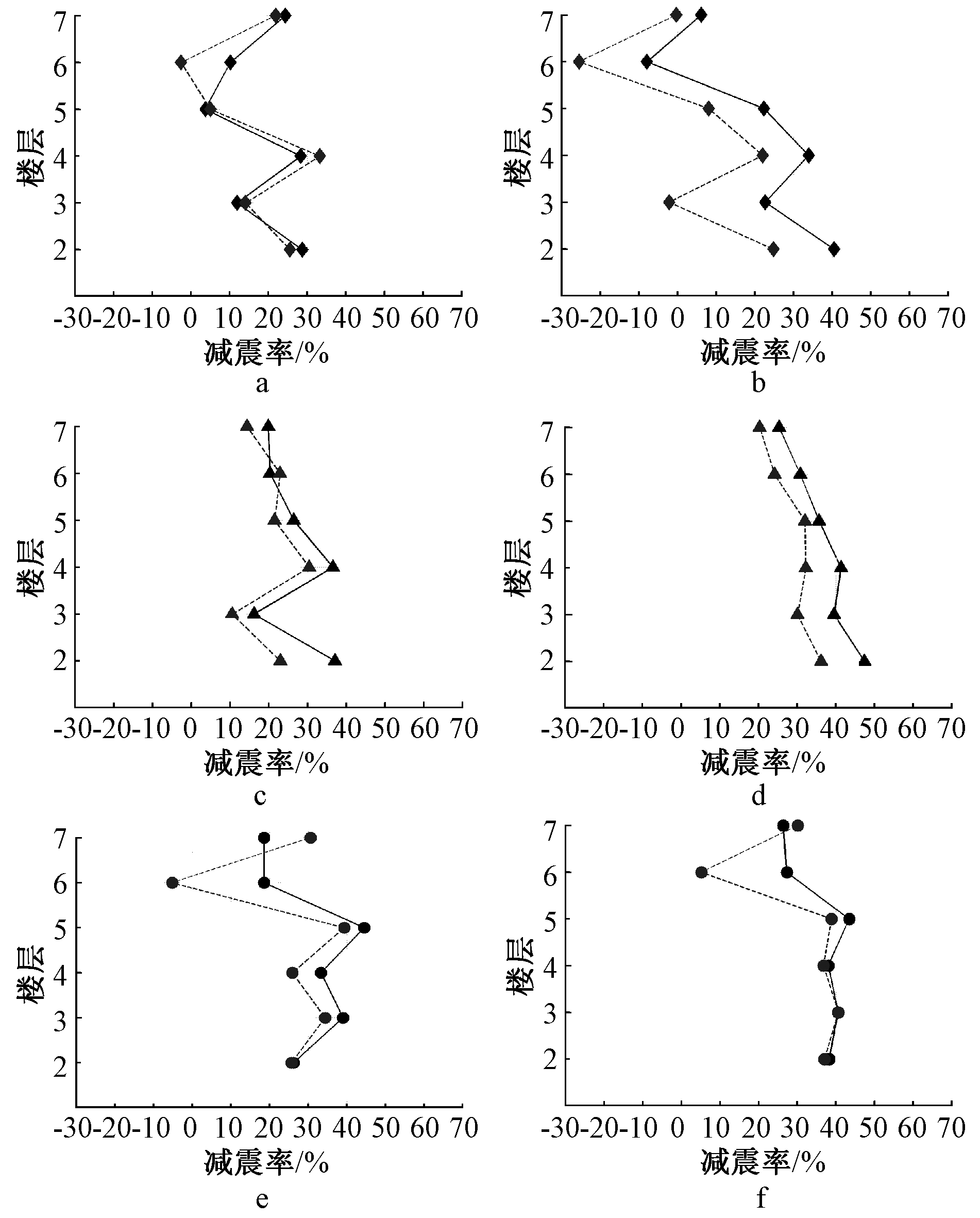
a—Saratoga-A波峰值; b—Saratoga-A波均方根; c—Petrolia波峰值; d—Petrolia波均方根; e—RGB波峰值; f—RGB波均方根。![]() —黏滞阻尼Saratoga-A波; --
—黏滞阻尼Saratoga-A波; --![]() ---无阻尼Saratoga-A波;
---无阻尼Saratoga-A波;![]() —黏滞阻尼Petrolia波; --
—黏滞阻尼Petrolia波; --![]() ----无阻尼Petrolia波;
----无阻尼Petrolia波;![]() —黏滞阻尼RGB波; --
—黏滞阻尼RGB波; --![]() ---无阻尼RGB波。
---无阻尼RGB波。
图16 Y向有无阻尼位移减震率
Fig.16 Damping rate of Y-direction damped and undamped displacement
1)有阻尼和无阻尼悬吊煤斗TMD结构都有显著位移减震效果,且有阻尼较无阻尼层间位移峰值和均方根减震率有提高,两方向位移峰值减震率平均提高19%,两方向均方根减震率平均提高33%。
2)多遇地震作用下,有阻尼悬吊煤斗TMD对结构加速度有一定控制效果,其X、Y两方向的加速度峰值和均方根的减震率明显优于无阻尼TMD结构的。
3)有阻尼悬吊煤斗TMD结构较无阻尼结构有更好的稳定性,在3组地震波三水准地震作用下,共得到的楼层位移减震率的72个结果中,仅有个别楼层出现放大现象,无阻尼结构两方向层间位移峰值和均方根的减震率分别出现7处和4处楼层放大现象,而有阻尼结构两方向层间位移峰值和均方根的减震率分别仅出现2处和1处楼层放大现象。
4)有阻尼和无阻尼悬吊煤斗TMD结构峰值减震率和均方根减震率都显示出在煤斗层(第4层)以上有下降的趋势,其中,Saratoga-A波、Petrolia波表现明显。
4.4 阻尼器荷载-位移曲线
阻尼器各工况的滞回曲线如图17所示,其中试验值曲线的位移和力值皆为振动台试验测得,理论值曲线的位移与振动台位移保持一致,力值为该位移求导测得的速度与最优阻尼系数的乘积,可以得出:
1)试验中黏滞阻尼器荷载-位移滞回曲线并非理论的椭圆形,阻尼器提供了一部分刚度,但刚度较小,对TMD减震装置频率影响较小。
2)三水准地震作用下,X方向阻尼器试验值与理论值更接近,有更好的减震效果,以设防烈度地震为例,X方向各层层间位移峰值减震率的平均值为24.8%,明显优于Y方向的8.0%。
3)随着地震水准的增加黏滞阻尼器幅值增大,阻尼力增大,滞回曲线越饱满,耗能能力增强。
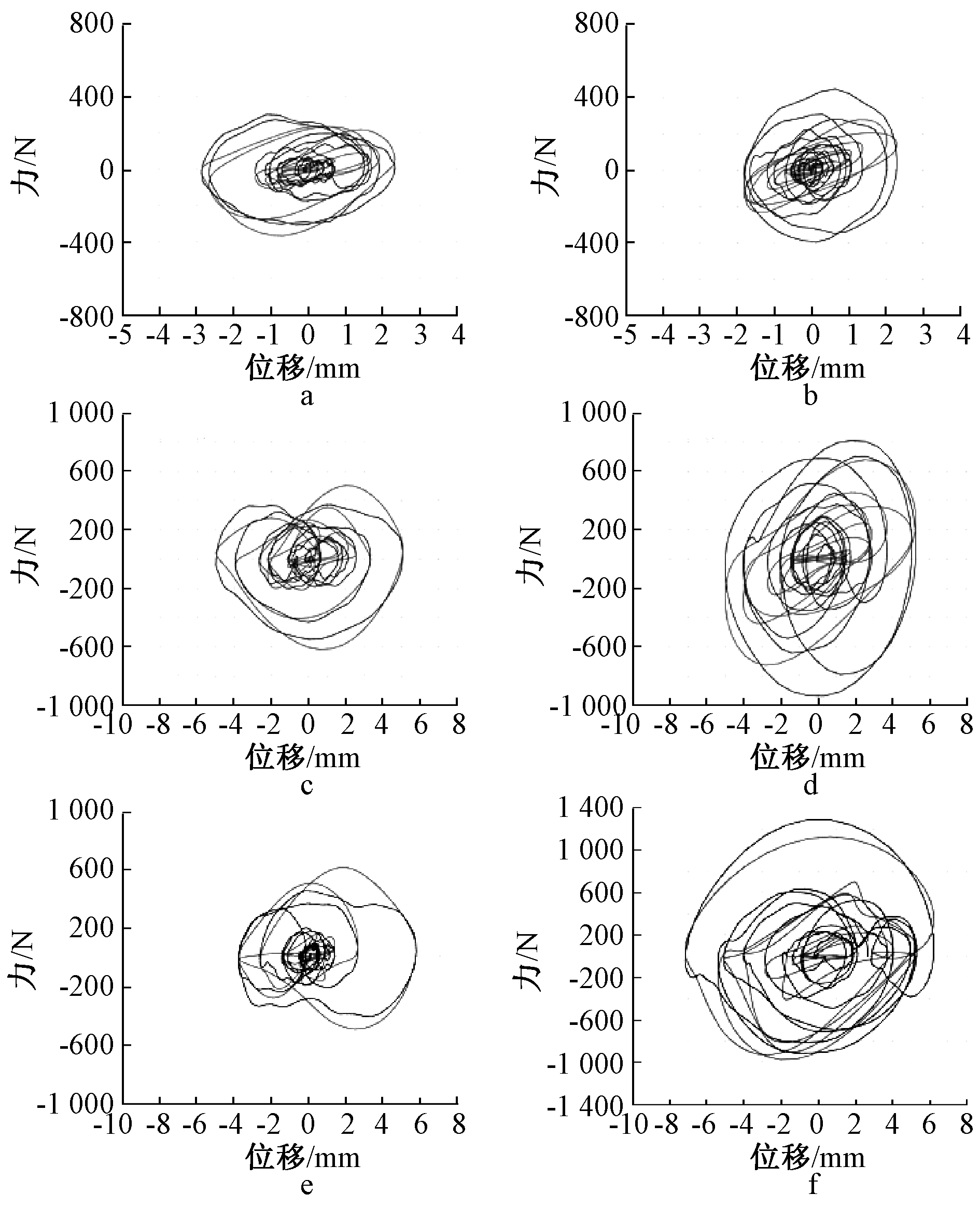
a—X向、多遇; b—Y向、多遇; c—X向、设防; d—Y向、设防; e—X向、罕遇; f—Y向、罕遇。
——试验值; ……理论值。
图17 Saratoga-A波三水准阻尼器滞回曲线
Fig.17 Hysteretic curve of Saratoga-A wave three-level damper
5 结束语
通过对悬吊煤斗TMD火电厂结构缩尺模型的有限元模拟以及振动台试验分析研究,得出如下结论:
1)地震作用下,悬吊煤斗TMD的多个煤斗同一时刻运动方向一致,TMD两方向耦合作用较小,即悬吊煤斗结构可基于TMD理论对结构的X、Y两方向分别独立地进行参数优化。
2)悬吊煤斗TMD结构对不同水准作用下结构位移控制效果显著,对多遇地震作用下加速度也有良好控制效果,且有阻尼悬吊煤斗TMD结构的位移和加速度减震效果优于无阻尼TMD结构。
[1] TANG B J, LI R, LI X Y, et al. An Optimal Production Planning Model of Coal-Fired Power Industry in China:Considering the Process of Closing Down Inefficient Units and Developing CCS Technologies[J]. Applied Energy, 2017, 206: 519-530.
[2] 吴涛,白国良,刘伯权. 大型火力发电厂钢筋混凝土框排架主厂房结构抗震性能试验研究[J].建筑结构学报,2007,28(3): 46-52.
[3] 秦丽. 结构风振与地震响应的TMD控制[D]. 北京:北京工业大学,2008.
[4] JOHN R S, RICHARD E K. Effect of Tuned-Mass Dampers on Seismic Response [J]. Journal of the Structural Division, 1983, 109(8): 2004-2009.
[5] 龙复兴, 张旭, 顾平, 等. 调频质量阻尼器系统控制结构地震反应的若干问题[J]. 地震工程与工程振动, 1996(2): 87-94.
[6] 秦丽, 李亚学, 徐福业. TMD对结构地震响应控制效果的研究[J]. 世界地震工程, 2010, 26(1): 202-206.
[7] 郑国琛, 祁皑, 阎维明. 加层减震结构振动台试验分析[J]. 地震工程与工程振动, 2007, 27(2): 164-170.
[8] 王博, 白国良, 代慧娟, 等. 火电厂主厂房型钢混凝土混合结构异型中节点抗震性能试验研究[J].建筑结构学报, 2013, 34(12): 26-34.
[9] CHEN G, WU J. Optimal Placement of Multiple Tune Mass Dampers for Seismic Structures[J]. Journal of Structural Engineering, 2001, 127(9): 1054-1062.
[10] FRANS R, ARFIADI Y. Designing Optimum Locations and Properties of MTMD Systems[J]. Procedia Engineering, 2015, 125: 892-898.
[11] SHU Z, LI S, ZHANG J, et al. Optimum Seismic Design of a Power Plant Building with Pendulum Tuned Mass Damper System by Its Heavy Suspended Buckets [J]. Engineering Structures, 2017, 136: 114-132.
[12] 廖翌棋, 高政国, 姚德康. 大型火电厂煤斗悬吊结构抗震性能研究 [J]. 建筑结构, 2008, 38(6): 30-33.
[13] 张士炼, 纪金豹, 郝晓敏, 等. 大型火电厂煤斗悬吊减震结构振动台试验研究 [J]. 电力建设, 2009, 30(8): 73-76.
[14] 何邵华,彭凌云,林娜,等.高烈度区大型火电厂混凝土主厂房支承式煤斗研究[J].武汉大学学报(工学版),2013,46(增刊1):85-89.