0 前 言
我国在建及建成的隔震建筑中,铅芯橡胶支座的应用十分广泛[1]。铅芯橡胶隔震支座具有较好的竖向抗压性能,但其受拉性能较差,当拉应力超过1 MPa时就会发生屈服从而导致刚度急剧下降[2],因此在实际工程中都尽可能地降低支座的受拉应力。在一些高层建筑或高宽比较大的基础隔震结构中,即便支座没有出现受拉破坏,支座的竖向拉压变形也会对上部结构的侧向位移机制产生较为显著的影响,变形机制见图1。
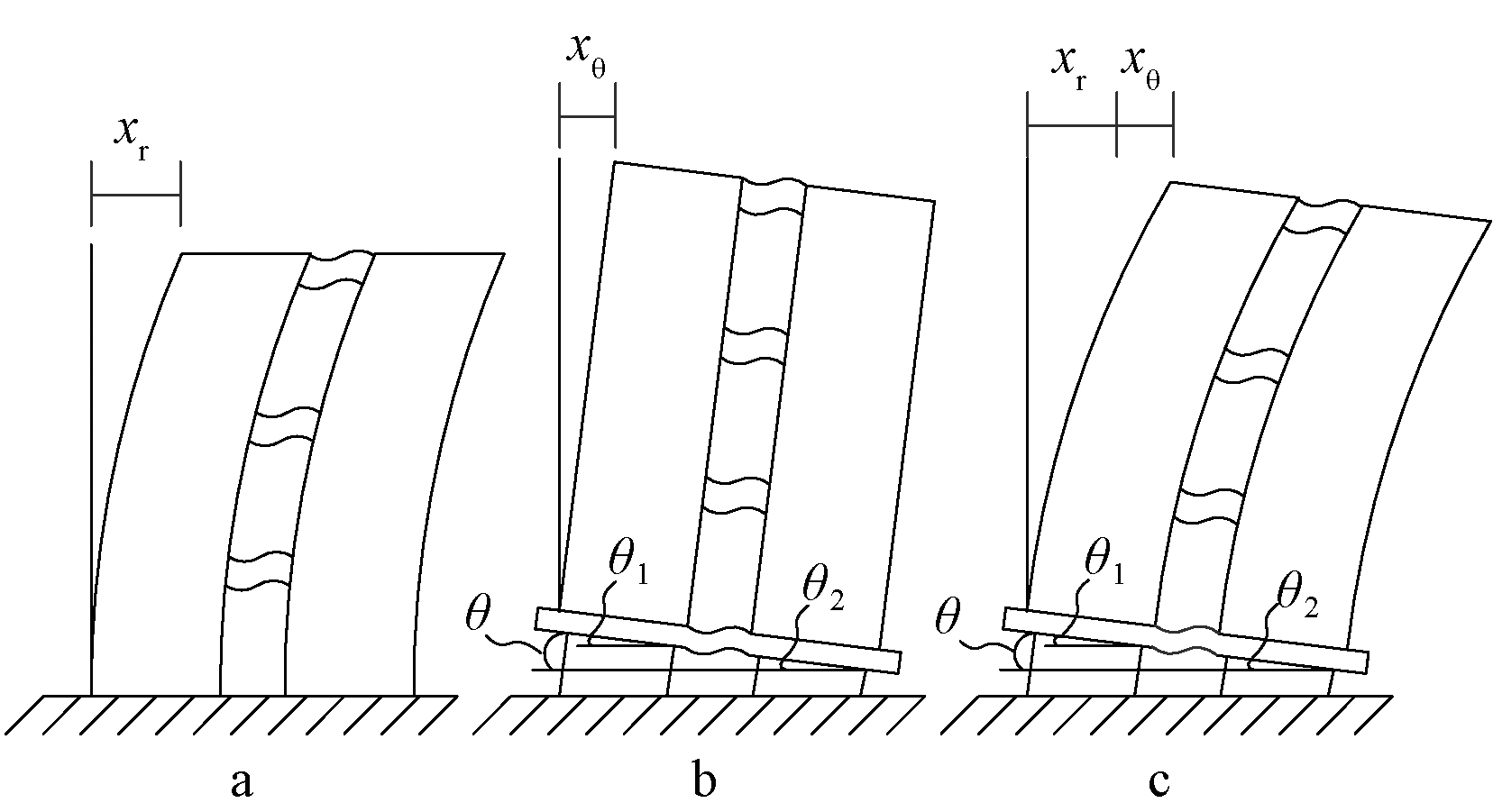
a—抗震结构变形; b—刚体转动; c—基础隔震结构变形。
图1 基础隔震结构变形示意
Fig.1 Schematic diagram of the deformation of base isolation structure
对于隔震层支座竖向变形对上部结构的响应影响,国内已有部分学者进行了相关的研究。谭平等基于Timoshenko理论,建立了隔震结构分布参数模型,通过采用虚拟激励法进行随机响应分析[3],研究表明:考虑隔震层转动对基础隔震体系结构各层转角有较大影响;随转动刚度降低,受支座摆动影响,结构转角增大;当隔震层转动刚度较小时,结构楼层转角甚至可能超过抗震结构响应。该模型的隔震层转动刚度为拉压等刚模型,与实际支座的变形模式有较为明显的差异。金建敏等建立了高宽比为4.5的高层建筑模型,通过改变拉伸刚度与压缩刚度比值,并采用与实测拉伸应力-应变曲线等效的双线性拉伸刚度模型,探讨了支座受拉后对高层隔震结构地震响应的影响[4]。但是该文中仅分析了框剪模型的地震响应,对于受隔震层转动影响较大的剪力墙结构没有做相应的研究。
本文对基础隔震联肢剪力墙结构进行深入分析研究。采用有限元分析软件ABAQUS建立基础隔震联肢剪力墙模型,重点研究在不同轴压比及不同高宽比情况下,通过改变隔震支座拉压刚度比,研究隔震层转动对上部结构抗侧刚度的影响。
1 有限元模型建立
1.1 模型建立
为选取一个合理的联肢剪力墙模型,选择文献[5]中HRCW-1试件尺寸及配筋情况建立抗震模型,并通过与文献[5]中的试验结果进行对比,验证有限元的合理性与可靠性。
整体模型采用1/4缩尺,转换梁截面尺寸为0.35 m×0.35 m,隔震支墩尺寸为0.4 m×0.4 m×0.4 m。在此基础上建立25个双肢剪力墙基础隔震有限元模型与5个抗震对比模型,隔震支座拉、压刚度比取值参考文献[6-7],模型基本参数见表1。
表1 模型基本参数
Table 1 Parameters of models

模型编号混凝土强度等级剪力墙高宽比轴压比隔震支座拉压刚度比K1C601.3(3层)0.1抗震K2C601.30.2抗震K3C601.30.3抗震K4C602.0(6层)0.2抗震K5C602.7(9层)0.2抗震G1C601.30.11/10G2C601.30.11/15G3C601.30.11/30G4C601.30.11/50G5C601.30.11/100G6~G10G11~G15G16~G20G21~G25C60C60C60C601.30.2 同G1~G51.30.3 同G1~G52.00.2 同G1~G52.70.2 同G1~G5
混凝土采用实体单元8结点6面体缩减积分单元(C38DR),既可以保证分析精度,又可以防止产生剪力自锁导致分析失败。钢筋采用线性三维桁架单元(T3D2)。隔震支座采用Connector单元定义连接属性。
1.2 本构关系
混凝土本构模型采用ABAQUS提供的混凝土损伤塑性模型(CDP)[8],本文CDP模型采用的混凝土应力-应变关系为GB 50010—2010《混凝土结构设计规范》[9]附录C中列出的混凝土单轴拉压本构关系。混凝土损伤参数由Lematire提出的损伤演化方程计算[10-11]所得。混凝土强度等级C60,弹性模量为36 GPa,泊松比为0.2。
采用von Mises屈服条件及相关的流动法则即可较为准确地描述钢筋的本构关系。本文采用文献[12]中建议的钢筋本构模型。该模型基于Légeron等的模型[13],加载路径上合理考虑了钢筋的Bauschinger效应,可以较好地反映钢筋单调加载时的屈服、硬化和软化现象。
隔震支座采用双线性模型。隔震结构分析通过对橡胶支座的屈服刚度和屈服力进行修正,得出其双线性模型[14]。其性能参数如表2所示,双线性模型本构如图4所示。
表2 隔震支座性能参数
Table 2 Parameters of isolation bearing

刚度/(kN·mm-1)竖向受压100%等效水平100%屈服前100%屈服后屈服力/kN橡胶剪切模量/MPa1 6629602.420.62430.4
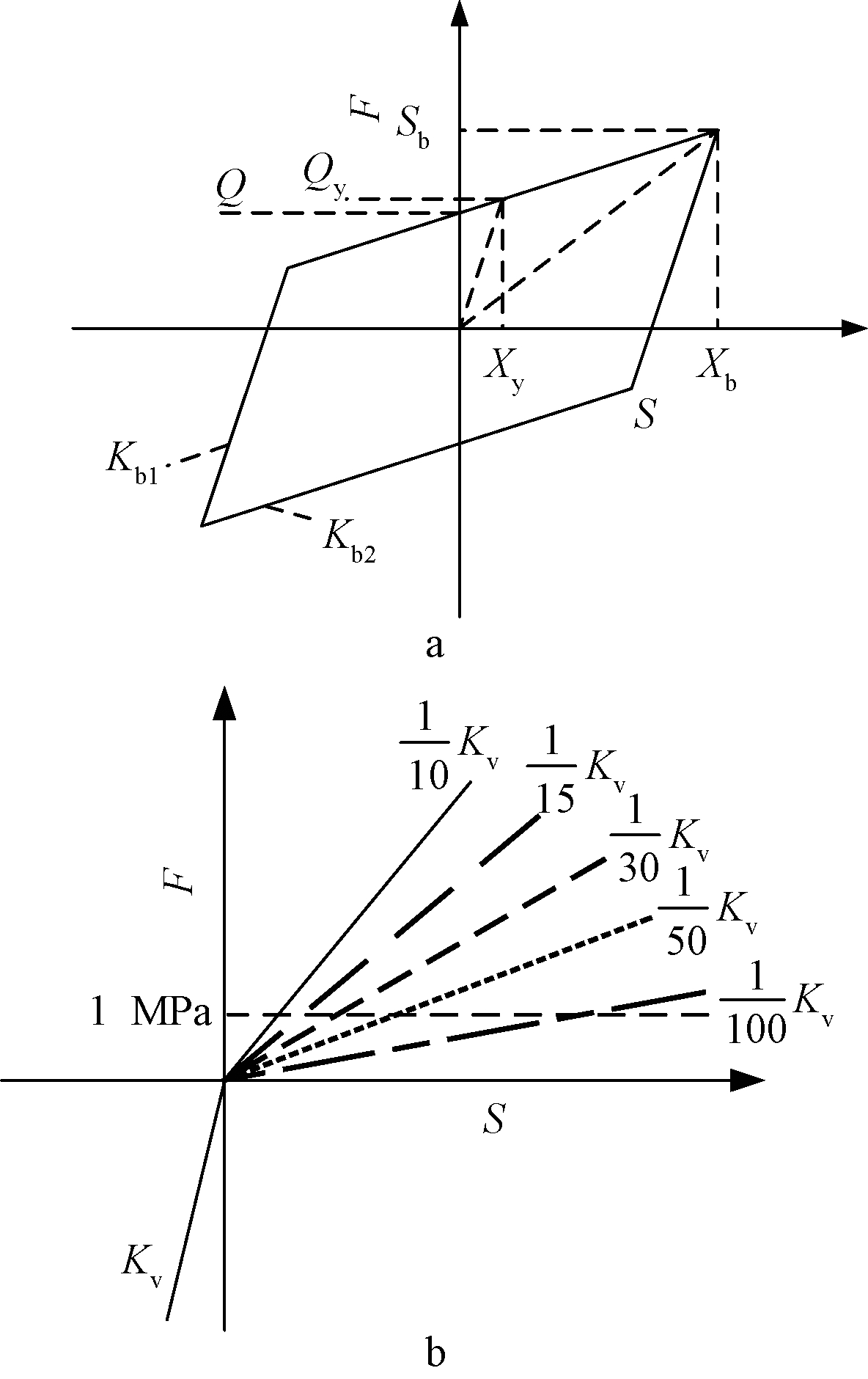
a—水平恢复力模型; b—竖向恢复力模型。
注:Sb为峰值点水平力;Q为截距;Qy为屈服力;Xy为屈服位移;Xb为峰值点位移;Kb1为屈服前刚度;Kb2为屈服后刚度;Kv为竖向受压刚度;1 MPa指GB 50011—2010《建筑抗震设计规范》中规定:隔震层橡胶支座最大拉应力不应大于1 MPa。
图4 隔震支座恢复力模型
Fig.4 Restoring force model of isolation bearing
1.3 加载方式
采用Push-over分析方法,如图5所示。首先施加重力荷载,其次在加载梁顶面施加轴力,然后在加载梁端部采用位移控制,从左至右进行水平推覆,直至试件破坏、无法继续加载或荷载下降至最大荷载的85% 左右为止。
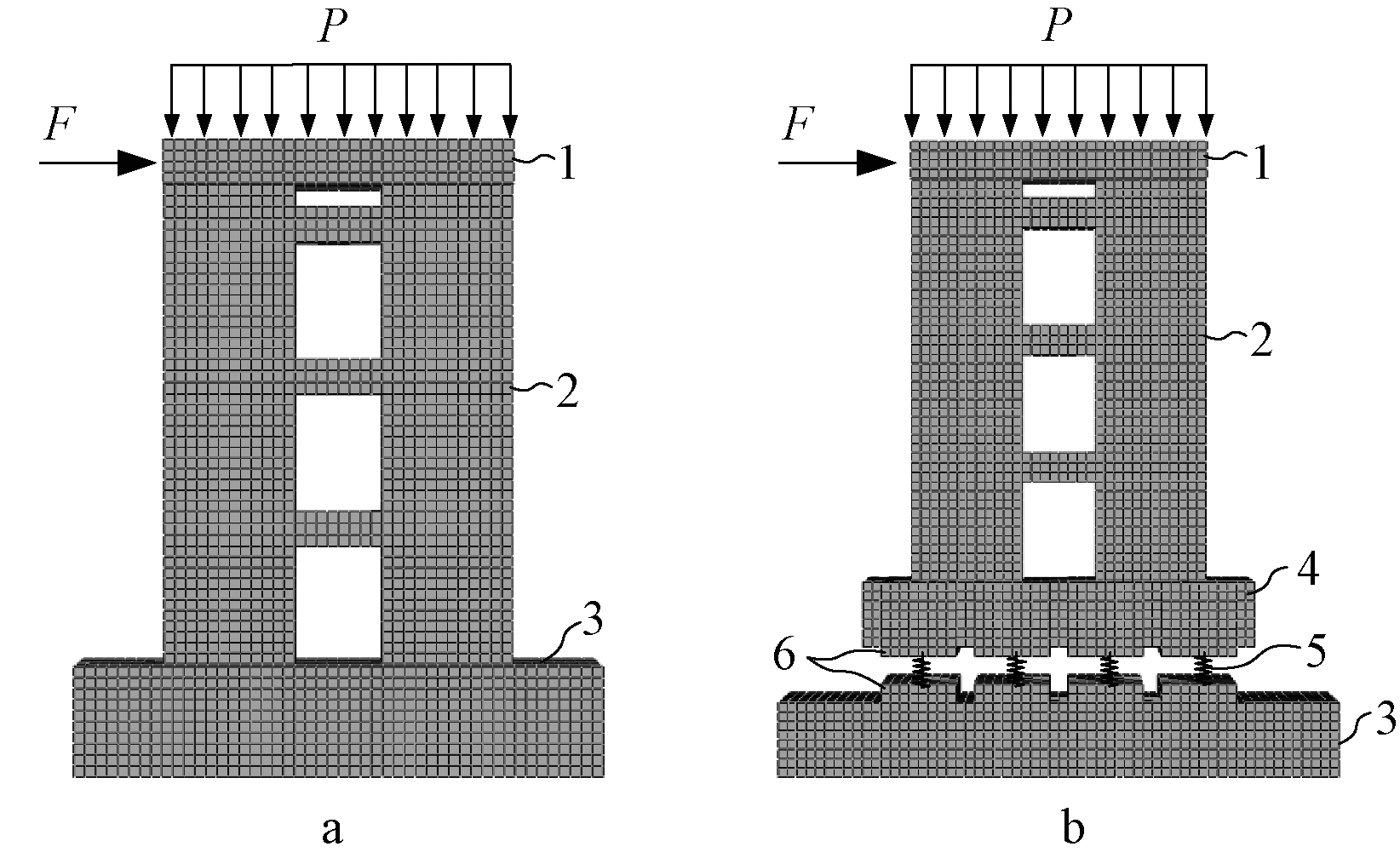
a—抗震模型; b—隔震模型。
1—加载梁; 2—双肢剪力墙墙体; 3—地梁;4—转换梁; 5—隔震支座; 6—隔震支墩。
图5 ABAQUS有限元模型
Fig.5 Finite element model of ABAQUS
1.4 模型验证
首先按验证模型分析得到的数据绘出骨架曲线,并将其与文献[5]中试验骨架曲线进行对比。图6为骨架曲线对比结果,可以看出,有限元分析模型曲线与试验骨架曲线能够较好地吻合。特别是初始弹性阶段吻合度较高,随着试件的开裂,有限元分析曲线与试验曲线出现了小幅度偏差。有限元分析模型峰值荷载与试验峰值荷载相比较小。当位移加载大于峰值荷载对应位移值之后,有限元分析曲线刚度下降明显小于试验曲线值。其原因在于有限元分析模型考虑混凝土为理想均质材料,而实际试验所用混凝土为非均质材料,试件内部存在一定的缺陷,并且有限元分析模型中忽略了混凝土与钢筋之间的黏结滑移。图7为试件HRCW-1验证模型中混凝土与钢筋峰值点应力云图。图中1、2、3层连梁端部纵筋屈服出现塑性铰,墙肢出现剪切斜裂缝,墙肢底部受拉纵筋屈服形成塑性铰,墙肢受压区混凝土压碎。故有限元分析模型的破坏形态与试件HRCW-1的能够较好吻合。从整体看,有限元分析曲线与试验曲线吻合较好,峰值荷载与峰值位移较为接近,总体走向趋势一致,破坏过程与破坏形态一致,验证了有限元模型的合理性与可靠性。
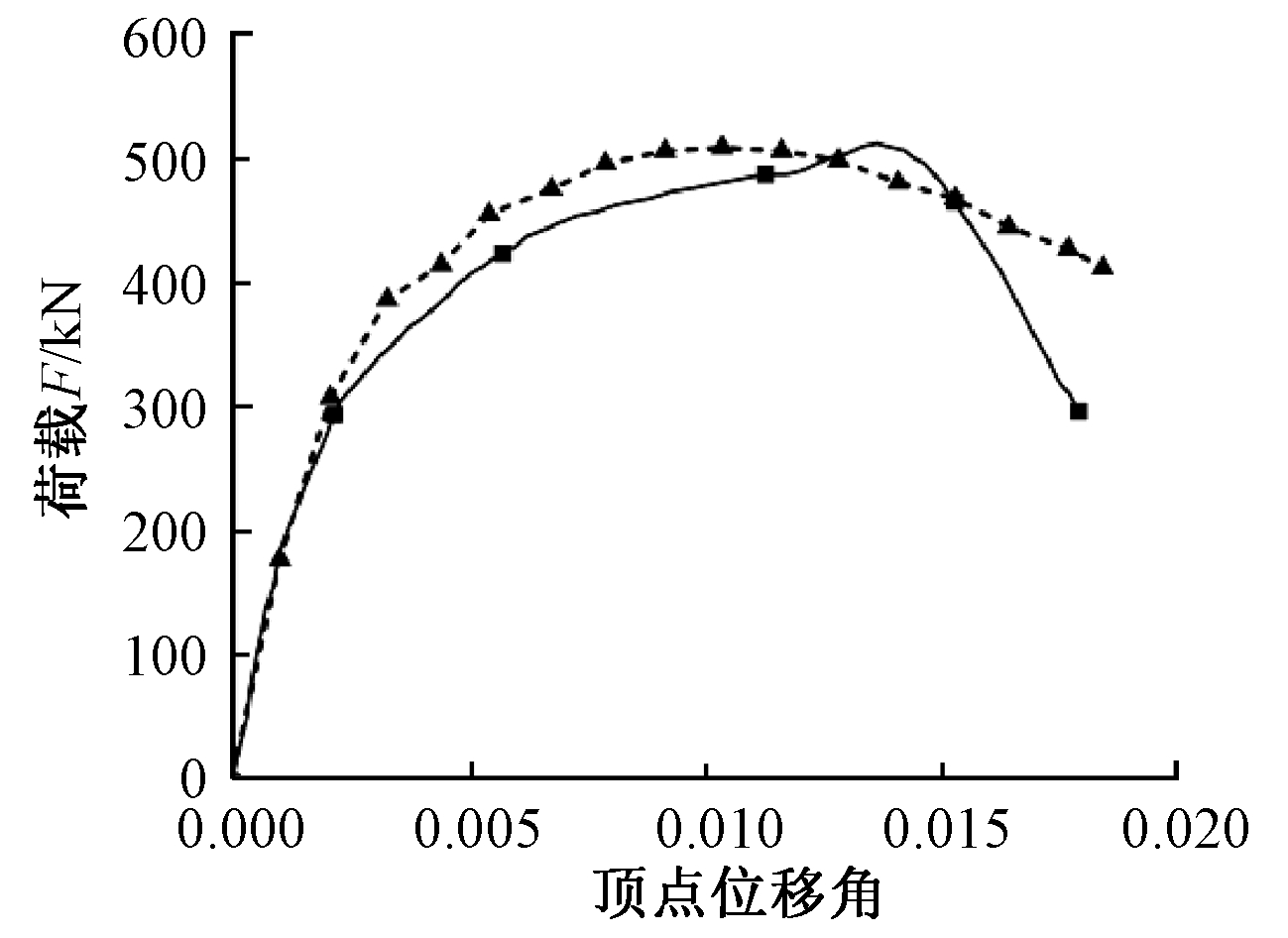
![]() —试验曲线;
—试验曲线; ![]() …有限元分析曲线。
…有限元分析曲线。
图6 有限元分析曲线与试验曲线对比
Fig.6 Comparison between simulation and test result
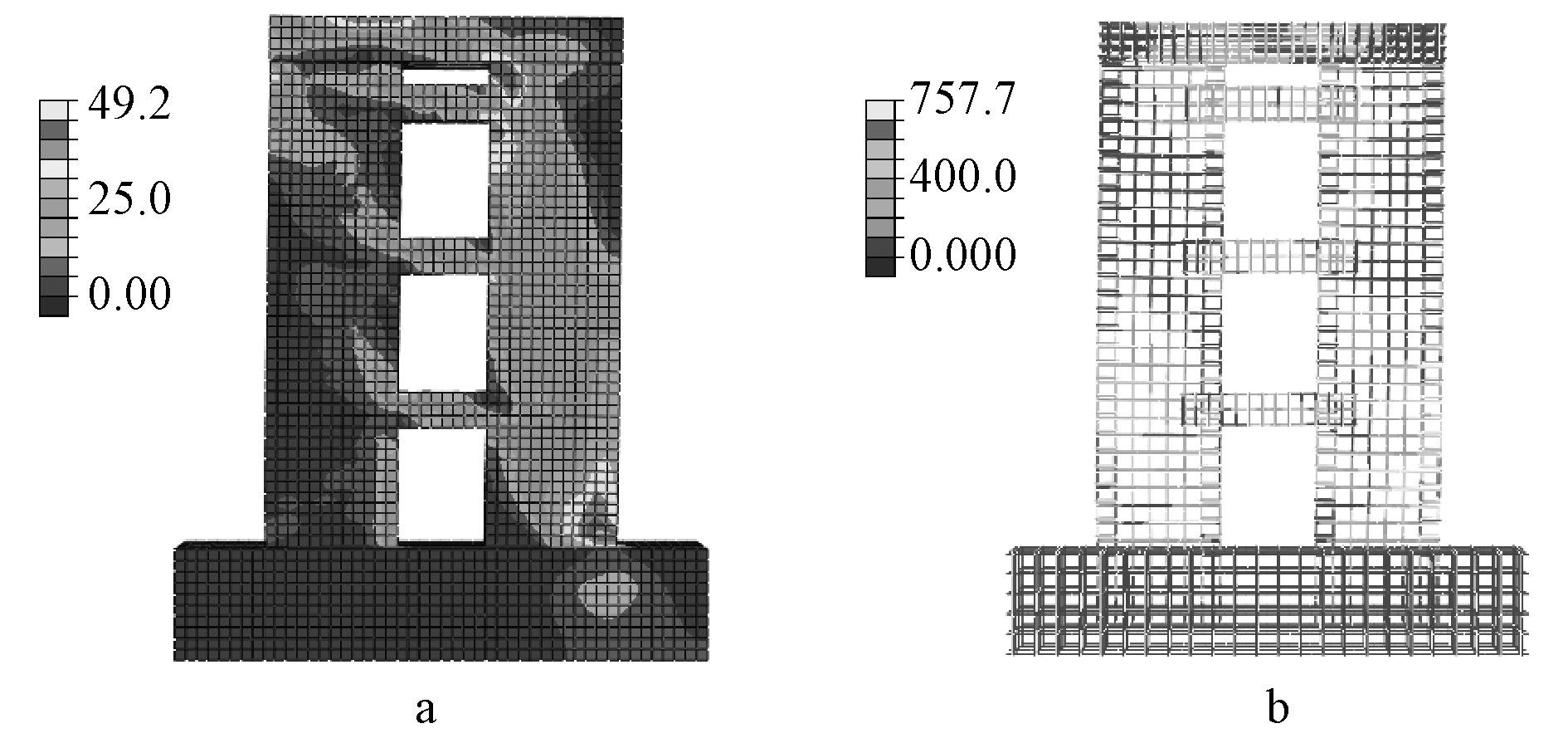
a—混凝土应力; b—钢筋骨架应力。
图7 峰值点应力云图 MPa
Fig.7 Stress nephogram of peak point
2 不同轴压比模型分析
2.1 骨架曲线
图8为模型K1~K3、G1~G15荷载-顶点位移角骨架曲线。可以看出:轴压比为0.1、0.2、0.3的三种情况下,抗震模型初始弹性刚度均大于相应隔震模型;抗震模型的极限承载力与隔震模型的大致相同,抗震模型极限位移均小于相应隔震模型的;相同轴压比时,随着隔震支座拉压刚度比由1/10降低至1/100,隔震模型的峰值位移有增大的趋势。
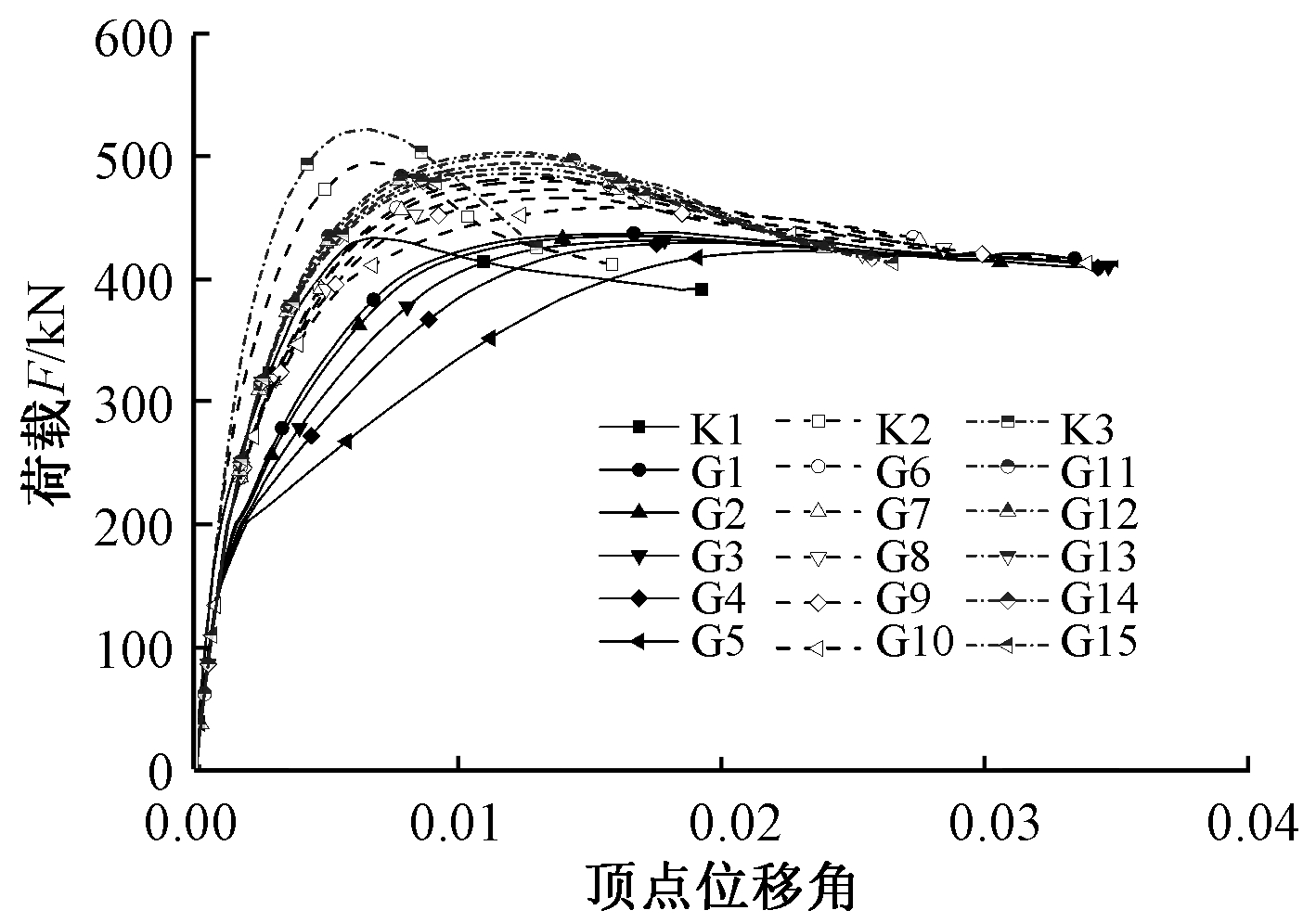
图8 不同轴压比模型的骨架曲线对比
Fig.8 Comparison of skeleton curves of specimens under different axial compression ratios
2.2 转 角
图9为模型K1~K3、G1~G15的转角对比。图中,θ1为左墙肢转角,取左墙肢下两隔震支座高度差值计算所得;θ2为右墙肢转角,取右墙肢下两隔震支座高度差值计算所得;θ为上部结构整体转角,取两端隔震支座高度差值计算所得(转角标志见图1)。由图9可以看出:上部结构整体转角θ值低于(θ1+θ2)/2,高于θ2;隔震支座拉压刚度比不变时,随着轴压比增大,其上部结构整体转角减小,说明轴压比的增大可以有效抑制上部结构的转动程度;轴压比不变时,隔震支座拉压刚度比越低,其整体转角越大。
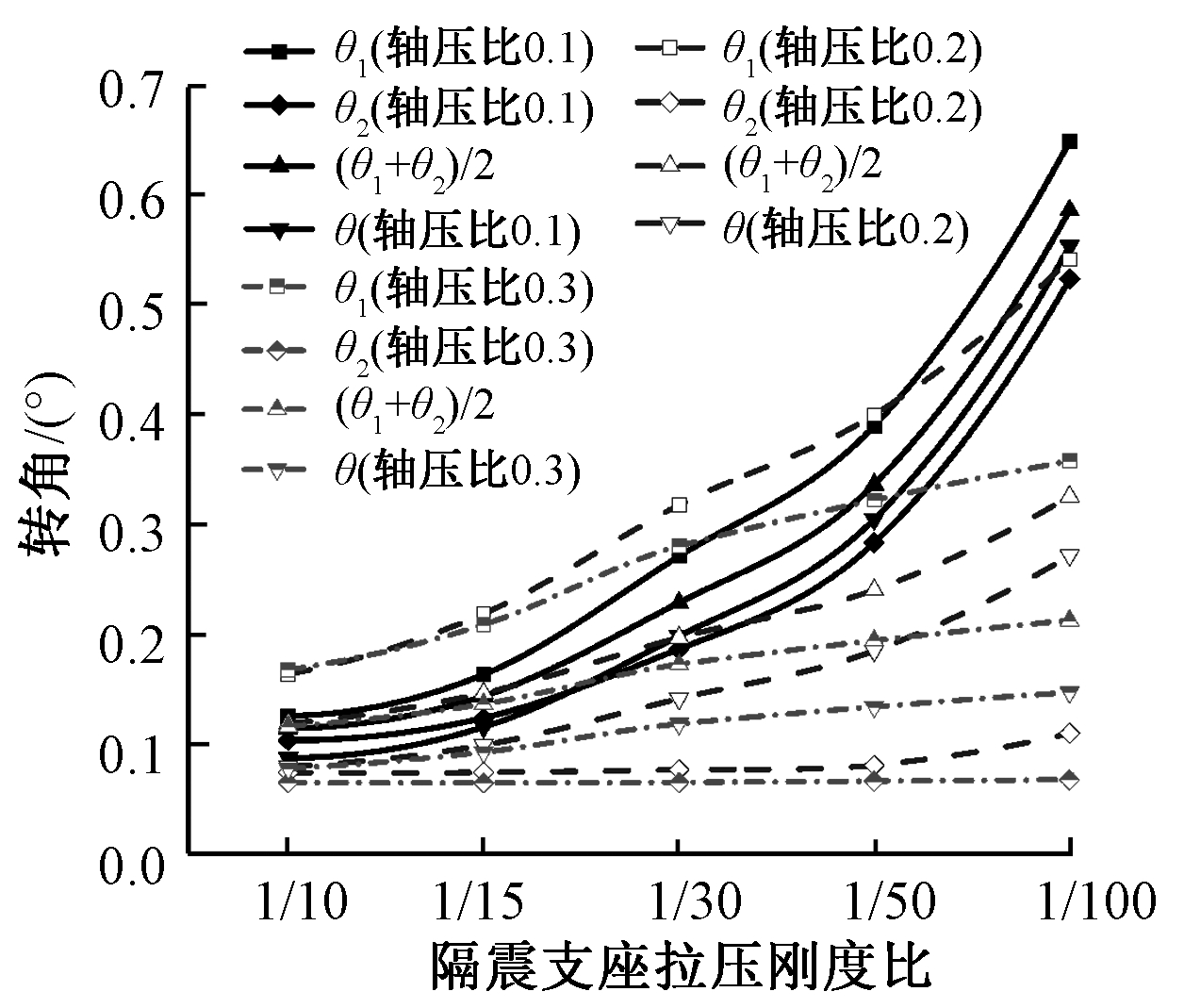
图9 不同轴压比模型的转角对比
Fig.9 Comparison of rotation comparison of specimens under different axial compression ratios
2.3 位移占比
图10中纵轴模型K1~K3、G1~G15中隔震支座竖向变形所引起上部结构刚体转动产生的水平位移占上部结构总水平位移的比值,其中转动位移按上部结构整体转角θ计算所得。可知:当轴压比为0.1时,G1~G5模型初始转动引起的水平位移占比为20.34%;轴压比为0.2时,G6~G10初始转动所引起的水平位移占比为17.94%;轴压比为0.3时,G11~G15初始转动所引起的水平位移占比为15.63%。即:轴压比越大,初始转动位移占比越小;隔震支座拉压刚度比对初始转动位移占比影响不大,随着顶点位移角的增大,减小隔震支座拉压刚度比会减小结构隔震层的转动刚度[15],导致其上部结构发生刚体转动的程度增大,所以转动位移所占总水平位移的比例增大。
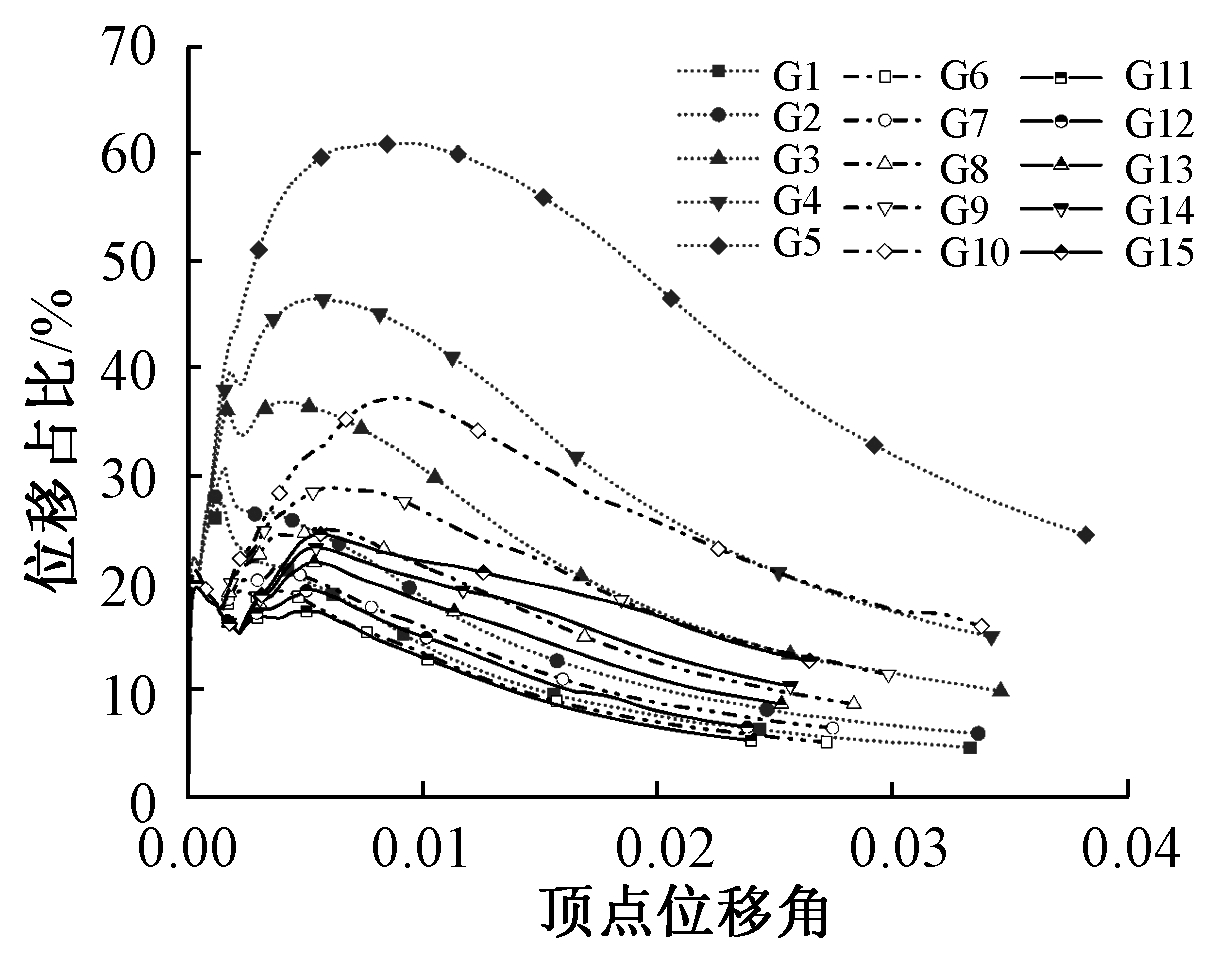
图10 不同轴压比模型刚体转动位移占比
Fig.10 Proportion of rigid body rotation displacement of models under different axial compression ratios
2.4 相对刚度比
图11a为模型K1~K3、G1~G15的屈服点与峰值点相对刚度比。其中,屈服刚度取屈服点切线刚度,峰值刚度取峰值点割线刚度;相对刚度比指隔震模型刚度与相应抗震模型刚度比值。由图11a可知:轴压比为0.1时,隔震支座拉压刚度比由1/10逐渐降低至1/100时,其屈服点与峰值点相对刚度比逐渐降低;轴压比增大至0.2时,隔震支座拉压刚度比值对上部结构水平刚度影响减小,其屈服点与峰值点相对刚度比下降缓慢;轴压比为0.3时,减小隔震支座拉压刚度比对其屈服点与峰值点相对刚度比值无明显影响。这是由于轴压比增大,隔震支座更不易出现受拉状态,其竖向变形相对较小,可以有效抑制上部结构的转动程度,隔震模型上部结构水平刚度越接近于抗震模型,故其相对刚度比值越大。
图11b为模型G1~G15最左侧隔震支座受拉应力为1 MPa时相对刚度比。可知:当轴压比一定,隔震支座拉压刚度由1/10降低至1/30,其受拉应力达到1 MPa时的相对刚度比值越低;而拉压刚度比为1/50、1/100时,过低的拉压刚度比会低估支座拉应力[4],从而导致最左侧支座拉应力未达到1 MPa;隔震支座拉压刚度比分别为1/10、1/15与1/30不变时,轴压比越大,其受拉应力达到1 MPa时相对刚度比越低;抗震模型取其对应的隔震模型最左侧隔震支座受拉应力达到1 MPa时相同荷载条件时刻为参照点。当轴压比为0.3、隔震支座拉压刚度比为1/50与1/100时,由于其最左侧隔震支座拉应力未达到1 MPa,图中数据取拉应力为0.881 MPa与0.596 MPa时相对刚度比值。
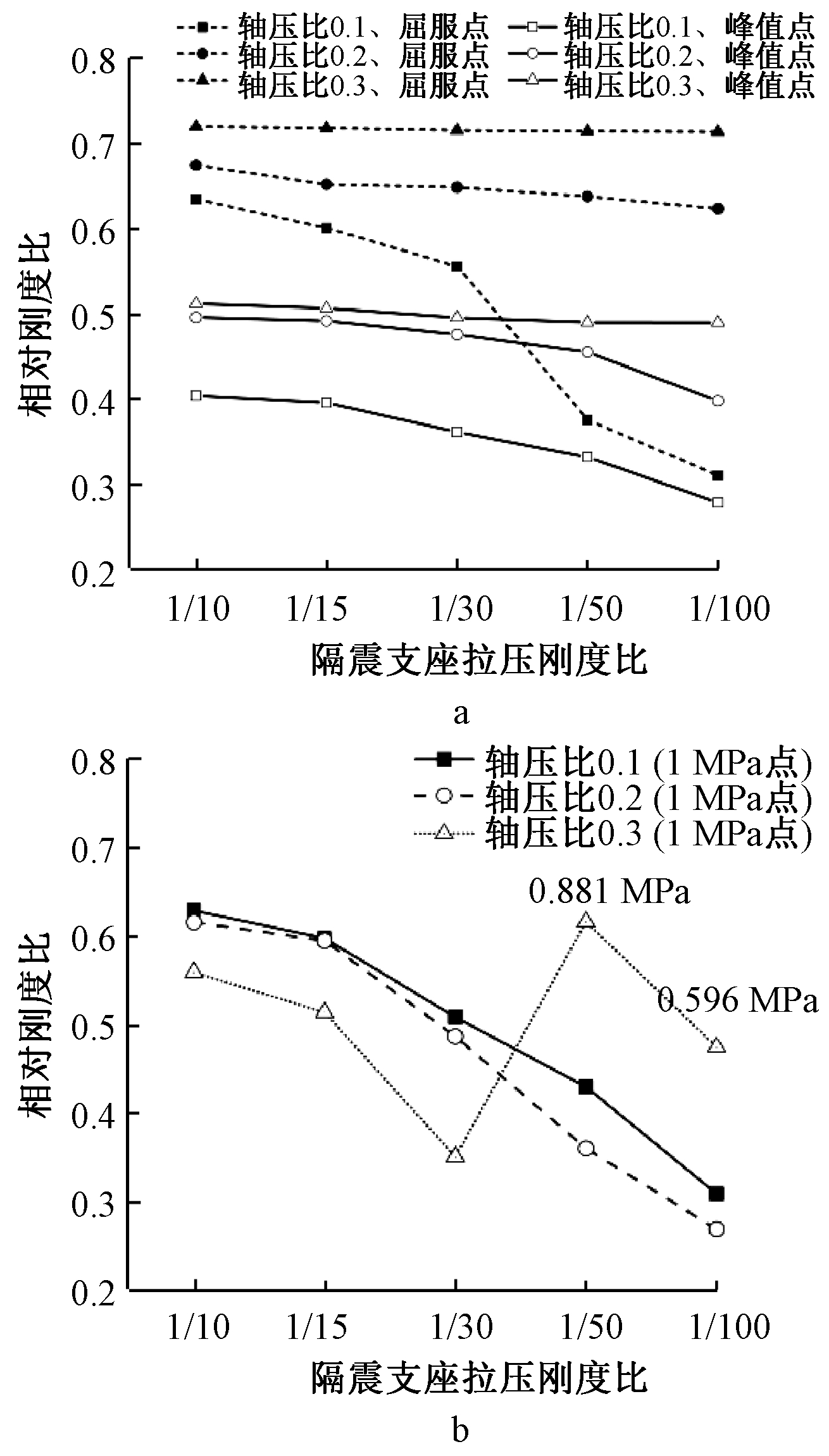
a—屈服点与峰值点; b—受拉应力为1 MPa。
图11 不同轴压比模型的相对刚度比值
Fig.11 Relative stiffness ratios of models under different axial compression ratios
3 不同高宽比模型分析
3.1 骨架曲线
图12为模型K2、K4、K5、G6~G10、G16~G25的骨架曲线。随着高宽比增大,其抗震与隔震模型的初始弹性刚度、屈服刚度、屈服位移、峰值刚度、峰值位移与峰值荷载均逐渐降低。
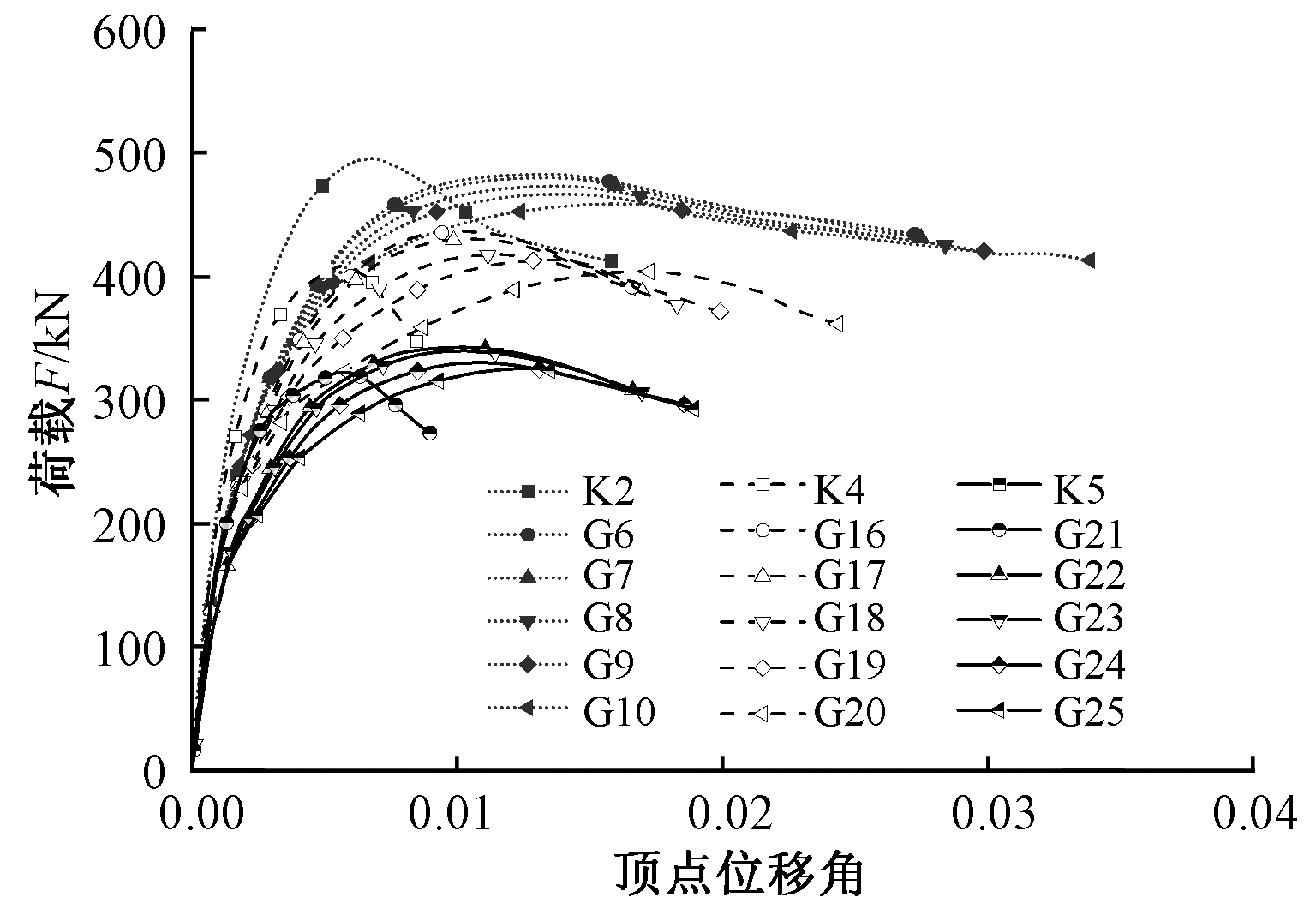
图12 不同高宽比模型的骨架曲线
Fig.12 Skeleton curves of models with different height-width ratios
3.2 转 角
图13为模型K2、K4、K5、G16~G25的转角对比。可以看出:高宽比为1.3时,模型整体转角θ低于 (θ1+θ2)/2,高于θ2;当高宽比增大至2.0时,其整体转角θ与 (θ1+θ2)/2无明显差异;当高宽比增大至2.7时,其整体转角θ大于 (θ1+θ2)/2,小于θ1。
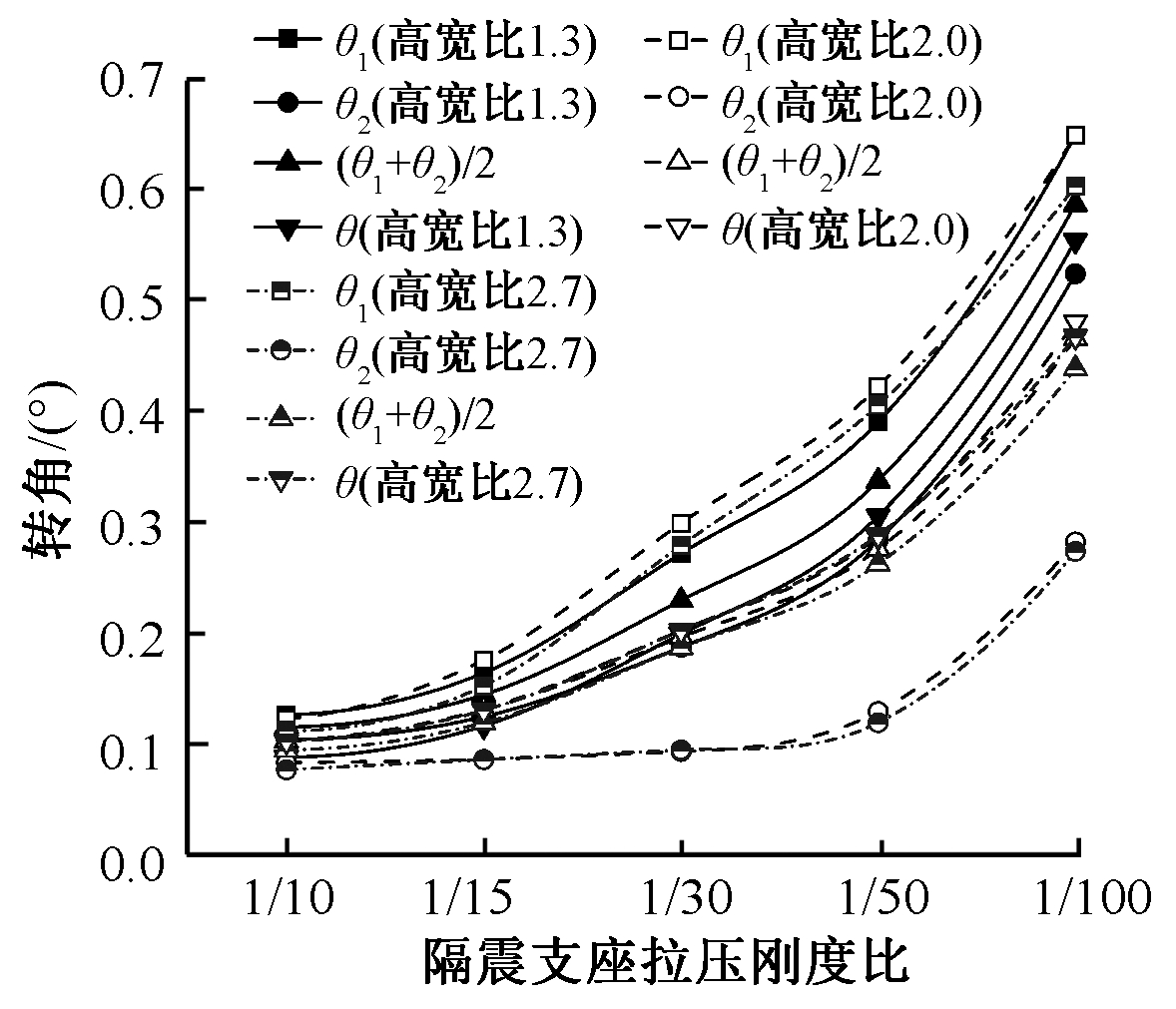
图13 不同高宽比模型的转角对比
Fig.13 Rotation comparison of models with different height-width ratios
3.3 位移占比
图14为模型K2、K3、K4、G16~G25的位移占比。可知:当高宽比由1.3增大至2.0时,转动位移占比明显增大;当高宽比由2.0增大至2.7时,转动位移占比增长幅度减小,即大高宽比结构,其整体刚度相对于柔软的隔震层刚度要大得多[15],上部结构整体反应近似刚体运动;随着高宽比的增大,结构质心越高,其隔震模型上部结构更易发生转动,结构由水平平动转为平摆耦合运动,继而向摇摆运动转变[4];但当高宽比超过一定范围时,增大高宽比对其转动程度的影响将减小。
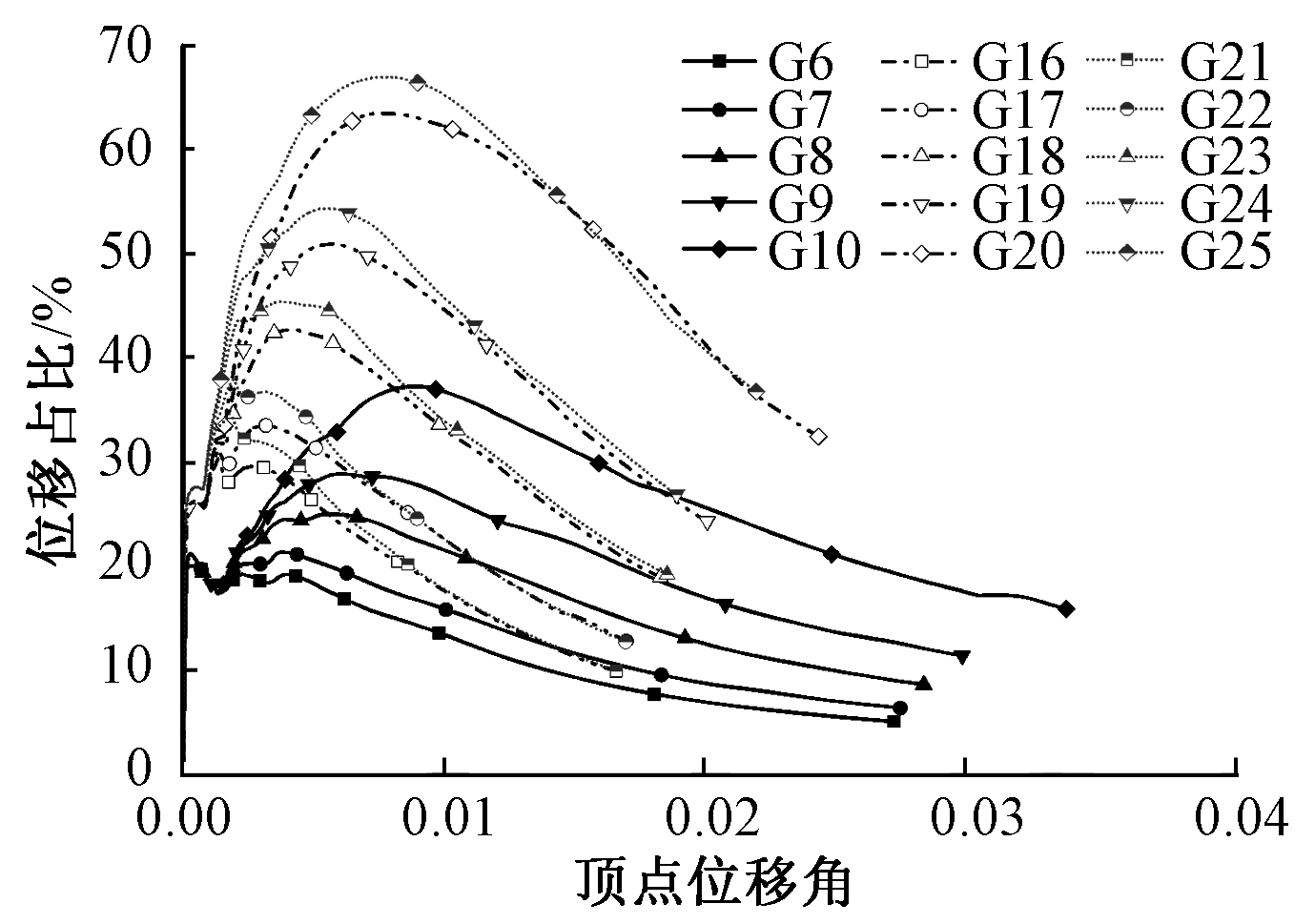
图14 不同高宽比模型的刚体转动位移占比
Fig.14 Proportion of rigid body rotation displacement of models with different height-width ratios
3.4 相对刚度比
图15a为模型K2、K4、K5、G16~G25的屈服点与峰值点相对刚度比。可知:随着隔震支座拉压刚度比逐渐降低,高宽比1.3的模型其屈服点与峰值点相对刚度降低缓慢,高宽比2.0与2.7的模型其屈服点与峰值点相对刚度比降低幅值较大;隔震支座拉压刚度比降低至1/15后,高宽比1.3的模型屈服点相对刚度比大于高宽比为2.0与2.7的模型;隔震支座拉压刚度比降低至1/50后,高宽比1.3的模型峰值点相对刚度比大于高宽比为2.0与2.7的模型。
图15b为模型K2、K4、K5、G16~G25的1 MPa点相对刚度比。可知:当高宽比一定时,随着支座拉压刚度的减小,其1 MPa点相对刚度比逐渐减小;当隔震支座拉压刚度比不变,高宽比由1.3增大至2.0时,其1 MPa点相对刚度比显著增大;当高宽比由2.0增大至2.7时,其1 MPa点相对刚度比小幅降低。

a—屈服点与峰值点; b—1 MPa点。
图15 不同高宽比模型的相对刚度比
Fig.15 Relative stiffness ratios of models with height-width ratios
4 结束语
通过建立ABAQUS有限元抗震和基础隔震双肢剪力墙模型,分析在竖向轴力和水平位移推覆加载作用下的相对刚度比,得到以下结论:
1)在隔震结构设计中应充分考虑隔震支座竖向变形引起隔震层与上部结构转动对其抗震性能的影响。
2)当轴压比与高宽比不变时,减小隔震支座拉压刚度比会减小结构隔震层的转动刚度,导致其上部结构发生刚体转动的程度增大,转动位移所占总水平位移的比例增大,其相对刚度比值越低。
3)当支座拉压刚度比、高宽比不变,轴压比增大时,隔震支座更不易出现受拉状态,其竖向变形相对较小,可以有效抑制上部结构的转动程度,其转动位移所占总水平位移的比例减小,隔震模型上部结构水平刚度越接近于抗震模型,故其相对刚度比值越大。
4)大高宽比结构,其整体刚度相对于柔软的隔震层刚度要大得多,上部结构整体反应近似刚体运动。随着高宽比的增大,结构质心越高,其隔震模型上部结构更易发生转动,结构由水平平动转为平摆耦合运动,继而向摇摆运动转变。但当高宽比超过一定范围时,增大高宽比对其转动程度的影响将减小。
5)选取θ作为上部结构刚体转动角度的方法较为简单,但不能反映其真实上部结构的转动情况。由于连梁以及转换梁的作用,上部结构的刚体转动角度介于θ1、θ2之间,且不能与墙体底部完全嵌固的情况等效。本文对该问题没有详细讨论,有待于进一步研究。
[1] ZHOU F L, TAN P, HEISHA W, et al. Earthquake M7.0 on 2013.4.12 and Recent Development on Seismic Isolation, Energy Dissipation & Structural Control in China [C]//The 13th World Conference on Seismic Isolation & JSSI 20th Anniversary International Symposium. Sendai, Japan: The Japan Society of Seismic Isolation, 2013.
[2] URYU M, NISHIKAWA T. Study on Stiffness, Deformation and Ultimate Characteristics of Base-Isolated Rubber Bearings: Horizontal and Vertical Characteristics Under Shear Deformation [J]. Journal of Structural and Construction Engineering, 1996, 479: 119-128.
[3] 谭平, 宋晓, 周福霖. 考虑SSI效应及支座转动的隔震体系性能研究[J]. 土木工程学报, 2016, 49(增刊1): 78-83.
[4] 金建敏, 冯德民, 谭平, 等. 隔震支座拉伸刚度及高层隔震建筑地震响应研究[J]. 地震工程与工程振动, 2015, 35(3): 177-182.
[5] 于敬海, 丁永君, 谢剑, 等. 高强钢筋高强混凝土双肢剪力墙抗震性能试验[J]. 天津大学学报, 2017, 50(2): 181-187.
[6] 罗佳润, 马玉宏, 沈朝勇, 等. 隔震设计中橡胶隔震支座拉压刚度取值的研究[J]. 地震工程与工程振动, 2013, 33(5): 232-240.
[7] 日本建筑学会. 隔震结构设计[M]. 北京: 地震出版社, 2006.
[8] 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M].北京: 机械工业出版社, 2006.
[9] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S]. 北京:中国建筑工业出版社, 2010.
[10] LEMAITRE J. A Continuous Damage Mechanics Model for Ductile Fracture[J]. Journal of Engineering Materials and Technology, 1985, 107: 83-89.
[11] 方自虎, 周海俊, 赖少颖, 等. ABAQUS混凝土损伤参数计算方法[J].建筑结构, 2014, 44(1): 719-721.
[12] 汪训流, 陆新征, 叶列平. 往复荷载下钢筋混凝土柱受力性能的数值模拟[J]. 工程力学, 2007, 24(12): 76-81.
[13] LÉGERON F, PAULTRE P, MAZAR J. Damage Mechanics Modeling of Nonlinear Seismic Behavior of Concrete Structures[J]. Journal of Structural Engineering, 2005, 131(6): 946-954.
[14] 濑户裕, 竹中康雄. 修正双线性模型表现隔震装置两方向非线性模型的延伸[C]//日本建筑学会学术讲演梗概集 (B-2). 东京 : 日本建筑学会, 1996:805-806.
[15] 马健. 大高宽比高层剪力墙隔震结构抗倾覆性能研究[D].昆明:昆明理工大学,2017.