在工厂对各模块进行预制并运输现场装配的工业化装配式钢结构具有施工快速、绿色环保、造价节省的优点。作为世界第一大产钢国,我国钢产量占世界的50%以上,但钢结构建筑仅占我国新建建筑的5%,而西方发达国家已达到50%以上。缺乏与钢结构主体相配套的“三板体系”(楼板、墙板、屋面板)是阻碍我国工业化装配式钢结构住宅推广的重要因素。目前,各种样式的楼板相继出现并不断发展,但满足建筑产业化、工业化的楼盖体系仍很缺乏[1-5]。
楼板作为“三板体系”之一,是结构的重要组成部分,能够传递竖向荷载和水平荷载,与梁柱连接共同承受外力和地震作用。国内外钢结构楼板发展经历了由现浇到预制、由重质到轻质的过程。目前工程实际应用中的楼板主要包括以下几种形式:现浇整体混凝土楼板、预制装配式钢筋混凝土楼板、压型钢板-混凝土组合楼板、混凝土叠合楼板等[6-7]。现浇整体混凝土楼板在现场与周围楼板整体浇筑形成,具有施工工艺简单、整体性和抗震性能良好的优点,但是现场工作量大,施工工期长,大量的湿作业造成环境污染[8-9]。预制装配式钢筋混凝土楼板在工厂绑扎钢筋、支模浇筑,能够缩短工期、节约成本,但是预制板与周边梁柱的连接不牢固,容易造成结构整体性差及抗震性能下降[10-11]。压型钢板-混凝土组合楼板现场施工时无需支模,方便施工,能够缩短工期,但是成本高,且楼板底部镀锌表面影响美观[12-13]。混凝土叠合楼板首先在工厂完成预制板的加工,再将其运输至现场后完成叠合层的浇筑,叠合楼板既具有现浇板整体性好和抗震性能好的优点,又具有预制板施工快速的优点[14-15]。
张季超等进行了装配整体式叠合楼板足尺加载试验研究[16],研究结果表明:该叠合连续板除具有单向叠合连续板的内力重分布特征外,还具有一定的双向板受力特性。聂建国等研究了不同叠合面对叠合楼板抗剪性能的影响[17],试验结果表明:对于无抗剪钢筋的混凝土叠合板,叠合面仍有足够的抗剪强度。武立伟等进行了4组预制叠合空心楼板静力性能试验[18],研究结果表明:叠合楼板在加载过程中并未出现沿叠合面的水平裂缝,挠度和裂缝宽度均满足规范限值。颜峰等对带接缝的混凝土叠合楼板进行了足尺试验[19],研究结果表明:该叠合板具有良好的受力性能并且拼缝处没有发生破坏。
目前对叠合楼板的研究着重于承载力,缺乏对短期刚度的研究。结合实际装配施工以及叠合楼板的特点,本文对一种高度可调节的装配式钢筋桁架叠合楼板进行了受力性能试验研究。对2块三角钢筋桁架叠合楼板的施工阶段进行模拟。施工阶段考虑楼板的吊装、现浇层的浇筑、人员施工的影响,测量钢筋的累计应变和挠度。通过对2块楼板使用阶段的静力性能进行试验研究,探明板底裂缝分布、钢筋应变及荷载大小与挠度的变化规律。
1 装配方式
高度可调节的装配式混凝土叠合楼板由带孔的角钢、L形丝杆、螺母、三角钢筋桁架叠合楼板组成。角钢和L形丝杆在工厂预制。三角钢筋桁架叠合楼板预制层在工厂完成加工,并在预制层上相应位置预留与角钢孔洞相同的圆孔,方便丝杆穿插。预制楼板通过两端外伸的钢筋桁架固定搭载在两侧的支座上,楼板安装如图1所示。在支座处相应位置放置混凝土预制块,将角钢开孔的一侧紧贴预制板,在孔洞处穿插L形丝杆,丝杆竖杆方向通过螺母固定,横杆方向固定搭载在混凝土预制块上,丝杆和角钢安装如图2所示。角钢与墙体之间放置软海绵条或其他填充物,防止由于墙体不平整进而导致浇筑混凝土时发生漏浆现象。在预制板的四角处架立水准尺,通过调节丝杆下部的螺母松紧调整楼板的平整度和高度。最后浇筑现浇层混凝土至丝杆横杆下边缘,养护完成后,拆除角钢并拔出丝杆。

a—楼板一侧连接; b—楼板另一侧连接。
图1 楼板安装
Fig.1 Floor installation

a—丝杆和角钢的构造; b—丝杆和角钢与楼板的连接。
图2 丝杆和角钢安装
Fig.2 Installation of screw and angle steel
2 试件设计及材性试验
2.1 试件设计
设计的高度可调节的装配式钢筋桁架叠合楼板,采用三角钢筋桁架的形式,1根上弦钢筋对应2根下弦钢筋,斜腹杆钢筋与上下弦钢筋焊接形成三角钢筋桁架。在上弦钢筋的上层和下弦钢筋的下层布置横向分布筋形成空间整体,钢筋等级为HRB400。考虑到材料性能、施工、养护等过程中的随机影响因素,设计制作2块相同的楼板试件SJ-B1和SJ-B2,并对其进行试验,第一阶段模拟预制板施工阶段的过程,第二阶段浇筑现浇层混凝土,待其达到设计强度后进行使用阶段的加载试验。所设计的楼板跨度为2 850 mm,宽度为1 270 mm,预制层厚度为60 mm,现浇层厚度为60 mm,混凝土强度等级为C30。试件尺寸及编号如表1所示。构件详图见图3。
表1 试件参数
Table 1 Specimen parameters mm
试件编号上弦钢筋直径下弦钢筋直径腹杆直径分布筋直径SJ-B1(B2)12868

a—施工阶段构造; b—使用阶段构造。
图3 SJ-B1构件
Fig.3 Specimen SJ-B1
2.2 材性试验
试验受力钢筋采用HRB400,取与试件所用钢筋同批次的钢筋试样进行材料性能试验,结果见表2。
表2 钢筋材料性能
Table 2 Material property of rebar

钢筋直径/mm屈服强度/MPa极限强度/MPa弹性模量/MPa6412.59595206 3258440.67598221 32512498.83601.78232 587
3 试验加载及测量方案
3.1 试验加载方案
首先在地面无应力状态完成楼板预制层的浇筑和养护。养护完成,采集钢筋应变,将楼板吊装放置在施工现场预定位置的混凝土墙体之上,调节楼板高度达到预定位置,记录吊装时的钢筋累计应变。按照正常施工模拟施工过程,浇筑混凝土,楼板承受施工人员、机械、湿混凝土荷载,记录浇筑时的钢筋累计应变和挠度。施工完成,开始养护28 d,养护完成再次测量钢筋应变。获得楼板在只有预制层不受力状态到叠合层达到设计强度装配的钢筋累计应变和挠度值,累计到楼板使用阶段试验中。使用阶段加载,将楼板从施工现场取下,运至实验室。
试验采用100 kN液压千斤顶进行静力加载,利用1根分配梁对楼板进行两点加载,加载点位于试件三分点处。为了更加贴近实际的荷载情况,板件两端搭载在钢梁上,搭在钢梁上的长度同楼板施工现场搭接长度。试验装置见图4,试验加载见图5。
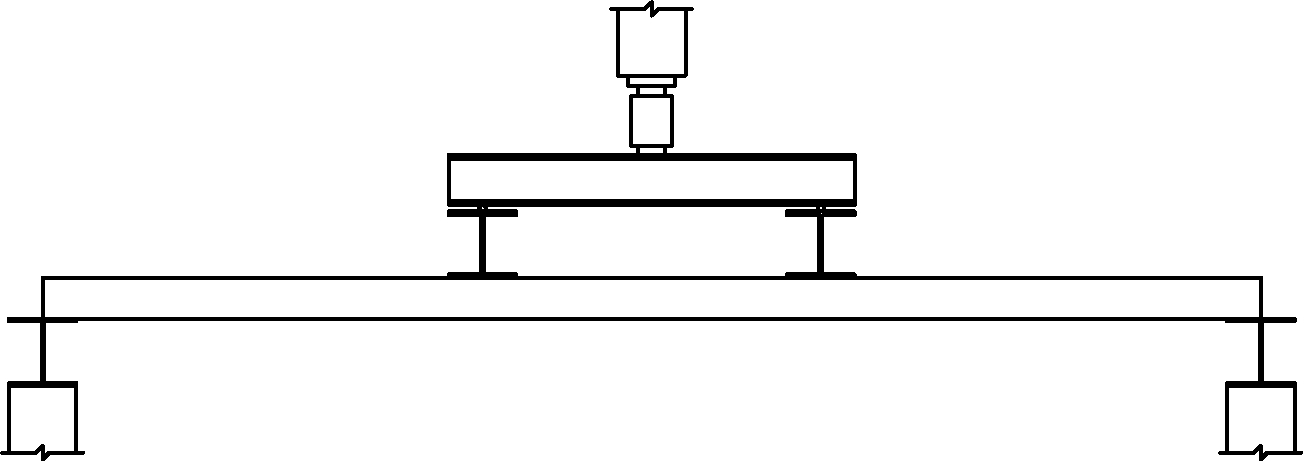
图4 试验装置示意
Fig.4 Schematic diagram of experimental setup

图5 试件加载
Fig.5 Specimen loading
开始加载时取2 kN为1级;出现裂缝后,以1 kN为1级,每1级加载完毕后持续稳定5 min,在稳定的时间内观察裂缝开展状况;楼板试件屈服后,以0.5 kN为1级,加载至试件破坏,破坏后以3 kN为1级分级卸载。
3.2 量测方案
试验的测量内容为钢筋应变、跨中位移值、1/3板跨位移值及板件两端的位移值。浇筑混凝土之前在钢筋上贴好应变片,分别布置在跨中位置和1/3板跨的上弦、下弦钢筋及支座处腹杆钢筋上。其中SX代表上弦钢筋,XX代表下弦钢筋,FG代表腹杆钢筋。在试件的跨中布置三个位移计(KS3、KS4、KS5),位移计量程为200 mm;在试件1/3板跨及支座处放置百分表(KS1、KS2、KS6、KS7),量程为50 mm。取楼板一半布置应变测点,具体见图6,位移测点见图7。
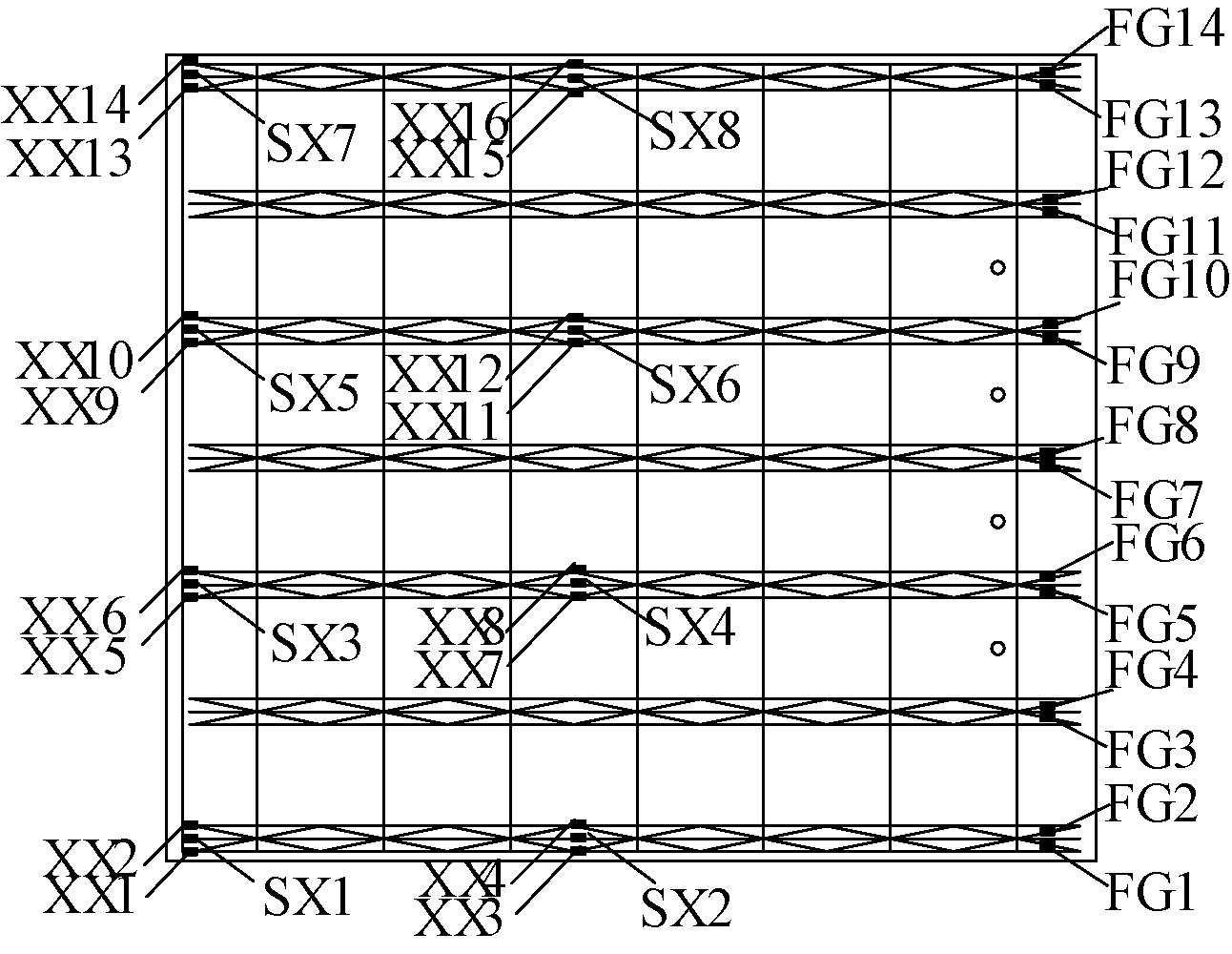
图6 应变测点布置
Fig.6 Arrangement of strain measuring point

图7 位移测点布置
Fig.7 Arrangement of displacement measuring point
4 试验过程描述
4.1 试件SJ-B1
在施工阶段,由现浇层的浇筑和预制层自重引起的挠度总计约为4.61 mm。在使用阶段,采用三分点加载,在三分点处放置传力梁,分配梁以及垫块,引起楼板的挠度约为2.41 mm,梁和垫块自重约为1.86 kN。在荷载未施加前,楼板预加荷载10.03 kN(跨中弯矩等效折算),总挠度7.02 mm。下文荷载-位移曲线均在此基础上叠加。
加载初期,随着荷载的缓慢增加,楼板跨中挠度同时增大,板底面和侧面无明显裂缝产生,此时楼板处于未裂弹性阶段;当荷载加至24.03 kN时,楼板加载点附近出现第一条裂缝,长度80 mm左右,宽度0.08 mm,板侧面无裂缝产生,此时楼板的挠度为13.11 mm;继续加载,楼板出现轻微震动,同时伴随荷载的突降,板底裂缝的数量增加并且裂缝宽度略有增加,板侧面没有出现新的裂缝;当荷载加载至28.14 kN,板底裂缝宽度明显增大,但尚未出现贯通裂缝,板侧面支座处出现细小裂缝,此时楼板挠度达到15 mm(跨度的1/200),裂缝宽度未达到GB/T 50010—2010《混凝土结构设计规范》[20]限值并且受拉钢筋尚未屈服,因此以28.14 kN作为承载力设计值。
随着荷载继续增大,板底逐渐出现贯通裂缝,主要分布在跨中及三分点处,板侧面加载点附近出现大量细微的斜裂缝。当荷载加至71.11 kN时,试件进入塑性阶段,板底出现6条贯通裂缝,板侧面裂缝变长并且加深,侧面裂缝逐渐延伸至板顶,此时楼板的挠度为42.45 mm;继续加载,楼板不断出现轻微地震动,伴随荷载突降,板的挠度增加速度较快,荷载增加速度较慢,侧面加载区附近裂缝显著增加。当荷载达到78.41 kN,板底发出巨大的撕裂声,试件破坏,板底最大裂缝宽度达到1.26 mm,挠度达到50 mm。图8a为楼板整体破坏情况,图8b为破坏时的板侧面裂缝,图8c为破坏时的板底面裂缝。

a—楼板破坏形态; b—板侧面裂缝; c—板底裂缝。
图8 SJ-B1的变形裂缝
Fig.8 Deformation cracks of SJ-B1
4.2 试件SJ-B2
试件SJ-B2与SJ-B1试验现象基本相同,仅一些特征点的数值稍有区别。对于试件SJ-B2,当荷载加至20.25 kN时,楼板加载点附近出现第一条裂缝,长120 mm左右,宽0.12 mm,板侧面无裂缝产生,此时楼板的挠度为10.37 mm;当荷载加载至28.84 kN,板底裂缝宽度明显增大,但尚未出现贯通裂缝,板侧面加载点附近出现斜裂缝,此时楼板挠度达到15 mm,裂缝宽度并未达到GB 50010—2010[20]限值并且受拉钢筋尚未屈服,因此以28.84 kN作为承载力设计值。当荷载加至66.73 kN时,试件进入塑性阶段,板底出现7条贯通裂缝,板侧面裂缝变长并且加深贯通至板顶,此时楼板的挠度为41.08 mm;当荷载达到72.11 kN,板底出现巨大的撕裂声,试件发生破坏,板底最大裂缝宽度达到1.48 mm,挠度达到50 mm。图9a为楼板整体破坏情况,图9b为板侧面裂缝分布情况,图9c为板底面裂缝分布情况。

a—楼板破坏形态; b—板侧面裂缝; c—板底裂缝。
图9 SJ-B2的变形裂缝
Fig.9 Deformation cracks of SJ-B2
图10、图11分别给出了各试件在极限荷载作用下的侧面和板底主要裂缝分布,从中可见:两组试件裂缝分布数量和分布范围基本一致,主要分布在加载点和跨中侧面及底面。这主要是由于加载点之间为单向板试件的纯弯段,弯矩较大,并且加载点下方应力较为集中,因此裂缝一般会在加载点的一定区域内出现。
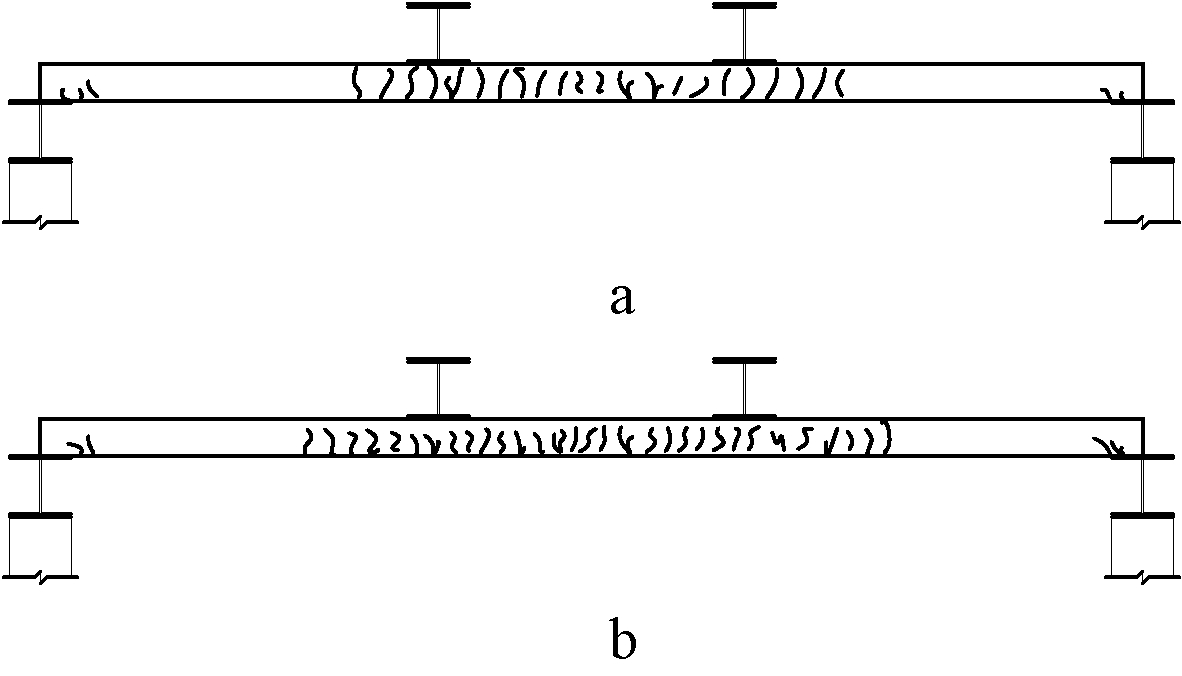
a—试件SJ-B1; b—试件SJ-B2。
图10 侧面主要裂缝分布
Fig.10 Distribution map of side major cracks

a—试件SJ-B1; b—试件SJ-B2。
图11 板底主要裂缝分布
Fig.11 Distribution map of major cracks at the bottom of floor
5 试验结果分析
5.1 荷载-挠度曲线
根据试验数据绘制2个试件的荷载-挠度曲线(图12),研究荷载与跨中挠度的关系。由图可知,两组试件的荷载-挠度曲线非常接近,大致分为以下几个阶段:1)未裂弹性阶段。开始加载时,荷载与挠度成线性关系,曲线斜率较大,荷载增加较快,挠度增加较慢,此时楼板的刚度较大,板底及板侧面未出现裂缝;2)开裂弹性阶段。荷载继续增加,曲线呈现锯齿状,荷载与挠度的关系仍为线性,曲线斜率略有降低,此时楼板受拉区局部混凝土退出工作,裂缝逐渐发展和扩散。3)屈服强化阶段。随着荷载继续增加,曲线出现明显拐点,荷载增加缓慢,挠度迅速增加,此时下弦钢筋屈服,裂缝不断扩展并交汇,此时受拉区大部分混凝土退出工作,楼板的刚度迅速下降。4)卸载阶段。达到极限状态后,继续加载,承载力不再提高,停止加载,当荷载卸载到0 kN时,两组试件的残余变形大致相同。

----SJ-B1; ——SJ-B2。
图12 荷载-挠度曲线
Fig.12 Load-deflection curves
5.2 试件性能指标
通过试验数据得到两组楼板的开裂荷载Pcr、设计承载力P1、屈服荷载Py、极限荷载Pu。
对于开裂荷载Pcr,以试件出现第一条裂缝时的外荷载为开裂荷载;对于设计承载力P1,根据GB/T 50010—2010受弯构件正常使用状态下的挠度限值为l0/200(15 mml0为跨度),裂缝宽度未达到0.2 mm,下弦钢筋尚未屈服,综合这3个指标确定设计承载力;对于屈服荷载Py,以试件纵向受拉主筋全部屈服时试件所受的外荷载为屈服荷载;对于极限荷载Pu,根据GB/T 50152—2012《混凝土结构试验方法标准》,跨中最大挠度达到跨度1/50(57 mm),受拉主筋处裂缝宽度达到1.5 mm,钢筋应变达到0.01或受压区混凝土受压开裂、破碎,综合这4个指标确定极限荷载。楼板试件的各个特征荷载值如表3所示。可知,从设计承载力到极限承载力有非常大的安全储备,开裂荷载与设计承载力非常接近。
表3 试件特征荷载值
Table 3 Primary performance indicators of the specimens

试件编号极限荷载Pu/kN开裂荷载Pcr/kNPcr/Pu设计承载力P1/kNP1/Pu屈服荷载Py/kNPy/PuSJ-B178.4124.030.3128.140.3671.110.91SJ-B272.1120.250.2828.840.4066.730.93
5.3 叠合楼板受力性能分析
通过对比试验现象,并结合试验数据,两个试件的设计承载力在28 kN左右,与极限荷载的比值在0.4左右。设计承载力仍处在开裂弹性阶段,说明此楼板的承载能力较高,满足正常使用阶段的各项要求,具有较高的安全储备。两个试件的开裂荷载为20~24 kN,因为两个试件配筋相同,同时浇筑,养护条件也相同,与极限荷载的比值为0.28~0.31。两个试件的屈服荷载为67~71 kN,与极限荷载的比值在0.9左右,从屈服至极限状态甚至破坏还有一定的强度富余。两个试件支座部位的混凝土预制方块在施工阶段主要起到吊挂调节丝杆的作用,在使用阶段的加载过程中,预制方块与混凝土楼板的黏结效果较好,未出现预制方块提前剥离结构的现象。
5.4 应变分析
各主要观测点荷载-应变曲线如图13所示。可以看出:上弦钢筋处于受压状态,下弦钢筋处于受拉状态。在施工阶段,主要采集了吊装和浇筑时的钢筋应变,上弦钢筋的累计应变达到2×10-4左右,下弦钢筋的累计应变达到4×10-4左右,这主要是由于下弦钢筋在吊装时,承受楼板自重以及受上部现浇层的影响。在使用阶段加载,刚开始钢筋的应变呈线性增加,当加至屈服荷载时,下弦钢筋进入屈服状态,但上弦钢筋尚未进入屈服状态。当荷载加载至极限荷载时,上弦钢筋逐渐进入屈服状态,下弦钢筋逐渐进入强化状态。其中,当楼板达到设计承载力时,上下弦钢筋均未进入屈服状态,说明楼板的承载力还有较大的富余。

a—SJ-B1的上弦钢筋; b—SJ-B1的下弦钢筋; c—SJ-B2的上弦钢筋; d—SJ-B2的下弦钢筋。
图13 荷载-应变曲线
Fig.13 Load-strain curves
6 短期刚度计算方法
根据结构力学基本原理可以得到跨中挠度计算式:
(1)
式中:F为梁跨中集中力;l0为楼板跨度;BS为受弯构件纯弯区段内平均的短期截面弯曲刚度。为了简化计算,GB 50010—1010给出了计算时所采用的“最小刚度原则”。
6.1 GB 50010—2010推荐的短期刚度计算法
对于叠合式构件,荷载准永久组合或标准组合下叠合式受弯构件正弯矩区段的短期刚度可按式(2)计算:
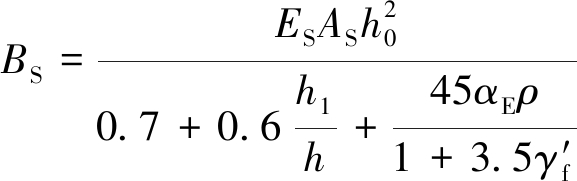
(2)
式中:ES为钢筋弹性模量;AS为受拉纵向钢筋截面面积;h1为叠合构件预制层高度;h0为叠合楼板的有效高度;h为叠合楼板的高度;αE为钢筋弹性模量与受压区材料弹性模量的比值;ρ为纵向受拉钢筋配筋率;γ′f为受压翼缘截面面积与腹板有效截面面积的比值,对于矩形截面取值为0。
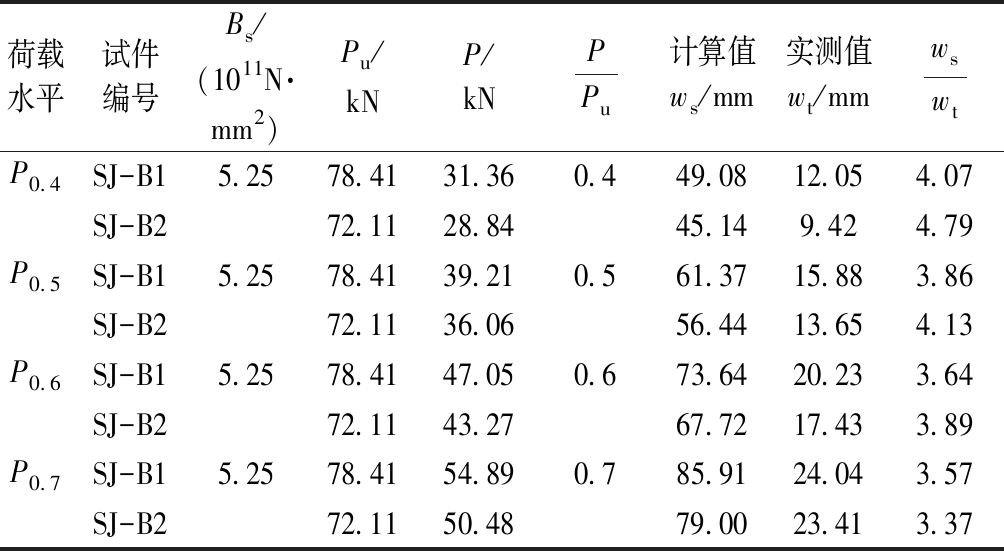
通过表4可以看出:在40%、50%、60%及70%的极限荷载作用下,试件的挠度计算值ws约是实测值wt的4倍。若按推荐算式计算,将会造成极大的材料浪费,构件的短期刚度值偏小,不适合本文提出的钢筋桁架楼板。
表4 P0.4,P0.5,P0.6和P0.7荷载作用下的刚度及挠度计算值(规范方法)
Table 4 Calculated values of stiffness and deflection under P0.4,P0.5,P0.6,P0.7 load(method in standard)
荷载水平试件编号Bs/(1011N·mm2)Pu/kNP/kNPPu计算值ws/mm实测值wt/mmwswtP0.4SJ-B15.2578.4131.360.449.0812.054.07SJ-B272.1128.8445.149.424.79P0.5SJ-B15.2578.4139.210.561.3715.883.86SJ-B272.1136.0656.4413.654.13P0.6SJ-B15.2578.4147.050.673.6420.233.64SJ-B272.1143.2767.7217.433.89P0.7SJ-B15.2578.4154.890.785.9124.043.57SJ-B272.1150.4879.0023.413.37
6.2 改进方法计算短期刚度
GB 50010—2010中对于受弯构件的短期刚度公式未考虑受压钢筋对刚度的影响,认为其对刚度的影响不大。但实际上受压钢筋对于短期刚度的影响不可忽略。
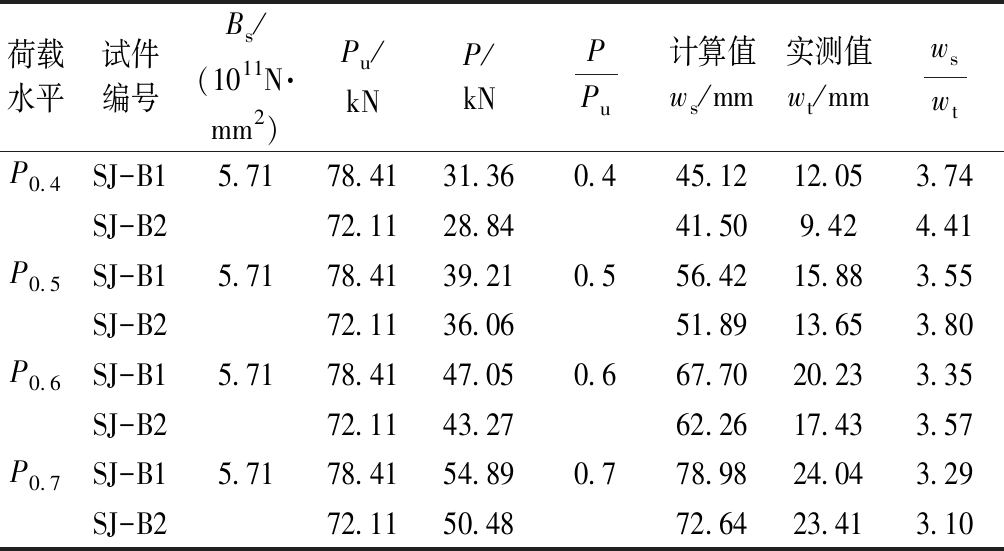
因此为考虑受压钢筋对于截面刚度的贡献,在受压翼缘加强系数中考虑受压钢筋的影响,取γ′f=αEρ′(ρ′为受压钢筋配筋率)。根据表5中计算值与实测值的挠度对比结果,可以看出,考虑受压钢筋后,楼板的刚度约提升9%,ws/wt的值大于3.10,计算值仍然偏大的原因是算式中仍未考虑钢筋桁架中腹杆钢筋对刚度的贡献以及空间桁架的整体作用。因此可以考虑通过引入钢筋桁架整体工作性能的刚度提高系数β进行修正,取β值为3。通过引入β后,各挠度计算值与实测值的比值基本一致。
表5 P0.4,P0.5,P0.6和P0.7荷载作用下的刚度及挠度计算值(改进方法)
Table 5 Calculated values of stiffness and deflection under P0.4,P0.5,P0.6,P0.7 load (improved method)
荷载水平试件编号Bs/(1011N·mm2)Pu/kNP/kNPPu计算值ws/mm实测值wt/mmwswtP0.4SJ-B15.7178.4131.360.445.1212.053.74SJ-B272.1128.8441.509.424.41P0.5SJ-B15.7178.4139.210.556.4215.883.55SJ-B272.1136.0651.8913.653.80P0.6SJ-B15.7178.4147.050.667.7020.233.35SJ-B272.1143.2762.2617.433.57P0.7SJ-B15.7178.4154.890.778.9824.043.29SJ-B272.1150.4872.6423.413.10
6.3 有效惯性矩法
有效惯性矩法采用截面换算的基本思想,将截面上的上弦钢筋、下弦钢筋等根据钢筋弹性模量与混凝土的弹性模量的比值,将钢筋截面换算为等效的混凝土截面,推导并建立相应的刚度计算式。
6.3.1 未出现裂缝时的换算惯性矩
受压区高度x由拉、压区对中和轴的面积矩相等的条件确定:
0.5b(h-x)2+(n-1)AS(h0-x)
(3)
式中:AS为下弦钢筋面积;A′S为上弦钢筋面积;a′S为受压区保护层厚度;h0为截面的有效高度;n为受拉钢筋的弹性模量与混凝土弹性模量的比值;n′为受压钢筋的弹性模量与混凝土弹性模量的比值。
换算截面的惯性矩为:
(4)
未出现裂缝时截面刚度为:
B0=ECI0
(5)
式中:EC为混凝土弹性模量。
6.3.2 出现裂缝后的换算惯性矩
当出现裂缝后,中和轴以下的混凝土不再受力,完全退出工作,拉力完全由受拉钢筋承担,将全部纵向钢筋的换算面积置于原截面高度处。受压区高度x由拉、压区对中和轴的面积矩相等的条件确定:
0.5bx2+(n′-1)A′S(x-a′S)=nAS(h0-x)
(6)
换算截面的惯性矩为:
(7)
出现裂缝时截面刚度为:
Bcr=ECIcr
(8)
在楼板开裂前,全截面参与工作,此时的刚度B0最大,开裂后受拉区混凝土退出工作,此时的刚度Bcr最小。设计时截面的平均刚度取:
B=0.625B0
(9)
美国土木工程协会(ASCE)规定[22-23]截面的平均刚度为:
B=(B0+Bcr)/2
(10)
文献[24]提出面惯性矩可以采用开裂截面惯性矩Icr和未开裂截面I0的几何平均值,即:
B=2B0Bcr/(B0+Bcr)
(11)
按式(9)计算的刚度记为B1,挠度值记为S1。按式(10)计算的刚度记为B2,挠度值记为S2。按式(11)计算的刚度记为B3,挠度值记为S3。经计算B1为36.78×1011N·mm2,B2为34.36×1011N·mm2,B3为16.91×1011N·mm2(其中B0为58.85×1011N·mm2,Bcr为9.88×1011N·mm2)。
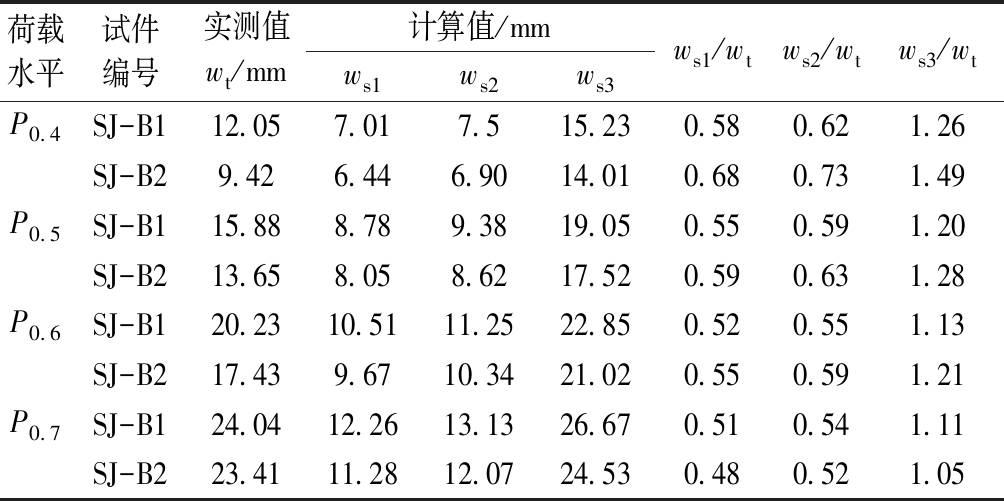
通过表6所示以上三种计算刚度方法的对比可以看出:式(9)和式(10)不符合本文所提出的楼板形式,式(11)与本文所提出的楼板形式比较吻合,ws/wt数值在1.1左右。
表6 P0.4,P0.5,P0.6和P0.7荷载作用下的计算值与理论值的比值
Table 6 Ratio of calculated value to theoretical value under P0.4,P0.5,P0.6和P0.7 load
荷载水平试件编号实测值wt/mm计算值/mmws1ws2ws3ws1/wtws2/wtws3/wtP0.4SJ-B112.057.017.515.230.580.621.26SJ-B29.426.446.9014.010.680.731.49P0.5SJ-B115.888.789.3819.050.550.591.20SJ-B213.658.058.6217.520.590.631.28P0.6SJ-B120.2310.5111.2522.850.520.551.13SJ-B217.439.6710.3421.020.550.591.21P0.7SJ-B124.0412.2613.1326.670.510.541.11SJ-B223.4111.2812.0724.530.480.521.05
6.4 数据回归法
在试验数据的基础上根据挠度计算公式反推出截面的抗弯刚度,如表7和图14所示,然后结合竖向荷载值对短期刚度计算值进行回归分析,从而总结出楼板屈服前的短期刚度简化计算公式。
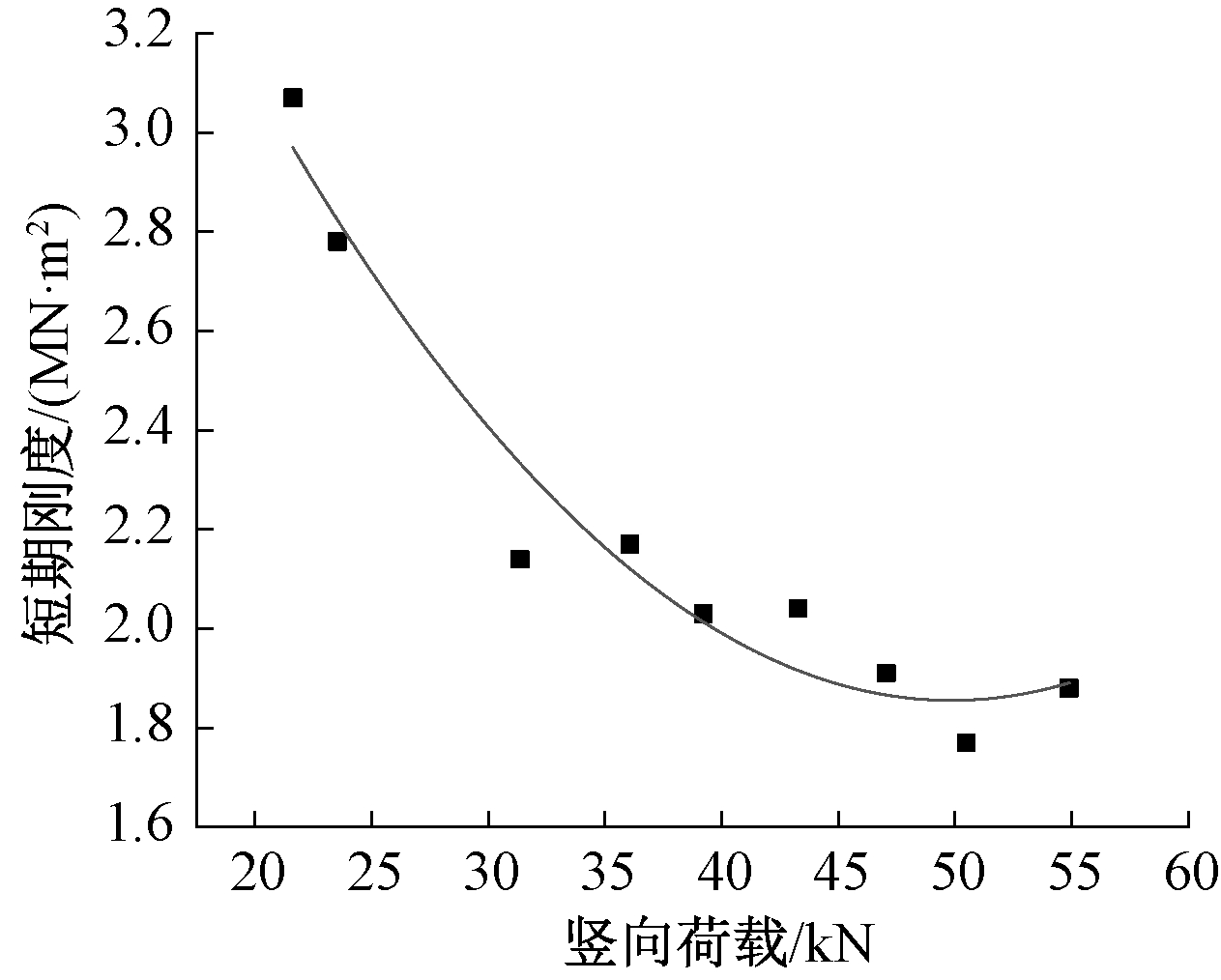
![]() 实测点; ——B=-0.139 51F+0.001 4F2+5.332 313。
实测点; ——B=-0.139 51F+0.001 4F2+5.332 313。
图14 短期刚度回归曲线
Fig.14 Short-term stiffness regression curve
对数据拟合,得到解析方程为:
B=-0.139 51F+0.001 4F2+5.332 313
(12)
式中:B为屈服前楼板使用阶段短期刚度;F为竖向荷载。
7 结束语
提出了一种高度可调节的装配式混凝土叠合楼板,对两个楼板进行静力加载,研究楼板的裂缝发展规律、钢筋应变、荷载-挠度曲线。通过理论分析与试验数据的分析,得到以下主要结论:
表7 P0.3 P0.4,P0.5,P0.6和P0.7荷载作用下的刚度值
Table 7 Calculated values of stiffness under P0.4,P0.5,P0.6,P0.7 load MN·m2

试件编号B0.3B0.4B0.5B0.6B0.7SJ-B12.782.142.031.911.88SJ-B23.072.522.172.041.77
1)两个试件荷载-挠度曲线发展趋势基本一致,都经历了未裂弹性阶段、开裂弹性阶段、屈服强化阶段和卸载阶段。在加载过程中,边缘两侧混凝土预制块并未提前剥离,说明混凝土预制块与混凝土楼板的黏结效果较好,能共同受力。
2)本文研究的楼板完全满足GB 50010—2010中对楼板正常使用状态下挠度限值的要求,楼板挠度达到规范限值时,受拉纵向钢筋并未屈服,处于开裂弹性阶段,楼板有较大的强度富余。
3)两个试件的设计承载力约为极限荷载的40%,从设计承载力到破坏有一定的安全储备,达到极限荷载后,荷载-挠度曲线近似为水平状态,并没有发生脆性的破坏,试件均具有良好的延性。
4)基于GB 50010—2010方法、有效惯性矩法和数据回归法推导出一种适用于所提出的叠合楼板使用阶段的短期刚度公式。
5)楼板装配性能良好,通过调节L形丝杆调整楼板四周的高差,调节螺母的松紧使楼板板面平整并达到同一标高,解决实际工程中由于梁或者墙上表面不平带来的装配和施工问题,提升施工的质量。
[1] LIU X C, ZHOU X J, ZHANG A L, et al. Design and Compilation of Specifications for a Modular Prefabricated High-Rise Steel Frame Structure with Diagonal Braces. Part I: Integral Structural Design [J]. The Structural Design of Tall and Special Buildings, 2017, 27(2):1-20.
[2] LIU X C, HE X N, ZHANG A L, et al. Design and Specification Compilation of a Modular Prefabricated High-Rise Steel Frame Structure with Diagonal Braces Part II: Elastic-Plastic Time-History Analysis and Joint Design [J]. The Structural Design of Tall and Special Buildings, 2017,27 (2):1-18.
[3] 张爱林,张艳霞. 工业化装配式高层钢结构新体系关键问题研究和展望[J]. 北京建筑大学学报,2016,32(3):22-27.
[4] 刘学春,商子轩,张冬洁,等.装配式多高层钢结构研究要点与现状分析[J].工业建筑,2018,48(5):1-10.
[5] ZHANG A L, LIU X C. The New Development of Industrial Assembly High-Rise Steel Structure System in China[C]// Pacific Structural Steel Conference. 2013:976-981.
[6] 吴晓鹏. 现浇预应力空心板梁楼盖体系受力特性研究[D]. 杭州:浙江大学,2005.
[7] 张爱林,赵越,刘学春. 装配式钢结构新型轻质叠合楼板设计研究[J]. 工业建筑,2014,44(8):46-49.
[8] 罗祥旺. 现浇混凝土楼板施工技术及控制措施分析[J]. 河南建材,2018(2):156-157.
[9] 张莫愁. 现浇混凝土楼板裂缝分析及综合控制措施[D]. 广州:中山大学,2014.
[10] 赵欣,母瑞强. 轻钢龙骨泡沫混凝土预制楼板受弯性能研究[J].建筑钢结构进展,2018,20(3):52-57.
[11] 张保金,李生之.混凝土现浇板与预制楼板的探讨[J].中国新技术新产品,2010(8):156-157.
[12] 祝延涛.压型钢板-再生混凝土组合楼板受弯性能试验研究[D].北京:北京工业大学,2015.
[13] 陈世鸣. 压型钢板-混凝土组合楼板的承载能力研究[J]. 建筑结构学报,2002, 23(3):19-26.
[14] 赵越. 装配式钢结构轻质钢筋桁架楼板承载能力与计算方法研究[D]. 北京:北京工业大学,2015.
[15] 刘轶,童根树,李文斌,等. 钢筋桁架叠合板性能试验和设计方法研究[J]. 混凝土与水泥制品,2006(2):57-60.
[16] 张季超,许勇,王蕴,等.装配整体式叠合楼板足尺加载试验研究[J].建筑结构,2009,39(5):116-120.
[17] 聂建国,陈必磊,陈戈,等.钢筋混凝土叠合板的试验研究[J].工业建筑,2003, 33(12):43-46.
[18] 武立伟,陈海彬,刘亦斌,等 .预制叠合空心楼板静力性能试验研究[J].建筑结构学报,2018,39(2):36-41.
[19] 颜锋,高杰,田春雨,等.带接缝的混凝土叠合楼板足尺试验研究[J].建筑结构,2016,46(10):57-60.
[20] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S]. 北京:中国建筑工业出版社,2010.
[21] 中华人民共和国住房和城乡建设部.混凝土结构试验方法标准:GB/T 50152—2012[S]. 北京:中国建筑工业出版社,2012.
[22] ASCE. Specification for the Design and Construction of Composite Slabs [S].New York: ASCE, 1984.
[23] JOHNSON R P. Composite Structures of Steel and Concrete [M].2nd ed. Oxford:Blackwell Scientific Publications,1994.
[24] 聂建国,易卫华,雷丽英,等.闭口型压型钢板-混凝土组合板的刚度计算[J].工业建筑,2003,33(12):19-21.