钢筋锈蚀是影响传统钢筋混凝土结构耐久性的主要因素之一。为控制钢筋锈蚀，国内外学术界与工程界提出了大量的方法，例如使用不锈钢、增加混凝土的抗渗性、增加结构保护层厚度、使用防水混凝土、钢筋外部涂刷防锈剂[1]等。然而，以上这些方法并不能完全彻底解决钢筋锈蚀问题。近30年来，由于纤维增强复合材料(FRP)具有良好的抗腐蚀、质量轻、强度大等优点，有望成为一种替换钢筋的新型材料，从而在根本上解决传统结构中钢筋锈蚀的问题。
诸多国内外学者针对FRP筋混凝土梁抗弯性能进行大量的理论分析研究，但是，这些分析大部分在钢筋混凝土梁的基础上进行修正。Branson通过对钢筋混凝土梁单元修正，得到了抗弯承载力计算式[2]，并提出了FRP筋混凝土梁的有效惯性矩计算模型。Yost等通过试验发现Branson模型计算值比试验值偏大，提出双线性模型预测弯矩-曲率的关系曲线并进行修正[3]。孔祥清等考虑GFRP筋与混凝土之间的黏结滑移以及材料非线性本构关系，建立了GFRP筋与钢筋混合配筋混凝土梁的三维有限元模型[4]，结果表明：为满足梁变形要求，应控制FRP筋的配筋率。张海霞考虑FRP筋与混凝土黏结-滑移本构关系，并利用ANSYS软件实现FRP筋混凝土梁非线性有限元模拟[5]，但未考虑到FRP筋与混凝土之间拉伸刚化现象。尽管国内外学者已在试验方面对FRP筋混凝土梁的受弯性能取得了一定的研究成果，但是目前在数值模拟方面的研究仍然较少。本文借鉴前人关于钢筋混凝土梁、FRP筋梁及混合配筋混凝土梁抗弯性能研究成果，建立适用于评估FRP筋混凝土梁受弯性能的理论分析模型和计算简化模型。
1 有限条带法
有限条带法基于以下基本假设：1)平截面假定，FRP筋与混凝土黏结完好，无相对滑移;2)不考虑剪切变形的影响；3)不考虑混凝土收缩、徐变和温湿度变化引起应力和变形状态。结合材料的本构模型、截面的静力平衡和变形协调建立截面的弯矩-曲率关系。图1 给出了典型的FRP筋混凝土梁截面上应力-应变分布，图中：
分别为受拉区和受压区FRP筋的面积；
分别为受拉区和受压区FRP筋的应变；εi为受压区混凝土的等效应变；Tf、Cf、Fc分别为受拉区和受压区FRP筋以及混凝土的合力。
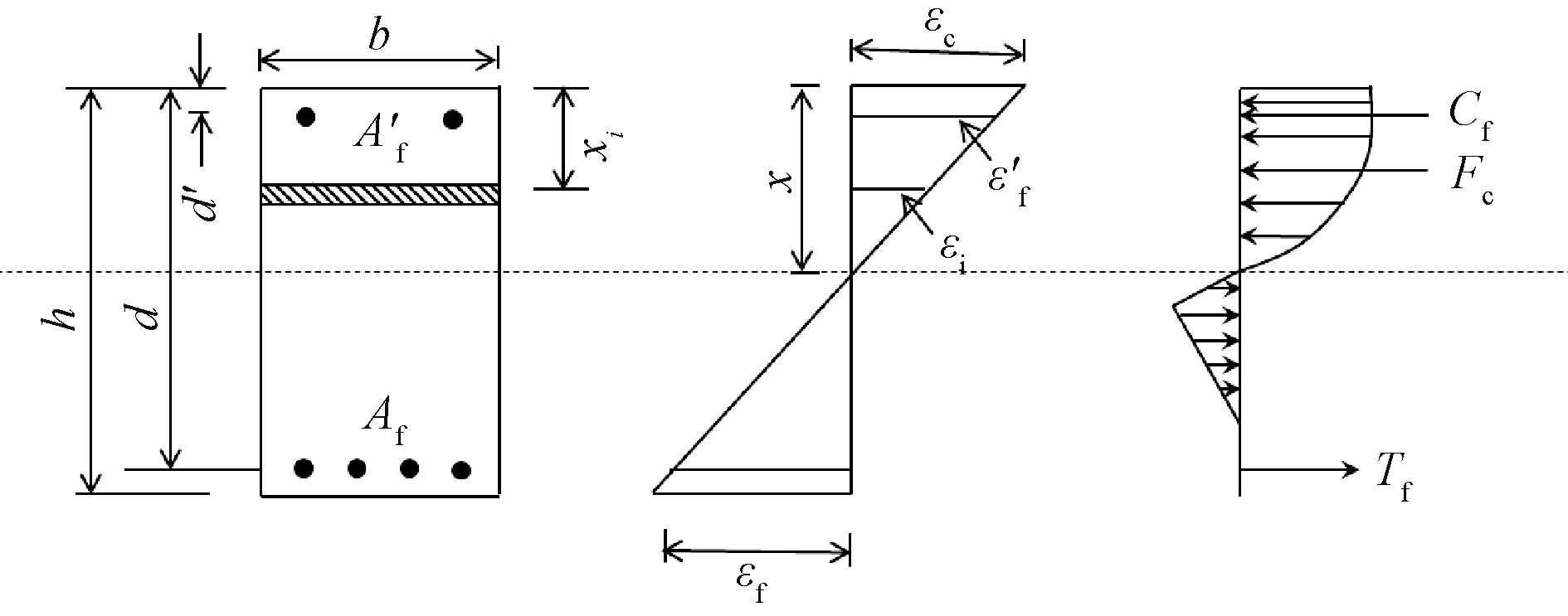
图1 FRP筋混凝土梁截面应力-应变分布
Fig.1 Stress strains distribution of cross section of concrete beam reinforced with FRP bars
1.1 材料应力-应变关系
混凝土单轴受压应力-应变曲线采用由Hognestad提出的分段模型[6](图2a)，其表达式为：
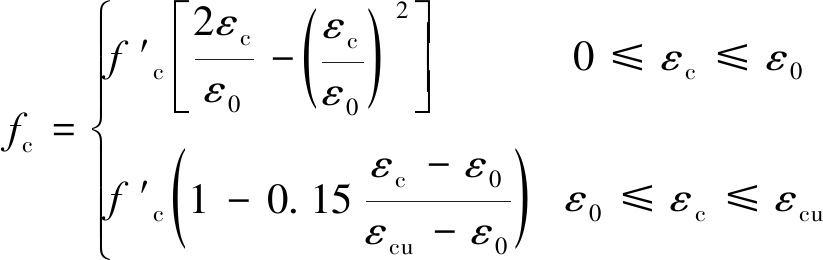
(1)
式中：fc、εc分别为混凝土压应力和压应变；f ′c为混凝土棱柱体抗压强度；ε0为相应于峰值压应力时的压应变，取值为0.002；εcu为极限压应变，取值为0.003 8。
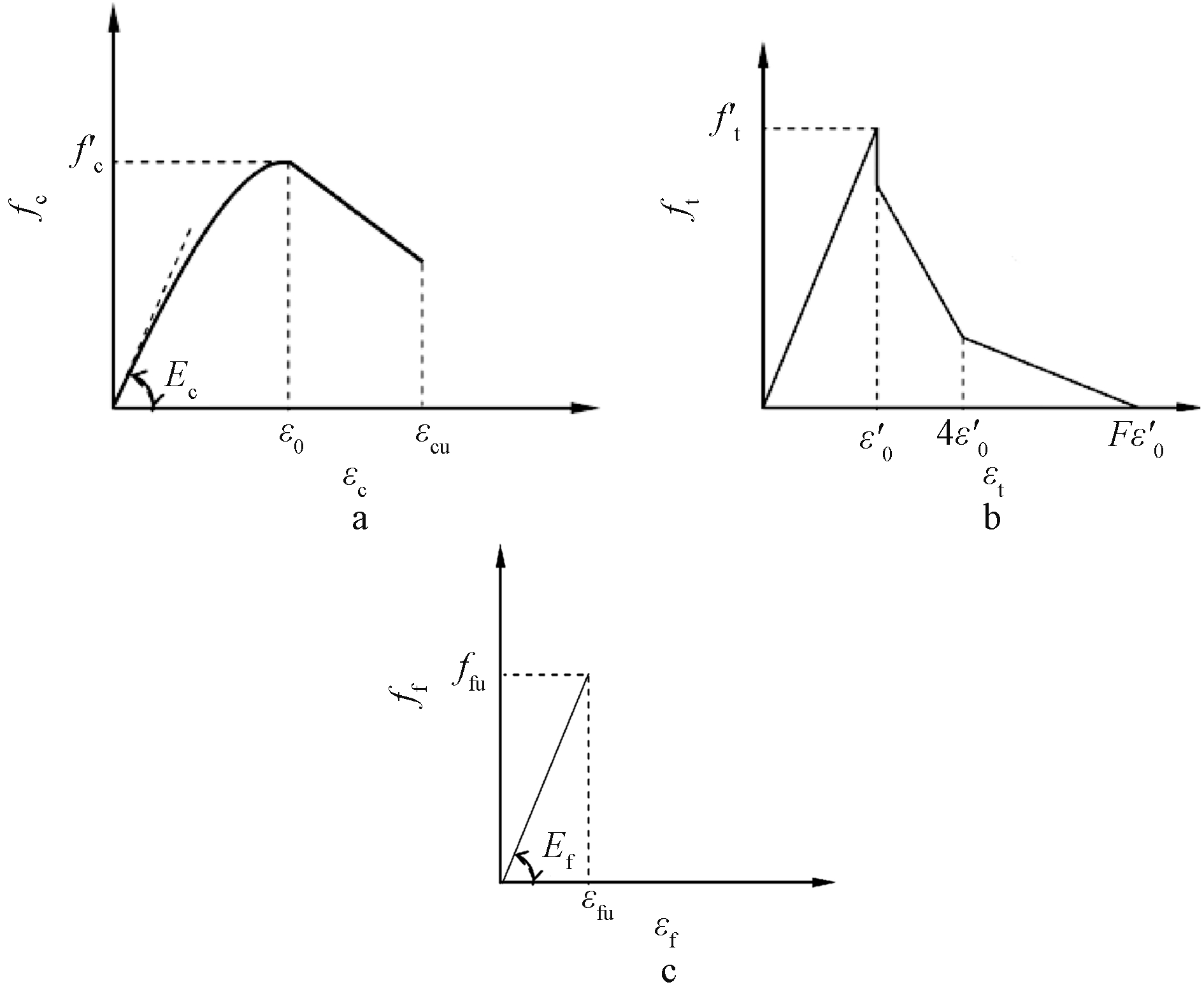
a—普通混凝土受压； b—混凝土受拉； c—FRP筋受拉。
图2 材料的应力-应变关系
Fig.2 Stress-strain relationships of materials
混凝土拉伸应力-应变关系采用Nayal-Rasheed提出的考虑了拉伸刚化[7]效应本构模型(图2b)，其表达式为：
(2)
其中
式中：Ec为混凝土弹性模量；
分别为混凝土极限拉应力和极限拉应变；ft、εt分别为混凝土拉应力和拉应变；As、Es分别为受拉区钢筋的面积和弹性模量；Af、Ef分别为受拉区FRP筋的面积和弹性模量；
分别为受拉区钢筋的根数和直径；
分别为受拉区FRP筋的根数和直径；Ft用来反映筋材拉伸刚化效应，对于FRP筋梁，Ft=100；对于钢筋混凝土梁，Ft=10；对于混合配筋梁，Ft的取值在10～100[7]。
FRP筋在破坏前其拉伸力学行为基本保持线弹性(图2c)，其应力-应变关系为：
ff=Efεf εf≤εfu
(3)
式中：ff、εf分别为FRP筋的应力和应变；Ef为FRP筋的弹性模量；εfu为FRP筋的极限应变。
1.2 数值模拟
有限条带法通过如下步骤[8]计算FRP筋混凝土梁的弯矩-曲率曲线：1)对于给定某一较小曲率，通过迭代法求出满足截面平衡方程的中性轴高度，得到该曲率所对应的弯矩值。2)增大曲率，重复过程1)直到满足程序终止条件。3)当满足以下条件时，程序终止：混凝土梁顶缘纤维应变达到混凝土极限压应变和FRP筋达到其极限抗拉应变时，程序终止。有限条带法分级加曲率法求弯矩-曲率关系具体流程可见图3。
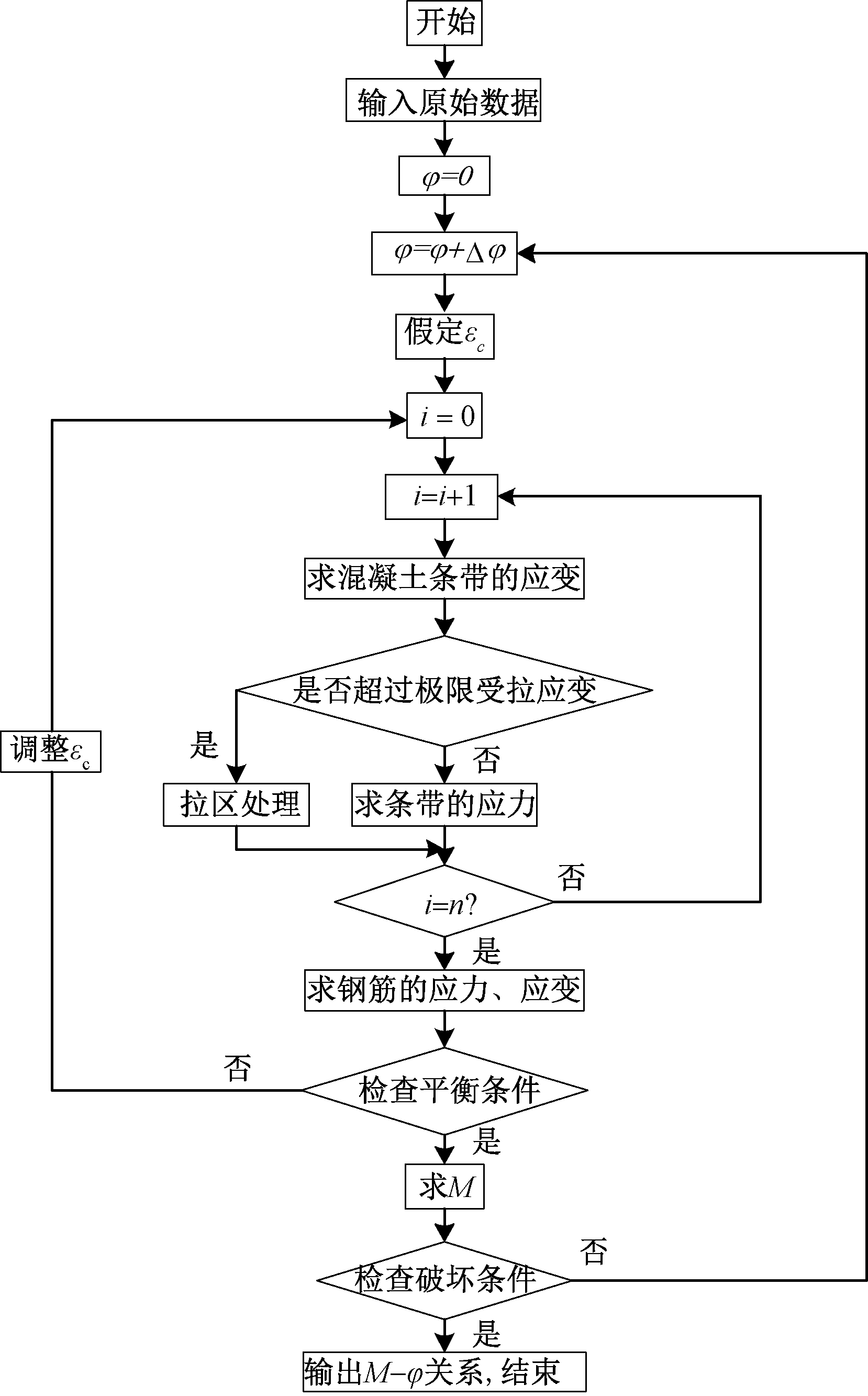
图3 弯矩-曲率流程
Fig.3 Flow chart of moment-curvature relationship
2 计算结果及参数分析
2.1 试验结果对比
为验证理论的正确性，本文选取文献[9]中试件Ⅱ、Ⅲ的试验曲线与数值模拟结果进行对比，对比结果如图4所示，试件II、III信息详见表1。另外，表1还比较了部分其他文献中FRP筋混凝土梁承载力试验值与数值计算结果。
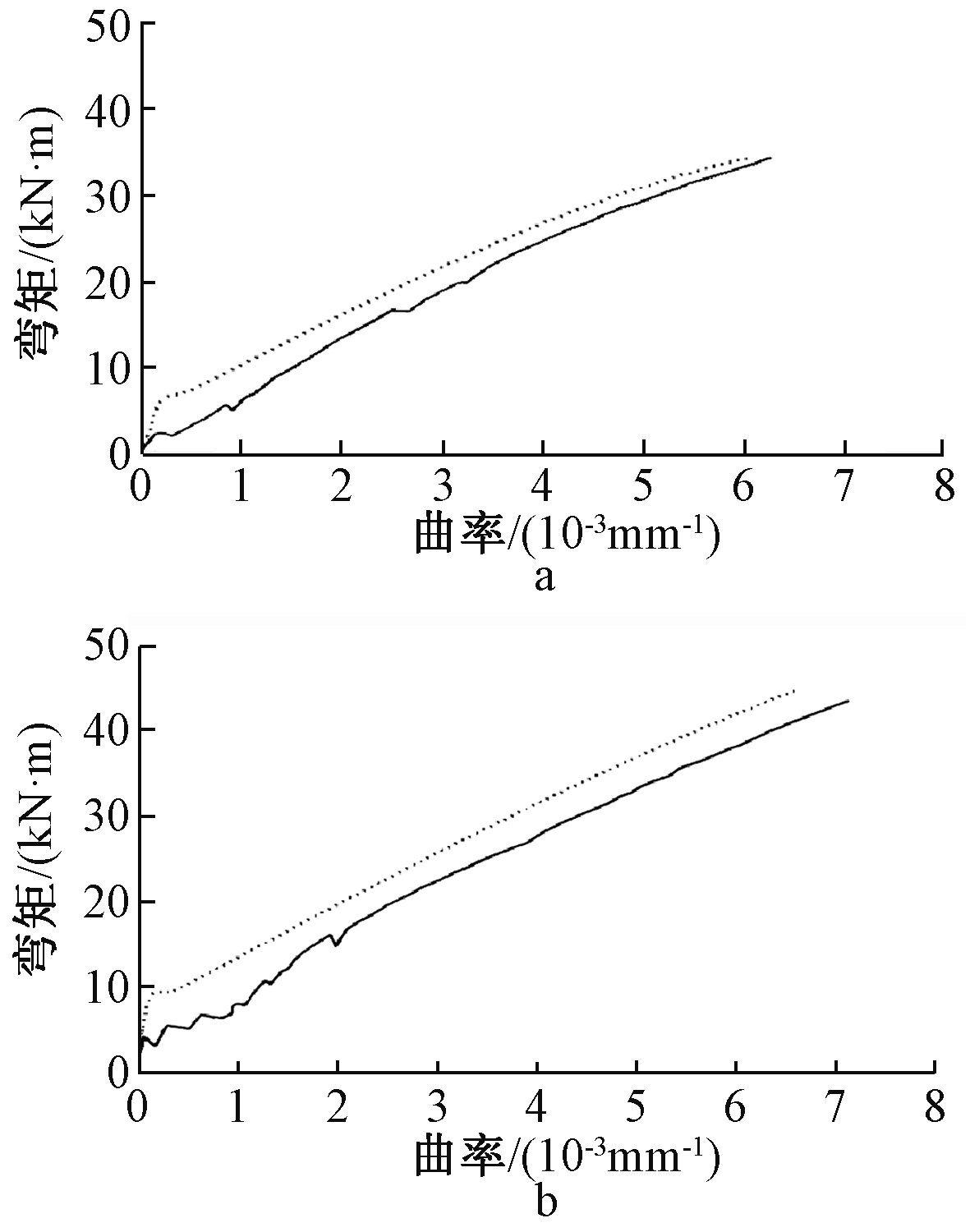
a—试件Ⅱ;b—试件Ⅲ。
试验曲线;
数值曲线。
图4 FRP筋混凝土梁试验、数值弯矩-曲率关系曲线
Fig.4 Test and numerical moment-curvature curves of FRP reinforced concrete beams
由图4可以看出：数值模拟结果与试验曲线吻合良好。FRP筋混凝土梁弯矩-曲率关系大致可以分为混凝土开裂前阶段和混凝土开裂后阶段。在开裂前，混凝土与FRP筋大致处于线弹性阶段，其弯矩-曲率呈线性变化；当荷载增加至开裂荷载时，梁受拉区混凝土开裂。开裂后，混凝土所承担拉力转移至FRP筋。随着曲率进一步增大，FRP筋混凝土梁所受弯矩随着曲率增加基本呈线性增长直至FRP筋梁截面破坏。另外，从图4中还可以看出，FRP筋混凝土梁的破坏属于脆性破坏。
表1 FRP筋混凝土梁极限抗弯承载力的理论值与试验值
Table 1 Experimental and theoretical ultimate moment in concrete beams reinforced with FRP bars
来源试件b/mmh/mmf′c/MPaρ/%Mexp/(kN·m)理论值/试验值条带法简化模型文献[9]Ⅱ20021031.33.6034.21.010.95Ⅲ20026031.31.2045.10.990.95Ⅳ20030040.71.1559.21.101.01Ⅴ20025040.72.8757.01.040.93文献[10]F250018530.00.7036.81.081.09F350018530.01.2260.70.860.82文献[11]BC2HA13018057.21.1619.70.960.82BC2VA13018097.41.1622.71.000.97文献[12]C-C-320030023.60.1644.80.900.91平均值0.990.94标准差0.080.08
注：ρ为配筋率。
2.2 参数分析
配筋率是影响FRP筋混凝土梁截面弯矩-曲率关系的重要参数。选取试件C-C-3，在截面尺寸，混凝土强度不变的情况下，采用不同配筋率，模拟得到梁截面弯矩-曲率的对比曲线，如图5所示。可以看出:在截面开裂前阶段，配筋率对FRP筋混凝土梁弯矩-曲率关系曲线影响较小，这是由于截面开裂前，混凝土承担着受拉区大部分拉力，而FRP筋承担的拉力较小，因此配筋率对开裂弯矩影响较小。正截面开裂后，随着配筋率增大，弯矩-曲率曲线越来越陡峭，即极限弯矩承载力逐渐增大，而极限曲率逐渐减小。对于不同FRP筋配筋率，FRP筋混凝土梁对应三种破坏形式，即FRP筋受拉破坏、平衡破坏和混凝土受压破坏。对于本次参数研究，当配筋率为0.17%时，FRP筋混凝土梁的破坏模式是FRP筋受拉破坏；当配筋率为0.22%时，其破坏模式是FRP筋拉坏和混凝土压碎同时发生；当配筋率大于0.22%时，FRP筋梁的破坏由混凝土压碎导致。从图5还可以看出:当FRP筋混凝土梁发生混凝土压碎破坏时，尽管其抗弯承载力较大，但是其延性较低配筋率FRP筋混凝土梁低，这在设计FRP筋混凝土梁时是值得注意的。
ρ=0.16%;
ρ=0.22%;
ρ=0.48%;
ρ=1.44%。
图5 不同配筋率的弯矩-曲率关系曲线
Fig.5 Moment-curvature relationships with different reinforcement ratios
混凝土强度是影响截面弯矩-曲率关系曲线的另一个重要因素。同样选取了C-C-3试验数据，并在此基础上增加混凝土强度f′c为30,40,50 MPa的试件，在截面尺寸不变，配筋率为0.16%的情况下，采用上述4种不同混凝土强度，计算得到截面弯矩-曲率的对比曲线，如图6所示。可以看出:混凝土强度越大，截面开裂弯矩与梁的承载力也就越大。在截面开裂前，混凝土承担了大部分拉力，混凝土抗压强度越高，其承担的拉力也越大。在截面开裂瞬间，受拉区混凝土退出工作，FRP筋承担大部分拉力，截面刚度较未开裂时迅速下降。在截面开裂后弯矩-曲率曲线大致呈线性关系，直至发生FRP筋拉坏或混凝土压碎。
f ′c=23.6 MPa;
f ′c=30 MPa;
f ′c=40 MPa;
f ′c=50 MPa。
图6 不同混凝土强度的弯矩-曲率关系曲线
Fig.6 Moment-curvature relationships with different concrete strengths
3 FRP筋混凝土弯矩-曲率简化模型
FRP筋混凝土梁的弯矩-曲率关系是进行FRP梁刚度计算的重要工具。前述有限条带法得到的弯矩-曲率关系尽管精度较高，但从工程计算的角度来看显得较为繁琐。根据FRP筋混凝土梁的弯矩-曲率曲线特点，本文提出了一个三线性简化模型，即由式(4)求解FRP筋混凝土梁在开裂时弯矩Mcr和曲率φcr，再由式(5)、式(6)或式(7)求解梁极限抗弯承载力及其对应极限曲率，将所求极限值与原点连成直线，在开裂弯矩处作一条水平线，两条线交点即为梁开裂至稳定的曲率φ0，在稳定曲率之前，弯矩不变，曲率增大至φ0，之后，弯矩-曲率继续呈线性变化，详见图7。
图7 FRP筋混凝土梁三线性弯矩-曲率关系
Fig.7 Trilinear moment-curvature relationship of FRP reinforced concrete beams
对于FRP筋混凝土梁，其开裂弯矩Mcr及对应的曲率φcr可以采用式(4)进行计算：
(4a)
(4b)
FRP筋混凝土梁破坏时根据其破坏状态分为混凝土压碎和FRP筋拉断。因此，其极限弯矩可按如下两种情况分别进行计算。
3.1 混凝土压碎
此时FRP筋混凝土梁极限弯矩Mu为：
(5)
式中:α为混凝土受压区矩形简化参数，取值0.85；β为混凝土强度折减系数[13]，其与f ′c有关当f ′c≤30 MPa时，β=0.85，当f ′c≥80 MPa时，β=0.65,当30 MPa≤fc′≤80 MPa时，β=1.09-0.008 f ′c。 极限弯矩Mu对应的极限曲率由式(6)确定：
αβf ′cbx=EfεfAf
(6a)
(6b)
(6c)
式中：Ef为FRP筋受拉区弹性模量；εf为FRP筋拉应变；εcu为混凝土极限压应变。
3.2 FRP筋拉断
此时FRP筋混凝土梁的极限弯矩Mu和对应的曲率为：
Mu=FfuAf(d-0.5x)
(7a)
αβf ′cbx=EfεfuAf
(7b)
(7c)
式中：Ffu为FRP筋极限抗拉强度；εfu为FRP筋极限拉应变。
从文献[9]中选取两组试验结果与三线性曲线进行对比，如图8所示。结果表明:试验曲线与三线性曲线吻合良好。为进一步说明该简化模型的可行性，选取部分文献中的FRP梁承载试验值与简化模型承载力计算值进行对比，得其平均值为0.94，标准差为0.08，具体数值详见表1。
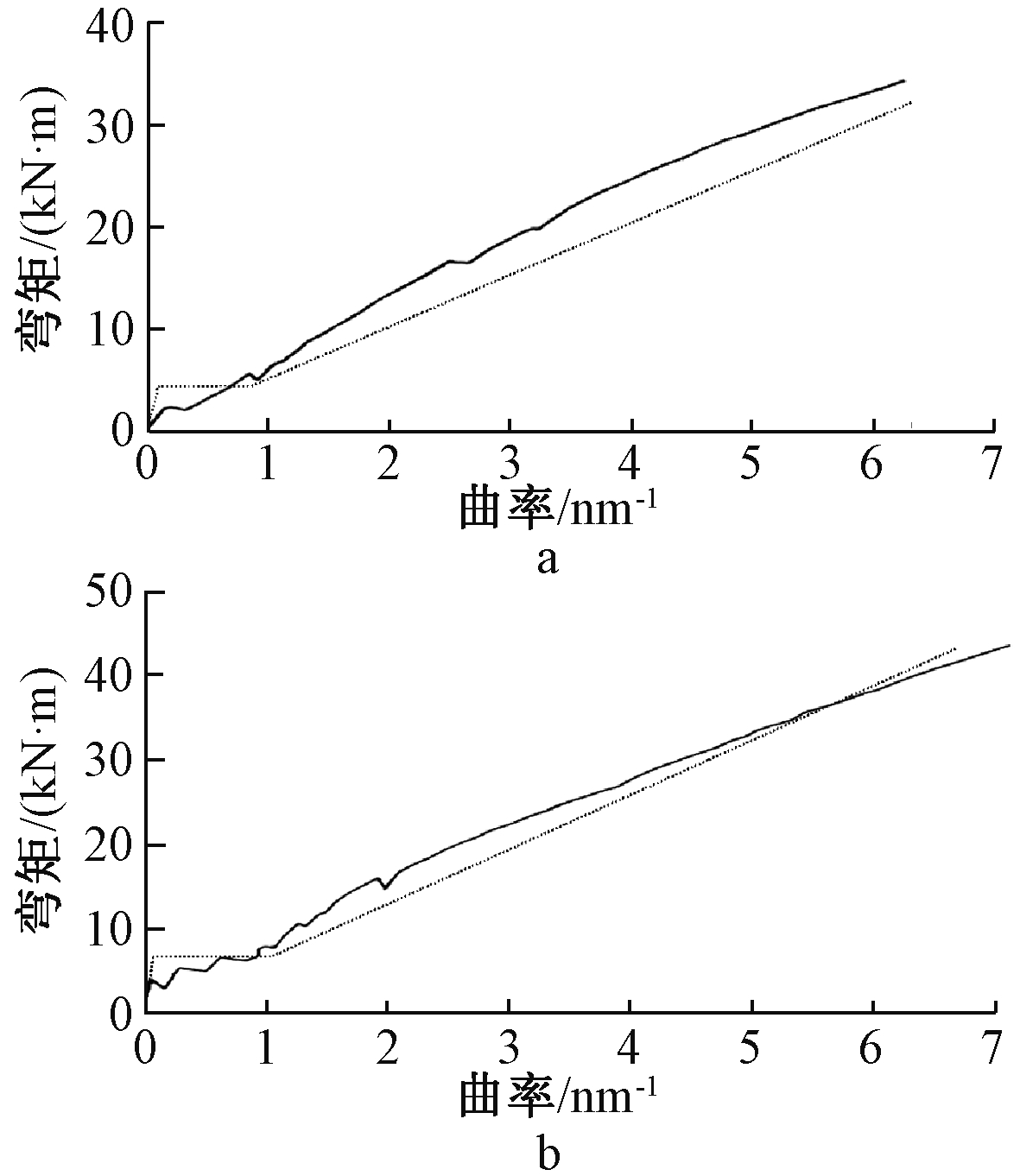
a—试件Ⅱ;b—试件Ⅲ。—试验曲线;
三线性曲线。
图8 FRP筋混凝土梁试验、三线性弯矩-曲率关系曲线
Fig.8 Test and trilinear moment-curvature curves of FRP reinforced concrete beams
4 结束语
采用有限条带法同时考虑拉伸强化的混凝土受拉应力-应变关系建立了FRP筋混凝土梁的弯矩-曲率模型。同时基于条带法计算结果提出了三线性弯矩-曲率简化模型。将与简化模型与试验结果进行对比及参数分析，可以得到如下结论：
1)有限条带法分析得到的FRP筋混凝土梁承载力及弯矩-曲率曲线与试验结果吻合良好。
2)参数分析表明配筋率与混凝土强度是影响FRP筋混凝土梁截面弯矩-曲率关系的重要因素。随着配筋率的增加，FRP筋梁的抗弯承载力也逐渐增大。同时，增大配筋率对FRP筋混凝土梁的延性有所降低。混凝土强度越高，截面的开裂弯矩和极限弯矩也越大。
3)提出简化的弯矩-曲率三线性模型，考虑了FRP筋混凝土梁变形的主要特征，得到的弯矩-曲率关系曲线与试验结果吻合较好，该模型可为后续探讨FRP筋混凝土梁的刚度提供理论基础。
[1] BROOMFIELD P J. Corrosion of Steel in Concrete: Understanding, Investigation and Repair[M]. 2nd ed. Swiss: CRC Press, 2003.
[2] BRANSON, D E. Deflections of Reinforced Concrete Flexural Members[J]. Journal of the American Concrete Institute, 1966, 63(6): 637-667.
[3] YOST J R, GOODSPEED C H, SCHMECKPEPER E R. Flexural Performance of Concrete Beams Reinforced with FRP Grids[J]. Journal of Composites for Construction, ASCE, 2001, 5(1): 18-25.
[4] 孔祥清, 鲍成成，章文姣，等．GFRP 筋和钢筋混合配筋混凝土梁受弯性能数值模拟研究[J]. 混凝土，2017,(7):50-54.
[5] 张海霞. FRP筋与混凝土粘结滑移性能研究[D]. 沈阳：东北大学, 2006.
[6] HOGNESTAD E, HANSON N W, MCHENRY D. Concrete Stress Distribution in Ultimate Strength Design[J].ACI Journal Proceedings, 1955, 52(12): 455-479.
[7] NAYAL R, RASHEED H A. Tension Stiffening Model for Concrete Beams Reinforced with Steel and FRP Bars[J]. Journal of Materials in Civil Engineering, ASCE, 2006, 18(6): 831-841.
[8] 顾祥林, 孙飞飞．混凝土结构的计算机仿真[M]. 上海: 同济大学出版社, 2002.
[9] ALSAYED S, AL-SALLOUM Y A, ALMUSALLAM T H. Performance of Glass Fiber Reinforced Plastic Bars as a Reinforcing Material for Concrete Structures[J]. Composites Part B, 2000, 31(6，7): 555-567.
[10] PECCE M, MANFREDI G, COSENZA E. Experimental Response and Code Models of GFRP RC Beams in Bending[J]. Journal of Composites for Construction, 2000, 4(4): 182-190.
[11] THERIAULT M, BENMOKRANE B. Effects of FRP Reinforcement Ratio and Concrete Strength on Flexural Behavior of Concrete Beams[J]. Journal of Composites for Construction, ASCE, 1998, 2(1): 7-16.
[12] ASHOUR A F, HABEEB M N. Continuous Concrete Beams Reinforced with CFRP Bars[C]// Proceedings of the Institution of Civil Engineers-Structures and Buildings. 2008: 349-357.
[13] 郑永峰, 徐新生. 纤维聚合物筋混凝土梁正截面承载力的计算方法[J]. 高科技纤维与应用, 2006, 31(6)：31-36.