T型钢-混凝土组合梁是由徐变特性各异的两种材料组合而成,依靠抗剪连接件将钢梁与混凝土板组合在一起,随着时间发展混凝土板在持续压应力作用下发生较钢梁大得多的徐变,在两者的变形协调过程中,钢梁要约束混凝土板的伸长,由此产生一组约束力和约束反力,而且钢梁弯曲刚度比混凝土板的大很多,将产生显著应力重分布,引起刚度折减和挠度显著增加等不利影响[1]。有限元软件操作人员对隐含的计算理论和方法常常了解不多。而且,大多数软件并没有植入混凝土徐变本构模型,植入的是适合于计算金属蠕变的一般的黏弹性本构模型,用这些模型来计算混凝土徐变时,还需要验证。当采用力法,在建立变形协调方程时可代入的徐变本构方程有很多,如积分本构、经典的迪辛格(Dischinger)微分本构、代数本构[2]。不同的徐变本构方程适用的结构分析方法和计算结果的精度不同,方程的形式和求解的难易与选择的徐变本构方程有关,对使用者要求高,因此在工程实用计算上存在选择和应用的不便。
为此,EN 1994-2《欧洲规范4钢-混凝土组合结构设计: 桥梁》[3]给出了一个非常实用的计算方法:基于经典的有效模量法,用反映组合梁徐变影响的定值徐变因子(永久荷载ψL=1.1)来修正,给出混凝土弹性模量折减系数的函数。本文将利用徐变微分本构方程推导徐变因子与徐变系数、刚度系数和组合系数等有关的计算式[4]。与数值积分法相比[5],优点是不依赖和取决于具体的徐变系数模型。相比EN 1994-2的定值徐变因子,提供了一种能够更为细致合理的分析方法。
1 算式推导
1.1 本构方程
徐变系数φt是指持时t时结构发生的应变值与加载龄期t0发生的弹性应变之比,是t0和t的二元耦合函数,表示为φ(t,t0)。按照黏弹性理论,徐变与应力关系的被积函数中含有徐变系数,自变量t同时出现在积分的上限和被积函数中,数学上称为Volterra积分方程,当φ是t和t0的耦合函数时,只能用数值积分法求解。
(1)
Dischinger于1937年对徐变系数提出了一个重大假定[6],使t和t0解耦,将积分本构转化为微分本构,得到一些徐变问题的经典的解析解,为工程实用计算带来了极大方便[7]。Dischinger假设在同一时刻不同加载龄期的徐变系数曲线具有相同的斜率,加载速率与加载龄期无关,不同加载龄期的徐变系数曲线可由初始时刻曲线向下平移获得,即有φ(t,τ)=φ(t,t0)-φ(τ,t0)。由此对式(1)进行分部积分、求导可导得徐变的微分本构方程为:
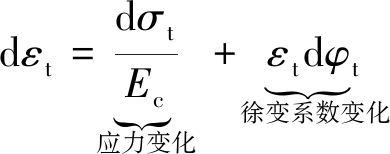
(2)
式(2)表示混凝土在任意t时刻的应变增量=应力增量引起的弹性应变+t时刻应变×徐变系数的增量,即应变增量分为两个部分:应力变化引起的弹性应变;徐变系数变化引起的非弹性应变。
1.2 组合梁的重分布内力
T型钢-混凝土组合梁的徐变截面分析模型如图1所示。
假设在任意时刻组合截面满足平截面假定,由此在t0、t和t+dt时刻的应变分布为三条直线。这三个时点之间有两个间隔,因此在部分截面上产生两组重分布内力。徐变引起的重分布内力为一组自平衡内力,不改变组合截面内力(弯矩M)的大小。
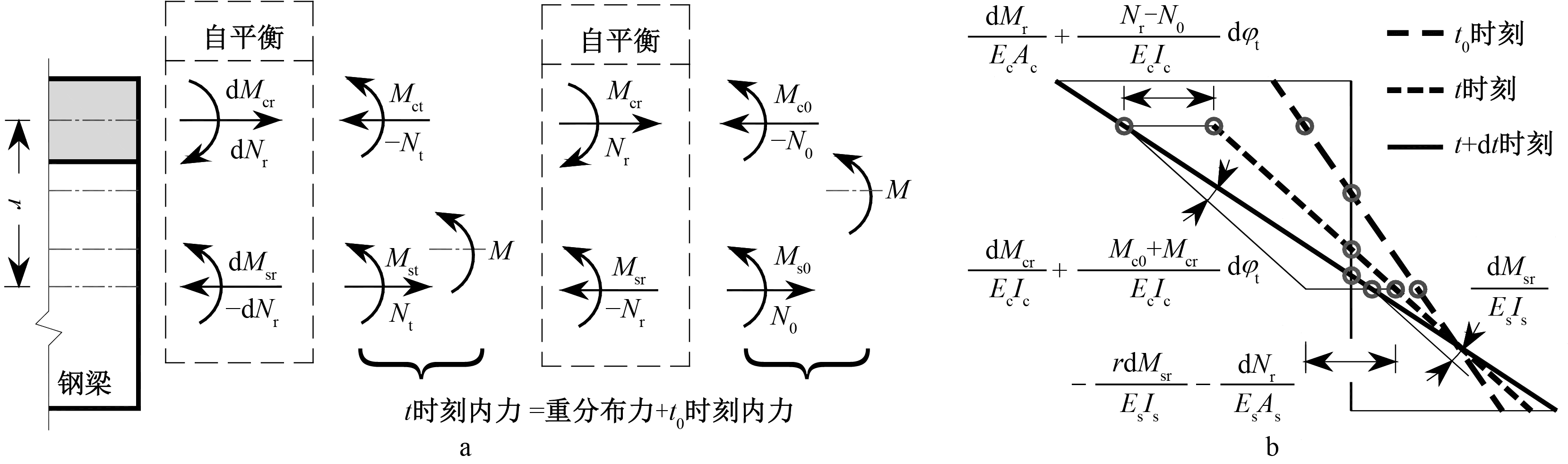
a—内力; b—应变。
注:1)下标c、s、0、t、r分别表示混凝土板、钢梁、t0时刻、t时刻和重分布;Mc0和Ms0分别为混凝土板和钢梁的初始弯矩,Mcr和Msr分别为重分布弯矩,Mct和Mst分别为t时刻弯矩,dMcr和dMsr分别为t 至t+dt时刻的重分布弯矩;N0为初始组合力,Nr为重分布组合力,Nt为t时刻组合力,dNr为t至t+dt时刻的重分布组合力;E、A和I分别为弹性模量、面积和惯性矩,r为混凝土板和钢梁形心之间的距离。
2)轴力以受拉为正;弯矩以使得截面下边缘受拉为正;截面高度坐标以向下为正。
图1 内力和应变分布
Fig.1 Internal force and strain distribution
从图1观察到:徐变使组合截面总形心轴下移了,这是因为虽然混凝土板和钢梁各自的形心位置不会改变,但Ect<Ec,混凝土板在t时刻的换算面积要减小(等效换算宽度减小),则必然总形心位置要下移。图1中部分截面内力的箭头标出了实际方向,N0、Nr和Nt表示受拉的组合力,为了方便计算,另一组与之平衡的组合力直接用添加负号来表示。
时间变化带来的是一组未知量(自平衡的重分布内力),除去平衡条件可求解得到,还有两个未知量,因此组合截面的徐变问题是内部二次超静定问题,需要补充两个变形协调方程。有了Dischinger微分本构方程[6],便可列出这两个微分形式的变形协调方程,而且可以导出未知量的解析式。
按照式(2),应变增量由两部分构成:重分布应力增量产生的应变;徐变系数增量引起的应变。而且注意到应力和应变可以是广义应力和广义应变,与弯曲变形对应的是弯矩和曲率。这样,写出t至t+dt时刻的应变和曲率在部分截面上的增量的计算式(图1),列出应变和曲率协调的增量方程,加之增量重分布内力的弯矩平衡方程,有:
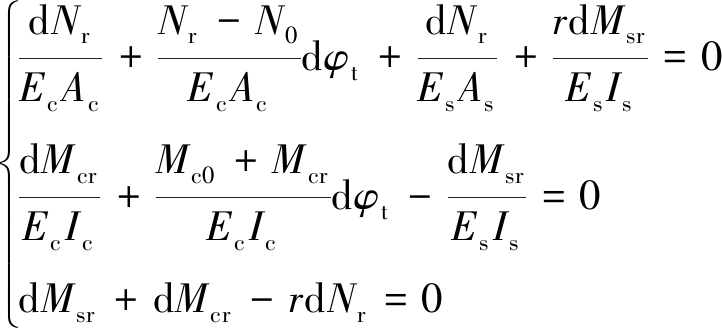
(3)
而t0时刻的初始内力为:

(4)
其中 EI=EcIc+EsIs+EAr2
式中:EI为组合截面刚度;EA为部分截面轴向串联刚度。
式(3)的电算求解没有难度,但导得的解析式冗长而复杂。为了获得简单的解析式,做一个合理的简化处理,令dMcr=0,代入式(3),有:
(5)
令![]()
则式(5)可表示成:
(6)
考查系数αs的物理意义:
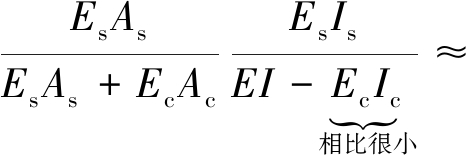

(7)
令![]()
则:
αs=αsNαsM
(8)
可见,αs表示的是两个刚度系数的乘积,其中αsN表示轴向刚度中钢梁对组合截面的比值,αsM表示弯曲刚度中钢梁对组合截面的比值。
由式(4)容易导得重分布轴力Nr的解析式,进而导得部分截面重分布弯矩的解析式,即:
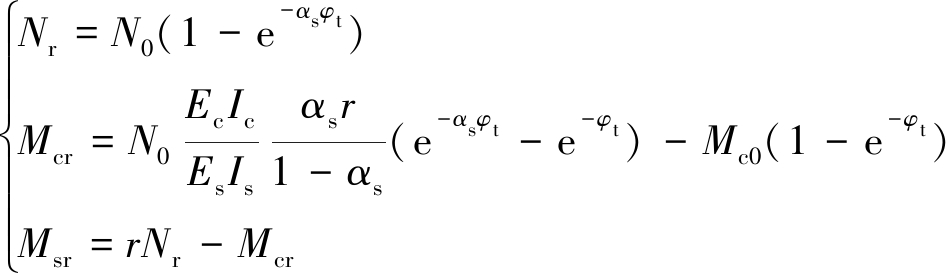
(9)
将重分布内力与初始内力叠加,得到t时刻的部分截面内力,即有:
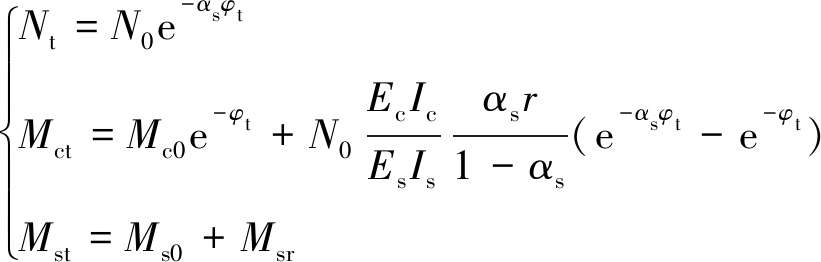
(10)
1.3 组合梁轴压徐变因子和弯曲徐变因子
如果知道弹性模量与时间的关系,则可直接按照Hooke定律由应力来计算应变。轴压力产生轴向应变的轴压徐变,弯矩产生曲率的弯曲徐变。所以按照荷载类型,将有效模量表示为两种:轴压弹性中的模量Ec1和弯曲弹性模量Ec2。参考EN 1994-2模型,有:
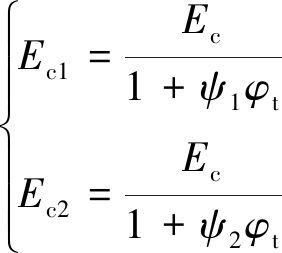
(11)
式中:ψ1和ψ2分别为轴压徐变因子和弯曲徐变因子。
这样,容易写出在部分截面上全量的协调方程和平衡方程,即:
(12a)
(12b)
Mst+Mct+rNt=M
(12c)
在平衡方程式(12c)中,弯矩按照钢梁、混凝土板和组合弯矩刚度三个部分分配,T型钢-混凝土组合梁的混凝土板弯曲刚度板为总刚度的1.5%以内(当钢梁高大于80 cm时)[8]。如果忽略混凝土板的t时刻弯矩,则有:
Mct=0
(13)
将Mst=M-rNt代入式(12a)和(12b)中,则有:
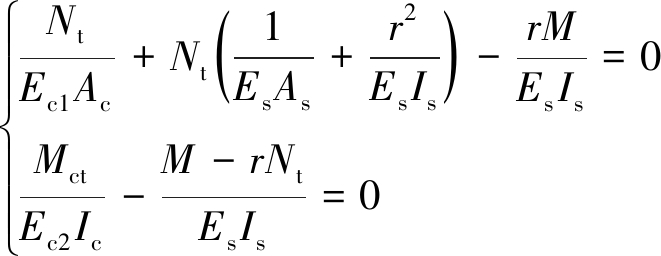
(14)
以徐变因子为因变量,将式(10)和式(11)代入式(14),整理化简,有:
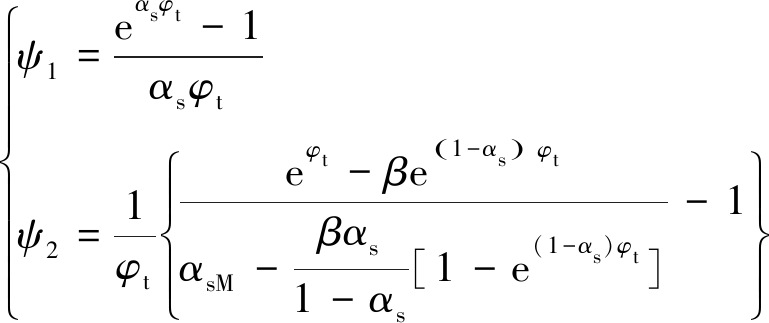
(15)
由式(15)可见,徐变因子与徐变系数、刚度系数和组合系数有关。
需要说明的是,在徐变因子的推导过程中进行了两次简化处理:式(5)的dMcr=0,式(13)的Mct=0。这一假定最早由Sontag于1951年提出[9]。钢梁的高度相比较大,弯曲刚度贡献就较大,混凝土板的弯曲刚度较小,分配到的重分布弯矩亦较小,因此在桥梁结构中可以忽略[10]。虽然进行了简化处理,但可导得徐变因子的解析式。由此产生多大的偏差,将在第2.2节进行比较分析。
1.4 组合梁换算截面的计算
由弹性模量按材料力学方法可计算持续荷载作用下的内力和变形,将混凝土换算为等效的钢在计算上更为方便,换算之后称为混凝土换算截面,计算过程和公式如图2所示。
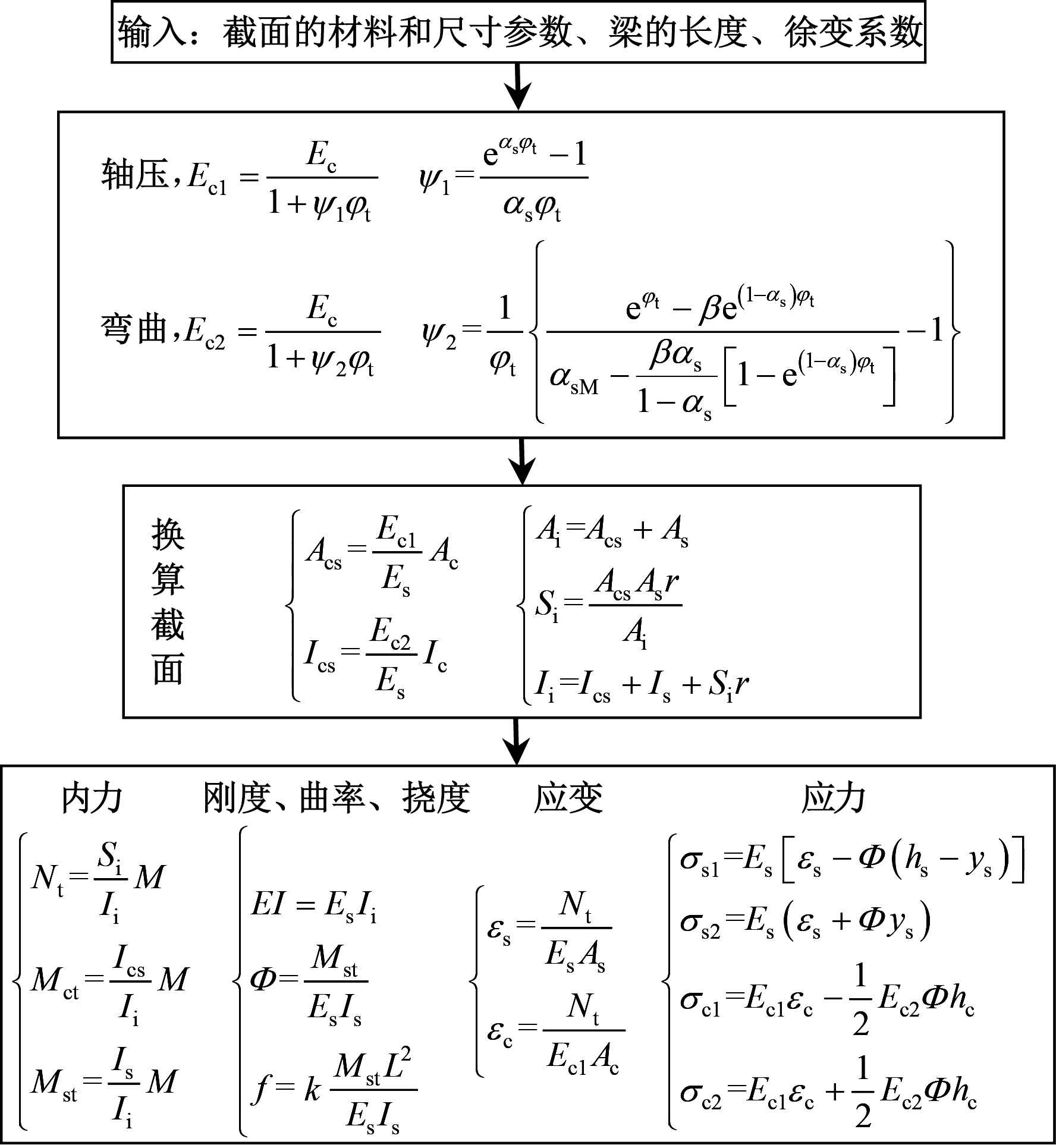
注:Φ为曲率;f为挠度;εs和εc分别为钢梁和混凝土板的形心应变;σs1和σs2分别为钢梁上、下边缘应变;σc1和σc2分别为混凝土板上、下边缘应变;hs和hc分别为钢梁和混凝土板的高度;ys为钢梁形心至截面下边缘的距离;k为与荷载分布相关的挠度系数,如均布荷载时,k=5/48。
图2 计算流程
Fig.2 Calculation flow
值得注意的是,在由应变计算应力时,混凝土板边缘应力计算必须用两个弹性模量,组合力产生的轴压应力用轴压模量Ec1,弯矩产生的弯曲应力用弯曲模量Ec2,否则会出现应力计算错误。
2 参数分析
2.1 徐变效应的计算
用文献[11]算例4.2-1的组合梁截面参数:钢梁为I30b,Es=2.1×105 MPa;混凝土板的有效宽度1 330 mm,高度100 mm,Ec=2.8×104 MPa。假设跨度9 m,长期均布荷载作用10 kN/m(跨中截面弯矩M=101.25 kN m)。假设t时刻徐变系数φt=4,采用四种方法计算组合梁在持续荷载作用后的t时刻的徐变效应,包括混凝土板的换算截面参数、部分截面重分布内力、应力和梁的变形(表2)。这四种方法分别是:
m)。假设t时刻徐变系数φt=4,采用四种方法计算组合梁在持续荷载作用后的t时刻的徐变效应,包括混凝土板的换算截面参数、部分截面重分布内力、应力和梁的变形(表2)。这四种方法分别是:
方法1,微分方程组(式(3))的电算解;
方法2,公式(15);
方法3,EN 1994-2中徐变因子ψL=1.1;
方法4,0.5Ec。
分析表2,可以归纳出以下五点。
1)从方法1的结果看,徐变使混凝土弹性模量降低,表现在混凝土板的等效面积退化至原来的18%左右,等效惯性矩至10%左右,组合截面刚度降低至59%左右,组合力削弱至73%,钢梁弯矩增加到约1.7倍,挠度增加到约1.7倍,钢梁上边缘的压应力增加到约29倍。显然,徐变对组合梁的长期力学性能影响是非常不利的,减小了刚度、增加了变形和显著加大了钢梁上翼缘的局部失稳的可能性。
2)方法4弹性模量折半的方法偏差较大,不能正确反映徐变效应的时随规律,高估了刚度,低估了变形和钢梁的压应力。
3)方法2与方法1吻合好。
4)方法2的轴压徐变因子(ψ1=1.19)与EN 1994-2的定值徐变因子1.1很接近。
5)令人惊讶的是,只用一个徐变因子定值的弹性模量的时间模型,竟然计算出与方法1吻合较好的结果(组合力、刚度、变形和钢梁压应力)。仔细分析不难发现其中原由。按照Sontag假定,混凝土板的弯曲刚度小可以忽略[9],如本例用方法1算得的混凝土板刚度为总刚度的0.8%,故即便用轴压徐变因子代替弯曲徐变因子,换算得到的等效惯性矩偏差大(如本例方法3为274 cm4, 方法1为146 cm4),对结果影响也较小。这也说明EN 1994-2的徐变因子是轴压徐变因子。
钢梁高度是影响钢梁惯性矩的最显著因素,当钢梁高度变化时,方法2与方法1的偏差情况,EN 1994-2用定值的一个徐变因子,其结果与轴压、弯两个徐变因子的吻合性,都需要做进一步的参数分析。
2.2 钢梁高度变化的影响
对2.1节的组合梁,选择钢梁I22b、I24b、I25b、I27b、I28b、I30b、I32b、I36b、I40b和I45b共十个型号进行参数分析(徐变系数为4)。
表2 计算结果
Table 2 Calculation resules

方法徐变因子混凝土弹性模量/MPa混凝土板换算截面ψ1ψ2Ec1Ec2Acs/cm2Ics/cm4Ii/cm4弯曲刚度EI/(kN·m2)形心轴高度y0/mm组合内力N/kN弯矩/(kN·m)McMs曲率MsEsIs/106 mm-1跨中挠度f/mm应力/MPaσc1σc2σs1σs211.192.284 8752 7683114618 01037 8202132380.8252.82.6822.6-2.16-1.42-48.95119.7121.192.644 8572 4253112817 97137 7382132380.7253.02.6822.6-2.11-1.46-49.14199.8831.11.15 1855 1853327418 50038 8492162421.5051.42.6122.0-2.49-1.14-46.18118.014——14 00014 0008973925 43653 4162643042.9437.41.901.6-4.97-1.32-19.85144.35t0——28 00028 0001771 47830 38163 8012953254.9231.31.5913.4-4.67-0.22-1.6698.32
注:最后一行数值为t0时刻的数值;其他为徐变系数φt=4时方法1~4的计算结果。
1)计算混凝土弹性模量的折减系数和徐变因子,见图3。
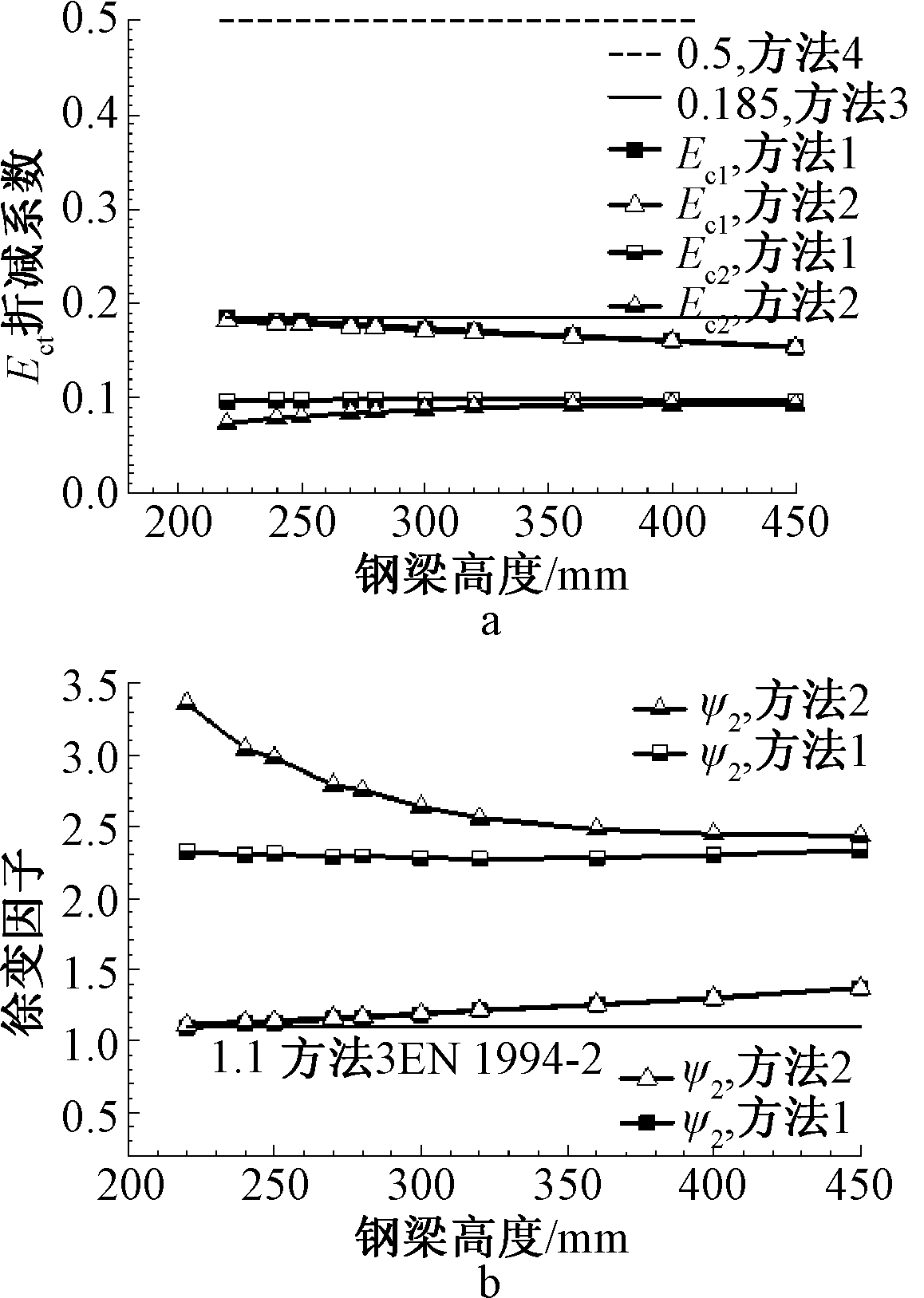
a—弹性模量的折减系数; b—徐变因子。
图3 弹性模量和徐变因子与钢梁高度关系
Fig.3 Relation of elastic modulus and creep multipier with steel beam heigth
从图3可以看出,EN 1994-2的折减系数和徐变因子与轴压模量Ec1在数值上很接近,但随着钢梁高度的增加偏差增大。方法2与方法1在数值上很接近,两者曲线在Ec1和ψ1上几乎重叠,在Ec2和ψ2上虽然在钢梁高度小时偏差大,但实际工程中为了充分利用材料,就本算例钢梁的高度不会小于300 mm,而且随着钢梁高度的增加偏差减小,说明在合理简化的基础上导得的徐变因子的近似计算式(式(15))合理。
2)徐变对组合截面内力和应力的不利影响,包括对组合力的削弱、对钢梁弯矩的增加、对混凝土压应力的卸载和对钢梁压应力的增加,见图4。从图4可见,方法2与方法1在数值上很接近,两者曲线几乎重叠,说明方法2可用。在曲线的数值和走势上虽然方法3与方法1接近,但还是在一定程度上低估了对组合力的削减程度、对钢梁弯矩的增大幅度、对混凝土应力的卸载和对钢梁压应力的增加,而且随着钢梁高度的增加这些偏差还在加大,说明用方法2的公式计算徐变因子比用EN 1994-2定值徐变因子进行计算的结果更精确。
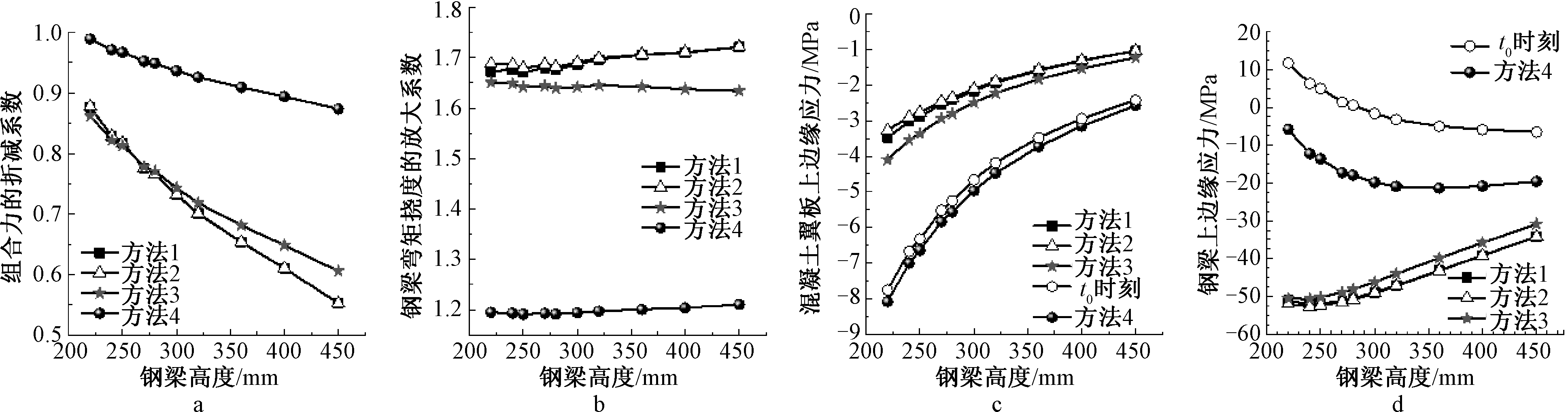
a—徐变对组合力的削弱; b—徐变对钢梁弯矩或挠度的增加; c—徐变对混凝土应力的卸载; d—徐变对钢梁应力的增加。
图4 钢梁高度的影响
Fig.4 Influences of steel beam height
图4b表示的也是挠度增加系数(组合梁的挠度增加系数与钢梁弯矩的放大系数相同),因为钢梁没有徐变,钢梁的弯曲刚度不会随着时间改变,组合梁挠度与钢梁弯矩呈线性关系(见图2的挠度计算公式)。另外,值得注意的是,从图4b观察,随着钢梁高度的增加按EN 1994-2计算的结果的偏差加大,而且曲线呈缓慢下降趋势,这不符合组合梁的时随规律(钢梁弯曲刚度越大,徐变引起的变形越大,曲线应呈上升趋势)。因此,相比EN 1994-2,方法2提供的挠度更合理。
3 结 论
组合梁徐变计算往往是设计人员感到十分棘手的问题之一。有了反映组合梁徐变特性的有效弹性模量,则可不用领会复杂的徐变本构方程,直接按照内力由刚度分配原则计算各种徐变效应。
EN 1994-2给出的用定值徐变因子和徐变系数表示的弹性模量折减模型,计算结果符合组合梁徐变的时随规律,与微分方程的电算结果比较偏差小,但会低估组合梁的各种不利影响,如低估挠度、低估钢梁上翼缘局部失稳和混凝土板开裂的可能性。而且随着钢梁高度的增加,这种偏差也在增加。
按照荷载类型,将徐变因子分为轴压徐变因子和弯曲徐变因子,能够更细致地描述组合梁的徐变行为。在合理简化的基础上(忽略混凝土板的弯矩),用微分方程解(式(10)),可导出徐变因子的计算式(式(15)),该式计算的结果与微分方程组的电算结果非常吻合,证明可用。相比EN 1994-2的定值徐变因子,式(15)可作为组合梁徐变效应分析的更细致和更精确的方法的一种补充。另外,当降低精确要求时,可不区分荷载类型,只用一个轴压徐变因子(式(15)中ψ1),因为混凝土板的弯曲刚度占比小,即便用轴压徐变因子代替弯曲徐变因子将混凝土换算为等效钢的惯性矩有较大的偏差,对结果的影响也较小。
[1] 周履, 陈永春. 收缩徐变[M]. 北京: 中国铁道出版社, 1994:115-374.
[2] 陈旭, 莫南明, 邱志刚, 等. 混凝土松弛系数的实用计算[J]. 公路交通科技, 2018, 35(3): 18-27.
[3] European Committee for Standardization. Eurocode 4. Design of Composite Steel and Concrete Structures-Part 2: General Rules and Rules for Bridges:EN 1994-2[S]. Brussels: CEN, 2005.
[4] KINDMANN R, XIA G. Erweiterung der Berechnungsverfahren für Verbundträger[J]. Stahlbau, 2000, 69(3):170-183.
[5] PARTOV D, KANTCHEV V. Gardner and Lockman Model in Creep Analysis of Composite Steel-Concrete Sections[J]. ACI Structural Journal, 2014, 111(1):59-69.
[6] SPECHT M. Spannweite der Gedanken: zur 100. Wiederkehr des Geburtstages von Franz Dischinger[M]. Berlin: Springer, 1987: 193-228.
[7] SOUICI A, TEHAMI M, RAHAL N, et al. Creep Effect on Composite Beam with Perfect Steel-Concrete Connection[J]. International Journal of Steel Structures, 2015, 15(2):433-445.
[8] ZHANG S P, CHEN X, LI G L. Study on the Influence of Reinforcement on Creep and Shrinkage Effects of Composite Beams[C]// IOP Conference Series: Earth and Environmental Science. UK: Institute of Physics Pubishing,2019.
[9] SONTAG H J. Beitrag zur Ermitlung der zeitabhängigen Eigenspannungen von verbundträgern[D]. Karlsruhe:Techn. Hochschule Karlsruhe, 1951.
[10] 陈旭,章胜平,莫南明,等. 组合梁截面重分布力的Volterra积分方程[J]. 铁道学报, 2019, 41(4):142-150.
[11] 朱聘儒. 钢-混凝土组合梁设计原理[M].2版.北京:中国建筑工业出版社, 2006.