依托大跨度桥梁构建观光平台和提升旅游景点,是开发旅游资源,谋求经济和社会利益的重大举措。在大跨度悬索桥桥塔顶部建设观光平台,需依附现有塔柱布设电梯井与楼梯间附属设施,如图1所示。附属设施的布置将改变塔柱的外形,并显著增大风荷载作用截面,可能影响已经建成桥梁的安全与正常使用。因此如何合理布置电梯井等附属设施以及较准确地计算新桥塔对应设计风速下的风荷载将成为结构设计重点关注的问题。
桥塔气动力系数是研究桥塔抗风性能的主要参数之一。近年来随着计算流体动力学(CFD)数值方法的飞速发展,CFD与风工程研究结合形成了计算风工程,相比风洞试验等研究方法,CFD模拟能形象而又细致地再现风工程的复杂流动,研究周期短、便于考虑多种方案、费用低,且易于揭示流动机理[1]。目前国内外对增设观光附属设施后桥塔的气动特性和干扰效应研究鲜有报道[2-6]。本文以杭瑞高速洞庭湖大桥观光平台项目论证为例,开展了原桥塔与增设附属设施后新桥塔断面绕流的二维雷诺时均Navier-Stokes(RANS)模型模拟。通过尝试5种气动优化措施的模拟计算,获得了新桥塔在不同气动外形布置下的气动力系数和漩涡脱落Strouhal(St)数,并与原桥塔进行了对比,确定了最优的新桥塔实施方案。同时,就结构设计重点关注的设计风速下风荷载值进行了对比研究,为同类工程应用提供参考。
1 工程背景
杭瑞高速洞庭湖大桥是杭州至瑞丽国家高速公路跨越洞庭湖的大跨度桥梁,主桥跨度组合为460 m+1 480 m+491 m,采用双塔不对称桁架梁悬索桥方案。其中原桥塔采用门形结构,由塔柱和横梁组成,包括上塔柱、下塔柱、上横梁和下横梁。经过多方论证拟在原君山侧桥塔顶(图1)约235.088 m位置进行双层观光平台的建设,因为垂直交通及消防疏散需要,需自塔底35.330 m标高位置布置如图1所示的电梯与楼梯。

图1 杭瑞高速洞庭湖悬索桥主塔塔柱增设观光电梯布置方案 m
Fig.1 The layout of adding sightseeing elevator to the main tower column of the Hangzhou—Ruili suspension bridge
2 CFD控制方程
基于文献[7-8]的数值方法来获得与桥梁等效静风荷载有关的气动力系数。桥梁风工程绕流属于不可压黏性流动,其雷诺时均Navier-Stokes方程可表示为:
(1a)
(1b)
式中:![]() 分别为直角坐标系xj下空气流动的平均速度和脉动速度; ρ、μ分别为空气密度和分子黏性; t为时间; p为压力;
分别为直角坐标系xj下空气流动的平均速度和脉动速度; ρ、μ分别为空气密度和分子黏性; t为时间; p为压力;![]() 为雷诺应力。上述雷诺应力的引入使得控制方程不封闭,需要引入湍流模型进行求解。基于涡黏假设,可将雷诺应力表示为:
为雷诺应力。上述雷诺应力的引入使得控制方程不封闭,需要引入湍流模型进行求解。基于涡黏假设,可将雷诺应力表示为:
(2)
其中![]()
式中:μ为湍流黏性; Cμ为经验常数;k和ε分别为流动湍动能和湍流黏性耗散率。
本文采用综合了标准k-ε模型和k-ω 湍流模型的SST k-ω湍流模型,SST k-ω湍流模型结合了上述两种湍流模型的优点,抛弃了它们各自的缺点。
3 研究对象与数值实现
为了获得原桥塔塔柱不同位置气动三分力系数,选取君山侧桥塔三个不同高度(图2)及对应的塔柱断面,也即G截面、H截面、I截面,其中H截面位于桥塔2/3高度处。
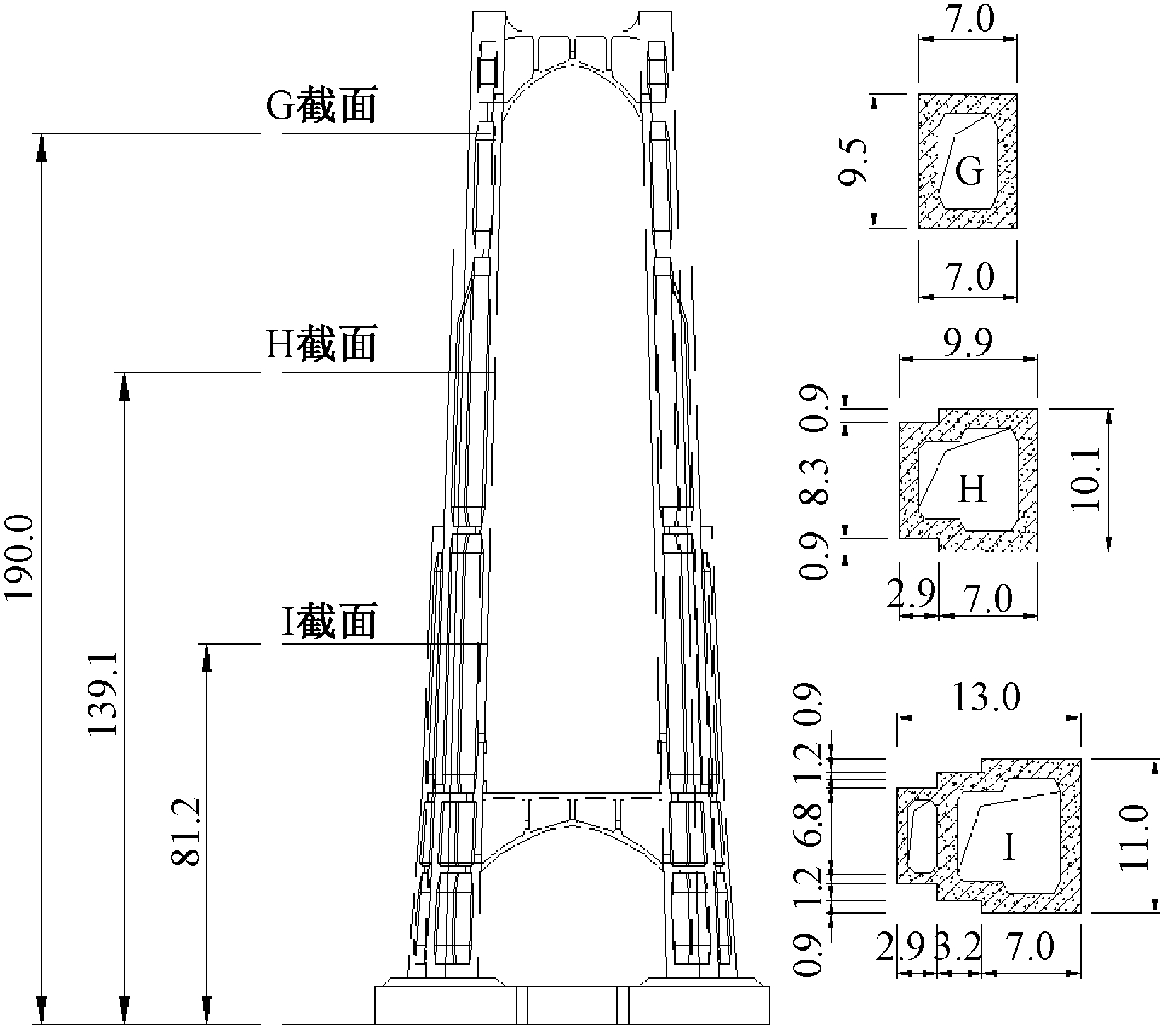
图2 原桥塔立面及塔柱横断面选取 m
Fig.2 The tower elevation and cross section of original bridge
3.1 计算域网格及流动条件
以G截面为例,其CFD模拟计算域如图3所示。计算域入口距离模型最前端为10D,上下两个侧边距离模型两端也为10D(其中D为模型最长边长)。计算域堵塞率为5%,满足风工程模拟对模型堵塞率不大于5%的要求[9]。
计算域入口边界定义为水平层流速度边界,下游出口施加纽曼边界条件;桥塔G断面表面为无滑移壁面;计算域上、下边界采用对称边界条件。计算域初始场采用入口速度条件初始化。
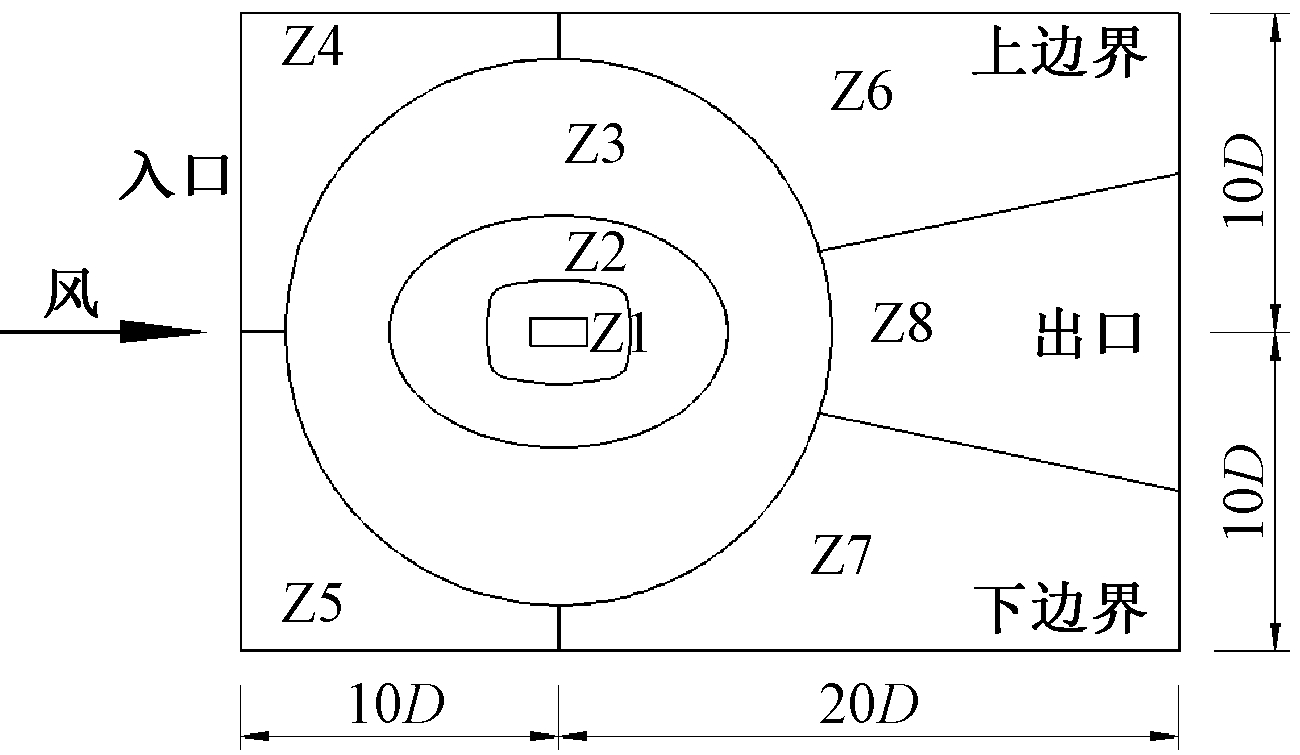
图3 计算域与分区
Fig.3 Grid partition in computational domain
3.2 CFD模拟的时间步及网格无关检查
对水平来流风作用下的主塔构件截面,气动力的作用点定义在扭转中心(图4)。定义桥塔断面的气动阻力、升力、扭矩系数分别为:
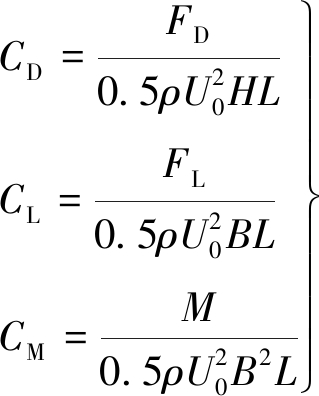
(3)
式中:ρ为空气密度,一般取1.225 kg/m3;U0为来流风速;FD为作用在截面上的阻力(来流风向为正);FL为作用在桥塔截面上的升力(垂直来流方向向上为正,也称之为横风向力);M为作用在桥塔截面上的扭矩;H为0°攻角时(来流垂直桥梁轴线,也即横桥向)截面在来流方向的投影高度;B为0°攻角时截面在平行来流方向的投影宽度;L为计算截面的展向长度,二维时L为单位长度1。
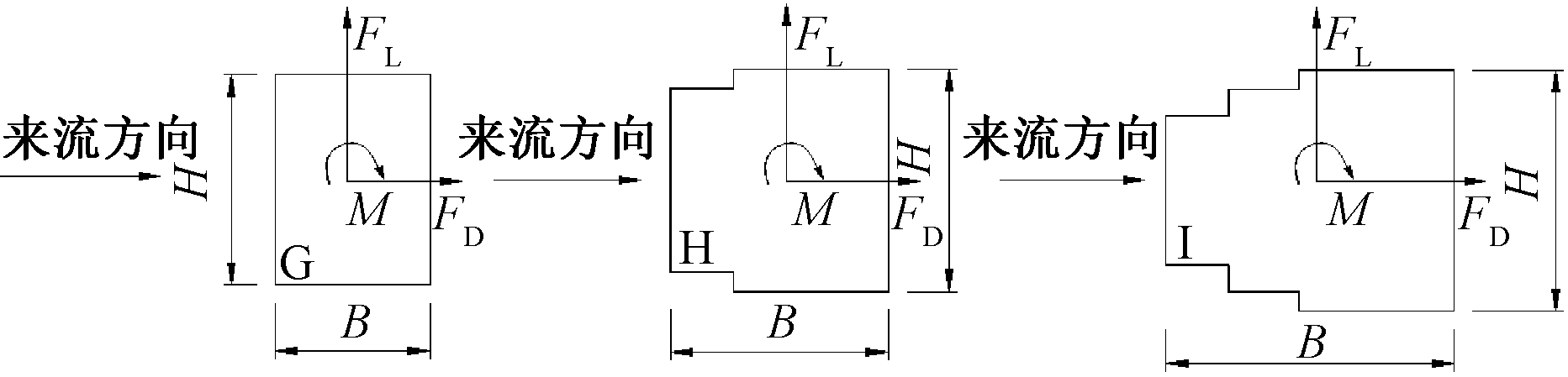
图4 G、H及I截面气动力定义
Fig.4 Aerodynamic definition of section G,H and I
定义桥塔断面漩涡脱落St数为:
St=fsB/U0
(4)
式中:fs为漩涡脱落频率。
为本文数值模拟方法在后继计算中的应用提供有利的基础与合理性证明,因此开展了CFD计算的时间步及网格无关性检查,对多个模型及时间步长进行了计算,CFD计算均能稳定和收敛,且模型表面的Y+(壁面雷诺数)值在各个时间步上均满足Y+<1的要求,其中G截面模型如图5所示。
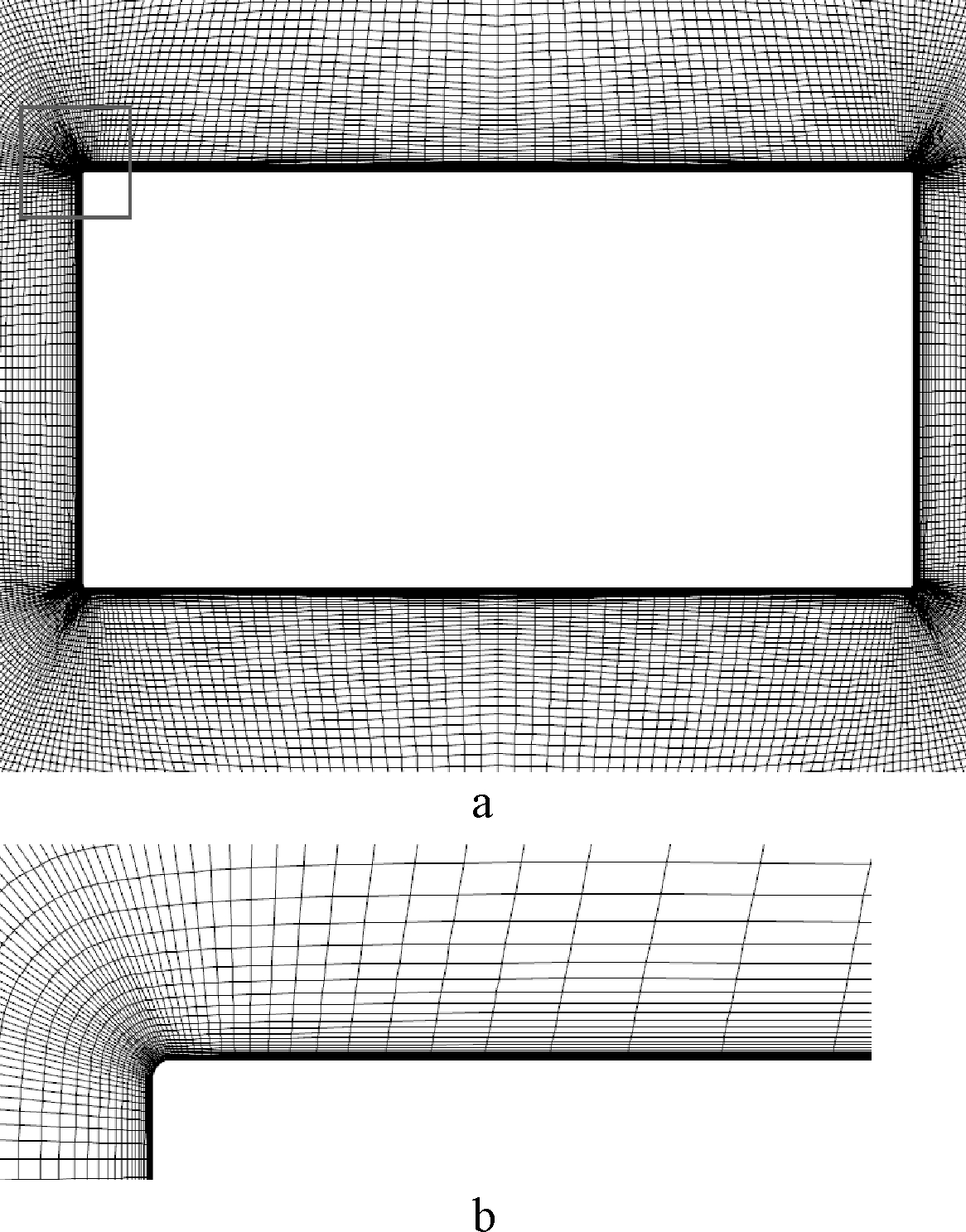
a—桥塔截面周围网格; b—角沿网格放大。
图5 桥塔截面周围网格布置
Fig.5 Grids arrangement around tower section
4 原塔柱气动力系数计算
对原桥塔柱G、H和I三个断面进行了数值计算,横桥向计算局部网格划分如图6所示(顺桥向计算时模型旋转90°),计算工况定义见图7。为了探究桥塔截面在各来流方向上的气动力特性,每种截面进行横桥向和顺桥向两种来流方向(来流方向定义见图7)计算,计算结果如表1所示。
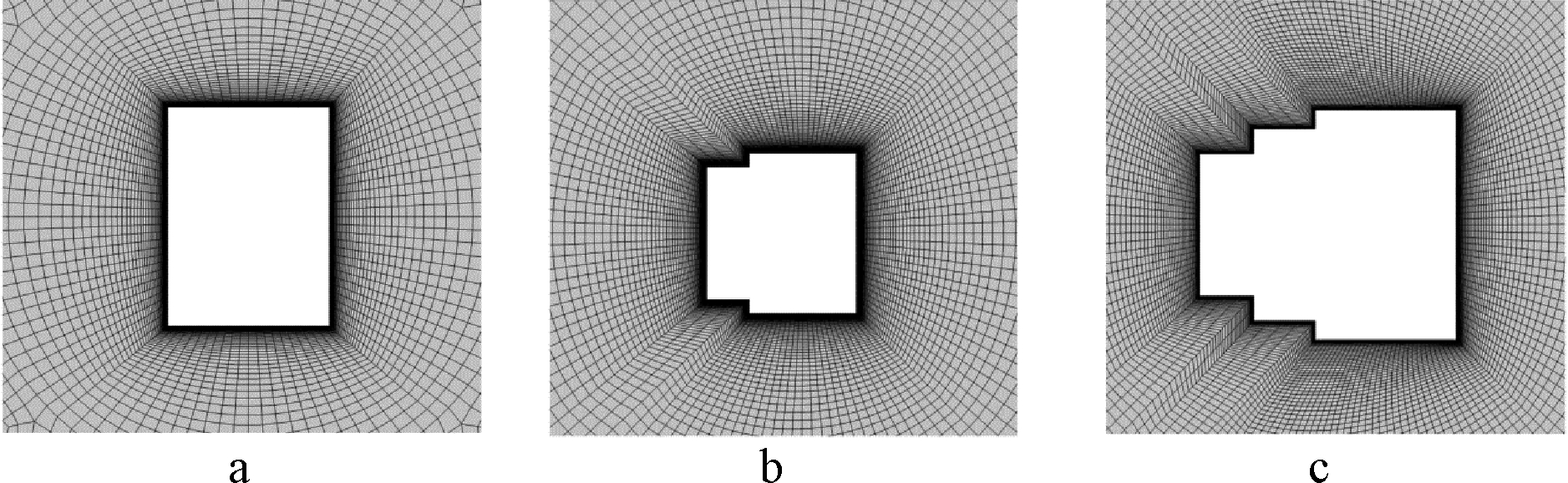
a—G截面; b—H截面; c—I截面。
图6 原桥塔计算截面网格划分局部
Fig.6 Mesh arrangement around the tower section
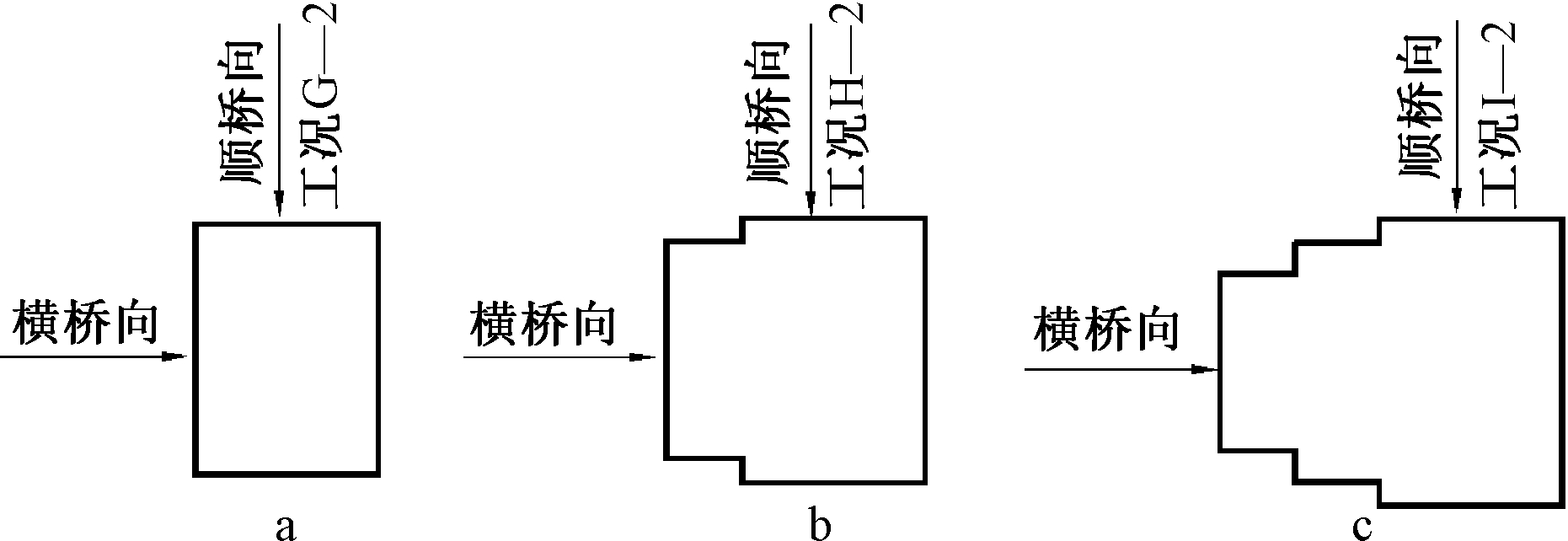
a—工况G-1; b—工况H-1; c—工况I-1。
图7 原桥塔计算截面横桥向及顺桥向计算工况定义
Fig.7 Calculation cases definition of tower sections
从表1数据可以看出:阻力系数在横桥向随宽高比(B/H)增大而变小;在顺桥向随宽高比(B/H)增大而增大。对H和I截面,在顺桥向为非对称截面,从而出现较大的升力系数值。
表1 原桥塔截面三分力系数和St数
Table 1 Three component coefficient and St number

来流工况B/HCLCDCMStG-10.740.062.79-0.010.15H-10.982×10-31.47-1.33×10-40.17I-11.18-1×10-31.122.19×10-40.21G-20.740.011.87-3.44×10-40.12H-20.98-0.352.570.030.14I-21.18-0.382.770.020.15
5 增加附属设施后桥塔柱气动力系数计算
原桥塔一旦建成,结构的抗力亦即确定。增加附属设施显著地增加了结构迎风面宽度,很可能导致荷载作用超过原结构的抗力允许范围。因此,附属设施的气动措施以及与原桥塔的合理连接将直接影响新桥塔的荷载取值,将成为工程可行性论证中的重点问题。为此,基于CFD手段,进行了5种工况a~e下的气动力系数计算,且每种情况下横桥向及顺桥向来流方向定义同图7一致,结果见表2。
表2 增设附属设施桥塔计算工况
Table 2 Calculation of additional auxiliary bridge towers

工况工况描述(三对象分别为原桥塔柱、电梯井及楼梯间)a三对象之间整体封闭连接(图8)b三对象之间整体封闭连接,且将外沿处理成圆角(图9)c原塔柱与楼梯间封闭连接,与电梯井透风处理(图10)d原塔柱与楼梯间及电梯井均透风,且将外沿处理成圆角(图11)e考虑上、下游塔柱,楼电梯井均透风,且将外沿处理成圆角(图12)
5.1 塔柱与附属设施封闭连接
原桥塔增设附属实施之后,电梯井与楼梯间分立原桥塔两侧,在原桥塔结构上先施工膨胀锚栓,再通过焊接件钢板与对应附属设施的钢梁实现结构连接;结构连接完成后,最后在外围安装玻璃幕墙结构实现围护结构的封闭连接。按研究对象所取断面,工况a在CFD中计算截面如图8所示,三分力系数计算结果如表3所示。
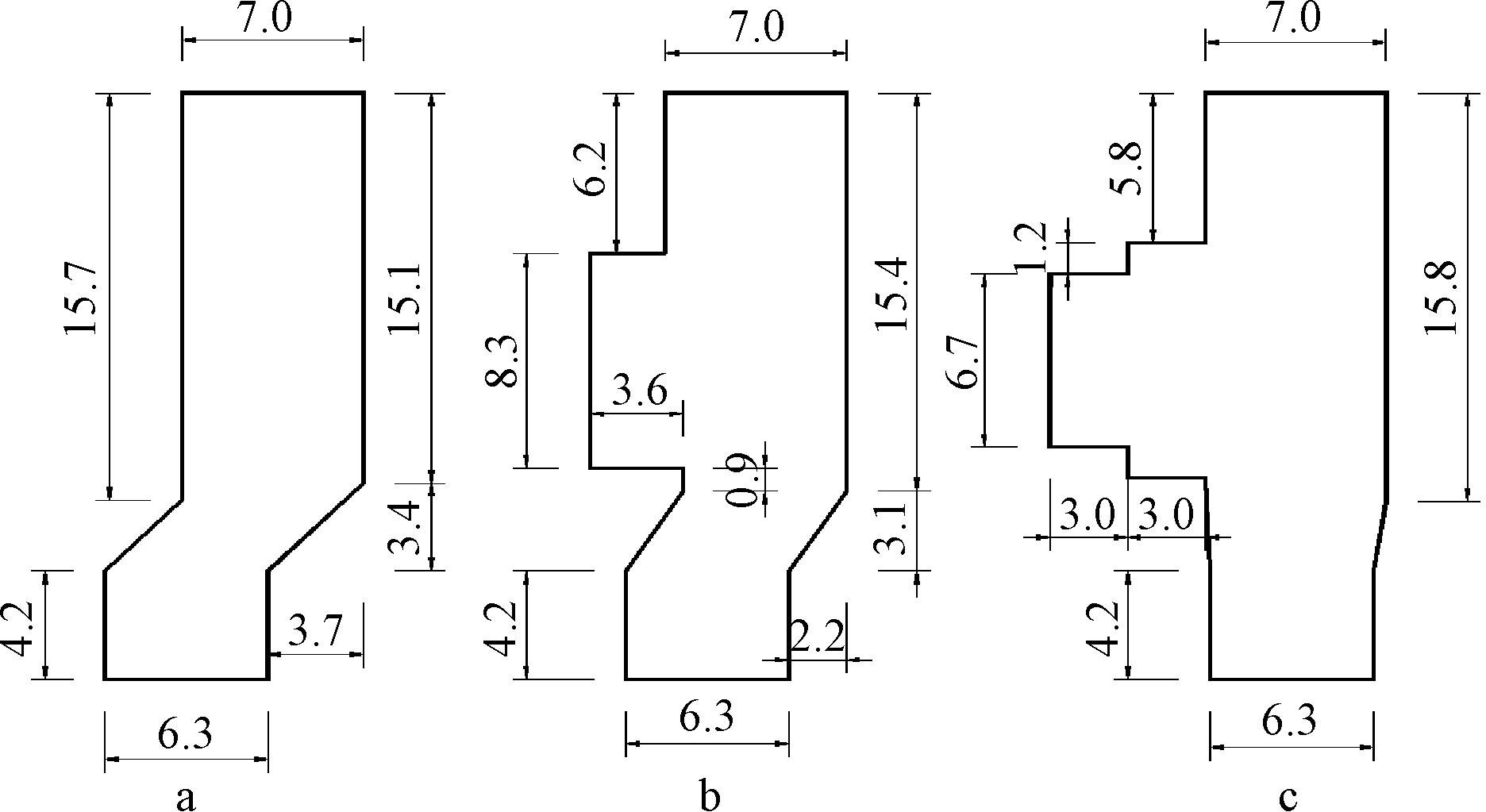
a—G计算截面; b—H计算截面; c—I计算截面。
图8 工况a计算截面 m
Fig.8 Calculation sections of case a
表3 工况a三分力系数和St数
Table 3 Three component coefficient and St number of case a
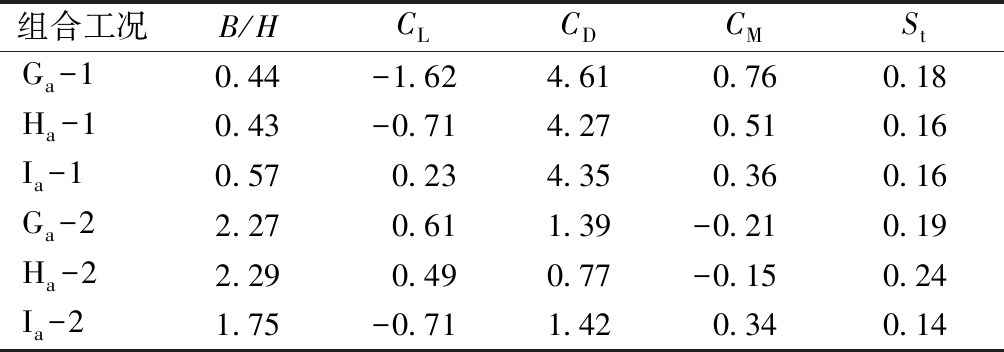
组合工况B/HCLCDCMStGa-10.44-1.624.610.760.18Ha-10.43-0.714.270.510.16Ia-10.570.234.350.360.16Ga-22.270.611.39-0.210.19Ha-22.290.490.77-0.150.24Ia-21.75-0.711.420.340.14
由以上计算结果可以看出:因为楼梯与电梯的增加,导致迎风面积增大,塔柱宽厚比明显增大。以H截面为例,其横桥向阻力系数原桥塔由1.47增大为4.27,增加约190%。而顺桥向由于加大矩形体顺来流方向的宽度后流动有可能再次附着在矩形表面上,于是尾流宽度变窄,阻力系数反而有所降低。本文将重点研究横桥向的阻力系数变化。
5.2 塔柱与附属设施封闭连接,且将外沿处理成圆角
工况b在工况a基础上再尝试外侧以R=0.6 m的圆角处理措施。按研究对象所取截面,工况b在CFD中计算截面如图9所示,三分力系数计算结果如表4所示。

a—G计算截面; b—H计算截面; c—I计算截面。
图9 工况b计算截面 m
Fig.9 Calculation sections of case b
表4 工况b三分力系数和St数
Table 4 Three component coefficient and St number of case b
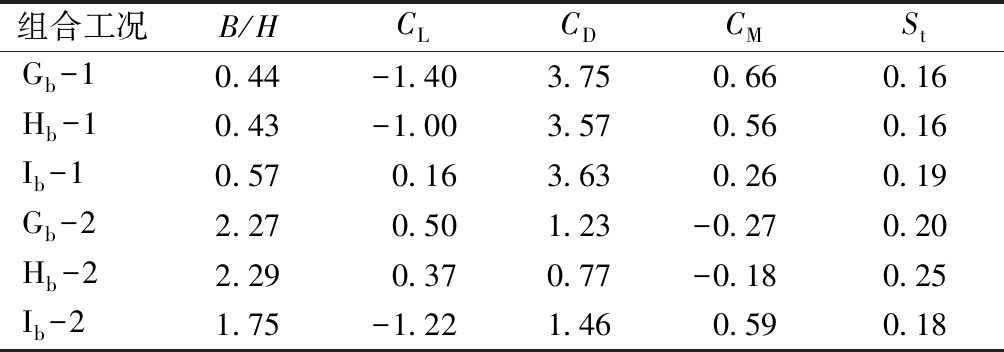
组合工况B/HCLCDCMStGb-10.44-1.403.750.660.16Hb-10.43-1.003.570.560.16Ib-10.570.163.630.260.19Gb-22.270.501.23-0.270.20Hb-22.290.370.77-0.180.25Ib-21.75-1.221.460.590.18
与工况a相比较,通过计算可以看出:采用外侧圆角气动措施后,以H截面为例,其横桥向阻力系数由4.27降低至3.57,降低约20%,而顺桥向阻力系数变化非常小。
5.3 塔柱仅与电梯井间透风
工况c在工况b的基础上采用单侧镂空处理措施来尝试进一步减小阻力系数。按研究对象所取截面,工况c在CFD中计算截面如图10所示,三分力系数计算结果如表5所示。
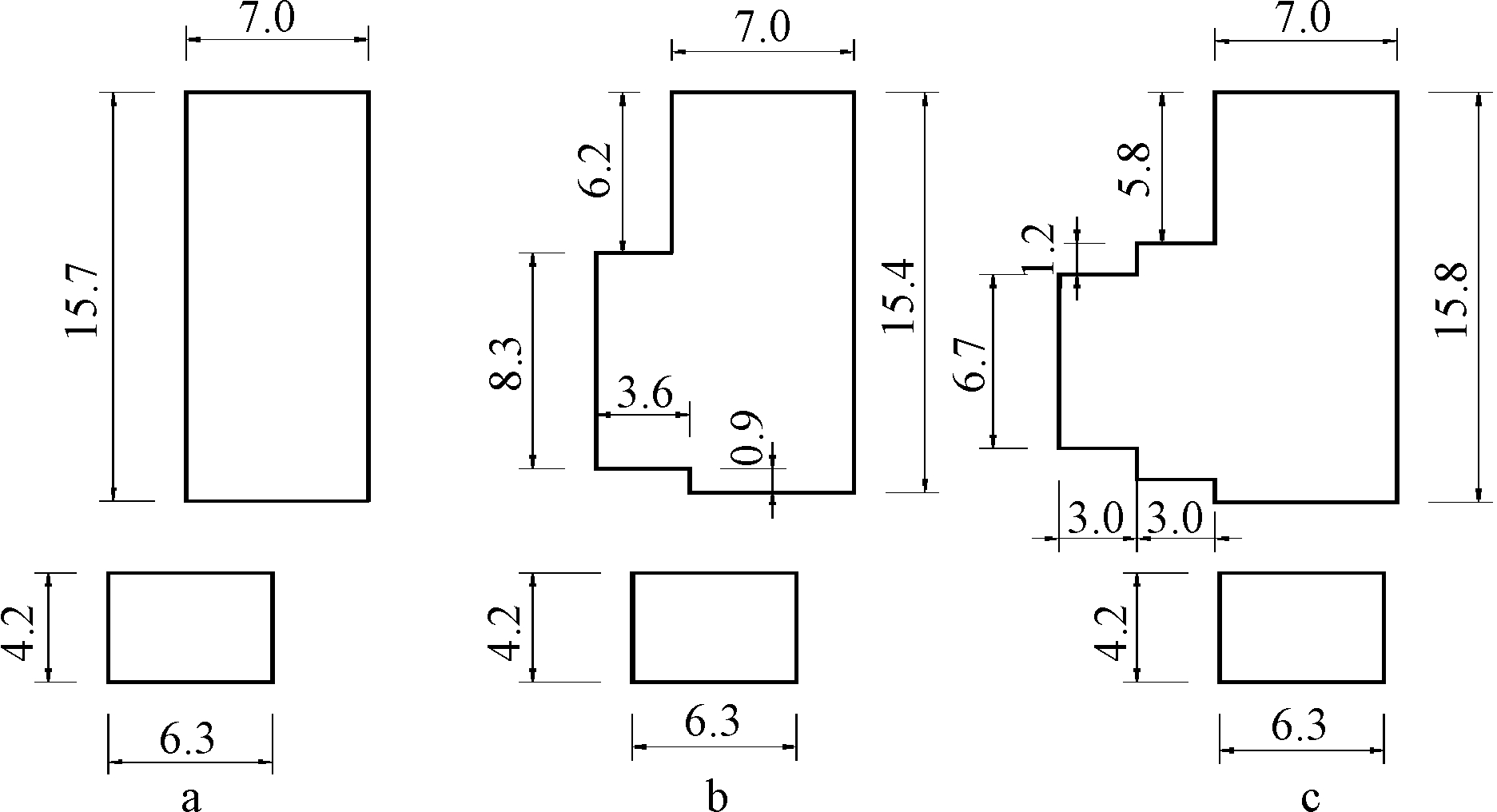
a—G计算截面; b—H计算截面; c—I计算截面。
图10 工况c计算截面 m
Fig.10 Calculation sections of case c
表5 工况c三分力系数和St数
Table 5 Three component coefficient and St number of case c
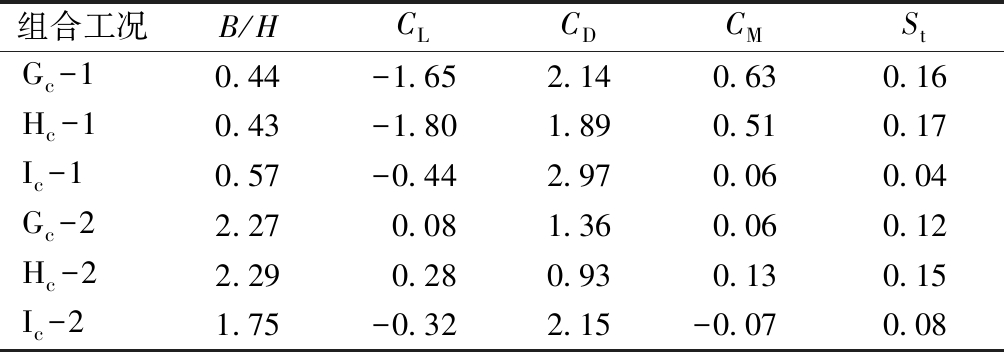
组合工况B/HCLCDCMStGc-10.44-1.652.140.630.16Hc-10.43-1.801.890.510.17Ic-10.57-0.442.970.060.04Gc-22.270.081.360.060.12Hc-22.290.280.930.130.15Ic-21.75-0.322.15-0.070.08
与工况b相比较,通过计算可以看出,原桥塔与新增附属设施单侧镂空连接后,以H截面为例,其横桥向阻力系数由3.57降低至1.89,降低约47%,效果非常显著。顺桥向阻力系数变化非常小。
5.4 塔柱与电梯井、楼梯井均透风连接,且外沿圆角处理
工况d采用双侧镂空处理措施及外沿圆角来尝试进一步减小阻力系数。按研究对象所取截面,工况c在CFD中计算截面如图11所示,三分力系数计算结果如表6所示。
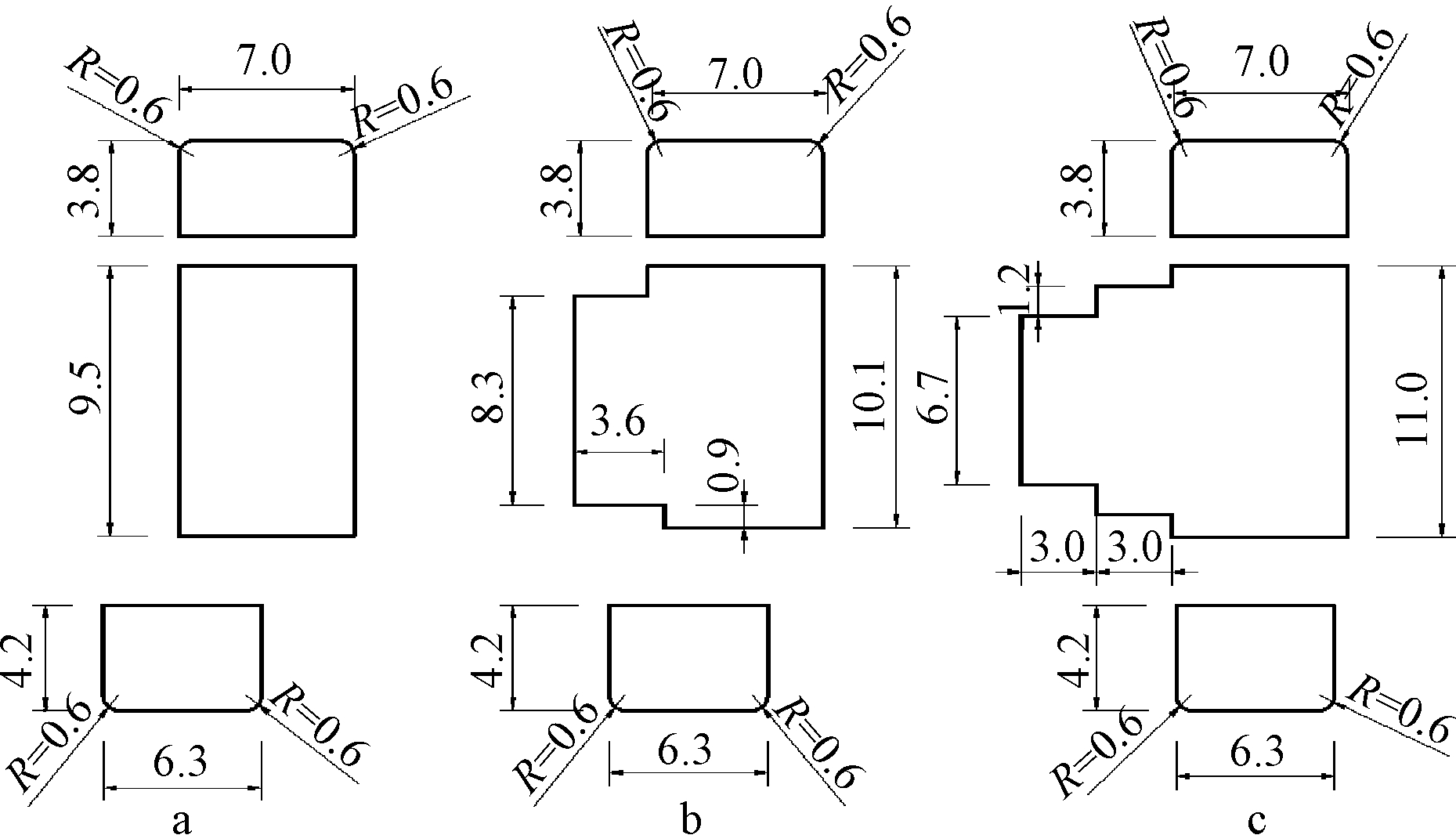
图11 工况d计算截面 m
Fig.11 Calculation sections of case d
表6 工况d三分力系数和St数
Table 6 Three component coefficient and St number of case d

组合工况B/HCLCDCMStGd-10.44-1.121.800.630.15Hd-10.43-0.381.540.510.03Id-10.57-0.161.630.060.01Gd-22.270.081.360.060.12Hd-22.290.280.930.130.15Id-21.75-0.322.15-0.070.08
与工况c相比较,通过计算可以看出:当采用双侧镂空连接的气动措施后,以H截面为例,其横桥向阻力系数由1.89降低至1.63,降低约14%,降低比例较单侧小,这是因为电梯与原桥塔的单侧镂空面积占双侧与原桥塔镂空面积的70%之多。顺桥向阻力系数变化非常小。
5.5 考虑上、下游塔柱气动干扰后的数值计算
从工况a~工况d计算的阻力系数结果可以看出,外侧圆角和双侧镂空措施能显著有效地降低阻力系数,从而达到降低结构荷载的目的。但是,以上计算均基于单肢桥塔本身,由于两塔柱之间最小间距为28.6 m,根据GB 50009—2012《建筑结构荷载规范》中8.3.2条[10]、Kwork[11]和Khanduri等[12]对高层建筑风荷载的干扰效应进行了较为详细的综述,表明任何结构均有可能遭受与其尺寸相近的邻近结构引起的荷载作用,由此可见塔柱间的干扰效应不能忽略。
为了进一步分析两塔柱之间干扰效应对气动力系数的影响,且考虑工况b~工况d的有利措施,工况e基于CFD计算考虑上游塔柱与下游塔柱之间的影响。在CFD模拟过程中将新增电梯井、新增楼梯井与主塔一并放入计算域中计算(图12),根据实际布置设计,采用1∶140的模型缩尺比。根据气动力的计算结果趋势,考虑来流风偏角范围为-50°~50°;在带风偏角的情况下,由于堵塞度增大,为了满足堵塞度的要求,计算域扩展至模型前方15D,上、下侧各15D,下游25D。当来流有风偏角,需要将风轴坐标系转换到体轴坐标系,使得风荷载分解到横桥向和顺桥向上。体轴坐标系与风轴坐标系共原点,对桥塔而言,其体轴阻力FH正方向定义为沿上下游塔柱中心的连线方向,也可称之为横桥向风力,体轴升力FS垂直FH。正方向定义如图13所示,也称之为顺桥向风力。其气动力到气动力系数的无量纲化与式(3)同,式中无量纲化计算高度H=hE+hT+hL,宽度B=b。风轴气动力转换到体轴气动力的转换关系式为:
(5)

a—G截面; b—H截面; c—I截面。
图12 考虑上下游塔柱间气动干扰效应的局部网格划分
Fig.12 Local meshing considering aerodynamic interference between upstream and downstream pylons
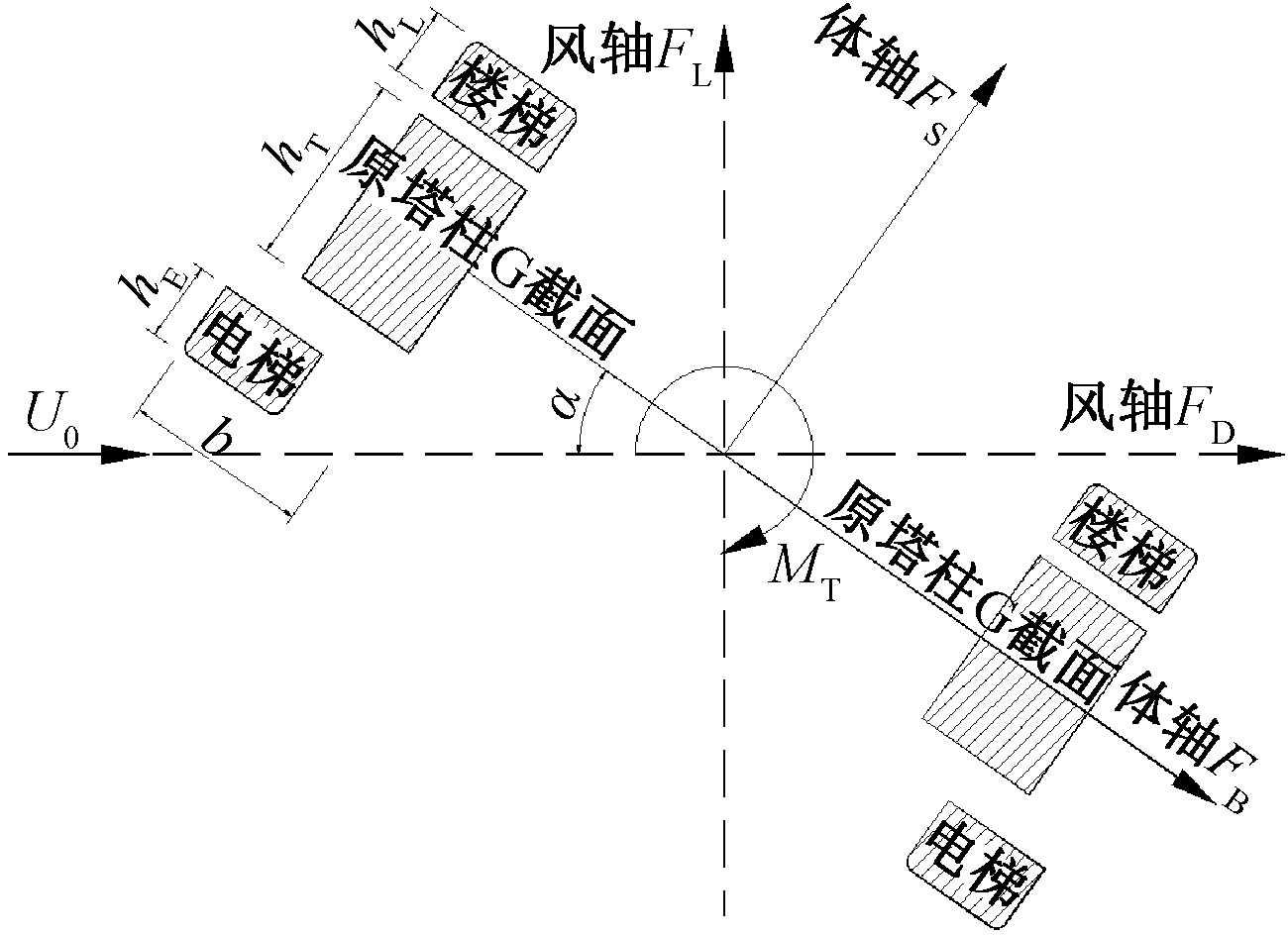
图13 考虑气动力干扰的上下游塔柱气动力定义
Fig.13 Aerodynamic definition of upstream and downstream pylons considering aerodynamic interference
不同来流攻角下,考虑上、下游气动干扰,且考虑外侧圆角和两侧透风连接的计算结果如图14所示。其中G截面阻力系数无量纲化高度为17.37;其中H截面阻力系数无量纲化高度为18.1;其中I截面阻力系数无量纲化高度为18.94。
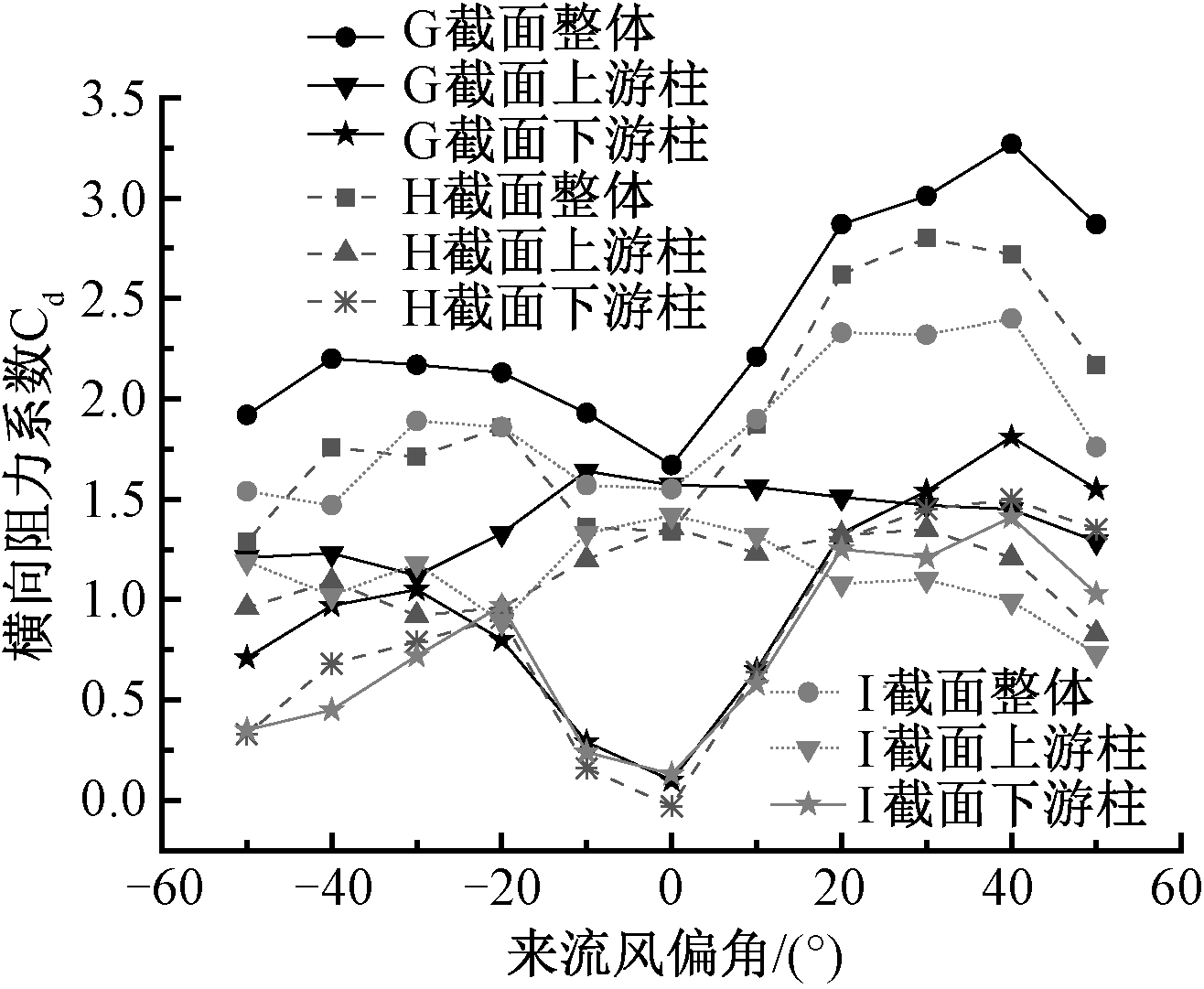
图14 不同来流风偏角下G、H和I截面横向阻力系数
Fig.14 Lateral resistance coefficient of G, H and I sections at different wind angles
通过考虑上、下游桥塔气动干扰现象,当来流风偏角为40°时,G截面横桥向整体体轴阻力系数最大值为3.27,其分塔各柱阻力系数为1.45和1.81;当来流风偏角为30°时,H截面横桥向整体体轴阻力系数最大值为2.8,其分塔各柱阻力系数为1.3和1.45;来流风偏角为20°时,I截面横桥向整体体轴阻力系数最大值为2.8,其分塔各柱阻力系数为1.08和1.25。
5.6 对比分析
由以上计算分析,对结构设计重点关注的阻力系数汇总各工况下对比见表7。在CFD中计算桥塔模型中,考虑塔柱的互相遮挡的情况下,外侧圆角和双侧镂空连接的气动措施对降低阻力系数最为有效。即工况e情况下既能真实反映结构受力状态,又能保证结构安全经济可靠。
表7 不同工况阻力系数对比
Table 7 Comparison of resistance coefficients under different cases

工况G截面H截面I截面说明a4.614.274.35单塔柱b3.753.573.63单塔柱c2.141.892.97单塔柱d1.801.541.63单塔柱e1.451.301.08上游塔柱e1.811.451.25下游塔柱
6 原塔柱与确定气动优化方案风荷载值对比
根据JTG/T 3360-01—2018《公路桥梁抗风设计规范》[13]式4.4.1计算桥塔在横桥向风作用下,桥梁运营状态及极限状态的静风荷载如表8所示。
由表8知,增加观光通道后,由于受风面积增加及索塔体型变化,索塔上塔柱横桥向风荷载增加约 7%,中塔柱约 69%,下塔柱约 78%。本桥索塔塔柱、横梁为横向风荷载控制,横向风载的增加需要重新验算桥梁各关键构件。
根据计算确定的荷载取值,通过验算塔柱、横梁各关键控制正截面抗弯承载力满足原设计要求,依然处于原设计安全贮备范围内。但通过验算横梁的斜截面抗剪发现,上横梁3/8跨、下横梁3/8跨及跨中截面斜截面抗剪承载力不足,上横梁最大剪力超
表8 工况e不同来流攻角H截面静力三分力
Table 8 Three component coefficient at
different wind angles of case e
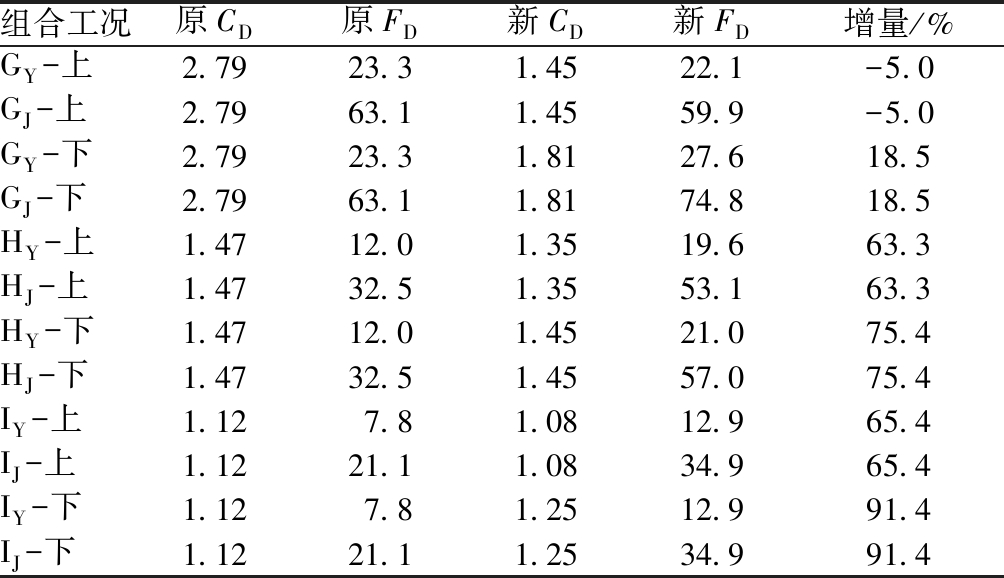
组合工况原CD原FD新CD新FD增量/%GY-上2.7923.31.4522.1-5.0GJ-上2.7963.11.4559.9-5.0GY-下2.7923.31.8127.618.5GJ-下2.7963.11.8174.818.5HY-上1.4712.01.3519.663.3HJ-上1.4732.51.3553.163.3HY-下1.4712.01.4521.075.4HJ-下1.4732.51.4557.075.4IY-上1.127.81.0812.965.4IJ-上1.1221.11.0834.965.4IY-下1.127.81.2512.991.4IJ-下1.1221.11.2534.991.4
注:G表示G截面;Y表示运营状态;J表示极限状态;上表示上游;下表示下游。
结构抗力约10%,下横梁最大剪力超结构抗力约11%。为了弥补增加观光楼电梯引起的横梁斜截面抗剪承载能力不足,应对上下横梁的斜截面抗剪能力采取补强措施。通过考虑在横梁内侧腹板贴10 mm的钢板或黏贴碳纤维布方案、以及在横梁箱形截面内增设剪刀撑的方案均可满足静力承载力验算要求。
7 结束语
1)与原桥塔相比,增设观光楼电梯和楼梯后桥塔横桥向阻力显著增大。
2)在增设观光电梯和楼梯的多个方案中,与原桥塔封闭连接的方案横桥向阻力最大;相反,用镂空替代封闭以及将外沿处理成圆角,可显著降低桥塔横向阻力。
3)增设观光电梯和楼梯后,主塔两侧塔柱的气动干扰效应不可忽视,在横桥向风作用下两塔柱存在最大的遮挡效应,而遮挡效应随着风向角的变化而变化。
4)增设观光电梯和楼梯导致桥塔横桥向风荷载明显增大,对悬索桥常采用的门式桥塔,与桥塔相连的上下横梁的斜截面抗剪承载力可能不足,在大桥上建造此类观光结构时,应注意横梁的抗剪设计。
[1] 祝志文.基于二维RANS模型计算扁平箱梁漩涡脱的可行性分析[J]. 中国公路学报,2015,28(6):24-22.
[2] 禹见达,李彬,竹剡锋.洞庭湖大桥桥塔塔顶风场与风压特性试验研究[J]. 湖南科技大学学报(自然科学版),2014,29(3):49-52.
[3] 李胜利,张通,陈淮,等.门型桥塔驰振气动干扰效应数值模拟[J]. 中国铁道科学,2012,33(1):27-34.
[4] 李永乐,刘多特,李少波,等.独柱式变截面倾斜桥塔气动特性风洞试验研究[J].实验流体力学,2023,27(5):38-43.
[5] 陶齐宇,李永乐,张明金,等.斜拉桥H形桥塔气动力系 数风洞试验研究[J]. 武汉理工大学学报,2009,31(13):64-68.
[6] 何旭辉,方东旭,王汉封,等.超高多肢斜拉桥桥塔气动力系数研究[J]. 中国铁道科学,2017,38(4):24-32.
[7] PLETCHER R H.TANNEHILL J C, ANDERSON D A. Computational Fluid Mechanics and Heat Transfer [M]. Washington D C: Taylor & Francis, 1997.
[8] JONES W P, LAUNDER B E. The Prediction of Linearization with a Two-Equation Model of Turbulence [J]. International of Heat and Mass Transfer, 1972, 15(2):301-314.
[9] TOMINAGA Y, MOCHIDA A, YOSHIE R,et al. AIJ Guidelines for Practical Applications of CFD to Pedestrian Wind Environment Around Buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11):1749-1761.
[10] 中华人民共和国住房和城乡建设部.建筑结构荷载规范: GB 50009—2012[S].北京:中国建筑工业出版社,2012.
[11] KWORK K C S. Aerodynamics of Tall Buildings:a State of Art in Wind Engineering[C]//Proceedings of the 9th International Conference on Wind Engineering. New Delhi:International Association for Wind Engineering, 1955:180-204.
[12] KHANDURI A C, STATHPOULOST, BEDARD C. Wind-Induced Interference Effects on Buildings:a Review of the State-of-the Art [J]. Engineering Structures, 1998, 20(7):617-630.
[13] 中国人民共和国交通运输部.公路桥梁抗风设计规范: JTG/T 3360-01—2018[S].北京:人民交通出版社股份有限公司,2019.