0 引 言
T形件螺栓连接所受外荷载一般未作用在螺栓轴线上,翼缘板将内力传递至螺栓时产生弯曲变形,使翼缘板边缘产生撬力,导致螺杆所受拉力增加并弯曲,节点承载性能下降。故撬力产生的不利影响不容忽视,应在设计中进行相应考虑。
当前国内外学者对钢结构T形件螺栓连接已经开展了试验研究和数值分析。吴兆旗等对T形件螺栓连接撬力与各参数的关系开展了数值模拟,并针对在T形件之间设置垫板对耗能能力的影响开展了试验研究[1-2];赵伟等对3个无加劲肋和6个有加劲肋T形件进行了试验研究[3];刘秀丽等对10个不同尺寸的T形连接试件开展了试验研究和有限元分析[4];暴伟等对高强螺栓T形连接进行拉伸试验,研究弯矩对螺栓受力的影响[5];郭宏超等开展了10个焊接T形件的单调拉伸试验[6];Faella等开展了螺栓预紧力对T形件承载性能影响的试验研究[7];Piluso等通过试验研究了28个T形件在循环荷载作用下的抗震性能[8];Zhao等完成了10个高性能钢结构T形件试件的试验研究[9];Chen等通过试验和有限元研究了焊接对高强度钢T形件承载性能的影响[10]。
不锈钢板及螺栓材料的非线性特性增加了T形件连接的承载性能的复杂性,因而需要对不锈钢T形件螺栓连接开展专门的研究。目前已发表的文献中,Bouchaïr等通过有限元分析了不锈钢T形件的承载力和撬力作用[11];杨成博完成了9个不锈钢T形件静力加载试验,通过开展参数分析探讨了各因素对不锈钢T形件节点力学性能的影响规律[12];袁焕鑫等完成了14个不锈钢T形件螺栓连接的单调拉伸试验,不锈钢T形件螺栓连接的相关研究仍然较少[13]。因此有必要对不锈钢T形件螺栓连接的承载性能开展深入研究。
采用有限元软件ABAQUS建立有限元数值模型,准确考虑不锈钢力学性能、接触关系和撬力作用,同时为得出主要参数对T形件螺栓连接静力承载性能的影响规律,进行参数分析,然后对不锈钢T形件力学模型进行简化,结合有限元计算结果,提出适用于不锈钢T形件螺栓连接承载力的建议计算方法。
1 不锈钢T形件有限元模型
1.1 T形件单调加载试验概况
文献[13]已经完成了14个不锈钢T形件螺栓连接试件的静力拉伸试验,得到了试件的荷载-位移曲线、破坏形态和撬力发展规律等。试件形式包括每排单个螺栓(T-S)和每排两个螺栓(T-D)两种,不锈钢牌号有奥氏体型S30408和双相型S22253,翼缘板厚度包括8 mm和12 mm两种,采用A4-70和A4-80两种不锈钢螺栓,螺栓直径包括12 mm和16 mm。
1.2 有限元模型建立
对不锈钢T形件螺栓连接(T-S类型)试验全过程进行有限元数值模拟,由于T形件的对称性,同时为降低计算量,取其一半建立有限元模型进行计算,有限元模型如图1所示。T形件翼缘厚度为实测板件厚度,翼缘腹板的角焊缝用三棱柱建模,焊脚尺寸为实测尺寸,为尽可能降低底座的变形,建模时考虑增大其刚度,取其弹性模量为普通钢材的100倍。试验采用了全螺纹螺栓,螺纹段对螺栓承载力有削弱作用,为此参考文献[14],将螺纹段面积换算为螺栓公称面积的80%进行建模。有限元模型采用C3D8R单元进行网格划分。
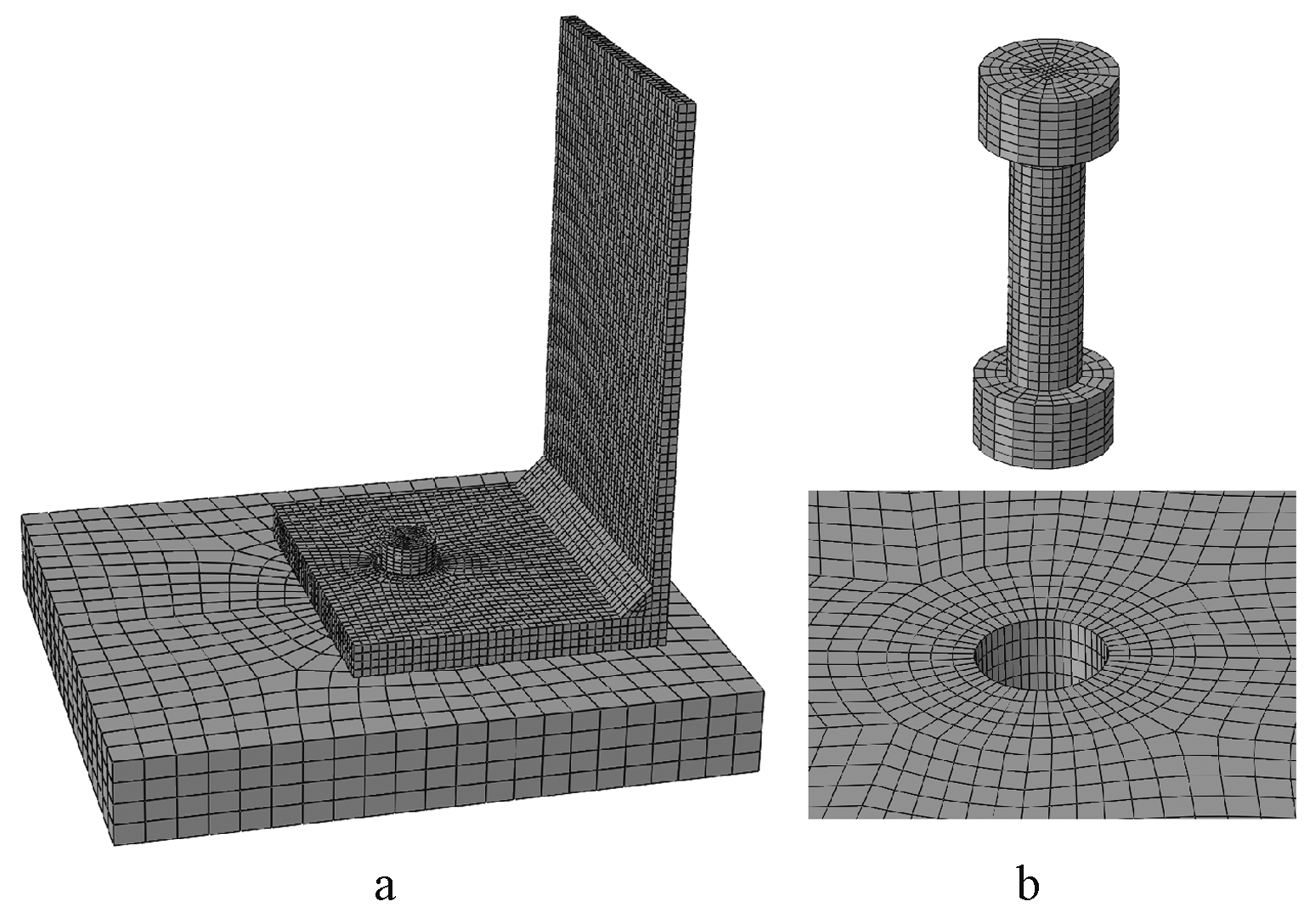
a—整体模型; b—模型细部网格。
图1 有限元模型
Fig.1 FE model
不锈钢板和螺栓的本构模型均采用CECS 410∶2015《不锈钢结构技术规程》[15]给出的两阶段模型,即式(1):
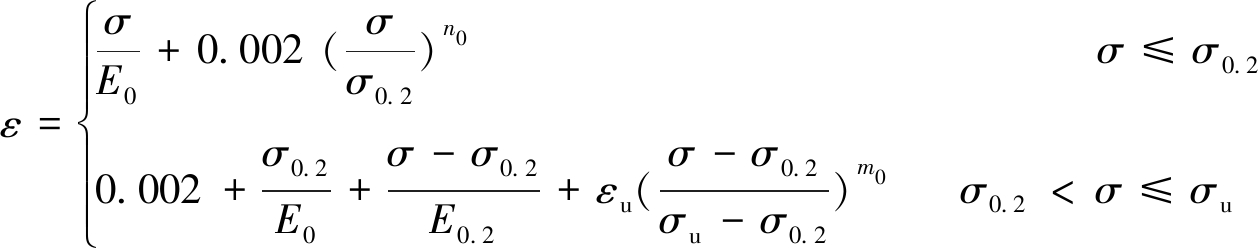
(1)
其中 εu=1-σ0.2/σu
m0=1+3.5σ0.2/σu
式中:E0.2为名义屈服强度σ0.2对应的切线模量;εu为材料抗拉强度σu对应的峰值应变;n为材料的应变硬化指数。不锈钢板和螺栓材料力学性能指标采用文献[13]中材性试验结果。
表1为有限元模型中接触关系设置,接触序号见图2。其中a为螺栓头下表面,b、c分别为T形件翼缘板上、下表面,d、e分别为刚性底座上、下表面,f为螺帽上表面,g为螺杆柱面,h为螺孔柱面。不锈钢与不锈钢抗滑移系数取为0.1,不锈钢与普通钢抗滑移系数取为0.12[16-17],螺栓杆与孔壁之间设置为无摩擦。有限元模型中不锈钢材料均采用各向同性弹塑性材料,硬化方式为同向硬化,屈服准则使用ABAQUS默认的Mises准则,关联塑性流动法则。
表1 接触关系设置
Table 1 Contact relationship setting

接触序号接触对接触类型法向属性切向属性①a,b②c,d③e,f④g,h面面接触硬接触库伦摩擦
边界条件如图2所示,此外,模型对称面为腹板中面,此处边界为X方向对称边界条件。
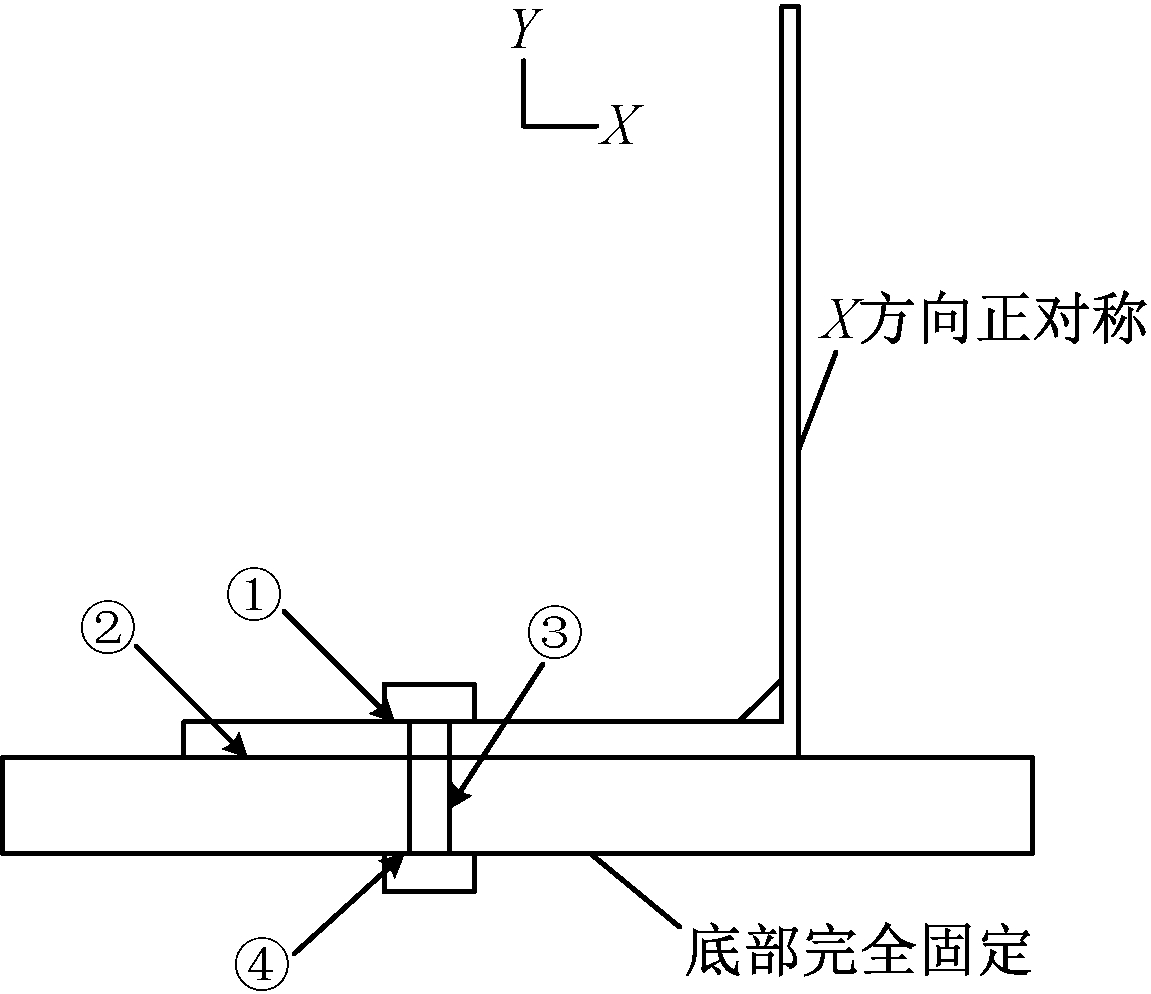
图2 有限元模型接触关系及边界条件
Fig.2 Contact configuration and boundary conditions in FE models
1.3 有限元模型验证
为验证所建立的有限元模型,对文献[13]中7个不锈钢T形件螺栓连接试件(T-S类型)进行有限元建模计算,有限元计算结果和试验结果对比如图3和图4所示。试验值和有限元计算结果列于表2中,表中Fu,Exp为试验所得极限承载力,Fu,FE为有限元计算所得极限承载力。综合对比荷载-位移曲线、破坏形态、承载力及其对应的峰值位移,有限元计算结果与试验结果十分接近。因此所建立的有限元模型是准确可靠的,可用于后续参数分析。
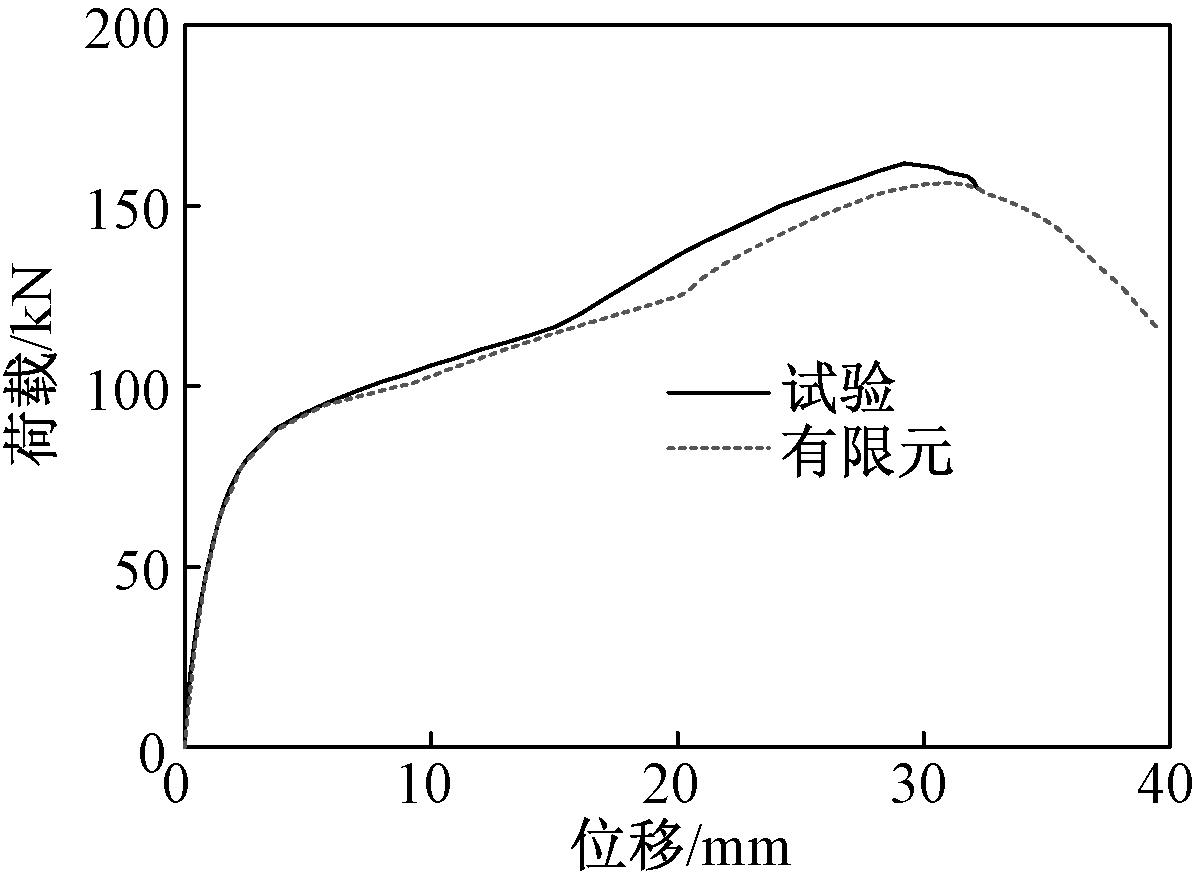
图3 试件(S4)荷载-位移曲线对比
Fig.3 Comparison of FE and test load versus deformation curves

a—试件S1; b—不锈钢螺栓。
图4 试件破坏形态对比
Fig.4 Comparison of FE simulated and test failure modes of specimens
表2 试验结果与有限元结果比较
Table 2 Comparison of FE and test results
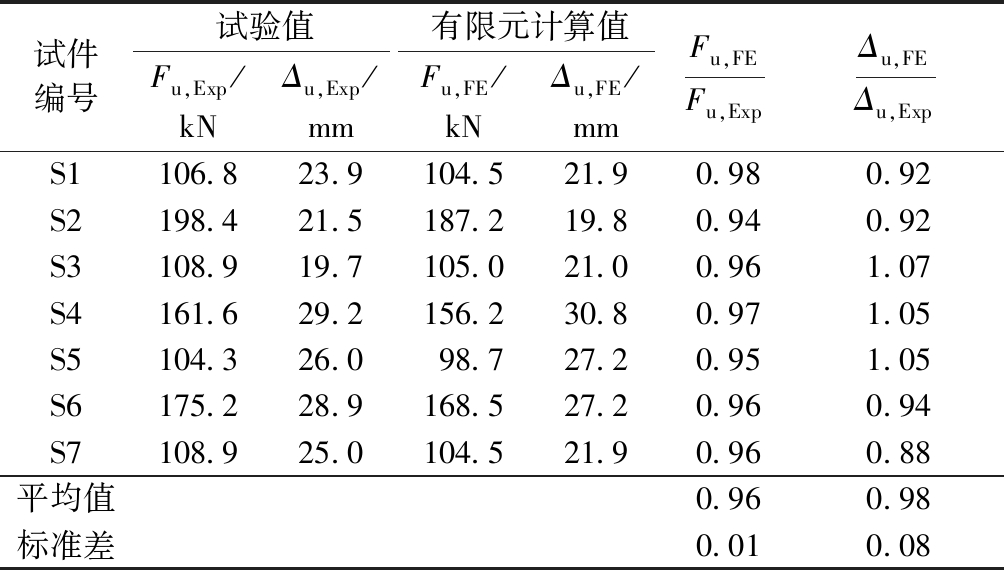
试件编号试验值有限元计算值Fu,Exp/kNΔu,Exp/mmFu,FE /kNΔu,FE /mmFu,FEFu,ExpΔu,FEΔu,ExpS1106.8 23.9 104.5 21.9 0.98 0.92 S2198.4 21.5 187.2 19.8 0.94 0.92 S3108.9 19.7 105.0 21.0 0.96 1.07 S4161.6 29.2 156.2 30.8 0.97 1.05 S5104.3 26.0 98.7 27.2 0.95 1.05 S6175.2 28.9 168.5 27.2 0.96 0.94 S7108.9 25.0 104.5 21.9 0.96 0.88 平均值0.960.98标准差0.010.08
2 有限元参数分析
采用前述有限元模型,对影响T形件承载性能的主要因素开展分析,所选取的关键参数及取值列于表3中。
2.1 翼缘厚度
根据欧洲标准EN 1993-1-8[18]中的三种破坏模式,即翼缘完全屈服为破坏模式1,翼缘屈服同时螺栓断裂为破坏模式2,螺栓完全断裂为破坏模式3,可以得到T形件的承载力和翼缘厚度平方的关系如图5a所示,破坏模式的分界点对应的翼缘厚度为临界翼缘厚度。因此对翼缘厚度tf进行参数分析时需考虑T形件的三种破坏模式均能涉及。选取参数为S30408、m=80 mm、db=20 mm的算例,有限元计算结果如图5b所示。从中可看出,有限元计算所得趋势与图5a相近,但对比二者破坏模式1的趋势可发现,计算所得趋势明显不会经过原点,故需要进一步研究属于破坏模式1的不锈钢T形件。
表3 关键参数及取值
Table 3 Key parameters and its values mm

翼缘厚度翼缘宽度b翼缘材料等级螺栓直径db螺栓孔到腹板边缘距离m螺栓孔到翼缘边缘距离n以能够涵盖三种破坏模式为原则120奥氏体型S30408、双相型S2225312,14,16,2040,50,55,60,65,8050
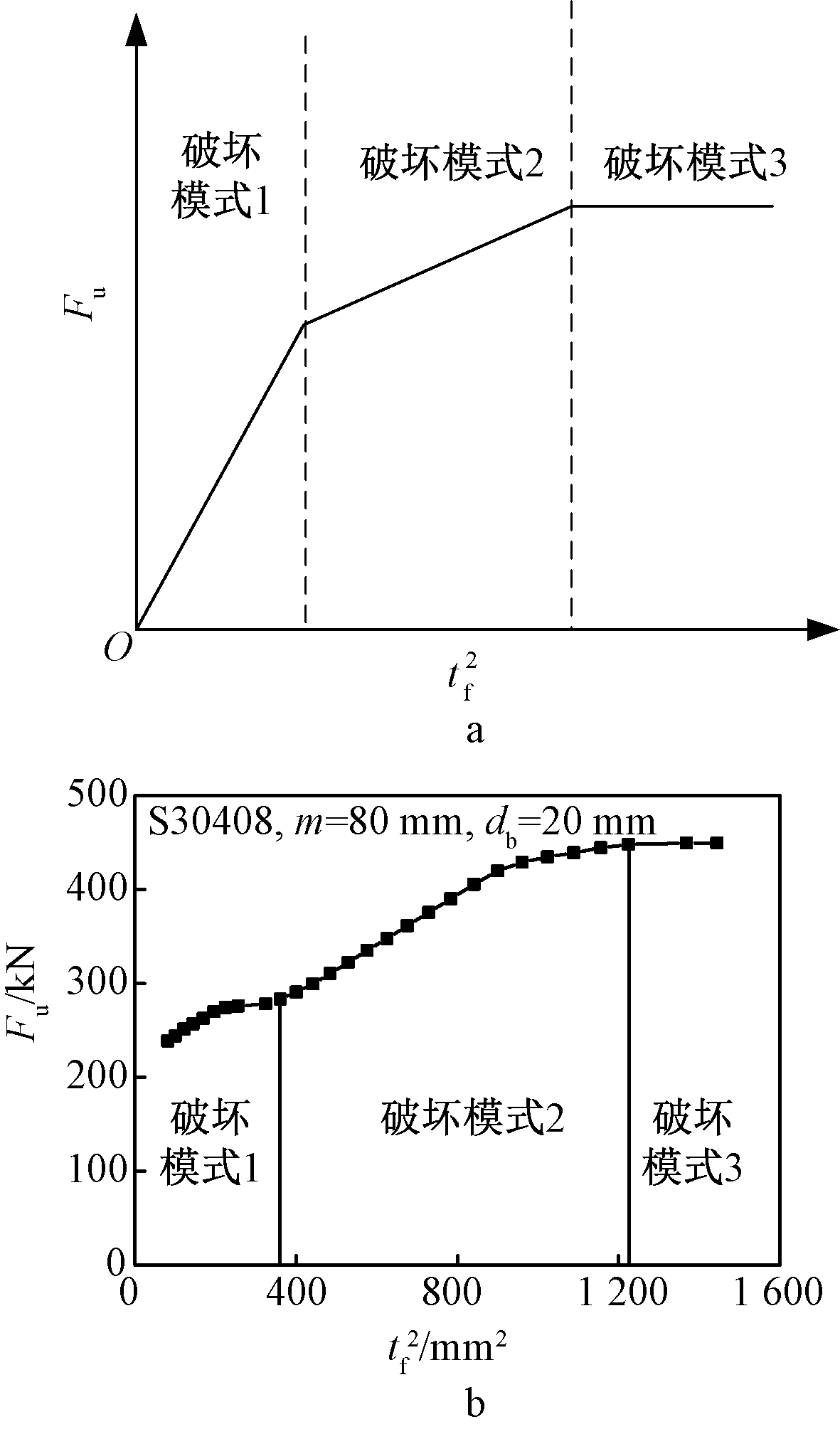
a—EN 1993-1-8理论关系; b—有限元计算结果。
图5 T形件极限承载力与翼缘厚度平方的关系
Fig.5 Relationship between ultimate bearing capacity and square of flange thickness of T-stub
图6为参数为S30408、m=80 mm、db=20 mm、tf=9 mm的算例有限元模拟加载至荷载-位移曲线峰值时的结果。其中灰色区域为Mises应力大于S30408名义屈服强度(280.4 MPa)的区域,可看出翼缘板已大面积屈服,此时翼缘板一侧形成两个塑性铰,故其属破坏模式1,且螺杆上部大部分区域塑性应变已超过螺栓最大塑性应变(0.295),表明螺栓先于模型整体破坏。由此认为:当螺栓破坏,即当螺栓的塑性应变达到材性试验所得最大塑性应变时,模型无法继续承载,此时对应的荷载为模型的极限承载力。
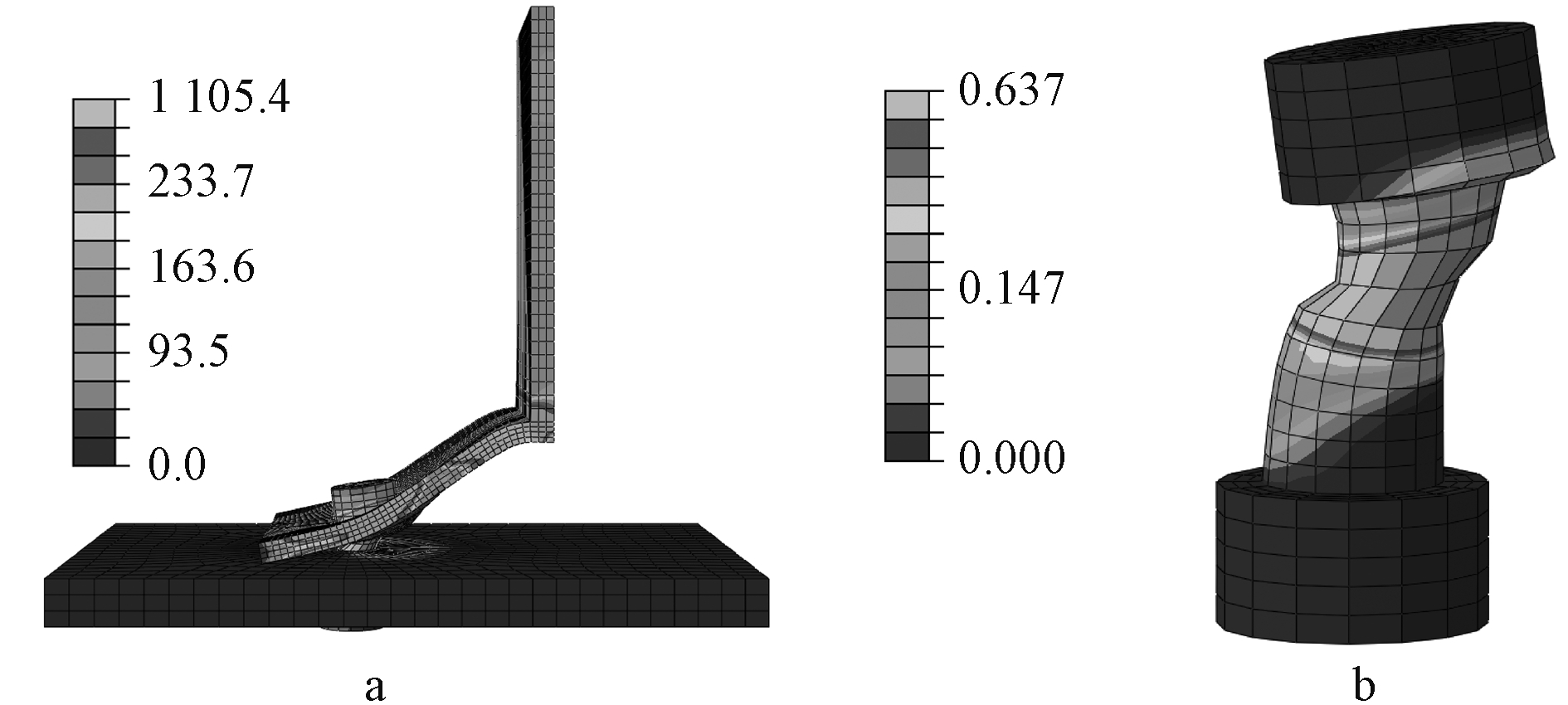
a—模型整体应力云图,MPa; b—螺栓塑性应变。
图6 算例有限元结果
Fig.6 FE result of the example
2.2 螺栓孔到腹板边缘的距离
螺栓孔到腹板边缘的距离m参数取值见表3,有限元计算结果如图7所示。
从图7可看出,对于破坏模式1和2的不锈钢T形件,增大m会降低其承载力,但对破坏模式3的承载力并无影响,原因在于破坏模式3的T形件翼缘板变形很小,破坏以螺栓被拉断为主,其承载力取决于螺栓强度。
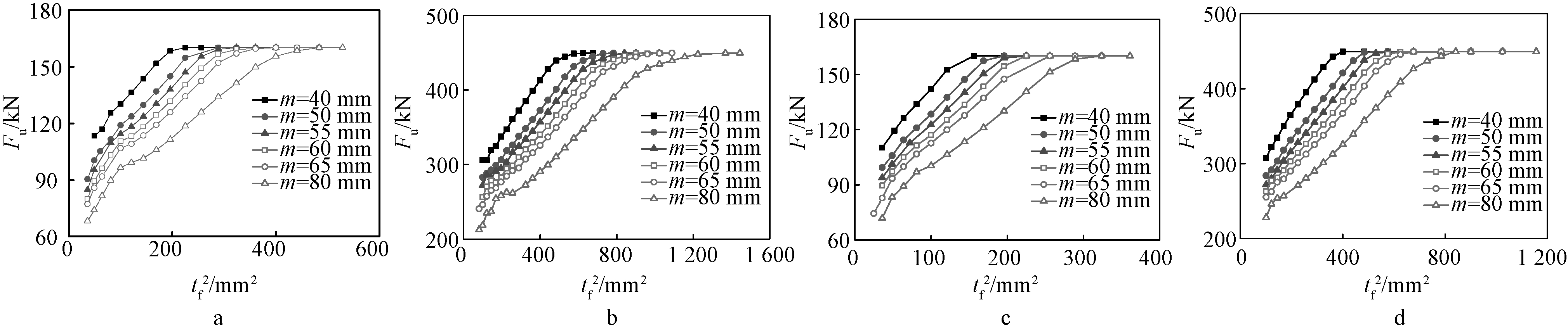
a—S30408、db=12 mm; b—S30408、db=20 mm; c—S22253、db=12 mm; d—S22253、db=20 mm。
图7 螺栓孔到腹板边缘距离m的影响分析
Fig.7 Effect analysis of the distance from the bolt hole to the web’s edge
2.3 材料等级
材料等级取奥氏体型S30408和双相型S22253两种,对不锈钢T形件极限承载力的影响分析如图8所示。从中可看出,对属破坏模式1和2的不锈钢T形件,取相同翼缘厚度时,S22253试件的承载力高于S30408试件,原因在于S22253的名义屈服强度相对较高。此外翼缘板厚度tf逐渐增大时,两种试件的承载力差距先增大后减小,当tf增大到使不锈钢T形件属于破坏模式3后,由于试件的承载力完全取决于螺栓强度,因此两种试件的承载力基本相同。
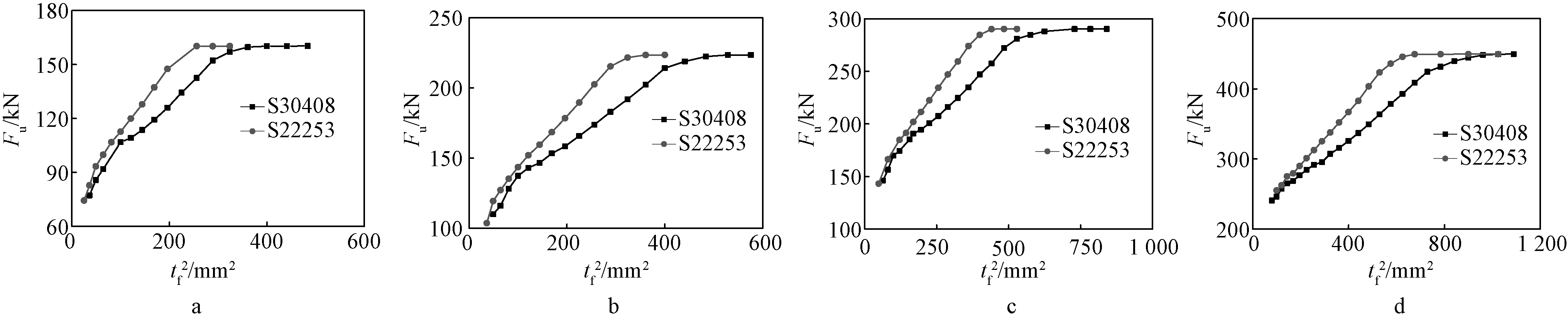
a—m=65 mm、db=12 mm; b—m=65 mm、db=14 mm; c—m=65 mm、db=16 mm; d—m=65 mm、db=20 mm。
图8 材料等级的影响分析
Fig.8 Effect analysis of the material grade
2.4 螺栓直径
螺栓直径db参数取值见表3,有限元计算结果如图9所示。从中可以看到,增大螺栓直径会提高不锈钢T形件的极限承载力。由于破坏模式2和模式3最终破坏均是螺栓被拉断而破坏,故螺栓直径的增大会提高螺栓受拉承载力,进而提高T形件的承载力;而对于破坏模式1的试件,欧洲标准EN 1993-1-8所给公式显示其承载力与螺栓直径无直接关系,但有限元计算结果则表明其承载力也会因螺栓直径的增大而有所提高。因此应该考虑螺栓直径对承载力的影响。
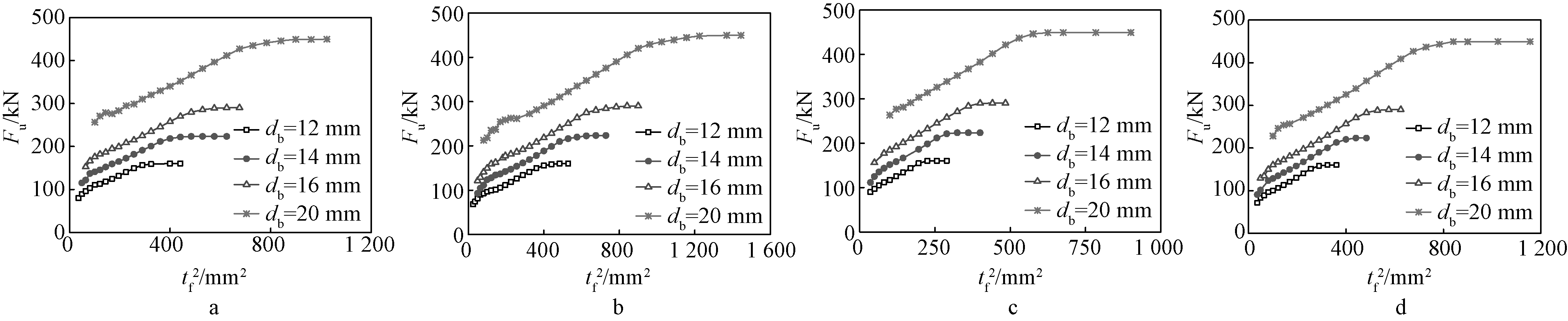
a—S30408、m=60 mm; b—S30408、m=80 mm; c—S22253、m=60 mm; d—S22253、m=80 mm。
图9 螺栓直径db的影响分析
Fig.9 Effect analysis of bolts’ diameters
3 建议计算方法
3.1 现有设计方法
对于普通钢结构T形件螺栓连接,欧洲标准EN 1993-1-8[18]、美国规范AISC[19]和中国规范JGJ 82—2011《钢结构高强度螺栓连接技术规程》[20]均给出了计算方法。欧洲规范EN 1993-1-8给出了考虑撬力时三种破坏模式对应的抗拉承载力计算公式:
模式1
(2a)
模式2
(2b)
模式3
F3,Rd=∑Ft,Rd
(2c)
其中 ew=dw/4
式中:Mf,1,Rd和Mf,2,Rd分别为对应破坏模式1和模式2的翼缘板塑性弯矩;dw为螺栓垫片直径;Ft,Rd为螺栓抗拉设计承载力。
美国规范AISC和中国规范JGJ 82—2011都是根据翼缘板厚度是否大于不考虑撬力的最小厚度来决定是否考虑撬力作用:若翼缘板厚度大于此最小厚度,则不考虑撬力作用,否则考虑撬力作用带来的不利影响。根据式(3b)和式(4b)计算可得到T形件设计承载力。
美国规范AISC中不考虑撬力时的翼缘最小厚度tmin和考虑撬力时的翼缘厚度te分别按式(3)计算。
(3a)
(3b)
其中![]()
式中:B为螺栓的受拉承载力;T为外荷载;p为翼缘的计算宽度;fu为翼缘材料的极限抗拉强度。
中国规范JGJ 82—2011中不考虑撬力时的翼缘最小厚度tec和考虑撬力时的翼缘厚度te分别按式(4)计算。
(4a)
(4b)
其中 ψ=1+δα′
式中:e2为螺栓中心到腹板边缘的距离;![]() 为单个螺栓的受拉承载力;Nt为外荷载;b为翼缘宽度;ψ为撬力影响系数;fy为翼缘材料的屈服强度。
为单个螺栓的受拉承载力;Nt为外荷载;b为翼缘宽度;ψ为撬力影响系数;fy为翼缘材料的屈服强度。
3.2 建议计算方法
欧洲标准EN 1993-1-8中,翼缘板塑性弯矩Mf,Rd按式(5)计算:
(5)
式(5)认为翼缘板全截面屈服时便破坏失效,未考虑不锈钢材料显著的应变硬化能力,导致计算得到的M偏小。参考连续强度法[21]将不锈钢材料本构模型简化为双折线模型,如图10所示,利用该简化本构模型对翼缘板塑性弯矩的计算方法进行修正,以充分利用不锈钢的应变硬化能力。
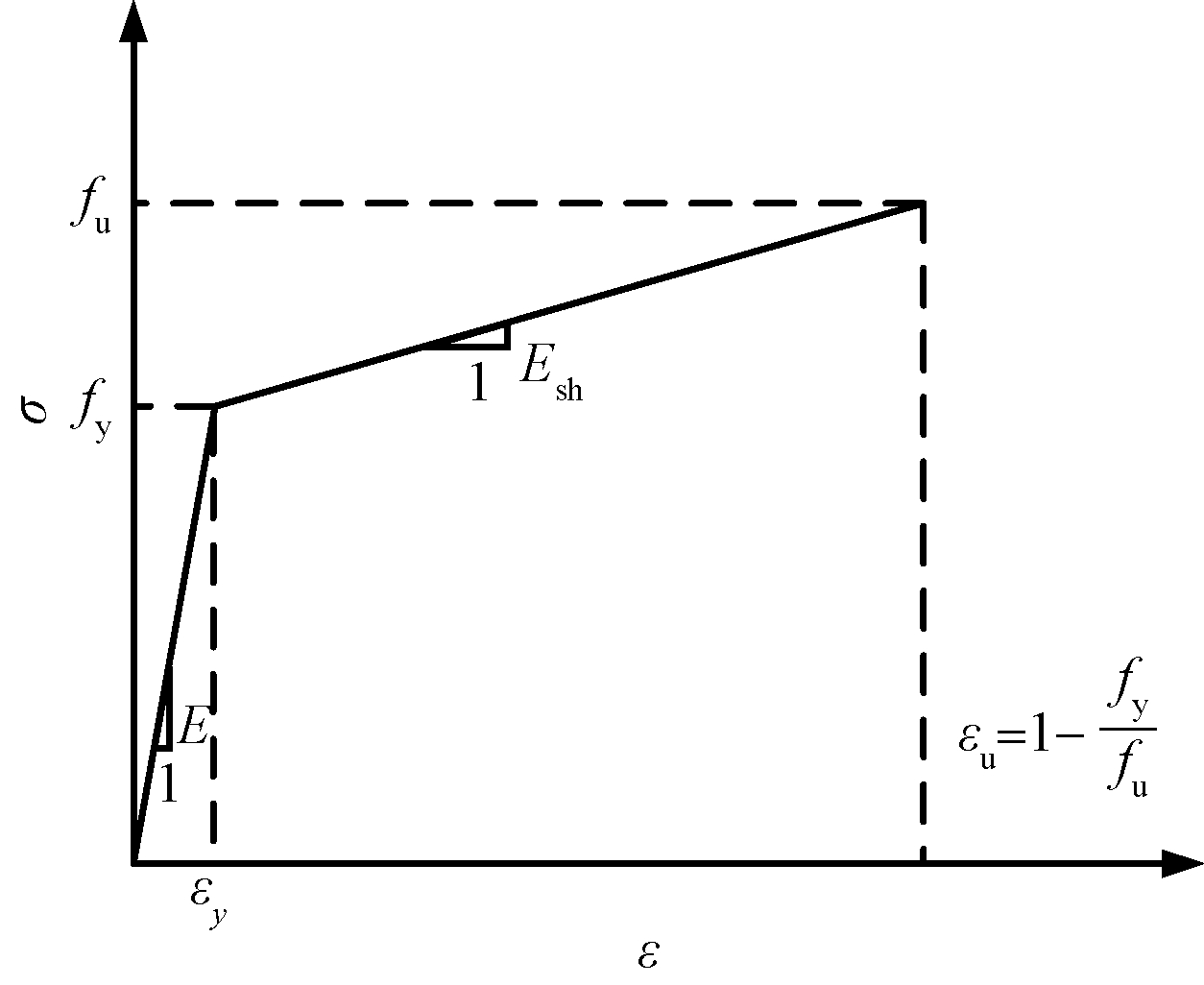
图10 不锈钢简化双折线本构模型
Fig.10 Simplified bilinear constitutive model of stainless steel
翼缘板塑性弯矩可按矩形截面弯矩计算方法计算,取翼缘板横截面为计算截面,由平截面假定可得计算简图如图11所示。对于奥氏体型S30408和双相型S22253不锈钢,计算可得二者极限应变与屈服应变比值εu/εy分别为398和135,均远大于1,故其应力分布可简化成图11c所示,由此推导可得M的计算式见(6),对比式(5)可知,式(6)将式(5)中的屈服强度fy改成了换算强度fy/3+2fu/3,从而合理利用了不锈钢应变硬化能力。
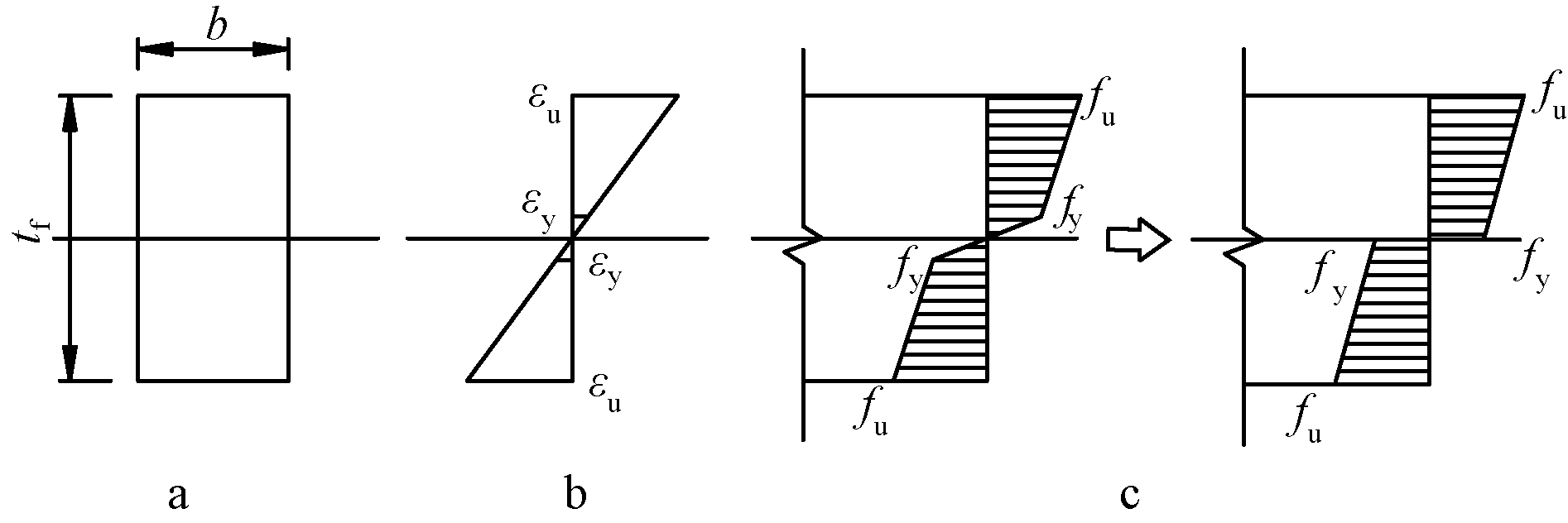
a—矩形截面; b—应变分布; c—简化应力分布。
图11 矩形截面应变、应力分布
Fig.11 Stress and strain distribution of rectangular section
(6)
对于破坏模式2,由于翼缘和螺栓二者刚度相近,螺栓随着翼缘的弯曲变形被拉离原螺孔中心线,使其对翼缘板的合力向腹板偏移,螺栓合力到翼缘板边缘和腹板边缘距离均有所改变,参考美国规范AISC对两距离进行修正,将式(2b)中的m和n分别换为 m′=m-db/2和n′=n+db/2。由图5和图7可拟合得到极限承载力Fu与翼缘厚度tf的计算式:
Fu=k1tf2+b1
(7)
因此考虑对螺栓孔到腹板边缘的距离m多次取值,代入模式2的计算公式中计算出Fu,根据上述拟合公式进行拟合,得到相应截距b1。为便于分析二者关系,将横轴取为1/(m′+n′),绘制曲线于图12中,当螺栓直径不变时,b1与1/(m′+n′)成正比,随着螺栓直径的增大,1/(m′+n′)对b1影响随之增大。因此,不锈钢T形件对应破坏模式2的承载力计算式见式(8)。
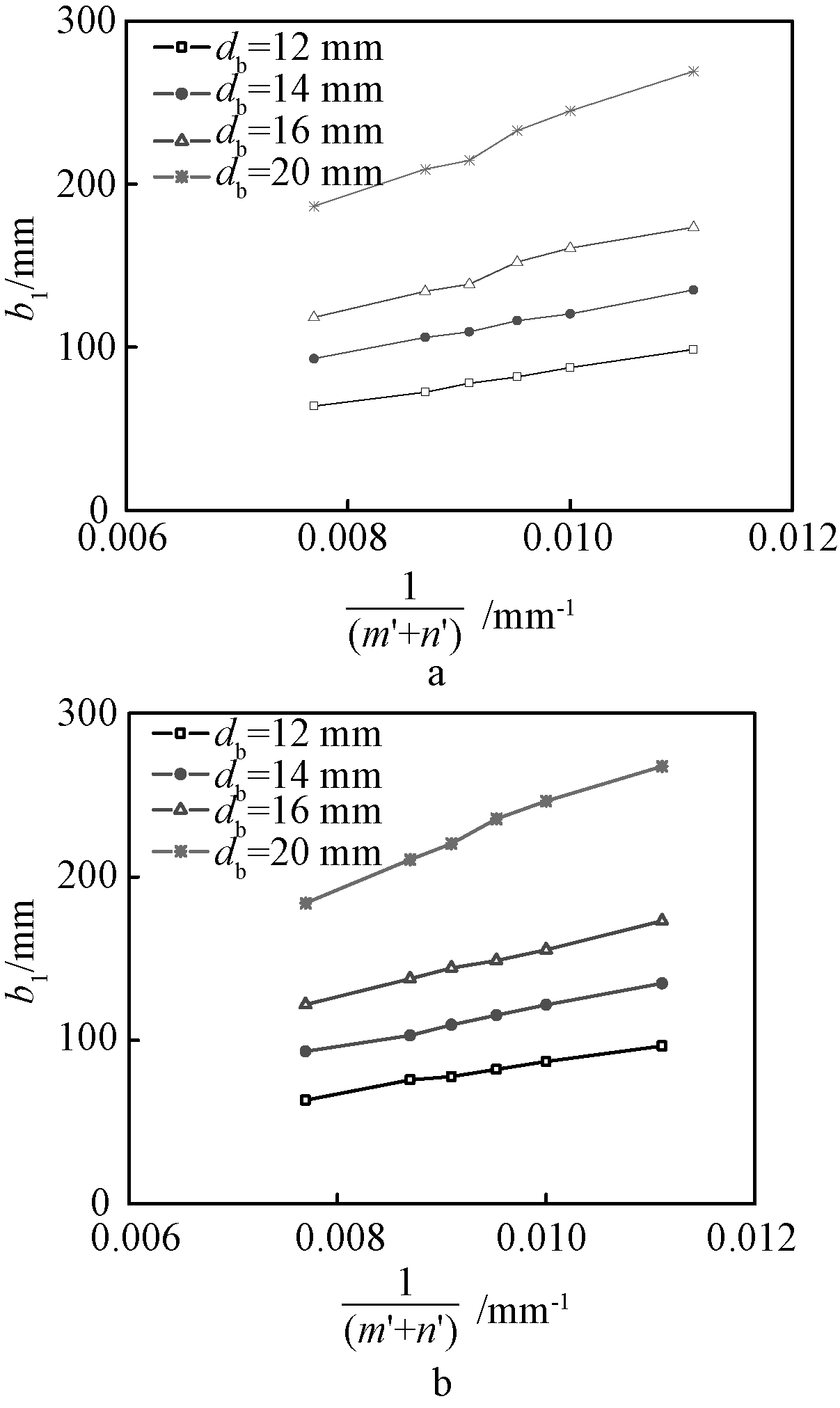
a—S30408; b—S22253。
图12 截距b1与m的关系
Fig.12 Relationship between intercept b1 and m
(8)
由于不锈钢翼缘板的塑性优于普通钢材,相对于普通钢材而言,不锈钢螺栓相对翼缘板的偏移量更大。在式(9)中引入系数β对n′/(m′+n′)进行修正,β与计算结果的比较见图13。
(9)
其中![]()
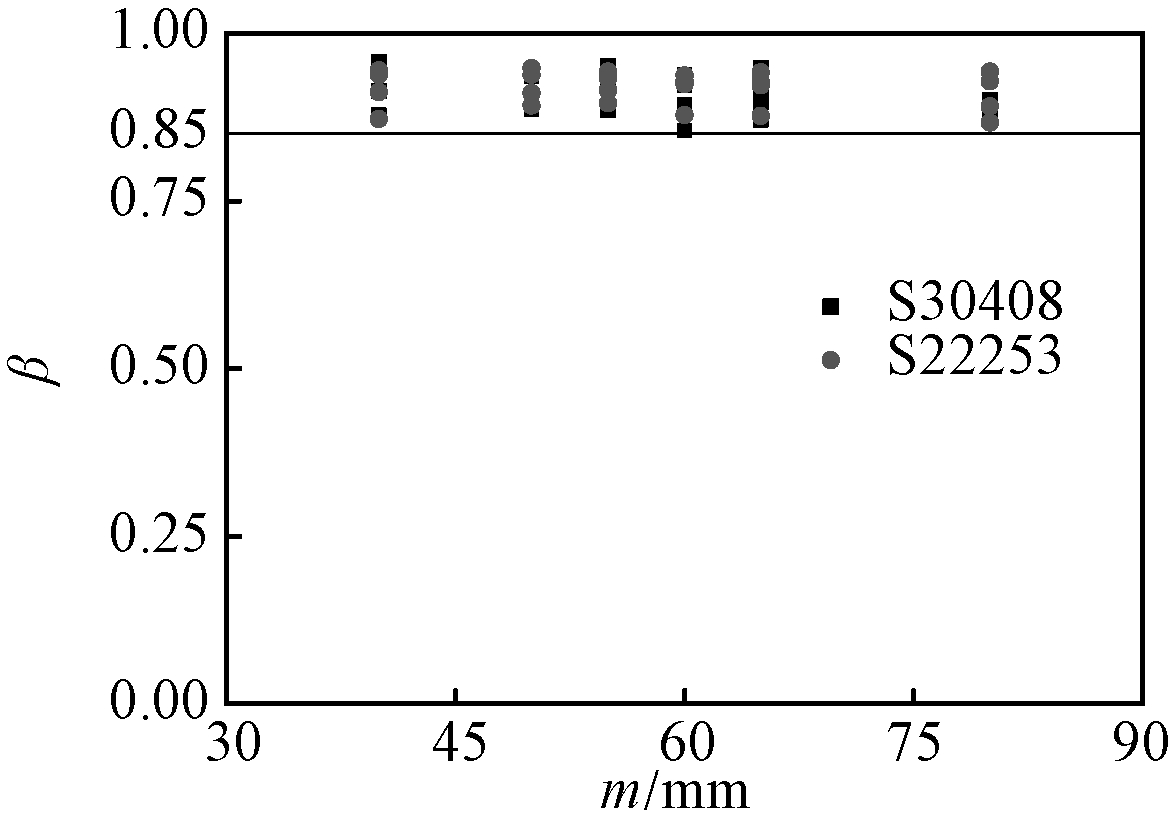
图13 系数β计算结果
Fig.13 Calculation result of coefficient β
从图中可看出,计算所得β均大于0.85,故出于安全考虑将β值取为0.85,则对于破坏模式2的不锈钢T形件承载力计算式见式(10)。
(10)
对于破坏模式1,由2.1节可知,螺栓先于模型整体破坏,故以螺栓破坏时试件承受的荷载为极限承载力,这与模式2的承载力计算原理相同,均以螺栓被拉断,且翼缘板在其与腹板连接处形成塑性铰为计算依据,因此破坏模式1的承载力计算式亦为式(10)。对于破坏模式3,破坏时螺栓被拉断,不锈钢T形件承载力即为螺栓抗拉承载力之和。综上,三种破坏模式下的不锈钢T形件螺栓连接承载力建议计算式如下。
模式1和2:
(11a)
模式3:
F3=∑Ft=∑fubAb
(11b)
其中 m′=m-db/2
n′=n+db/2
式中:M为翼缘板塑性弯矩,见式(6);db为螺栓直径;fub为螺栓的极限抗拉强度;Ab为螺栓的螺杆面积。
图14为不锈钢T形件建议计算式的计算结果Fu与有限元结果FFE的比较。可知,Fu/FFE大部分数据点介于0.9~1.1之间。S30408不锈钢T形件Fu/FFE的平均值为0.99,标准差为0.03,而S22253不锈钢T形件Fu/FFE的平均值为0.93,标准差为0.04。表明建议算式可以准确计算不锈钢T形件的承载力。
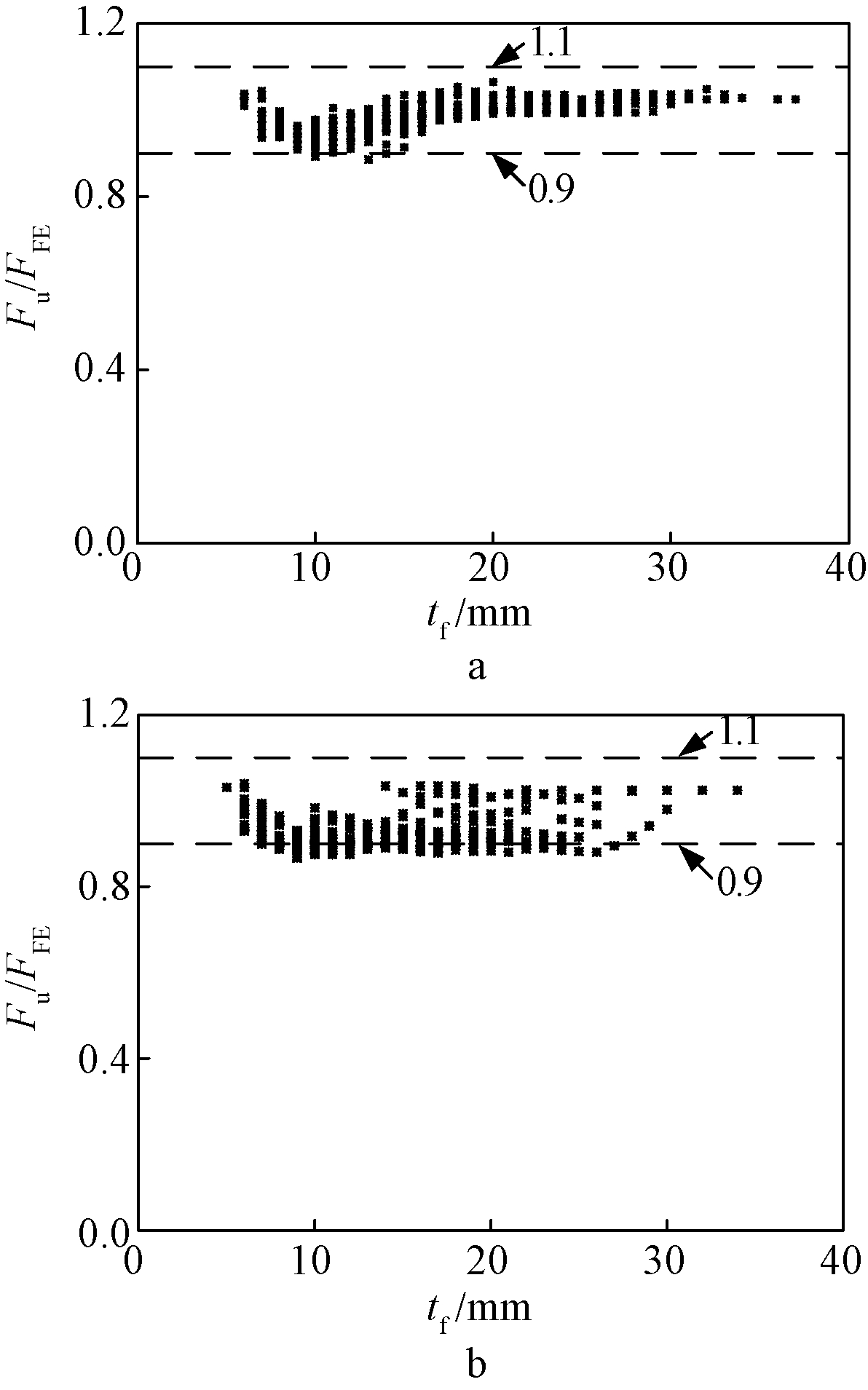
a—S30408; b—S22253。
图14 建议算式计算结果与有限元结果比较
Fig.14 Comparison of calculation results from proposed formula with FE results
4 结 论
1)对不锈钢T形件螺栓连接建立了精细有限元数值模型,有限元计算结果与试验结果十分接近,表明所建立有限元模型准确可靠。
2)参数分析表明:随着翼缘厚度的增加,T形件破坏模式由破坏模式1逐渐变为破坏模式3;螺栓孔到腹板边缘距离的增大及翼缘材料名义屈服强度的降低会降低破坏模式1和2的T形件的承载力,但不影响破坏模式3的T形件的承载力;螺栓直径的增大会提高3种破坏模式下的T形件的承载力。
3)由于不锈钢板具有良好的塑性变形能力,破坏模式1的试件在荷载未到峰值时螺栓已经破坏,从而定义螺栓塑性应变达到最大塑性应变时对应的荷载为试件的极限承载力。
4)考虑利用不锈钢的应变硬化能力对翼缘板塑性弯矩进行了修正,提出了不锈钢T形件螺栓连接承载力的建议计算方法,其计算结果与有限元结果吻合良好,可以应用于不锈钢T形件螺栓连接设计计算。
[1] 吴兆旗, 张素梅. 撬力对螺栓抗拉连接承载力的影响[J]. 地震工程与工程振动, 2008, 28(6): 220-225.
[2] 吴兆旗, 姜绍飞, 喻露, 等. 设置垫板的T形件螺栓连接滞回性能试验研究[J]. 工程力学, 2014, 31(2): 164-169, 176.
[3] 赵伟, 童根树. 加劲T形件连接节点试验研究[J]. 浙江大学学报(工学版), 2008, 42(1): 66-71.
[4] 刘秀丽, 王燕, 李关红, 等. 钢结构T形连接高强度螺栓受力分析及数值模拟[J]. 建筑科学与工程学报, 2016, 33(2): 63-70.
[5] 暴伟, 周向前, 班敏, 等. 受拉T形连接件高强螺栓受力性能研究[J]. 建筑结构学报, 2016, 37(增刊1): 380-387.
[6] 郭宏超, 梁刚, 刘云贺, 等. 预拉力螺栓连接焊接T形件受力性能研究[J]. 建筑结构学报, 2018, 39(5):156-163.
[7] FAELLA C, PILUSO V, RIZZANO G. Experimental Analysis of Bolted Connections: Snug Versus Preloaded Bolts [J]. Journal of Structural Engineering, 1998, 124(7):765-774.
[8] PILUSO V, RIZZANO G. Experimental Analysis and Modelling of Bolted T-Stubs Under Cyclic Loads [J]. Journal of Constructional Steel Research, 2008, 64(6): 655-669.
[9] ZHAO M S, LEE C K, CHIEW S P. Tensile Behavior of High Performance Structural Steel T-Stub Joints [J]. Journal of Constructional Steel Research, 2016, 122: 316-325.
[10] CHEN C, ZHANG X, ZHAO M, et al. Effects of Welding on the Tensile Performance of High Strength Steel T-Stub Joints [J]. Structures, 2016(9): 70-78.
[11] BOUCHAïR A, AVERSENG J, ABIDELAH A. Analysis of the Behaviour of Stainless Steel Bolted Connections [J]. Journal of Constructional Steel Research, 2008, 64(11): 1264-1274.
[12] 杨成博. 不锈钢螺栓高温本构关系构建及其T型连接受力性能研究[D]. 重庆:重庆大学,2017.
[13] 袁焕鑫, 胡松, 杜新喜, 等. 不锈钢T形件螺栓连接承载性能试验研究[J]. 工程力学, 2019,36(2):218-226.
[14] DE MATTEIS G, NAQASH M T, BRANDO G. Effective Length of Aluminium T-Stub Connections by Parametric Analysis [J]. Engineering Structures, 2012, 41(3): 548-561.
[15] 中华人民共和国住房和城乡建设部.不锈钢结构技术规程:CECS 410∶2015[S]. 北京:中国计划出版社, 2015.
[16] 王元清, 关建, 张勇, 等. 不锈钢构件螺栓连接摩擦面抗滑移系数试验[J]. 沈阳建筑大学学报(自然科学版), 2013, 29(5): 769-774.
[17] 关建, 王元清, 张勇, 等. 不锈钢结构螺栓连接节点设计方法比较[J]. 建筑科学与工程学报, 2012, 29(1): 115-120.
[18] European Committee for Standization. Eurocode 3: Design of Steel Structures-Part 1-8: Design of Joints: EN 1993-1-8[S].Brussels: European Committee for Standardization, 2005.
[19] AISC. Steel Construction Manual[S]. 14th ed. Chicago: American Institute of Steel Construction, 2011.
[20] 中华人民共和国住房和城乡建设部.钢结构高强度螺栓连接技术规程:JGJ 82—2011[S]. 北京: 中国建筑工业出版社, 2011.
[21] AFSHAN S, GARDNER L. The Continuous Strength Method for Structural Stainless Steel Design [J]. Thin-Walled Structures, 2013, 68: 42-49.