2017年4月26日,住建部发布《建筑节能与绿色建筑发展“十三五”规划》[1]并提出建筑节能及绿色建筑发展目标。围护结构节能是建筑节能的主要部分,因此楼板节能措施至关重要。赵欣等通过对轻钢龙骨泡沫混凝土预制楼板受弯性能的研究发现:泡沫混凝土能够延缓轻钢龙骨整体或局部失稳破坏,提高构件整体承载力,另外提出了适用于该楼板的承载力计算理论[2];肖凌云等对预制混凝土保温空心楼板进行了抗弯试验并发现空心板破坏形态与实心板类似,在保证空心率和板厚不变时,泡沫板下部混凝土厚度越大,其对应的抗弯刚度、开裂荷载、屈服荷载都会相应降低[3];吴方伯等提出一种预应力混凝土叠合空心楼板并进行静力试验,试验结果表明预应力混凝土叠合空心楼板与预应力现浇空心楼板受力性能较为接近[4];王新堂等通过对开孔薄壁钢梁-轻骨料混凝土装配式组合楼板进行静力试验发现,组合效应系数可以较好地反映组合楼板整体特性及内部损伤[5];冯鹏等基于CTSRC楼板静力试验结果,提出了等效钢筋混凝土梁计算方法和条带法[6];侯和涛等提出了一种新型灌浆钢管桁架混凝土叠合板并通过受弯试验研究发现[7]:现有技术标准推荐的计算方法满足工程设计的要求。研究人员对轻质楼板和型钢楼板研究较多,但对两者相结合的楼板研究较少。
在国内相关研究基础上,本课题组提出一种M型型钢组合楼板。该楼板结合型钢和保温板的特点,能够有效提高楼板整体保温和受力性能。通过对两块M型型钢组合楼板的静力试验和理论分析,探究其受力性能。
1 试验概况
1.1 构件设计
考虑不同厚度M型型钢对楼板受力性能的影响,制作了两块编号为SB1、SB2的M型型钢桁架楼板,其设计几何尺寸为4 500 mm×1 300 mm×200 mm。楼板混凝土强度等级为C30,采用聚苯板作为保温层并内置于楼板中。试件楼板骨架设计参数如表1所示,楼板截面如图1所示,型钢构造如图2所示,所用材料力学性能试验结果见表2、表3所示。
表1 楼板骨架设计参数
Table 1 Floor frame design parameters mm
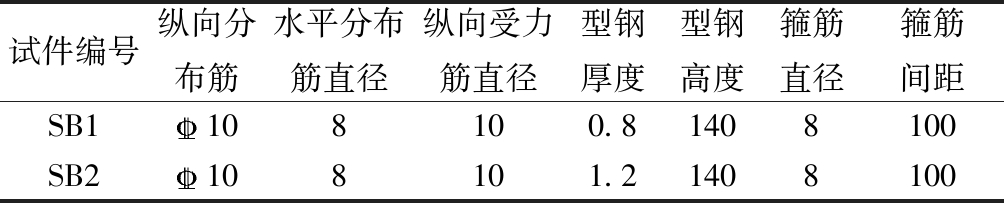
试件编号纵向分布筋水平分布筋直径纵向受力筋直径型钢厚度型钢高度箍筋直径箍筋间距SB1108100.81408100SB2108101.21408100
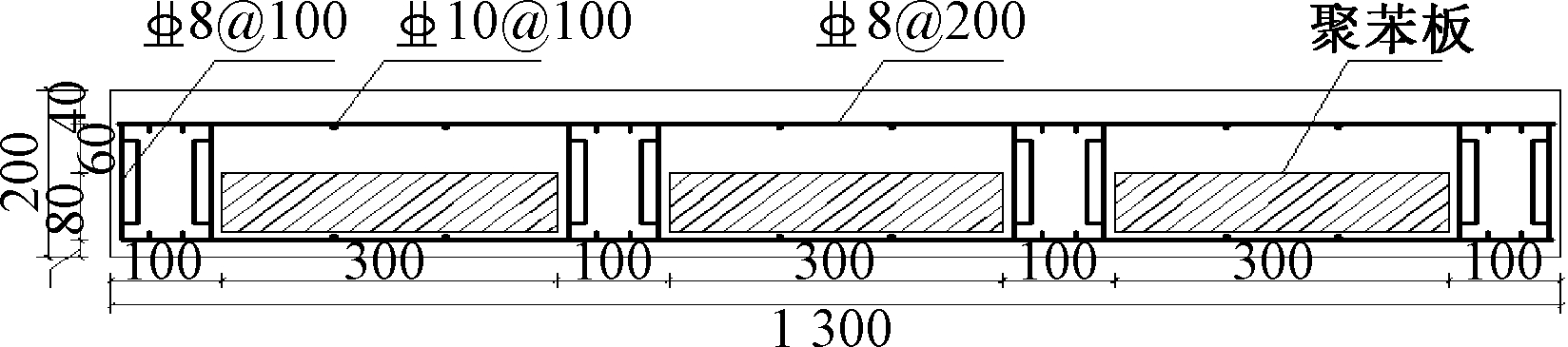
图1 M型型钢桁架楼板截面
Fig.1 Section diagram of M-shaped steel truss floor
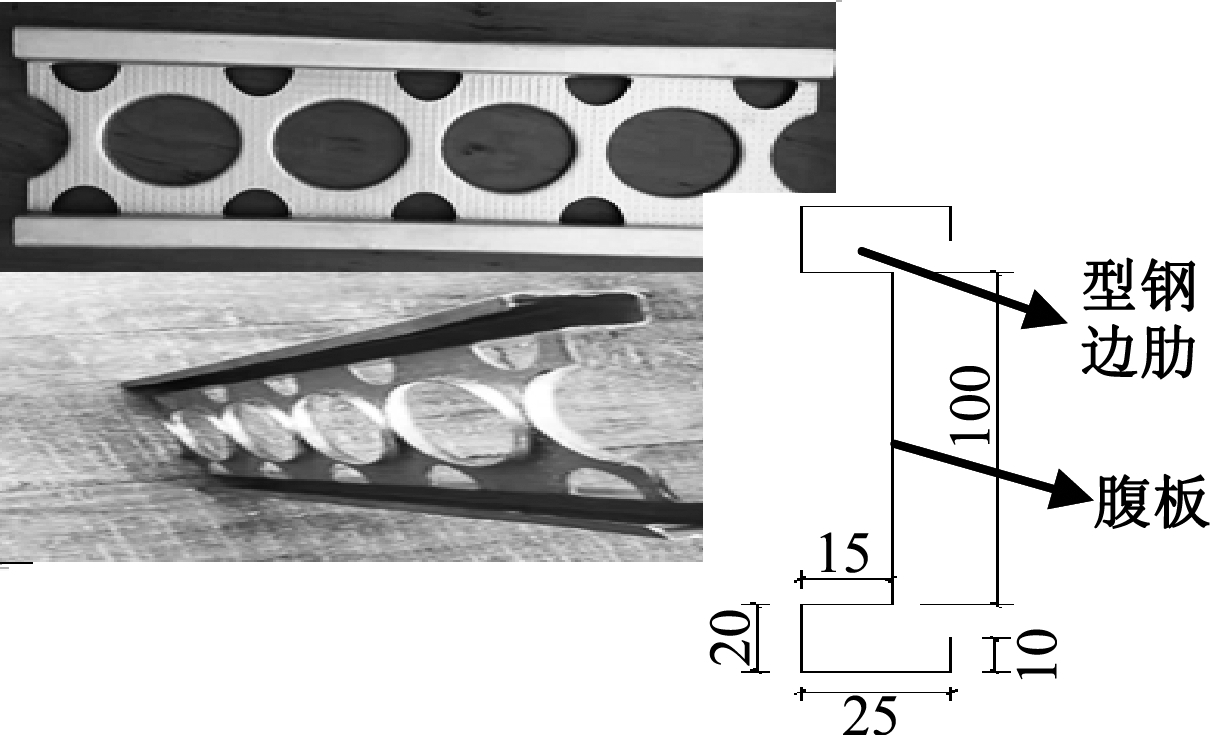
图2 型钢构造
Fig.2 Steel structure
表2 混凝土性能参数
Table 2 Performance parameters of concrete MPa

编号立方体抗压强度平均值fcu,m轴心抗压强度平均值fc,m轴心抗拉强度平均值ft,mSB143.833.33.2SB242.332.13.2
表3 钢材材性试验结果
Table 3 Results of steel properties test
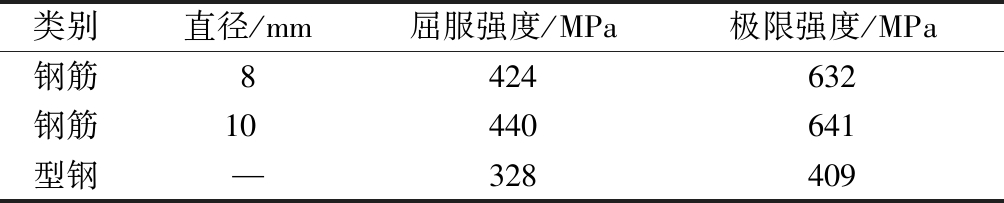
类别直径/mm屈服强度/MPa极限强度/MPa钢筋8424632钢筋10440641型钢—328409
1.2 试验方案设计
1.2.1 试验装置和加载方案
试件按照四分点加载方式进行试验,楼板两端支座简支,一端为固定铰支座,另一端为滚动铰支座,分别布置在距离试件两端150 mm处,计算跨度为4 200 mm。试验过程中,采用液压千斤顶施加集中荷载,并通过分配梁将荷载传递到两个加载点上,两个加载点分别距离试件两端1 200 mm处,具体试验装置如图3所示。本文加载方案采用分级加载方式,每级加载值为使用状态短期试验荷载的10%,直至试件破坏。
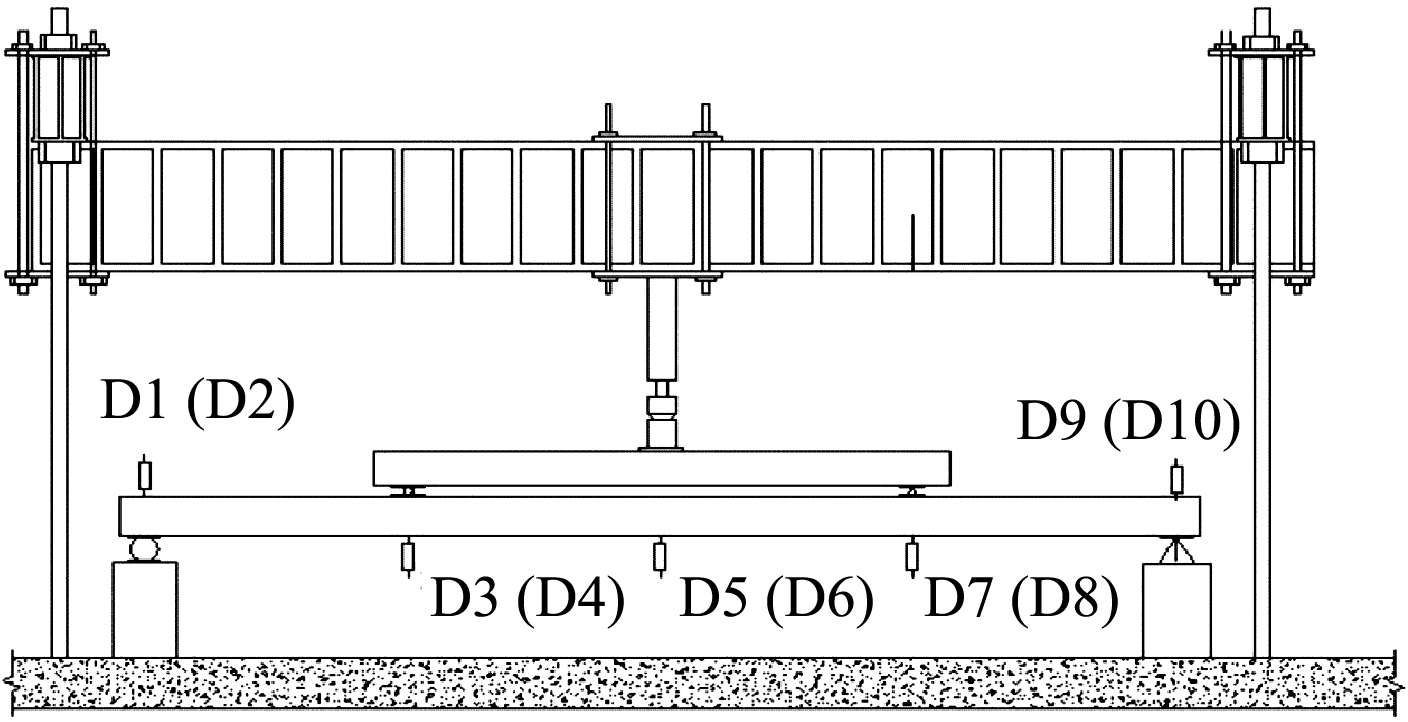
图3 试验装置
Fig.3 Experimental equipment
1.2.2 测点布置
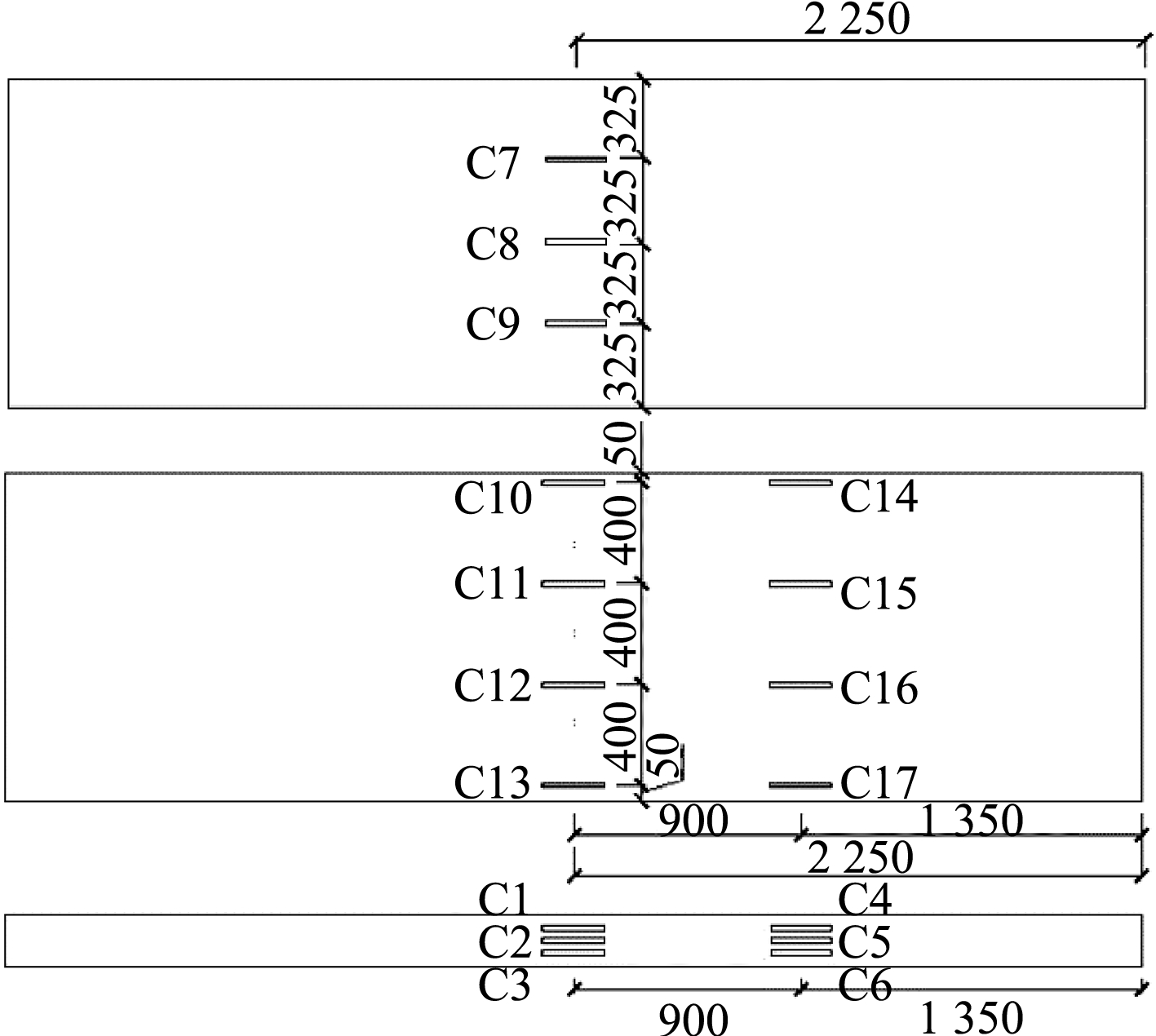
图4 混凝土应变片布置
Fig.4 Arrangement of concrete strain gauges
为了测量楼板不同部位挠度变化,在试件跨中、加载点、支座处共布置10个位移计,位移计具体布置如图3所示。计算跨中挠度时需考虑支座沉降。试验前,在试件跨中上表面、侧面、下表面粘贴应变片,用于验证楼板截面是否满足平截面假定,混凝土应变片布置如图4所示。其中楼板上表面应变片编号为C7~C9,侧面应变片编号为C1~C6,下表面应变片编号为C10~C17。钢筋应变片布置在钢筋骨架的跨中位置,布置如图5所示。其中型钢应变片编号为XG1,纵向受力筋应变片编号为ZJ1,下部水平钢筋应变片编号为SJ1。

图5 钢材应变片布置
Fig.5 Arrangement of steel strain gauges
2 试验结果与分析
2.1 试验现象
试件SB1和试件SB2的裂缝分布基本一致,如图6所示,故以SB1板为例介绍楼板整个破坏过程。冷弯型钢桁架楼板的破坏形式为弯曲破坏,整个破坏过程可分为三个阶段。
a—SB1; b—SB2。
图6 裂缝分布
Fig.6 Crack distribution
1)第一阶段为线弹性阶段,荷载从零开始直至达到开裂荷载,试件始终保持弹性状态,试件表面无裂缝出现。
2)第二阶段为带裂缝工作阶段,当荷载加载到22 kN时,在跨中附近出现第一条竖向裂缝;随着荷载继续增加,纯弯段陆续出现竖向裂缝并向上延伸。
3)第三阶段为破坏阶段,随着荷载继续增加,弯剪段也出现较短的竖向裂缝,纯弯段处的裂缝继续向上延伸、变宽;当跨中挠度增加到19.6 mm时,型钢应变达到了1 600×10-6,型钢屈服;当跨中挠度为31.5 mm时,荷载达到了峰值荷载(69.2 kN);当千斤顶继续加载,楼板跨中挠度增加,已有裂缝变宽,试件承载力逐渐下降,直至试件破坏。
2.2 试验结果分析
2.2.1 跨中截面应变分析
SB1跨中截面应变变化规律见图7。可知:试件处于弹性状态时,随着荷载增加,楼板截面高度与平均应变的关系仍然保持直线趋势。由此表明:试件截面的平均应变满足平截面假定。
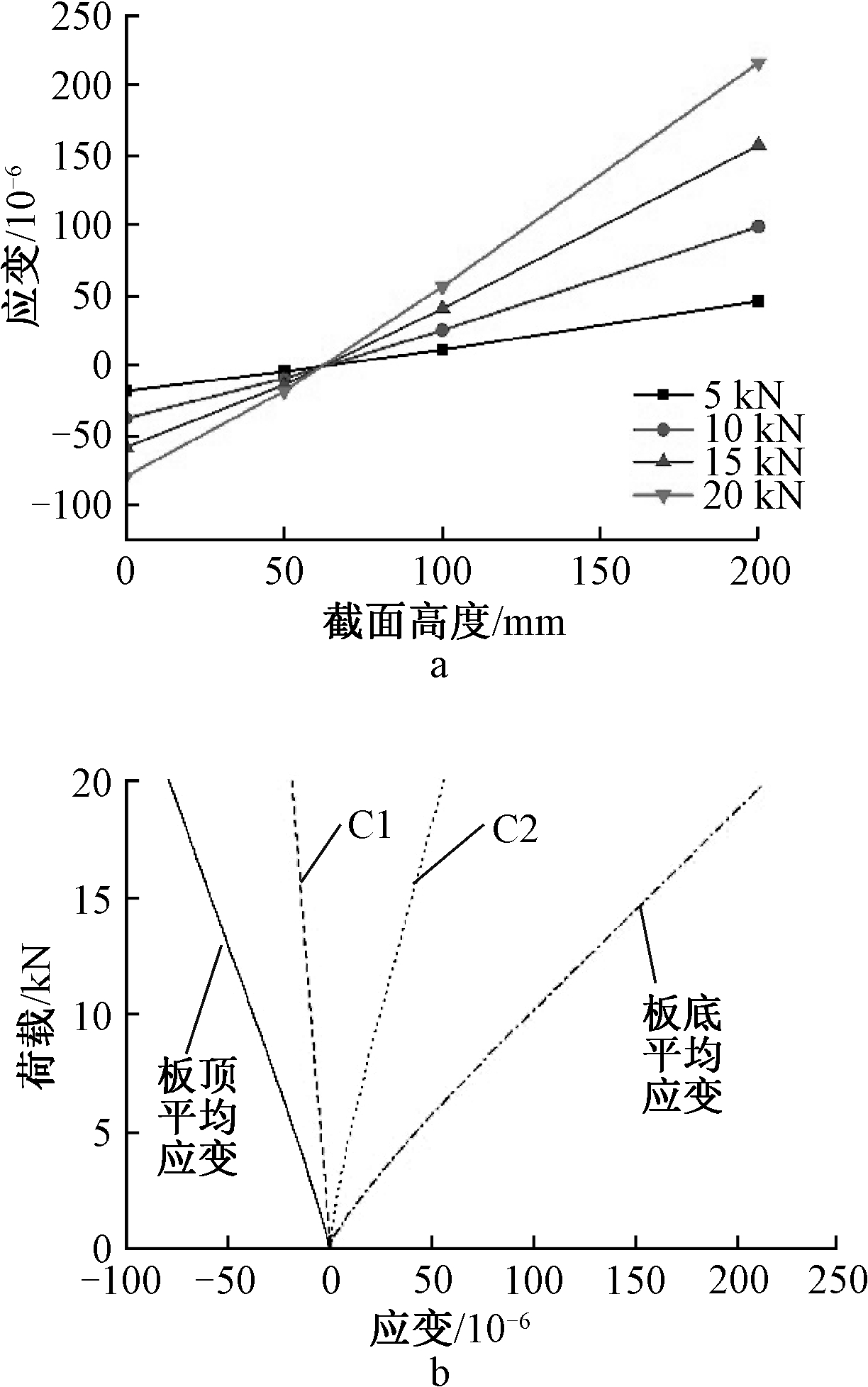
a—不同荷载下截面应变分布; b—荷载-应变曲线。
图7 SB1截面应变变化规律
Fig.7 Change law of section strain of SB1
2.2.2 荷载-跨中挠度曲线
试件荷载-跨中挠度曲线如图8所示。试件SB1和SB2的荷载-跨中挠度曲线走势基本一致,特以试件SB2为例描述曲线。试件SB2开裂荷载为25 kN,当荷载超过开裂荷载后,荷载-跨中挠度曲线斜率开始下降,试件刚度降低;当跨中挠度为48.8 mm时,荷载达到峰值荷载(73.6 kN);跨中挠度继续增加,承载力开始下降,直至破坏。试件SB1、SB2的试验结果如表4所示。可知:型钢厚度由0.8 mm提高到1.2 mm时,试件开裂荷载、峰值荷载、峰值位移分别提高了13.6%、6.3%、54.9%。试验结果表明:型钢厚度越厚,试件开裂荷载、峰值荷载越大。
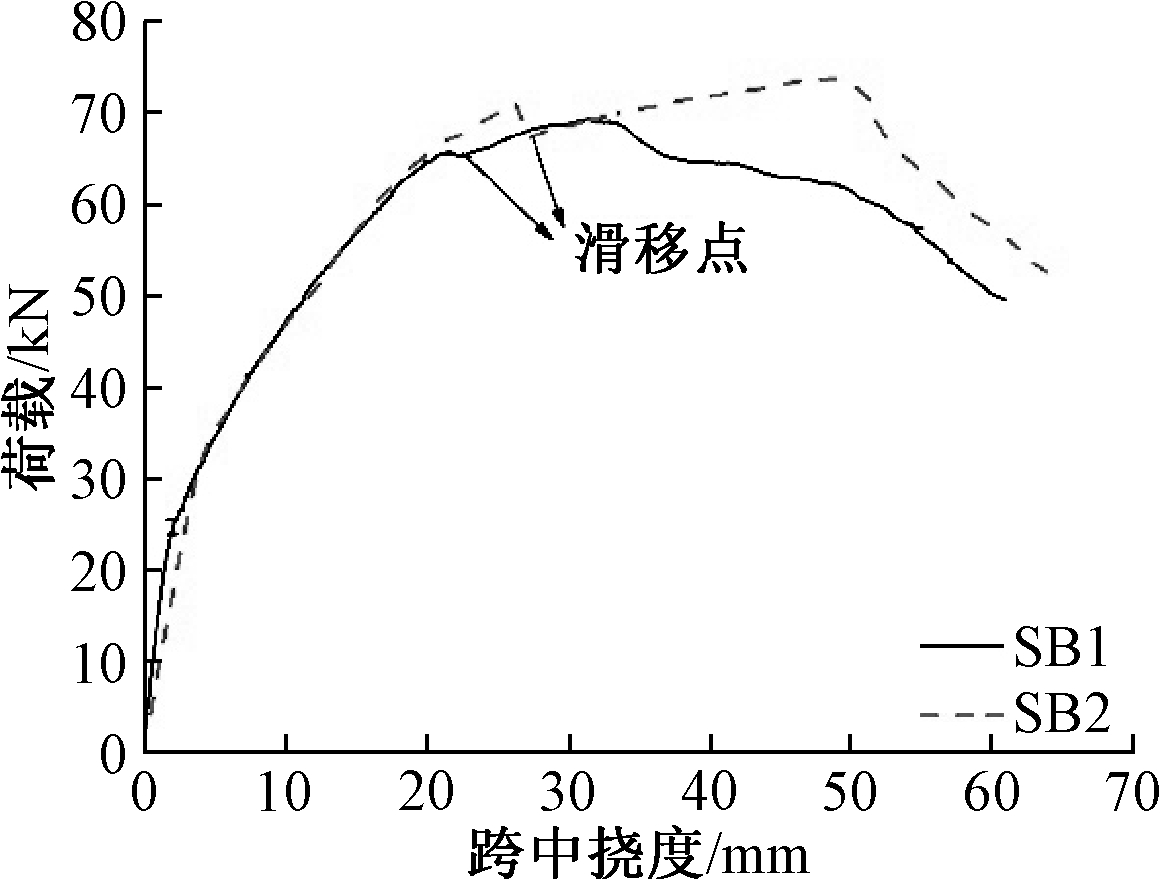
图8 荷载-跨中挠度曲线
Fig.8 Load versus mid-span deflection curves
表4 试验结果
Table 4 Test results
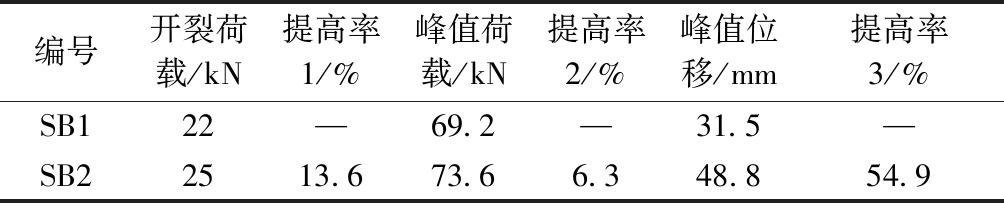
编号开裂荷载/kN提高率1/%峰值荷载/kN提高率2/%峰值位移/mm提高率3/%SB122—69.2—31.5—SB22513.673.66.348.854.9
如图8所示:试验过程中SB1和SB2钢筋均发生不同程度的滑移,这是因为浇筑问题导致下部纵向受力钢筋混凝土包裹量不足(图9),混凝土与钢筋的黏结力小于受拉钢筋的拉力,荷载-跨中挠度曲线的表现形式为荷载下降。当下部纵向受力钢筋与混凝土不再发生局部滑移时,荷载继续提高。
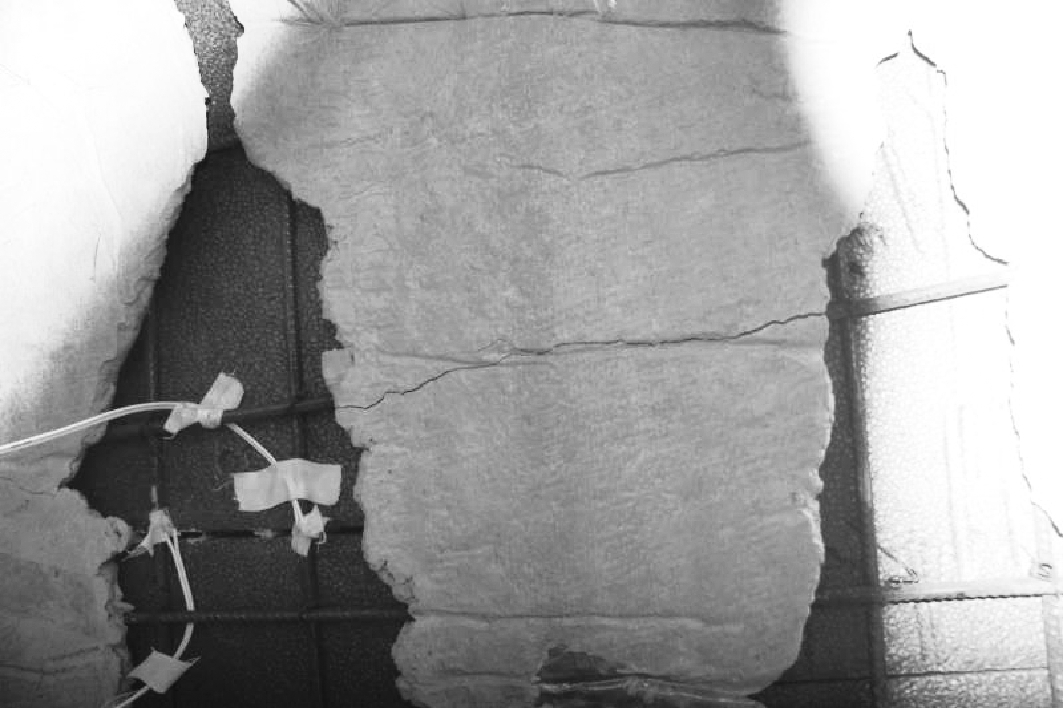
图9 楼板板底
Fig.9 The bottom of the floor
2.2.3 延性系数
延性系数是反映楼板性能的重要指标之一[8],试件延性系数如表5所示,试件型钢厚度从0.8 mm提高到1.2 mm时,延性系数从4.98下降到3.73,下降程度为25%。试验结果表明:试件延性随着型钢厚度的增大而减小。具体表达式为:
(1)
式中:Δu为极限位移;Δy为屈服位移(按作图法[9]取值)。
表5 延性系数
Table 5 Ductility coefficients

编号屈服位移/mm极限位移/mm延性系数提高率/%SB110.652.84.98—SB215.056.03.73-25
2.2.4 特征刚度
如表6和图8可知,试件SB1与试件SB2使用阶段荷载设计值对应的挠度值分别为6.62,6.54 mm,均远小于GB 50010—2010《混凝土结构设计规范》规定的1/200跨度(21 mm)。试件SB1的Ke值、Km值分别是试件SB2对应值的1.57、1.45倍。试验结果表明,增加型钢厚度会降低Ke和Km,但对Ks基本没有影响。
表6 特征挠度与刚度
Table 6 Characteristic deflection and stiffness

编号Δe/mmΔm/mmKe/(kN·mm-1)Ks/(kN·mm-1)Km/(kN·mm-1)SB11.6731.513.175.892.19SB22.9848.88.395.961.51
注:Δe为弹性极限挠度;Δm为峰值荷载对应的挠度;Ke为弹性刚度;Ks为荷载设计值7.14 kN/m2(荷载标准值为3.78 kN/m2、活荷载为2 kN/m2)对应的割线刚度;Km为峰值荷载对应的割线刚度。
3 等效计算方法研究
基于试验分析结果,并考虑楼板构造的复杂性,在前人研究[6]基础上提出一种适用M型型钢等效计算式,推导楼板开裂荷载和承载力计算式。同时与试验结果对比,验证该等效计算式及计算式的正确性和适用性。
3.1 型钢等效计算式
M型型钢构造特殊,考虑最薄弱截面等因素,忽略型钢腹板对楼板承载力的贡献,仅考虑型钢边肋对试件受力性能的影响,并在此基础上将型钢等效为钢筋即等效筋。
按照惯性矩的平行移轴式,型钢或等效筋对楼板截面的中和轴的惯性矩算式为:
I=A+B
(2a)
A=Ic
(2b)
B=a2S
(2c)
式中:Ic为型钢或等效筋截面对形心轴的惯性矩;a为型钢或等效筋截面形心轴到中和轴的距离;S为型钢或等效筋截面面积。
由于型钢边肋的钢材厚度h较薄,其值远小于a,因此h2≪a2;等效筋直径d远小于a,因此d2≪a2,故在计算型钢边肋和等效筋对中和轴惯性矩时,可以忽略A对I的影响,等效时按照式(3)进行惯性矩计算:
I=B=a2S
(3)
将型钢等效成等效筋时采用的等效原则为:
ExIx=EsIs
(4a)
Exax2Sx=Esas2Ss
(4b)
式中:Ex和Es分别为型钢和等效筋弹性模量;Ix和Is分别为型钢和等效筋对中和轴惯性矩;ax和as分别为型钢和等效筋截面形心到中和轴距离;Sx和Ss分别为型钢和等效筋惯性矩。
由于将等效筋布置在与型钢形心重合的位置,即ax=as,因此式(4b)可以简化为:
ExSx=EsSs
(5)
令
(6)
(7)
将式(6)和式(7)代入式(5)中,得等效筋直径d的等效算式:
(8)
3.2 截面等效方法
由于楼板的原始截面构造复杂,为了简化计算,按照截面对重心轴惯性矩不变、截面重心不变、截面面积不变三个原则[9]将空心矩形截面等效成工字形截面,截面等效如图10所示。图中A、B、C、D分别对应混凝土截面区域,具体等效过程如下:
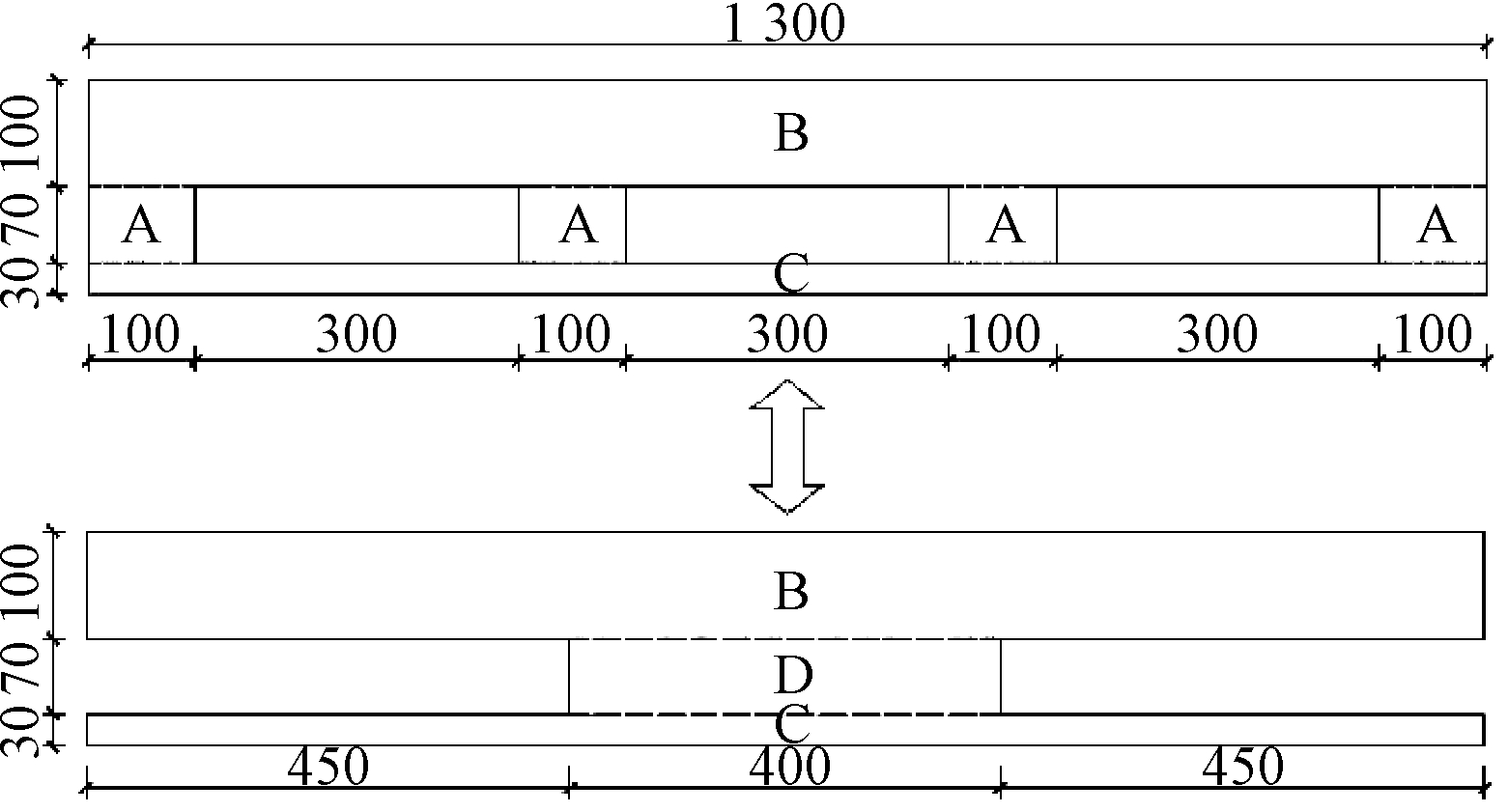
图10 截面等效
Fig.10 Section equivalent
1)对于B、C部分,当截面等效时,保持B、C部分尺寸、形状和位置不变,其对中和轴的惯性矩不会改变。
2)对于A部分,当截面等效、A部分截面形心到中和轴距离不变时,将A部分按照平移方式进行合并,即4Ab(A部分截面宽度)=Db(D部分截面宽度);Ah(A部分截面高度)=Dh(D部分截面高度)。合并后D部分相对于A部分对中和轴的惯性矩不变,截面重心不变、截面面积不变。因此,A、B和C部分按照上述方式进行截面等效后,截面特性未发生变化,满足等效要求。
3.3 开裂荷载计算公式
根据《钢筋混凝土原理》[10]可知:按照几何中心不变的原则将钢筋面积等效成相应的混凝土的面积,即按式(9)进行计算:
Ac=(β-1)As
(9)
其中![]()
式中:Ac为等效的相应混凝土面积;As为钢筋面积;Ec为混凝土弹性模量;Es为钢筋弹性模量。
即将钢筋混凝土截面等效成单一材料的混凝土截面。截面处任一纤维处混凝土的应力可以按照材料力学式进行计算。
δci=My0/I0
(10)
式中:δci为任一纤维处的混凝土应力;y0为任一纤维至换算截面中和轴距离;I0为换算截面惯性矩。
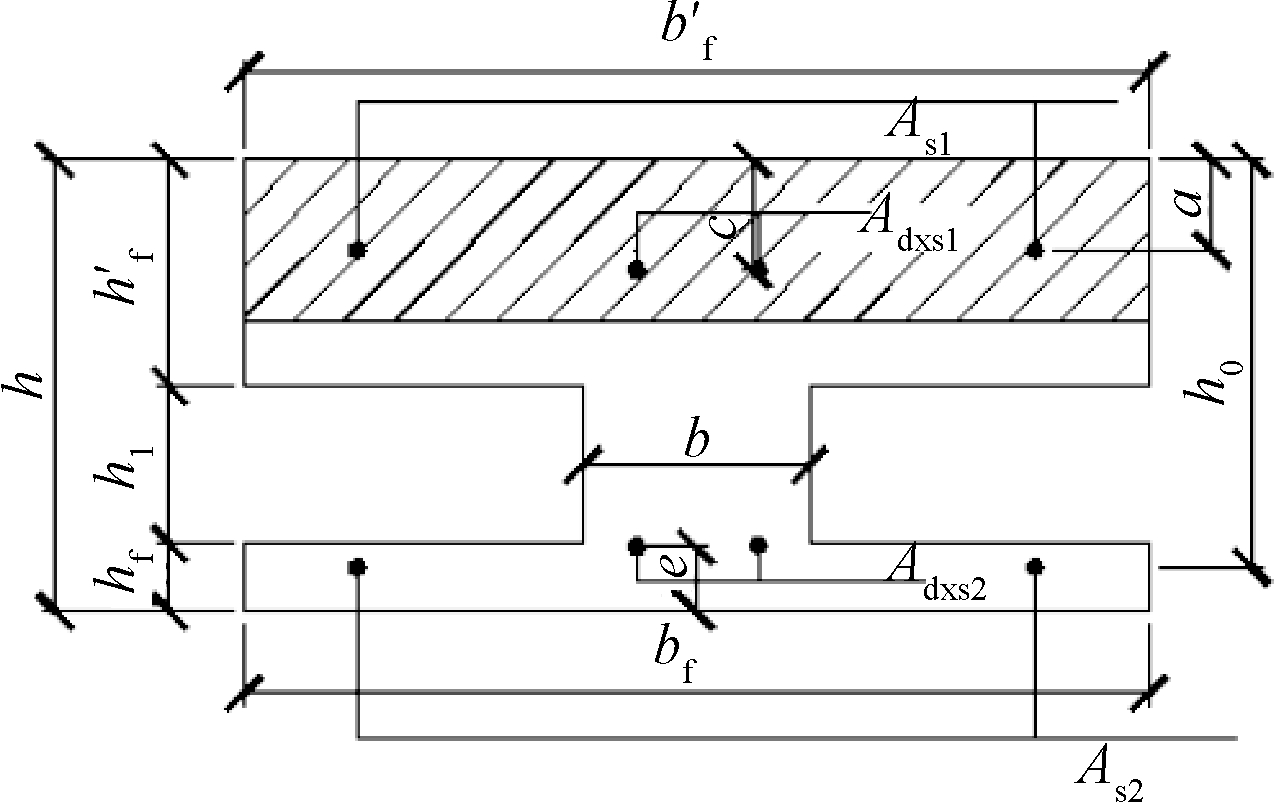
图11 第一种情况下的开裂荷载计算简图
Fig.11 Schematic diagram for the calculation of cracking load in the first case
第一种情况:假设受压区高度为x,中和轴在上翼缘内,如图11所示。图中:![]() 为上翼缘宽度,
为上翼缘宽度,![]() 为上翼缘高度,bf为下翼缘宽度,hf为下翼缘高度,b为腹板宽度,h1为腹板高度,h为楼板高度,h0为楼板有效高度,a为分布筋到上翼缘顶部距离,c为上部等效筋到上翼缘顶部距离,e为下部等效筋到下翼缘底部距离,As1为上部分布筋总面积,Adxs1为上部等效筋总面积,As2为下部分布筋总面积,Adxs2为下部等效筋总面积。
为上翼缘高度,bf为下翼缘宽度,hf为下翼缘高度,b为腹板宽度,h1为腹板高度,h为楼板高度,h0为楼板有效高度,a为分布筋到上翼缘顶部距离,c为上部等效筋到上翼缘顶部距离,e为下部等效筋到下翼缘底部距离,As1为上部分布筋总面积,Adxs1为上部等效筋总面积,As2为下部分布筋总面积,Adxs2为下部等效筋总面积。
按截面相对中和轴面积矩为零的条件得平衡等式:
(h-e-x)+(β-1)(h0-x)As2
(11)
利用式(11),解出x,代入式(12),求出惯性矩I0:
(h-e-x)2+As2(β-1)(h0-x)2
(12)
第二种情况:假设受压区高度为x,中和轴在腹板内,如图12所示。
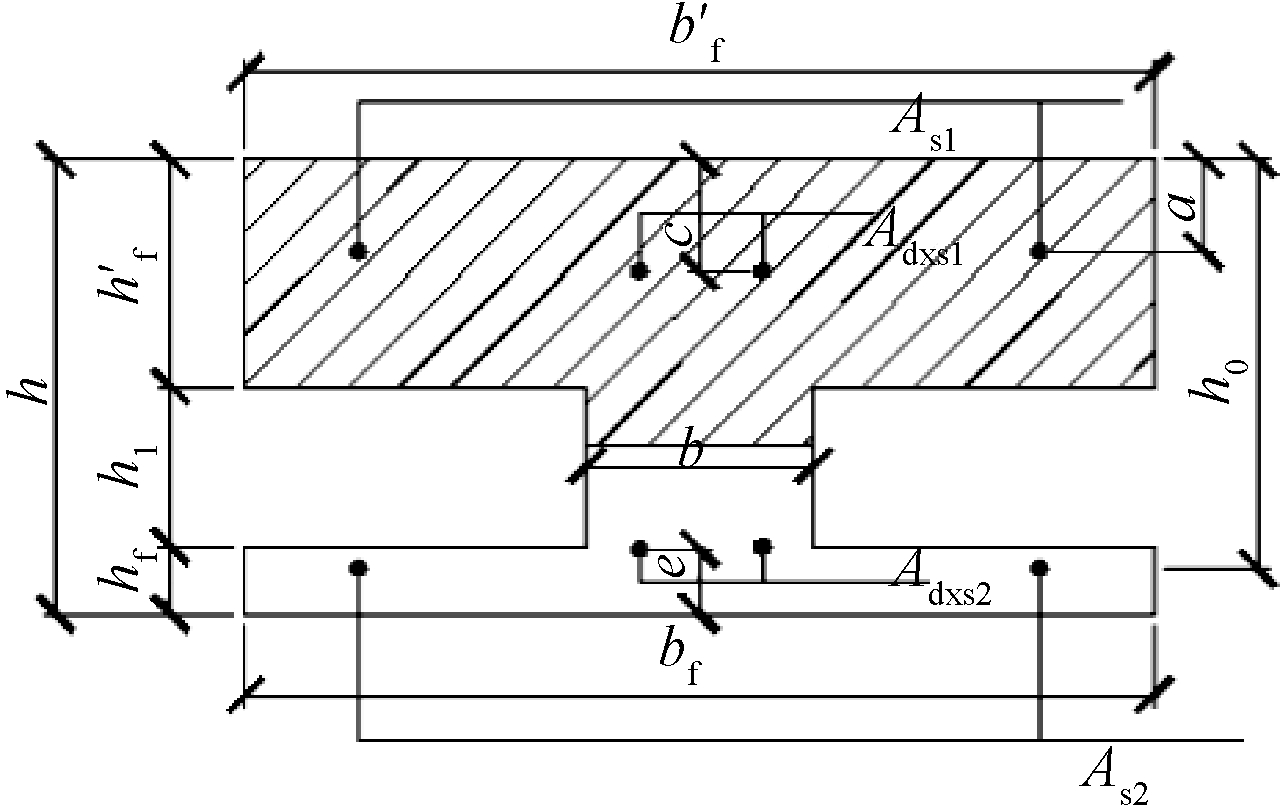
图12 第二种情况下的开裂荷载计算简图
Fig.12 Schematic diagram for the calculation of cracking load in the second case
按截面相对中和轴面积矩为零的条件得平衡等式:
(β-1)As1(x-a)+(β-1)Adxs1·
(h-x-e)+(β-1)As2(h0-x)
(13)
利用式(13)解出x,将x代入式(14),求出惯性矩I0:
(h-x-e)2+(β-1)As2(h0-x)2
(14)
从施加荷载到截面开裂,截面下边缘应力由零变化至γft,则δcr表示为:
(15a)
则
Mcr=γftW0
(15b)
式中:δcr为开裂应力;Mcr为截面的开裂弯矩;W0为换算截面受拉边缘的抵抗矩;γ为截面抵抗矩塑性影响系数;ft为混凝土的轴心抗拉强度。
3.4 承载力计算方法
由于As1与Adxs1、As2与Adxs2重心离中和轴距离近似,为了简化计算,假设As1与Adxs1、As2与Adxs2重心离中和轴距离相等,即a=c,令As3=As1+Adxs1;As4=As2+Adxs2。
第一种情况:假设受压区高度为x,中和轴在上翼缘内,如图13所示。
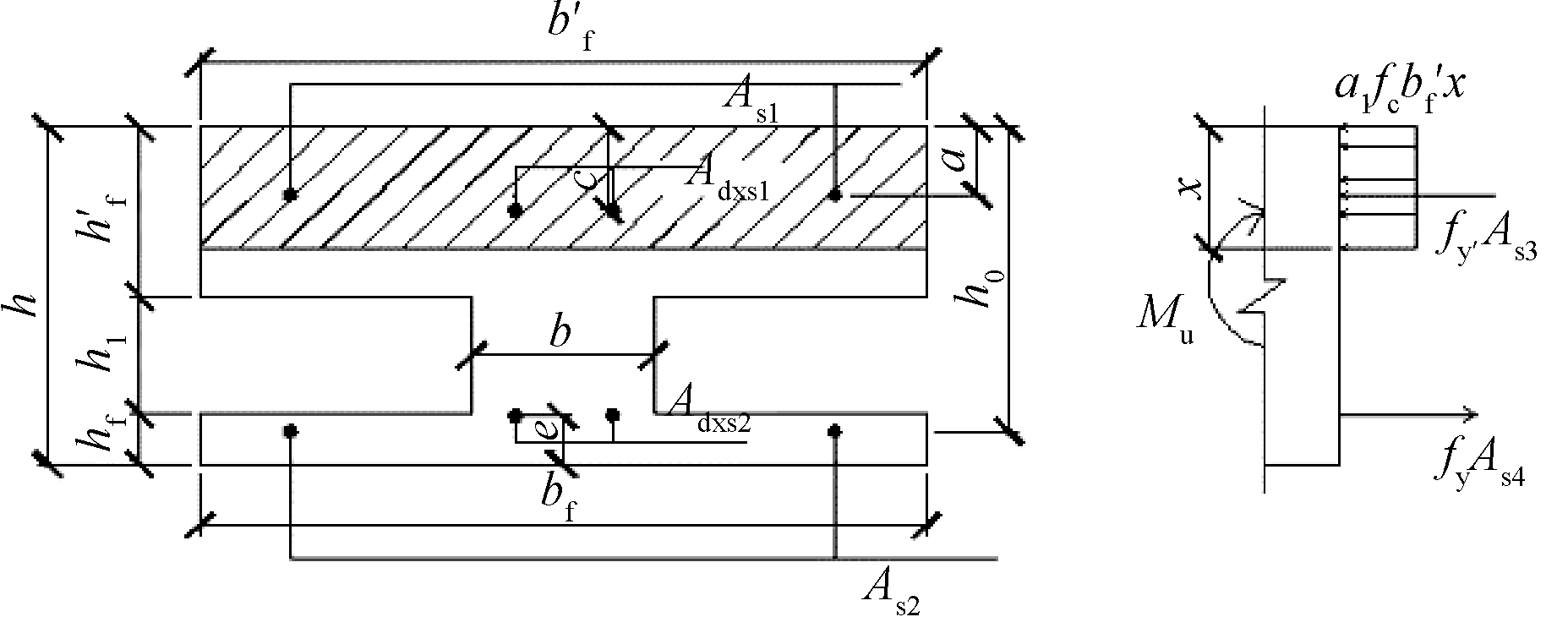
图13 第一种情况下承载力计算简图
Fig.13 Calculation diagram of the bearing capacity in the first case
在计算正截面承载力时,由于不考虑受拉区混凝土参加受力,截面破坏时实质上相当于![]() 由静力平衡方程得:
由静力平衡方程得:
(16a)
(16b)
其中 f ′yAs3=fsAs1+fxAdxs1
fyAs4=fsAs2+fxAdxs2
式中:fs为钢筋屈服强度;fx为型钢屈服强度;fy和f ′y分别为受拉筋和受压筋屈服强度;α1fc为等效后混凝土的压应力。
当受压钢筋不能屈服时,根据《混凝土结构基本原理》[11]相关式,推导得出双筋截面承载力的计算公式:
(17a)
(17b)
其中 ![]()
式中:![]() 为受压筋应力;εcu为混凝土的极限压应变;ξ为相对受压区高度;β1为矩形应力图受压区高度与中和轴高度的比值。
为受压筋应力;εcu为混凝土的极限压应变;ξ为相对受压区高度;β1为矩形应力图受压区高度与中和轴高度的比值。
第二种情况:假设受压区高度x,中和轴在腹板内,如图14所示。
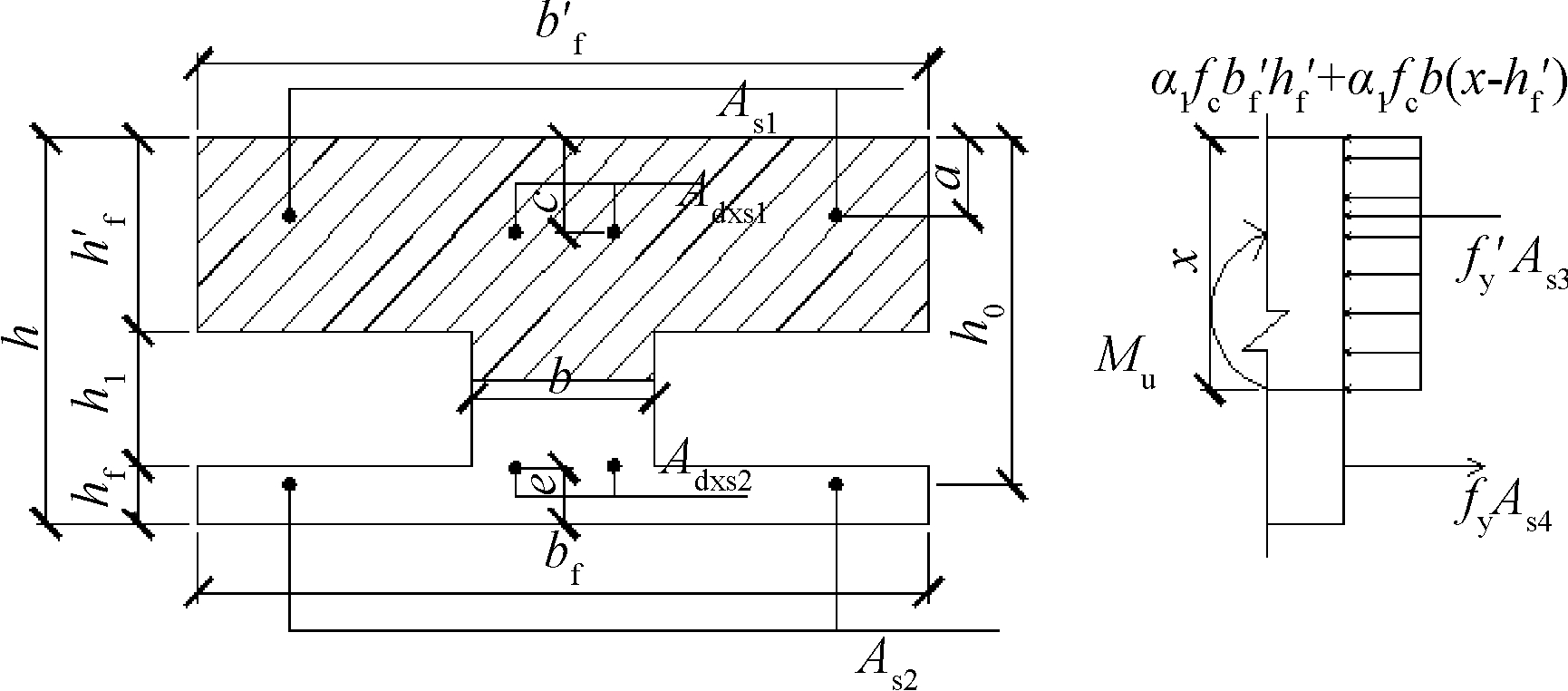
图14 第二种情况下承载力计算简图
Fig.14 Calculation diagram of the bearing capacity in the second case
由静力平衡方程得:
(18a)
(18b)
当受压钢筋不能屈服时,按下式求双筋截面的承载力:
(19a)
(19b)
其中![]()
3.5 开裂荷载与承载力理论计算值对比
将计算参数(表7)代入式(9)~式(19)中,得出试件SB1与SB2的开裂荷载和承载力理论计算结果,如表8所示。
试验值与理论值见表9。对于试件SB1,开裂荷载、峰值荷载理论值分别是试验值的1.32和0.96倍;对于试件SB2,开裂荷载、峰值荷载理论值分别是试验值的1.18和1.04倍。由于混凝土浇筑时底板出现大量空鼓现象,对楼板开裂荷载影响显著,导致开裂荷载的理论值与试验值误差较大。对比结果表明:峰值荷载理论值与试验值相差4%,误差较小,可以应用于后期楼板设计,具有较高的实际应用价值。
表7 计算参数
Table 7 Calculated parameters

参数b′f/mmbf/mma/mmb/mmc/mme/mmh′f/mmhf/mmh1/mmh/mm数值1 3001 3004040050301003070200参数αAs1/mm2As2/mm2h0/mmft/MPafys/MPaγl/mmfydxs/MPa数值1.034714711803.24241.354 200328
注:l为楼板两支座间净距。
表8 计算结果
Table 8 Calculated results

试件编号Mcr/(kN·m)Mu/(kN·m)Fcr/kNFu/kNSB130.5770.0829.1166.7SB231.0781.0529.5977.2
注:Mcr为开裂弯矩;Mu为极限弯矩;Fcr为开裂荷载;Fu为极限荷载。
表9 试验值与理论值
Table 9 Experimental and theoretical values

编号开裂荷载/kN峰值荷载/kN试验值理论值试验值理论值SB12229.1169.266.7SB22529.5973.677.2
4 结束语
基于M型型钢桁架楼板静力试验和理论分析结果,得到以下结论:
1)楼板具有较大的整体刚度和承载力,当均布荷载达到荷载设计值7.14 kN/m2时,楼板跨中变形远小于GB 50010—2010的要求,具有较大的安全储备。
2)静力试验过程中的应变分析表明楼板处于弹性阶段时,随着荷载增加,楼板截面高度与平均应变的关系保持直线趋势,符合平截面假定。
3)M型型钢尺寸对楼板受力性能影响显著,型钢厚度越厚,试件的开裂荷载、峰值荷载越大,延性越差。
4)增加M型型钢厚度会降低楼板的弹性刚度Ke和峰值荷载对应的割线刚度Km,但对荷载设计值对应的割线刚度Ks基本没有影响。
5)SB1开裂荷载、峰值荷载理论值与试验值误差分别为32%、4%,SB2开裂荷载、峰值荷载理论值与试验值误差分别为18%、4%,峰值荷载理论值与试验值误差较小,表明型钢等效计算公式和承载力计算公式合理有效。
[1] 中华人民共和国住房和城乡建设部.建筑节能与绿色建筑发展“十三五”规划[EB/OL].[2020-04-08]. http://www.mohurd.gov.cn/wjfb/201703/t20170314_230978.html.
[2] 赵欣,母瑞强,张驰,等.轻钢龙骨泡沫混凝土预制楼板受弯性能研究[J].建筑钢结构进展,2018,20(3):51-57.
[3] 肖凌云,张炳顺,沈万玉,等.预制混凝土保温空心楼板抗弯力学性能试验研究[J].安徽建筑,2018,24(2):195-197.
[4] 吴方伯,刘彪,邓利斌,等.预应力混凝土叠合空心楼板静力性能试验研究[J].建筑结构学报,2014,35(12):10-19.
[5] 王新堂,杨景,王万祯.开孔薄壁-轻骨料混凝土装配式组合楼板受力性能试验研究[J].建筑结构学报,2016,37(5);39-47.
[6] 冯鹏,初明进,林旭川,等.CTSRC楼板承载力计算及实荷试验[J].清华大学学报(自然科学版),2010,50(9):1325-1329.
[7] 侯和涛,蓝如海,冯明远,等.灌浆钢管桁架混凝土叠合板抗弯性能试验研究[J].工业建筑,2017,47(7):29-33.
[8] 陈博珊. 蒸压加气混凝土板力学试验及数值模拟研究[D].北京:北京建筑大学,2016.
[9] 金灵芝. 预应力混凝土空心叠合板的受力性能和设计计算研究[D].长沙:中南大学,2008.
[10] 过镇海.钢筋混凝土塬理[M].北京:清华大学出版社,1999.
[11] 梁兴文.混凝土结构基本原理[M].重庆:重庆大学出版社,2011.