钢板剪力墙是一种新型的抗侧力构件,由内置钢板与约束边缘构件组成[1-2],目前,钢板剪力墙已在我国一些标志性的高层建筑和超高层建筑中得到应用。与混凝土剪力墙相比,钢板剪力墙具有较大的延性,但钢板剪力墙由于其内嵌平钢板自身厚度及材料的原因,存在承受重力荷载时易屈曲的问题,为此,将波纹腹板钢梁的概念[3-4]引入到钢板剪力墙设计中,提出波形钢板剪力墙,将内嵌的钢板截面几何形状设计为波形,提高其垂直于波折方向的承载力(当波纹肋沿竖直方向时,即提高竖向承载力)和柱面刚度、抗剪屈曲荷载,波纹的设置可以提高内嵌钢板的平面外刚度从而抑制内嵌钢板的平面外鼓曲。
目前国内外对于波形钢板剪力墙的研究较少,郭彦林等对波形钢板竖放和横放进行了有限元数值模拟,以分析其滞回性能,发现波形钢板竖放和横放对滞回性能几乎没有影响[5]。赵秋红等对梯形波纹钢板剪力墙进行的试验研究表明,内嵌钢板与边缘框架的连接构造对剪力墙承载能力具有重要的作用,边缘框架柱最后屈服并耗能[6]。王威课题组对内嵌钢板分别为平钢板、波形钢板竖向放置、横向放置的钢板剪力墙进行了试验研究[7-8],结果表明:三面剪力墙试件最终均在墙趾处的约束边缘构件变形过大,而当约束边缘构件变形过大时内嵌钢板无明显变形,导致钢板剪力墙整体失稳,丧失承载力,钢板剪力墙未充分发挥其耗能性能。
近年来建筑的抗震思想已经向可修复转变,即地震(设防或罕遇地震) 后经修复或在部分使用状态下稍许修复即可恢复结构的使用功能,且结构体系易于建造和维护,全寿命成本效益高。2012年吕西林等介绍了一种带有可更换墙脚构件剪力墙的构造并给出详细的设计过程。墙角可更换试件是新型拉压组合减震支座,由叠层橡胶和软钢板组合而成[9]。2014年毛苑君等对比了带可更换墙脚构件剪力墙与普通剪力墙的抗震性能的差别[10]。
为充分发挥钢板剪力墙的耗能性能,防止约束边缘构件过早屈曲,保护剪力墙主体不受破坏,本课题组设计了一面在墙趾处带有可更换阻尼器的波形钢板剪力墙,并在更换阻尼器前和更换阻尼器后进行了两次低周往复加载,在试验过程中发现内嵌钢板与阻尼器刚度的匹配关系对剪力墙的整体受力机制和抗震性能有重要的影响,通过有限元软件进行数值分析,验证了有限元分析与试验结果的吻合度,并研究了内嵌钢板与阻尼器的刚度匹配关系对剪力墙抗震性能的影响,确定出一种两者合理的匹配关系。
1 试验研究
1.1 试件设计
试件为一片单肢带有可更换阻尼器的波形钢板剪力墙(CSPSWD),试件采用1∶2缩尺模型,针对其更换阻尼器前、后的力学性能进行两次低周往复加载。剪力墙内嵌波形钢板波纹肋沿竖直方向布置,厚度为3 mm,具体构造尺寸如图1所示。剪力墙四边连接约束构件,顶梁H型钢为H244×175×7×11,底梁H型钢为H294×200×8×12,两侧约束边缘构件采用方钢管,厚度为10 mm,外边缘尺寸为150 mm×150 mm。墙体高度为1 978 mm,宽度为1 300 mm,剪跨比为1.5。内嵌波形钢板的波角均为45°,试件横截面如图2所示。
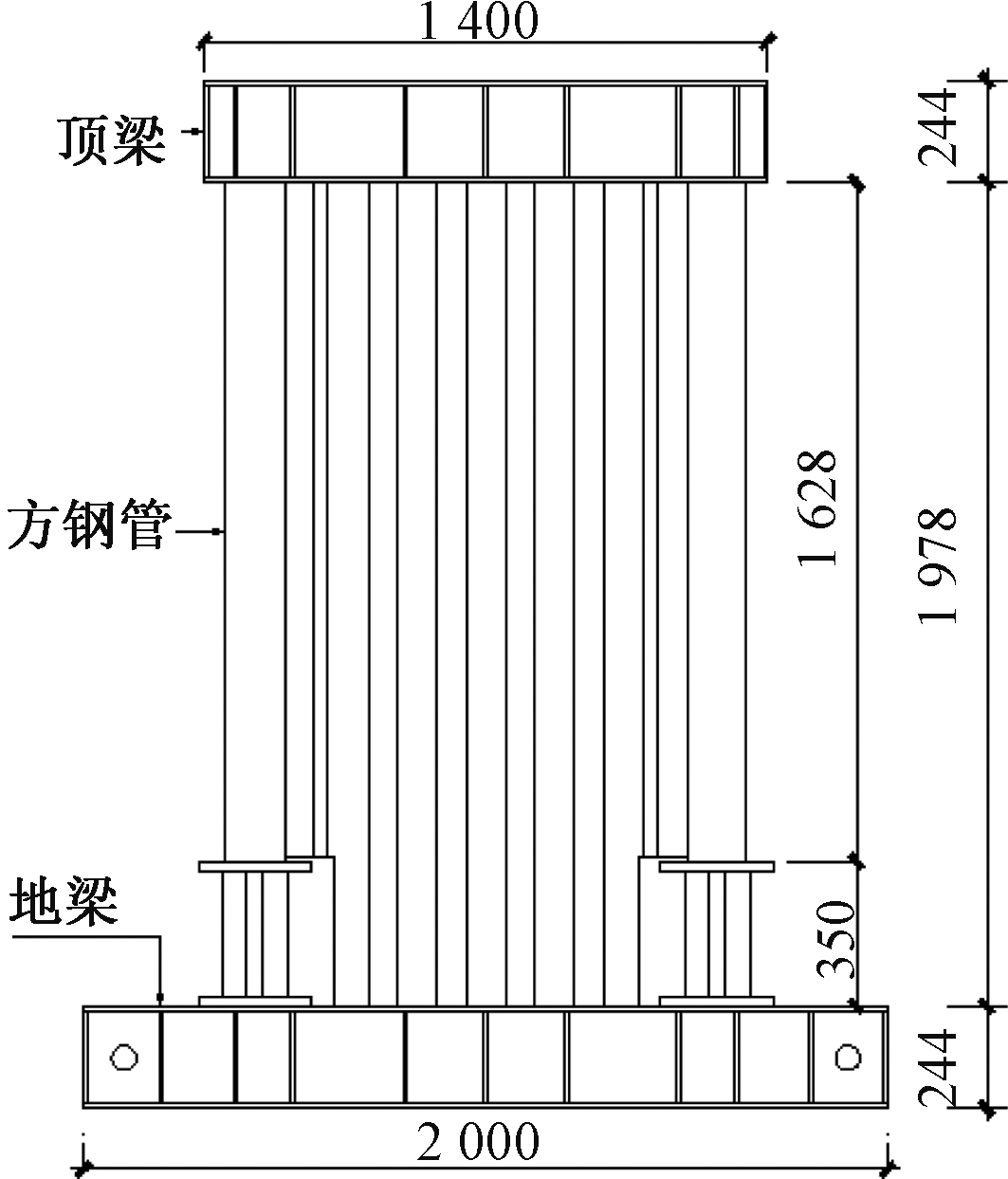
图1 带可更换阻尼器的波形钢板剪力墙
Fig.1 Corrugated steel plate shear wall with replaceable damper
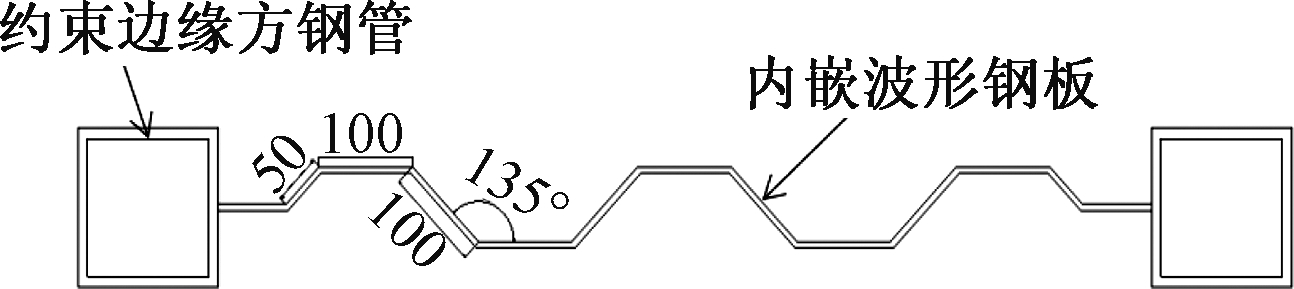
图2 剪力墙横截面
Fig.2 Cross section of shear wall
阻尼器是在课题组前期的试验研究基础之上改进而成的,由中间两块波形腹板与上下矩形端板组成,上连接端板与下连接端板分别与母墙、底梁的连接板采用统一预设的预紧力通过螺栓连接,腹板起主要耗能作用,消耗传至剪力墙墙趾处的荷载。该阻尼器采用弯曲变形耗能的力学原理,腹板截面形式为波形,波形板的几何特征类似手风琴,其受力时沿波纹方向存在“手风琴效应”,克服了钢板平面内单点屈服这一缺陷,残余变形较小,具有良好的耗能能力和塑性变形能力。同时该阻尼器结构形式简单,易于加工制作,价格低廉。更换前的阻尼器的腹板厚度为6 mm,更换后的阻尼器的中间钢板的厚度为3 mm。阻尼器示意如图3所示,材料性能列于表1。
1.2 试验加载
竖向集中荷载为150 kN,试验过程保持恒定,水平往复荷载由MTS电液伺服加载作动器施加,作动器一端与反力墙相连,一端与剪力墙加载梁相连。底梁两端与台座通过压梁锚固,试验加载依据JGJ/T 101—2015《建筑抗震试验规程》[11]的规定,两次加载均采用荷载-位移双控制,试件屈服前采用荷载控制加载,屈服后采用位移控制加载,加载至试件承载力下降,并降至峰值承载力85%时停止加载。根据GB 50011—2010《建筑抗震设计规范》[12]规定的剪力墙结构允许的最大层间位移角,当试件的层间位移角达到1/100时,更换阻尼器且对剪力墙进行第二次低周往复水平荷载加载。
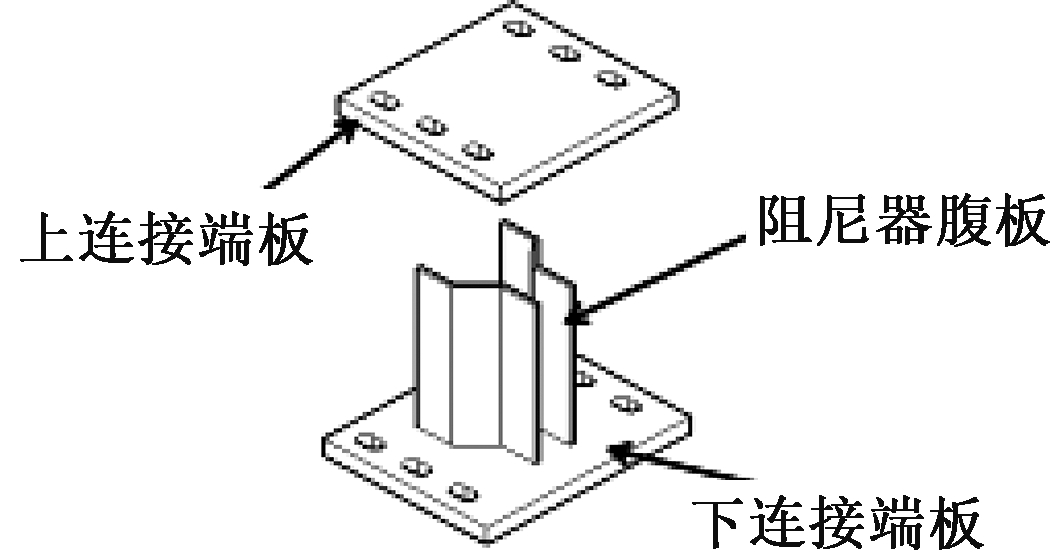
图3 阻尼器构造
Fig.3 Details of dampers
表1 材料力学性能
Table 1 Mechanical properties of materials
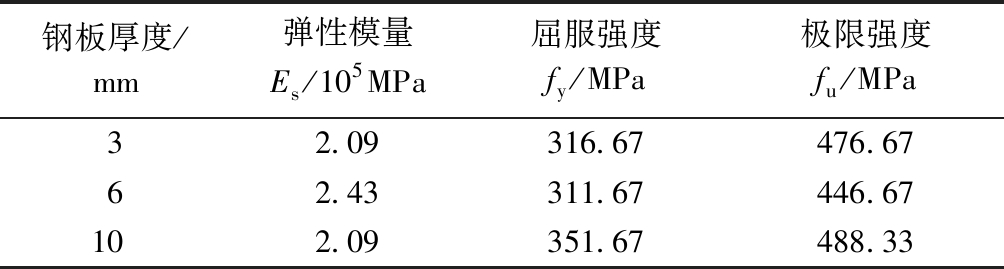
钢板厚度/mm弹性模量Es/105MPa屈服强度fy/MPa极限强度fu/MPa32.09316.67476.6762.43311.67446.67102.09351.67488.33
1.3 试验结果及分析
1.3.1 试验现象
本文规定推力为正,拉力为负。为方便记录试验现象,将更换阻尼器之前的试件命名为CSPSWD-1,更换阻尼器之后的试件命名为CSPSWD-2。
1)试件CSPSWD-1在承受荷载初期处于弹性状态。加载至+150 kN,内嵌波形钢板下部东侧开始发生略微鼓曲且伴随着响声;加载至-250 kN,内嵌波形钢板下部西侧距离地梁20 cm处向平面外鼓曲达到2 mm;加载至+300 kN,阻尼器的钢板略微发生屈曲,试件的荷载-位移曲线偏离直线。改为位移控制加载,加载至18.9 mm,西侧底部墙体向南鼓曲,阻尼器的钢板产生较小鼓曲,如图4a所示,此时试件的层间位移角接近规定的最大层间位移角1/100,需更换墙体的阻尼器。更换后的阻尼器,采用厚度为3 mm的腹板,以降低阻尼器刚度。
2)试件CSPSWD-2加载至+50 kN,焊缝连接处有焊渣脱落;阻尼器的腹板外侧鼓曲程度随荷载增大而增大,当水平荷载加载至+150 kN,东侧阻尼器腹板外侧下部鼓曲明显,同时荷载-位移曲线出现明显偏离直线的现象。改用位移控制加载,当水平位移加载至10.1 mm第一圈,东侧阻尼器腹板外侧鼓曲约6 mm,内侧上部向南方向鼓曲约2 mm,中部发生复杂鼓曲变形;加载至10.1 mm第三圈时,西侧阻尼器南侧腹板发生较大变形,呈S形;当加载至13.2 mm,阻尼器的腹板整体发生复杂变形,试件丧失承载力,如图4b所示。

a—CSPSWD-1; b—CSPSWD-2。
图4 试验现象
Fig.4 Test phenomenon of specimens
1.3.2 试验分析
试件CSPSWD-1和试件CSPSWD-2的试验滞回曲线如图5所示,试件CSPSWD-1的初始刚度较大,进入强化阶段后的试件随着水平荷载的增大,滞回曲线逐渐饱满,试件开始耗能。在试件层间位移角达到GB 50011—2010规定的1/100时,由于阻尼器与内嵌钢板匹配度较差,内嵌钢板早于阻尼器产生变形,未能充分发挥试件的承载能力和耗能能力。试件CSPSWD-2初始刚度较大,未见明显降低,滞回曲线较饱满,耗能能力较好,试件的极限承载力相比于试件CSPSWD-1降低较多,达到峰值承载力之后,滞回曲线斜率下降,这是因为阻尼器发生了整体变形而丧失了承载力。试件CSPSWD-2的滞回曲线更加饱满,这是因为试件CSPSWD-2的阻尼器刚度与母墙匹配度更高,试件更好地发挥了其耗能性能。
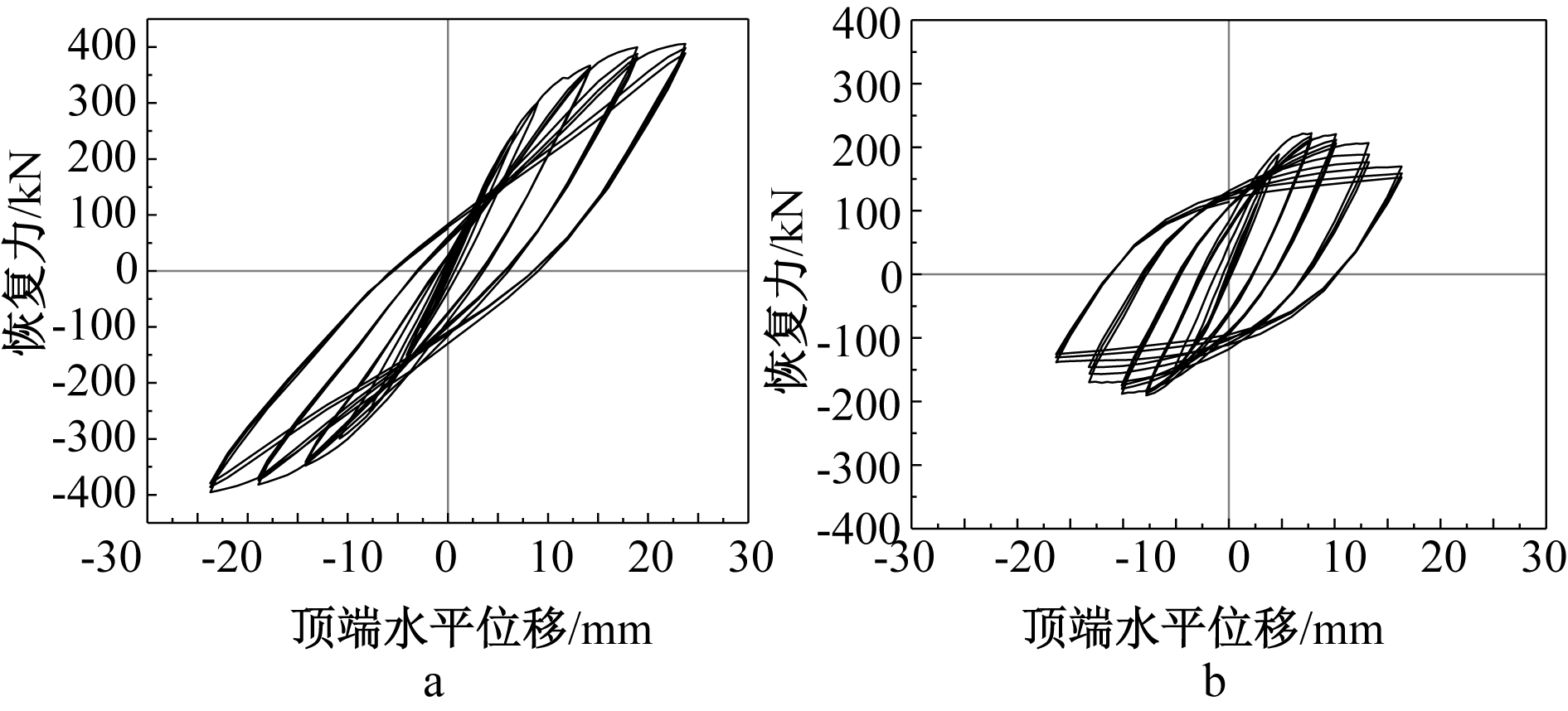
a—CSPSWD-1; b—CSPSWD-2。
图5 试件滞回曲线
Fig.5 Hysteretic curves of specimens
变形能力采用位移延性系数μ衡量,其计算式为μ=Δu/Δy。其中:Δu为试件的极限位移,取峰值承载力下降至85%时所对应的位移;Δy为试件的屈服位移,试件CSPSWD-2的特征点数值列于表2。
表2 试件CSPSWD-2的特征荷载和位移
Table 2 Characteristic load and displacement of specimen CSPSWD-2

屈服点峰值点极限点Fy/kNΔy/mmFd/kNΔd/mmFu/kNΔu/mmμ183.84.3213.47.9181.413.93.2
2 有限元分析
通过试验可以看出,试件第一次加载时,试件CSPSWD-1由于阻尼器刚度与母墙匹配度较低,随着荷载的增大,内嵌波形钢板底角处先于阻尼器产生较明显变形,试件的耗能性能未能充分发挥。试件第二次加载时,削弱了阻尼器中间钢板的厚度,试件CSPSWD-2的初始刚度较高,耗能性能发挥较好,但承载力下降。因此,对于带有阻尼器的钢板剪力墙,剪力墙与阻尼器刚度的合理匹配关系是充分发挥剪力墙抗震性能的关键所在。本文采用ABAQUS有限元软件,建立32个有限元模型,通过改变阻尼器中间钢板的厚度来改变阻尼器的刚度,意图利用数值模拟找出波形钢板剪力墙与阻尼器刚度的最佳匹配关系。
内嵌钢板采用S4R单元,阻尼器和钢梁、约束边缘方钢管等构件采用C3D8R六面体线性缩减积分壳单元,整个试件中各个构件之间的接触统一采用Tie接触,以模拟试验中构件之间的焊接连接。
2.1 试验与数值模拟对比
模型的钢材采用三折线本构模型、von Mises屈服准则、关联的流动法则以及运动硬化准则的弹塑性模型。边界设置中,底梁固定六个自由度,顶梁中心竖向荷载加载点六个自由度中除竖向向下外全固定,顶梁侧面中心水平荷载加载点除沿作用力方向,垂直作用力上下和绕垂直作用力旋转方向外全固定。ABAQUS数值模拟的滞回曲线和骨架曲线与试验结果的对比如图6、图7所示。可以看出:模型CSPSWD-1的初始刚度略微高于试验中试件的刚度,有限元模拟的滞回曲线更加饱满,骨架曲线趋势相同,这是由于数值分析中考虑的均为理想状态,而试验中材料的离散性、试件加工及固定误差和初始缺陷都会对试验结果造成一定的影响;模型CSPSWD-1极限承载力为414.8 kN,试验值为405.6 kN;模型CSPSWD-2初始刚度与试验中试件的刚度大致相同,有限元模拟的滞回曲线更加饱满,滞回曲线和骨架曲线的趋势和试验相同,模型的极限承载力为230.28 kN,试验值为222.03 kN,误差均在合理范围内。综上所述,有限元数值模拟与试验值吻合度高,可以利用有限元数值模拟进行拓展来分析阻尼器刚度与母墙的合理匹配关系。
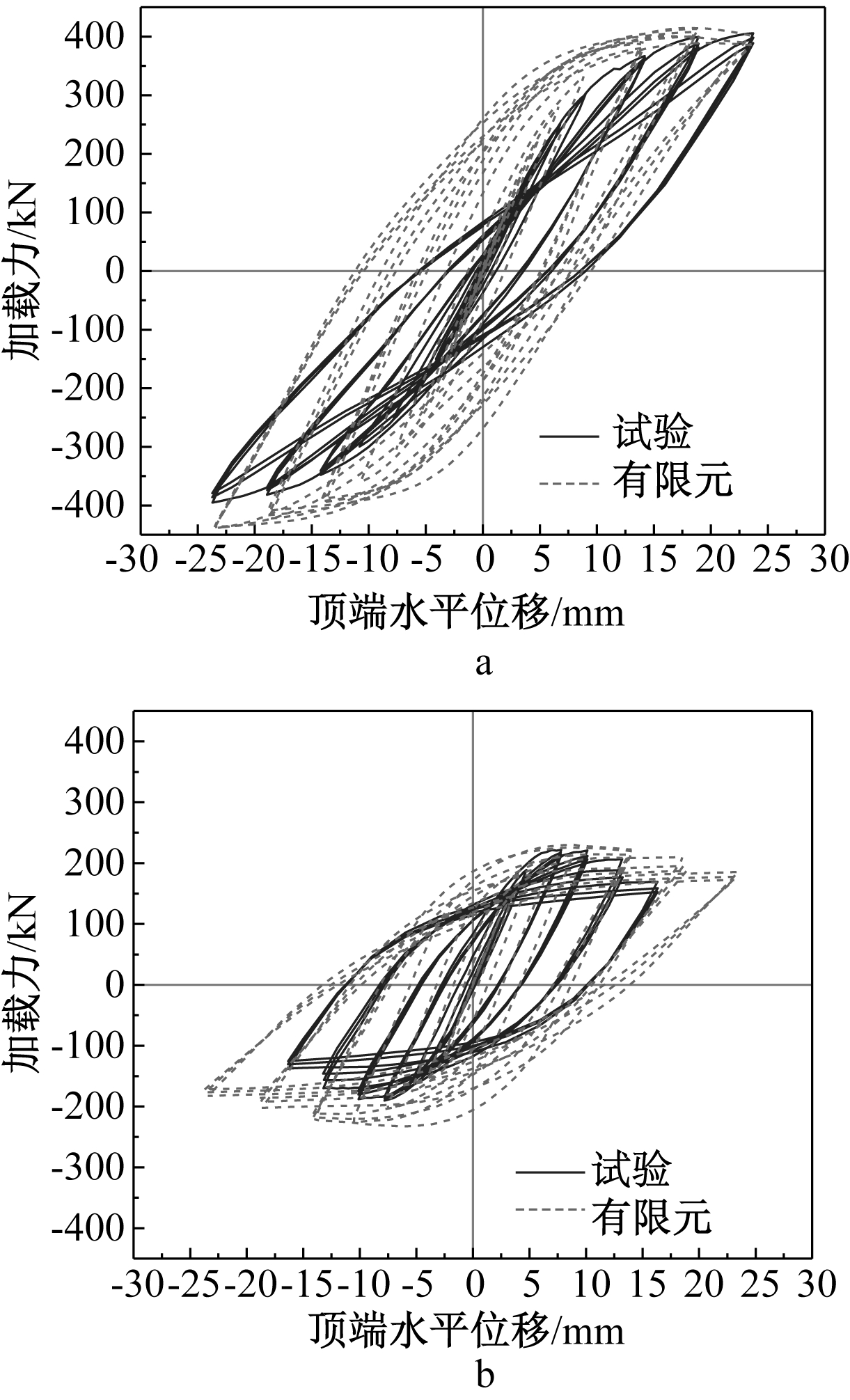
a—CSPSWD-1; b—CSPSWD-2。
图6 滞回曲线对比
Fig.6 Comparision of hysteretic curves

a—CSPSWD-1; b—CSPSWD-2。
图7 骨架曲线对比
Fig.10 Comparison of skeleton curves
有限元分析中,试件CSPSWD-1在承受水平荷载初期,先在内嵌波形钢板底角部出现屈曲,并且随着荷载的持续施加,屈曲程度逐渐增大。在承受水平荷载后期,阻尼器中间钢板出现变形。通过有限元模型的von Mises应力云图的变化可以看出,试件在加载初期,应力先集中在波形钢板的下部两侧底角处,然后沿着水平方向慢慢向中间增大,加载后期,阻尼器的外侧腹板应力开始增大,外侧腹板出现变形(图8)。

a—东侧阻尼器; b—西侧阻尼器。
图8 CSPSWD-2阻尼器变形
Fig.8 Deformation of damper of CSPSWD-2
试件CSPSWD-2在承受水平荷载初期,阻尼器中间钢板外侧下部首先开始发生屈曲,并且屈曲程度随着荷载的持续施加而增大。当荷载加载到一定程度时,内嵌波形钢板的底角处开始发生变形。最终试件由于阻尼器腹板变形过大丧失承载力,而导致整体剪力墙承载力下降。有限元模型的von Mises应力云图(图8)表明,模型在承受水平往复荷载初期,应力首先集中在阻尼器外侧腹板的下端,并且阻尼器外侧钢板的应力从下往上逐渐增大,且向内延伸。
2.2 内嵌钢板与阻尼器刚度匹配分析
2.2.1 模型的建立
通过试验加载以及有限元数值模拟均可见,试件CSPSWD-1由于内嵌钢板与阻尼器刚度匹配度较差,导致内嵌钢板先于阻尼器发生屈曲变形,导致剪力墙试件在达到GB 50011—2010规定的极限位移角时,阻尼器腹板变形较小,未充分发挥其集中耗能能力,导致试件CSPSWD-1整体抗震性能未得到充分发挥。试件CSPSWD-2在改变了阻尼器腹板厚度之后,在荷载加载至一定程度时,其阻尼器腹板先于内嵌钢板产生变形,集中耗散水平荷载施加的能量,较大地提高了剪力墙整体耗能性能,滞回曲线饱满,但试件CSPSWD-2极限承载力却下降较大。由此可见,内嵌钢板与阻尼器的刚度合理匹配关系对剪力墙的承载能力以及耗能性能有关键的影响。因此,本文对不同的内嵌钢板形式及厚度与阻尼器腹板厚度进行任意排列组合,通过ABAQUS软件建立32个有限元模型对这些组合进行数值模拟分析,探究钢板剪力墙中内嵌钢板与阻尼器的合理匹配关系,优化带阻尼器钢板剪力墙的抗震性能。
2.2.2 不同参数组合的对比
表3为32个有限元模型的参数,模拟的变量为内嵌波形钢板波纹肋的方向,钢板的厚度以及阻尼器腹板的厚度。表4为当内嵌钢板波纹肋沿竖直方向布置时,各个试件的特征荷载和位移,包括屈服荷载Fy和屈服位移Δy、极限荷载Fu和极限位移Δu、破坏荷载Fm和破坏位移Δm以及延性系数μ。通过表4可以更加清楚地反映各组试件之间承载力和延性变化的幅度、以及更好地对比不同对照试件组之间的抗震性能变化。
表3 有限元模型参数
Table 3 Parameters of finite element models
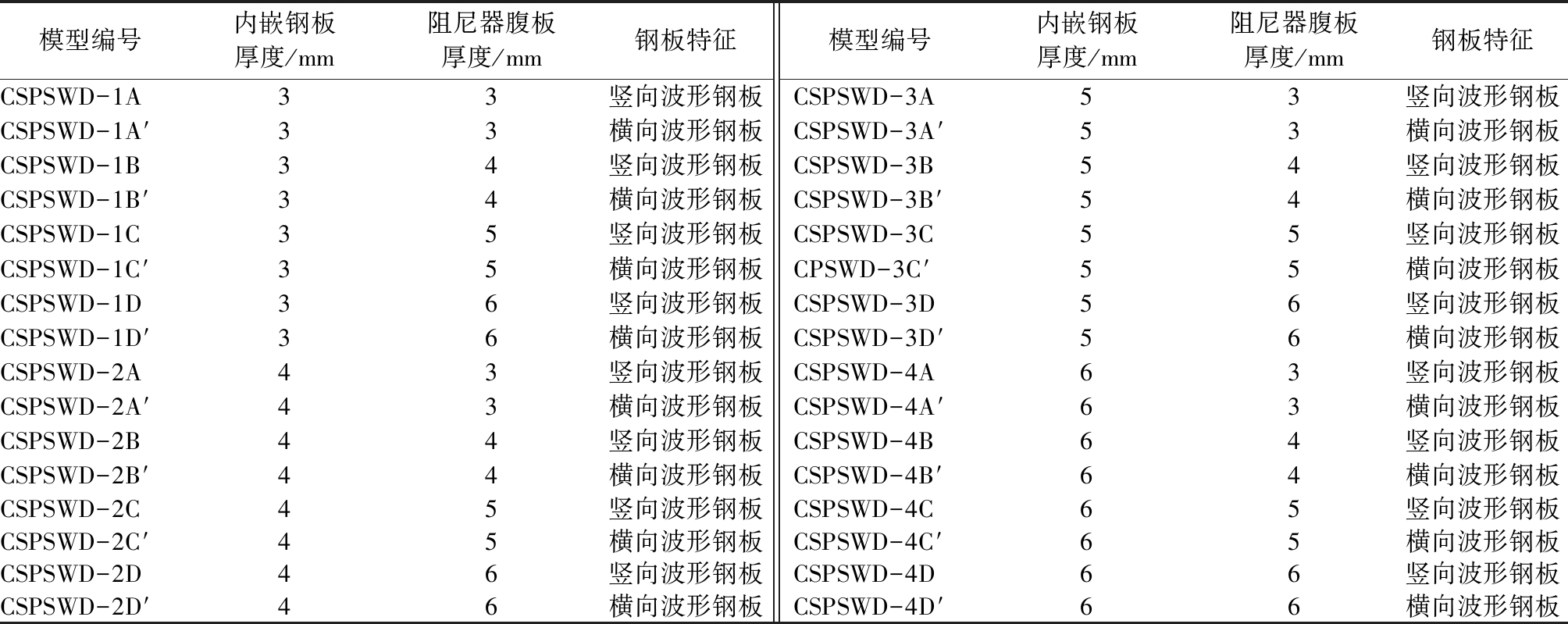
模型编号内嵌钢板厚度/mm阻尼器腹板厚度/mm钢板特征模型编号内嵌钢板厚度/mm阻尼器腹板厚度/mm钢板特征CSPSWD-1A33竖向波形钢板CSPSWD-3A53竖向波形钢板CSPSWD-1A′33横向波形钢板CSPSWD-3A′53横向波形钢板CSPSWD-1B34竖向波形钢板CSPSWD-3B54竖向波形钢板CSPSWD-1B′34横向波形钢板CSPSWD-3B′54横向波形钢板CSPSWD-1C35竖向波形钢板CSPSWD-3C55竖向波形钢板CSPSWD-1C′35横向波形钢板CPSWD-3C′55横向波形钢板CSPSWD-1D36竖向波形钢板CSPSWD-3D56竖向波形钢板CSPSWD-1D′36横向波形钢板CSPSWD-3D′56横向波形钢板CSPSWD-2A43竖向波形钢板CSPSWD-4A63竖向波形钢板CSPSWD-2A′43横向波形钢板CSPSWD-4A′63横向波形钢板CSPSWD-2B44竖向波形钢板CSPSWD-4B64竖向波形钢板CSPSWD-2B′44横向波形钢板CSPSWD-4B′64横向波形钢板CSPSWD-2C45竖向波形钢板CSPSWD-4C65竖向波形钢板CSPSWD-2C′45横向波形钢板CSPSWD-4C′65横向波形钢板CSPSWD-2D46竖向波形钢板CSPSWD-4D66竖向波形钢板CSPSWD-2D′46横向波形钢板CSPSWD-4D′66横向波形钢板
表4 模型的特征荷载和位移(竖直波纹肋)
Table 4 Characteristic loads and displacements of the model(vertical corrugated rib)
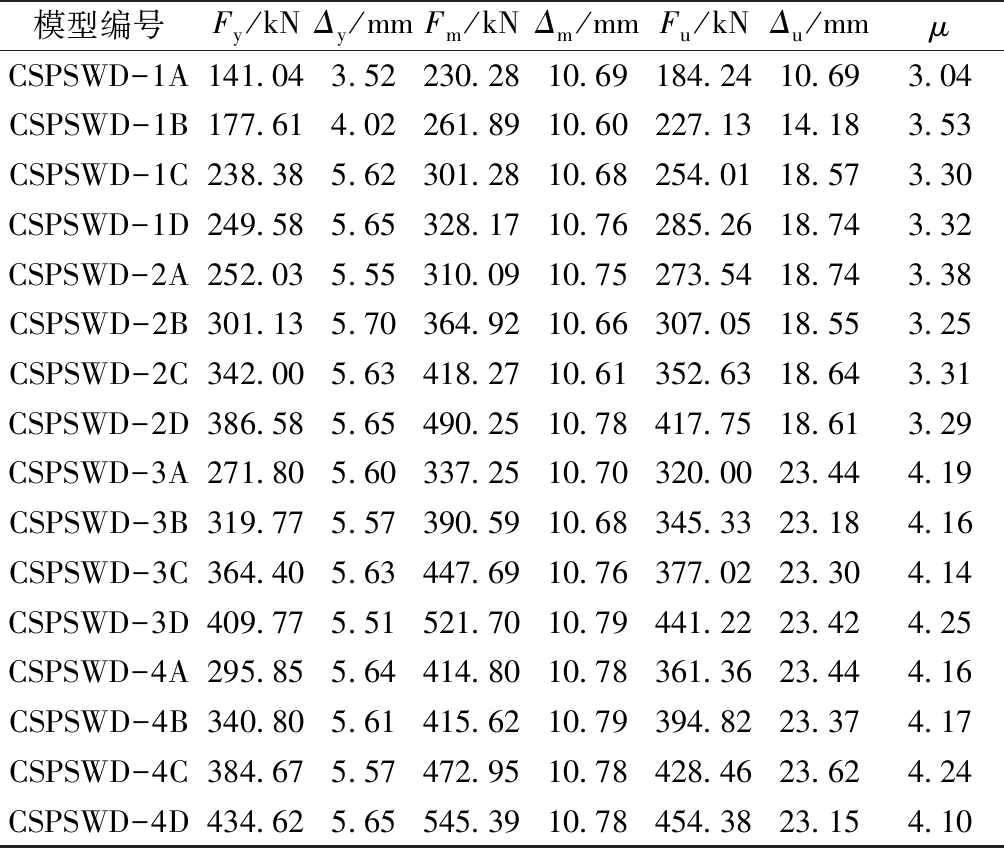
模型编号Fy/kNΔy/mmFm/kNΔm/mmFu/kNΔu/mmμCSPSWD-1A141.043.52230.2810.69184.2410.693.04CSPSWD-1B177.614.02261.8910.60227.1314.183.53CSPSWD-1C238.385.62301.2810.68254.0118.573.30CSPSWD-1D249.585.65328.1710.76285.2618.743.32CSPSWD-2A252.035.55310.0910.75273.5418.743.38CSPSWD-2B301.135.70364.9210.66307.0518.553.25CSPSWD-2C342.005.63418.2710.61352.6318.643.31CSPSWD-2D386.585.65490.2510.78417.7518.613.29CSPSWD-3A271.805.60337.2510.70320.0023.444.19CSPSWD-3B319.775.57390.5910.68345.3323.184.16CSPSWD-3C364.405.63447.6910.76377.0223.304.14CSPSWD-3D409.775.51521.7010.79441.2223.424.25CSPSWD-4A295.855.64414.8010.78361.3623.444.16CSPSWD-4B340.805.61415.6210.79394.8223.374.17CSPSWD-4C384.675.57472.9510.78428.4623.624.24CSPSWD-4D434.625.65545.3910.78454.3823.154.10
图9~图11对比了各组试件在内嵌钢板波纹肋方向和钢板厚度不变的情况下,阻尼器腹板厚度变化时试件的承载力滞回曲线和骨架曲线的变化。通过对比可以反映各组试件在阻尼器和内嵌钢板不同的刚度匹配关系中,承载能力、刚度变化、耗能能力和延性等抗震性能的差别。图中:Vplate代表内嵌钢板竖向放置时的钢板厚度,Hplate代表内嵌钢板横向放置时的钢板厚度。
2.2.3 模拟结果分析
1)通过图9~图11可以看出:当内嵌钢板波纹肋沿竖直方向时,在同一内嵌钢板厚度的情况下,随着阻尼器腹板厚度的增大,试件的刚度和极限承载力逐渐增大,耗能能力有所上升,但达到极限承载力之后承载力下降速度也逐渐增大,原因是当阻尼器腹板厚度从3 mm增大到6 mm的过程中,因为其刚度的增大,导致试件在承受水平荷载时,内嵌钢板早于阻尼器发生变形,阻尼器未能充分发挥其耗能能力,在达到极限承载力后,试件的内嵌钢板已经发生失稳,试件的承载力下降较快;内嵌钢板厚度为6 mm,阻尼器腹板厚度为6 mm时,试件的承载力最大,但其延性在内嵌钢板厚度为6 mm时最差;内嵌钢板厚度为5 mm,阻尼器腹板厚度为6 mm 时,试件的延性最好,且承载力较高。通过图9以及表3可以得出,在每一种内嵌钢板厚度不变的情况下,试件的极限承载力随着阻尼器腹板厚度的增大比例大致相同,阻尼器腹板的厚度每增加1 mm,试件承载力大致增大13%~20%,说明试件的承载力与阻尼器腹板厚度变化呈正比。

a—内嵌钢板竖向放置; b—内嵌钢板横向放置。
图9 试件承载力变化趋势
Fig.9 Change trend of bearing capacity of specimens
在同一阻尼器腹板厚度的情况下,随着内嵌钢板厚度的增大,试件的极限承载力增大,当内嵌钢板厚度从3 mm变到4 mm时,试件承载力增大40%~50%,而内嵌钢板厚度从4 mm继续每增加1 mm,试件承载力增大4%~8%,说明在阻尼器腹板厚度不变的情况下,内嵌钢板厚度为3 mm会导致试件承载力降低,内嵌钢板继续增大,试件的承载力则变化不大。延性在内嵌钢板厚度为3 mm和4 mm时相差不大,且相比于在内嵌钢板厚度为5 mm和6 mm时较低。
2)通过图9~图11可以看出:内嵌钢板波纹肋沿水平方向时,其试件的承载力相比于内嵌钢板波纹肋沿竖直方向时明显下降较多,在内嵌钢板厚度保持不变的情况下,随着阻尼器腹板厚度的增大,试件的承载力增大,当阻尼器腹板厚度增大至6 mm时,试件承载力不再增加;试件滞回环的面积逐渐增大,说明试件的耗能能力逐渐增大,当阻尼器腹板厚度增大至6 mm时,试件的耗能能力大致相同;试件的刚度随着阻尼器腹板厚度的变化而变化较小;试件达到极限承载力之后承载力下降均较小;内嵌钢板波纹肋沿水平方向时试件的延性相比于波纹肋沿竖直方向时要好;在阻尼器腹板厚度保持不变的情况下,随着内嵌钢板厚度的变化,试件的承载力和延性变化不大,说明内嵌钢板厚度对阻尼器的匹配度和试件的抗震性能影响较小。

a—竖向波形钢板厚度3 mm; b—竖向波形钢板厚度4 mm; c—竖向波形钢板厚度5 mm; d—竖向波形钢板厚度6 mm; e—横向波形钢板厚度3 mm; f—横向波形钢板厚度4 mm; g—横向波形钢板厚度5 mm; h—横向波形钢板厚度6 mm。![]() 阻尼器腹板厚度3 mm;
阻尼器腹板厚度3 mm;![]() 阻尼器腹板厚度4 mm;
阻尼器腹板厚度4 mm;![]() 阻尼器腹板厚度5 mm;
阻尼器腹板厚度5 mm;![]() 阻尼器腹板厚度6 mm。
阻尼器腹板厚度6 mm。
图10 模型的滞回曲线对比
Fig.10 Comparison of hysteretic curves of models

a—竖向波形钢板厚度3 mm; b—竖向波形钢板厚度4 mm; c—竖向波形钢板厚度5 mm; d—竖向波形钢板厚度6 mm; e—横向波形钢板厚度3 mm; f—横向波形钢板厚度4 mm; g—横向波形钢板厚度5 mm; h—横向波形钢板厚度6 mm。![]() —阻尼器腹板厚度3 mm;
—阻尼器腹板厚度3 mm; ![]() 阻尼器腹板厚度4 mm;
阻尼器腹板厚度4 mm;![]() —阻尼器腹板厚度5 mm;
—阻尼器腹板厚度5 mm; ![]() 阻尼器腹板厚度6 mm。
阻尼器腹板厚度6 mm。
图11 模型的骨架曲线对比
Fig.11 Comparison of skeleton curves of models
综上所述,内嵌钢板波纹肋沿竖直方向时,在内嵌钢板厚度一定的情况下,随着阻尼器腹板厚度的增加,试件的承载力大致呈正比增加,延性变化不大,且这种变化随着内嵌钢板厚度的增大越来越小。在阻尼器腹板厚度一定的情况下,随着内嵌钢板厚度的增加,试件承载力增大,但内嵌钢板厚度增大至5 mm以后,试件的承载力增加微小。
内嵌钢板波纹肋沿水平方向时,在内嵌钢板厚度一定的情况下,随着阻尼器腹板厚度的增加,试件承载力增加,当阻尼器腹板厚度增加到5 mm以后,承载力不再增加。试件的耗能能力逐渐增大,延性相差不大。在阻尼器腹板厚度一定的情况下,随着内嵌钢板厚度的增加,试件的承载力和延性均变化较小。
3 结束语
1)带有阻尼器的钢板剪力墙,内嵌钢板与阻尼器的刚度匹配对试件的抗震性能有重要影响。
2)其余参数不变时,剪力墙内嵌钢板波纹肋竖直要比波纹肋水平的承载力和延性好。
3)内嵌钢板波纹肋竖直时,剪力墙承载力随着阻尼器腹板厚度的增大而增加,极限承载力下降速度增大,延性变化较小。
4)内嵌钢板波纹竖直方向时,剪力墙承载力随着内嵌钢板厚度的增大而增加,但承载力增加有限,延性增大较大。
5)试验结果与有限元模拟结果吻合度较高,可以为后续研究提供参考。
[1] OZCELIK Y, CLAYTON P M. Behavior of Columns of Steel Plate Shear Walls with Beam-Connected Web Plates[J]. Engineering Structures, 2018, 172:820-832.
[2] ZHANG X, GUO Y. Behavior of Steel Plate Shear Walls with Pre-Compression Adjacent Frame Columns[J]. Steel Construction, 2014, 77:17-25.
[3] 聂建国,朱力,唐亮.波形钢腹板的抗剪强度[J].土木工程学报,2013,46(6):97-109.
[4] 聂建国,李法雄,樊健生.波形钢腹板梁变形计算的有效刚度法[J].工程力学,2012,29(8):71-79.
[5] 郭彦林,王小安,张博浩,等.波浪腹板钢结构设计理论研究及应用现状[J].工业建筑,2012,42(7):1-13,73.
[6] 赵秋红,邱静,李楠,等.梯形波纹钢板剪力墙抗震性能试验研究[J].建筑结构学报,2018,39(增刊2):112-120.
[7] 王威, 张龙旭, 苏三庆, 等. 波形钢板剪力墙抗震性能试验研究[J]. 建筑结构学报, 2018, 39 (5): 36-44.
[8] 王威, 高敬宇, 苏三庆, 等. 波形钢板剪力墙抗侧性能的有限元分析[J]. 西安建筑科技大学学报(自然科学版), 2017, 49(5): 630-636.
[9] 吕西林, 毛苑君. 带有可更换墙脚构件剪力墙的设计方[J]. 结构工程师, 2012, 28(3): 12-17.
[10] 毛苑君, 吕西林. 带可更换墙脚构件剪力墙的低周反复加载试验[J]. 中南大学学报(自然科学版), 2014, 45(6): 2029-2040.
[11] 中国建筑科学研究院. 建筑抗震试验规程:JGJ/T 101—2015 [S].北京:中国建筑工业出版社, 2015.
[12] 中华人民共和国住房和城乡建设部. 建筑抗震设计规范:GB 50011—2010[S]. 北京:中国建筑工业出版社, 2010.