索拱桁架结构综合了刚性拱桁架与柔性索撑体系两种结构的优点,具有结构整体刚度大、施工方便、支座水平推力小、结构内力分布均匀、造型优美等众多优点,已被广泛应用于大跨度建筑结构中,如新广州站主站房[1-2]、日本关西机场、德国柏林火车站等。但是索拱结构的平面外稳定性较差,一定程度上限制了其向更大跨度的方向发展。单层柱面网壳因节点简单、杆件布置规则、形态优美、受力合理、计算理论成熟,也往往成为大跨度空间结构的常用结构形式,如天津火车西站等,但由于稳定性较弱及较大的水平推力使得单层柱面网壳的经济跨度限制在40 m以内。为充分发挥常见大跨度空间结构的优势,扬长避短,将索拱桁架与单层柱面网壳结构组合起来,形成索拱桁架-单层柱面网壳复合结构,一方面单层柱面网壳为索拱桁架结构提供了平面外支撑,可提高拱桁架的侧向稳定性;另一方面索拱桁架作为柱面网壳结构的弹性支承,减小了网壳结构的纵向跨度,实现单层柱面网壳跨度的飞跃。
目前,对索-拱结构的研究相对比较充分,清华大学郭彦林课题组对多种索拱结构的基本力学性能、动力特性、参数分析、弹性稳定及弹塑性稳定进行了系统研究,为索-拱结构的推广应用奠定了基础[3];Chen等研究了节点坐标、结构构件、运动约束等对对称杆系结构稳定性的影响[4],这对空间结构的稳定性分析提供了新思路;王振等也对V形腹杆内凹式索拱结构的主要参数对稳定承载力的影响规律进行了研究[5]。综观已有研究可以发现:索-拱结构选型不同,其承载力和具体的力学特性也随之不同[6]。在索拱桁架的研究方面,赵曦辉等对索拱桁架的结构原理和稳定性也进行了研究[7];贺拥军[8],袁婷[9]等分别介绍了对不同类型索-拱桁架结构的各个参数对结构稳定性影响的研究;朱奕锋等对基于剪式单元的索-拱开合结构进行了静力分析和稳定性研究[10]。在单层网壳结构方面,国内外学者也进行了较为充分的研究,张竟乐等对单层网壳结构的板式节点刚度进行了研究,为网壳结构发展奠定了基础[11];朱奕锋等对华能大厦单层网壳结构的整体稳定性及结构的受力性能进行了研究[12];马凯等对厦门东海火炬科技园S3号楼大跨度多曲面单层网壳在考虑初始缺陷情况下的极限承载力进行了全过程分析[13];张烨等在试验中通过人造缺陷得到单层网壳结构的破坏形式,并与有限元分析出的结构破坏形式进行了对比研究[14];随着单层网壳结构发展,其结构的理论也越来越完善,马肖彤等基于能量原理,对单层网壳结构抗冲击性能的简化分析方法进行了研究[15]。从上述分析可以看出:索-拱结构和网壳结构的研究已非常充分,国内外学者对其基本特性已有比较全面的了解,但将其与单层柱面网壳结合后的力学性能,以及在跨度上是否有大的突破,需要加以论证。本文结合一拟建内凹式索拱桁架-单层柱面网壳复合空间结构煤棚,开展了结构的预应力设计与力学性能分析工作,从结构受力的合理性论证了该结构的适用性,为以后类似工作的设计提供参考。
1 工程概况
拟建特大跨煤棚的水平投影为矩形,投影尺寸为640 m×198 m,如图1所示,其横向跨度为198 m,纵向支承于柱距为9 m/18 m的15 m高柱列上。由于场地条件限制,柱子截面尺寸为800 mm×800 mm,采用C40混凝土。为确保棚内正常堆料以及设备的正常运行,整个钢结构煤棚有严格的净空要求,需控制在柱顶标高以上,即图1b所示虚线范围内。设计过程中,需考虑的荷载或作用如表1所示。其中风荷载计算中,初步设计时,根据工程经验取风振系数βz=1.4,风压高度变化系数uz、体型系数us按GB 50009—2012《建筑结构荷载规范》取值,us根据封闭式拱形屋面分块取值[16]。
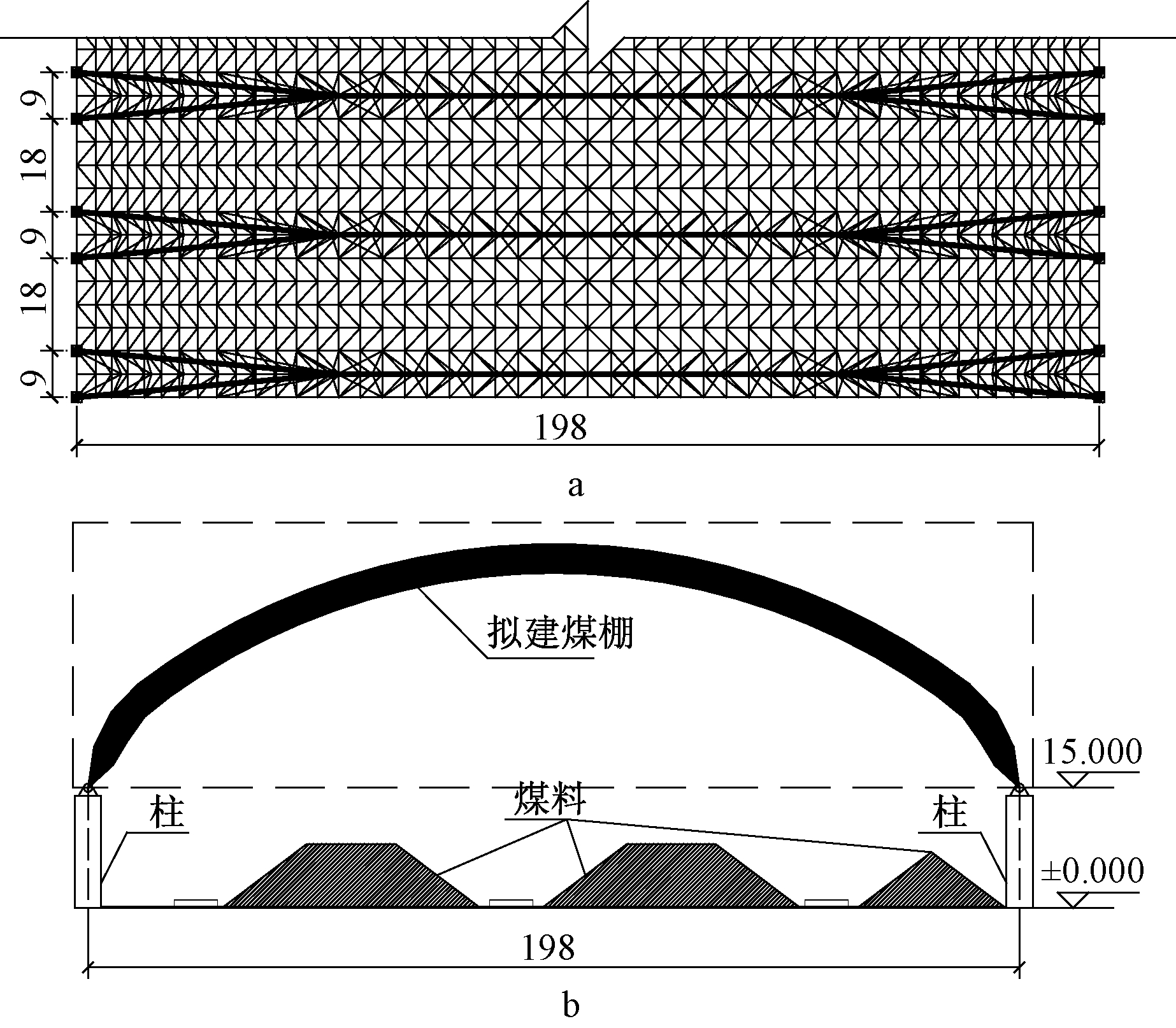
a—平面投影; b—横向剖面。
图1 结构平面 m
Fig.1 Structural plan
表1 结构设计荷载/作用
Table 1 Structural design load/action kN/m2

自重g1屋面恒载g2活荷载q基本风压w0基本雪压μr地震作用根据屋盖结构具体形式计算0.15(因跨度大,采用单层压型钢板)0.5(不上人屋面)0.4 0.4基本地震加速度0.10g;设计地震分组为第三组;场地类别为Ⅱ类。
2 结构布置
鉴于本项目上部钢结构煤棚跨度大、净空要求高且拱架无法落地等特点,拟采用内凹式索拱桁架作为主要承载结构,并结合屋面弧形要求采用单层柱面网壳作为屋面承载结构。根据工程现有条件,整个煤棚仅支承于15 m高的柱列上。由于柱列高、截面小,其侧向刚度小,下部支承结构能承受的水平荷载非常有限。因此,采用内凹式索拱桁架结构时,一方面在竖向荷载作用下,内凹式拉索能平衡支座处的水平推力,极大减小了支承结构的水平荷载;另一方面,索撑体系施加预应力后能在拱桁架内产生与竖向荷载作用下相反的内力,可优化上部拱桁架的内力。上部屋面支承结构采用的单层柱面网壳支承于拱桁架上,同时在拱桁架所在区域,柱面网壳与立体拱桁架上弦平面共用。拱桁架作为单层柱面网壳的弹性支承,减小了单层柱面网壳的纵向跨度,可大幅减小柱面网壳的自重,同时柱面网壳为拱桁架提供侧向支撑形成空间受力体系,提高结构承载力,实现结构跨越较大的跨度。
图2所示索拱桁架-单层柱面网壳复合空间结构示意,上部单层柱面网壳采用人字形斜杆布置方式(图2a),所形成的三角形网格在提高稳定性的同时,也尽可能实现杆件等长。作为主要的承载结构体系,索拱桁架结构的上部拱桁架采用倒三角形立体拱桁架(图2b),且尽可能增大桁架上弦受压截面积。根据已有工作经验,上弦拱桁架截面高度取为h=6.5 m,拱桁架矢高取f=48 m。下弦拉索采用内凹式布置,保证下部净空需求,如图2c所示。下弦拉索在索撑节点处自中间向两端由单根拉索分离为双拉索,至支座处分别锚固于拱桁架的两肢上弦杆端支座处,形成自平衡体系,如图3所示。新型索拱桁架-单层柱面网壳柔性索、刚性拱与网壳结构有机结合在一起,既充分利用了索结构传力高效、构造轻巧、刚度较大的优点,又借助刚性网壳提高了结构的整体稳定性,大大提高了结构效率。
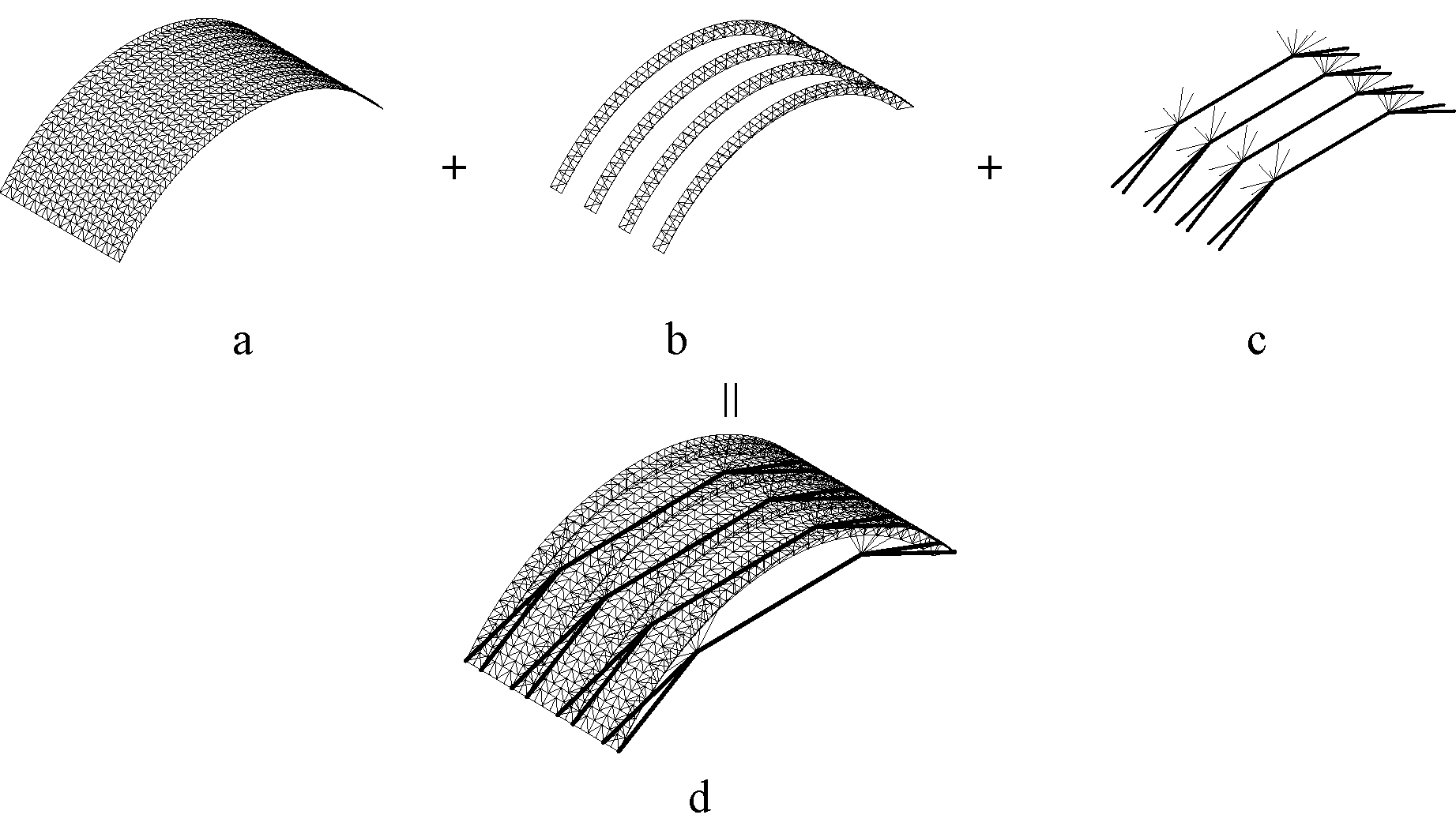
a—单层网壳; b—拱桁架; c—索撑体系; d—索拱桁架-单层柱面网壳结构。
图2 索拱桁架-单层柱面网壳结构示意
Fig.2 Schematic diagram of structure composed of cable-supported arch truss and single-layer cylindrical reticulated shell structure
根据市场钢管供应情况,上部单层网壳、拱桁架及索撑体系中的撑杆拟选用的杆件包括φ60×3.5、φ89×4.5、φ108×5.5、φ133×6、φ159×6.5、φ180×8、φ203×8、φ245×10、φ273×10、φ299×12、φ325×12、φ351×12、φ377×12、φ402×14等规格,钢材均选用Q345,为方便施工,所有杆件均采用焊接空心球节点连接;初步设计时下弦拉索采用φ7×163钢丝束,裸索直径为98.8 mm,抗拉强度标准值取为1 570 MPa,破断荷载为9 850 kN[17]。
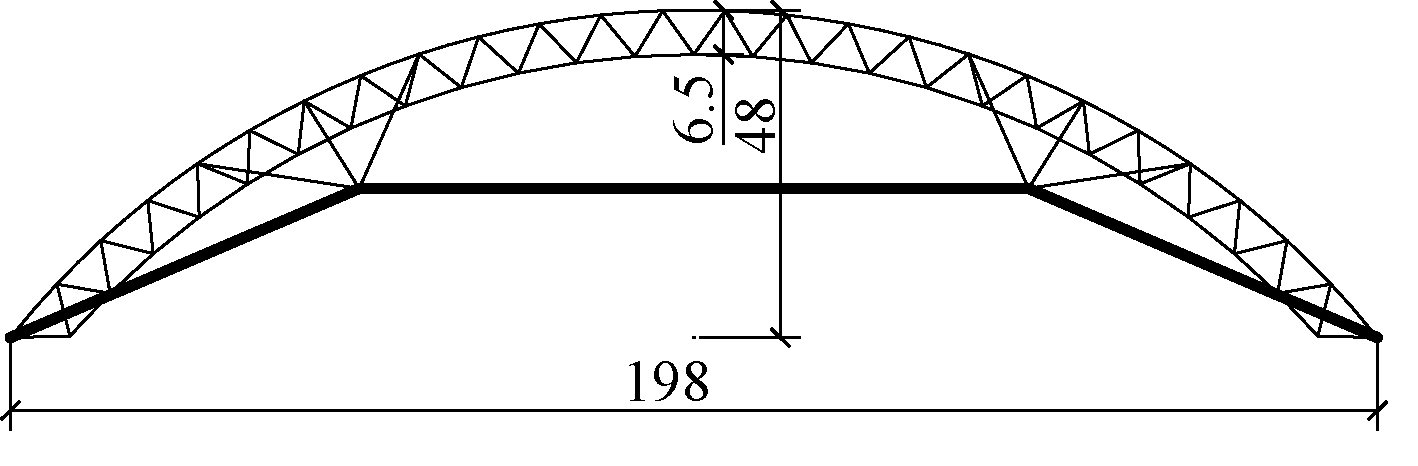
图3 索拱桁架示意 m
Fig.3 Schematic diagram of cable-supported arch truss
3 结构力学性能分析
拟建钢煤棚跨度大、下部支承条件较差,结构形式复杂,为保证结构的安全适用性,需对其力学性能进行系统分析。此外,结构中的预应力如果施加不当,不仅不能起到优化上部结构内力、减小支座反力的效果,反而会对结构受力有不利影响,因此,结构的预应力应进行严格设计。
3.1 有限元模型
利用有限元软件Midas/Gen建立煤棚预应力钢结构的有限元模型。上部网壳与拱桁架的杆件均采用梁单元模拟,索撑体系中的撑杆采用桁架单元模拟,拉索采用桁架索单元模拟。为方便屋面均布荷载的施加,在网壳上建立虚面单元。考虑到该煤棚纵向长度为640 m,尺度大,但结构布置相同,为节省计算成本,截取其中的4榀索拱桁架及对应的柱面网壳组成的结构作为分析对象,其有限元模型如图4所示。

图4 结构有限元模型
Fig.4 Finite element model of the structure
对于边界约束条件,将上部钢结构与下部柱顶三向铰接,但由于柱子较高,其水平抗侧移刚度较小,于是将柱子对上部钢结构的水平约束简化为横向弹性约束。根据支承柱的截面尺寸及C40混凝土材料的弹性模量,可知单根柱子的抗弯刚度为EcIc=1.11×1015 N·mm2,由结构力学知识可得在柱顶单位水平力作用下的水平位移如式(1)所示:
(1)
式中:h为柱高。
进而可由式(2)求得单根柱子对其柱顶支座的水平弹性刚度为986 N/mm。为计算简便,实际计算时取K=1 000 kN/m。
(2)
3.2 预应力设计
预应力是预应力钢结构中的关键因素,预应力过大会降低拉索本身的可靠性;预应力过小则起不到优化结构力学性能、平衡支座推力的作用。因此,计算出合理的预应力值是预应力钢结构的设计关键。通常情况下,预应力钢结构的预应力设计原则包括:1)任何工况下拉索均不能出现松弛,即拉索内力应大于0 kN;2)拉索最大内力不能过大,应留足2~3倍的安全储备;3)索的最佳张拉力应使拱在最不利工况下的应力和挠度尽可能小;4)在通常情况下,以平衡恒载产生的支座反力为宜。因此结构应在满足所有要求的前提下,使预应力水平尽量降低[18]。
根据上述原则,本工程中索拱桁架结构的预应力设计以优化上部结构内力和支座水平推力最小为目标进行预应力的优化设计。为提高分析效率,并结合本结构的受力特点,提取其中一榀索拱桁架进行预应力的优化分析,应用ANSYS有限元软件的优化模块OPT,考虑结构在施加阶段(1.0恒载+0.5活载)下,以支座水平推力最小为优化目标对预应力设计值进行优化计算。
对于ANSYS中的优化方法,主要有零阶方法和一阶方法。一种合理的优化方法是联合运用两种优化方法得出比较理想的解,如先采用零阶方法或是随机搜索在全局范围内找到一个粗糙的合理解,然后在前面分析基础上使用一阶优化方法局部精确寻优[12]。本文首先分别采用零阶和随机搜索方法各寻找出一组最优预应力值,后又分别用一阶方法计算,从而保证了优化结果的可靠性。两种优化方法计算的拉索初始应变如表2所示,其中拉索编号如图5所示。对比表2中两种优化结果,因“随机+一阶”优化结果在上部结构组合应力相差不大的情况下,支座反力更小,故选取“随机+一阶”分析方法得到的预应力为参考。
图5 拉索编号
Fig.5 Cable number
表2 预应力优化结果
Table 2 Prestress optimization results

优化方法荷载工况ε1ε2F1/kNF2/kNF3/kNF4/kNF5/kNRmax/kN零阶+一阶随机+一阶1.0恒+0.5活1.476×10-39.970×10-42 928.41 401.51 401.51 367.11 367.1179.091.109×10-31.457×10-32 938.81 495.51 495.51 448.71 448.7171.87
注:ε1为①号拉索的初始应变优化值;ε2为②~⑤号拉索的初始应变优化值;F1~F5分别为①~⑤号拉索在1.0恒载+0.5活载作用下的内力值;Rmax为最大支座水平推力。
3.3 静力性能
根据上述分析结果,对3.1节建立的Midas有限元模型引入拉索的初始应变以模拟预应力的施加。然后对结构施加恒载、屋面活载、风荷载等荷载并进行工况组合,典型的荷载工况如表3所示,为简化,将预应力视为恒载,其分项系数按恒载考虑。
表3 典型荷载效应组合工况
Table 3 Typical load effect combination

工况荷载组合工况荷载组合11.2恒载+1.4活载(全/半跨)71.2恒载+1.4活载(全/半跨)+0.98风载21.0恒载+1.4风载81.35恒载+0.98活载(全/半跨)+0.98风载31.0恒载+0.98活载(全/半跨)+1.4风载91.35恒载+0.98活载(全/半跨)41.0恒载+1.4活载(全/半跨)+0.98风载101.35恒载+0.98风载51.2恒载+0.98活载(全/半跨)+1.4风载11包络工况
应用基于构件的设计准则评判结构设计的安全性,提取结构在包络工况下所有单元的应力比图,如图6所示。可知:大部分构件的应力比均在0.7以下,表明结构留有足够的安全储备。此外,图7列出了包络工况下梁单元的组合应力云图。可以看出,包络工况下梁单元最大组合应力为228.2 MPa,小于钢材的设计强度f=310 MPa,满足设计要求。总体来看,索拱桁架-单层柱面网壳结构的应力分布均匀,结构受力合理。
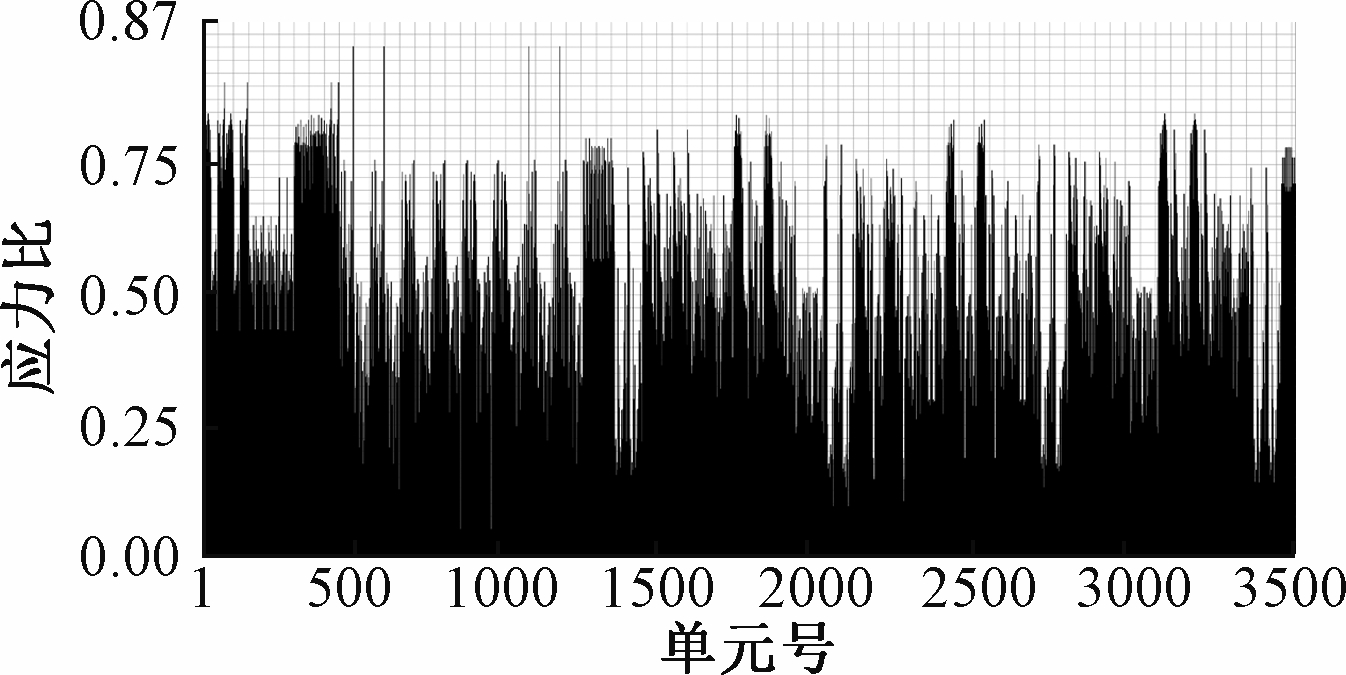
图6 构件应力比
Fig.6 Stress ratio diagram of member
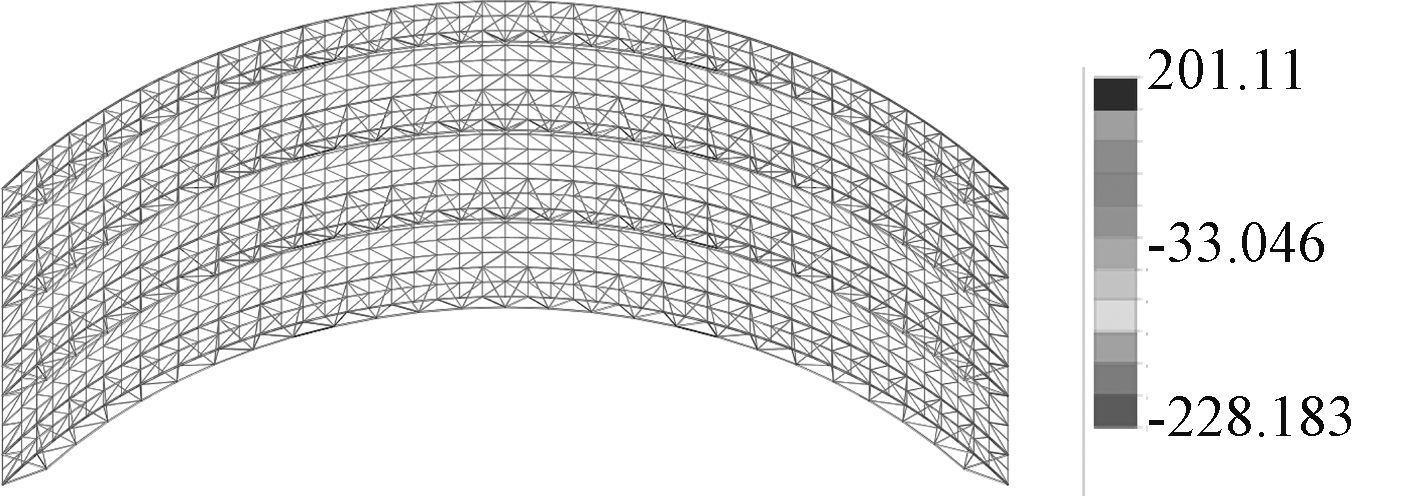
图7 包络工况下组合应力云图 MPa
Fig.7 Combined stress cloud map under envelope condition
具体来看,梁单元的最大组合拉应力为201.1 MPa,在靠近索撑体系撑杆区域的下弦杆上,出现在1.2恒载+1.4半跨活载工况时,在竖直向下最不利荷载作用下,拱桁架上弦受压,下弦受拉,但受拉最大位置位于施加半跨活荷载一侧的撑杆连接区域。这也说明,对于大跨度空间结构不能忽视半跨荷载的作用。梁单元的最大组合压应力为228.2 MPa,在拱桁架的上弦杆件处,出现在1.2恒载+1.4全跨活载工况时。索拱桁架-单层柱面网壳结构的最大内力分布规律体现了索拱桁架为主要传力构件的受力特征。
提取荷载效应标准组合工况(1.0恒载+1.0活载)下的结构变形云图,如图8所示,结构跨中最大挠度为498.3 mm,小于JGJ 7—2010《空间网格结构技术规程》所规定的L/250=792 mm,满足JGJ 7—2010的要求。此外,从变形分布规律来看,结构变形均匀,由跨中区域向撑杆连接区域再向支座逐渐减小,跨中区域在中间拉索和内侧撑杆的作用下,对减小跨中挠度有一定的作用。

图8 标准工况下竖向变形云图 MPa
Fig.8 Vertical deformation nephogram under standard operating conditions
本项目设计主要难点在于由于净空要求,钢结构屋盖不能落地而支承于15 m高单排柱列上,对钢结构的支座水平推力提出了较高要求。提取典型工况下支座的水平推力计算结果,如表4所示。
表4 支座最大水平推力
Table 4 Maximum support horizontal thrusts kN

荷载工况1.0恒载+1.0预应力1.0恒载+1.0预应力+1.4风载1.2恒载+1.2预应力+1.4活载支座最大横向水平推力132393720
由表4可以看出:结构沿横向的支座水平推力最大出现在1.2恒载+1.4活载工况时,仅为720 kN,15 m高的柱可满足其承载力。
拉索是索拱桁架-单层柱面网壳结构中的核心构件,为保证结构的正常安全运营,除了保证拉索在各工况下的内力不能超过其设计强度外,还应保证在所有工况下不出现松弛。其中,拉索的拉力设计值可按式(3)进行计算[19]。
(3)
式中:Ftk为拉索的极限抗拉力标准值,即拉索的公称破断索力;γR为拉索的抗力分项系数,取2.0。
由式(3)计算得到拉力值为4 925 kN。
提取最不利工况下的拉索内力值如表5所示。可以看出,拉索在所有工况作用下均是安全和可靠的。
表5 各最不利工况下的拉索内力
Table 5 Cable internal forces under the most unfavorable conditions kN
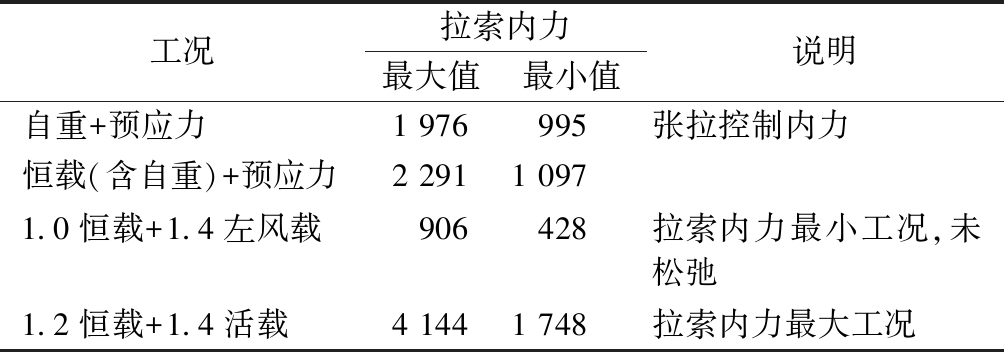
工况拉索内力最大值最小值说明自重+预应力1 976995张拉控制内力恒载(含自重)+预应力2 2911 0971.0恒载+1.4左风载906428拉索内力最小工况,未松弛1.2恒载+1.4活载4 1441 748拉索内力最大工况
3.4 动力性能
自振特性是结构重要的固有动力特性,它除了直接影响动力荷载作用于结构所产生的效应外,也是衡量结构质量与刚度是否匹配、刚度是否合理的重要指标。图9列出了索拱桁架-单层柱面网壳结构的前6阶振型,表6列出了相应的前6阶自振频率。
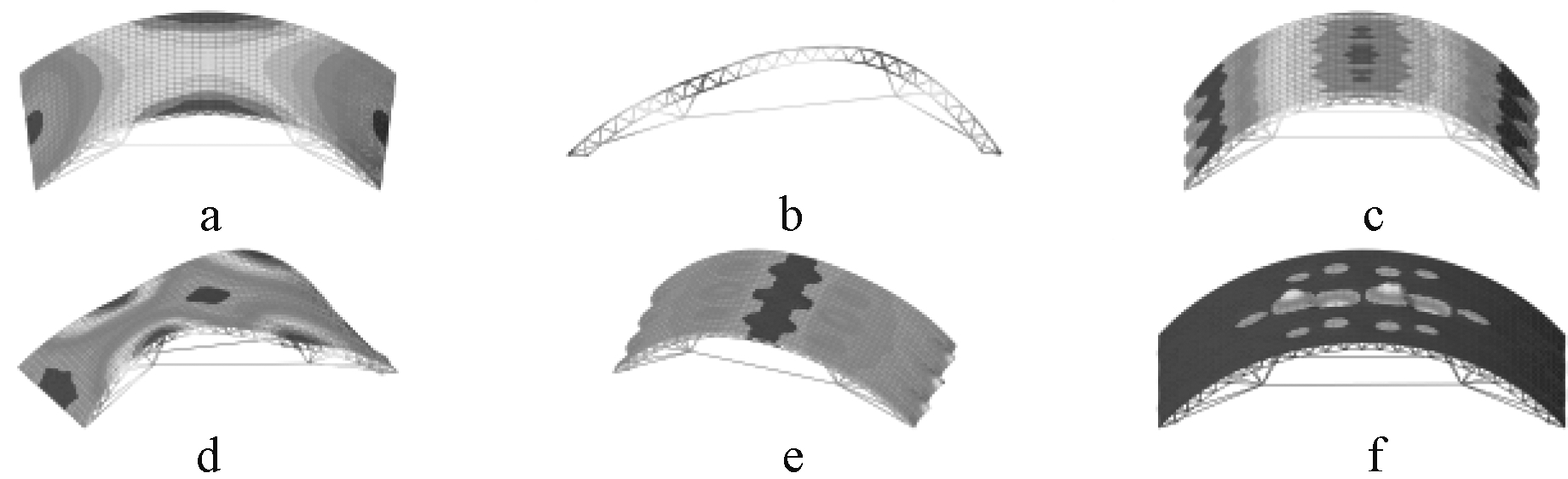
a—第1阶; b—第2阶; c—第3阶; d—第4阶; e—第5阶; f—第6阶。
图9 前6阶振型
Fig.9 Diagram of the first six modes of vibration
表6 前6阶自振频率
Table 6 The first six order natural frequencies Hz
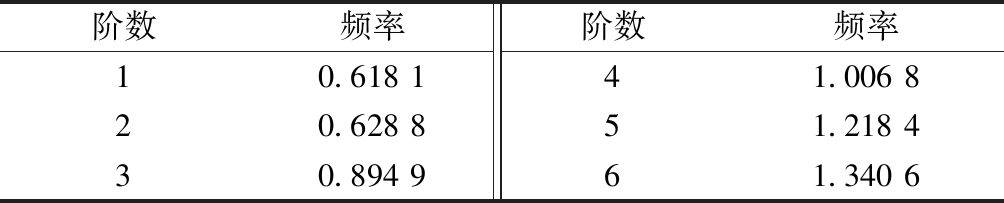
阶数频率阶数频率10.618 141.006 820.628 851.218 430.894 961.340 6
由图9可以看出:结构的第1阶振型以纵向平动为主,第2阶振型以横向平动为主,第3阶振型为竖向振动,第4阶振型为扭转振型,第5、6阶振型均为结构的局部竖向振动。由表6可以看出:结构的前3阶自振频率较小,结构较柔,尤其是第1阶与第2阶自振频率较为接近,说明结构在纵、横两个方向的刚度相差不大,结构刚度分布均匀;第3阶自振频率有一较小突变,由振型图知其为竖向振动,可预测结构的竖向刚度大于其水平刚度;后续自振频率增大较为均匀平缓,表明结构的刚度分布均匀,与质量匹配较为合理,可预测结构的动力性能较为可观。
4 结构稳定性分析
单层柱面网壳的面外刚度较差,在竖向荷载作用下,几何非线性很强,常发生失稳破坏;相对而言,索拱桁架的刚度较大,结构的几何非线性减弱,极限荷载作用下部分构件达到屈服后引起结构内力重分布,结构可能会发生弹塑性失稳。索拱桁架-单层柱面网壳由以上两种结构组合而成,其失稳形态可能更加复杂。结构的稳定性分析包括特征值屈曲分析和非线性屈曲分析,特征值屈曲分析不考虑初始缺陷及非线性效应影响,对结构失稳临界力的预测往往是过于保守的,仅用作非线性屈曲分析的依据,而通过非线性屈曲分析的结果往往更加接近实际情况。鉴于大型通用有限元分析软件ANSYS强大的非线性分析功能,本文拟采用ANSYS对索拱桁架-单层柱面网壳的稳定性进行系统分析。
4.1 特征值屈曲分析
结构的特征值屈曲分析基于小位移线弹性理论假设,以结构的初始位移为参考构型,计算其从一个平衡态突变到另一个平衡态的过程,其特征屈曲方程如式(4)所示。
([KE]+λ[KGz]){ψ}={0}
(4)
式中:[KE]+λ[KGz]为结构的切线刚度矩阵,对于预应力钢结构,其中的[KE]为弹性刚度矩阵,与结构的变位等无关;[KGz]为引入结构预应力和荷载作用后的初应力刚度矩阵或几何刚度矩阵[20-21]。因此在预应力钢结构的特征值屈曲分析中,荷载因子λ的实际意义是结构在λ倍预应力和λ倍外荷载作用下的屈曲现象,这与实际需要的荷载因子不符。为了消除预应力对荷载因子的影响,可以修改{P},使得在λ{P}和1倍预应力作用下,结构特征值屈曲分析得到的荷载因子接近于1[22]。
按上述方法,通过不断调试,当对索拱桁架-单层柱面网壳施加8.07倍屋面恒载(g2=0.15 kN/m2)、结构自重和1倍预应力作用时,计算出第一阶屈曲特征值λ1=1.005≈1,可认为结构的实际第一阶屈曲特征值为8.07。同样的方式,通过不断调整荷载因子为8.5时,计算出第二阶屈曲特征值λ2=1.000 5;当荷载因子为8.62时,计算第三阶屈曲特征值λ3=1.000 8≈1。按上述原则确定的前三阶屈曲模态如图10a~10c所示。
从图10可以看出:理想完善模型前3阶失稳均表现为局部失稳破坏,其薄弱部位为单层柱面网壳区域。显然这与单层柱面网壳的面外刚度较弱的定性分析是吻合的。通过进一步分析发现:结构的前100阶特征值屈曲模态均为单层网壳发生局部失稳,只是各阶模态的具体失稳局部区域有所不同,其中第22阶是失稳区域相对较大的最低阶失稳模态,如图10d所示,仍然是拱桁架之间的单层网壳出现了较大范围的失稳形态,但拱桁架未发生较大变形。
4.2 考虑初始缺陷的双重非线性分析
单层柱面网壳结构作为一种缺陷敏感性结构,当其组合到索拱桁架-单层柱面网壳结构中时,也应考虑初始缺陷对结构极限承载力的影响。此外,结构稳定性分析时如忽略了材料和几何双重非线性的影响有可能高估结构的实际承载力。因此,为研究本结构的实际承载力,为以后类似工程提供可靠参考,本文考虑初始缺陷以及几何与材料双重非线性的影响,根据一致缺陷模态法(一般情况下可根据首阶屈曲模态施加初始缺陷,但考虑到本结构的低阶屈曲模态均为局部失稳,不足以反映结构的整体情况),本文选取特征值屈曲区域相对较大的第22阶特征值屈曲模态,并按缺陷最大值为L/300(L为结构跨度,本工程中最大初始缺陷值取为0.66 m)对结构施加初始缺陷后,对结构进行全过程跟踪分析。分析过程中,所有钢材均采用双折线非线性本构关系,其中钢材屈服强度取为fy=345 MPa,钢丝束的名义屈服强度取为f0.2=1 570 MPa,超过材料的屈服强度后,假定切线模量均为0。

a—第1阶,λ1=8.07; b—第2阶,λ2=8.50; c—第3阶,λ3=8.62; d—第22阶,λ22=13.9。
图10 部分特征屈曲模态
Fig.10 Partial characteristic buckling modal diagram
选取结构位移最大点绘制结构的荷载-位移曲线,如图11所示。可知,当荷载小于7.18倍屋面恒载时,荷载与节点位移近似呈线性关系;当荷载大于7.18倍屋面恒载后,结构将发生一突变,节点位移随荷载呈非线性迅速增长,可初步判定结构在7.18倍屋面恒载附近将发生失稳。
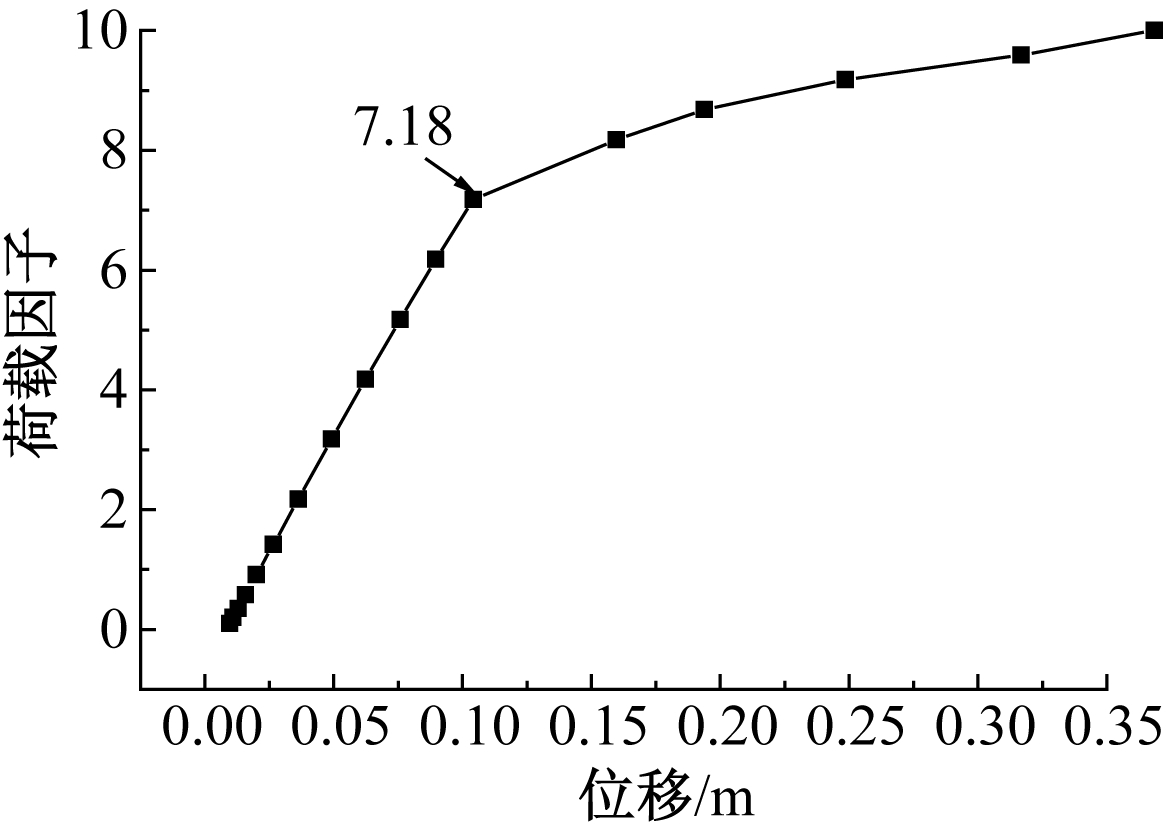
图11 荷载-位移曲线
Fig.11 Load-displacement curve
为进一步考察结构在7.18倍屋面恒载附近所发生的突变情况,提取结构在7.18倍屋面恒载g2所在荷载步及后一相邻荷载的位移云图与von Mises等效应力云图,分别如图12~图14所示。由图12可知,在结构进入塑性前,结构最大变形发生在靠近跨中区域的单层柱面网壳上,同时其拱桁架部分也发生了相应的均匀变形,此时结构尚处于弹性阶段,最大von Mises等效应力仅为186 MPa(图14a);当荷载略微增大后,结构的变形将向集中到跨中区域的单层网壳上发展,而拱桁架上的变形将不再增加,如图13所示,且最大von Mises等效应力也突增到345 MPa(图14b),结构进入塑性阶段。
分析发生上述突变的原因,主要是因为单层柱面网壳的面外刚度弱、稳定性差,柱面网壳子结构部分在7.18倍屋面荷载作用下刚好处于分支点失稳临界状态;随着荷载的进一步增大,结构发生微小变形后即达到一种新的承载力更高的稳定结构。这与ANSYS计算过程中,刚好在荷载因子为7.18时出现结构总体刚度矩阵奇异,而后需通过调整荷载步重新继续求解的情况相吻合。这一过程也可简单理解为,拱桁架之间的单层柱面网壳结构在荷载较小时为向上“凸起”的网壳形式;在屋面荷载为7.18倍屋面荷载时,变为接近“水平”的随遇临界平衡状态;随后荷载继续增大,即变为向下“凹陷”的另一种稳定结构形式。虽然,结构进入弹塑性阶段还可继续承载,但通过上述分析可知,此时单层柱面网壳部分已突变为另一种结构形式,已达到结构失稳破坏的标准。因此,可将结构的考虑初始缺陷的双重非线性极限荷载因子定义为7.18。
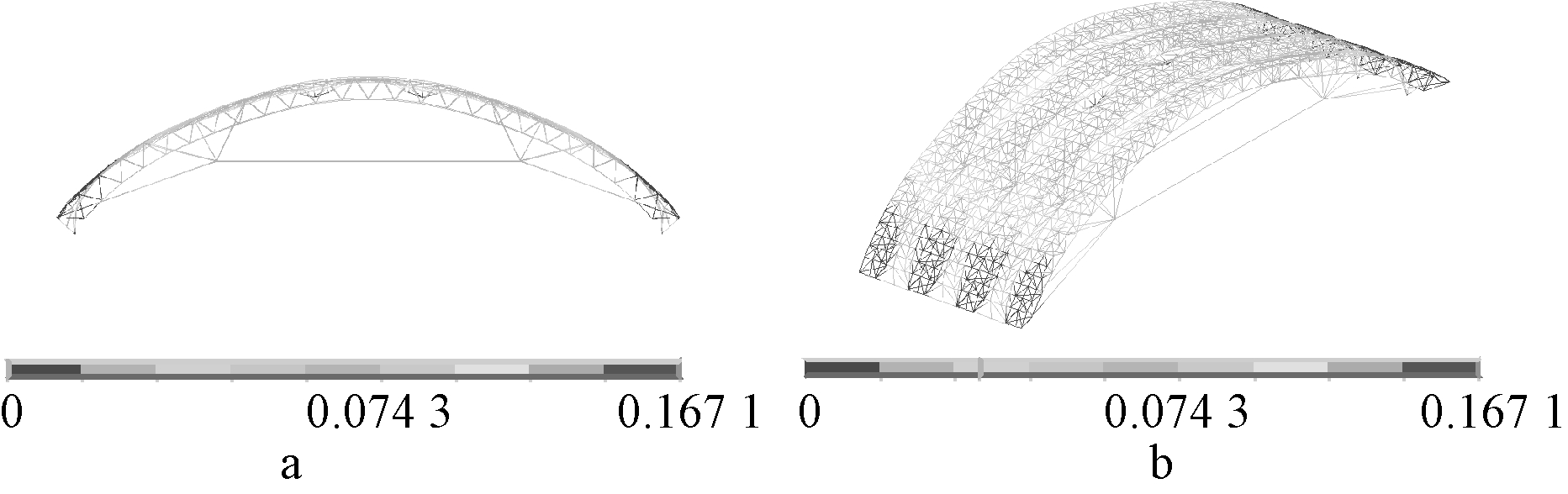
a—立面; b—轴测。
图12 7.18倍屋面恒载作用下变形云图(放大50倍) m
Fig.12 Deformation nephogram of 7.18 times roof load (magnified 50 times)

a—立面; b—轴测。
图13 突变后结构变形云图(放大50倍) m
Fig.13 Structural deformation nephogram after mutation (magnified 50 times)
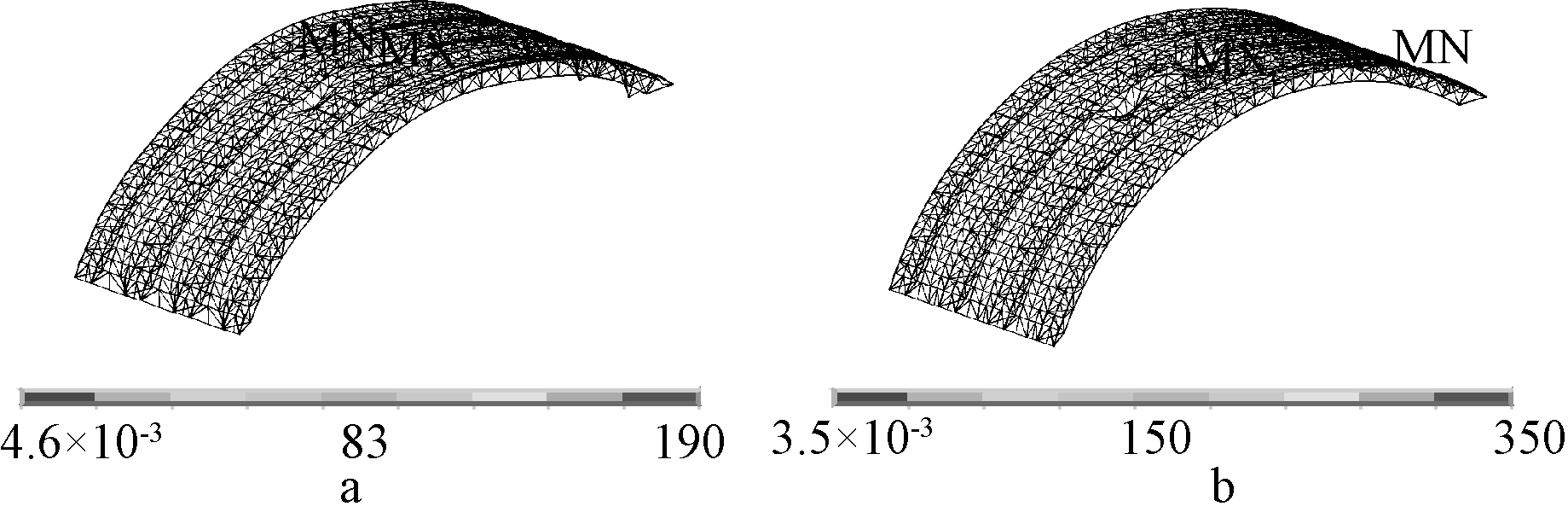
a—失稳前时刻; b—失稳后时刻。
图14 von Mises等效应力云图 MPa
Fig.14 von Mises equivalent stress nephogram
对比结构的特征值屈曲分析结果与弹塑性极限承载力分析结果,发现结构在引入初始缺陷并考虑材料与几何双重非线性后,计算得到的极限荷载因子7.18与线弹性屈曲特征值8.07较为接近,说明其对初始缺陷不甚敏感。其原因:一方面主要在于索拱桁架-单层网壳复合空间结构的薄弱区域位于单层网壳部分,线弹性分析时主要为网壳局部失稳,考虑非线性影响后,变形亦主要集中在网壳局部区域,因此两者失稳形式相似;另一方面,相比于传统的单层网壳结构,由于刚度和稳定性较好的索拱桁架为单层柱面网壳提供了有力的弹性支承,减小了网壳结构的跨度,增强了网壳结构的侧向约束,从而克服了单层网壳对安装缺陷较为敏感的问题。
5 结 论
1)索拱桁架-单层柱面网壳结构的内凹式索撑体系极大减小了支座处水平推力;上部单层网壳弹性支承于拱桁架上,减小了单层网壳的纵向跨度,从而可减轻结构自重、提高网壳稳定性;同时柱面网壳为拱桁架提供了侧向支撑,提高了结构的整体稳定性,可实现结构跨越更大的跨度。
2)索拱桁架-单层柱面网壳在静力荷载作用下,拉索未出现松弛现象且留有一定的安全储备,保证了预应力钢结构核心构件——拉索工作的可靠性,且最不利荷载工况下支座水平推力仅为720 kN,为近200 m级大跨度煤棚支承于15 m高单排柱列的实现提供了可能性。
3)在竖向荷载作用下,结构的应力与变形均满足设计要求,结构受力最大位置位于与索撑体系中撑杆连接区域的拱桁架上,表明索拱桁架是结构的主要传力构件,且半跨荷载作用较全跨对结构更为不利;在变形方面,结构变形均匀,由跨中向撑杆连接区域再向支座逐渐减小,索撑体系对减小跨中挠度起到有益作用。
4)结构的自振特性分析结果表明,索拱桁架-单层柱面网壳结构的刚度分布均匀,与质量匹配较为合理,结构扭转振型出现在第4阶,但结构整体较柔。
5)由于索拱桁架-单层柱面网壳复合结构的单层网壳稳定性较差,其线弹性特征屈曲的低阶失稳模态均表现为单层网壳的局部屈曲;而索拱桁架的几何非线性不明显,为结构的主要传力子结构体系,且有效减小了网壳的跨度、增强了网壳的侧向约束,因此,考虑初始缺陷以及材料、几何双重非线性的极限荷载与弹性屈曲特征值较为接近。
[1] 陈耀, 冯健, 盛平, 等. 新广州站内凹式索拱结构索夹节点抗滑性能分析[J].建筑结构学报, 2013, 34(5): 27-32.
[2] 黄利锋, 冯健, 赵建, 等. 新广州站内凹式索拱结构模型静力试验研究[J]. 建筑结构学报, 2010, 31(7): 111-117.
[3] 剧锦三, 郭彦林. 索-拱结构的平面内稳定性研究[J].建筑结构学报, 2001, 22(2): 84-87.
[4] CHEN Y, SAREH P , FENG J. Effective Insights into the Geometric Stability of Symmetric Skeletal Structures Under Symmetric Variations[J]. International Journal of Solids and Structures, 2015, 69-70: 277-290.
[5] 王振, 杨大彬, 周观根, 等. 一次张拉V形腹杆内凹式索拱结构稳定承载力参数分析[J]. 建筑结构, 2017, 41(1): 84-87.
[6] 郭彦林, 吕晶, 黄李骥, 等. 几种新型结构及构件的稳定性承载力研究与应用[J]. 工业建筑, 2004,34 (增刊1): 151-165.
[7] 赵曦辉, 吴碧野. 索拱桁架在大跨度干煤棚结构中的应用[J]. 建筑结构, 2016, 46(增刊1): 519-522.
[8] 贺拥军, 张相扬, 周绪红. 交叉布索预应力立体桁架拱静力与稳定性研究[J]. 铁道科学与工程学报, 2016, 13(12): 2420-2426.
[9] 袁婷. 索-拱结构平面外弹塑性稳定分析[J]. 低温建筑技术, 2011, 33(8): 53-55.
[10] 朱奕锋, 赵伟, 蔡建国, 等. 基于剪式单元的预应力索拱开合结构的分析研究[J]. 钢结构, 2016, 31(7): 37-41.
[11] 张竟乐, 赵金城, 许洪明. 单层网壳板式节点的刚度分析[J]. 工业建筑, 2005, 35(4): 88-90.
[12] 朱奕锋, 吴向东, 曾滨, 等. 华能大厦单层柱面网壳的设计及分析[J]. 工业建筑, 2011, 41(7): 96-100.
[13] 马凯, 杨勇. 厦门东海火炬科技园S3#楼大跨度多曲面单层网壳整体受力及稳定分析[J]. 建筑结构, 2017, 47(15): 11-15.
[14] 张烨, 吕玉惠, 孙保金. 复杂曲面单层网壳结构的非线性稳定性分析研究[J]. 钢结构, 2017, 32(11): 53-57.
[15] 马肖彤, 包超, 王秀丽, 等. 基于能量原理的单层网壳结构抗冲击性能简化分析方法研究[J]. 工业建筑, 2017, 47(11): 155-162.
[16] 中华人民共和国住房和城乡建设部.建筑结构荷载规范: GB 50009—2012 [S]. 北京: 中国建筑工业出版社, 2012.
[17] 中华人民共和国建设部.塑料护套半平行钢丝拉索: CJ 3058—1996[S].北京:中国标准出版社,1996.
[18] 盛平, 柯长华, 甄伟, 等. 一种新型预应力索拱结构设计及工程应用[J]. 建筑结构, 2008, 38(1): 117-120.
[19] 中华人民共和国住房和城乡建设部. 索结构技术规程:JGJ 257—2012[S]. 北京: 中国建筑工业出版社, 2012.
[20] CHEN Y, FENG J. Generalized Eigenvalue Analysis of Symmetric Prestressed Structures Using Group Theory [J]. Journal of Computing in Civil Engineering, 2012, 26(4): 488-497.
[21] 张沛, 冯健. 张拉整体结构的稳定性判定及刚度分析[J]. 土木工程学报, 2013, 46(10): 48-57.
[22] 陈志华. 空间钢结构APDL参数化计算与分析[M]. 北京: 中国水利水电出版社, 2013.