混凝土材料由于原材料丰富,使用方便,抗压强度高,造价低等优点在土木工程领域得到了广泛使用。但是普通混凝土也有抗拉强度低,延性和韧性差等缺点[1],影响结构的正常使用和耐久性。因此,新型超高韧性工程水泥基复合材料(ECC)应运而生[2-3]。ECC由于具有优越的抗裂性、超高延性和韧性等优点,已经成功应用于建筑、桥梁、隧道、道路、大坝输水渡槽等工程结构中[4-5]。
抗压性能是ECC力学性能的重要方面,国内外诸多学者对聚乙烯醇纤维(PVA)-ECC的抗压性能及本构关系展开了研究。徐世烺等对273个PVA-ECC进行了单轴受压试验,提出了PVA-ECC的受压应力-应变关系全曲线模型[6];胡春红等讨论了龄期、纤维类型对PVA-ECC受压性能的影响[7];梁济丰等通过试验研究发现PVA纤维掺量的增加对混凝土抗压强度的影响不大[8]。Cavdar对不同温度下的纤维增强水泥基复合材料进行了试验,发现掺入纤维可以提升水泥基材料的高温力学性能[9]。Zhou等通过单轴抗压试验研究提出了ECC受压本构模型[10]。
虽然诸多国内外学者对ECC的受压性能进行研究,但研究仍很有限,且对ECC的受压应力-应变关系模型并未得到统一结论。因此,本文对PVA-ECC(简称“ECC”)的单轴受压本构关系进行试验和理论研究,分析了不同的PVA纤维掺量、水胶比对ECC棱柱体抗压性能的影响规律,并基于对试验测得的ECC受压应力-应变全曲线特征的分析,提出ECC受压应力-应变关系模型。
1 试验研究
1.1 试验方案设计
试验原材料有普通硅酸盐水泥、粉煤灰、微硅粉、细沙、聚羧酸高效减水剂及可饮用的自来水、REC15型PVA纤维,PVA的具体性能指标见表1。
表1 PVA纤维性能指标
Table 1 Performance index of PVA fiber

直径/μm长度/mm抗拉强度/MPa弹性模量/GPa断裂延伸率/%密度/(g·cm-3)40121560416.51.3
试验考虑PVA纤维掺量、水胶比的影响,ECC试件分为6组,每组对应一种配合比,每种配合比均制作6个相同的试件。试验采用尺寸为100 mm×100 mm×200 mm的棱柱体试件。基于其中50%的试件确定其峰值荷载,并得到应力-应变全曲线,通过其余的试件测定棱柱体试件的弹性模量和泊松比。各组试件配合比主要参数如表2所示。
表2 ECC配合比设计
Table 2 Mix proportion design of ECC
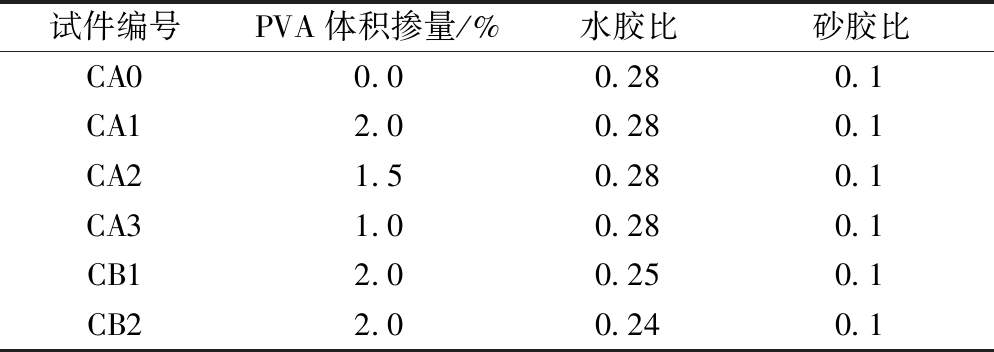
试件编号PVA体积掺量/%水胶比砂胶比CA00.00.280.1CA12.00.280.1CA21.50.280.1CA31.00.280.1CB12.00.250.1CB22.00.240.1
试件的制作过程为:首先用电子称称量好所需的材料的质量;再将水泥、砂、粉煤灰、微硅粉倒入搅拌桶中并干拌均匀;随后向桶中缓慢加入水和减水剂并低速搅拌120 s;之后将PVA纤维沿着搅拌桶边缘缓慢加入搅拌桶中,待PVA全部加入桶中后再搅拌180 s直至纤维均匀分布;最后将浆体浇筑成型,并在温度为(20±2)℃、湿度为95%以上的标准养护条件下养护24 h后,方可拆模。ECC试件拆模后在标准养护条件下养护28 d后进行试验。
1.2 试验现象分析
未掺加PVA纤维的水泥基体试件(CA0)从开始加载到达到峰值荷载之前均未出现明显征兆。当CA0试件达到极限荷载时,试件表面形成一条贯穿的斜向裂缝,发生脆性破坏。破坏形态见图1。

图1 水泥砂浆基体试件破坏形态
Fig.1 Failure mode of cement mortar matrix specimen
掺加纤维的试件(CA1~CA3和CB1、CB2)从开始加载到峰值荷载30%以下时没有出现裂缝;当加载至峰值荷载的30%~50%时,ECC表面出现第一条细小裂缝,继续加载,ECC表面不断出现新的细小裂缝,且原有裂缝不断发展,并向两端延伸;当荷载增加至极限荷载时,试件表面多处开裂,且裂缝迅速变宽,多条裂缝之间相互连接形成贯通斜向裂缝;随后试件承载力开始降低,当荷载降低至峰值荷载的30%左右时,试件表面裂缝宽达1 cm,之后停止加载。典型的ECC棱柱体破坏形态如图2所示。

图2 CA1试件破坏形态
Fig.2 Failure mode of specimen CA1
1.3 试验结果分析
通过试验得到各组ECC试件的试验数据如表3所示(表中数据均取每组试验数据平均值)。
由表3可见:ECC泊松比与PVA纤维体积掺量、水胶比和ECC的轴心抗压强度的大小基本无关,且ECC棱柱体泊松比平均值为0.27。这与文献[11]中立方体结构的泊松比0.26接近。
表3 试验结果
Table 3 Test results
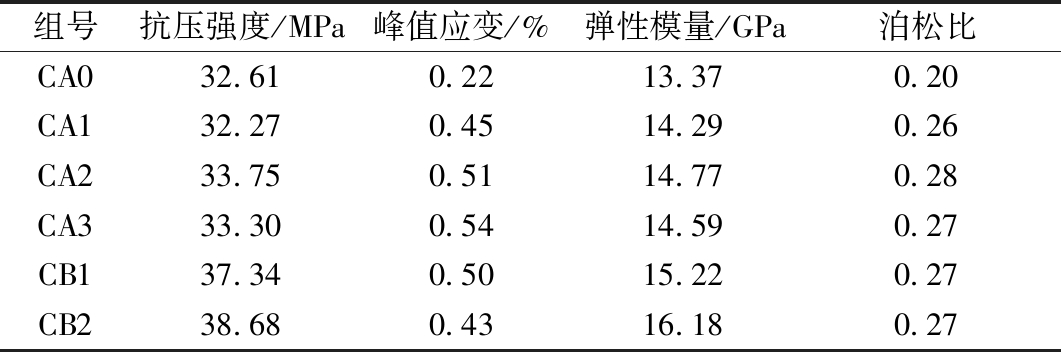
组号抗压强度/MPa峰值应变/%弹性模量/GPa泊松比CA032.610.2213.370.20CA132.270.4514.290.26CA233.750.5114.770.28CA333.300.5414.590.27CB137.340.5015.220.27CB238.680.4316.180.27
根据表3,相比于没有掺加纤维的CA0试件,纤维含量为1%和1.5%时,ECC试件抗压强度分别提高了2%、3.4%;纤维掺量为2.0%时,ECC试件抗压强度降低了1.0%。由此说明:当PVA纤维掺量较小时,ECC抗压强度随PVA纤维掺量的增加而增大;当PVA纤维掺量过多时,反而会降低ECC抗压强度。但总体来说,PVA纤维掺量的变化对ECC抗压强度影响不大。文献[12]也得到了相同的结论。
根据表3,对比CA1、CB1和CB2三组试件的试验结果,可以发现ECC抗压强度随着水胶比的减小而增大,与文献[13]中得到的结论相同。
对比表3中所有ECC试件的试验结果,发现ECC棱柱体弹性模量随其抗压强度提高而逐渐增大。文献[14]也得到了相同的结论。
2 ECC受压应力-应变曲线分析
图3为基于试验结果得到的各组ECC棱柱体受压应力-应变曲线。可知,在应变为0.5%左右时,ECC棱柱体受压应力最大。当应力达到峰值应力后,随着应变的增加,应力下降较快,但当应力降到峰值应力的30%左右时,随着应变的增加,应力下降缓慢,具有一定的残余强度,即在水泥基砂浆基体中加入PVA纤维可以使其受压极限应变显著提高。
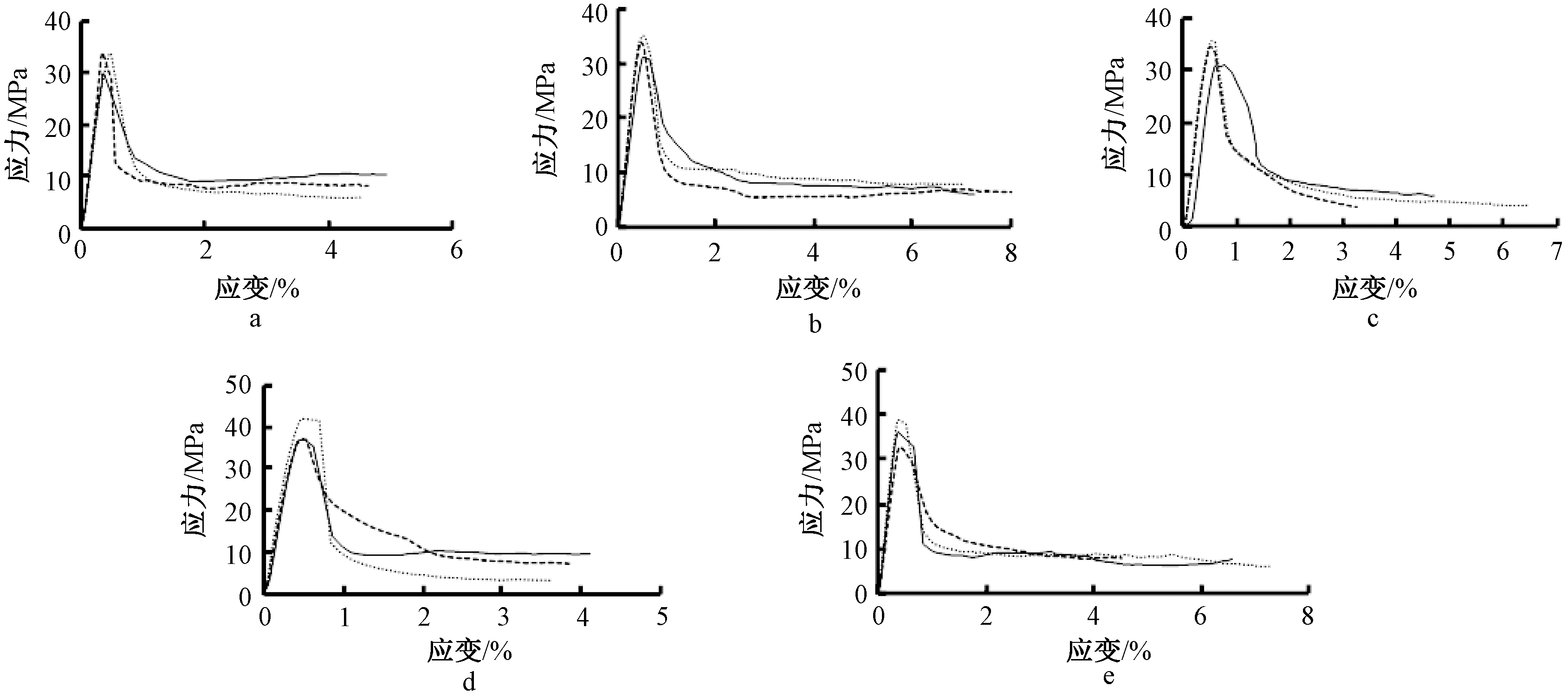
a—CA1;b—CA2;c—CA3;d—CB1;e—CB2。
图3 ECC试件实测受压应力-应变全曲线
Fig.3 Complete stress-strain curve of ECC specimens under compression
本文采用分段函数描述ECC受压应力-应变曲线。将应力、应变用无量纲表示,如式(1)所示。
(1)
式中:σu为峰值应力;εu为与σu对应的应变。

图4 典型ECC受压应力-应变全曲线
Fig.4 Typical complete stress-strain curve of ECC under compression
通过式(1)得到无量纲化典型ECC受压应力-应变曲线如图4所示。基于图4中ECC受压应力-应变曲线的特征,可分为以下四个阶段:
第一阶段为弹性阶段(OA),在该阶段外荷载主要由水泥砂浆基体承担,PVA纤维发挥作用很小,应力与应变呈线性关系。
第二阶段为裂缝稳定扩展阶段,即从比例极限到峰值点的曲线段AB。随着应力的增大,应变的增加速率不断增大,在此阶段ECC内部裂缝缓慢扩展延伸裂,表面出现多条细小裂缝,由于PVA纤维开始发挥桥联作用,裂缝稳定地扩展延伸。
第三阶段为裂缝不稳定发展阶段,即从峰值点B到下降段拐点C之间的凸曲线段BC。当应力至峰值后,荷载快速下降,相应的裂缝快速地扩展变宽,由于纤维的桥联作用,ECC裂而不碎。
第四阶段是破坏阶段,即下降段反弯点C与下降段曲率最大点D之间的凹曲线段CD。在该阶段ECC内部的纤维逐渐被拔出或拉断,表面的裂缝也相互贯通变宽,最后在表面出现一条贯通斜裂缝。
第五阶段是残余应力阶段,即D点之后曲线接近水平线,进入残余应力阶段。在该阶段裂缝宽度仍不断增加,但由于纤维的桥联作用,ECC棱柱体裂而不碎,仍能作为整体承担残余荷载。
3 受压应力-应变关系模型研究
3.1 应力-应变曲线特征
ECC棱柱体受压应力-应变曲线的几何特征可以描述如下:
1)x=0,y=0;
2)0≤x≤1.0,且![]() 时,
时,![]() 为一常量;
为一常量;
3)x=1时,![]()
4)坐标xC(≥1.0)处,![]() 即下降段曲线有一拐点;
即下降段曲线有一拐点;
5)坐标xD(≥xC)处,![]() 为下降段曲线上曲率最大点;
为下降段曲线上曲率最大点;
6)当x→∞时,![]()
7)全部曲线x≥0,0≤y≤1.0。
3.2 应力-应变关系模型提出
根据ECC受压应力-应变全曲线特征,可将曲线分为上升段和下降段分别进行分析。上升段:从开始加载到比例极限点,应力-应变曲线斜率为弹性模量,并保持不变;超过比例极限点后,曲线斜率逐渐降低,本文采用六次多项式对上升段曲线进行拟合,如式(2)所示。
y=b+ax+cx5+dx6
(2)
式中:a、b、c、d均为待定常数。
根据ECC受压应力-应变曲线几何特征1)和3),经计算可得式(2)中,b=0、c=6-5a、d=4a-5,所以,上升段曲线函数表达式如式(3)所示。
y=ax+(6-5a)x5+(4a-3)x6
(3)
根据式(3),对每组试件中典型试验曲线进行拟合,拟合曲线与试验曲线对比如图5所示。
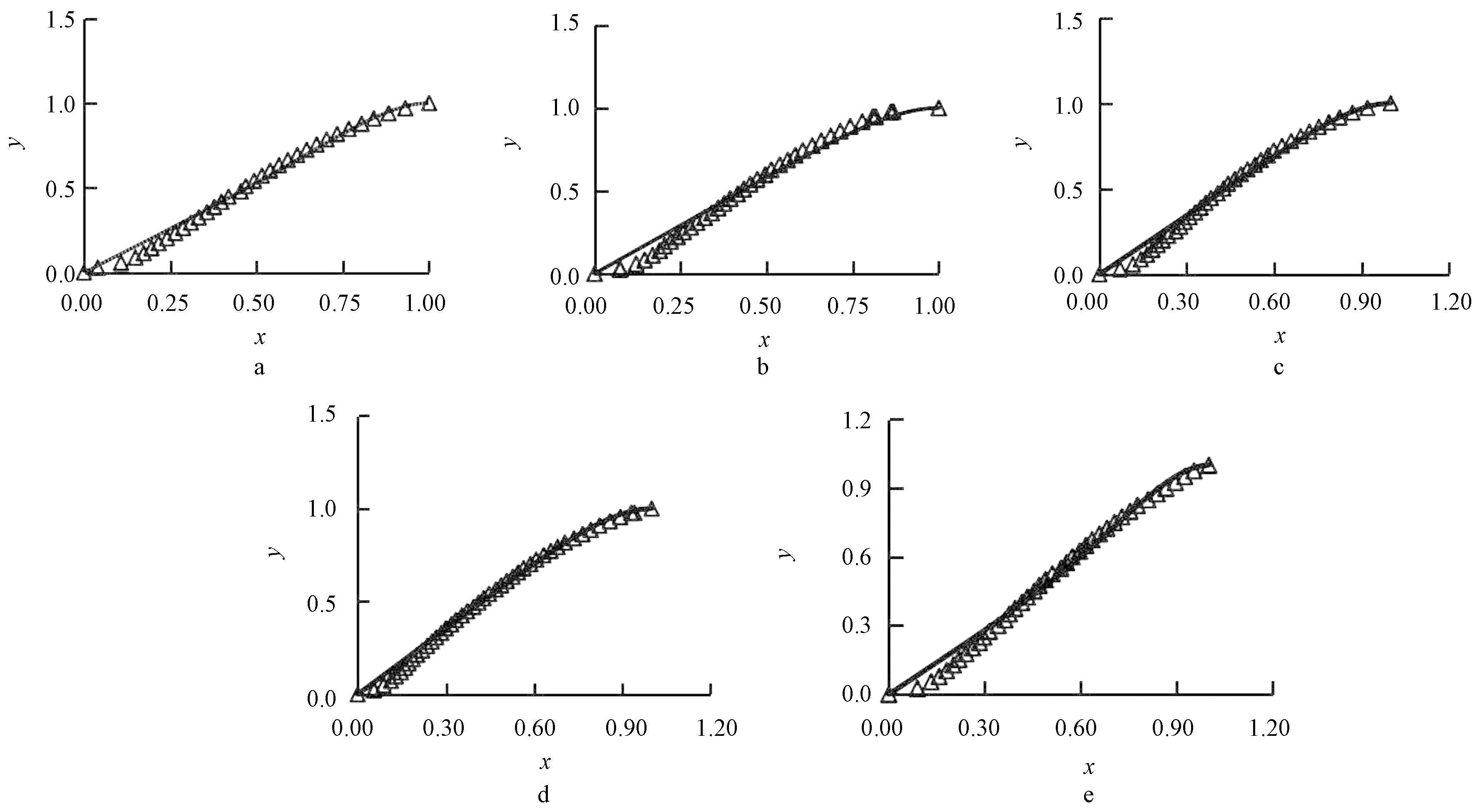
a—CA1-3上升段;b—CA2-3上升段;c—CA3-3上升段;d—CB1-3上升段;e—CB2-3上升段。![]() 为试验数值;——为拟合曲线。
为试验数值;——为拟合曲线。
图5 上升段拟合曲线与试验曲线对比
Fig.5 Comparisons between fitting curves of ascending stage and test curves
根据ECC受压应力-应变曲线特征,下降段函数表达式如式(4)所示:
(4)
式(4)符合3.1节所述的3)~7)项ECC棱柱体受压应力-应变曲线几何特征。根据式(4),对每组试件中典型试验曲线进行分析,分析结果如图6所示。
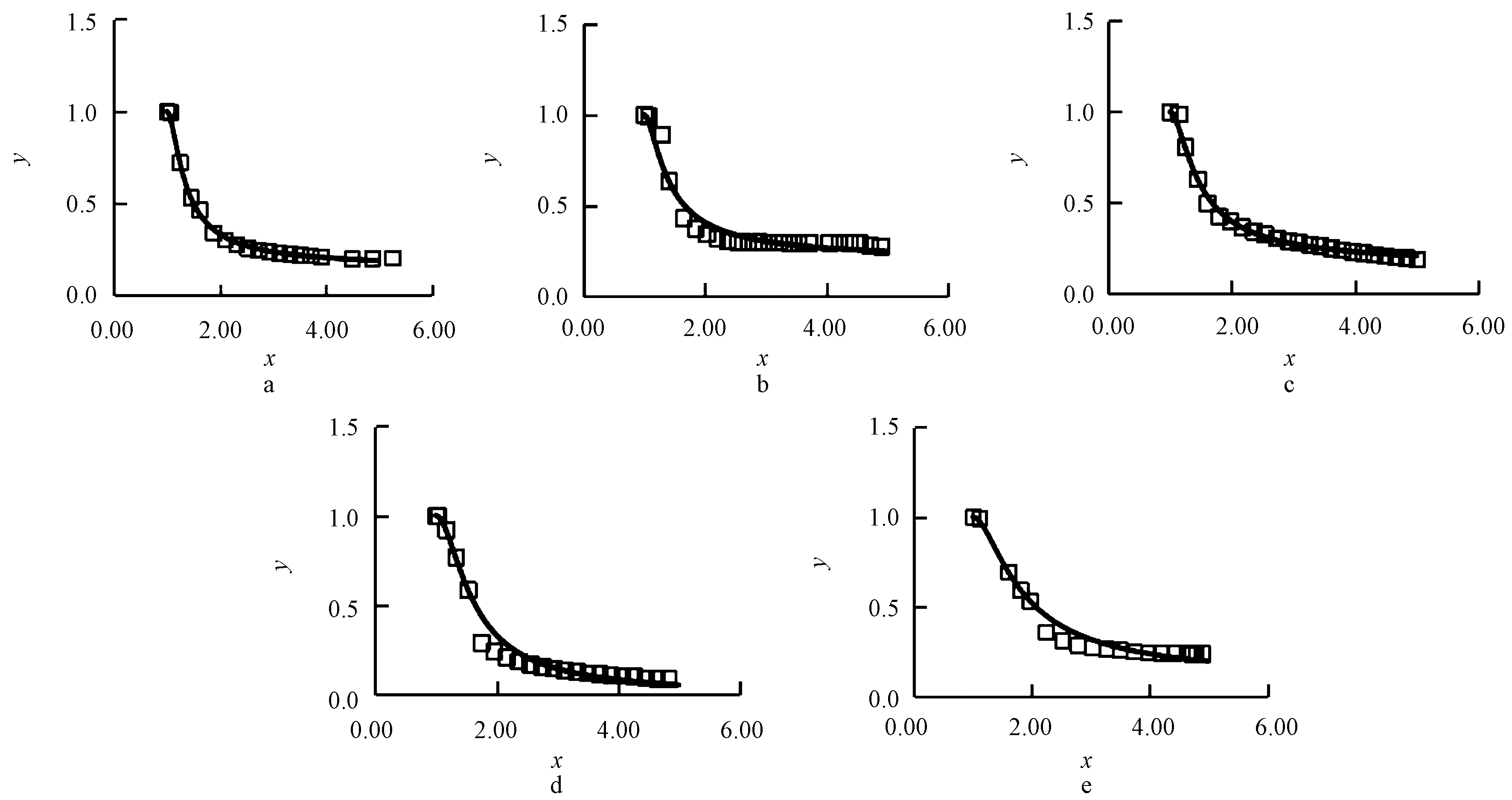
a—CA1-3下降段;b—CA2-3下降段;c—CA3-3下降段;d—CB1-3下降段;e—CB2-3下降段。![]() 为试验数值;——为拟合曲线。
为试验数值;——为拟合曲线。
图6 下降段拟合曲线与试验曲线对比
Fig.6 Comparisons between fitting curves of descending stage and test curves
根据式(3)、式(4),采用最小二乘法对试验数据进行分析,可得到式(3)、式(4)中待定常数值(见表4)。根据表4,由于各组a、k值相差不大,因此取各试件a、k的平均值作为待定常数a、k的值,即a=1.10,k=1.15。因此可以得到ECC受压应力-应变关系模型如式(5)所示。
σ=

(5)
表4 待定常数a、k的拟合结果
Table 4 Fitting results of undetermined constants a and k
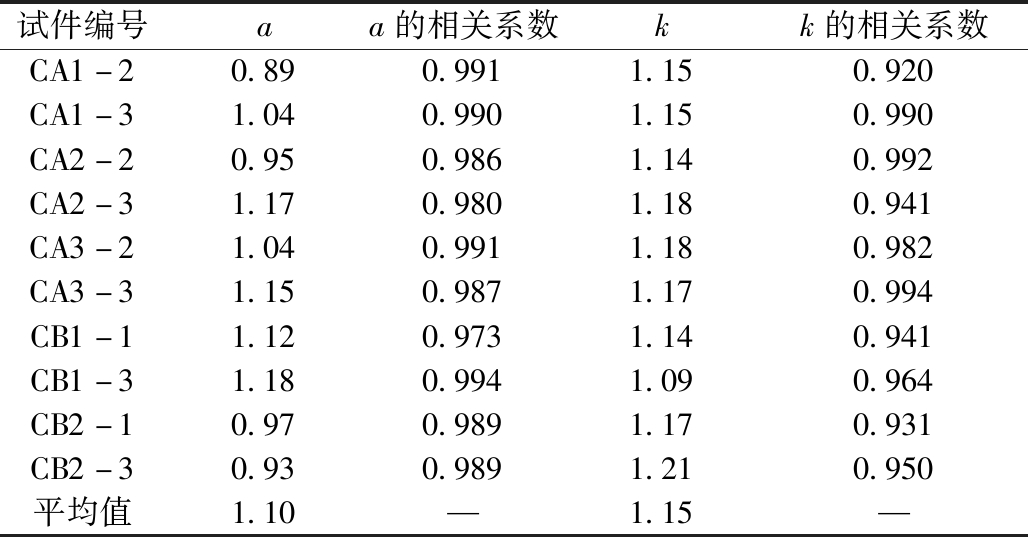
试件编号aa的相关系数kk的相关系数CA1-20.890.9911.150.920CA1-31.040.9901.150.990CA2-20.950.9861.140.992CA2-31.170.9801.180.941CA3-21.040.9911.180.982CA3-31.150.9871.170.994CB1-11.120.9731.140.941CB1-31.180.9941.090.964CB2-10.970.9891.170.931CB2-30.930.9891.210.950平均值1.10—1.15—
3.3 受压应力-应变关系模型验证
本文进行了以下的试验,用来验证ECC受压应力-应变关系模型的适用性。试验各组试件的尺寸为100 mm×100 mm×200 mm,表5所示为配合比主要参数,每组配合比6个试件,用来测试每组试件的单轴受压应力-应变全曲线。
表5 验证试件配合比
Table 5 Mix proportion of validation test specimens

试件编号PVA体积掺量/%水胶比砂胶比YCA1Z2.00.280.1YCB1Z2.00.250.1
将YCA1Z、YCB1Z两组试件的受压应力-应变全曲线与按照3.2节提出的受压模型式(5)计算所得的应力-应变曲线进行对比,如图7所示。可以看出:YCA1Z、YCB1Z两组试件的应力-应变曲线的试验结果与本文所提模型吻合良好,相关系数分别为0.947、0.978。由此说明本文提出的ECC受压应力-应变关系模型能够较好地表征ECC单轴受压应力-应变关系特性。

a—YCA1Z;b—YCB1Z。
……试验曲线;——本构模型。
图7 验证试验与模型结果对比
Fig.7 Comparisons between the verification experimental results and the modeling results
4 结束语
本文通过ECC棱柱体受压试验,探究了PVA掺量、水胶比对ECC受压性能的影响以及ECC受压本构关系模型,得到的主要结论如下:
1)当PVA纤维掺量小于1.5%时,ECC的抗压强度随着纤维掺量的增加而略有增大;当纤维掺量大于1.5%小于2%时,ECC的抗压强度随着纤维掺量的增加略有降低。但PVA纤维掺量的变化对ECC抗压强度影响不大。
2)ECC棱柱体抗压强度随水胶比的降低而增加。ECC棱柱体弹性模量随着ECC抗压强度的提高而逐渐增大。
3)ECC的水胶比和PVA体积掺量对其泊松比影响不大,本文得到的ECC棱柱体泊松比平均值为0.27。
4)提出了ECC单轴受压应力-应变关系模型,并根据试验结果确定了模型参数,该模型与验证试验结果吻合良好,表明了该模型的准确性。
[1] 王玉清,孙亮,刘曙光,等.PVA-ECC受压弹性模量与泊松比试验研究[J].混凝土,2018(10):17-21.
[2] LI V C,LEUNG C K Y.Theory of Steady State and Multiple Cracking of Random Discontinuous Fiber Reinforced Brittle Matrix Composites[J].Journal of Engineering Mechanics,ASCE,1992,118(11):2246-2264.
[3] LI V C,WU H C,CHAN Y W.Effect of Plasma Treatment of Polyethylene Fibers on Interface and Cementitious Composite Properties [J].Journal of the American Ceramic Society,1996,79(3):700-704.
[4] 李艳,程格格,刘泽军.聚乙烯醇纤维增强水泥基复合材料单轴受压强度与变形特性分析[J].工业建筑,2017,47(4):122-126,158.
[5] 刘曙光,邓轶涵,张菊,等.PVA纤维水泥基复合材料与钢筋粘结性能研究[J].功能材料.2016,46(1):1110-1116.
[6] 徐世烺,蔡向荣,张英华.超高韧性水泥基复合材料单轴受压应力-应变全曲线试验测定与分析[J].土木工程学报,2009,42(11):79-85.
[7] 胡春红,高艳娥,丁万聪.超高韧性水泥基复合材料受压性能试验研究[J].建筑结构学报,2013,34(12):27-32.
[8] 梁济丰,吕磊,余晓青.聚乙烯醇纤维增强水泥基复合材料力学性能试验研究[J].混凝土与水泥制品,2013(11):48-51.
[9] CAVDAR A.A Study on the Effects of High Temperature on Mechanical Properties of Fiber Reinforced Cementitious Composites [J].Composite Part B:Engineering,2012,43(5):2452-2463.
[10] ZHOU J J,PAN J L,LEUNG C K Y.Mechanical Behavior of Fiber-Reinforced Engineered Cementitious Composites in Uniaxial Compression [J].Journal of Material in Civil Engineer,2015,27(1).DOI:10.1061/(ASCE)MT.1943-5533.0001034.
[11] 李可,金蕾蕾,刘伟康,等.考虑多参数影响的水泥基复合材料单轴抗压试验性能试验研究[J].工业建筑,2018,48(2):139-143,148.
[12] 刘桐,张继红,刘友忠,等.PVA纤维增强水泥基复合材料力学性能研究[J].混凝土与水泥制品,2016(4):63-65.
[13] 韩冠生,车佳玲,李权威,等.沙漠砂PVA-ECC材料力学性能试验研究[J].施工技术,2018(3):27-31.
[14] 王娟,李秀领,罗敏.GHPFRCC轴心抗压强度和弹性模量的试验研究[J].防灾减灾工程学报,2013,33:52-62,77.