0 引 言
现浇式、装配式及装配整体式是最常见的三种楼盖形式。其中现浇楼盖具有整体性好、水平刚度大等优点，但现场湿作业量大、模板工程量大，现场作业噪声和环境污染严重，且现浇混凝土的收缩变形和温差变形很难控制。相比现浇楼盖，装配式楼盖可避免现浇作业的诸多问题，但最大的缺点是整体性和抗震性较差。装配整体式楼盖又称为叠合楼盖，其整体性和抗震性介于现浇楼盖与装配式楼盖之间[1-2]。传统叠合板的预制部分采用实心平板，GB/T 16727—2007《叠合板用预应力混凝土底板》 规定，由于叠合板预应力反拱度难以控制，预制板厚度较大，导致叠合层混凝土厚度小，常按单向板设计，故降低了叠合板的经济效应，同时由于预制板间以及板端与支撑结构之间缺少有效的连接，导致楼盖整体性能差、楼板平面刚度小、抗震性能相对一般，该楼盖不适用受振动的结构，进而影响了其推广使用[3-6]。为此文献[7]提出了预制带肋底板混凝土双向叠合楼板，围绕预制带肋底板混凝土双向叠合楼板的静力性能进行了研究。文献[8]鉴于预制带肋楼盖与后浇混凝土的整体作用，借助ANSYS 10.0进行了该楼板双向受力效应理论分析。文献[9-13] 提出了一种实用的弹性计算方法，解决了单向叠合板设计时传力模式不合理和刚度各向异性板求解困难的问题。文献[14]结合静力破坏试验提出了考虑刚度各向异性特征影响的实用塑性设计方法。上述研究主要限于叠合板的静力计算问题，国内外标准有关疲劳验算的方法仅建立在容许应力法基础之上[15]。以往对预应力混凝土受弯构件的疲劳受力性能研究多采用梁式受弯构件，对于工程实际中常用的板式受弯构件疲劳性能研究很少[16-17]。因此，有必要对该叠合板的疲劳受力性能进行研究。本研究通过对T形肋与矩形肋两种板肋形式的叠合板试件在相同疲劳荷载上限和疲劳荷载下限的弯曲疲劳对比试验，以及矩形板肋试件在不同疲劳荷载上限的弯曲疲劳性能对比试验，分析板肋形状以及疲劳幅值在疲劳循环加载过程中，对试件的内部损伤和破坏模式的影响，并提出相应的弯曲疲劳验算方法。
1 试验概况
1.1 试件设计及制作
设计制作了矩形和T形两种不同肋底板叠合板试件，其中矩形肋底板叠合板试件编号分别为DHB2-1～4，T形肋底板叠合板试件编号为DHB4-2。在肋内预留孔洞内布设间距100 mm的横向穿孔钢筋，两种带肋底板叠合板试件的构造及几何尺寸分别见图1、图2，试件的长×宽×高均为3 000 mm×490 mm×120 mm。矩形肋底板和T形肋底板都采用先张法张拉，锚固端采用双夹头形式，张拉端采用单夹头形式，端部横向分布筋采用冷拔低碳钢丝，直径为4 mm。带肋底板在70 m张拉台座上完成混凝土的浇筑，养护7 d后开始浇筑叠合层混凝土，采取分阶段浇筑的方法确保板肋预留孔洞内混凝土浇筑密实。带肋底板及叠合层的混凝土材性参数见表1。所有预制底板中的预应力筋均采用1 470 MPa级螺旋肋高强预应力钢丝，张拉控制应力σcon=0.48fptk，通过在板肋内配置2φ6避免反拱过大导致板肋开裂、在支座处配4根冷拔低碳钢丝避免支座局部破坏。带肋底板及叠合层的非预应力钢筋材性参数见表2。
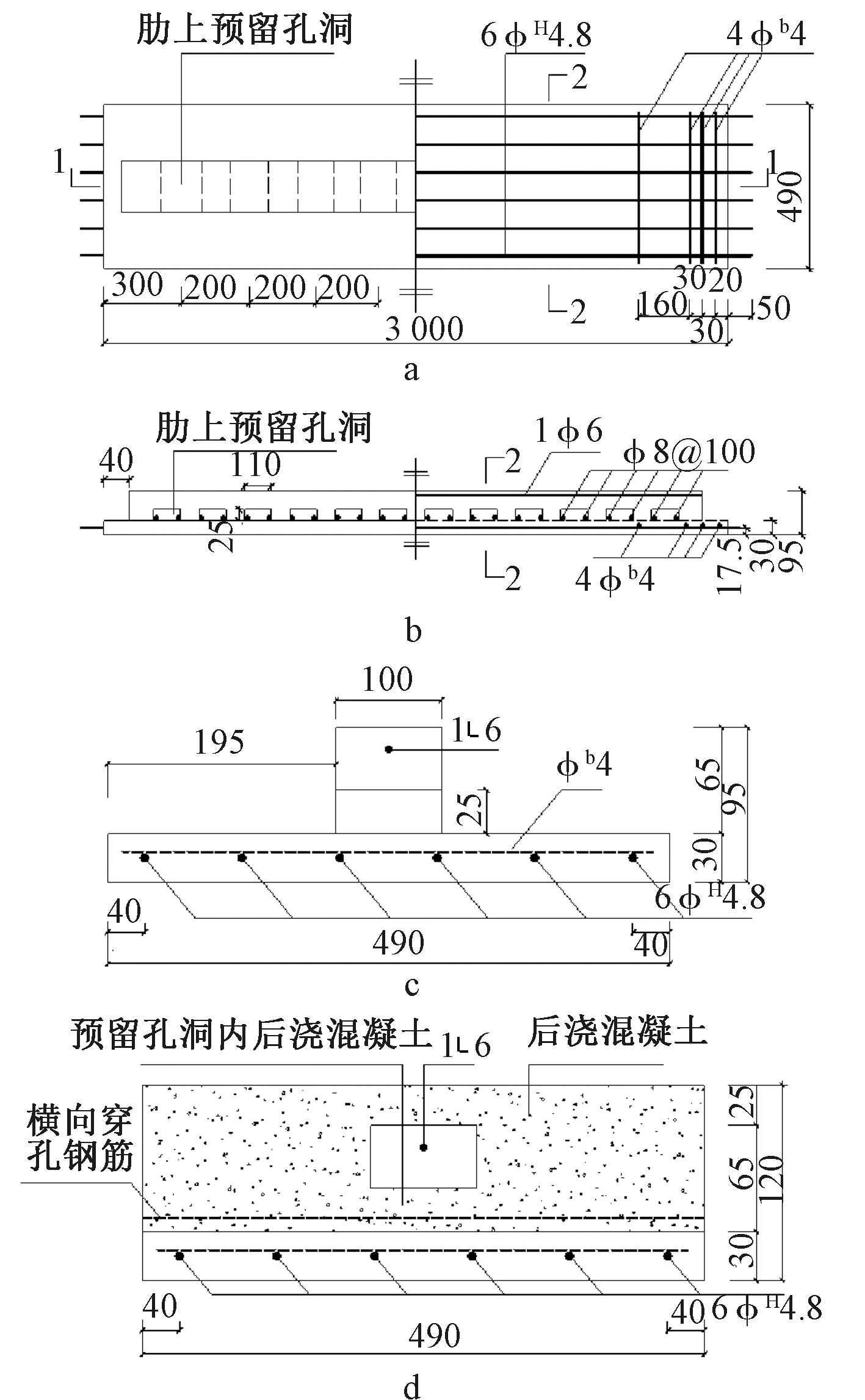
a—模板配筋；b—1—1剖面；c—2—2剖面；d—2—2剖面在叠合后的横断面示意。
图1 预制矩形肋底板叠合板试件构造及几何尺寸
Fig.1 Details and geometry dimension of precast rectangular ribbed composite slab
1.2 加载装置
试验主要采用了液压脉动疲劳试验机、BLR-1型10T动态拉压传感器、4通道DC-104R小型动态应变仪、线性可变差动变压器传感器，加载装置示意见图3。试验采用两端简支、两点集中对称的同步分级加载方式。为了保证疲劳试验中试件没有滑移，一级支座两端加焊钢架并填塞橡胶垫片，二级支座置于板面三分点位置，通过分配梁实现两点加载。为了确定脉动荷载的上限和下限，疲劳试验前先进行静载破坏试验，详细的疲劳荷载加载参数见表3。
1.3 加载方案及测点布置
疲劳试验前先作2次加载卸载循环的静载试验。在加载和卸载各阶段结束后，分别对上部叠合层混凝土和下部预制楼板的预应力筋进行应力测量。并观察记录试件的挠度和裂缝发展情况。当疲劳加载达到1万、5万、10万、30万、50万、70万、100万、150万、200万次时，分别进行静载试验，当疲劳循环加载次数达到200万次时进行静载破坏试验。
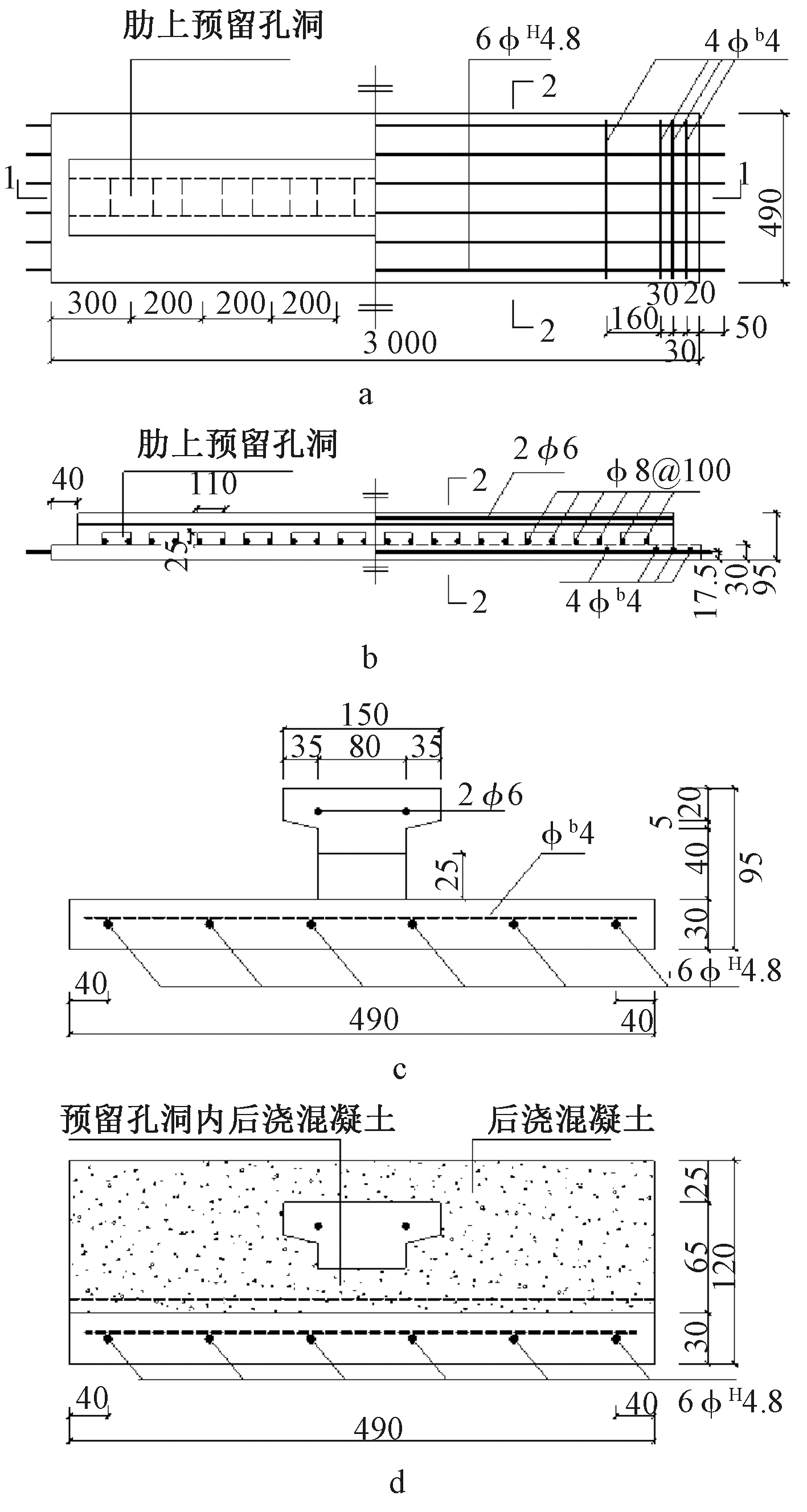
a—模板配筋；b—1—1剖面；c—2—2剖面；d—2—2剖面在叠合后的横断面示意。
图2 预制T形肋底板叠合板试件构造及几何尺寸
Fig.2 Details and geometry dimension of precast T-ribbed composite slab
表1 混凝土材性参数
Table 1 Material properties of concrete
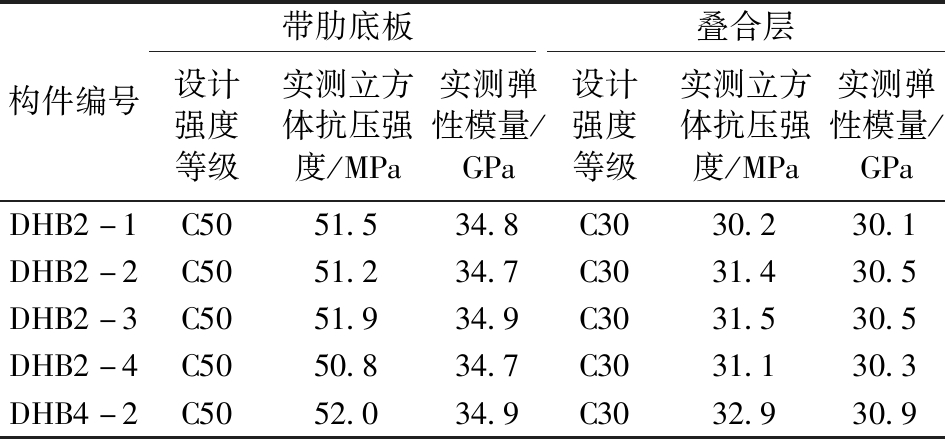
构件编号带肋底板叠合层设计强度等级实测立方体抗压强度/MPa实测弹性模量/GPa设计强度等级实测立方体抗压强度/MPa实测弹性模量/GPaDHB2-1C5051.534.8C3030.230.1DHB2-2C5051.234.7C3031.430.5DHB2-3C5051.934.9C3031.530.5DHB2-4C5050.834.7C3031.130.3DHB4-2C5052.034.9C3032.930.9
表2 钢筋材性参数
Table 2 Material properties of steels
型号直径/mm面积/mm2屈服强度/MPa极限强度/MPa弹性模量/GPaϕH4.84.818.081618205ϕ6628.26250320200
在试件表面布置电阻应变片，用来测量板顶、板底以及侧面混凝土的应变。为确定加载前预应力筋的初始应力状态，所有应变片在预应力筋张拉后进行粘贴，应变片粘贴位置为跨中截面及加载点处。具体测点布置见图4。
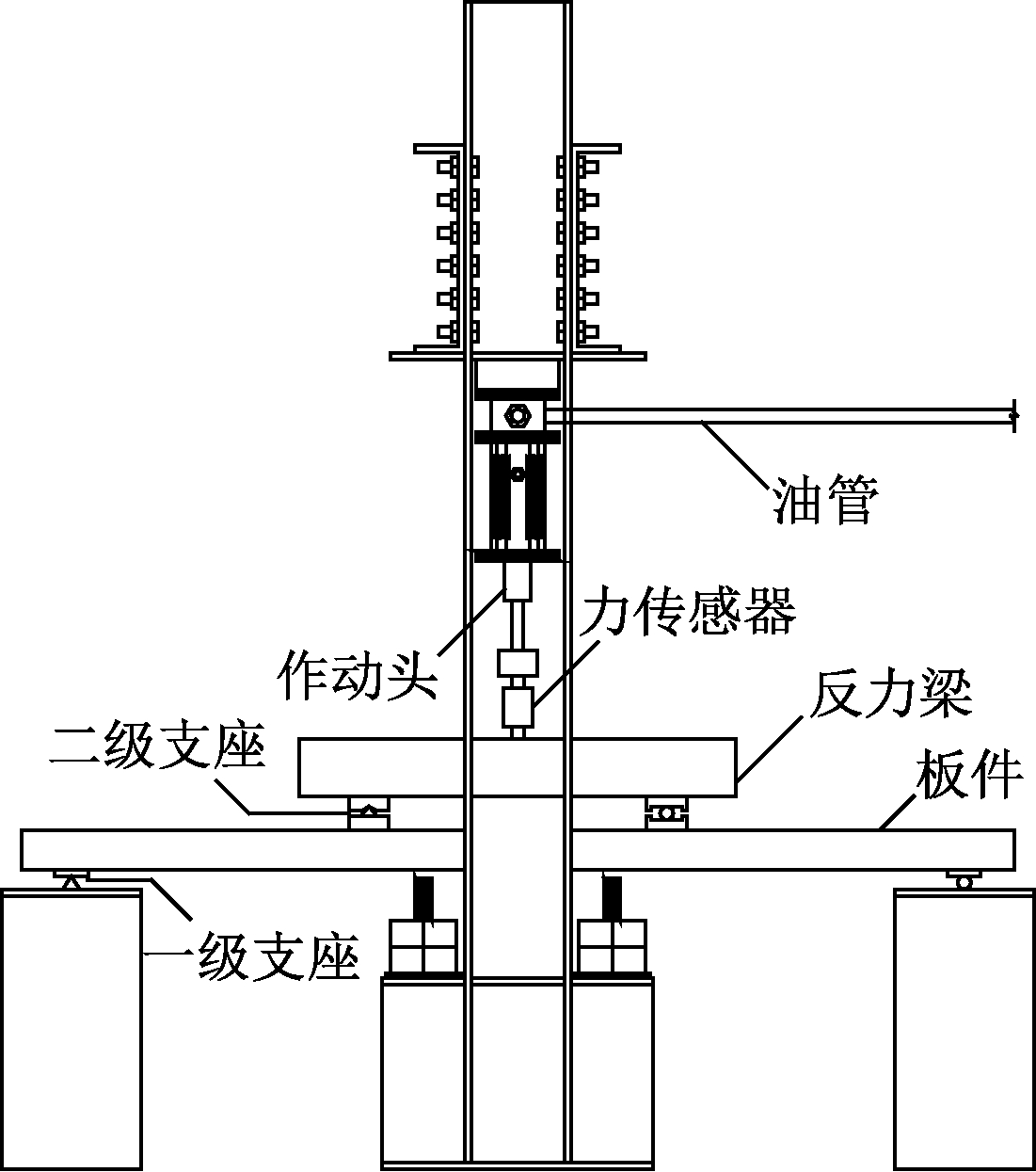
图3 疲劳试验加载装置
Fig.3 Loading set-up for fatigue test
表3 试件疲劳荷载加载参数
Table 3 Parameters of fatigue load on specimens
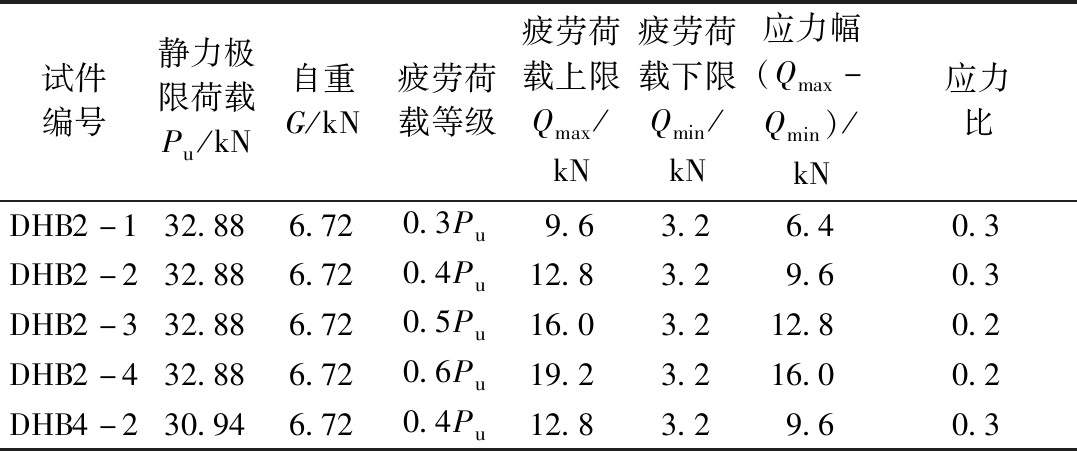
试件编号静力极限荷载Pu/kN自重G/kN疲劳荷载等级疲劳荷载上限Qmax/kN疲劳荷载下限Qmin/kN应力幅(Qmax-Qmin)/kN应力比DHB2-132.886.720.3Pu9.63.26.40.3DHB2-232.886.720.4Pu12.83.29.60.3DHB2-332.886.720.5Pu16.03.212.80.2DHB2-432.886.720.6Pu19.23.216.00.2DHB4-230.946.720.4Pu12.83.29.60.3
注：Pu为预估极限荷载。
a—位移测点及侧面混凝土应变测点；b—板底混凝土应变测点；c—板顶混凝土应变测点；d—预应力筋应变测点。
图4 应变片及位移测点布置
Fig.4 Arrangement of strain gauge and displacement measurement point
2 试验结果及其分析
2.1 破坏形态
由于疲劳加载时超过了荷载上限，导致DHB2-1、DHB2-3分别在疲劳循环次数为5万和30万次出现裂缝，随着疲劳循环加载次数的增加，裂缝基本处于稳定状态，试件端部的预应力锚固良好，当裂缝经过叠合面后并未沿接触面发展，表明随着疲劳循环加载次数的增加，试件弯曲刚度无明显退化。根据200万次疲劳后的静载破坏试验得到的试件裂缝分布规律见图5。根据静载破坏试验得到的裂缝展开不难看出，DHB2-1、DHB2-2、DHB2-3、DHB4-2的裂缝均匀分布在试件的纯弯段内，卸载后试件的残余裂缝宽度较小，这是由于高强预应力使得试件历经疲劳加载后仍表现出较强的裂缝闭合能力。但在不同的疲劳荷载上限情况下，叠合板混凝土疲劳累积损伤与预应力筋松弛随着疲劳荷载上限的增加而增加。由于疲劳荷载上限过大，DHB2-4加载至31.7万次时预应力筋被拉断并且停止试验。
a—DHB2-1；b—DHB2-2；c—DHB2-3；d—DHB2-4；e—DHB4-2。
图5 200万次疲劳循环后试件静载破坏试验裂缝侧面展开
Fig.5 Crack profile on the sides of the specimens under static load failure test after 2 million fatigue cycles
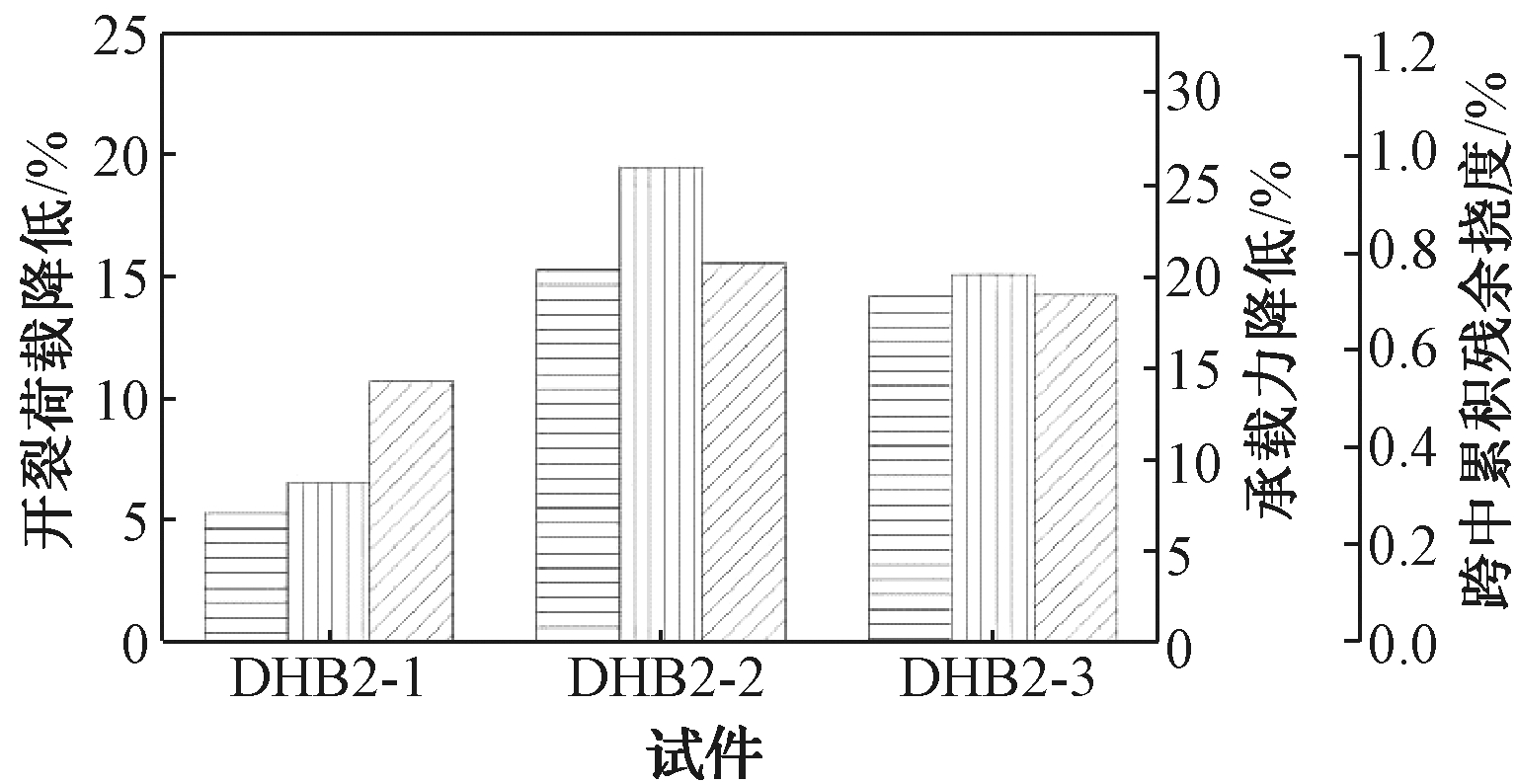
表4与图6对比分析了相同板肋形状下，不同疲劳荷载上限对试件疲劳性能的影响，结果表明：较小的疲劳荷载不会导致试件发生疲劳破坏；对带有裂缝的试件进行疲劳加载，疲劳荷载较小时，对试件的弯曲刚度和疲劳破坏模式影响较小，但当疲劳荷载较大时，试件的疲劳弯曲刚度和承载力显著降低，当疲劳荷载上限超过70%的静载开裂荷载时，会引起预应力筋疲劳断裂，导致试件疲劳破坏。随着疲劳上限的增加，裂缝不会沿着叠合面发展，表明叠合面的存在不会影响叠合板的受力性能。
表4 不同疲劳荷载参数对试件疲劳受力性能的影响
Table 4 Effect of different fatigue load parameters on the fatigue behavior of specimens
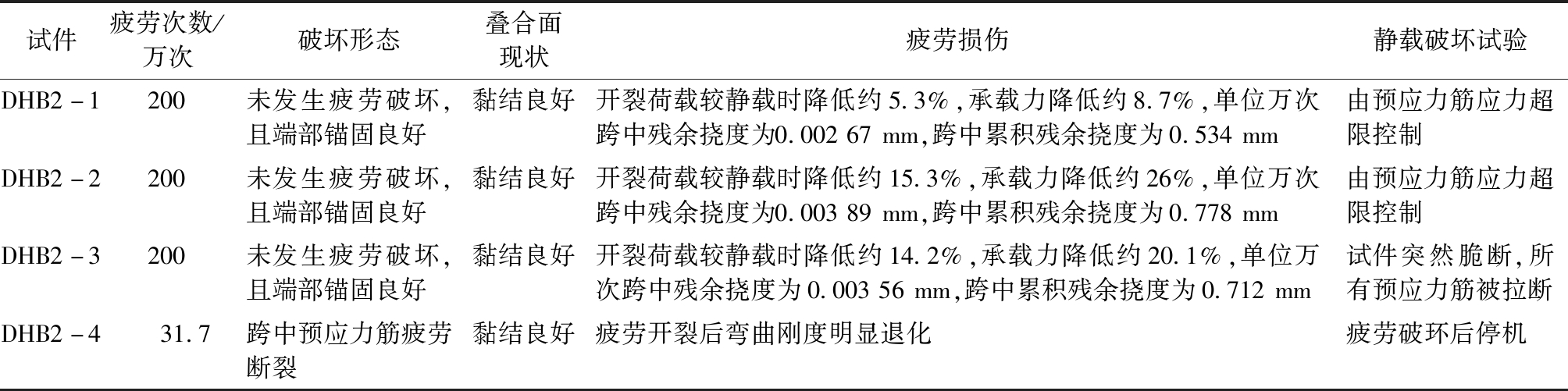
试件疲劳次数/万次破坏形态叠合面现状疲劳损伤静载破坏试验DHB2-1200未发生疲劳破坏,且端部锚固良好黏结良好开裂荷载较静载时降低约5.3%,承载力降低约8.7%,单位万次跨中残余挠度为0.00267mm,跨中累积残余挠度为0.534mm由预应力筋应力超限控制DHB2-2200未发生疲劳破坏,且端部锚固良好黏结良好开裂荷载较静载时降低约15.3%,承载力降低约26%,单位万次跨中残余挠度为0.00389mm,跨中累积残余挠度为0.778mm由预应力筋应力超限控制DHB2-3200未发生疲劳破坏,且端部锚固良好黏结良好开裂荷载较静载时降低约14.2%,承载力降低约20.1%,单位万次跨中残余挠度为0.00356mm,跨中累积残余挠度为0.712mm试件突然脆断,所有预应力筋被拉断DHB2-431.7跨中预应力筋疲劳断裂黏结良好疲劳开裂后弯曲刚度明显退化疲劳破环后停机
开裂荷载降低；
承载力降低；
跨中累积残余挠度。
图6 不同疲劳荷载上限对试件疲劳受力性能影响
Fig.6 Effect of different fatigue loads on fatigue behavior of the specimens
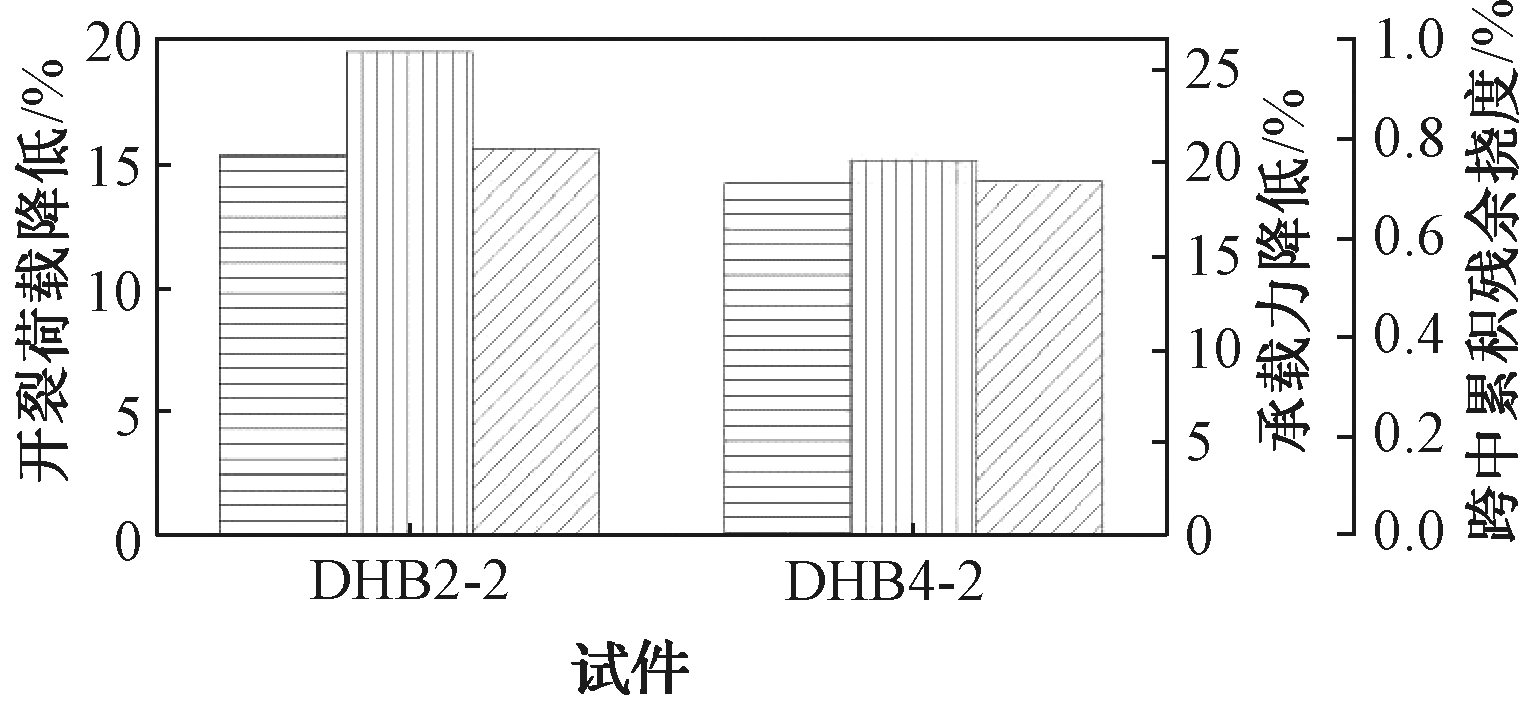
表5和图7对比分析了不同板肋形式对叠合板试件弯曲疲劳性能的影响，结果表明：两种试件均未发生疲劳破坏，疲劳后停机静载破坏试验均由预应力筋应力超限控制，基本表现出相同的破坏形式。经历200万次循环后的疲劳损伤，DHB4-2的开裂荷载降低百分比、承载力降低百分比、单位万次跨中残余挠度、跨中累积残余挠度分别为DHB2-2的92.8%、77.3%、91.5%、91.5%。可见，矩形肋底板叠合板与T形肋底板叠合板的疲劳性能基本相同，改变板肋形式对叠合板的疲劳性能影响不大。
表5 不同板肋形式对试件疲劳受力性能的影响
Table 5 Effect of different slab-rib forms on the fatigue behavior of specimens
试件疲劳次数/万次破坏形态叠合面现状疲劳损伤静载破坏试验DHB2-2200未发生疲劳破坏,且端部锚固良好黏结良好开裂荷载较静载时降低约15.3%,承载力降低约26%,单位万次跨中残余挠度为0.00389mm,跨中累积残余挠度为0.778mm,疲劳弯曲刚度无明显退化由预应力筋应力超限控制DHB4-2200未发生疲劳破坏,且端部锚固良好黏结良好开裂荷载较静载时降低约14.2%,承载力降低约20.1%,单位万次跨中残余挠度为0.00356mm,跨中累积残余挠度为0.712mm,疲劳弯曲刚度无明显退化由预应力筋应力超限控制
开裂荷载降低；承载力降低；跨中累积残余挠度。
图7 不同板肋形状对试件疲劳受力性能影响
Fig.7 Effect of different rib shapes on the fatigue behavior of specimens
2.2 挠度变化曲线
图8为矩形肋底板叠合板经历各次疲劳循环加载后，由静载试验所得跨中荷载-挠度曲线，结果表明：在相同疲劳加载上限条件下，随着疲劳循环加载次数的增加，矩形肋底板叠合板DHB2-1、DHB2-2、DHB2-3、DHB2-4从1万～10万次，各次静载试验跨中荷载-挠度曲线基本重合且斜率变化不大，表明叠合板在经历疲劳循环加载后弯曲刚度无明显退化；在相同疲劳循环加载次数下，随着疲劳加载上限的增加，DHB2-1～4试件发生较为明显的疲劳弯曲刚度退化，同时疲劳损伤也有明显增大。在加载过程中DHB2-1、DHB2-3由于操作失误，疲劳荷载达到疲劳荷载上限导致试件出现非疲劳裂缝，荷载-挠度曲线分别在5万和30万次开始呈抛物线，这是因为疲劳循环加载时非疲劳裂缝使得试件刚度明显被削弱。对比DHB2-2和DHB4-2，随着疲劳加载次数的增加，弯曲刚度没有显著的退化，进一步说明了矩形肋底板叠合板与T形肋底板叠合板的疲劳性能基本相同。
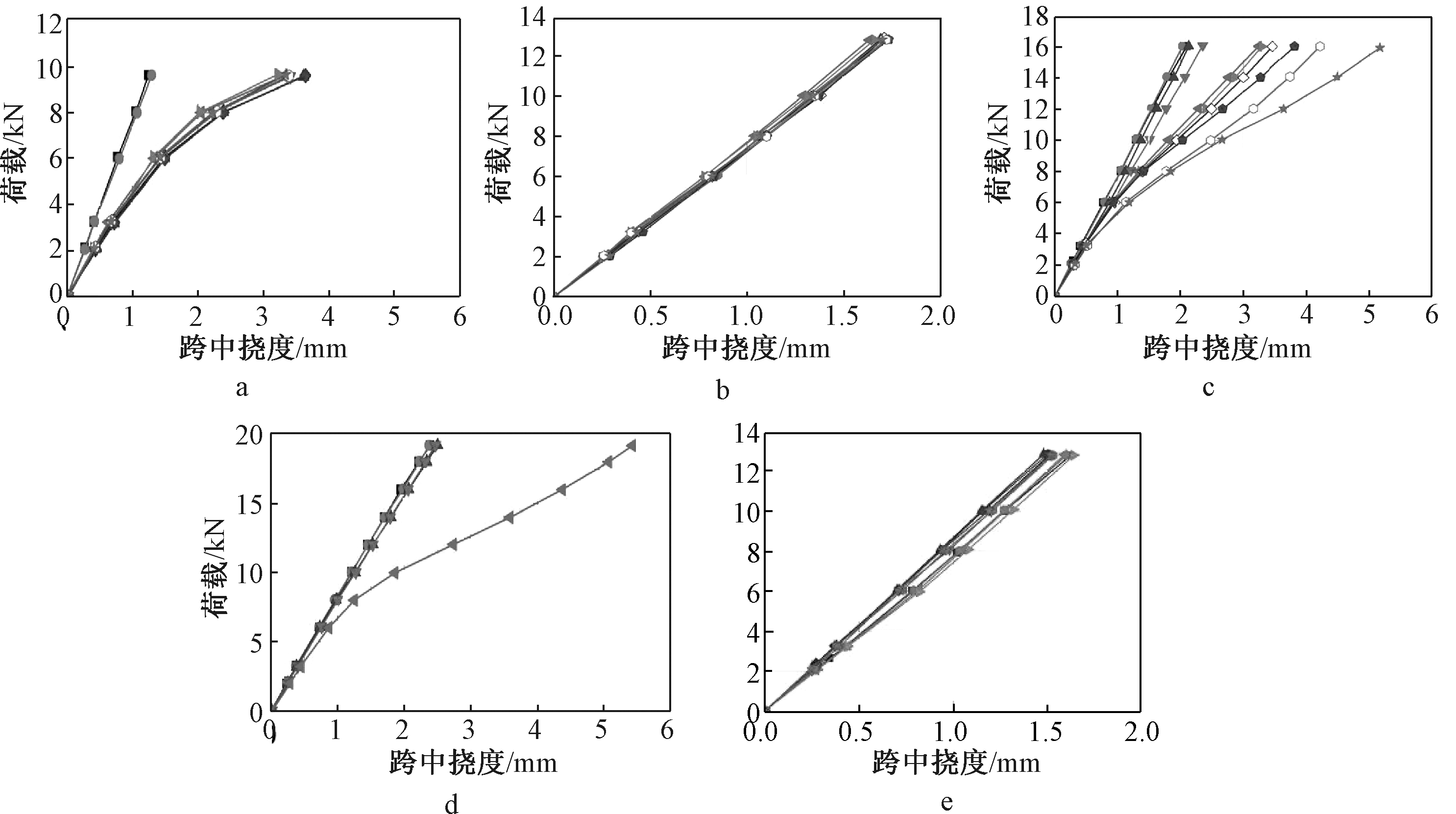
a—DHB2-1；b—DHB2-2；c—DHB2-3；d—DHB2-4；e—DHB4-2。
— 0万次；
— 1万次；
— 5万次；
— 10万次；
— 30万次；
— 50万次；
— 70万次；
— 100万次；
— 150万次；
— 200万次。
图8 试件疲劳循环后荷载-跨中挠度曲线
Fig.8 Load versus mid-span deflection curves of specimens after being subjected to fatighe cycles
图9为T形肋底板叠合板与矩形肋底板叠合板试件跨中累积残余挠度与加载循环次数的关系曲线。试件DHB2-1、DHB2-2、DHB2-3、DHB4-2在200万次疲劳循环后的跨中残余挠度分别为0.534，0.778，2.532，0.712 mm。由于DHB2-4疲劳荷载上限过大，加载至31.7万次试件破坏，没有达到预期的200万次疲劳循环加载，其跨中残余挠度为0.527 mm。图中曲线表明：曲线的斜率随着加载循环次数的增加而增大，表明试件疲劳弯曲刚度都有明显退化，且叠合板试件内部的疲劳累积损伤也在不断发展。当疲劳荷载上限过大甚至会导致试件发生疲劳破坏。通过对比两种不同板肋形式DHB2-4与DHB4-2可知：两者曲线基本呈现相同规律，甚至出现重合，表明相同加载循环次数下跨中残余挠度和最终累积残余挠度基本接近，进一步证明板肋形式对叠合板的疲劳损伤影响较小。
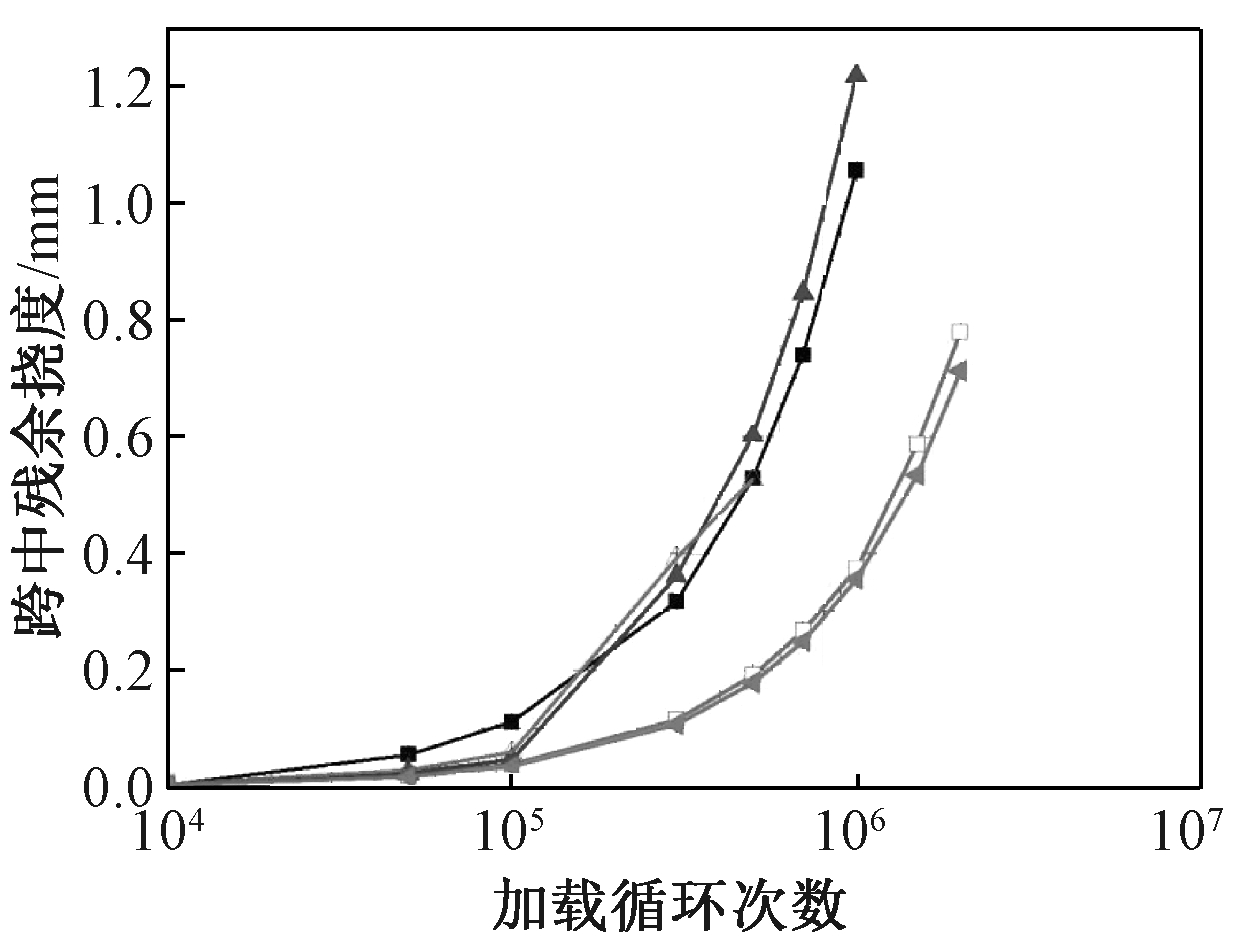
— DHB2-1；
— DHB2-2；
— DHB2-3；
— DHB2-4；
— DHB4-2。
图9 试件跨中累积残余挠度-加载循环次数曲线
Fig.9 Relationship between accumulated residual deflection and loading cycle number in the mid-span of specimens
2.3 荷载-应变关系曲线
图10对比分析了DHB2-2、DHB2-4、DHB4-2的荷载-应变关系曲线，结果表明：DHB2-2与DHB4-2的跨中板顶受压混凝土和受拉预应力筋的应变峰值和谷值基本保持不变，只是在较小的范围内波动。由于疲劳荷载上限的增大，DHB2-4混凝土的压应变和预应力筋的拉应变急剧增加，最后在31.7万次试件疲劳破坏。根据荷载-应变关系曲线可知，应变大小与板肋形状无关，与疲劳加载上限大小成正相关。
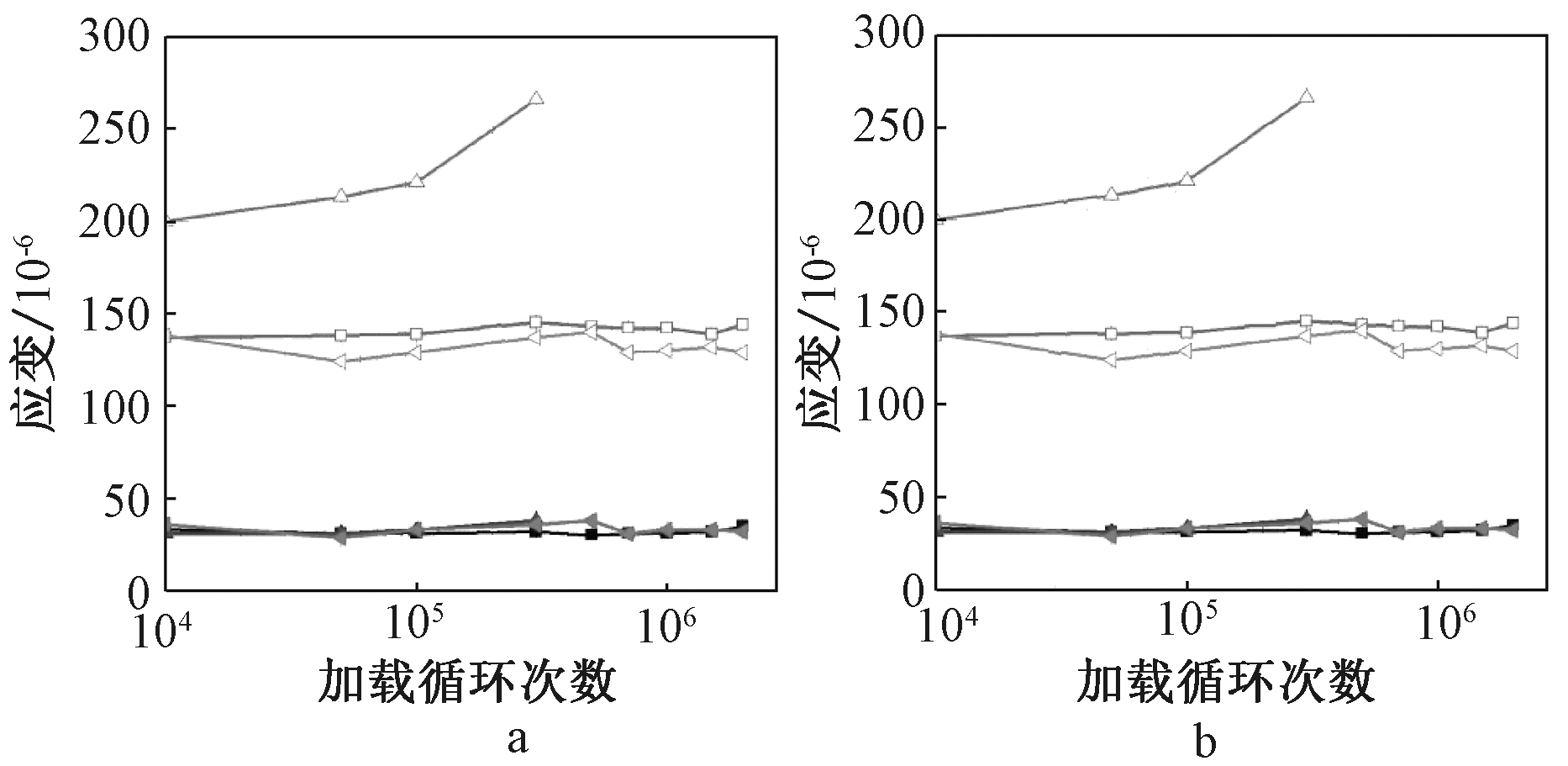
a—试件跨中板顶面混凝土压应变；b—试件跨中板底预应力筋拉应变。— DHB2-2谷值；
— DHB2-2峰值；— DHB2-4谷值；
— DHB2-4峰值；— DHB4-2谷值；
— DHB4-2峰值。
图10 试件跨中应变-加载循环次数曲线
Fig.10 Relationship between mid-span strain and load cycle times of specimens
图11为试件DHB2-2疲劳加载过程中动态应变仪采集的跨中动态应变-时间曲线，预应力筋和混凝土的动态应变变化呈现出相同的规律，即：预应力筋拉应变与混凝土压应变曲线关于X轴对称，且与疲劳荷载产生的脉动正弦曲线参数吻合良好，表明试验过程中采集数据的可靠性。同时跨中受拉区混凝土与预应力筋应变传递同步，且预应力筋动态拉应变被混凝土动态拉应变曲线包裹，说明试件处于弹性工作阶段，整个疲劳过程中没有出现疲劳裂缝。最后进行静载破坏试验，叠合板跨中混凝土开裂前沿截面高度分布的应变曲线见图12。由图12可知：混凝土开裂前沿截面高度应变分布呈直线，说明经过疲劳加载后试件仍满足平截面假定，其他试件开裂前基本呈现出与DHB2-2相同的应变分布特征，限于篇幅不一一介绍。
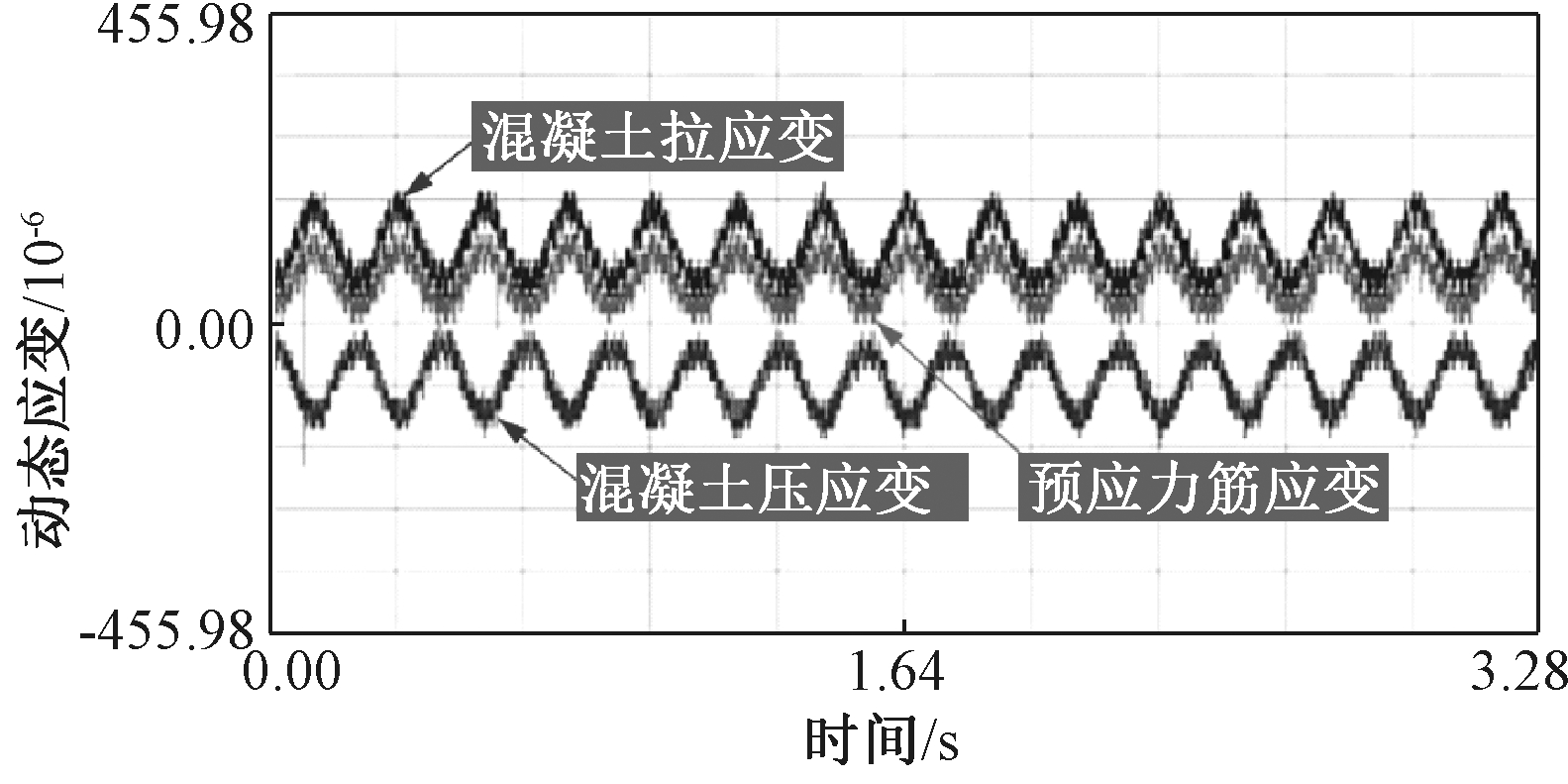
图11 跨中动态应变采集曲线
Fig.11 Mid-span dynamic strain acquisition curves
— 2.04 kN;— 3.22 kN;— 6.02 kN;— 8.01 kN;— 10.03 kN;— 12.83 kN;— 14.02 kN;— 16.00 kN;— 17.99 kN;— 19.98 kN。
图12 开裂前沿截面高度混凝土应变分布
Fig.12 Strain distribution of concrete along section heigh before cracking
2.4 疲劳荷载对残余承载力的影响
经历200万次疲劳循环加载后进行静载破坏试验，DHB2-1、DHB2-2、DHB2-3、DHB4-2的残余承载力分别为25.21，24.29，25.10，24.71 kN，试件DHB2-4加载至31.7万次时，跨中预应力筋突然疲劳断裂，试件停止加载。静载破坏试验中破坏形态都是由于预应力筋应力超限控制。较小的疲劳荷载上限对试件内部的累积疲劳损伤影响较大，会随着加载循环次数的增加有所增大。当疲劳荷载上限大于试件静力开裂荷载时，容易出现疲劳破坏。DHB2-2与DHB4-2区别在于采用了不同板肋形式，经历相同的疲劳荷载幅值及疲劳循环加载次数后，残余承载力十分接近，并且在静载试验中表现出相同的破坏形式，进一步表明两种不同带肋形式对叠合板的疲劳性能影响较小。
3 弯曲疲劳验算
3.1 基本假定
通过总结T形和矩形两种带肋底板混凝土叠合板的疲劳破坏模式及疲劳损伤可知，两种不同带肋形式的混凝土叠合板试件表现出相同的疲劳性能，并且预制带肋底板混凝土叠合板在正常使用条件下一般按不出现裂缝的构件进行设计，为了简化其正截面弯曲疲劳应力验算，引入以下假定：1)平截面假定；2)混凝土法向应力图形取为三角形；3)采用换算截面计算。
3.2 验算方法
预应力混凝土构件进行截面疲劳强度验算时，一般按弹性受力情况考虑，本文以矩形肋底板混凝土叠合板疲劳计算为例，根据上述基本假定并参考文献[17]的方法，计算预应力筋和混凝土在疲劳荷载作用下的应力，然后各自与试件加载前的应力叠加。可得相应组合作用下混凝土边缘纤维处的拉、压应力σctf与σccf。图13为叠合板在不同荷载下产生的应力示意。
(1a)
(1b)
式中：σpc、σqc、σgc分别为预应力、疲劳活载标准值、疲劳恒载标准值在混凝土受拉区边缘纤维处产生的混凝土法向预压应力；σpt、σqt、σgt分别为以上荷载混凝土受压区边缘纤维处产生的混凝土法向预拉应力；MQf、MGf为疲劳活载、恒载标准值在计算截面产生的弯矩；I0为截面换算惯性矩。
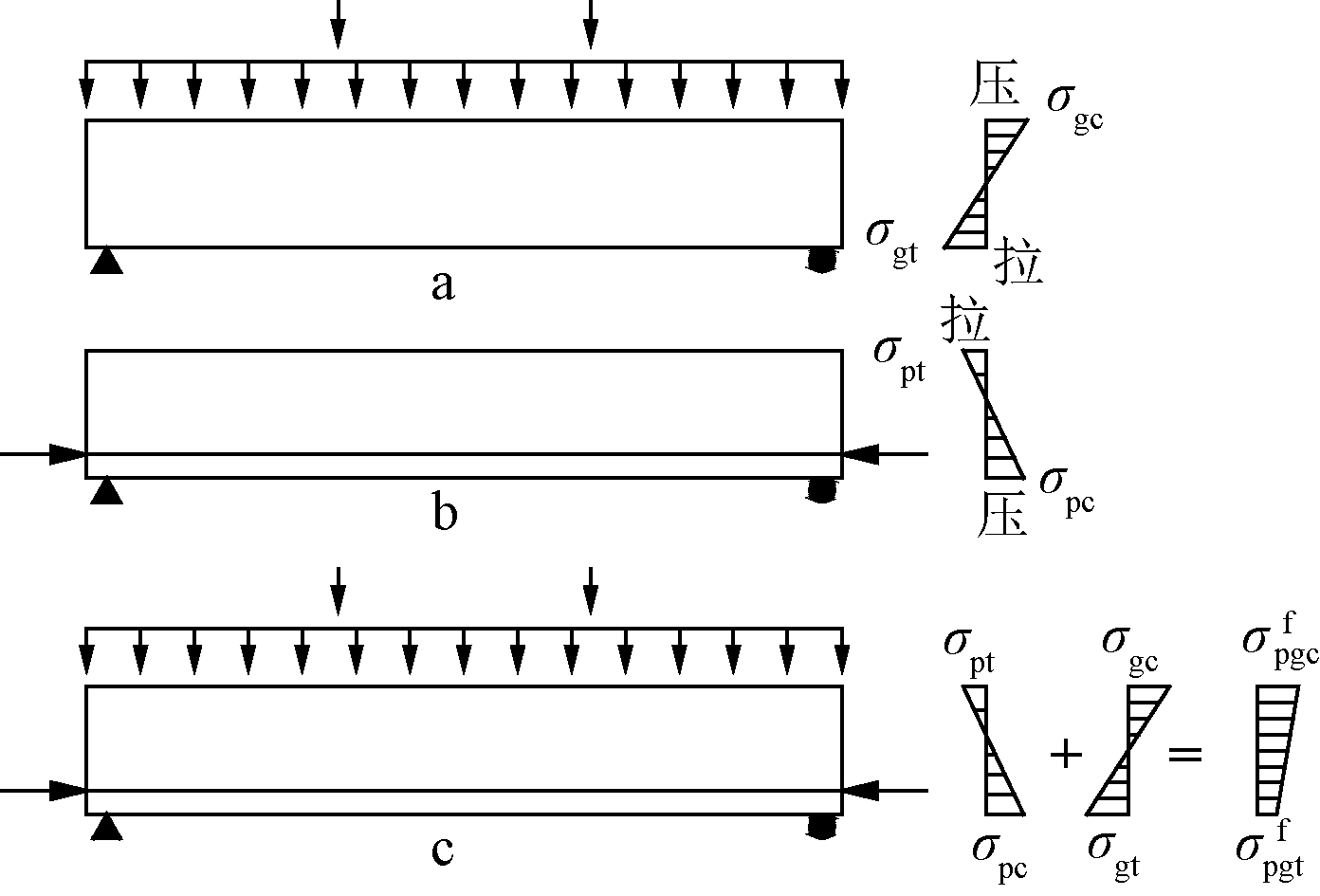
a—疲劳恒载作用；b—预应力作用；c—两种应力状态叠加。
图13 叠合板在不同荷载作用下产生的应力示意
Fig.13 Stress diagram of composite slabs under different loads
疲劳验算时，一次应力循环中受拉区预应力筋的最小应力σpf,min、最大应力σpf,max及应力幅Δσpf分别为：
(2a)
(2b)
Δσpf=σpf,max-σpf,min
(2c)
式中：αpE为预应力筋、混凝土两种不同材料的弹性模量之比；σpe为受拉预应力筋的有效预应力；Mf,min、Mf,max分别为疲劳恒活荷载标准值在计算截面产生的最小、最大弯矩；y0p为受拉区预应力筋截面到换算截面的重心距离。
采用上述方法进行疲劳验算，应力应符合下列要求。
边缘纤维的混凝土应力：
压应力时
σccf,max≤fcf
(3a)
拉应力时
σctf,max≤ftf
(3b)
受拉区预应力筋的应力幅值：
Δσpf≤Δfpyf
(3c)
式中：fcf、ftf、Δfpyf分别为混凝土轴心抗压、抗拉疲劳强度设计值、预应力筋疲劳应力幅限值。
本文对试件DHB2-2进行疲劳验算。根据相关已知材性和几何参数，可知：I0=6.6×107 mm4，y1=58.1 mm，σpc=4.6 MPa，σpe=649.5 MPa，αpE=40.6，MGf=1.28 kN·m，MQf,min=1.44 kN·m，MQf,max=5.76 kN·m。
1)板底混凝土边缘纤维的应力验算。根据式(1)、式(2)，可得：σctf=1.59 MPa，σccf=-2.2 MPa，ftf=γp×ft=0.9×1.92=1.73 MPa(γp为疲劳受拉强度修正系数，查GB 50010—2010《混凝土结构设计规范》，可取0.9)，则：σctf=1.59 MPa<ftf=1.73 MPa。
计算表明板底受拉区边缘混凝土最大受拉应力满足式(3b)条件。
2)受拉区预应力筋的应力幅值验算。根据式(3a)、式(3b)，可得：σpf,min=659.5 MPa，σpf,max=675.2 MPa。所以，Δσpf=15.7 MPa,ρpf=σpf,min/σpf,max=659.5/675.2>0.9。
根据GB 50010—2010可不作预应力筋疲劳验算。
4 结束语
1)在相同的疲劳加载上限条件下，预制T形肋底板混凝土叠合板试件与预制矩形肋底板混凝土叠合板试件具有相同的疲劳性能，每次疲劳加载后的静载试验所得荷载-跨中挠度曲线、荷载-应变关系曲线、最终累积残余承载力基本接近。
2)叠合板试件在疲劳加载过程中，较小的疲劳荷载不会导致试件发生疲劳破坏；对带有裂缝的试件进行疲劳加载，疲劳荷载较小时，对试件的弯曲刚度和疲劳破坏模式影响较小，但当疲劳荷载较大时，试件的疲劳弯曲刚度和承载力显著降低，当疲劳荷载上限超过70%的静载开裂荷载时，会引起预应力筋疲劳断裂，导致试件疲劳破坏。
3)叠合板试件经历200万次疲劳循环加载后进行静载破坏试验，混凝土开裂前沿截面高度应变分布曲线基本呈直线，表明试件经历疲劳循环加载后平截面假定仍成立。
4)叠合板试件按一般不允许出现裂缝构件进行正截面疲劳强度验算时，应计算受拉区预应力筋的应力幅值、受压区与受拉区混凝土边缘纤维的应力。
[1] 周绪红，吴方伯，张敬书，等.新型单向预应力双向配筋混凝土叠合楼盖在震后重建中的应用[C]//2008年汶川地震建筑震害分析与重建研讨会论文集.北京：2008：448-454.
[2] 周绪红，吴方伯，刘占科，等.新型装配整体式房屋结构体系[C]//2008年汶川地震建筑震害分析与重建研讨会论文集.北京：2008：455-462.
[3] 姜忻良，岳建伟.陶粒叠合层叠合板的承载能力研究[J].四川大学学报(工程科学版)，2006，38(6):6-12.
[4] 沈春祥.预应力混凝土双向叠合板试验研究[D].天津：天津大学，2005：5-20.
[5] 刘汉朝，蒋青青.倒“T”形叠合简支板的试验研究[J].中南大学学报(自然科学版)，2004，35(1):147-150.
[6] 安海玉，贾莉，丁永君.预应力混凝土双向叠合板力学性能试验研究及应用[J].建筑结构，2012，42(12):90-93.
[7] 曾垂军，吴方伯，刘锡军，等.新型叠合结构体系的设计与施工[J].建筑科学，2006，22(4):67-71.
[8] 吴方伯，黄海林，陈伟，等.预制预应力带肋底板-混凝土叠合板双向受力效应理论研究[J].工业建筑，2010，40(11)：55-58.
[9] 黄海林，李金华，曾垂军，等.预制带肋底板混凝土双向叠合板等效各向同性板的弹性计算方法[J].应用力学学报，2018，35(3)：624-630，694.
[10] 黄海林，李金华，曾垂军，等.均布荷载作用下四边简支预制带肋底板混凝土双向叠合板的简化弹性计算方法[J].湖南科技大学学报(自然科学版)，2016，31(4)：46-51.
[11] 黄海林，李金华，曾垂军，等.均布荷载作用下一边固支三边简支预制矩形肋底板混凝土双向叠合板的简化弹性计算方法[J].建筑科学与工程学报，2017，34(1)：58-67.
[12] 吴方伯，黄海林，陈伟，等.预制带肋底板混凝土双向叠合板实用弹性计算方法[J].建筑结构，2012，42(4)：99-103.
[13] HUANG H L,LI J H,ZENG C J,et al.Simplified Elastic Design Method Using Equivalent Span Ratio for Two-Way Concrete Composite Slabs with Precast Ribbed Panels[J].Structural Concrete,2019，20(1)：213-224.
[14] 吴方伯，黄海林，陈伟，等.预制带肋底板混凝土双向叠合板极限承载力[J].土木建筑与环境工程，2011，33(5)：34-40.
[15] 赵顺波.钢筋混凝土板正截面疲劳性能试验研究[J].应用基础与工程科学学报，1999，7(3)：289-297.
[16] 黄海林.预制带肋底板混凝土叠合楼板受力性能及设计方法[D].长沙：湖南大学，2013.
[17] 黄海林，吴方伯，祝明桥，等.预制T形肋底板混凝土叠合板弯曲疲劳性能试验研究[J].建筑结构学报，2016,37(5)：233-241.