超高性能混凝土(UHPC)具有较高的强度、优异的耐久性和体积稳定性,是性能优越的建筑材料[1];钢筋桁架混凝土叠合板作为装配整体式楼板的一种新形式,保持了装配式构件施工的便捷性,提升了楼板的整体刚度,同时在抗弯和抗剪承载力等方面具有显著的优点。国内外专家学者对叠合结构已经进行了大量试验研究与理论分析,20世纪70年代法国和德意志联邦共和国在混凝土叠合层间配置抗剪钢筋,制作混凝土叠合楼盖,并颁布了设计、施工规程;陈科分析了叠合构件的承载力、整体性和抗裂性能,证明了其较高的承载力和刚度[2];叶献国通过静力加载试验,对比现浇混凝土整体板和在跨中拼接的混凝土叠合板的受弯性能及承载力机理,提出了改进叠合式楼板设计的建议[3];刘轶通过4块钢桁架混凝土叠合板、两块钢桁架混凝土整浇板在施工、养护、使用阶段受弯力学性能的试验,结合有限元分析,提出预制构件短期刚度的计算式[4]。研究表明:将超高性能混凝土UHPC运用于叠合构件,可充分发挥两者的优势。廖莎等对3根活性粉末混凝土无黏结预应力叠合梁受弯性能进行了研究,表明:UHPC 叠合梁的截面应变符合平截面假定,还建立了试验梁的开裂弯矩和刚度计算式[5];聂建国等将高强混凝土和钢筋桁架结合在一起形成的高强混凝土叠合板[6]是一种具有较高综合效益的新型承重体系,开展这方面的试验研究在实际工程领域具有广阔的前景。但是有关高性能混凝土钢筋桁架叠合构件的研究目前还比较少,本研究以1块UHPC整浇板和2块钢筋桁架UHPC叠合板为对象,进行了三分点加载试验,探讨钢筋桁架UHPC叠合板的抗弯性能,并建立钢筋桁架UHPC简支叠合板的正截面承载力简化计算模型,为实际工程应用提供参考。
1 试验概况
1.1 试件制作
设计3块试验板,分别为1块UHPC整浇板和2块钢筋桁架UHPC叠合板。3块板均为3 020 mm×600 mm×130 mm,净跨长2 700 mm,整浇板一次性浇筑完成,板底配筋由纵筋和分布筋构成;叠合板分两次浇筑,先浇筑70 mm底板,养护完成达到设计强度后,再浇叠合层60 mm。钢筋桁架UHPC叠合板除设置与整浇板一样的纵筋和分布筋外,还配有纵向钢筋桁架。其配筋与尺寸如表1、图1所示。
表1 试验板详细配置情况
Table 1 Detailed configuration of test boards

试件编号试件宽度/mm试件高度/mm底板纵筋分布筋抗剪键加载方式DB-160070+60412+2108@200钢筋桁架反向DB-260070+60412+2108@200钢筋桁架正向ZB-36001305128@200无反向
1.2 原材料力学性能指标
UHPC力学性能指标严格按照GB/T 50152—2012《普通混凝土结构试验方法标准》[7]和国家标准GB/T 31387—2015《活性粉末混凝土》[8]进行测试,试块与试验板由同一批材料浇筑和养护,配合比见表2,其实测结果均值见表3。
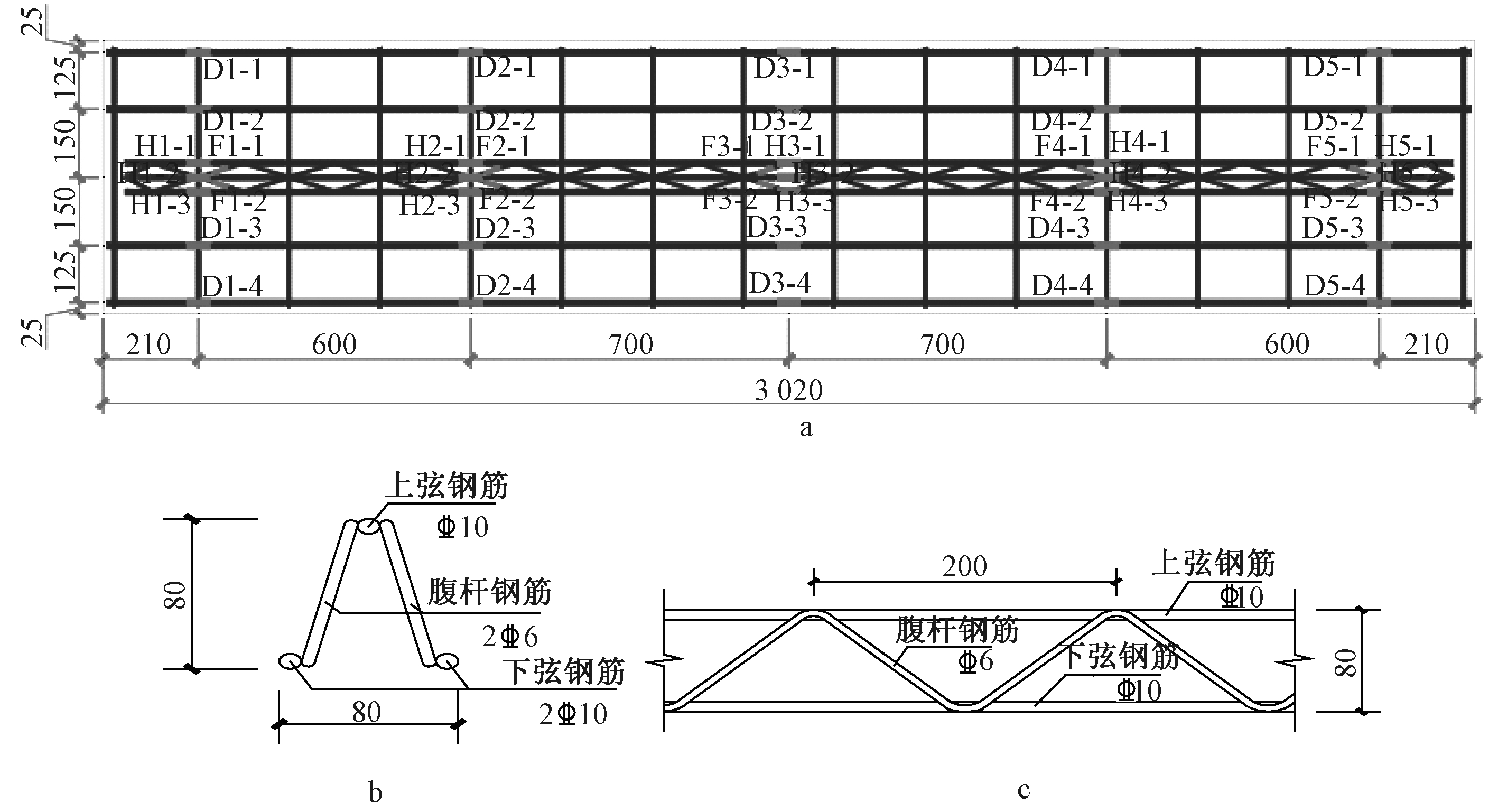
a—板配筋及测点;b—钢筋桁架剖面;c—钢筋桁架立面。
图1 叠合板配筋及钢筋桁架详图
Fig.1 Details composite slab reinforcement and steel truss
表2 UHPC配合比
Table 2 Mix proportion of UHPC kg

水泥石英砂粗砂中砂细砂钢纤维硅灰减水剂水10.20.80.20.020.30.020.23
HRB400级钢筋的力学指标严格参考GB/T 228.1—2010《金属材料 拉伸试验 第1部分:室温试验方法》进行实测,所测钢筋与试验板所用的钢筋为同一批材料,每种钢筋取3根样本做材性试验。
表3 UHPC材料性能
Table 3 Material properties of UHPC MPa
focufocfoccfotsfof135.71119.37120.628.3625.38
注:![]() 为混凝土立方体抗压强度实测值;
为混凝土立方体抗压强度实测值;![]() 为混凝土棱柱体抗压强度实测值;
为混凝土棱柱体抗压强度实测值;![]() 为圆柱体试件抗压强度实测值;
为圆柱体试件抗压强度实测值;![]() 为劈裂抗拉强度实测值;
为劈裂抗拉强度实测值;![]() 为抗折强度实测值。
为抗折强度实测值。
1.3 试验方法
根据GB/T 50152—2012[7]采用两个集中力按三分点加载。为便于观察试验板受拉区裂缝,DB-1与ZB-3采用反向加载,DB-2采用正向加载与反向加载板进行对比修正,其中反向加载的分配梁刚度必须足够大,试验加载装置由支座、试验构件、分配梁、千斤顶和反力架组成,现场加载情况如图2所示。

a—反向加载照片;b—正向加载照片。
图2 试验加载照片
Fig.2 Photos of loading test
2 试验现象及分析
2.1 试验现象描述
根据试验现象将板的加载过程分为五个阶段:开裂、侧裂缝到达叠合面、板底裂缝0.3 mm、破坏(板底裂缝1.5 mm)、极限状态(荷载无法施加)。试验板在各阶段施加的荷载P、跨中弯矩M、挠度af、裂缝宽度ω如表4所示。
由于试验板和分配梁的自重,试验板存在初始挠度,正向加载板DB-2的挠度随着荷载的增加继续增长,在跨中、加载点附近和板侧不断产生新的裂缝,少数裂缝贯穿板底。而反向加载板DB-1和DB-3必须首先抵消自重产生的挠度,然后随荷载的增加反拱增加。叠合板DB-1和DB-2的板侧裂缝到达叠合面后均发生滞留,在一定时间内并未继续向上发展,同时板底几乎不产生新裂缝,只是已有裂缝持续延伸、分叉、交汇和贯穿板底。三块试验板的最大裂缝宽度达到0.3 mm左右时,可清晰地听到钢纤维被拔出的声音,临近破坏时,试验板的挠度和裂缝宽度急速增长,板顶混凝土被压碎,并可明显看到裂缝之间的钢纤维和纵筋,各试验板的裂缝及破坏情况如图3所示。
表4 试验板各阶段试验数据
Table 4 Test data of test slabs at each stage

阶段DB-1(反)DB-2(正)ZB-3(反)P/kNM/(kN·m)af/mmω/mmP/kNM/(kN·m)af/mmω/mmP/kNM/(kN·m)af/mmω/mm开裂8.111.71.304.57.81.508.111.71.50叠合面55.935.616.00.2543.127.213.40.170.3mm65.940.619.80.3260.936.022.70.3250.432.918.50.30破坏77.746.532.81.5472.741.937.21.4059.137.224.01.37极限80.948.140.773.642.452.461.438.426.5
2.2 试验现象分析
将3块试验板受荷过程的裂缝开展及破坏情况进行分析归纳,其数据汇总于表5。
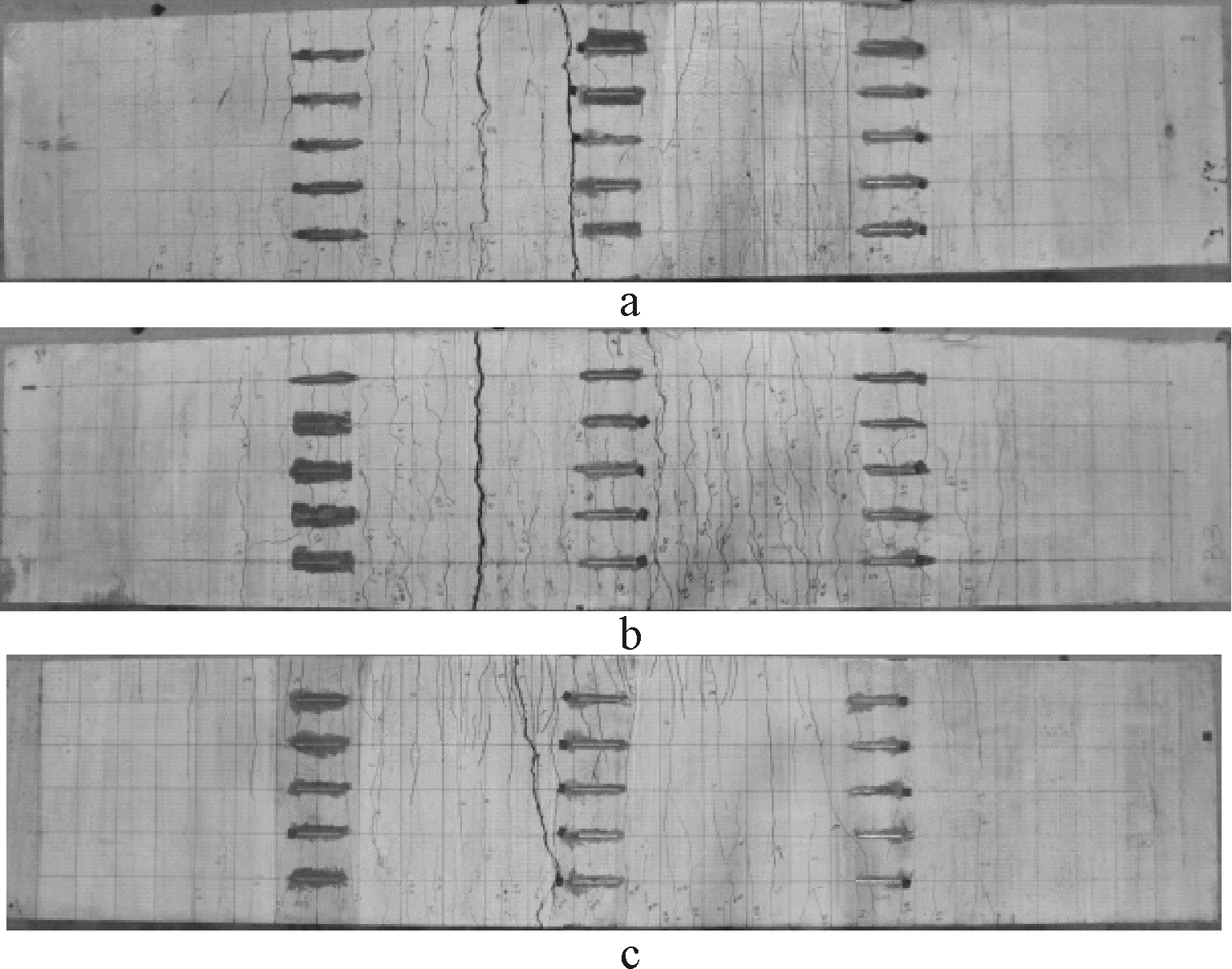
a—DB-1;b—DB-2;c—ZB-3。
图3 试验板裂缝及破坏情况
Fig.3 Cracks and failure mode of test slabs
表5 试验板各阶段试验数据对比
Table 5 Comparison of test data of test slabs at each stage %

阶段DB-1(反)DB-2(正)ZB-3(反)加载方式比较整浇与叠合比较M1i/M1uaf1i/af1uM2i/M2uaf2i/af2uM3i/M3uaf3i/af3uM2i/M1iaf2i/af1iM3i/M1iaf3i/af1i开裂24318330667115100115叠合面7439642676840.3mm844985438670891158193破坏978199719791901138073极限100100100100100100881298065
注:M1i、af1i表示试验板DB-1各阶段的跨中弯矩和挠度;M1u、af1u表示试验板DB-1承载力极限状态下的跨中弯矩和挠度。其余参数含义以此类推。
比对叠合板DB-1和DB-2的数据可以发现:正向加载板DB-2各阶段弯矩、挠度和极限状态下弯矩、挠度的百分比值低于反向加载的DB-1,这是因为DB-1为反向加载,需要首先抵消试验板及分配梁自重的受荷效应,荷载应力相对滞后,经验算可知考虑自重影响后,两块板在各阶段的承载力、裂缝开展情况与挠度都比较接近,说明加载方式对板的承载力和挠度影响不大,DB-1的试验结果可信,以下有关叠合板与整浇板的对比分析在同为反向加载的DB-1和ZB-3中展开。
对比分析表4和表5中DB-1和ZB-3的数据可以发现:在开裂阶段,叠合板与整浇板的开裂荷载均为8.1 kN左右,整浇板挠度1.5 mm稍大于叠合板1.3 mm,因为开裂前试验板主要由UHPC承受荷载,钢筋桁架并未受力,但是却可以提高板的整体刚度。裂缝开展到0.3 mm直至破坏,钢筋桁架已经发挥作用,叠合板的承载力为65.9 kN明显高于整浇板的50.4 kN。ZB-3的承载力和挠度在各阶段占其极限值的百分比均略高于DB-1,可以推断整浇板的整体性还是优于叠合板,UHPC叠合板仍然存在一定的应力滞后现象。
2.3 平截面假定
为了验证钢筋桁架UHPC叠合板在荷载作用下是否符合平截面假定,在试验板侧的纯弯段跨中位置沿高度均匀布置5枚应变片,试验板的开裂荷载较小,DB-1靠近板底的部分应变片在试验早期被破坏未采集到,3块板板侧的应变分布如图4所示。
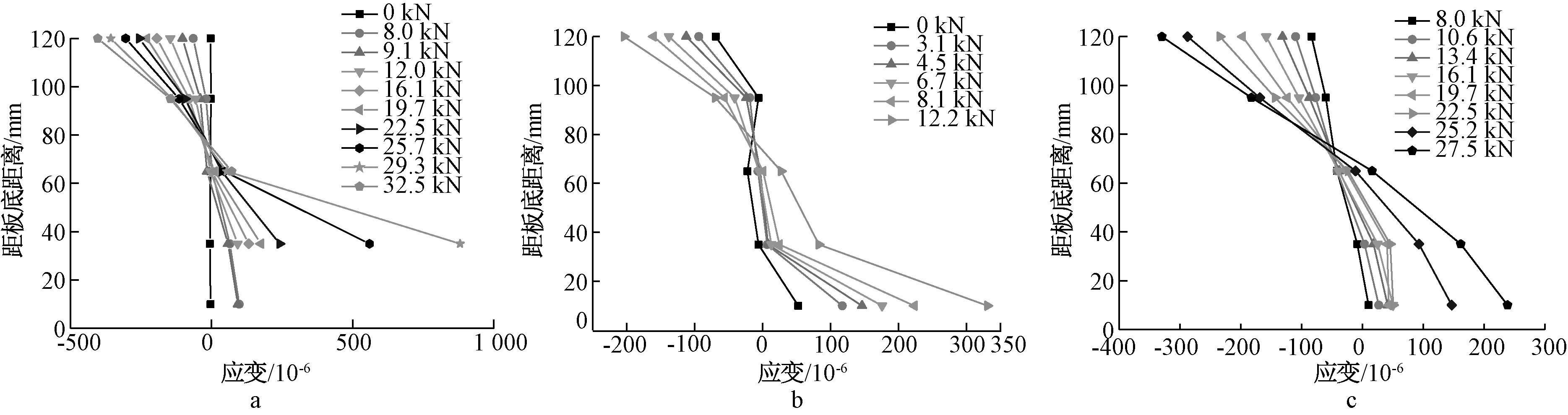
a—DB-1;b—DB-2;c—ZB-3。
图4 试验板跨中正截面混凝土应变分布
Fig.4 Strain distribution of normal cross-section concrete in mid-span of test slabs
试验板的纯弯段只受弯矩作用,截面上UHPC的应变基本呈直线分布,由图4可以看出,DB-1和ZB-3的应变分布情况基本符合平截面假定,DB-2的应变分布有点异常,距离板底35 mm处的应变数据出现小幅偏离,这可能是由于先浇部分板自重产生的应力超前现象,但截面应变仍然基本保持平面。3块板中性轴位置均处于距离板底70~80 mm处,随着荷载的增加,板底产生裂缝并向上开展,靠近板底的应变值不断增大,中性轴位置随之上移,只是其上升幅度比较小。
2.4 板侧面混凝土应变
为探究叠合面上下UHPC的应变变化情况,在试验板距支座500 mm处的叠合面处,沿预制和后浇部分的水平接缝上下分别布置应变片LD与LY,再在垂直于叠合面的接缝处布置应变片(LT),如图5所示。
图5 试验板侧面应变片布置
Fig.5 Arrangement of strain gauges of test slab sides
在试验过程中,DB-1、DB-2板侧的应变片始终完好,说明测点位置的变形较小,不足以使应变片损坏,且没有超过应变片的量程。
将DB-1、DB-2板侧的荷载-混凝土应变曲线绘制于图6,图6a中,DB-1未破坏之前,各测点的应变波动范围不大,测点上下波动不超过±100×10-6,但达到极限荷载后,LY的应变突增,而LD应变波动不大。说明受荷初期测点位置板叠合面接缝的连接较好,得益于钢筋桁架优异的抗剪作用和新旧UHPC结合面良好的黏结性能,有效降低了叠合板的二次受力效应,但临近破坏时,后浇层还是存在一定的应变滞后现象。图6b中,DB-2除LT测点受压外,其余测点均处于受拉状态,并且各点的荷载-应变曲线比较一致,说明测点处叠合面上下层整体性良好;LT测点数据异常,可能是由于应变片粘贴的位置偏差,且LT在加载点附近,靠近最大裂缝一侧,受压区的应力相对另一端更大。
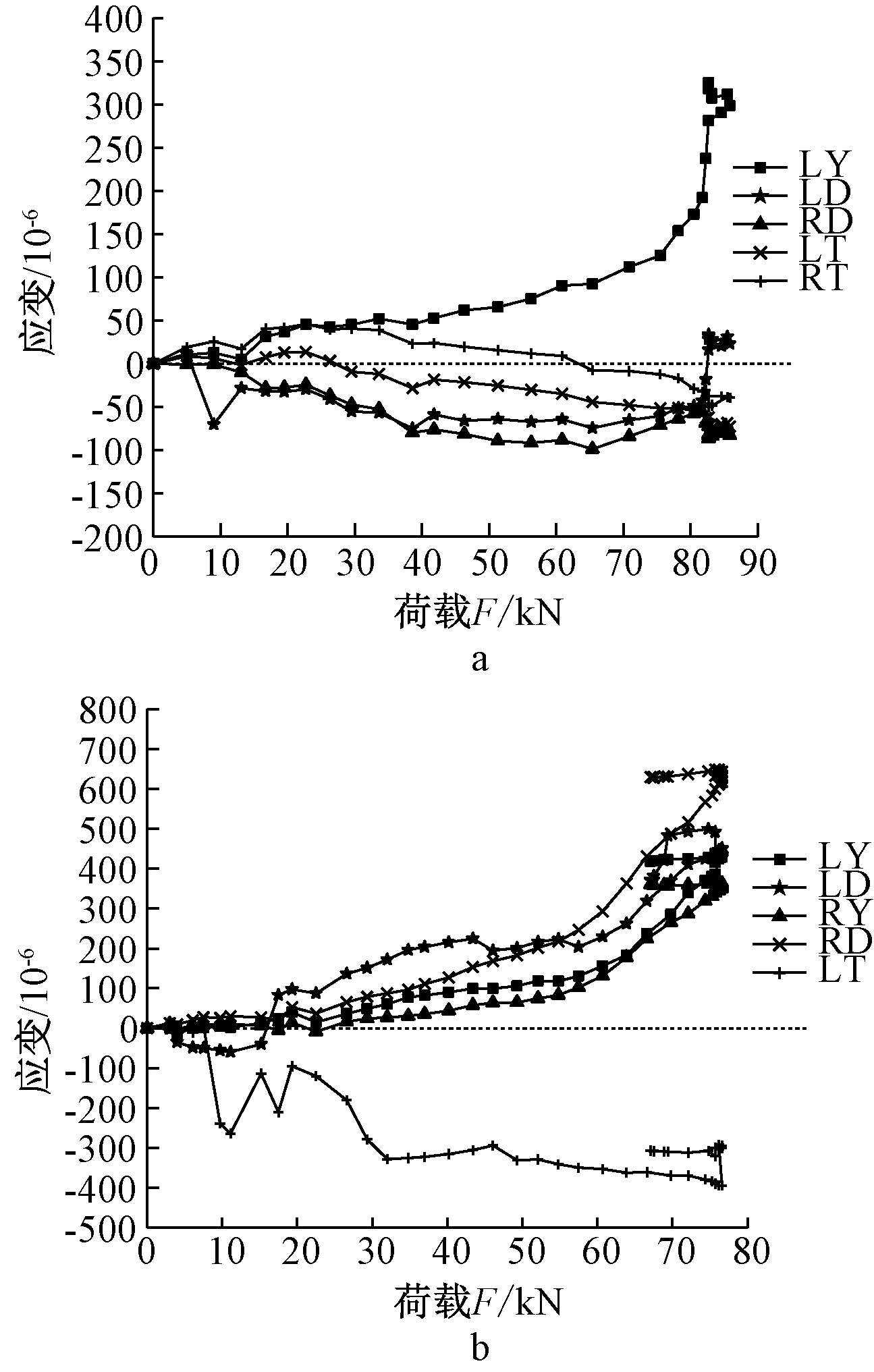
a—DB-1;b—DB-2。
图6 试验板侧面荷载-混凝土应变曲线
Fig.6 Load-concrete strain curves of test slab sides
![]() — F1-1;
— F1-1;![]() — F1-2;
— F1-2;![]() — F2-1;
— F2-1;![]() — F2-2;
— F2-2;![]() — F3-1;
— F3-1;![]() — F3-2;
— F3-2;![]() — F4-1;
— F4-1;![]() — F4-2;
— F4-2;![]() — F5-1。
— F5-1。
图7 DB-1桁架腹杆荷载-应变曲线
Fig.7 Load-strain curves of truss web member of truss DB-1
2.5 桁架腹杆荷载-应变
叠合板钢筋桁架腹杆的内力往往受到剪力影响而变得复杂,文献[9]对现浇钢筋桁架混凝土楼板中的桁架腹筋进行了试验测定和有限元模拟,其两个测点的数值显示一侧受压一侧受拉,基本大小相等符号相反,认为可以假定腹杆为桁架二力杆。在本试验中,穿过叠合面的腹杆承担抗剪键作用。从图7中DB-1的桁架腹杆荷载-应变曲线中可以发现:DB-1桁架腹杆的应变随荷载增大而增大,且跨中测点F3的数值最大,两侧支座处测点F1和F5的较小,与试验板的受力情况比较一致。钢筋桁架可以连接上、下弦杆,传递叠合面剪力,使得叠合层与预制层的连接更为可靠,而且还能够提高板的刚度,承担部分受弯承载力。
2.6 二次受力分析
文献[10]指出:普通混凝土叠合受弯构件,其预制部分高度小于叠合后的截面总高度,与一次成型受弯构件相比,存在受拉钢筋“应力超前”,后浇混凝土“受压应变滞后”现象和“荷载预应力”。前述通过试验板有关平截面假定及叠合层上下应变的分析,表明由于预制部分的自重作用形成一次受力,预制板存在一定高度的受压区,后浇混凝土浇筑完成并加载后,整浇层的混凝土应变有所滞后。
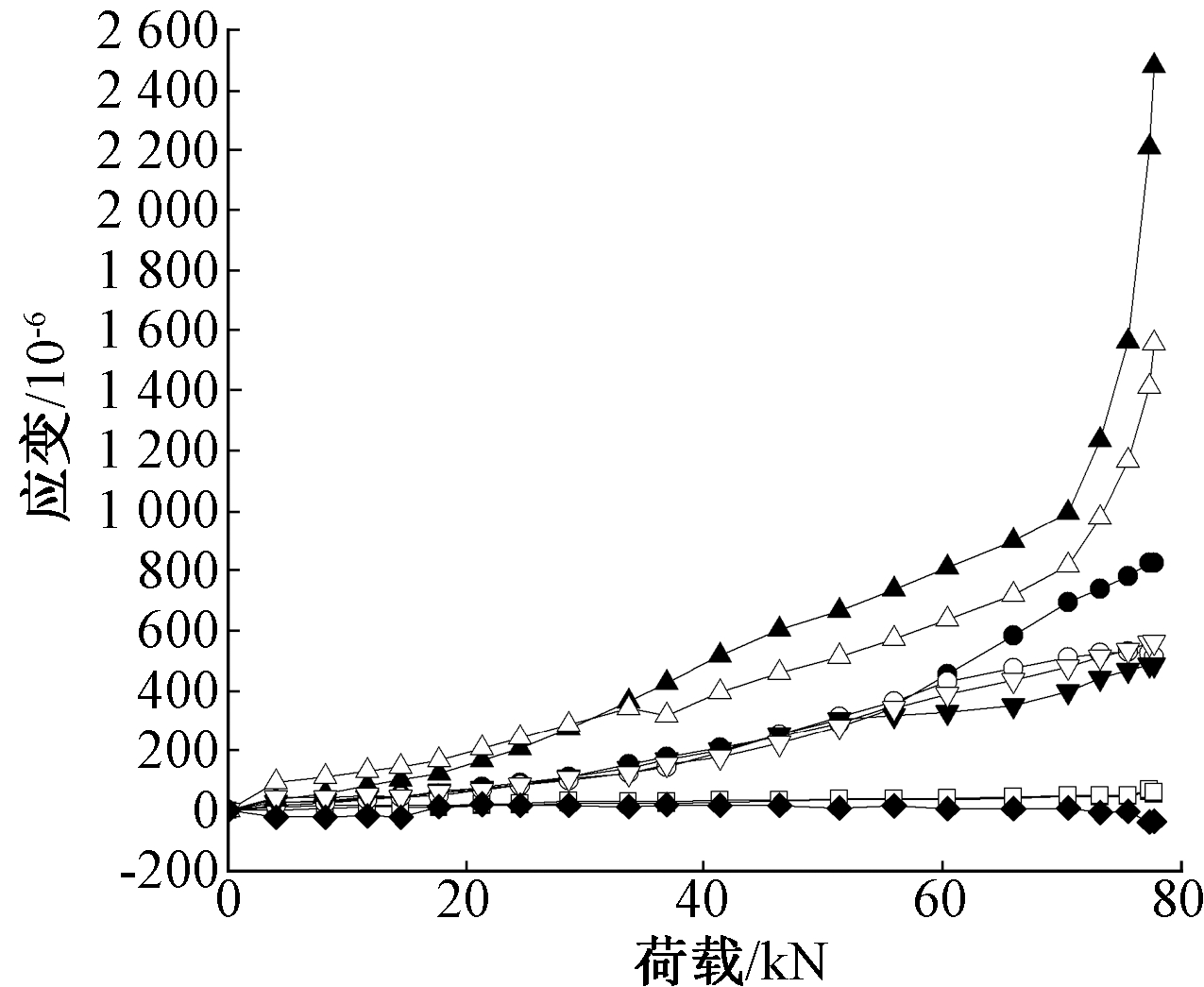
钢筋“应力超前”是指二次受力叠合构件的受拉钢筋应力、挠度、曲率都比相同弯矩作用下整浇构件的相应值大。观察图8试验板的纵筋荷载-平均应变曲线发现,整浇板与叠合板跨中位置的纵筋平均应变在试验前期非常贴近,随着荷载的增加,整浇板的纵筋平均应变水平甚至逐渐高于叠合板,说明叠合板跨中位置纵筋的“应力超前”并不明显,这是由于钢筋桁架的存在,减弱了钢筋的“应力超前”效应,同时下弦杆分担纵筋所受拉力,延缓了其应力增长。

![]() — DB-1;
— DB-1;![]() — DB-2;
— DB-2;![]() — ZB-3。
— ZB-3。
图8 试验板纵筋荷载-平均应变曲线
Fig.8 Load-average strain curves of longitudinal reinforcement of test slabs
本试验中叠合板侧的裂缝开展至叠合面附近发生停滞,并没有立刻继续向上开展,而是沿叠合界面产生小段水平裂缝,在多级加载后再继续向上延伸,其原因是本试验板材料为超高性能混凝土(UHPC),没有粗骨料,且硅灰等活性材料后期强度高,叠合面的混凝土结合比较紧密,加上钢筋桁架为叠合面提供了强有力的抗剪作用等,避免了水平裂缝继续延伸而导致构件叠合面的滑移破坏。
2.7 构件延性分析
延性是指材料的结构、构件或构件的某个截面从屈服到破坏,或达到承载能力后的变形能力。本文以试验构件裂缝宽度达到1.5 mm为破坏标志,继续进行后期加载,达到极限受荷状态,然后将构件受压区边缘混凝土被压碎,定义为终止标志,混凝土被压碎后,逐级卸载,以卸掉板上全部荷载为恢复标志,观察构件的后续变形情况。试件各阶段的跨中弯矩和跨中挠度及关系曲线分别如表6、图9所示。
分析表6和图9,3块板在后期施载过程中的试验现象,具有如下共同点:1)荷载增长缓慢或下降幅度很小,同一荷载值可持续多级;2)挠度持续增长,最大裂缝持续增宽,板侧裂缝缓慢向上发展;3)在加载过程中,构件发出明显钢纤维拔出或崩开的声音;4)卸载后,板的挠度有明显恢复现象。
表6 试件变形数据
Table 6 Deformation data of specimens
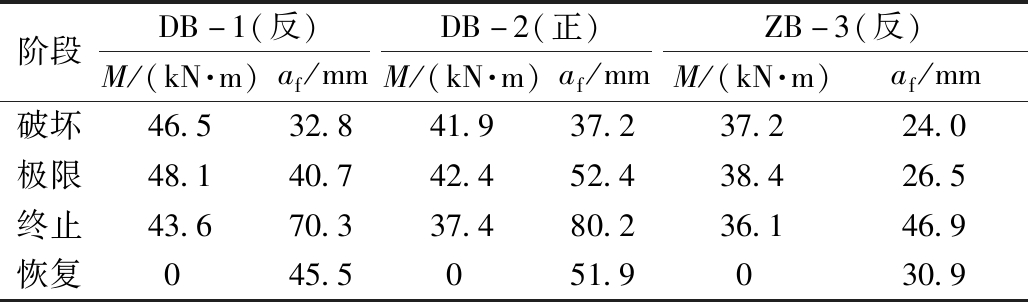
阶段DB-1(反)DB-2(正)ZB-3(反)M/(kN·m)af/mmM/(kN·m)af/mmM/(kN·m)af/mm破坏46.532.841.937.237.224.0极限48.140.742.452.438.426.5终止43.670.337.480.236.146.9恢复045.5051.9030.9
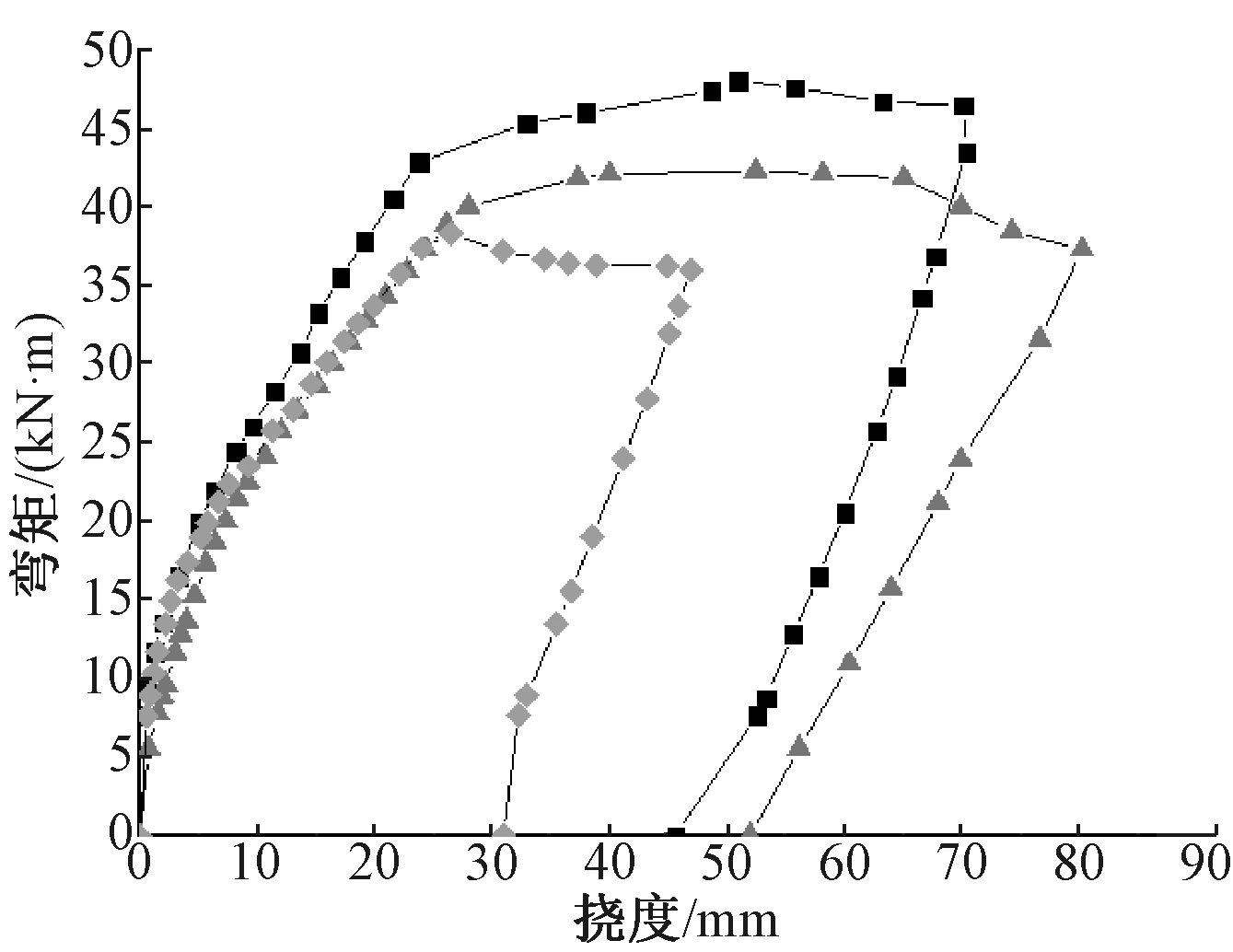
![]() — DB-1;
— DB-1;![]() — DB-2;
— DB-2;![]() — ZB-3。
— ZB-3。
图9 UHPC试验板跨中弯矩-挠度曲线
Fig.9 Bending moment-deflection curves in the mid-span of UHPC test slabs
从破坏标志到极限状态,再到混凝土被压碎,DB-1、DB-2和ZB-3都是荷载稍有增大然后回落,挠度值持续增大。从极限状态到压碎,挠度分别增加29.6,27.8,20.4 mm。整浇板ZB-3的荷载变化最小,挠度增大也最小。叠合板至其受压区边缘混凝土被压碎时,承载能力下降才比较明显,说明叠合板的延性优于整浇板。引入构件延性系数λ=μm/μy,以混凝土被压碎为构件的后续加载变形μm,以构件裂缝宽度达到1.5 mm时的变形为μy,可得叠合板DB-1、DB-2和整浇板ZB-3的延性系数分别为2.14、2.16和1.95,叠合板的延性系数均值比整浇板提高10.3%,证明钢筋桁架UHPC叠合板相对整浇板具有更好的延性。
结构构件在加载过程中,随着荷载的增加挠度增大,由加载初期的弹性挠度转变为弹塑性挠度,并产生不可恢复挠度,也称残余挠度,如图9所示。随着荷载的增大,残余挠度也会逐渐增大。本文试验板混凝土被压碎后卸载,试件DB-1、DB-2和ZB-3的跨中挠度恢复量分别为24.8,28.3,16.0 mm,恢复率分别为35.3%、35.3%、34.1%,其中钢筋桁架叠合板较高,说明UHPC叠合板具有非常好的弹性恢复能力,从另一个侧面反映了其良好的延性。
3 抗弯承载力
3.1 应力等效图形
在进行超高性能混凝土叠合构件正截面承载力计算时,受拉区混凝土的拉应力[11]和受压区混凝土的压应力均可简化成等效矩形应力图形,其应力分布如图10所示。设受压区混凝土等效矩形应力图的压应力值为αfc,高度为x,受拉区混凝土等效矩形应力图形的拉应力值为fftu,fftu=k3ft,k3为混凝土等效抗拉影响系数,受拉区高度为xt。
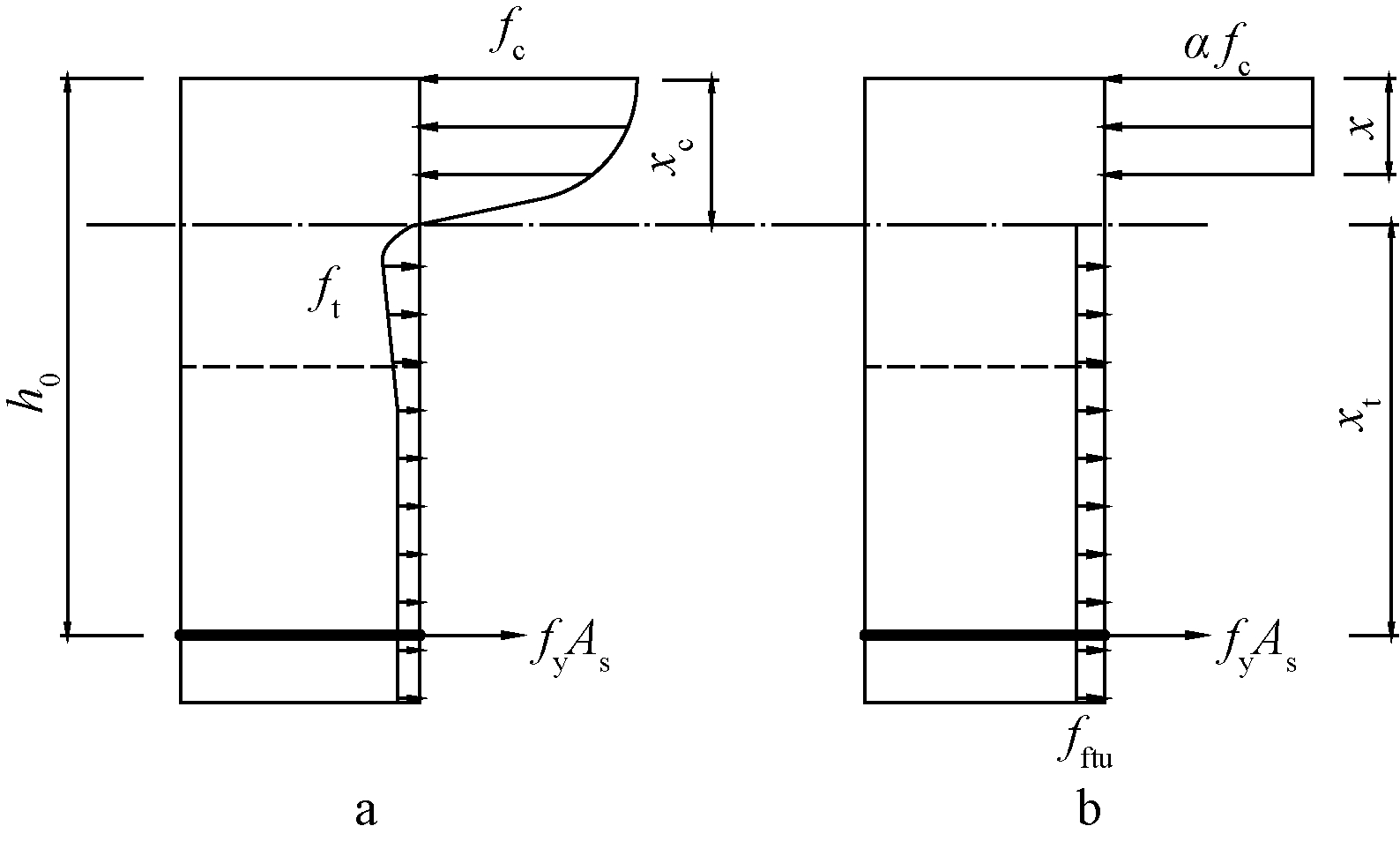
a—实际应力分布;b—等效应力分布。
图10 适筋钢筋桁架UHPC叠合板正截面应力分布
Fig.10 Normal section stress distribution of UHPC composite slabs with suitable reinforcement trusses
UHPC抗拉强度比较高,进行截面受力分析时不可忽略其抗拉作用,参考文献[12],取α=0.85,β1=0.71,k3=0.35。
3.2 受弯承载力计算式
根据截面应力等效图形10b,由平衡条件分析得到钢筋桁架UHPC适筋叠合板的抗弯承载力计算式:
(1a)
(1b)
式中:b为混凝土构件截面宽度;fy为纵向高强钢筋屈服强度;As为纵向高强钢筋截面面积;as为受拉钢筋合力点至截面受拉边缘的距离;As1为下弦钢筋截面面积;fy1为下弦钢筋屈服强度。
将本次试验UHPC受弯叠合板的各项参数代入式(1)得到其抗弯承载力计算值![]() 与试验值
与试验值![]() 进行比较,结果如表7所示。
进行比较,结果如表7所示。
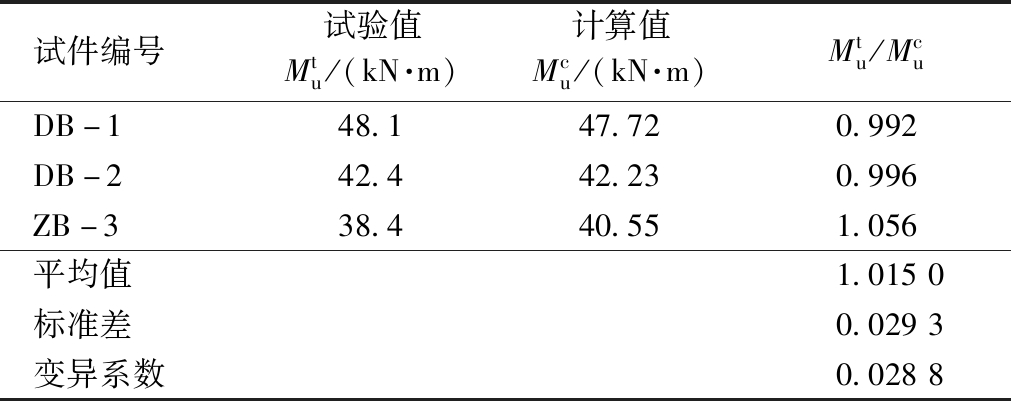
表7显示:3块试验板的受弯承载力计算值与试验值均比较接近,其比值的平均值为1.015,标准差为0.029 3,变异系数为0.028 8,说明UHPC的系数α、β1和k3取值比较合理,式(1)具有一定的可信度。从表中还可以看出,整浇板的承载力低于叠合板,且叠合板的试验值高于计算值,表明UHPC叠合板的钢筋桁架发挥了一定的抗弯作用。
表7 试验板承载力计算值与试验值比较
Table 7 Comparison between the calculated bearing
capacity of test slabs and the test value
试件编号试验值Mtu/(kN·m)计算值Mcu/(kN·m)Mtu/McuDB-148.147.720.992DB-242.442.230.996ZB-338.440.551.056平均值1.0150标准差0.0293变异系数0.0288
4 结束语
1)钢筋桁架UHPC叠合板具有良好的受弯性能,在受力过程中,其截面应变与钢筋桁架PC叠合板一样基本符合平截面假定,但是其中性轴上升幅度比较小。
2)由于超高性能混凝土UHPC优异的材料性能,叠合面的混凝土结合比较紧密,加上钢筋桁架的抗剪作用,钢筋桁架UHPC叠合板叠合面的水平裂缝延伸非常有限,一般不会发生叠合面的滑移破坏。
3)由于UHPC致密的微观结构和钢筋桁架的存在,UHPC叠合板的二次受力效应并不明显,而且其延性和恢复性能均优于UHPC整浇板,钢筋桁架不但可以使叠合层和预制层的抗剪连接更为可靠,而且还能提高叠合板的整体刚度。
4)根据截面应力等效原则,得到受弯构件截面的等效矩形应力图形,取混凝土等效抗拉影响系数为0.35,推导出适用于钢筋桁架UHPC叠合板的正截面承载力计算式,其计算值与试验值吻合较好,说明计算式具有一定的可信度,可以为工程应用提供一些参考。
[1] RICHARD P,CHEYREZY M.Composition of Reactive Powder Concrete Research[J].Cement and Concrete Research,1995,25(7):1501-1511.
[2] 陈科.大跨度PK预应力混凝土叠合板的试验研究与理论分析[D].长沙:湖南大学,2009.
[3] 叶献国,华和贵.叠合板拼接构造的试验研究[J].工业建筑,2010,40(1):59-63.
[4] 刘轶.自承式钢筋桁架混凝土叠合板性能研究[D].杭州:浙江大学,2006.
[5] 廖莎,马远荣.活性粉末混凝土(RPC)预应力叠合梁受弯性能研究[J].湖南大学学报(自然科学版),2005,32(1):57-62.
[6] 聂建国,陈必磊.钢筋混凝土叠合板的试验研究[J].工业建筑,2003,33(12):43-46,33.
[7] 中华人民共和国住房和城乡建设部.普通混凝土结构试验方法标准:GB/T 50152—2012[S].北京:中国建筑工业出版社,2012.
[8] 中国国家标准化管理委员会.活性粉末混凝土:GB/T 31387—2015[S].北京:中国建筑工业出版社,2015.
[9] 邓莎莎.现浇钢筋桁架混凝土楼板试验与理论研究[D].重庆:重庆交通大学,2017.
[10] 装配整体梁板研究专题科研组.装配整体梁板设计方法的试验研究[J].建筑结构学报,1982,3(6):1-19.
[11] 郑文忠,李莉.钢筋活性粉末混凝土简支梁正截面受力性能试验研究[J].建筑结构学报,2011,32(6):125-134.
[12] 吴欣柯.配置高强钢筋的RPC梁正截面抗裂性能试验研究[D].桂林:桂林理工大学,2014.