1 概 述
方案设计阶段是自然通风设计的基础和关键环节,有关空间形态因子的设计决策将会对自然通风性能产生根本性的影响。近年来,随着流体动力学计算(CFD)数值模拟技术与人工智能的发展,已有研究开始在方案设计阶段对两者耦合并展开迭代计算,实现自然通风性能引导下建筑形态的自动寻优[1-4]。以上自然通风性能优化流程均遵循如下步骤:首先在设计空间中生成一定数量的样本,通过CFD平台进行自然通风性能的批量模拟,然后利用优化算法调用模拟结果进行分析和比较,以比较的结果作为指导,再获取下一批更好的样本,如此循环往复直至“优化”的目标达成[5]。整个优化进程由优化算法进行驱动,无需人力参与,实现了自然通风性能引导下空间形态的“自动生成”。然而在优化进程中,利用优化算法评价的基础是对大量样本自然通风性能的批量模拟,而每一次CFD数值模拟都需要建模—网格—模拟—后处理等一系列复杂流程,动辄需要几十分钟到几小时甚至更长时间,巨大的计算成本难以对方案阶段的快速决策进行有效支持。针对上述问题,既有研究尝试搭建满足建筑初期设计需求的可视化物理风洞[6-7],替代计算耗时的CFD数值模拟,进行建筑风环境的模拟、数据测量及性能反馈。利用风洞试验可以快速获得流场数据,通过优化算法驱动机械装置的运动,实现建筑形态的自动优化和生成。以上基于风洞试验的优化方法,可以解决计算周期和精度的问题,但限于试验成本和建造难度,目前难以在方案设计阶段广泛应用。
针对上述问题,本研究提出基于响应面的自然通风性能优化流程,并搭建相应的优化平台。选取全民健身中心作为研究对象展开实践探讨,提取典型空间模型11个几何形态参数作为输入变量,选取空气龄、温度和风速三个评价指标作为优化目标。应用参数化建模技术、CFD数值模拟技术获得200组数据,采用Kriging算法构建响应面模型;采用多目标遗传算法调用响应面模型数据进行快速寻优,获得了优化候选方案以及几何参数的优化区间。
2 基于响应面的自然通风优化流程及平台
2.1 优化流程
响应面法(response surface methodology,RSM)[8]最早由数学家Box和Wilson于1951年提出,是一种试验设计与数理统计相结合的优化方法。基本思想是利用有限数量的样本点拟合一个连续的响应面来模拟真实极限状态曲面,以此构建输入变量与输出变量之间复杂的映射关系(图1)。通过把复杂的物理求解问题转化为数学问题,有效减少计算量,因此可以利用响应面模型替代流程复杂、求解耗时的CFD模型,通过优化算法调用响应面模型快速获得输出变量进行迭代寻优,实现自然通风性能的快速优化。
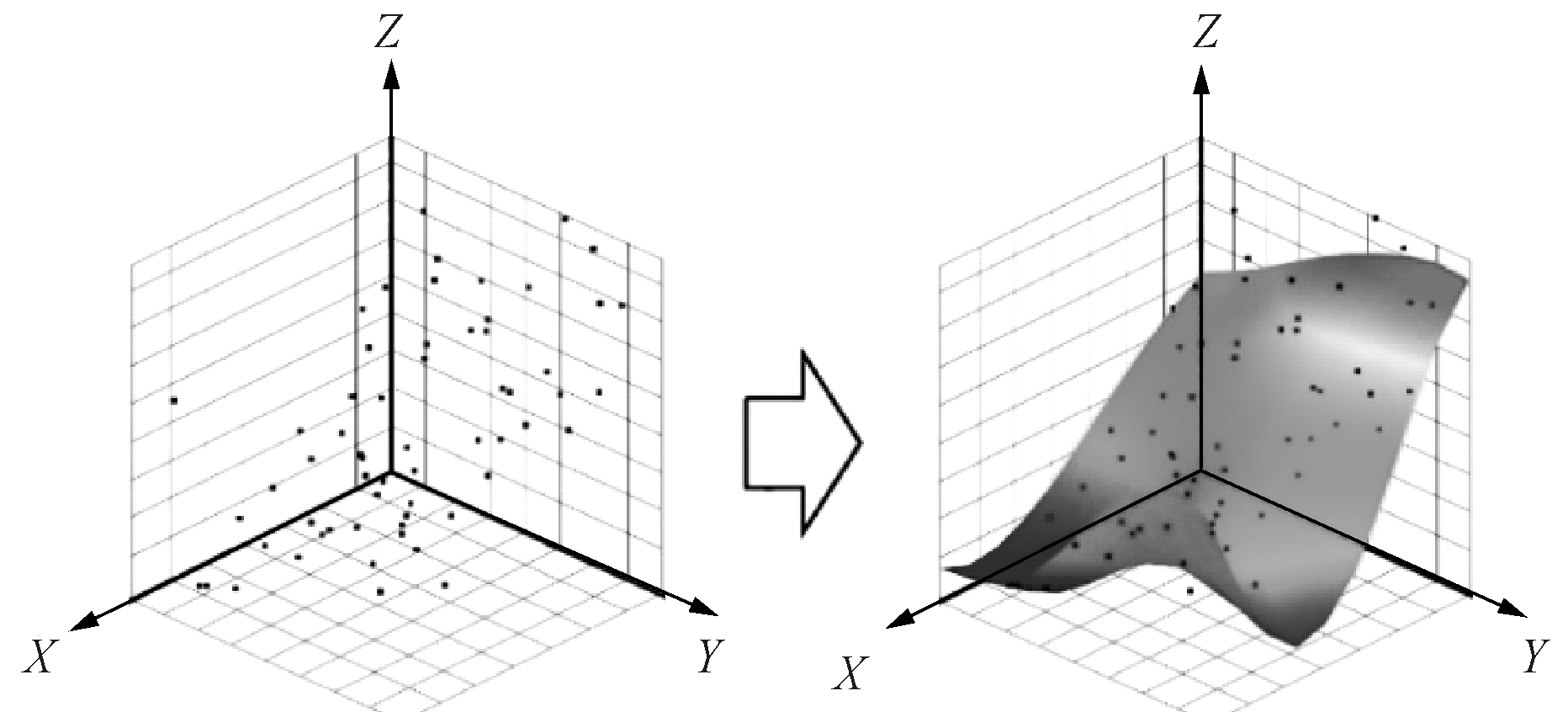
图1 响应面基本原理
Fig.1 Basic principle of response surface
基于响应面的自然通风优化的完整流程如图2所示。首先提取空间模型的几何参数,确定自然通风评价指标,并采用参数化建模技术进行建模。采用敏感性分析方法计算各几何参数的敏感性指标,筛选关键几何参数。通过试验设计对关键参数组合进行抽样,形成一定数量均匀分布的样本,利用CFD数值模拟程序调用参数化模型进行批量计算,获得样本的输出数据。以试验设计环节的离散数据为基础,采用相应算法进行数据的拟合与插值,构建响应面模型。同时对其预测精度进行验证,若满足精度要求则进入优化环节,反之则进行新一轮的试验设计。最后,利用优化算法调用响应面模型进行迭代寻优,直至优化目标达成。
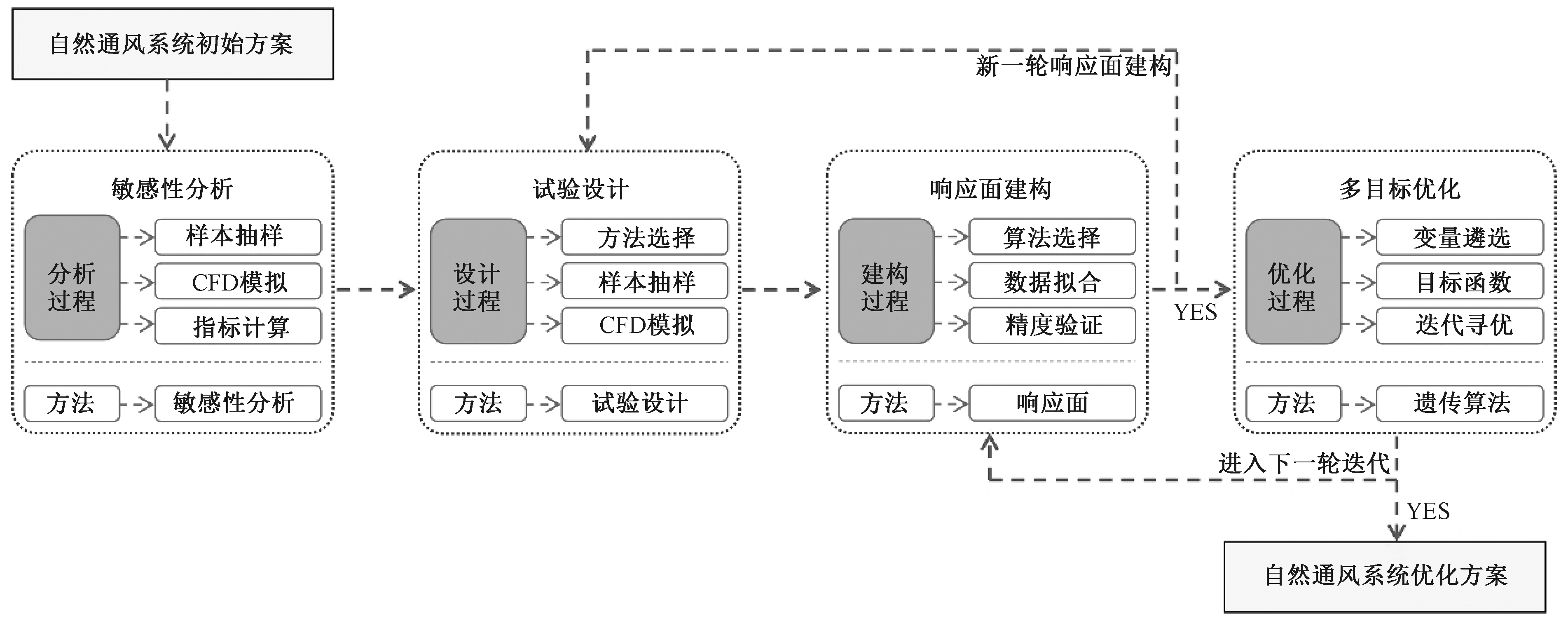
图2 基于响应面的多目标优化流程
Fig.2 Multi-objective optimization process based on response surface
2.2 平台搭建
采用ANSYS 17.0搭建优化平台。ANSYS Workbench提供了与优化流程相对应的多个功能模块和各模块协同工作的环境,模块相互之间数据可以自由读取与调用。与优化流程相对应,优化平台包含以下五个模块:参数化建模模块、CFD数值模拟模块、敏感性分析模块、响应面建构模块、多目标优化模块(图3)。Design Modeler为参数化建模模块,通过内置的参数管理器编译参数间的函数表达式,建立起各参数间的耦合关系。Fluent为CFD数值模拟模块,通过调用参数化模型,对自然通风性能指标展开批量计算,计算后的数据导入参数管理器(Parameter Set)。Parameter Correlation为敏感性分析模块,可读取参数管理器数据,通过相关性分析确定各几何参数敏感性指标,筛选关键参数。Response Surface为响应面建构模块,通过读取参数管理器数据,选择合理的试验设计方法和响应面算法对关键参数展开响应面模型建构和精度验证。Response Surface Optimization为多目标优化模块,可选择适宜优化算法调用响应面模型数据展开迭代寻优,获得优化候选方案。
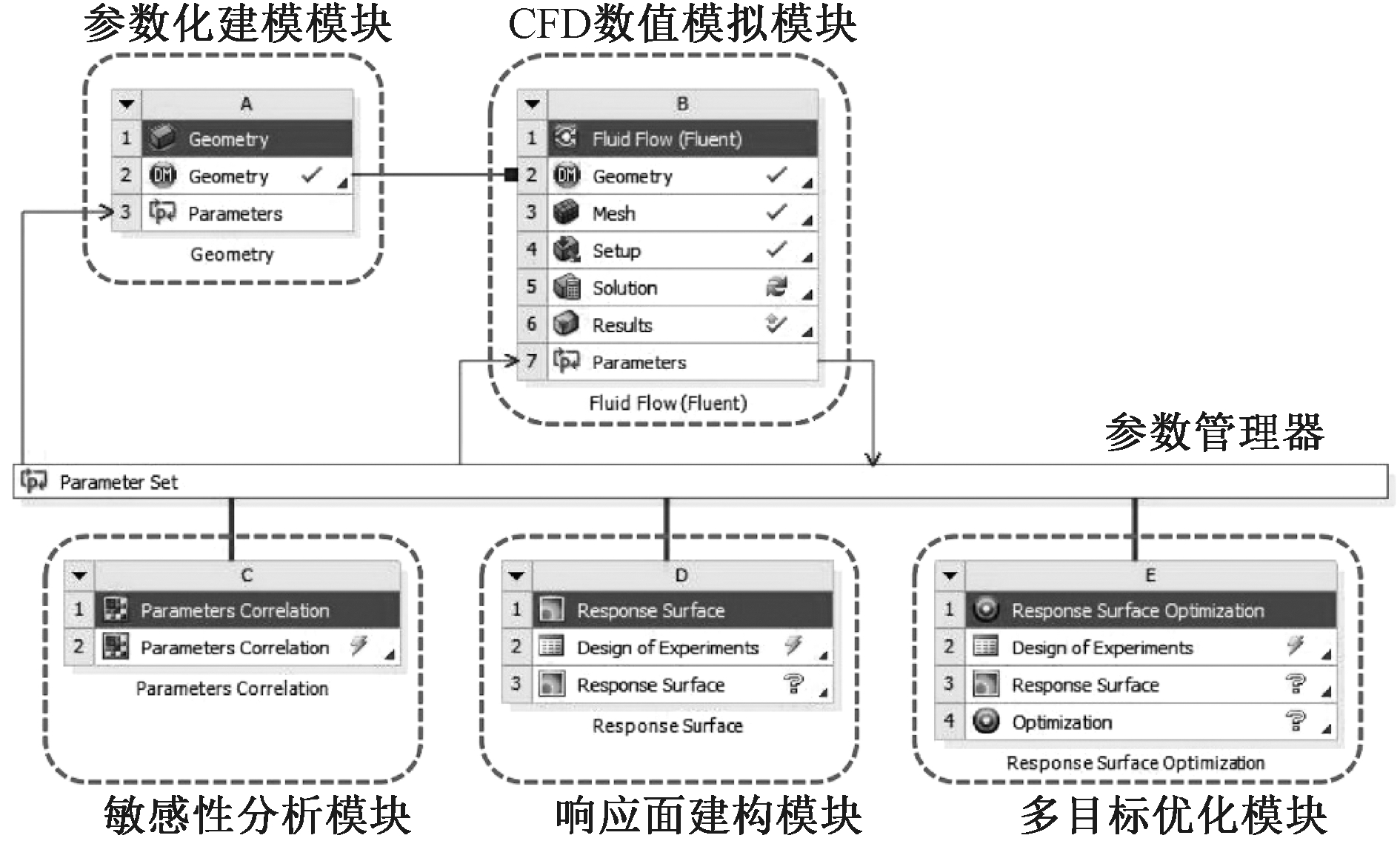
图3 基于响应面的多目标优化平台
Fig.3 Multi-objective optimization platform based on response surface
3 基于响应面的自然通风优化实践
3.1 典型模型
全民健身中心是指由国家体育总局命名,专用于开展群众性体育健身活动,具有一定规模的公益性多功能综合体育设施[9]。作为一种全新的体育建筑类型,全民健身中心的使用主体由专业运动员转化为广大健身人群,功能强调群众参与性、弱化观演性,取消大规模坐席,内部多个大空间运动厅立体叠加组合。全民健身中心的空间模式反映了当前大型公共建筑空间布局紧凑的特征,以及由此导致的自然通风设计难点,因此围绕全民健身中心展开的自然通风优化设计研究具有典型意义。
对全国范围内50座典型全民健身中心进行调研,提取典型空间模型(图4):两层多功能运动厅竖向层叠,周围四层附属空间L型围合。每层运动厅平面尺寸为40 m×60 m,高度为12 m,可容纳1块手球场、3块篮球场、3块网球场、4块排球场、12块羽毛球场、24块乒乓球场,根据不同的运动需求可进行场地的灵活转换与组合。

图4 典型模型 m
Fig.4 Typical model
为形成气流运动的连续路径,需在建筑纵深部位植入竖向腔体构建自然通风系统。在各类腔体中,通风竖井平面尺寸小,周边布置的方式保证了大空间运动的完整性,具有广泛的应用潜力,因此本研究采取周边竖井的腔体植入方式。按照空气流经建筑的次序,将影响自然通风的形态因子分为4个层级:进风口、交界面、腔体、出风口(图5)。提取4个层级形态因子的11个几何参数,结合调研数据确定值域(表1)。
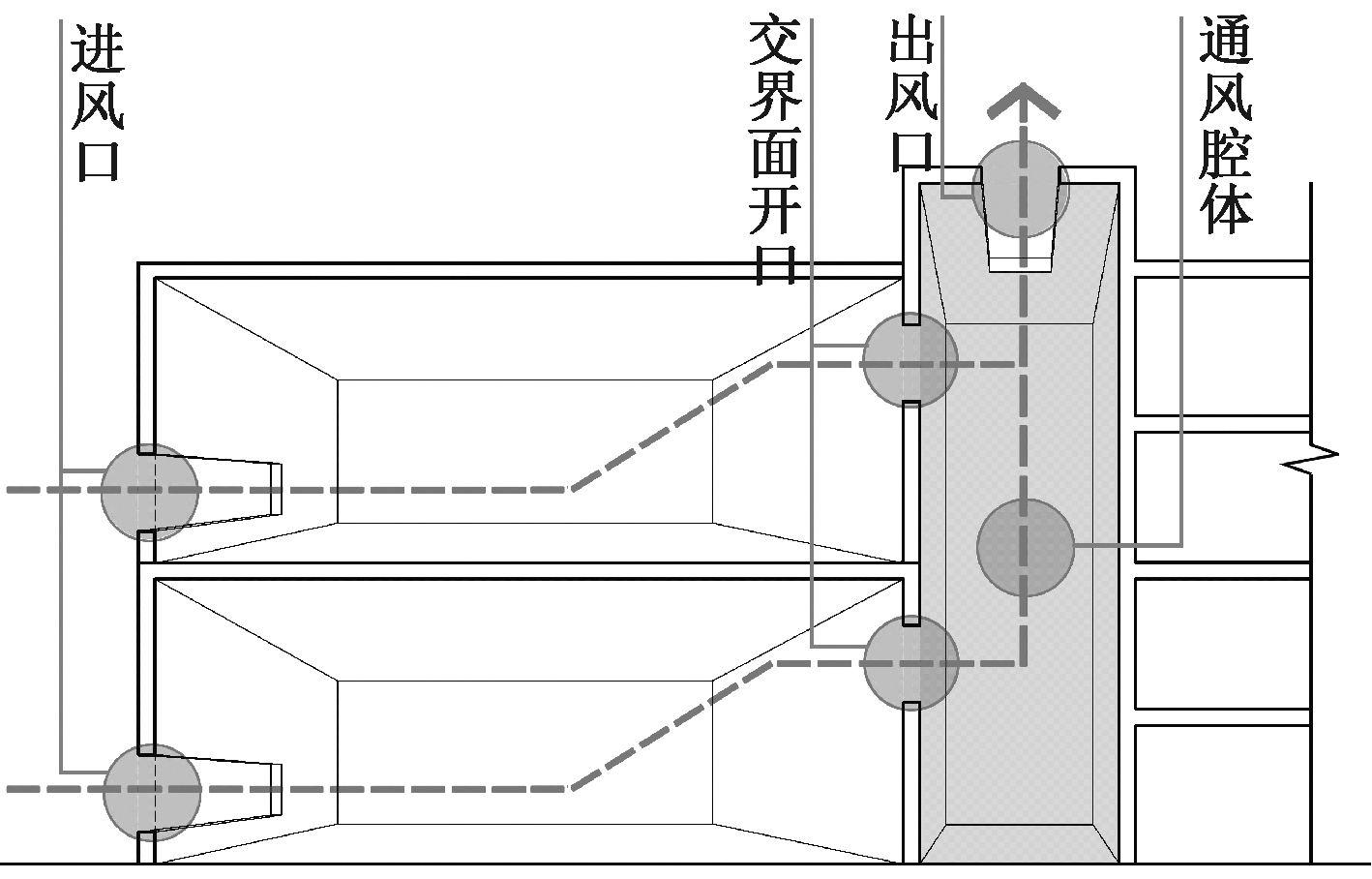
图5 典型模型内部的气流组织
Fig.5 The airflow organization inside a typical model
从空气品质、热舒适性和体育运动的工艺要求三方面出发,采用空气龄、温度和风速三个指标对自然通风性能进行评价。在CFD数值模拟中,分别提取第1、2层1.5 m高处参考平面的空气龄值、温度值和风速值,并计算各指标第1、2层的平均值作为输出结果。
3.2 参数敏感性分析
建构响应面所需样本数量会随着输入参数的数量显著增长,从而大幅增加计算成本。因此首先对参数进行敏感性分析,筛选关键参数。采用随机抽样方法获得100组输入参数数据,利用参数化模型调用CFD数值模拟软件Fluent 17.0对模型的空气龄、温度和风速进行计算。在Parameter Correlation敏感性分析模块中采用spearman等级相关性系数法对计算结果进行分析。各几何输入参数敏感性指标如图6所示,其中参数P7(交界面开口距地距离)和P10(腔体高度)对自然通风性能的各项指标均不敏感,因此选取P1、P2、P3、P4、P5、P6、P8、P9、P11共9个参数作为输入参数,进入试验设计环节。
表1 几何参数及其值域
Table 1 Geometric parameters and ranges

进风口交界面腔体出风口P1P2P3P4P5P6P7P8P9P10P11进风口个数进风口宽度/m进风口距地距离/m进风口高度/m交界面开口个数交界面开口宽度缩放系数交界面开口距地距离/m交界面开口高度/m腔体截面边长/m腔体高度/m出风口边长缩放系数3~301~100.5~111~11.53~180.1~10.5~10.51~111~624~300.1~1
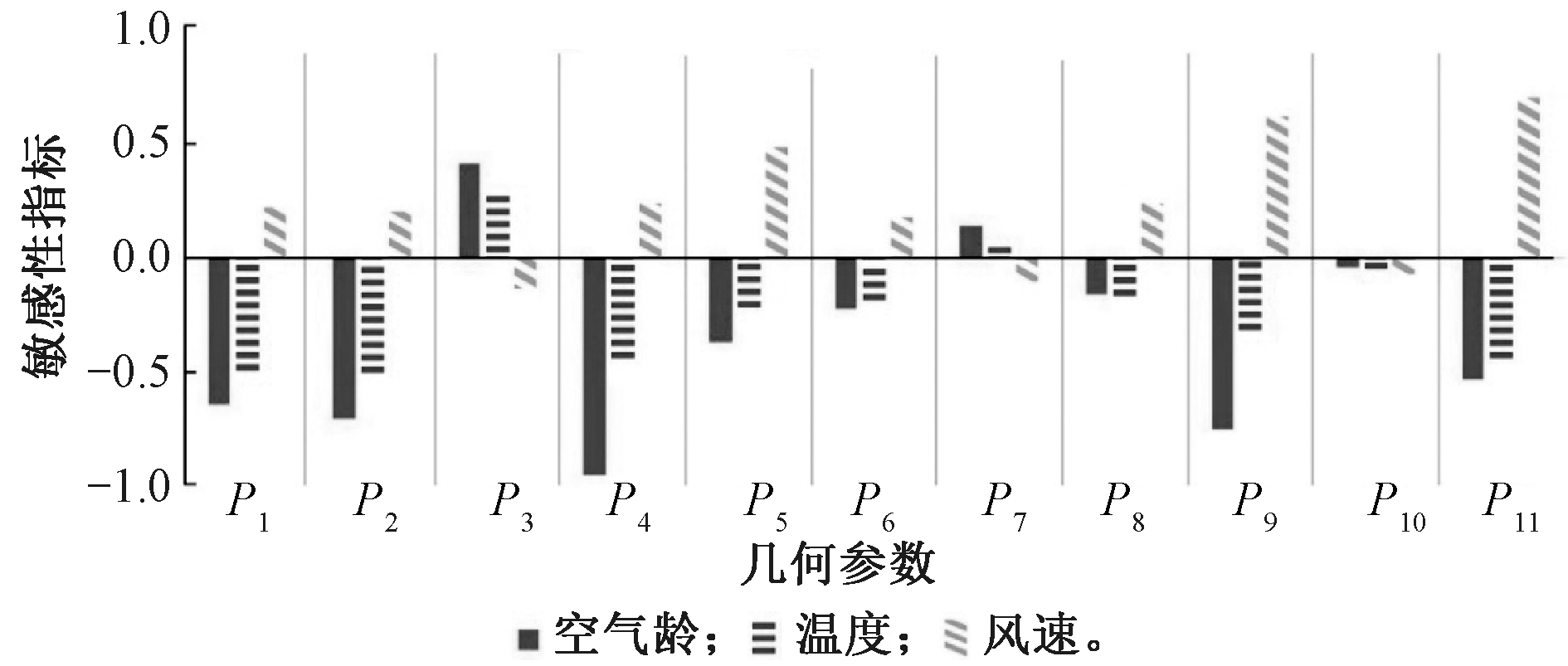
图6 11个几何参数的敏感性分析
Fig.6 Sensitivity analysis of 11 geometric parameters
3.3 试验设计
试验设计(Design of Experiments,DOE)是指对输入参数的组合进行有限次的抽样,使其尽可能反映整个设计空间的特征[10]。其目的是利用尽可能少的CFD仿真次数,获取尽可能多的关于输入参数与输出参数之间的映射关系。DOE是构造响应面模型的基础,直接影响响应面模型的预测精度,进而影响后续优化的准确性。在各种DOE方法中,拉丁超立方设计是一种广泛采用的均匀抽样方法,所有输入参数的设计空间都被均匀划分为数目相同的分区,所有水平随机组合在一起,每个输入参数的每个水平只被抽样一次,可以使有限个样本点均匀填充整个设计空间。由于拉丁超立方抽样具有效率高,均匀性好的特点,可在抽样较少的情况下获得较高的计算精度,本研究选用该方法进行抽样。根据Loeppky的建议[11],样本数量不应少于10倍的输入参数数量。权衡计算成本与响应面质量,选取该方法对9个输入参数组合抽样200次。采用Fluent 17.0对200个抽样样本展开批量模拟计算,提取平均空气龄值、平均温度值、平均风速值建构响应面模型。
3.4 响应面模型建构
响应面模型的构造方法包括二阶多项式、神经网络、Kriging法等,不同类型的算法适用于解决不同的问题。二阶多项式算法是一种常用的数值拟合方法,通过最小二乘原理获取近似多项式的参数而建立响应面模型[12]。构造简单、计算量小,输入与输出参数关系明确,但该方法对非线性拟合能力不足。神经网络算法通过模拟人脑神经元网络的结构和特征实现对各种复杂信息的处理,具有很强的自适应学习功能和非线性映射能力[13]。但利用神经网络算法构造响应面需要数量较大的样本进行训练,增加了计算成本。考虑到本研究输入与输出参数间高度非线性的情况,并权衡计算成本,最终选用Kriging算法构造响应面。
Kriging算法由南非地质学者Danie Krige提出,早期用来预测矿产储量的分布,后引入优化领域。Kriging是一项多维插值技术,结合了标准二阶多项式的全局算法和局部偏差测定,函数表达式如式(1):
y(x)=PT(x)·a+Z(x)
(1)
式中:y(x)为响应面的输出参数;PT(x)·a为类似标准响应面的多项式模型;Z(x)是一个特殊随机过程。
PT(x)·a是y(x)中的确定性回归部分,提供近似模型的全局逼近,Z(x)提供对模型局部偏差的近似[13]。由于兼具局部和全局估计的特点,Kriging算法在解决高度非线性问题时可获得理想的拟合效果(图7)。在Response Surface模块中选择Kriging算法,对DOE中200个样本进行数据拟合与插值,建构响应面模型。
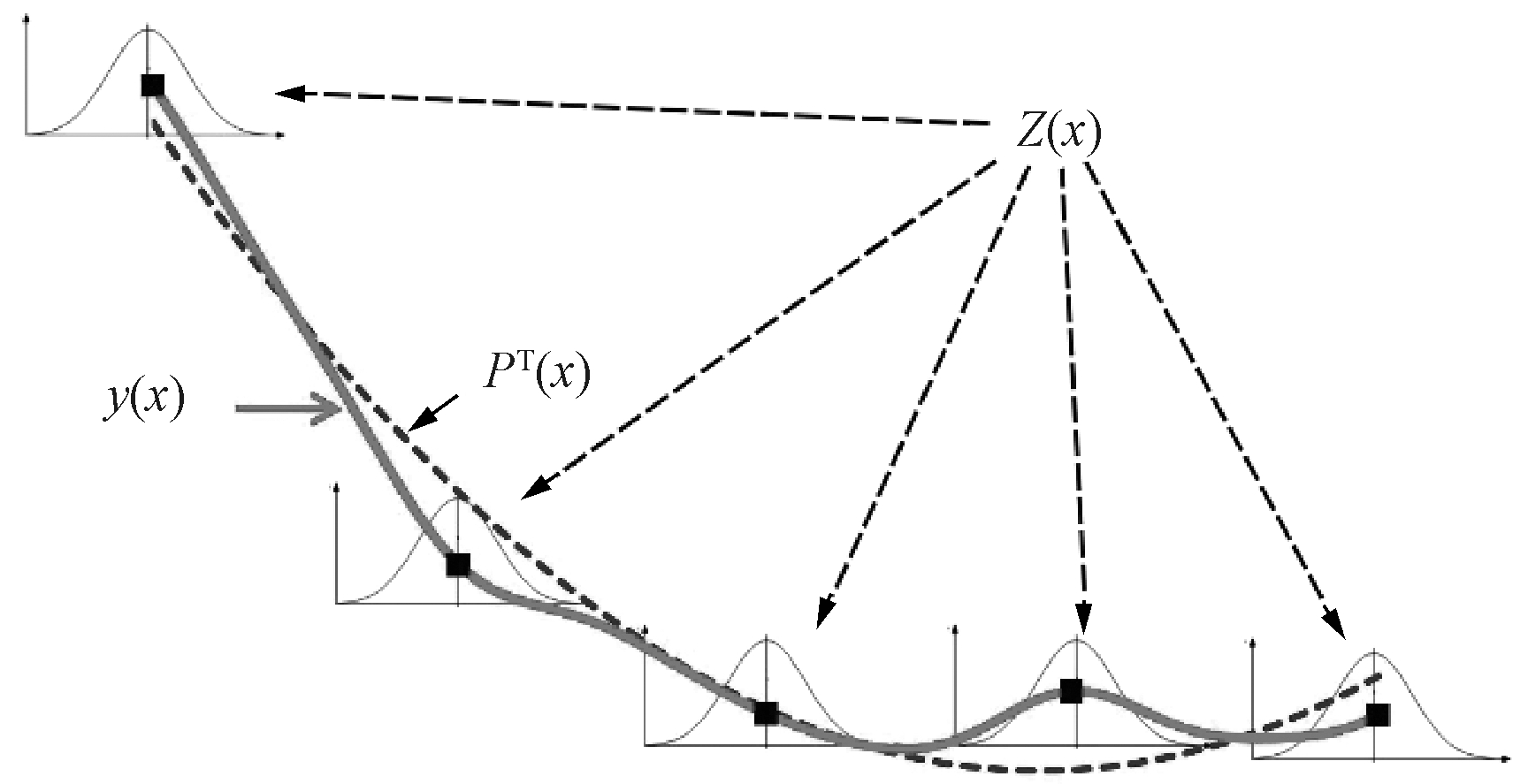
图7 Kriging算法
Fig.7 Kriging algorithm
响应面实质是多维的超曲面,为方便图示表达,以任意两个输入参数作为横坐标,以输出参数作为纵坐标绘制三维曲面(图8)。以输入参数P2和P4为例,分别绘制3个输出参数的三维响应面图。由于响应面是数学模型,无需复杂的物理求解过程,对于一组输入参数的组合,可以快速获得相应的输出参数,对于需要大量迭代的优化过程可进行有效支持。
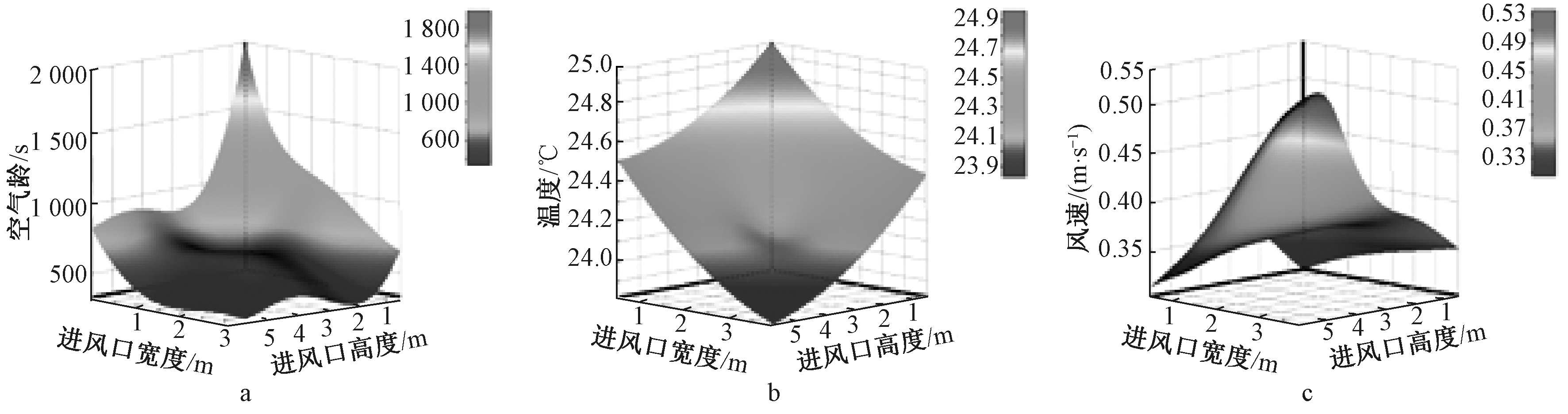
a—空气龄;b—温度;c—风速。
图8 响应面模型
Fig.8 Response surface model
响应面模型是一种近似的预测模型,输入与输出参数的映射关系是建立在数值拟合与插值的基础之上,因此对其精度的验证至关重要。响应面模型建构完成之后,选择测试样本利用复相关系数R2对预测数据和模拟值进行验证(式(2))。
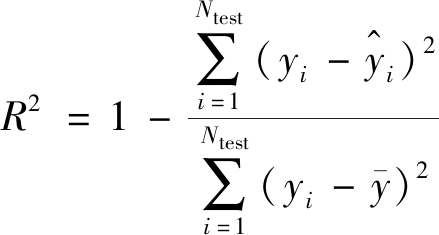
(2)
其中![]()
式中:yi为测试样本实际模拟值;![]() 为响应面预测值;Ntest为测试样本数量;
为响应面预测值;Ntest为测试样本数量;![]() 为测试样本的平均值。经计算,空气龄、温度、风速的目标值与预测值的接近程度为0.937 36、0.921 05、0.955 52(图9)。说明响应面模型达到了较高的预测精度,可以替代CFD数值模拟进入优化环节。
为测试样本的平均值。经计算,空气龄、温度、风速的目标值与预测值的接近程度为0.937 36、0.921 05、0.955 52(图9)。说明响应面模型达到了较高的预测精度,可以替代CFD数值模拟进入优化环节。

a—空气龄;b—温度;c—风速。
图9 响应面模型的精度验证
Fig.9 Accuracy verification of response surface model
3.5 多目标优化
优化过程中的输入变量为去除P7和P10后的9个关键几何形态参数;3个目标函数为:平均空气龄Z1(X)、平均温度Z2(X)、平均风速Z3(X),且三者数值越低越好:
Min Z1(X)=AirAge(X)
(3a)
Min Z2(X)=Temperature(X)
(3b)
Min Z3(X)=Velocity(X)
(3c)
式中:AirAge为平均空气龄;Temperature为平均温度;Velocity为平均风速。
X=(P1,P2,P3,P4,P5,P6,P8,P9,P11)
(4)
采用多目标遗传算法(Multi-Objective Genetic Algorithm,MOGA)调用响应面模型进行迭代寻优。为保持优化解集样本的多样性,并防止优化提前收敛,初始样本种群设为2 000个,每次迭代计算500个,最大迭代100代。当帕累托百分比达到80%时,优化进程收敛。首先,几何参数信息传递至Response Surface Optimization多目标优化模块,由遗传算法随机生成2 000个初始样本。随后2 000个样本的输入参数传递至响应面模型,快速计算输出参数,计算结果反馈至遗传算法。遗传算法根据目标函数对2 000个样本的输出数据执行选择、交叉与变异操作,形成新一代500个样本,输入参数再次传递至响应面,计算结果由遗传算法判断是否满足优化终止条件,若满足,则终止优化进程,输出优化结果,否则进入新一轮迭代,直至优化目标达成。遵循上述流程,本次优化迭代计算11次后优化进程收敛(图10),共调用响应面模型计算6 141次,而实际的CFD模拟计算仅需200次,显著降低计算成本。

图10 优化过程的迭代次数
Fig.10 Iterations of the optimization process
由于3个目标函数彼此之间的变化趋势是相互矛盾的(如风速的提升引起室内气流的加快,必然导致温度和空气龄的下降),某一性能指标的提升,必然会引起其他指标的下降。因此,多目标优化的结果并非是一个最优方案,而是一系列“非支配解”的集合——帕累托前沿(图11)。非支配解均是权衡各项指标计算得出的优化方案,不同的是非支配解对各项性能的倾斜程度不同,如有的风速值较好,但其他指标相对较差。可以结合不同的设计要求对非支配解集进行选择(如可倾向于某一目标函数),本研究围绕“综合平衡三个目标函数、使各项性能均较为均衡”的原则展开筛选。
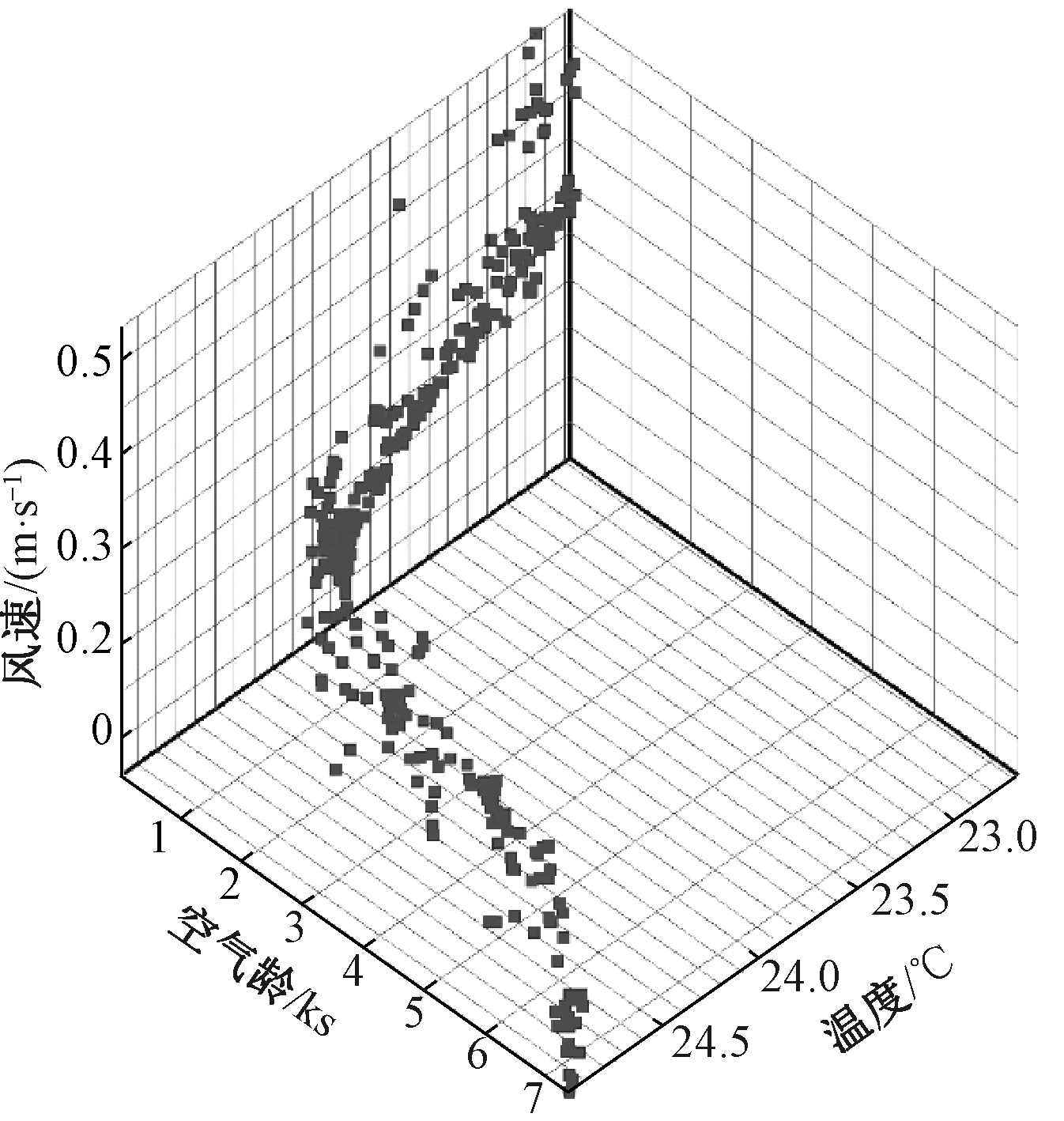
图11 帕累托前沿
Fig.11 Pareto front
首先确定风速限值,参考JGJ 31—2016《体育建筑设计规范》中风速小于0.5 m/s的规定,取0.5 m/s为优化方案中风速的上限值。随着风速降低(图11),非支配解的温度和空气龄均呈上升趋势,因此应在临近0.5 m/s的区域选择,以保证温度和空气龄值不至过高。非支配解的温度值随着风速降低呈均匀上升趋势;非支配解的空气龄在风速0.3~0.5 m/s范围内保持不变,风速降低至0.3 m/s以下,空气龄迅速增加(图12)。因此风速0.3~0.5 m/s的范围为优化方案分布区域,此范围内50个方案的参数空间分布见图13,各参数优化区间的取值见表2。在优化方案分布区域内,ABCDEF六个非支配解的风速值和空气龄相比于其他方案更具优势,因此作为最终优化备选方案(表3)。其中非支配解E的温度值和风速值与其他非支配解十分接近,但空气龄最低,所以最终选择非支配解E为优化方案。
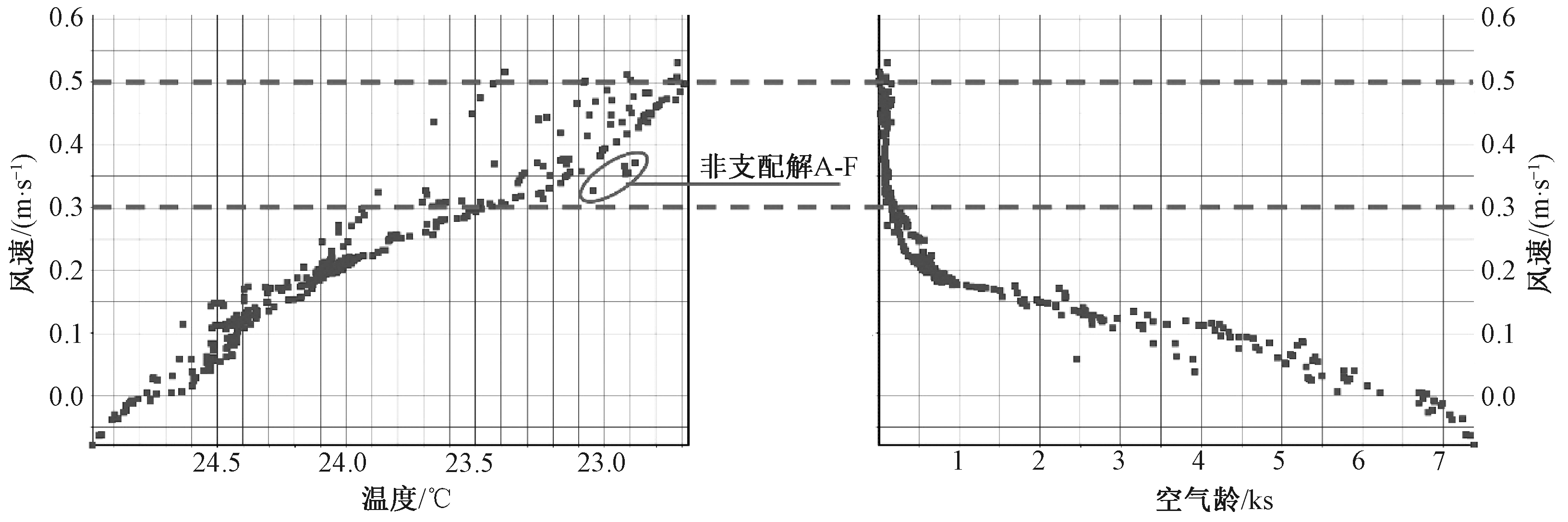
图12 非支配解中的优化方案分布
Fig.12 Optimal schemes distribution in non-dominated solution set
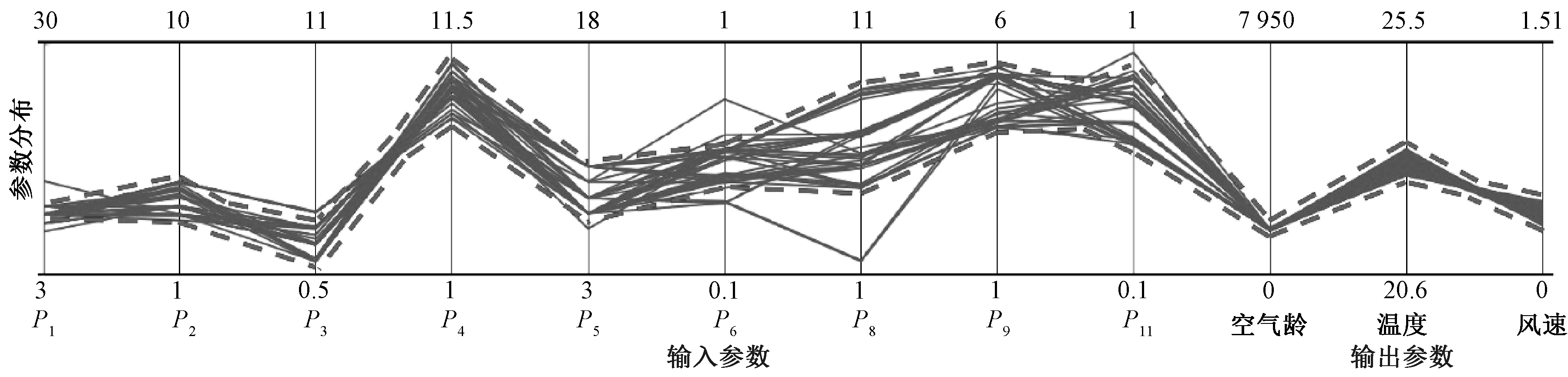
图13 优化方案的参数区间分布
Fig.13 Parameter interval distribution of optimal schemes
表2 几何参数及其优化区间
Table 2 Geometric parameters and optimization intervals

输入参数输出参数P1P2P3P4P5P6P8P9P11P12P13P14进风口个数进风口宽度/m进风口距地距离/m进风口高度/m交界面开口个数交界面开口宽度缩放系数交界面开口高度/m腔体截面边长/m出风口边长缩放系数平均空气龄/s平均温度/℃平均风速/(m·s-1)7~103.12~4.600.92~3.258.06~10.496~90.44~0.624.76~5.734.17~5.470.61~0.8966.22~146.2622.69~23.260.31~0.53
表3 优化备选方案
Table 3 Alternative optimization schemes

编号P1P2P3P4P5P6P8P9P11空气龄/s温度/℃风速/(m·s-1)A9.4.2311.48210.4960.4535.7195.1070.605121.3323.040.3283B94.2421.07810.3770.5516.6665.0050.602112.6522.920.3539C94.2491.07810.5370.4784.3875.2280.642124.9122.920.3563D94.2491.07810.5370.4785.5415.2280.633124.9222.910.3565E94.1301.07810.1960.5776.0185.2400.62298.67122.920.3673F94.1301.07810.2570.5776.0185.2400.622100.2822.880.3717
4 结束语
方案阶段的自然通风优化设计需要对大量方案的自然通风性能进行快速预测和寻优,响应面则为上述问题提供了新的研究视角。
1)提出基于响应面的自然通风优化流程:参数敏感性分析、试验设计、响应面模型建构、多目标优化,实现自然通风性能引导下的建筑形态的快速生成,为方案阶段自然通风优化设计提供有效支持。
2)基于ANSYS Workbench构建协同优化平台,整合了参数化建模技术、CFD数值模拟技术、响应面方法、遗传优化搜索技术,实现建筑自然通风性能的快速优化。
3)以全民健身中心典型模型为研究对象,应用上述自然通风优化流程和平台展开实践探讨,获得优化方案的参数空间分布以及优化方案。
[1] 谭子龙.基于建筑风环境分析的Grasshopper与Fluent接口技术研究[D].南京:南京大学,2016.
[2] KARAGKOUNI C,SCHIECK A F,TSIGKARI M,et al.Facade Apertures Optimization:Integrating Cross-Ventilation Performance Analysis in Fluid Dynamics Simulation[C]∥Orlando:Symposium on Simulation for Architecture and Urban Sign,2013.
[3] KYLE K,ALEJANNDRO G,KAREN K.Passive Performance and Building Form-An Optimization Framework for Early-Stage Design Support [J].Solar Energy,2016,125(2):161-179.
[4] WANG B,MALKAWI A.Genetic Algorithm based Building Form Optimization Study for Natural Ventilation Potential [C].Proceedings of BS,2015:640-647.
[5] 吉国华.参数化图解与性能化设计[J].时代建筑,2016(5):44-47.
[6] MENICOVICH D,GALLARDO D,BEVILAQUA R,et al.Generation and Integration of an Aerodynamic Performance Database within the Concept Design Phase of Tall Buildings [C]∥San Francisco:ACADIA 2012.2012.
[7] 袁烽.从图解思维到数字建造[M].上海:同济大学出版社,2016.
[8] BOX G E P,WILSON K B.On the Experiment Attainment of Optimum Conditions [J].Journal of the Royal Statistical Society Series B,1951,13(3):1-45.
[9] 国家体育总局.全民健身活动中心命名资助暂行办法[EB/OL].2008-06-12[2014-09-01].http://www.sport.gov.cn/n16/n33193/n33208/n33418/n33598/642310.html.
[10] 刘文卿.试验设计[M].北京:清华大学出版社,2005.
[11] LOEPPKY J L,SACKS J,WELCH W J.Choosing the Sample Size of a Computer Experiment:A Practical Guide[J].Technometrics,2009(51):366-376.
[12] CAVAZZUTI M.Optimization Methods:from Theory to Design [M].Berlin:Spring-Verlag,2013.
[13] 李坚.代理模型近似技术研究及其在结构可靠度分析中的作用[D].上海:上海交通大学,2013.