0 引 言
桁架式多腔体钢板组合剪力墙在双钢板内的钢腔及端柱内灌注混凝土,采用平面钢筋桁架作为钢板间的连接件,钢筋桁架由弯折的钢筋和角钢焊接而成,角钢通过焊接机器人自动焊接在两侧钢板内侧[1]。该组合墙体能够充分利用钢材与混凝土的组合效应,即钢腔内的混凝土约束钢腔较早产生屈曲,而钢材壁板的约束作用使得腔内的混凝土处于空间受压状态,两者相互作用保证发挥混凝土抗压的同时,提高钢板稳定承载力。
桁架式多腔体钢板组合剪力墙用于框架-剪力墙结构中需要与钢梁可靠连接,墙-梁连接节点是结构体系的重要组成部分,其抗震性能对结构的抗震性影响显著。近年来,国内外学者对组合结构连接节点的抗震性能研究多集中于钢管混凝土柱梁节点[2-4],但对墙-梁节点研究较少[5]。
本文参考已有方钢管混凝土柱梁节点构造形式,提出4类不同构造的桁架式多腔体钢板组合剪力墙与H型钢梁节点,利用有限元软件ANSYS对4种类型的墙梁节点在拟静力工况下的受力性能进行了系统研究,得到各节点试件的滞回能力、破坏特征等分析结果,并与试验结果进行对比。同时对钢梁翼缘和竖向外肋板部位的应力分布进行分析,进一步揭示节点的破坏过程。
1 有限元模型的建立
1.1 模型设计
本文提出的4类不同构造的墙-梁节点包括标准节点、盖板节点、立板节点和全板节点,节点构造如图1所示。
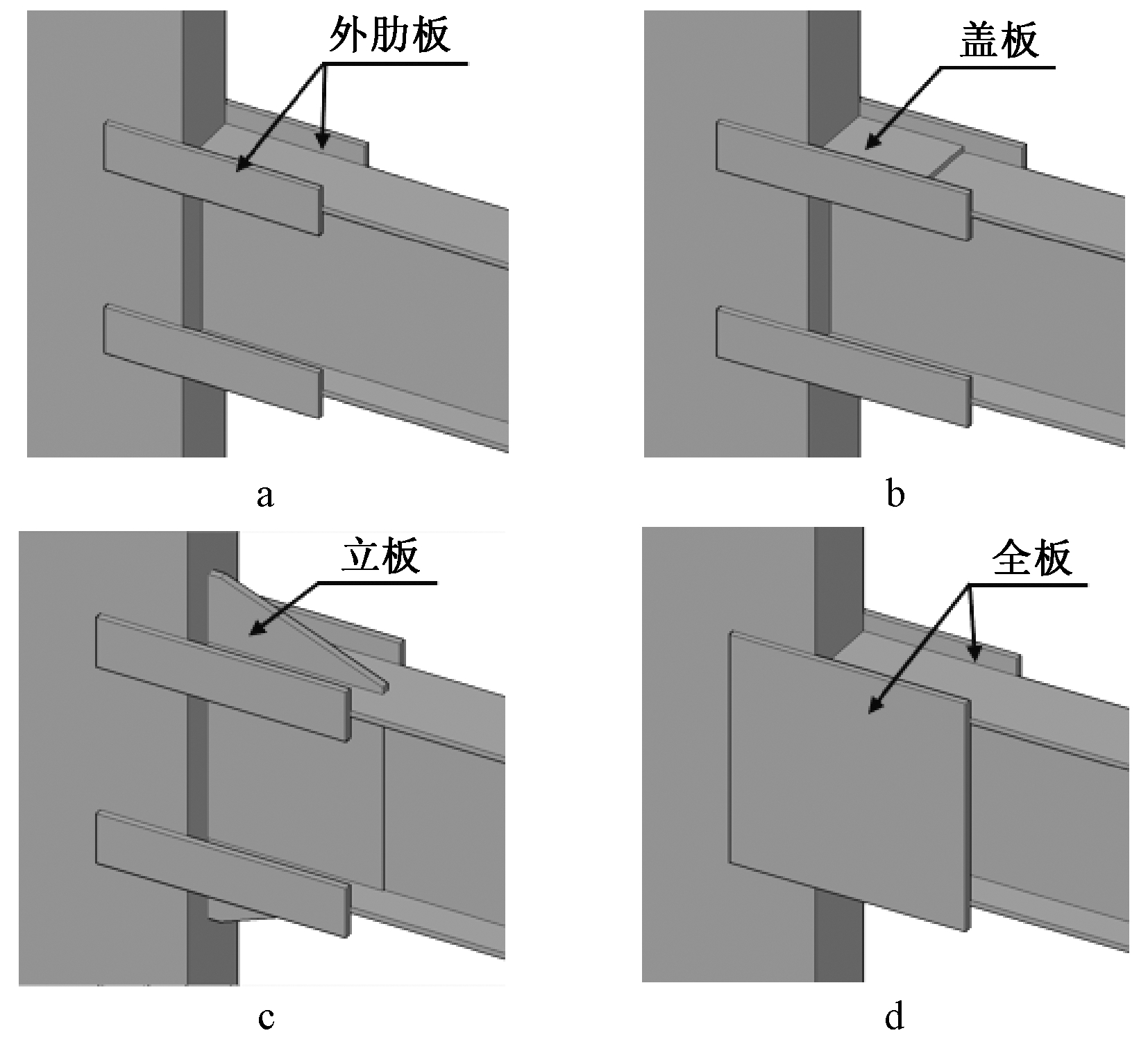
a—标准节点;b—盖板节点;c—立板节点;d—全板节点。
图1 墙-梁节点构造
Fig.1 Configuration of wall-beam connections
共设计了4个不同构造的桁架式多腔体钢板组合剪力墙与H型钢梁节点足尺模型,模型的墙体均为桁架式多腔体钢板组合剪力墙,墙体尺寸均为1 500 mm×150 mm×3 000 mm,墙体壁厚为4 mm,墙体由两侧端柱外加双钢板焊接组成,中间由钢筋桁架将中部墙体分为多腔,钢筋桁架间距为200 mm,腔内灌注混凝土。钢梁截面尺寸均为H400×150×8×12。墙体及钢梁的钢材均为Q235B钢材,混凝土强度等级为C25,试件参数见表1,材性结果见表2。
表1 模型设计参数
Table 1 Design parameters of models

编号墙体尺寸/mm梁长/mm轴压比n说明QL-11500×150×300017500.2标准节点QL-21500×150×300017500.2盖板节点QL-31500×150×300017500.2立板节点QL-41500×150×300017500.2全板节点
由于各节点试件的墙体和钢梁尺寸相同,因此以标准节点为例给出模型大样如图2所示,各模型节点区(虚线框部分)放大如图3所示。竖向外肋板与钢梁翼缘采用双面角焊缝,与墙体端柱采用三面围焊连接;盖板与端柱采用“大坡口焊”[6];立板与端柱采用对接焊缝,与钢梁翼缘和腹板分别采用角焊缝和对接焊缝连接。
表2 材性试验结果
Table 2 Properties of steel plates and concrete
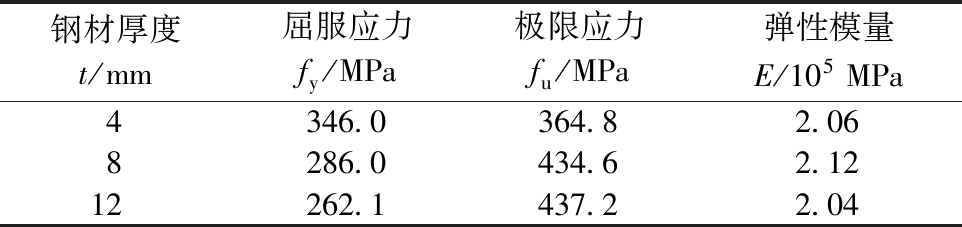
钢材厚度t/mm屈服应力fy/MPa极限应力fu/MPa弹性模量E/105MPa4346.0364.82.068286.0434.62.1212262.1437.22.04
注:混凝土的立方体试块抗压强度标准值为23.9 MPa。

1—端柱□150×150×4;2—竖向外肋板,t=12 mm;3—悬臂梁段H400×150×8×12;4—钢筋桁架φ8。
图2 节点大样
Fig.2 Detail drawing of the joint
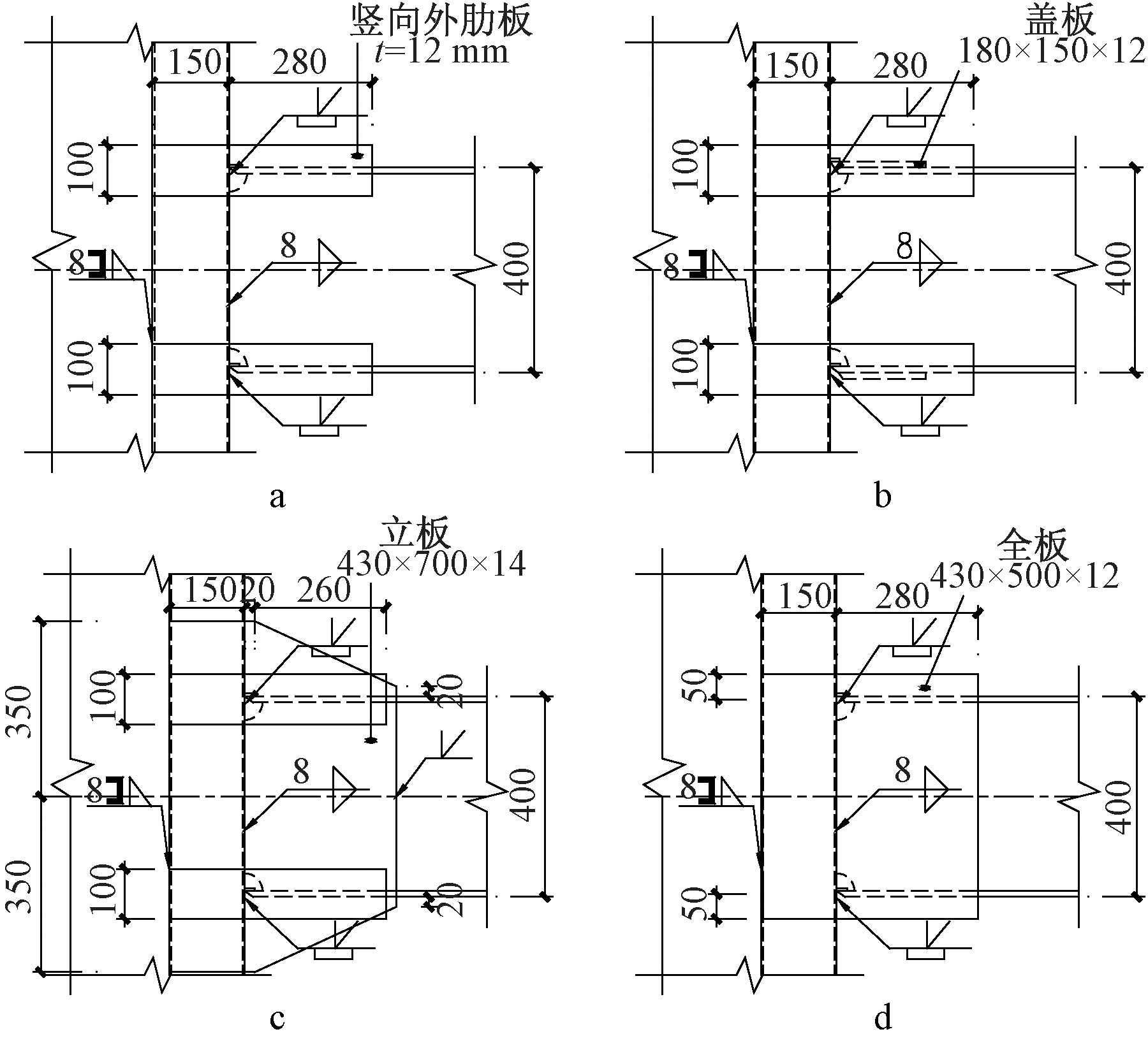
a—标准节点;b—盖板节点;c—立板节点;d—全板节点。
图3 节点区构造详图
Fig.3 Detail drawing of joint zone
1.2 材料本构模型
材料本构关系中,节点的钢材采用Q235B。钢材的本构模型选用三折线模型,图中三段直线分别代表为弹性段、强化段和水平段。钢材本构的特征参数取值为:σy=310 MPa,σu=440 MPa,E=206 000 MPa,Et=6 200 MPa,钢材的泊松比为ν=0.3[6],钢材本构模型见图4。
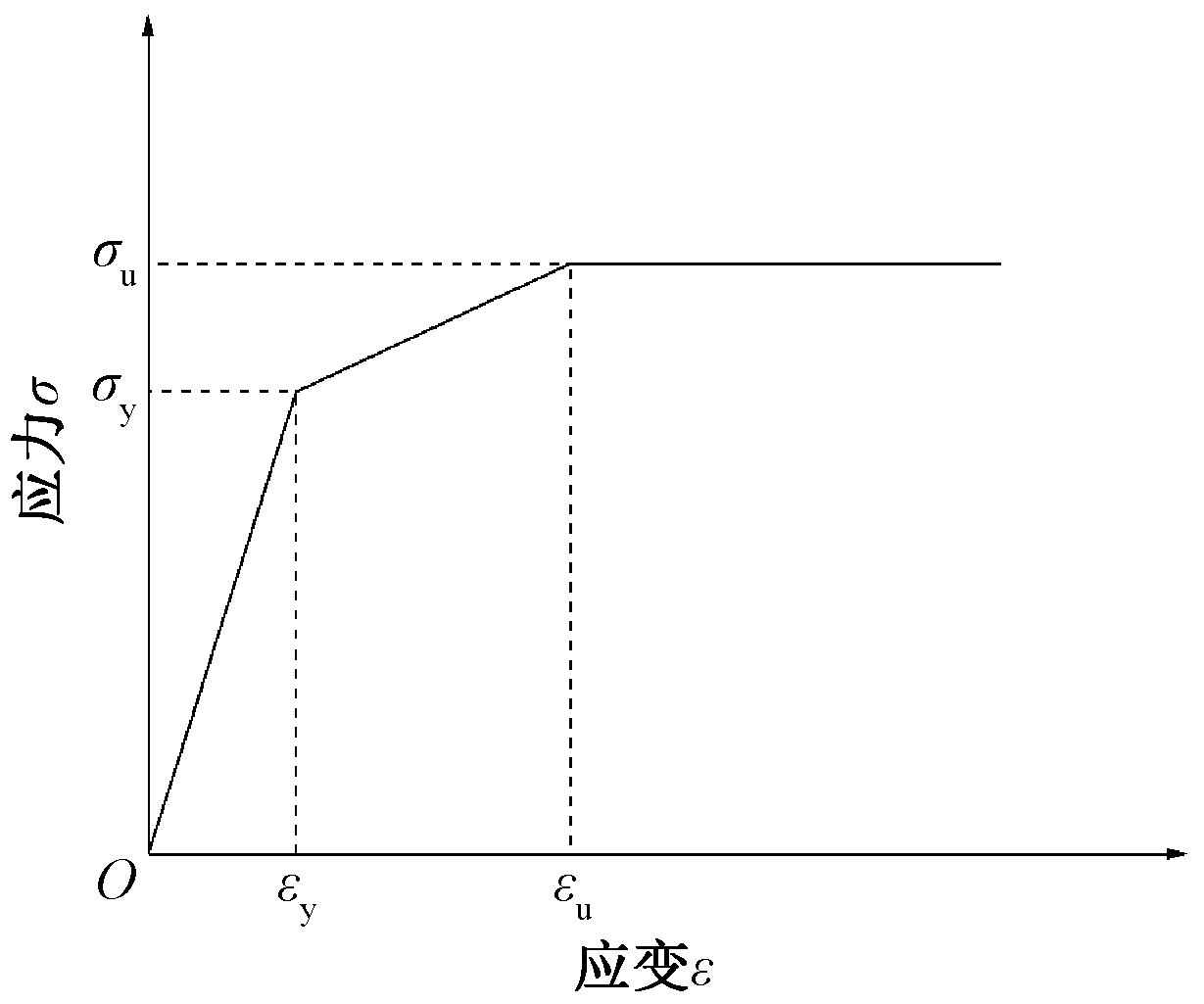
图4 钢材本构模型
Fig.4 Steel constitutive model
混凝土是一种脆性且具有各向异性特性的材料,国内外学者基于不同的力学理论建立了各种本构关系模型。对于钢管混凝土结构,比较有代表性的为韩林海建立的核心区混凝土本构模型[7],该模型的主要参数与截面含钢率有关,本文的多腔体钢板组合剪力墙体钢腔壁厚仅有4 mm,钢腔对混凝土的约束作用有限,故本文选用GB 50010—2010《混凝土结构设计规范》采用的模型[8]。混凝土为C25,各参数取值为:ftk=2.01 MPa,fck=20.1 MPa,Ec=1 970 MPa,ν=0.2。混凝土本构模型见图5。
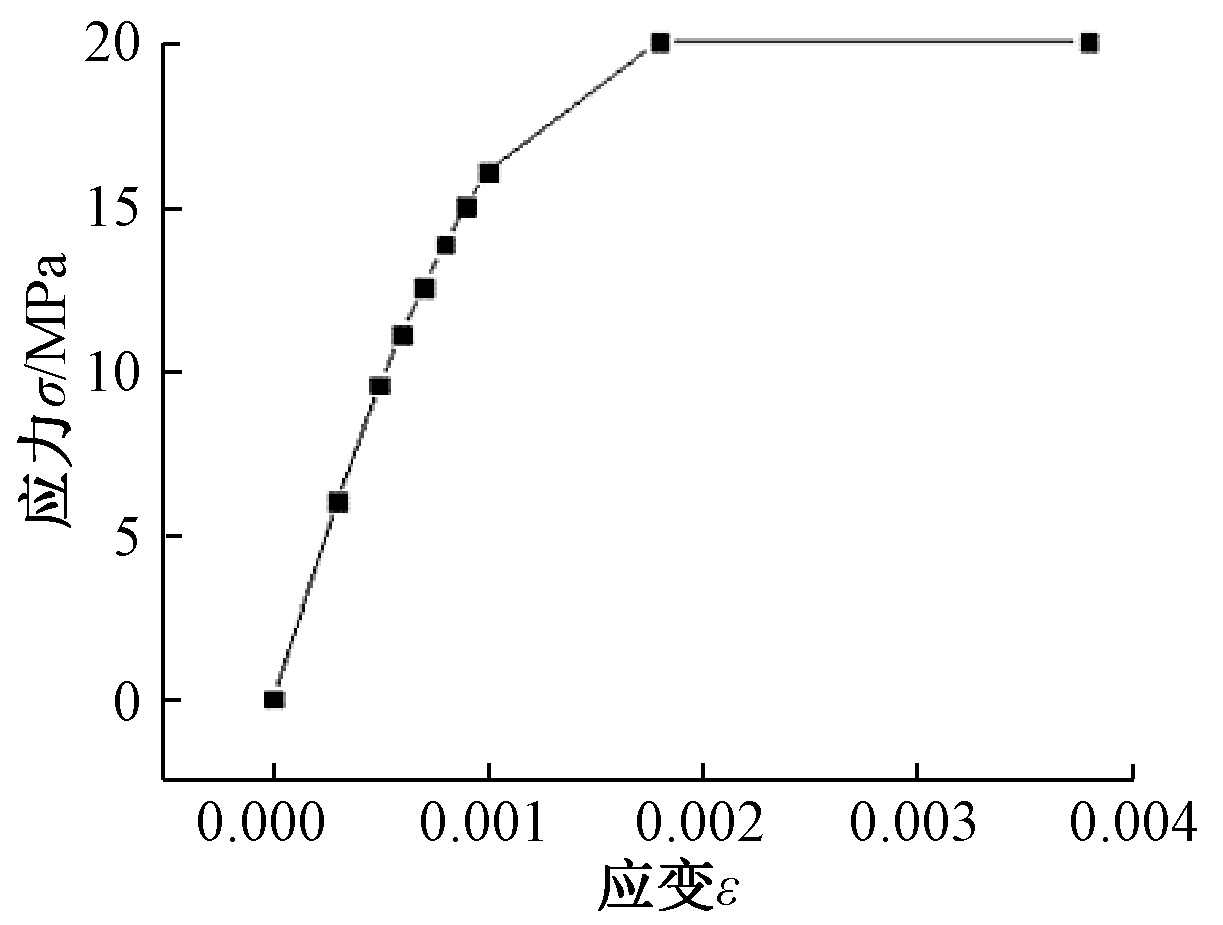
图5 混凝土本构模型
Fig.5 Concrete constitutive model
在有限元模型中,混凝土采用多线性等向强化模型(MISO),采用等向强化Mises屈服准则。钢材采用双线性随动强化模型(BKIN),采用Mises屈服准则和随动强化准则。
1.3 单元选用及网格划分
钢板和钢梁选用Solid 45单元,该单元是8结点6面体单元,用于模拟3D实体结构。混凝土选用Solid 65单元,该单元称为3D加筋混凝土单元,可用于模拟无筋或加筋的3D实体结构,Solid 65与Solid 45相似,但可以模拟混凝土的弹性开裂(三个正交方向)、压碎、塑性变形和收缩徐变,同时考虑钢筋的轴向变形、塑性发展,忽略钢筋的剪切。本文主要研究钢腔与钢梁的变形与破坏,未见混凝土压碎,因此为了便于收敛,在分析时关闭混凝土压碎功能[9]。
连接钢板两侧角钢的钢筋桁架采用梁单元Beam 188,该单元属于三维空间线单元,每个单元由2个结点组成,每个结点包含6个或7个自由度,可以考虑剪切变形。
为了模拟组合剪力墙体钢腔与混凝土的接触行为,模型采用Targe 170单元和Conta 174单元引入目标面和接触面。在端柱与柱内混凝土、端柱与腔内混凝土、腔内混凝土与钢板、角钢肢尖与腔内混凝土和角钢肢背与腔内混凝土之间建立接触对。
网格划分采用自由网格划分与映射网格划分相结合的方法,对墙体与钢梁连接节点域部分采用较小的网格尺寸进行划分,远离节点域部分则降低网格密度。
1.4 边界条件与加载制度
墙梁连接节点单元是从结构中墙体上下1/2墙高范围中抽取出来的,其中组合剪力墙上下端部的边界条件为刚接,用来模拟墙体不存在反弯点的约束条件,组合剪力墙上端部不存在面外变形。在ANSYS中,选中组合剪力墙端部所有结点直接施加结点约束。在组合剪力墙底端和顶端施加X、Y、Z三个方向的平动约束。在钢梁自由端将端板上沿墙体高度方向结点的竖向自由度(Z向)进行耦合,并限制Y方向的平动以避免钢梁发生侧向失稳[10],如图6所示。
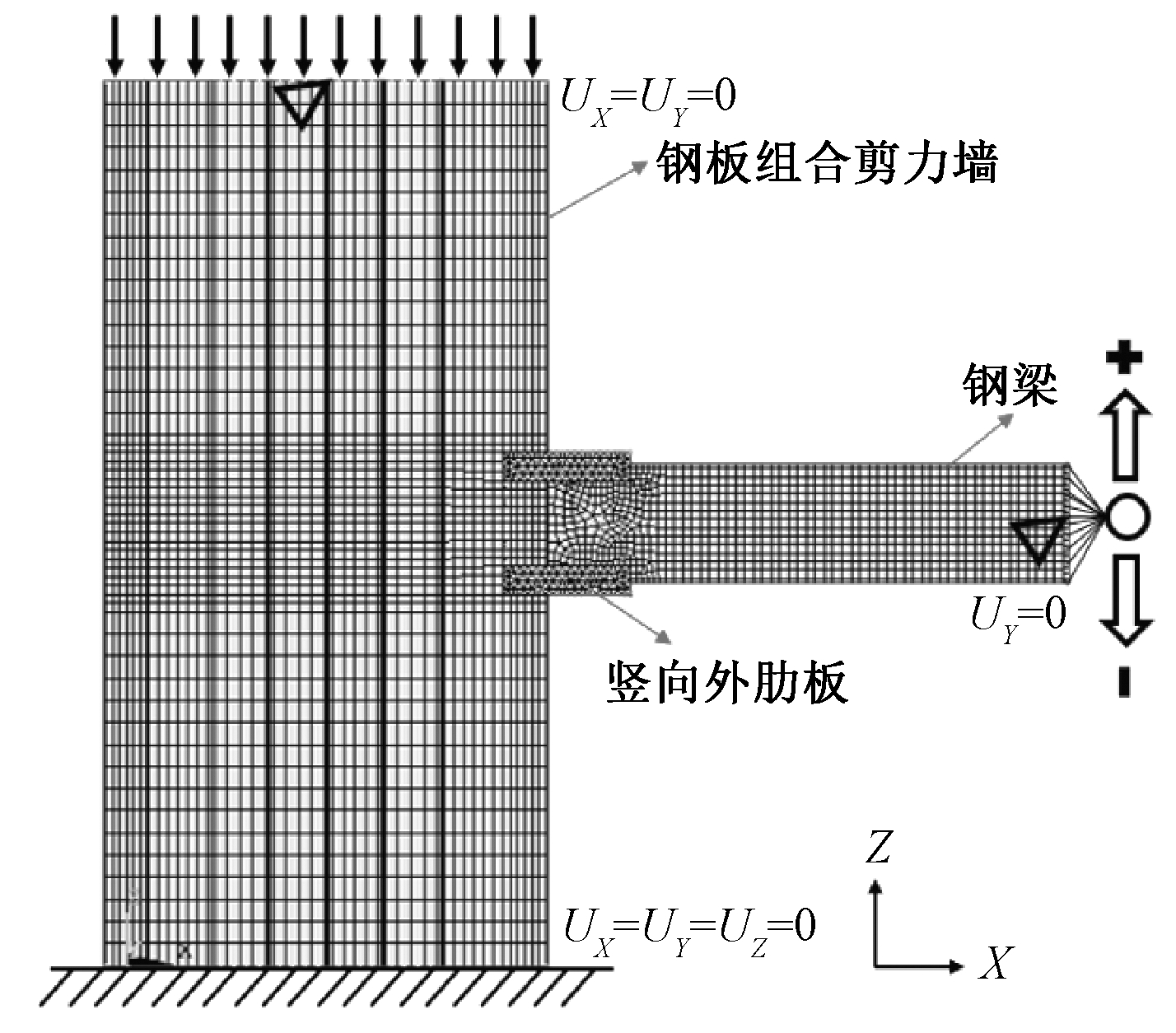
图6 节点模型边界条件
Fig.6 Boundary conditions of finite element model
有限元的荷载分步施加。第一荷载步施加墙端的轴压力,采用自动时间步(AUTOTS),按0.2轴压比施加于墙体顶端,分10~20个子步进行施加;从第二荷载步开始,在梁端耦合点上施加低周往复循环荷载。先按±0.5Fy、±0.75Fy、±0.9Fy进行三级力加载,分10~50个子步进行施加,每级荷载步循环一次。达到屈服位移之后,按10 mm的级差进行位移加载,分20~200个子步进行施加,每个荷载级别循环3次。
2 有限元分析结果
2.1 破坏特征
为了研究节点在循环加载过程中的应力状态,本文以QL-1为例,采用von Mises应力云图进行分析,同时与文献[11]中的试验结果做对比,验证有限元模型的正确性。
从图7可以看出,有限元计算分析所得的高应力区和变形模态与试验结果基本一致。试件进行到-30 mm位移加载过程中,有限元应力云图表明,高应力区集中在钢梁上翼缘与外肋板对接位置处和竖向外肋板与桁架式多腔体钢板组合剪力墙墙体端柱接合处,据此推测这两个位置在节点进入塑性后发生破坏的可能性较高。加载后期,钢梁翼缘受压鼓曲,并相继发现有翼缘开裂现象,-70 mm位移荷载级别时,试件上翼缘表面在外肋板端部位置处断裂并扩展至钢梁腹板,有限元分析结果与试验吻合较好。
2.2 滞回曲线
提取有限元计算所得与文献[11]中试验相同荷载级别的滞回曲线,与MTS得到滞回曲线比对,如图8所示。不难发现两者吻合较好,同时有限元计算中因为没有考虑焊缝及其残余应力等不利因素,加之边界约束条件较为理想,因此其所得的滞回曲线更加饱满(对比QL-2及QL-3试件与有限元的滞回曲线,可以发现,实际构件中发生节点端部焊缝撕裂,直接引起节点承载力退化,而ANSYS中未考虑焊缝的影响,未发生明显的强度退化)。

a—上翼缘裂缝扩展至腹板;b—下翼缘鼓曲。
注:各分图中左图为试验现象,右图为有限元分析结果。
图7 节点破坏时现象对比
Fig.7 Comparison of failure characteristic

a—QL-1(标准节点);b—QL-2(盖板节点);c—QL-3(立板节点);d—QL-4(全板节点)。
图8 滞回曲线对比
Fig.8 Comparison of hysteretic curves
进一步观察可以发现:有限元分析计算所得滞回曲线与MTS作动器提取的滞回曲线在卸载阶段的曲线斜率相差很小,由此表明,有限元分析节点的整体刚度和试验中节点的实际刚度十分接近;对于弹性段有限元分析所得的曲线斜率略高于试验所得曲线,分析原因可能是装置之间存在间隙,使得加载过程中梁端位移内包含着试件的整体平移,表现出来试件的刚度较小;加载后期,则由于出现侧向变形,使得试验所得梁端荷载有所偏大。
2.3 骨架曲线
ANSYS计算得到的节点QL-1~QL-4的骨架曲线见图9。
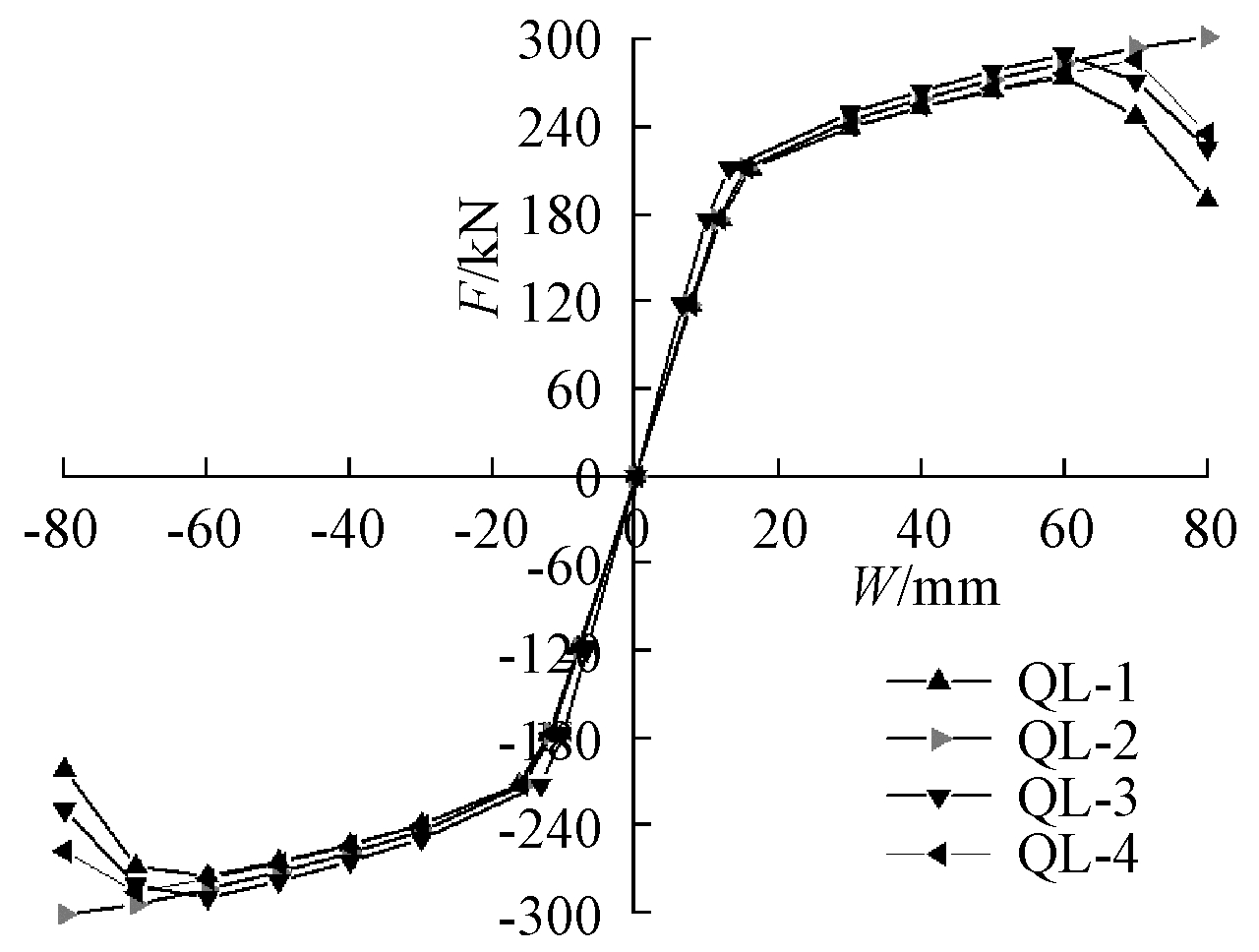
图9 骨架曲线对比
Fig.9 Comparison of skeleton curves
可以看出,有限元分析所得各试件的骨架曲线基本关于原点对称,在进入塑性后曲线下降平缓,说明理想状态下该新型节点延性较好;4种不同构造形式的节点试件的骨架曲线在力持荷阶段保持为线性,屈服后梁翼缘边缘进入塑性,骨架曲线斜率降低,加载至梁翼缘全部达到极限应力,塑性铰形成,骨架曲线下降明显。相较于标准竖向外肋板节点(QL-1),盖板节点、立板节点和全板节点(QL-2,QL-3和QL-4)在加载阶段后期表现出了很好的受力性能,因此,节点进入塑性后,采用盖板的方式对节点的加强作用最为显著,其次,采用立板能增加节点域的腹板厚度,也能较大程度上提高节点域的抗剪承载力。相比于标准节点,加强效果稍弱的是全板节点,分析原因为中间板对梁截面的惯性矩增大作用有限。
2.4 节点梁翼缘应力分布
从沿梁翼缘横向应力分布(图10)可以看出,加载初期各测点的应力分布保持线性,随着荷载的增大,梁翼缘表面应力值线性上升。各节点模型的翼缘测点峰值应力均出现在距离梁端约300 mm(竖向外肋板的长度)处。随着荷载的进一步加大,钢梁翼缘应力达到屈服强度后,原本的应力峰值点处由于腹板相继进入屈服状态,参与承担节点抗弯的贡献达到最大而不再增大。观察应力数值可以发现,距墙壁300 mm范围以外的梁翼缘相继达到极限应力,根据分析结果不难发现,塑性铰长度逐渐增长,这种应力分布模式与塑性铰出现的试验现象吻合较好。
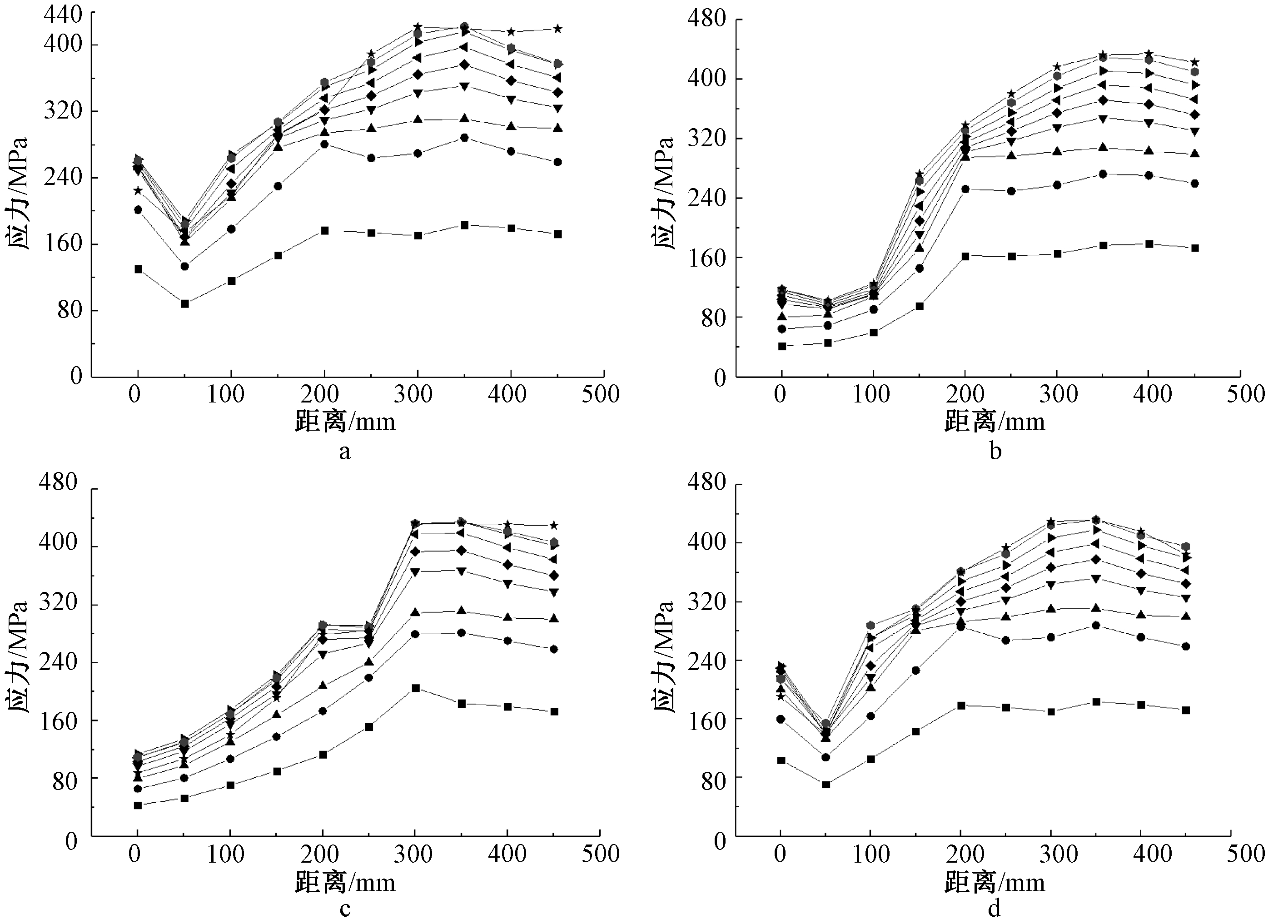
a—QL-1(标准节点);b—QL-2(盖板节点);c—QL-3(立板节点);d—QL-4(全板节点)。![]() —0.5Fy;
—0.5Fy;![]() —0.75Fy;
—0.75Fy;![]() —0.9Fy;
—0.9Fy;![]() —30 mm;
—30 mm;![]() —40 mm;
—40 mm;![]() —50 mm;
—50 mm;![]() —60 mm;
—60 mm;![]() —70 mm;
—70 mm;![]() —80 mm。
—80 mm。
图10 梁翼缘横向应力分布
Fig.10 Transverse stress distribution of flange
3 结束语
通过对4个不同构造形式的桁架式多腔体钢板组合剪力墙与H型钢梁连接节点试件和模型进行数值模拟研究,表明节点满足GB 50011—2010《建筑抗震设计规范》的设计要求,可以在桁架式多腔体钢板组合剪力墙结构中应用。结论如下:
1)4个不同构造的节点模型破坏前在钢梁翼缘处均出现了明显的塑性变形,避免了墙体的破坏,塑性铰外移明显,表明本文提出的墙-梁节点符合“强墙弱梁,强节点弱构件”的原则。
2)各个模型的滞回曲线都较为饱满稳定,整体都呈梭形,无捏拢现象,表明4类节点形式均具有较好的抗震性能。
3)4种节点构造均能实现塑性铰的外移,竖向外肋板在整个加载过程中处于弹性工作状态,满足使用要求。
[1] QIN Y,SHU G P,ZHOU X L,et al.Height-Thickness Ratio on Axial Behavior of Composite Wall with Truss Connector[J].Steel and Composite Structures,2019,30(4):315-325.
[2] 聂建国,秦凯,张桂标.方钢管混凝土柱内隔板式节点的抗弯承载力研究[J].建筑科学与工程学报,2005,22(1):42-49.
[3] 庄磊.方管柱-H型钢梁隔板贯通式节点抗震性能研究[D].上海:同济大学,2006.
[4] 陈志华,苗纪奎.方钢管混凝土柱-H型钢梁外肋环板式节点研究[J].工业建筑,2005,35(10):61-63.
[5] 李杰.钢管束组合剪力墙与钢梁节点抗震性能研究[D].天津:天津大学,2015.
[6] 中华人民共和国住房和城乡建设部.钢结构设计标准:GB 50017—2017[S].北京:中国建筑工业出版社,2018.
[7] 韩林海.钢管混凝土结构:理论与实践[M].北京:科学出版社,2007.
[8] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S].北京:中国建筑工业出版社,2016.
[9] 王新敏,李义强,许宏伟.ANSYS结构分析单元与应用[M].北京:人民交通出版社,2011.
[10] 林坤洪.新型方钢管柱与H型钢梁下贯上环隔板式节点受力性能研究与应用[D].南京:东南大学,2016.
[11] QIN Y,SHU G P,ZHANG H K,et al.Experimental Cyclic Behavior of Connection to Double-Skin Composite Wall with Truss Connector[J].Journal of Constructional Steel Research,2019,162:1-17.