目前,我国建筑行业已进入新建与维修并重的阶段,由于施工质量低下、外部灾害损伤、设计用途改变等因素,许多建筑物不仅无法满足日常使用要求,更成为潜在安全隐患,危害群众生命财产安全,必须进行加固维修,因此采用何种加固技术已成为一项热点问题。传统的加固技术,加固材料往往要等混凝土构件发生较大的横向变形才能发挥作用,主动约束效果差,而预应力加固技术在构件发生较大横向变形前便对构件施加水平或环向预应力,更早发挥加固材料约束作用。预应力钢带加固技术通过使用打包机在混凝土构件表面等间距布置钢带,起到限制构件横向变形和提高构件承载力的作用,具有施工方便、节约成本等优点。
杨勇等对预应力钢带加固混凝土构件的研究表明经钢带加固后,构件的轴压承载力、抗剪承载力及侧移刚度和耗能能力均有较大提升[1-4];张磊等对预应力钢带加固混凝土偏压柱受力性能的研究表明:钢带加固构件的初裂荷载及极限承载力显著提高,极限荷载对应的侧向挠度增大,变形能力增强[5];陈建华对预应力钢带加固火灾后型钢混凝土柱抗震性能的研究表明,火损后经钢带加固的构件,其承载力较火损后未加固构件明显提高[6]。
目前针对这项加固技术的试验大多基于小尺寸混凝土构件,与工程实际存在差异,有关预应力钢带加固混凝土构件尺寸效应的研究未见报道。相关研究表明:FRP加固混凝土构件[8-10]的力学性能存在尺寸效应,本文在已有钢带加固柱轴压性能试验研究[11]基础上,采用ANSYS建立相应分析模型,利用试验结果验证模型正确性,并分析构件截面尺寸对构件轴向力学性能的影响,建立考虑尺寸效应的预应力钢带加固柱轴压承载力计算式。
1 有限元分析模型
1.1 材料的本构关系
混凝土采用德国Rüsch建议的模型(图1),该模型上升段为二次抛物线,下降段为水平直线:
ε≤ε0
(1a)
σ=fc
ε0≤ε≤εcu
(1b)
式中:fc为混凝土轴心抗压强度;取ε0=0.002;εcu=0.003 5。
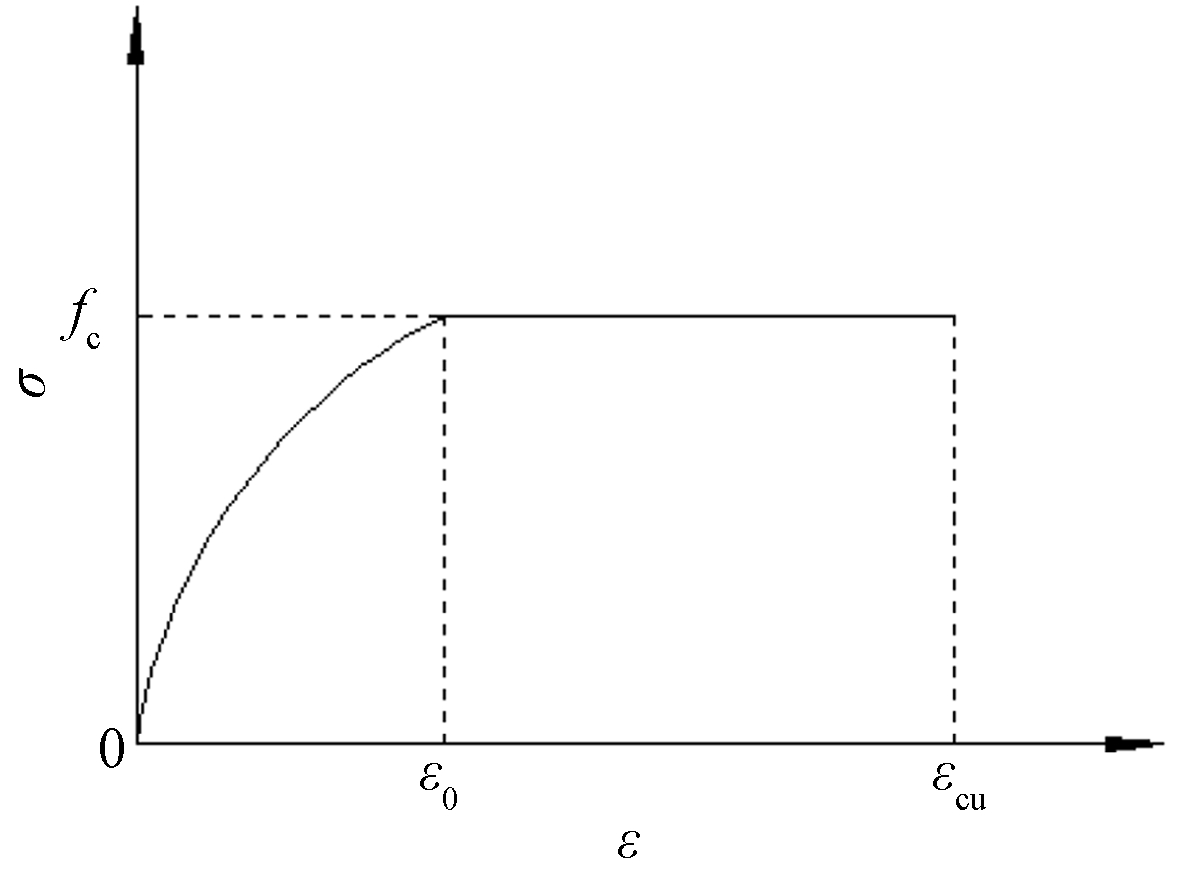
图1 混凝土应力应变曲线
Fig.1 Concrete stress-strain curve
钢筋采用双折线模型(图2),该模型不计屈服强度上限和由于应变硬化而增加的应力:
σx=Exεs
εs≤εy
(2a)
σx=fy
εy≤εs≤εs,h
(2b)
其中 Ex=fy/εy
式中:fy及εy为钢筋弹性阶段屈服下限对应的应力及应变;εs,h为钢筋塑性阶段应力强化对应的应变。
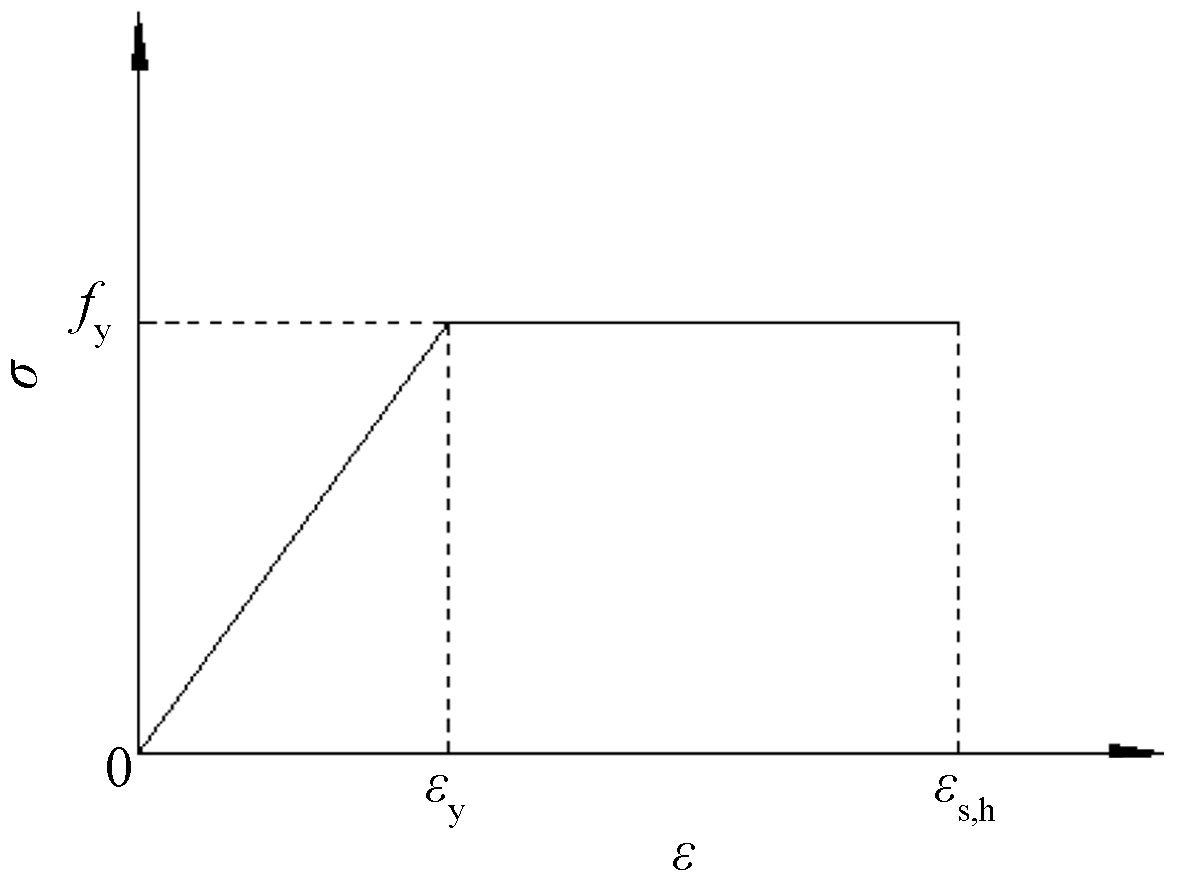
图2 钢筋应力应变曲线
Fig.2 Steel bar stress-strain curve
钢带本构模型同钢筋。
1.2 界面的模拟
研究表明加固构件因钢带间未受约束的混凝土破坏失效引起构件发生破坏[11],破坏时钢带、钢筋并未与混凝土发生滑移或剥离现象。模型中混凝土、钢筋与钢带三者之间完全黏结,不考虑相对滑移和剥离破坏,使用约束方程对钢筋单元与混凝土单元建立约束,使用“MERGE”命令合并钢带单元与混凝土单元的结点。
1.3 单元选取及网格划分
使用Link 180单元模拟钢筋,该单元可模拟钢筋受拉压行为;使用Solid 65单元模拟混凝土,该单元可模拟混凝土的开裂、压碎等力学现象;使用Shell 41单元模拟钢带,该单元通过参数设置可仅承受压应力或拉应力。采用映射网格划分技术,各单元网格模型见图3。
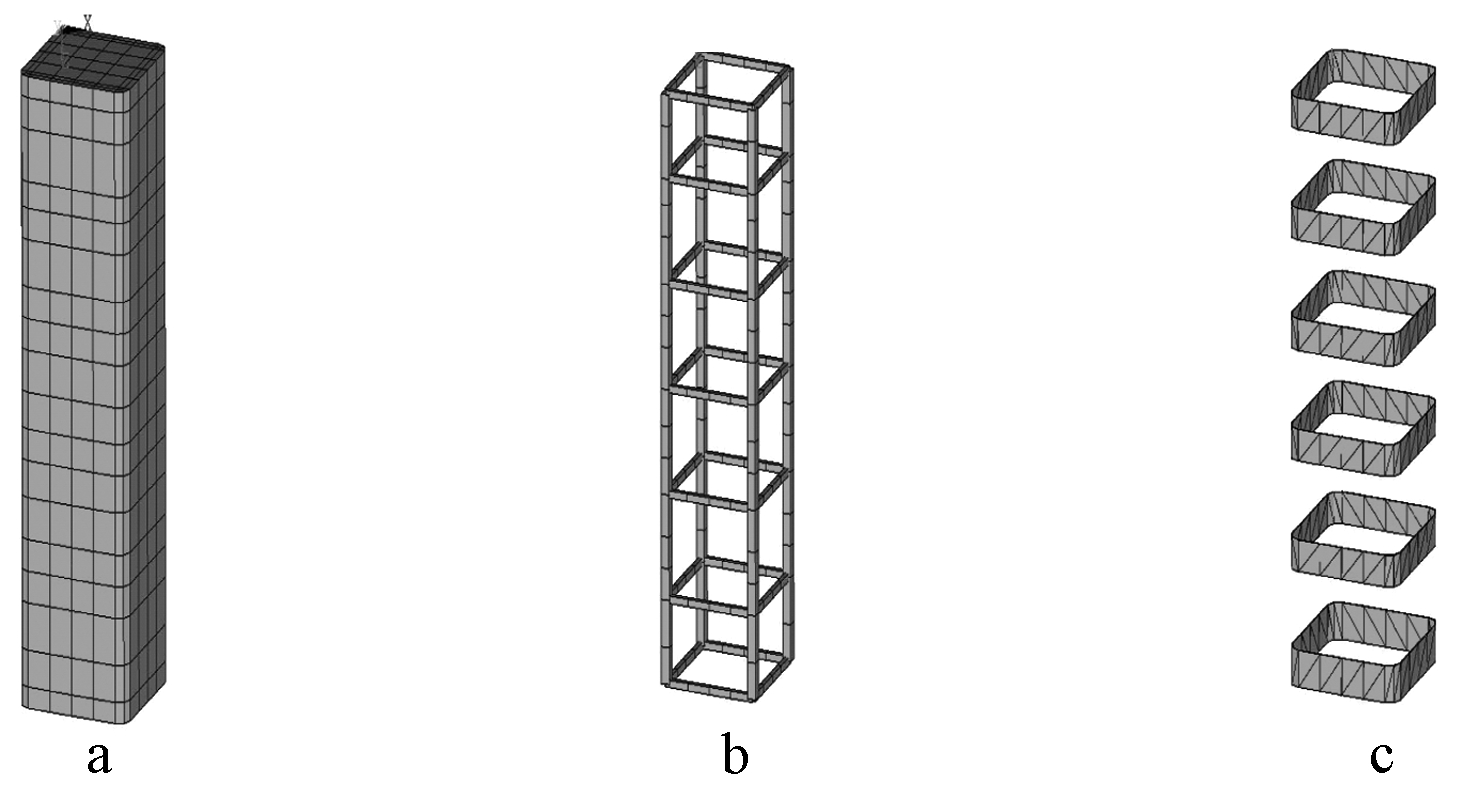
a—混凝土网格模型; b—钢筋网格模型; c—钢带网格模型。
图3 有限元模型
Fig.3 Finite element models
1.4 边界条件及加载
通过对钢带单元定义温度膨胀系数,施加温度荷载使钢带单元收缩,对构件施加侧向约束应力;施加荷载时,对柱底部ux、uy、uz和柱顶部ux、uy共五个方向自由度进行固定,构件顶部uz方向自由度施加位移载荷,保证柱顶只产生竖向位移。
1.5 有限元模型验证
采用上述建模方法,对已有试验[11]中的构件建模并进行轴压分析。构件承载力试验值和模拟值结果见表1,两者比值的平均值为1.005,比值的方差为0.036,吻合程度较好。
表1 试验值与模拟值
Table 1 Test values and simulated values
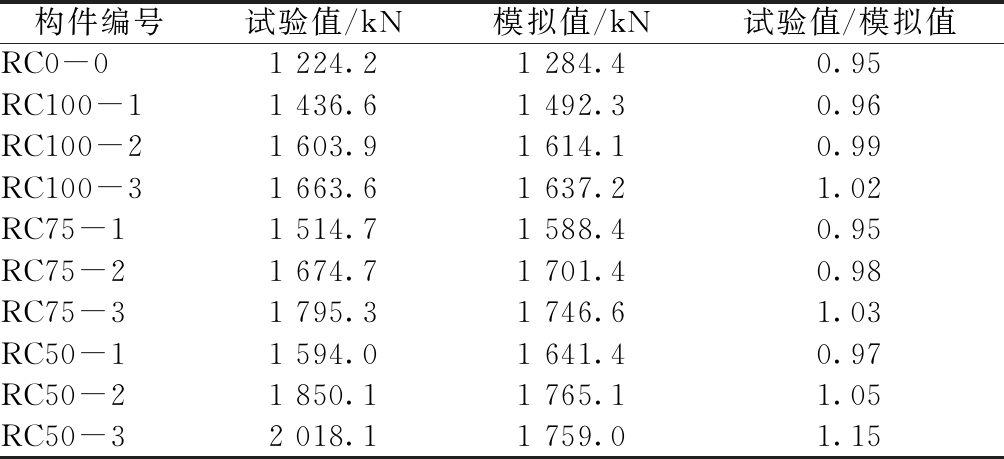
构件编号试验值/kN模拟值/kN试验值/模拟值RC0-01 224.21 284.40.95RC100-11 436.61 492.30.96RC100-21 603.91 614.10.99RC100-31 663.61 637.21.02RC75-11 514.71 588.40.95RC75-21 674.71 701.40.98RC75-31 795.31 746.61.03RC50-11 594.01 641.40.97RC50-21 850.11 765.11.05RC50-32 018.11 759.01.15
2 尺寸对轴压性能影响分析
为研究构件截面尺寸对加固构件轴压力学性能的影响,基于前文得到验证的有限元分析模型,设计了不同尺寸的构件并进行了轴压模拟。
2.1 构件尺寸设计
试验主要考虑构件截面尺寸对加固效果的影响,设计了4组构件,构件形状为矩形,尺寸分别为300 mm×300 mm×1 800 mm、400 mm×400 mm×2 400 mm、500 mm×500 mm×3 000 mm、600 mm×600 mm×3 600 mm。每组构件均有四种钢带体积配置率。构件截面保持相似关系,受到构件尺寸和钢筋直径的影响,配筋形式无法保持相同,通过控制纵筋横截面面积、箍筋横截面面积和间距、钢带间距和层数[7],保持配筋率与钢带体积配置率一致,控制无关变量。构件设计详细参数见表2。材料本构关系选取、建模过程及边界条件与加载同上文。材料属性定义: 混凝土轴心抗压强度为26.8 MPa,纵筋屈服强度为411 MPa,箍筋屈服强度为359 MPa,钢带屈服强度为778 MPa。
表2 构件设计参数
Table 2 Component design parameters
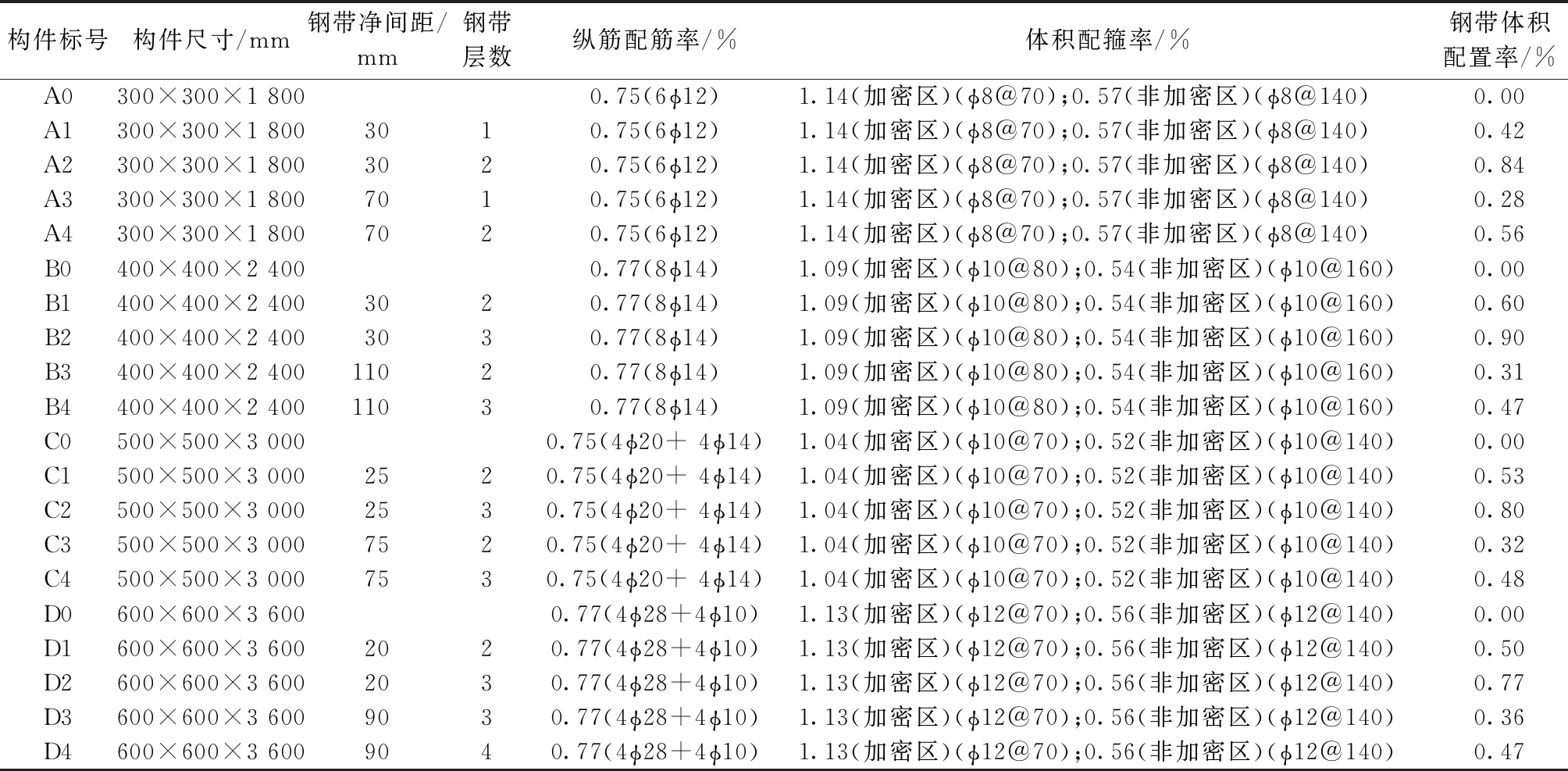
构件标号构件尺寸/mm钢带净间距/mm钢带层数纵筋配筋率/%体积配箍率/%钢带体积配置率/%A0300×300×1 8000.75(6ϕ12)1.14(加密区)(ϕ8@70);0.57(非加密区)(ϕ8@140)0.00A1300×300×1 8003010.75(6ϕ12)1.14(加密区)(ϕ8@70);0.57(非加密区)(ϕ8@140)0.42A2300×300×1 8003020.75(6ϕ12)1.14(加密区)(ϕ8@70);0.57(非加密区)(ϕ8@140)0.84A3300×300×1 8007010.75(6ϕ12)1.14(加密区)(ϕ8@70);0.57(非加密区)(ϕ8@140)0.28A4300×300×1 8007020.75(6ϕ12)1.14(加密区)(ϕ8@70);0.57(非加密区)(ϕ8@140)0.56B0400×400×2 4000.77(8ϕ14)1.09(加密区)(ϕ10@80);0.54(非加密区)(ϕ10@160)0.00B1400×400×2 4003020.77(8ϕ14)1.09(加密区)(ϕ10@80);0.54(非加密区)(ϕ10@160)0.60B2400×400×2 4003030.77(8ϕ14)1.09(加密区)(ϕ10@80);0.54(非加密区)(ϕ10@160)0.90B3400×400×2 40011020.77(8ϕ14)1.09(加密区)(ϕ10@80);0.54(非加密区)(ϕ10@160)0.31B4400×400×2 40011030.77(8ϕ14)1.09(加密区)(ϕ10@80);0.54(非加密区)(ϕ10@160)0.47C0500×500×3 0000.75(4ϕ20+ 4ϕ14)1.04(加密区)(ϕ10@70);0.52(非加密区)(ϕ10@140)0.00C1500×500×3 0002520.75(4ϕ20+ 4ϕ14)1.04(加密区)(ϕ10@70);0.52(非加密区)(ϕ10@140)0.53C2500×500×3 0002530.75(4ϕ20+ 4ϕ14)1.04(加密区)(ϕ10@70);0.52(非加密区)(ϕ10@140)0.80C3500×500×3 0007520.75(4ϕ20+ 4ϕ14)1.04(加密区)(ϕ10@70);0.52(非加密区)(ϕ10@140)0.32C4500×500×3 0007530.75(4ϕ20+ 4ϕ14)1.04(加密区)(ϕ10@70);0.52(非加密区)(ϕ10@140)0.48D0600×600×3 6000.77(4ϕ28+4ϕ10)1.13(加密区)(ϕ12@70);0.56(非加密区)(ϕ12@140)0.00D1600×600×3 6002020.77(4ϕ28+4ϕ10)1.13(加密区)(ϕ12@70);0.56(非加密区)(ϕ12@140)0.50D2600×600×3 6002030.77(4ϕ28+4ϕ10)1.13(加密区)(ϕ12@70);0.56(非加密区)(ϕ12@140)0.77D3600×600×3 6009030.77(4ϕ28+4ϕ10)1.13(加密区)(ϕ12@70);0.56(非加密区)(ϕ12@140)0.36D4600×600×3 6009040.77(4ϕ28+4ϕ10)1.13(加密区)(ϕ12@70);0.56(非加密区)(ϕ12@140)0.47
2.2 试验结果
通过ANSYS后处理器可得到构件轴向位移,并对加载端处结点力轴向力求和,可得到构件轴压承载力。定义名义强度:
σ=F/A
(3)
式中:F为构件轴向承载力;A为构件净横截面面积,采用名义强度σ以描述构件轴向抗压强度。定义名义应变:
ε=ΔL/L
(4)
式中:ΔL为构件轴向位移;L为构件原长,采用名义应变ε以描述构件轴向变形程度,各个构件模拟试验结果见表3。
2.3 σ-ε曲线
图4为不同尺寸构件名义强度名义应变曲线。构件相似时,不同截面尺寸构件的σ-ε曲线存在差异,弹性阶段,小尺寸构件曲线斜率相对大尺寸构件曲线斜率更大,小尺寸构件最终名义强度σ和名义应变ε较大尺寸构件更大。
表3 模拟试验结果
Table 3 Simulation test results

构件编号轴压承载力F/kN轴向位移ΔL/mm名义强度σ/MPa名义应变ε/10-6A02 7103.53930.291 966A12 9453.88432.912 158A23 0464.39634.042 442A32 8553.63131.922 017A42 9573.90933.052 172B04 7934.57430.131 906B15 1465.09532.322 123B25 2655.55633.072 315B34 9904.65831.181 941B45 0545.02831.582 095C07 4875.53530.071 845C17 9145.98531.781 995C28 0956.36032.512 120C37 7285.62831.041 876C47 8295.92231.441 974D010 6876.48429.791 800D111 2036.86931.241 908D211 3867.43031.742 064D311 0016.55630.671 821D411 1556.89431.101 915
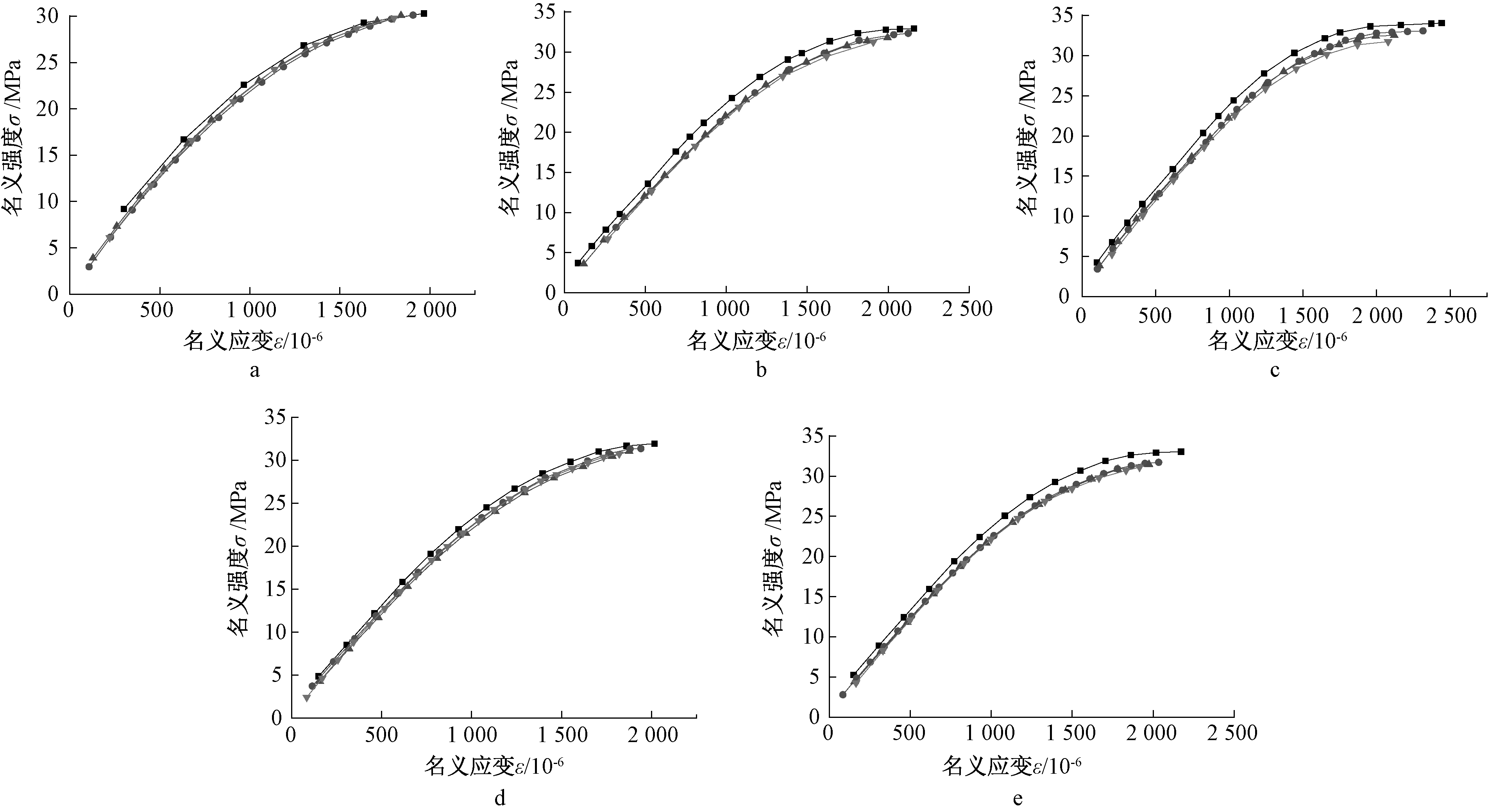
a—A0~D0; b—A1~D1; c—A2~D2; d—A3~D3; e—A4~D4。 ![]() —A0~A4;
—A0~A4; ![]() —B0~B4;
—B0~B4; ![]() —C0~C4;
—C0~C4;![]() —D0~D4。
—D0~D4。
图4 名义强度σ-名义应变ε曲线
Fig.4 Relationship between nominal strength σ and nominal strain ε
2.4 尺寸对强度加固效果的影响
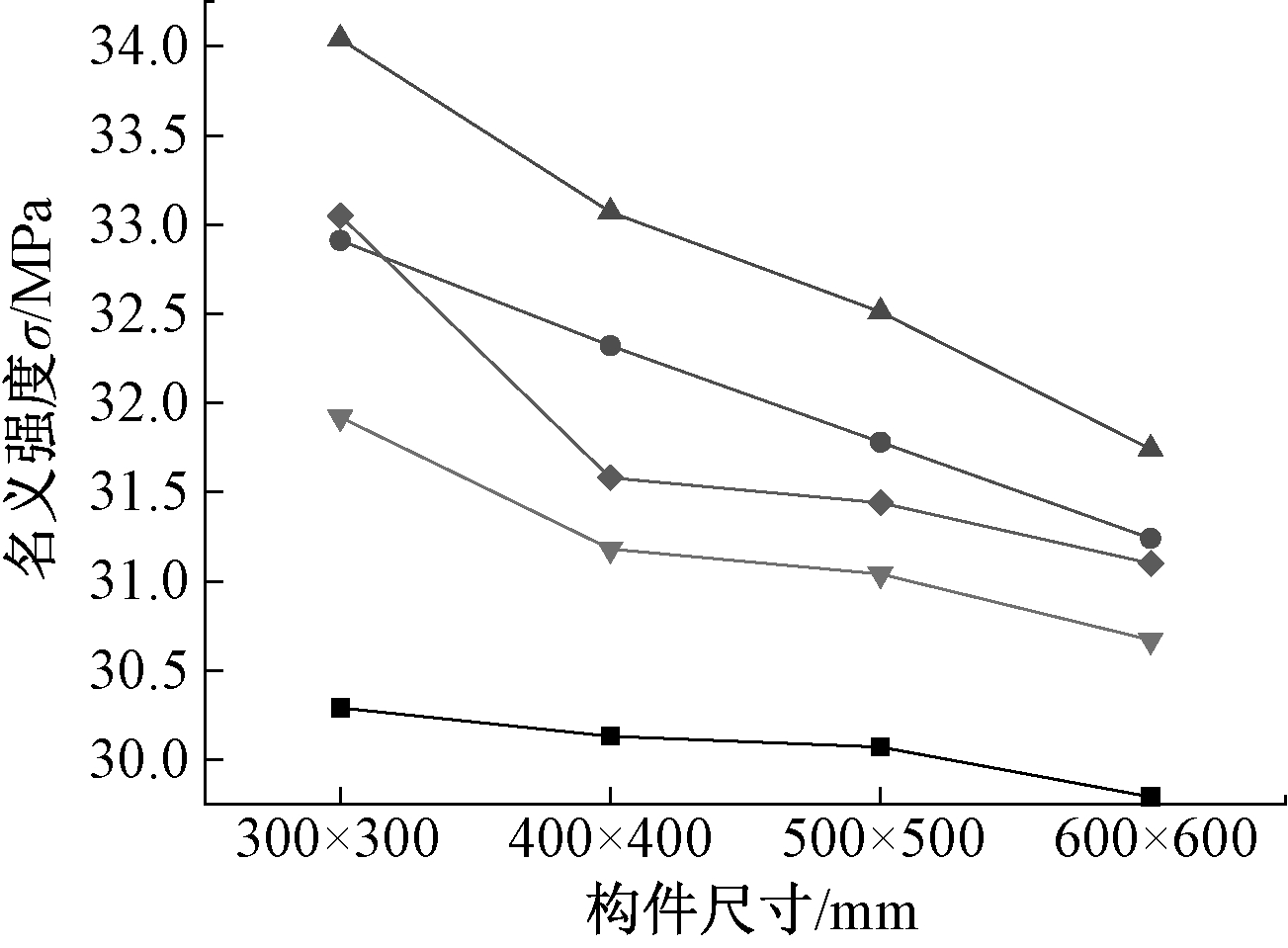
图5为构件名义强度σ-构件尺寸关系曲线。由图5可知:相较未加固构件,经钢带加固后,不同尺寸构件名义强度均有提升;当加固构件尺寸从 300 mm×300 mm 增加到 600 mm×600 mm时,不同钢带体积配置率的构件名义强度均呈下降趋势。
![]() —A0、B0、C0、D0;
—A0、B0、C0、D0; ![]() —A1、B1、C1、D1;
—A1、B1、C1、D1; ![]() —A2、B2、C2、D2;
—A2、B2、C2、D2; ![]() —A3、B3、C3、D3;
—A3、B3、C3、D3; ![]() —A4、B4、C4、D4。
—A4、B4、C4、D4。
图5 名义强度σ-构件尺寸关系曲线
Fig.5 Reeationship between nominal strength σ and member size
图6为各尺寸构件名义强度σ提升幅度与构件尺寸的柱状图。由图6可知:当构件尺寸从300 mm×300 mm增加到600 mm×600 mm时,各组加固构件名义强度提升幅度呈下降趋势,构件相似时,钢带对构件的轴向抗压强度的加固效果随构件尺寸的上升而下降。
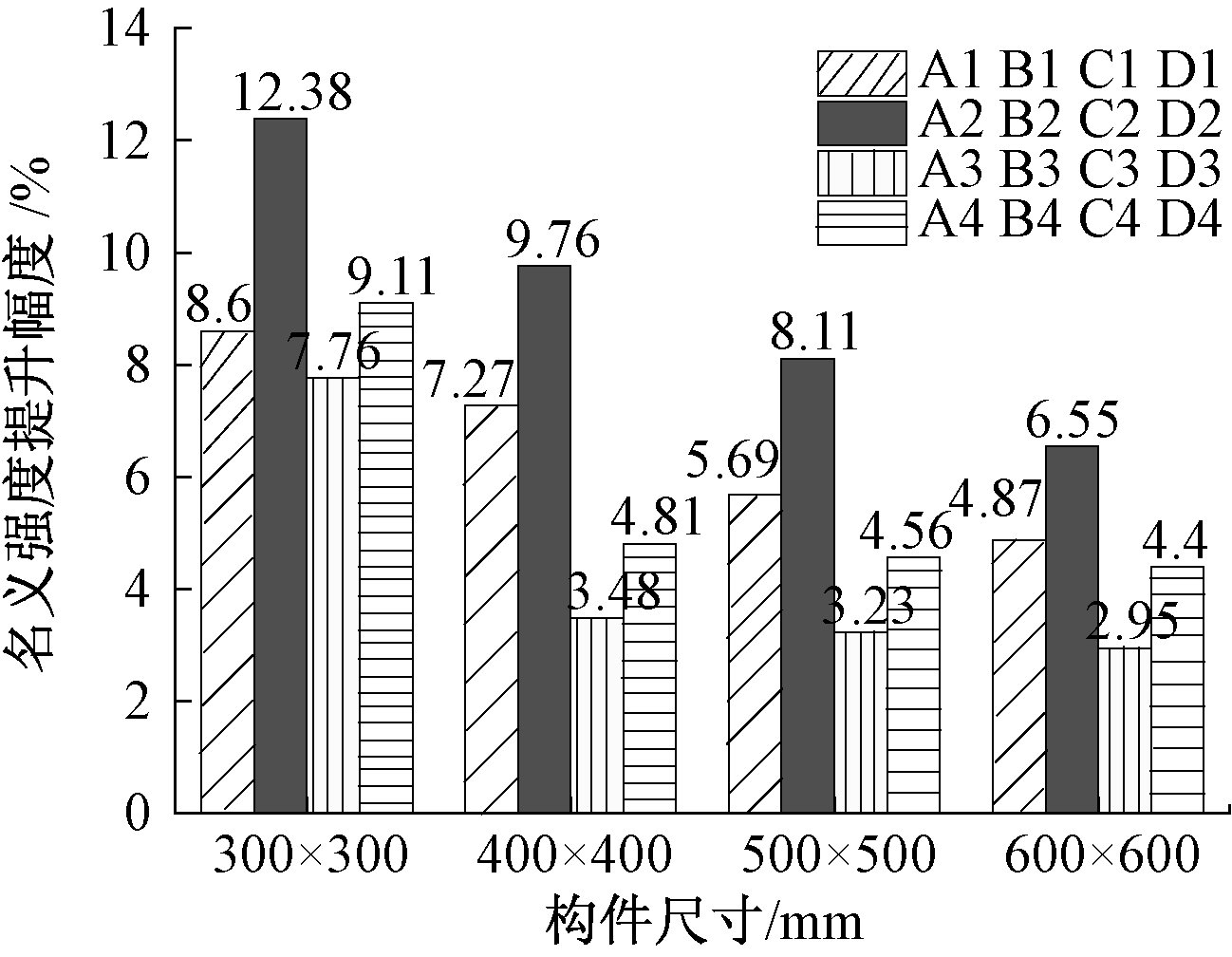
图6 名义强度σ提升幅度与构件尺寸的柱状图
Fig.6 Histogram of nominal strength σ enhancement and component size
分析上述现象,以Mander创立的有效约束区模型[12]为例,该模型中有效约束区如图7所示。
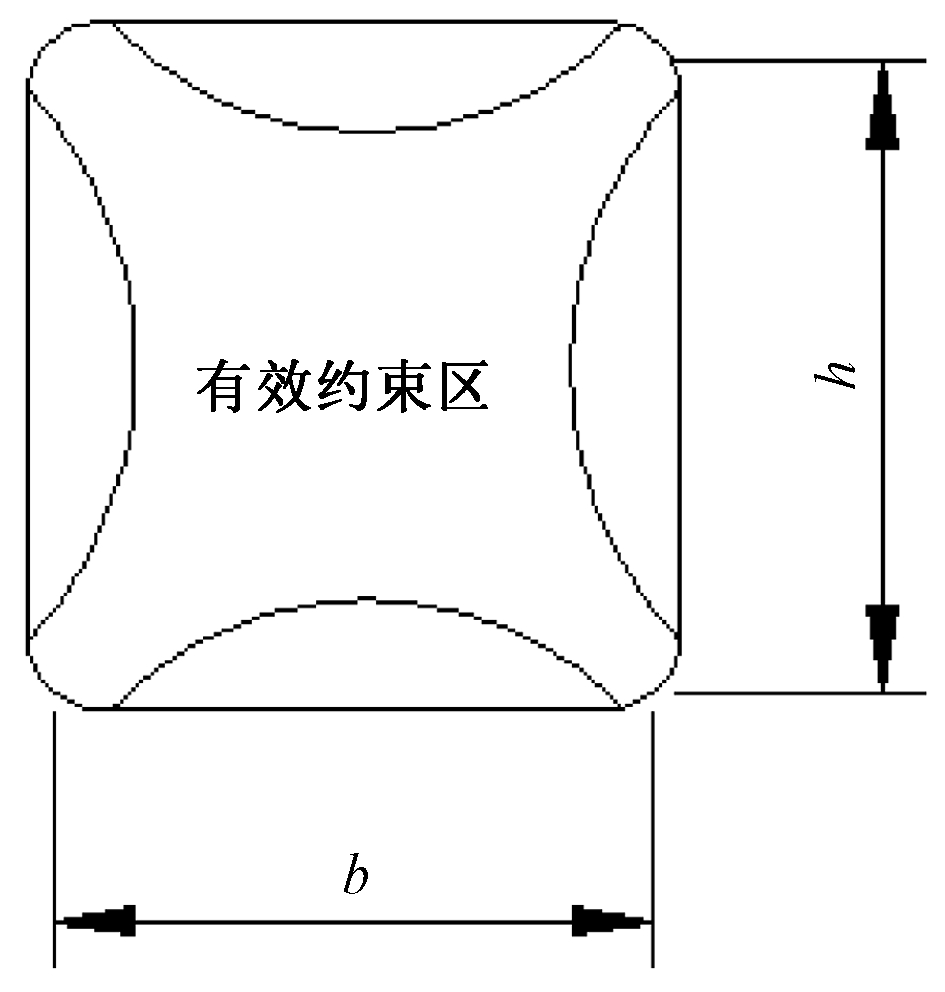
图7 有效约束区域
Fig.7 Effective constraint area
当轴压荷载引起构件内部的混凝土应力到达临界应力后,混凝土发生横向体积膨胀使钢带受拉,导致钢带对混凝土的侧向约束作用变强。由于有效约束区内角部的混凝土受到钢带约束作用较中部的混凝土更强,所受侧向约束应力更大,在混凝土三向受压时,角部的混凝土轴向的抗压强度较中部的混凝土增长更多。当构件表面钢带体积配置率一致且施加相同的预应力度时,构件表面受到的钢带侧向约束应力fel一致,相较小尺寸构件有效约束区内中部的混凝土,大尺寸构件有效约束区内中部的混凝土由于距离其角部处钢带更远,钢带对其约束作用更弱,所受侧向约束应力更小,因此大尺寸构件中部混凝土轴向的抗压强度增长程度较之小尺寸构件更小,构件整体抗压强度提升幅度下降。
以A2、B2、C2、D2四组构件为例,图8为A2、B2、C2、D2四组构件受钢带约束处混凝土横截面轴向应力云图。由图可知,四组构件轴向应力云图分布形状符合有效约束区模型,角部混凝土相较中部混凝土受钢带约束效果更强,轴向应力更大;A2中部混凝土轴向应力为31.902 2 MPa,B2中部混凝土轴向应力为30.349 2 MPa,C2中部混凝土轴向应力为29.957 6 MPa,D2中部混凝土轴向应力为29.288 3 MPa,应力值随着构件截面尺寸的增大而减小,符合上述分析。
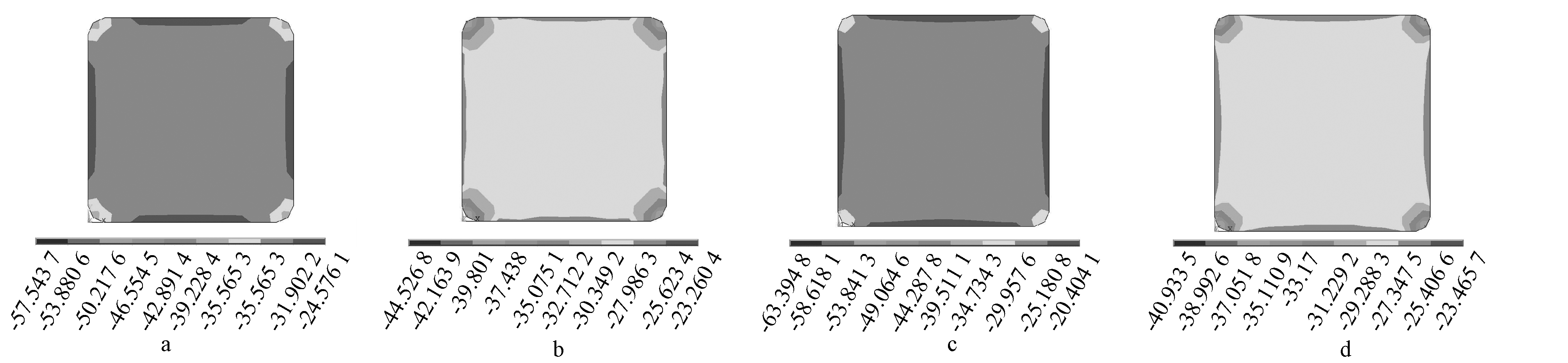
a—A2; b—B2; c—C2; d—D2。
图8 轴向应力云图MPa
Fig.8 Axial stress nephogram
2.5 尺寸对刚度加固效果的影响
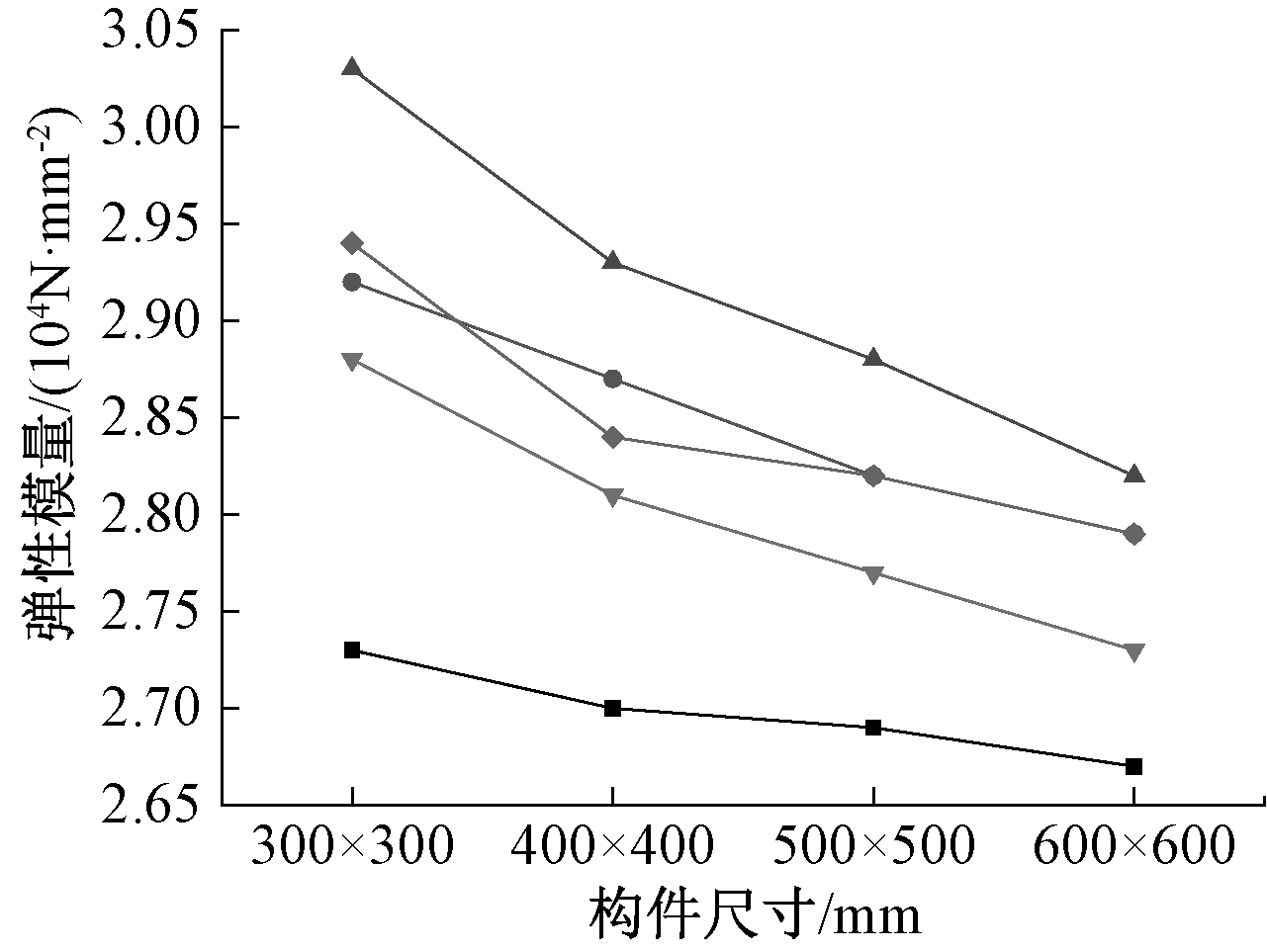
根据胡克定律ε=σ/E,可知σ-ε曲线斜率值大小等于弹性模量E,采用该指标可侧面反映构件轴向刚度大小。比较不同尺寸构件的曲线斜率,可知弹性阶段小尺寸加固构件的刚度较大尺寸构件更大。为定量描述构件尺寸对刚度加固效果的影响,采用ORIGIN数据处理软件,对弹性阶段曲线数据点处求切线处理,可得到各曲线斜率值。图9为不同尺寸构件σ-ε曲线对应的弹性模量E和构件尺寸的关系曲线,由图可知弹性模量E随着构件尺寸的增大而减小。
![]() —A0、B0、C0、D0;
—A0、B0、C0、D0; ![]() —A1、B1、C1、D1;
—A1、B1、C1、D1; ![]() —A2、B2、C2、D2;
—A2、B2、C2、D2; ![]() —A3、B3、C3、D3;
—A3、B3、C3、D3; ![]() —A4、B4、C4、D4。
—A4、B4、C4、D4。
图9 弹性模量E-构件尺寸关系曲线
Fig.9 Relationship between elastic modulus E and component size
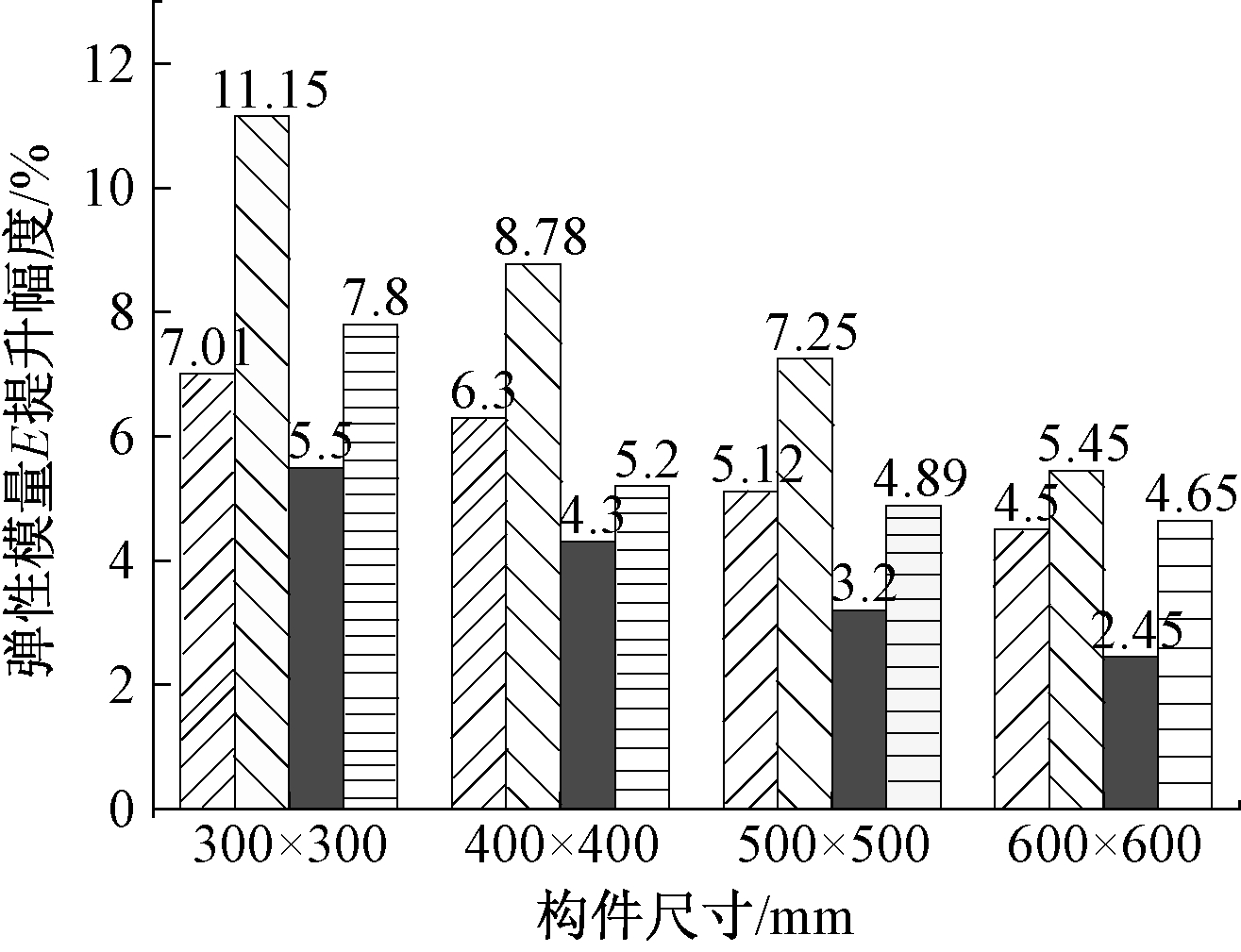
图10为不同尺寸构件曲线弹性模量E提升幅度与构件尺寸的柱状图。由图10可知:当构件截面从300 mm×300 mm增加到600 mm×600 mm时,各组加固构件曲线的弹性模量E提升幅度呈下降趋势,构件相似时,钢带对构件轴向刚度的加固效果随构件尺寸的上升而下降。
![]() A1、B1、C1、D1;
A1、B1、C1、D1;![]() A2、B2、C2、D2;
A2、B2、C2、D2; ![]() A3、B3、C3、D3;
A3、B3、C3、D3;![]() A4、B4、C4、D4。
A4、B4、C4、D4。
图10 弹性模量E提升幅度与构件尺寸的柱状图
Fig.10 Histogram of elastic modulus E enhancement and component size
分析上述现象原因,当相似构件受到相同的钢带侧向约束应力时,大尺寸构件中部混凝土因距离钢带角部区更远,所受钢带约束作用越弱,当受到轴压荷载时,大尺寸构件中部的混凝土会因侧向约束较弱,更易发生轴向变形,宏观上表现为轴向刚度的下降。
通过对不同尺寸构件名义强度σ和弹性模量E分析可知,对于相似构件,钢带加固效果随构件尺寸的增大而减小,引起构件抗压强度和轴向刚度下降,表明钢带加固效果存在尺寸效应,应对现有钢带加固柱轴压承载力计算式进行修正。
3 承载力尺寸效应计算式
钢带加固柱轴压承载力分为三部分:未约束混凝土受压承载力fcoAcor、纵向钢筋受压承载力fyAs、钢带约束混凝土提高的承载力(fcc-fco)Ae,按照式(5)计算:
N=fcoAcor+fyAs+(fcc-fco)Ae
(5)
其中![]()
式中:fco为未约束混凝土抗压强度;Acor为核心混凝土面积;fy为纵筋屈服强度;As为纵筋截面面积;fcc为钢带约束混凝土抗压强度;Ae为钢带约束混凝土有效面积;bc为混凝土柱边长;r为柱倒角半径;s为钢带净间距。
钢带约束混凝土抗压强度算式参考Richart的研究[13]和Lam-Teng的研究[14],计算式如下:
(6)
其中 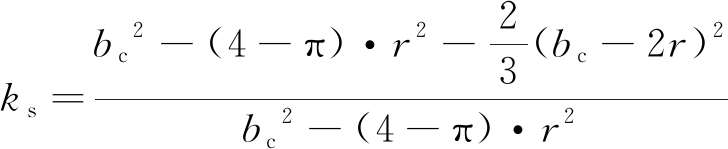
式中:k1为混凝土强度提高的有效系数; ks为截面形状影响系数;fel为钢带侧向约束应力;fg为钢带屈服应力;![]() 为钢带强度发挥系数,本文取0.52;tg为钢带总厚度;sg为钢带宽度。
为钢带强度发挥系数,本文取0.52;tg为钢带总厚度;sg为钢带宽度。
采用上述算式对数据分析,得到各组构件混凝土强度提高的有效系数K1,见表4。
表4 系数K1
Table 4 CoefficientK1
构件边长/mm300400500600K12.731.821.711.45
由表4可知:K1随着构件尺寸的增大而减小,引起fcc下降。按现有算式计算轴压承载力偏于不安全,应在原有式(6)的基础上进行修正,通过引入尺寸效应系数ke,得到考虑尺寸效应的约束混凝土抗压强度计算式:
(7)
为得到尺寸效应系数ke与构件截面几何尺寸的换算关系,利用线性、多项式、幂指数型和指数型四种函数进行数据拟合,拟合结果见表5。
表5 尺寸效应系数和几何尺寸的换算关系
Table 5 Conversion relationship between size effect coefficient and geometric size

编号拟合公式函数表达式决定系数R21线性拟合ke=-0.17x+1.130.817 72多项式拟合ke=0.05x2-0.38x+1.270.917 43幂指数拟合ke=0.84x-0.260.843 54指数拟合ke=0.19e-0.23x0.898 7
注:x=(bc/300)2,bc为构件截面边长。
当决定系数R2的值越接近1时,拟合效果越好,则采用多项式拟合可以较好的反映ke与几何尺寸的换算关系。代入上述算式,可得不同尺寸构件的ke值见表6。
表6 尺寸效应系数ke
Table 6 Size effect coefficient ke
构件边长/mm300400500600ke0.940.750.600.55
考虑尺寸效应的钢带加固柱轴压承载力计算式如下:
N=fcoAcor+fyAs+k1kskefelAe
(8)
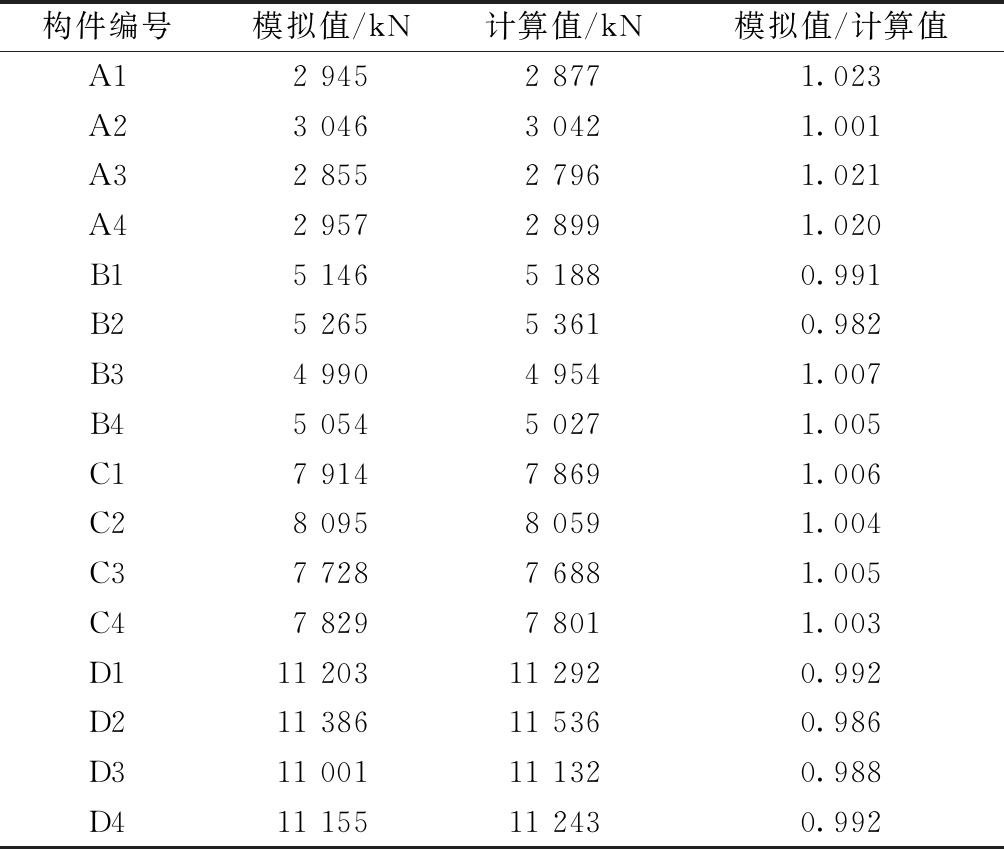
根据拟合所得的算式进行计算,结果见表7,所得的计算值和模拟值吻合度较好。
表7 模拟值与计算值
Table 7 Calculated values and simulated values
构件编号模拟值/kN计算值/kN模拟值/计算值A12 9452 8771.023A23 0463 0421.001A32 8552 7961.021A42 9572 8991.020B15 1465 1880.991B25 2655 3610.982B34 9904 9541.007B45 0545 0271.005C17 9147 8691.006C28 0958 0591.004C37 7287 6881.005C47 8297 8011.003D111 20311 2920.992D211 38611 5360.986D311 00111 1320.988D411 15511 2430.992
4 结束语
1)通过比较不同尺寸构件之间的名义强度σ和构件σ-ε曲线对应的弹性模量E,可知随着构件尺寸的增大,名义强度σ提升幅度和弹性模量E提升幅度减小,表明预应力钢带对构件轴向抗压强度和轴向刚度的加固效果存在尺寸效应。
2)根据混凝土矩形柱有效约束区模型,结合各尺寸构件的轴向应力云图,明确预应力钢带对构件的加固效果产生尺寸效应的原因。
3)分析数值模拟数据并结合ORIGIN数据处理软件,在已有承载力计算式的基础上,引入尺寸效应系数ke,通过数据拟合,得到ke和构件几何尺寸的换算关系,建立考虑尺寸效应的钢带加固柱的轴压承载力计算式。
[1]刘义,高宗棋,杨勇,等.预应力钢带加固钢筋混凝土梁柱受力性能试验研究[J].建筑结构学报,2013,34(10):120-127.
[2]杨勇,田静,刘如月.预应力钢带加固混凝土梁斜截面开裂荷载及抗剪承载能力分析[J].工业建筑,2015,45(3):19-21.
[3]杨勇,王欣林,刘义.预应力钢带加固钢筋混凝土柱轴压承载力试验研究[J].工业建筑,2012,42(增刊1):183-187.
[4]杨勇,李少语,刘义,等.预应力钢带约束混凝土轴心抗压强度试验研究[J].工业建筑,2015,45(3):1-5
[5]张磊,宁国荣,李俊华,等.预应力钢带加固钢筋混凝土柱试验研究[J].工业建筑,2016,46(3):155-159
[6]陈建华.火灾后型钢混凝士柱抗震性能及加崮修复研究[D].宁波:宁波大学,2014.
[7]BAZANT Z P, YU Q. Designing Against Size Effect on Shear Strength of Reinforced Concrete Beams Without Stirrups[J]. Journal of Structural Engineering, 2005, 131(12): 1877-1897.
[8]BASE Y H, LEE J H, YOON Y S. Prediction of Shear Strength in High-Strength Concrete Beams Consideration Size Effect[J]. Magazine of Concrete Research, 2006, 58(4): 193-200.
[9]SENE S, BARRB I G, ABUSIAF H F. Size Effect in Axially Loaded Reinforced Concrete Columns [J]. Journal of Structural Engineering, 2004, 130(4): 662-670.
[10]张波,杨勇,刘义,等.预应力钢带加固钢筋混凝土柱轴压性能试验研究[J].工程力学,2016,33(3):107-108.
[11]杜修力,符佳,张建伟.钢筋混凝土柱轴心受压性能尺寸效应的大比尺试验研究[J].土木工程学报,2010,43:2.
[12]MANDER J B , PRIESTLEY M J N, PARK R. Theoretical Stress-strain Model for Confined Concrete [J]. Journal of Structural Engineering, 1998, 114(8): 1804-1826.
[13]RICHART F E, BRANDTZAEG A, BROWN R L. A Study of Failure of Concrete Under Combined Compressive Stresses [R]. Engineering Experiment Station, University of Illinoi, Urbana,1928.
[14]LAM L, TENG J G. Ultimate Condition of Fiber Reinforced Polymer-Confined Concrete [J]. Journal of Composites for Construction, 2004, 8(6): 539-548.