1 研究概况
随着科学技术的不断发展,通过拓扑优化结合三维打印、激光切割等工具实现的智能建造,逐渐成为科学研究的热点问题。智能建造[1-3]技术的发展,可以结合传统材料和新的加工工艺,在结构的关键部分大幅度提高性能。本文的研究对象主要是轴向或切向的板式构件,通过拓扑优化和激光切割等智能建造方法,提升材料和结构的力学性能,例如空间结构中关键承重部位的轴向受压加劲板,被动耗能减震的钢板阻尼器等[4]。通过钢板的适当开孔设计,可以在保证材料和结构强度的基础上,实现其更好的延性,从而提升材料和结构的耗能能力。
负泊松比材料[5-6]拥有良好的吸声、吸振能力,将这种负泊松比效应应用在结构设计上,能够通过适当的拓扑优化设计,有效提高结构的使用性能,使其在诸如声学、耗能和阻尼等方面展现优势。本项研究通过适当的钢板开孔设计,结合负泊松比拓扑结构,设计出具有负泊松比效应的新型结构,相比传统实心构件,在满足轴向受力条件和截面积相同的条件下,实现构件耗能的最大化。
为了分析方便,本文选取典型的负泊松比结构——内凹六边形结构作为研究对象,设计了一种内凹六边形结构形式的钢板。为寻求在约束条件下能量最大的内凹六边形单元拓扑,结合响应曲面法,针对内凹六边形单元结构设计整体结构模型,并基于能量最大化准则建立目标函数,进行参数优化,确定最优的内凹六边形单元尺寸。
2 负泊松比结构模型设计
2.1 单元结构几何参数的选取
在优化过程中,优化变量是在不断变化的,故在建立模型前,须选择能够表现结构尺寸且独立的几何参数来准确表达结构的拓扑。本文选用内凹六边形负泊松比单元结构,其几何参数如图1所示。
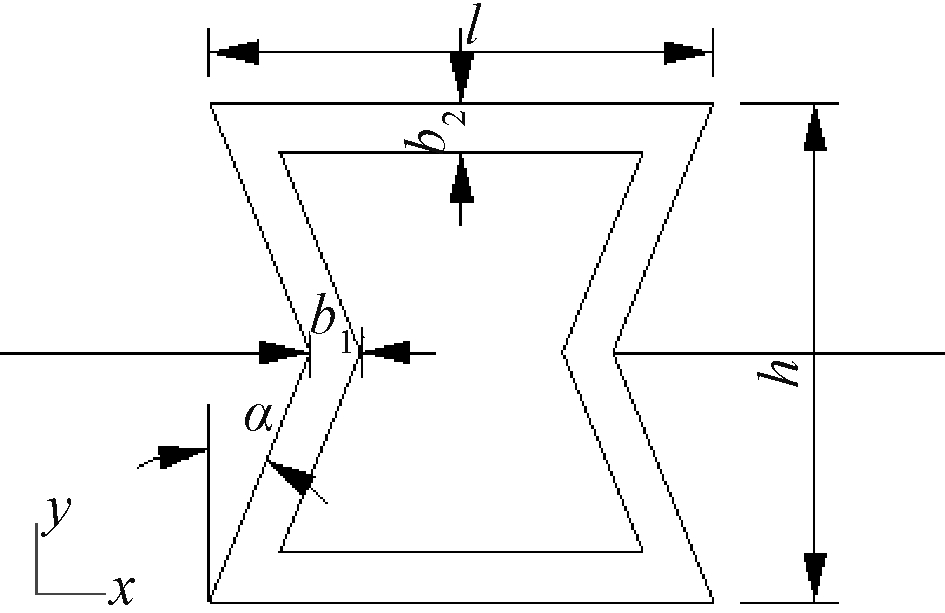
图1 内凹六边形负泊松比单元的几何参数
Fig.1 Geometrical parameters of concave hexagonal negative Poisson’s ratio unit
针对模型的几何特点,其独立参数有:纵向单元长度h、横向单元长度l、纵向单元厚度b2、横向单元厚度b1、构件厚度t、内凹角度α。
为确保模型满足刚度和承载力的要求,设计时采用Q235钢,其设计轴向承载力为100 kN。此外,为避免单元体内的“斜短柱”发生弹塑性失稳导致试件过早破坏,需确定纵向长度方向尺寸h以及横向单元厚度b1。其截面积可由承载力公式求出,如式(1)所示:
N=σsAs
(1)
式中:N为轴心承载力;σs为钢材的屈服强度;As为构件受力截面面积。
由式(1)求出As=4 255.3 mm2。
考虑到上述设计要求,试件厚度初步确定为t=20 mm,初步确定横向的开孔个数为5,则有As=6b1t,求出b1=35.5 mm,取b1=35 mm,得出内凹六边形斜短柱的截面面积为(35×20) mm2。根据斜短柱的回转半径和长细比计算式确定纵向单元长度h,如式(2)所示:
(2a)
(2b)
(2c)
式中:l0x、l0y分别为围绕截面主轴即x轴和y轴的构件计算长度;[λ]为GB 50017—2017《钢结构设计标准》[7]规定的容许长细比。
求出纵向单元长度h≤58 mm,为设计方便,h取值为55 mm。此外,为确保内凹六边形单元的物理结构实现,构型的各个独立参数还应满足一定的几何相容性约束,例如为避免结构发生图2所示的内凹尖端部重叠,可通过下列不等式达到要求:
(3)

图2 尖端重叠示意
Fig.2 Schematic diagram of tips overlap
将不等式化简,得到式(4):
(4)
在保证刚度和构型成立的前提下,最终选取的设计变量为:纵向单元长度与横向单元长度之比h/l、横向单元厚度与纵向单元厚度之比b1/b2、内凹角度α共3个参数。
2.2 约束条件
约束条件就是指在满足刚度和构型成立的前提下,各个设计变量的取值范围。
设计变量的取值范围主要依据以下几点:1)确保几何构型能够成立;2)根据断裂指标[8],单元开孔率最好控制在30%~50%;3)为了具有足够的承载力,需保证有效的截面面积。考虑到以上因素,各个设计变量的取值范围如表1所示。
表1 设计变量的取值范围
Table 1 The range of design variables

α/(°)h/lb1/b2最小值最大值最小值最大值最小值最大值5450.11110
另外,根据式(4),为了更加直观地表现3个变量之间的函数关系,用空间中的点表示不同设计变量组合下的内凹六边形单元,为了确定其在空间中的位置,以内凹角度α为x轴,纵向与横向单元长度之比h/l为y轴,横向与纵向单元厚度之比b1/b2为z轴,建立三维空间直角坐标系。将上述确定的h=55 mm、b1=35 mm代入式(4)中,得到对应的函数关系,结合表1中各个设计变量的取值范围,得出代表内凹六边形单元的点区间如图3所示。另外,由于内凹六边形单元构件的内凹尖端重叠,产生了图中虚线所示的碰撞区域,该碰撞区域中的点代表实际中因为内凹点碰撞接触而无法成立的内凹六边形单元。

图3 内凹六边形单元存在区间
Fig.3 The existence interval of the concave hexagonal unit
2.3 整体模型设计
本文设计的负泊松比整体结构几何模型如图4所示,中间部分选取内凹六边形单元交叉排列,考虑到刚度满足轴向力和截面积的要求,横向的单元数初步定为5个,厚度为20 mm,横向和纵向的长度根据变量而异。数值分析过程中,在模型两端均设置一个夹持端,夹持端不影响结构的力学性能,亦不是分析关注目标。

图4 结构整体模型
Fig.4 Configuration of overall model
3 结构优化设计
3.1 能量最大化的优化模型
优化设计的问题首先是建立数学模型[9],即把实际问题转化为数学模型的形式。通过优化模型的建立,运用各种优化方法[10-12],在满足设计要求的条件下进行迭代计算,求得目标函数的极值,得到最优设计方案。本次研究的负泊松比结构的设计变量较多,优化目标为在满足约束条件的前提下求得能量最大的构型。从模型来看,能量值应由纵向单元长度与横向单元长度之比h/l、横向单元厚度与纵向单元厚度之比b1/b2、内凹角度α三个变量组成的函数方程确定,最后根据方程中的函数关系可求得能量的最大值。本次研究的优化设计的数学模型可表述为:
Max f(X)=f(x1,x2,…,xn)
(5)
式中:X=(x1,x2,…,xn)为设计变量,即纵向单元长度与横向单元长度之比h/l、横向单元厚度与纵向单元厚度之比b1/b2、内凹角度α;目标函数f(X)为模型的能量值;![]() 和
和![]() 分别表示每个设计变量的下限和上限。
分别表示每个设计变量的下限和上限。
得到数学模型后,采用响应曲面法来拟合结构的目标函数,并求取最大值。响应曲面法[13-14]是一种有效的拓扑优化设计方法,它通过适当的设计,利用分析点的结果数据进行回归拟合,建立响应曲面模型,使用该响应模型近似地反映响应与影响因子之间的函数关系,然后再对该模型进行分析,寻找使响应输出变量最接近其目标值的自变量最佳组合。
3.2 试验点选取
Design-Expert[15-16]是由美国State-ease公司开发的优化设计软件,该软件广泛应用于多参数的优化设计和分析中。本次研究基于响应曲面法,针对能量最大化的优化目标,结合表1各参数合理的取值范围,采用Design-Expert软件中的box-behnken正交设计,按3因素、3水平对本次参数分析进行设计。
分析中的模型参数点不仅要求能够客观反映实际,还要包括最佳的设计条件,因此试验点的选取至关重要。一般情况下,三因素BBD设计的试验点分布情况如图5所示。但根据上述图3中的单元存在区间,为了避免碰撞区域以及分析数据便于统计,本次模型试验点的选取以及各设计变量取值情况分别如图6和表2所示(包括2个随机点)。
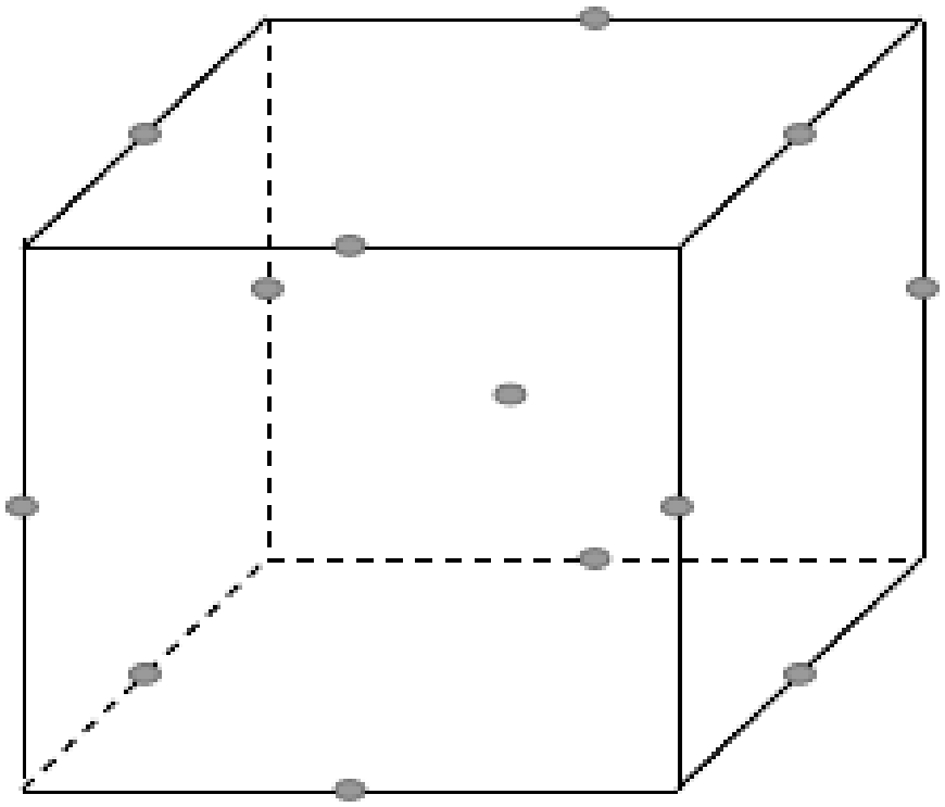
图5 三因素BBD设计试验点分布情况
Fig.5 Distribution of experimental points in a three-factor BBD experimental design
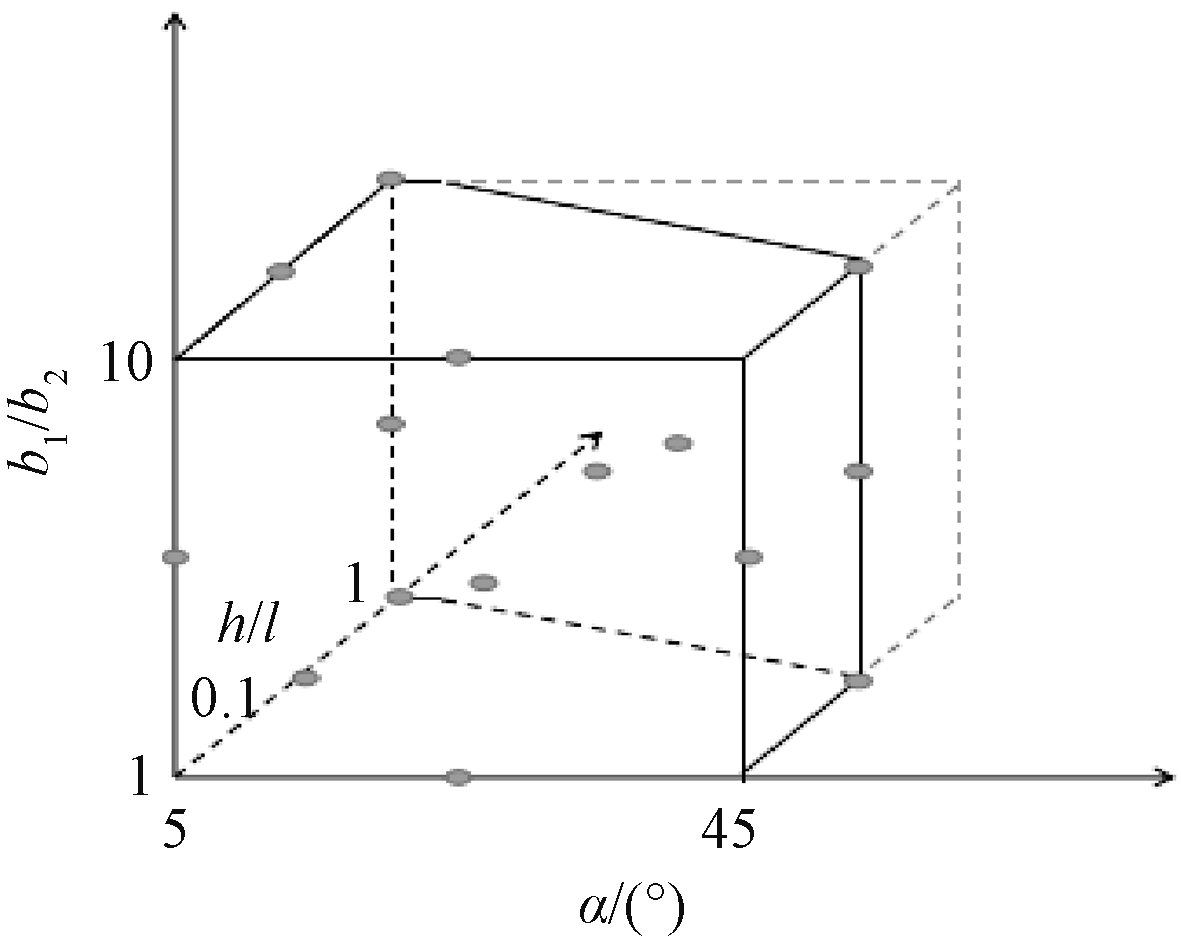
图6 本次设计试验点选取分布情况
Fig.6 The distribution of experimental points in the design
表2 试验点设计变量的具体取值
Table 2 Specific values of the design variables in the experimental points
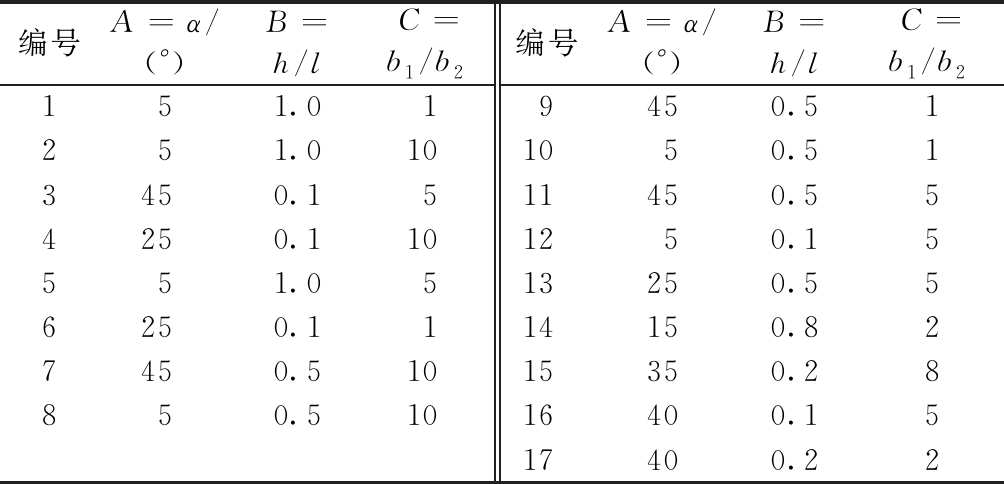
编号A=α/(°)B=h/lC=b1/b2编号A=α/(°)B=h/lC=b1/b2151.019450.51251.0101050.513450.1511450.554250.1101250.15551.0513250.556250.1114150.827450.51015350.28850.51016400.1517400.22
3.3 塑性损伤模型
本次优化的目标是在满足约束条件下求得耗能最大的结构,即模型塑性变形过程中塑性损伤指标达到1.0时,认为结构发生断裂,此时的能量最大。根据上述所取试验点,分别在ABAQUS中建立弹塑性损伤模型,固定一端,在另一端施加一个较大的竖向位移进行有限元分析,求得各个模型的极限位移值,取其中的最小值作为试验点的竖向位移值重新施加位移约束,以内凹角度α=15°、纵向与横向单元长度之比h/l=0.8、横向与纵向单元厚度之比b1/b2=2的内凹六边形单元尺寸为例,如图7所示,设置相关弹塑性参数,进行拉伸分析,得到极限位移下的塑性损伤(图8)和损伤指标为1.0时的力-位移曲线(图9),对此力-位移曲线积分,最终得到如表3所示各试验模型断裂时的耗能。
图7 α=15°、h/l=0.8、b1/b2=2的损伤模型
Fig.7 Damage model diagram of α=15°、h/l=0.8、b1/b2=2
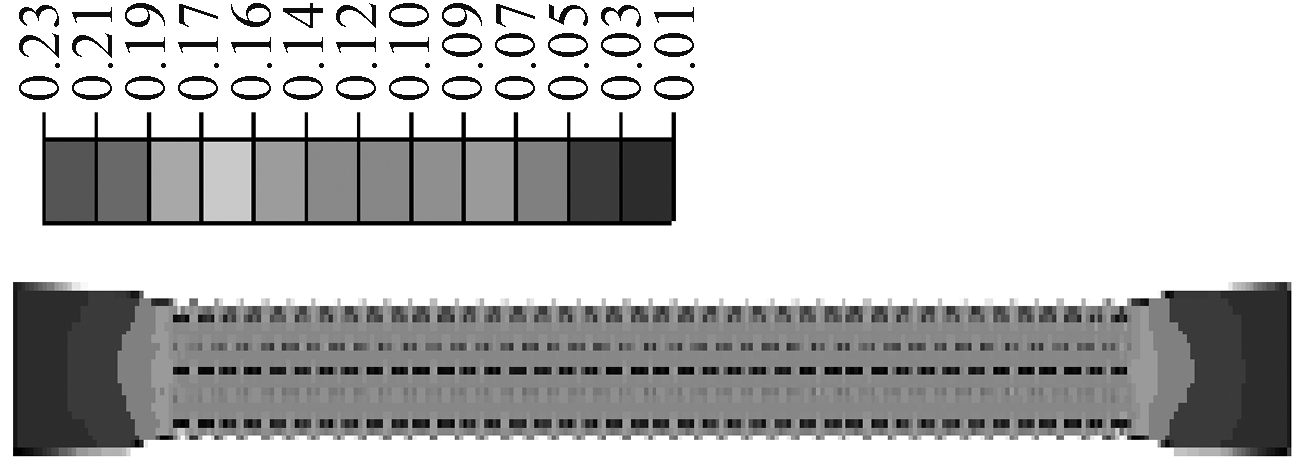
图8 塑性损伤
Fig.8 Plastic damage
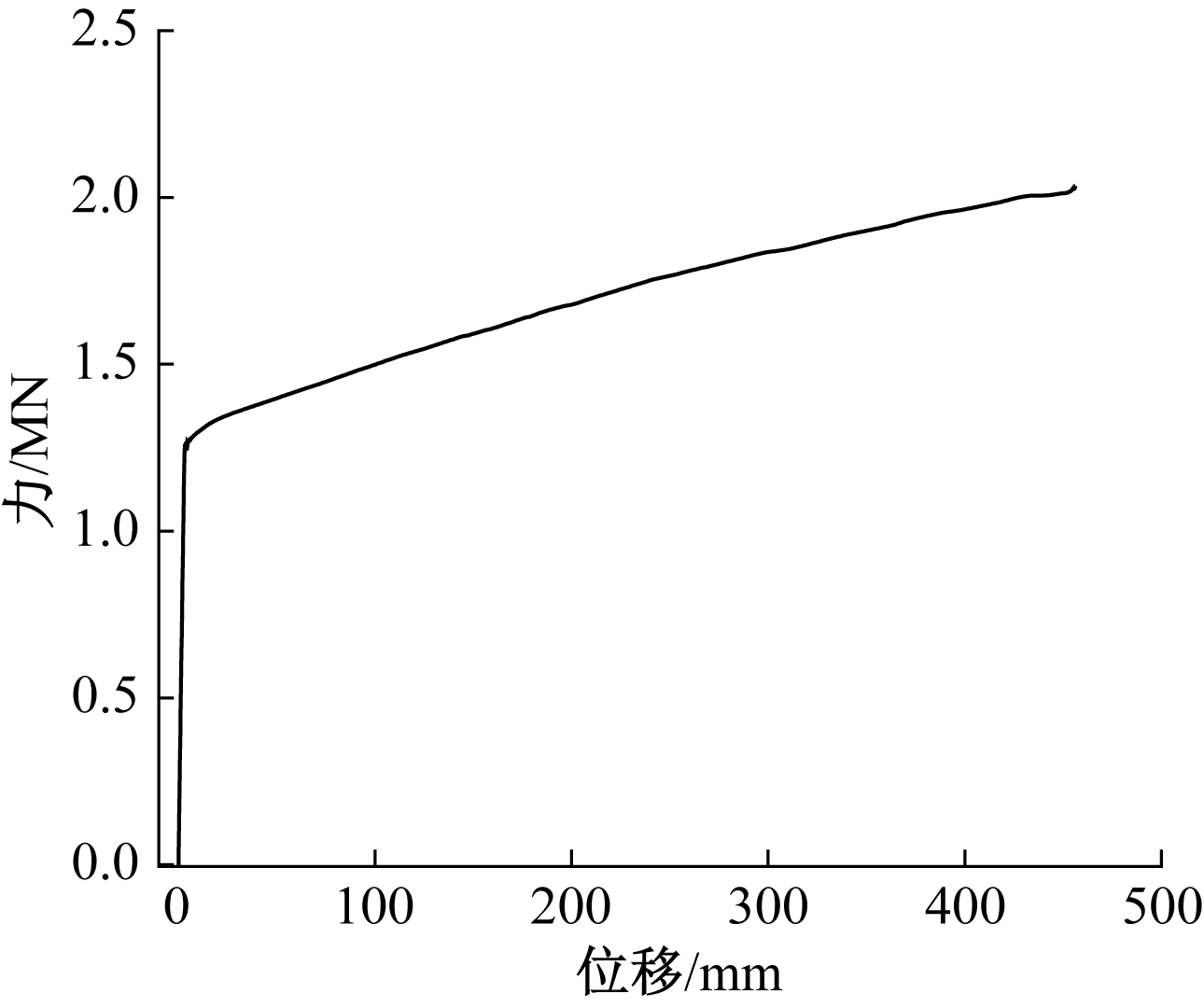
图9 损伤指标为1.0时的力-位移曲线
Fig.9 Force-displacement curve with the damage index of 1.0
表3 各试验点的耗能
Table 3 Energy dissipation of each experimental point
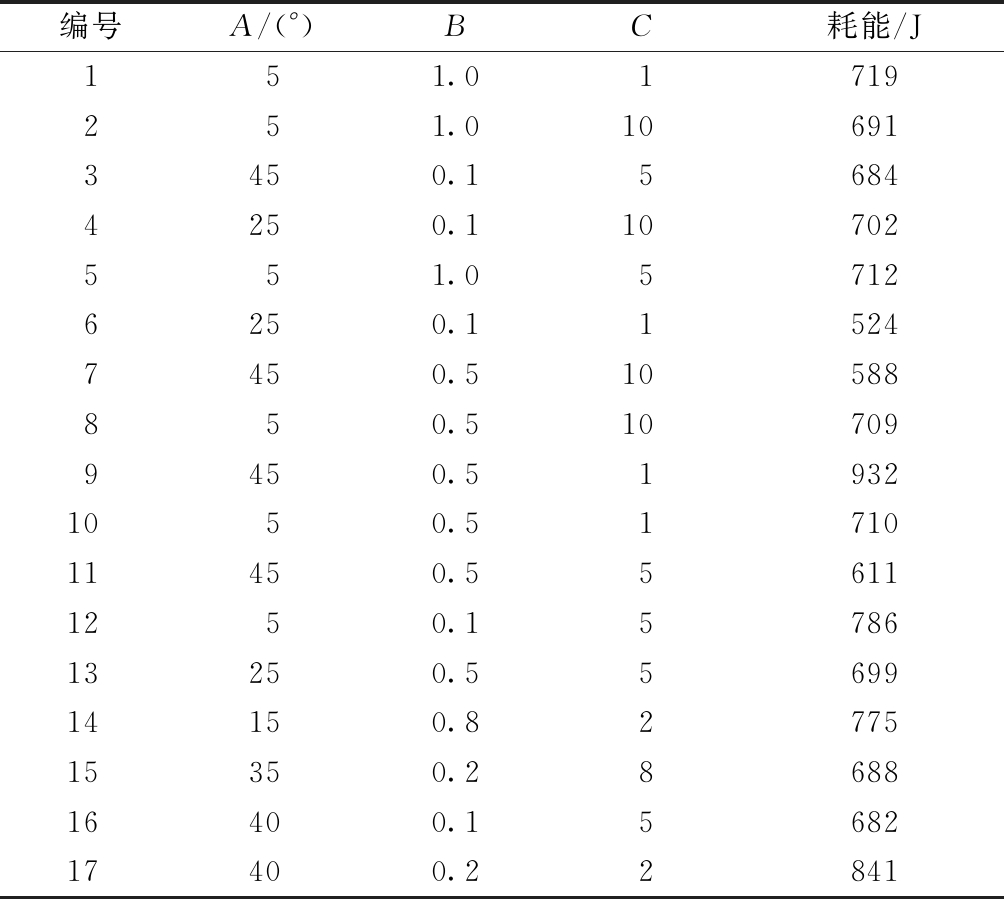
编号A/(°)BC耗能/J151.01719251.0106913450.156844250.110702551.057126250.115247450.510588850.5107099450.519321050.5171011450.556111250.1578613250.5569914150.8277515350.2868816400.1568217400.22841
3.4 回归模型的建立及其分析
通过不同模型的方差比较、失拟检验结果以及各模型的综合统计分析,最终确定二次方程数模型较其他模型能更好地拟合参数分析数据,并反映出耗能指标与各参数之间的关系,表示耗能与各影响参数之间关系的响应面拟合方程为:
E=1.167 93×109-5.773 94×107 A-8.257 83×108B-5.714 80×107C+6.962 54×107AB+4.863 25×106AC-1.881 29×107BC+1.344 27×106A2+3.918 85×108B2+3.568 13×106C2+2.348 33×106ABC-1.548 83×106A2B-1.393 81×105A2C
图10为拟合模型的残差分布,从正态概率图可看出,残差分布与累计概率分配函数值近似于直线关系,表明该模型的拟合效果比较好,同时说明分析数据可靠。

图10 耗能指标残差分布
Fig.10 Residual distribution of energy dissipation indexes
通过Design-Expert对拟合二次多项式回归方程的置信度分析,可得出各参数对耗能指标的影响程度,参数估计栏中的绝对值越大,说明该参数对耗能指标的影响程度越大。根据分析结果,结合表3中的参数模型编号,各参数交互作用对耗能指标的影响顺序为:A2B>A2C>A2>ABC>BC>B2>AC>C2>AB。得出单参数对能量指标影响顺序为: B>C>A。
3.5 响应面分析
图11~图13为响应面和耗能分析结果响应面等高线图,该图组根据回归方程绘制,可直观地反映并预测各参数及其交互作用对耗能指标的影响结果。分析当内凹角度α、纵向与横向单元长度之比h/l、横向与纵向单元厚度之比b1/b2中有一个参数固定时,另外两个参数及其交互作用对耗能的影响。
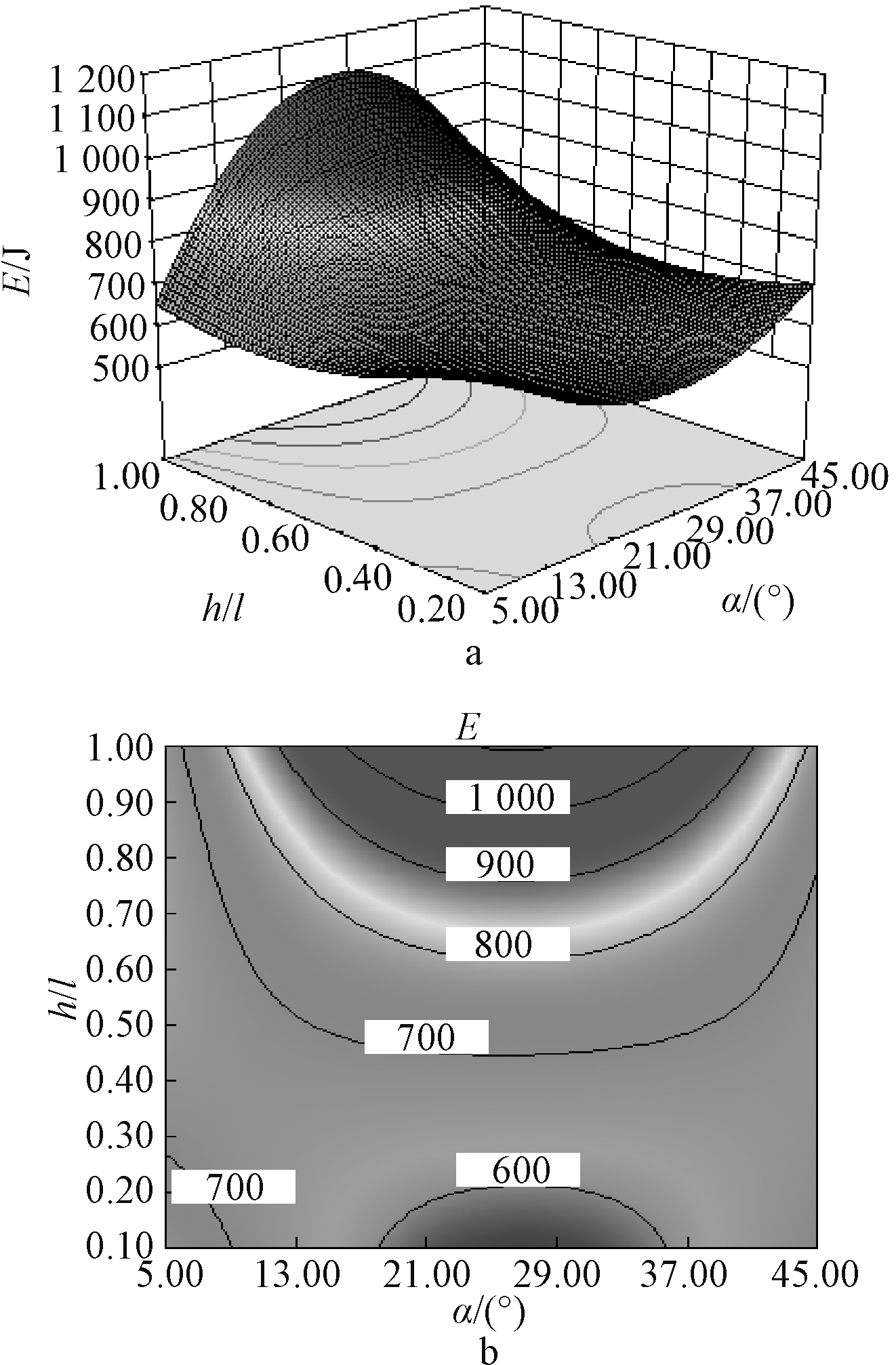
a—响应面; b—等高线,J。
图11 内凹角度α、纵向与横向单元长度之比h/l对耗能影响
Fig.11 Effects of concave angle α and ratio of longitudinal to transverse unit length h/l on energy dissipation

a—响应面; b—等高线,J。
图12 内凹角度α、横向与纵向单元厚度之比b1/b2对耗能的影响
Fig.12 Effects of concave angle α and the ratio of transverse to longitudinal unit thickness b1/b2 on energy dissipation
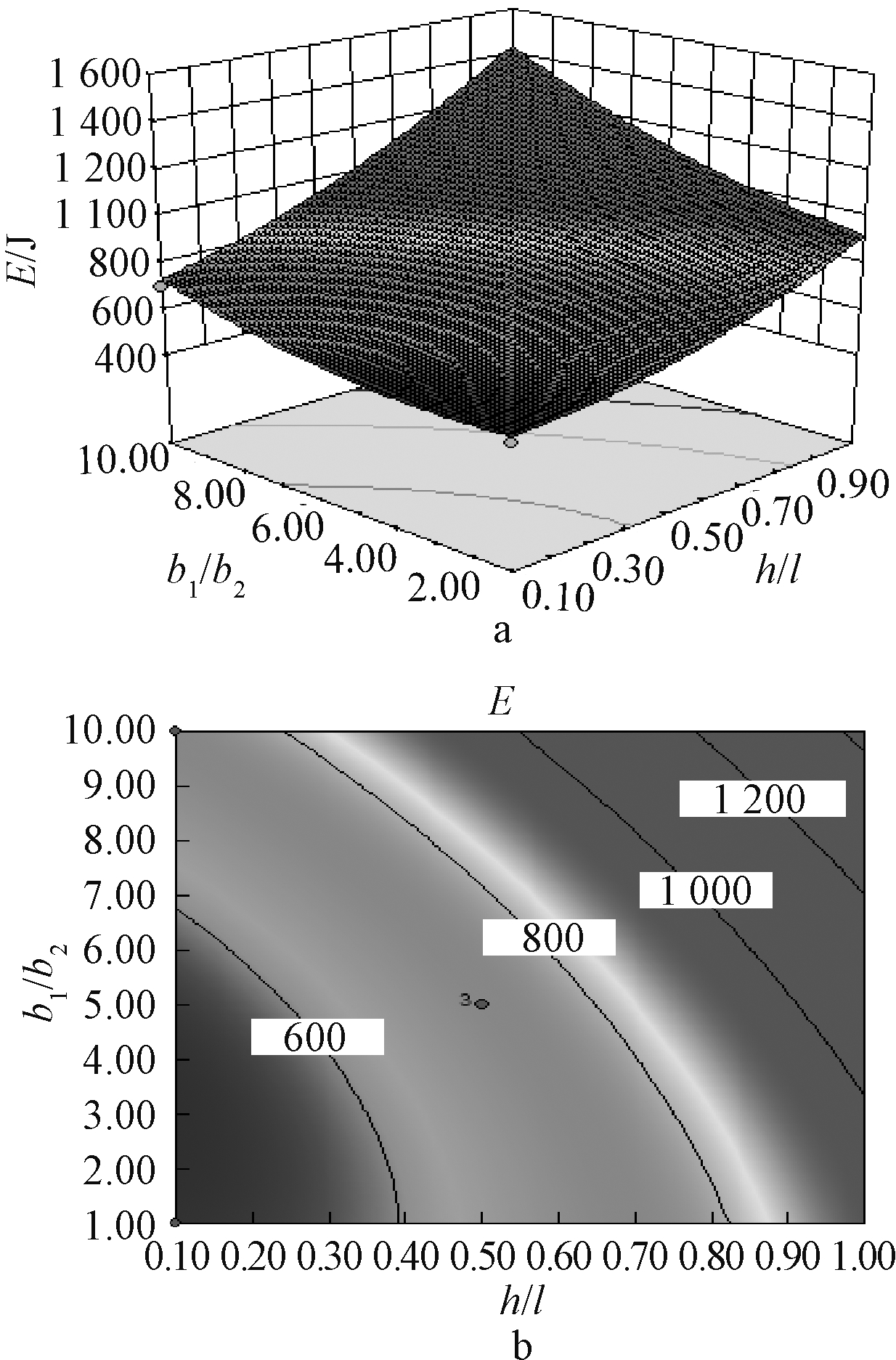
a—响应面; b—等高线,J。
图13 纵向与横向单元长度之比h/l、横向与纵向单元 厚度之比b1/b2对耗能量的影响
Fig.13 Effects of ratio of longitudinal to transverse unit length h/l and ratio of transverse to longitudinal unit thickness b1/b2 on energy dissipation
由图11可以看出:等高线分布密集,内凹角度α、纵向与横向单元长度之比h/l影响较显著;纵坐标上等高线分布较其在横坐标上的分布更为密集,说明纵向与横向单元长度之比h/l对影响值的显著性要高于内凹角度α;同时图形存在一定的扭曲,说明两因素间具有一定的交互作用。
由图12可看出:在内凹角度α取值(尤其是内凹角度α的值在21°~29°之间时)以及b1/b2取值一定时,耗能随b1/b2或内凹角度α取值的改变而改变,且改变的单步长变化幅度都较大,具体表现在此时等高线密集及曲面陡峭,说明:α、b1/b2对响应值的影响较显著(与前文选定拟合方程的分析结果一致);一参数对响应值的影响规律与另一参数的初始取值有关,表现为参数不同初始值对应的等高线值变化趋势不同以及三维图形中的扭曲程度不同,这也说明α、b1/b2间具有一定的耦合作用。
由图13可知:当纵向与横向单元长度之比h/l或横向与纵向单元厚度之比b1/b2中一参数为其选定水平范围的上限或下限时,耗能指数随着另一值的变化趋势均较陡,说明纵向与横向单元长度之比h/l、横向与纵向单元厚度之比b1/b2对耗能的影响较为显著;等高线分布趋势与参数水平有关,且三维曲面图存在一定的扭曲,因为二者共同影响单元结构,因而产生了一定的耦合作用,但耦合作用较弱,体现为曲面图的扭曲幅度小。
考虑到碰撞区域,横向与纵向单元厚度之比b1/b2对模型边界条件影响不大,由图11、图12可看出:就单参数而言,耗能的最大值位于内凹角度α值在21°~29°的区间之内和α=45°附近,但是由于碰撞区域的存在,且边界处随着参数纵向与横向单元长度之比h/l、横向与纵向单元厚度之比b1/b2的增加,耗能指数呈减小的趋势,因此能量的最大值位于内凹角度α值在21°~29°的区间之内。
综上所述,不同参数组成的二次项反映了参数间的耦合作用,结合响应面分析并根据前文对模型各项的方差分析认为,二次项参数间耦合作用的排序仍为:A2B>A2C>A2>ABC>BC>B2>AC>C2>AB。就单参数而言,在碰撞区域以外的空间中,随着内凹角度α、纵向与横向单元长度之比h/l、横向与纵向单元厚度之比b1/b2的增加,耗能指数呈增加的趋势,但随着各参数增加到一定程度之后,耗能指标呈减小的趋势。
3.6 参数优化及验证
在满足约束条件的前提下,利用Design-Expert对模型参数进行优化,从优化结果中选取前4组推荐参数进行分析验证,优化方案中的前10个及前4组验证结果列于表4。
结果表明:理论耗能值和数值模拟出的能耗值接近,说明软件建立的内凹角度α、纵向与横向单元长度之比h/l、横向与纵向单元厚度之比b1/b2的关系模型准确可靠。根据实际进行取整后得到最佳构型参数组合为α=24.73°、h/l=0.7、b1/b2=10。最终优化预测结果为:理论能量值为1 130 J,实际能量值为1 110 J。
表4 前10优化方案及验证结果
Table 4 Top 10 optimization plans and verification results
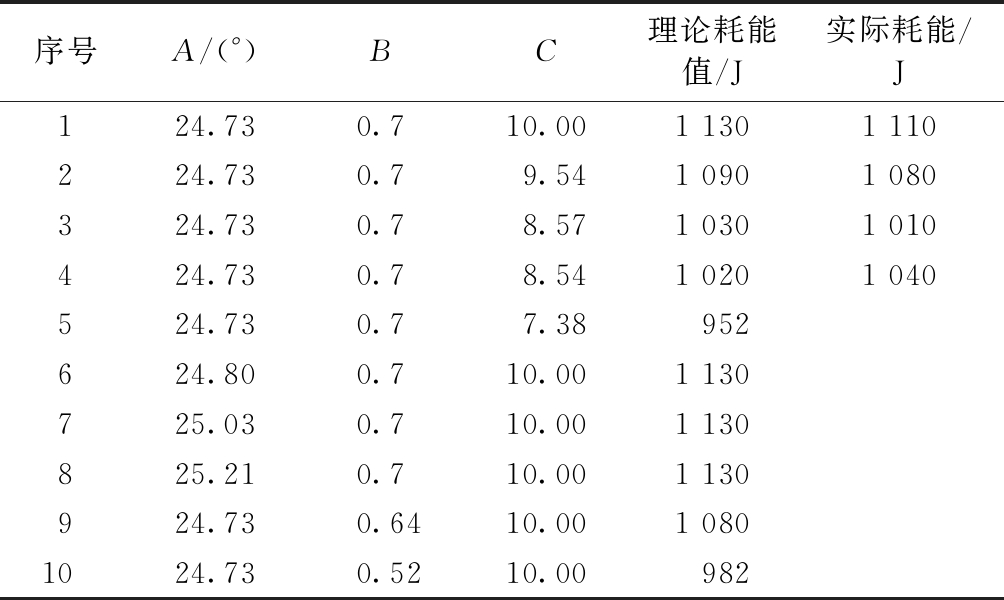
序号A/(°)BC理论耗能值/J实际耗能/J124.730.710.001 1301 110224.730.79.541 0901 080324.730.78.571 0301 010424.730.78.541 0201 040524.730.77.38952624.800.710.001 130725.030.710.001 130825.210.710.001 130924.730.6410.001 0801024.730.5210.00982
4 结束语
本文结合负泊松比拓扑结构,使其刚度在满足轴向受力要求和截面积不变的同时,具有较好的耗能能力。本文基于负泊松比结构优异的变形能力,以内凹六边形负泊松比结构作为研究对象,建立了内凹六边形负泊松比结构的有限元模型,并应用响应曲面法对其单元结构建立回归方程,进行优化设计分析,使之在满足相关约束条件的情况下,通过不同参数控制,得到能量最大的设计方案,在此基础上完成了负泊松比整体模型设计。
其次,本文对内凹六边形负泊松比结构的设计优化采用响应曲面法,设计合理的参数分析,使用基于有限元塑性损伤模型的数值模拟方法,在相关约束条件下对结构多个目标参数进行优化,实现了参数化的反应曲面方法与有限元的损伤影响因子结合的创新性分析成果。
[1]袁烽,胡雨辰.人机协作与智能建造探索[J].建筑学报,2017(5):24-29.
[2]袁烽,柴华,谢亿民.走向数字时代的建筑结构性能化设计[J].建筑学报,2017(11):9-16.
[3]LU C F,LIU J F,LIU Y H,et al.Intelligent Construction Technology of Railway Engineering in China[J].Frontiers of Engineering Management, 2019,6 (2):503-516.
[4]李霞昭,曾明会.阻尼器在耗能减震结构中的应用[J].四川建材, 2013,39(4):32-36.
[5]任鑫,张相玉,谢亿民.负泊松比材料和结构的研究进展[J].力学学报, 2019,51(3):656-687.
[6]杨智春,邓庆田.负泊松比材料与结构的力学性能研究及应用[J]. 力学进展,2011,41(3):335-350.
[7]中华人民共和国住房和城乡建设部. 钢结构设计标准:GB 50017—2017[S]. 北京:中国建筑工业出版社,2018.
[8]刘中华,黄明鑫,朱邵宁.钢结构构件断裂韧性指标的选取[J]钢结构, 2008,23(11):50-53.
[9]许素强,夏人伟.结构优化方法研究综述[J].航空学报,1995,16(4):2-13.
[10]XIE Y M, STEVEN G P. Evolutionary Structural Optimization[M]. London: Springer-Verlag, 1997(13):12-29.
[11]HUANG X, XIE Y M. Convergent and Mesh-Independent Solutions for the Bi-Directional Evolutionary Structural Optimization Method[J]. Finite Elements in Analysis & Design, 2007,43(14):1039-1049.
[12]HUANG X, XIE Y M. Evolutionary Topology Optimization of Continuum Structures: Methods and Applications[M]. Chichester: John Wiley & Sons, 2010.
[13]BASTÜRK E, ALVER A.Modeling Azo Dye Removal by Sono-Fenton Processes Using Response Surface Methodology and Artificial Neural Network Approaches[J]. Journal of Environmental Management,2019(10):248-256.
[14]SHIMA G N, ABOLFAZL S, MEGHDAD K, et al. Synthesis of Ion-Imprinted Polymer-Decorated SBA-15 as a Selective and Efficient System for the Removal and Extraction of Cu(ii) with Focus on Optimization by Response Surface Methodology[J].The Analyst,2019,144(15):4596-4612.
[15]MONTGOMERY D C.Design and Analysis of Experiments 8th Edition with Student Solutions Manual and Design Expert 8.0.7 Set[J].Technometrics,2001,48(1):158.
[16]徐仁崇,刘君秀,曾冲盛,等.采用Design-Expert软件优化透水混凝土配合比设计[J].新型建筑材料, 2010,37(7):17-20.