0 引 言
雷达天线罩是雷达系统的重要组成部分,不但为天线提供发射和接收的电磁窗口,保证雷达正常工作,还为雷达提供独立、封闭的空间,防止雷达受周围环境影响,保障雷达设备安全[1-2]。为保证天线罩有高透波率和低指向误差,满足雷达越来越高的精度指标,同时又要适应极端恶劣的自然环境条件,对天线罩的结构设计提出了更苛刻的要求。因此,在进行天线罩结构设计时,必须对其整体力学性能进行详细的分析,以保证结构的安全性。
柔性蒙皮分块金属桁架天线罩是一种新型的地面雷达天线罩,主要应用于大型地面固定式雷达[3-4]。作为典型的单层球面网壳结构,其整体的稳定性是结构设计中的关键问题[5-9]。同时,柔性蒙皮分块金属桁架天线罩采用施加预张力的柔性蒙皮结构,蒙皮效应对整体结构的承载能力的贡献也是值得研究的问题[10-12]。本文以某28.5 m金属桁架天线罩为例,介绍了柔性蒙皮分块金属桁架天线罩的力学性能分析流程,并对该天线罩进行了仿真计算和校核,同时开展了天线罩蒙皮效应的试验研究,验证了柔性蒙皮对天线罩整体力学性能的影响。
1 柔性蒙皮分块金属桁架天线罩概述
某金属桁架天线罩直径28.5 m,截球比为83.37%,采用空间三角网架结构,由745个三角单元块按准随机排列方式拼装而成,相邻的两个三角形的边对拼形成天线罩的肋,边之间的连接采用螺栓、螺母对穿的形式两两连接成整体,相邻三角单元块顶角形成天线罩的节点(图1)。
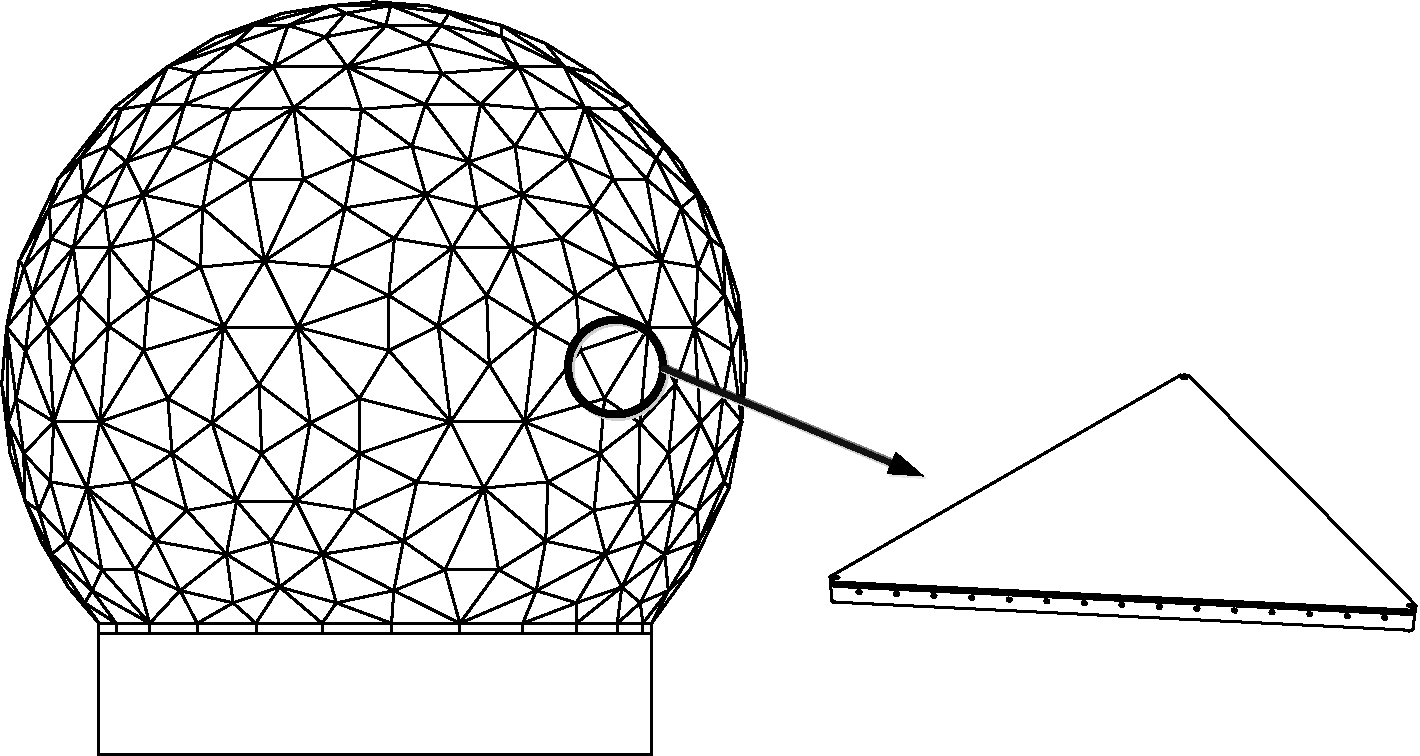
图1 天线罩整罩示意
Fig.1 Schematic diagram of radome
三角单元块由金属骨架和柔性蒙皮组成,金属骨架采用矩形截面金属杆件和节点柱焊接而成,柔性蒙皮需施加预张力,张拉固定在金属骨架上,如图2所示。根据电讯设计结果,为满足雷达电性能指标的要求,确定杆件截面尺寸为15 mm×100 mm。为了实现高透波率、低指向误差性能,透波窗口的插入损耗和插入相移必须尽可能得小,结合结构强度和环境适应性的要求,最终选择具有优异力学和耐候性能的聚四氟乙烯膜材作为天线罩的蒙皮材料。
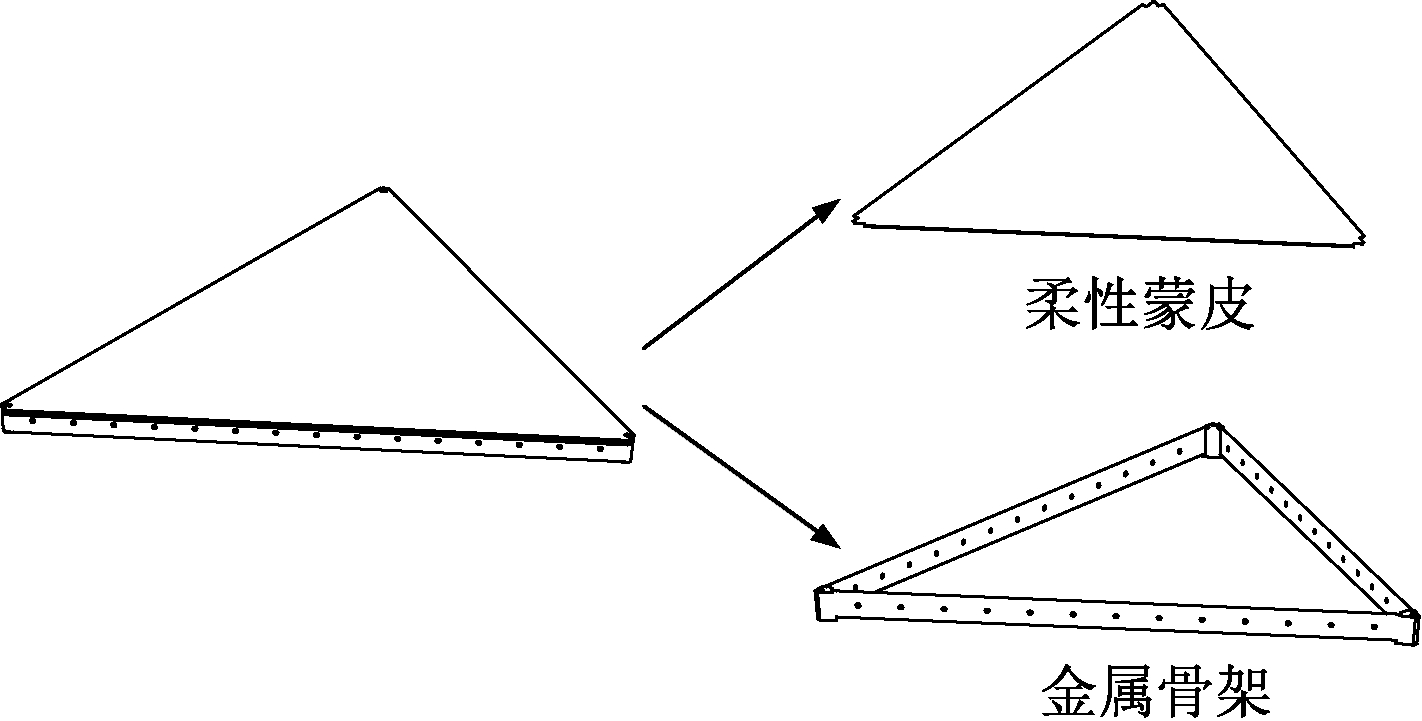
图2 三角单元块结构
Fig.2 The triangle unit block
2 柔性蒙皮分块金属桁架天线罩力学性能分析
2.1 分析流程概述
天线罩的仿真分析是对天线罩在严酷环境荷载下结构强度的评价。本文所述天线罩采用的是张拉薄膜结构结合空间金属桁架的形式。传统的天线罩结构仿真分析流程主要包括了有限元建模、边界条件和荷载的施加、结构的静力特性和动力特性分析、整体的稳定性分析以及局部强度校核等流程,而本天线罩由于采用施加预张力的薄膜结构作为天线罩蒙皮,需增加对膜结构的找形分析,以得到天线罩的初始构型,并且膜结构作为天线罩承载的一部分结构,本身的结构强度也需要进行校核。具体的仿真流程如图3所示。

图3 柔性蒙皮金属桁架天线罩力学性能分析流程
Fig.3 Mechanical properties analysis process of block metal frames radome with flexible skin
2.2 荷载条件
地面雷达天线罩作为雷达系统的保护罩,直接暴露于户外环境中,作用于罩体的荷载主要有风荷载、雪荷载、自重、温度荷载等等。
参考GB 50009—2012《建筑结构荷载规范》[13],作用在建筑表面上的风荷载应按照下列规定确定:
w=βzμsμzw0
(1)
式中:w0为基本风压;v为风速;βz为风振系数; μz为风压高度变化系数,μz=1.20~1.52(按高度6~30 m梯度取值);μs为风荷载的体型系数。球体的体型系数为:
μs=-1.3+0.180 1sin φcos θ+1.56sin2φcos2θ+0.559sin3φcos3θ
(2)
式中:φ,θ为天线罩球坐标系数。
雪荷载应按照下列规定计算:
sk=μrs0
(3)
式中:s0为基本雪压;μr为屋面积雪分布系数。
参照GB 50009—2012,依据风载、雪荷载、温度荷载条件,选取合理的荷载系数及荷载组合工况,可开展天线罩的力学性能分析。
一般情况下,考虑如下4种荷载组合工况:
工况1,1.0×恒载+1.0×雪荷载+1.0×初始预张力;
工况2,1.2×恒载+1.4×风荷载+1.0×初始预张力;
工况3,1.2×恒荷载+1.4×风荷载+1.4×0.7×雪荷载+1.0×初始预张力;
工况4,1.2×恒荷载+1.4×雪荷载+1.4×0.6×风荷载+1.0×初始预张力。
其中工况1为第一类荷载组合,表征了结构在长期正常使用荷载效应组合下的受力状态,工况2~4为第二类荷载组合,表征了结构在短期(临时)荷载效应组合下的受力状态。
2.3 有限元建模
采用通用有限元计算软件ABAQUS进行分析,依照天线罩的三维模型建立有限元仿真分析模型,其中金属桁架采用B31梁单元,材料采用Q345钢,杨氏模量为210 GPa,屈服强度为345 MPa,泊松比为0.3;柔性蒙皮采用M3D3膜单元,材料为聚四氟乙烯膜材,弹性模量为1.6 GPa,厚度为0.5 mm,经、纬向抗拉强度分别为170,160 MPa。膜单元采取500 mm的网格尺寸进行划分,蒙皮的膜单元与桁架的梁单元采用绑定连接,天线罩底部周圈与环墙连接处采取固支约束,如图4所示。

图4 膜结构有限元模型
Fig.4 Finite element model of membrane structure
2.4 找形分析
传统结构如钢结构、混凝土结构等, 是依靠本身的刚度来承受荷载,并且结构的初始形状是已知的。而张拉膜结构是柔性材料,在没有预应力的情况下结构不存在刚度, 也就无法定义形状,必须通过施加适当的预应力获得一定的刚度和形状,才能承受外部荷载[14]。在给定的边界条件下,所施加的预应力大小与所形成的结构是相互联系的,确定随结构自平衡的预应力分布状态以及张拉膜结构的初始形状即为膜结构的初始形态分析,也称膜结构的找形分析。
膜结构找形分析一般流程如下:
1)采用最小曲面约束条件的弹性模量法,设定膜材的虚拟弹性模量。一般情况下的弹性模量比实际的低3个数量级。
2)利用预定义温度场,膜单元通过降温施加预应力。
3)设定合理的膜初始应力值,找形后的形状和膜面应力必须满足要求,用几何非线性的解法,实施第1 次找形,然后更新结点坐标。
4)恢复膜单元的实际弹性模量,恢复膜单元的实际预应力。
5)进行第1 次自平衡迭代求解。
6)重复4)~5)步,即可找到一定应力水平及一定矢高下的等应力曲面。直到结构两次自平衡迭代求解的结构误差达到5%以内,即可得到天线罩膜面的初始分析模型。
图5是天线罩找形后的结果,可以看到,初始状态的膜面应力分布非常均匀,膜面最大应力为3.604 MPa,最小应力为3.452 MPa,大部分区域膜面应力为3.55 MPa,符合预设的膜面预应力要求。

图5 找形分析结果 MPa
Fig.5 Form-finding analysis results
2.5 非线性静力分析
参考天线罩部署地的气象数据,得到基本风压0.65 kN/m2,基本雪压0.15 kN/m2。按照该荷载条件,对四种荷载组合工况下天线罩的膜材和杆件分别进行校核。
经过非线性静力分析得出,四种工况下荷载工况2最为严酷,膜面最大应力为25.899 MPa,如图6所示。杆件最大应力为140.27 MPa,最大位移为36 mm,如图7所示。
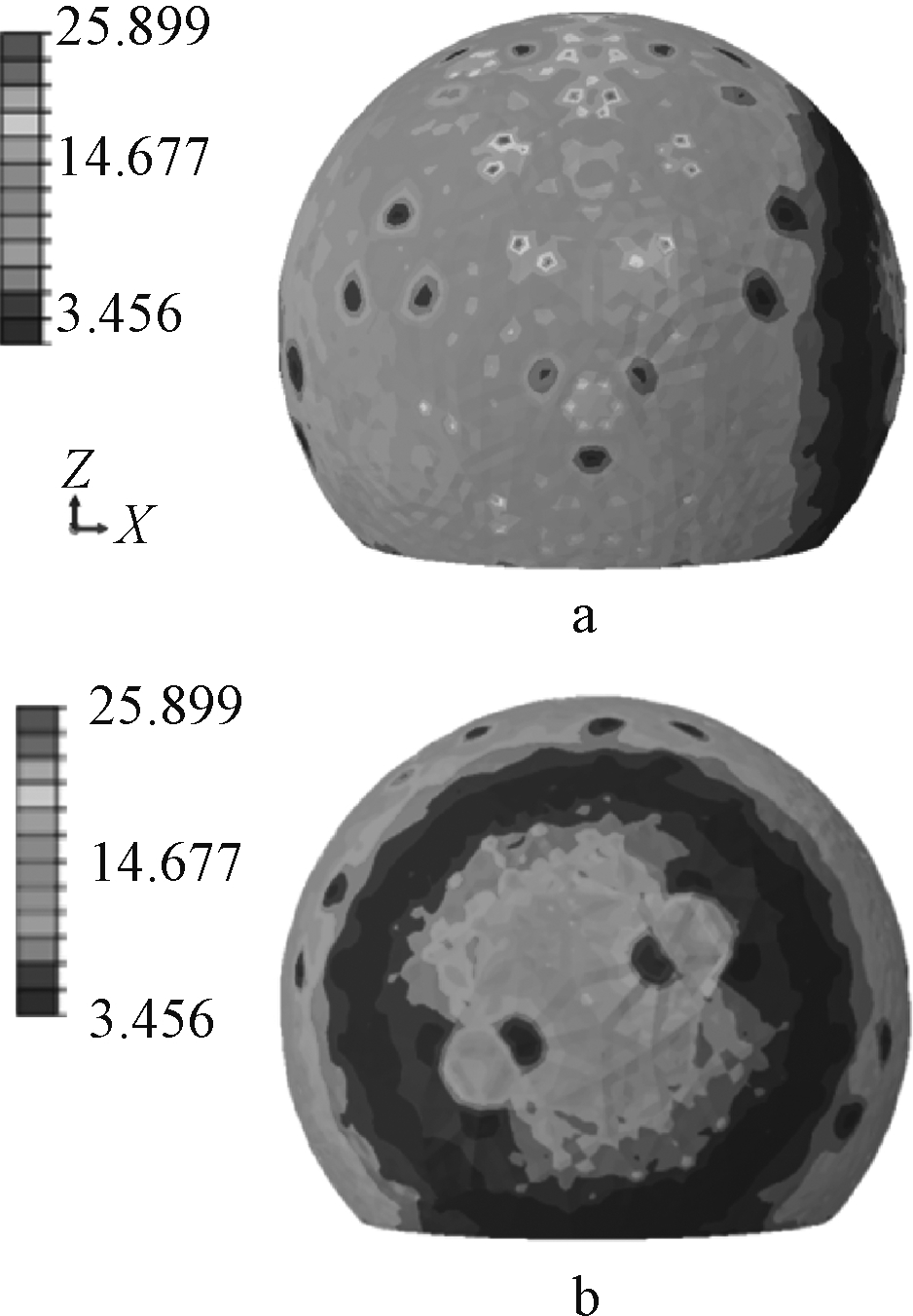
a—迎风面; b—背风面。
图6 膜面应力静力分析结果 MPa
Fig.6 Static analysis results of membrane surface stress

a—杆件应力云图,MPa; b—杆件位移云图,mm。
图7 杆件静力分析结果
Fig.7 Static analysis results of bar
这是因为天线罩的顶部为负压区,风荷载在膜结构顶部产生较大的风吸力,使得膜结构顶部膜张力达到最大值,如果同时考虑风荷载和雪荷载作用的情况,雪荷载的作用会抵消一部分风吸力的不利影响,反而没有单独考虑风荷载严酷,因此一般情况下球形天线罩最不利荷载条件为考虑自重、膜结构初始预张力和风载的荷载工况2。
2.6 骨架动力特性分析
通过模态分析(图8)可得出,结构一阶振型的自振频率为6.511 4 Hz,自振周期为0.154 s。
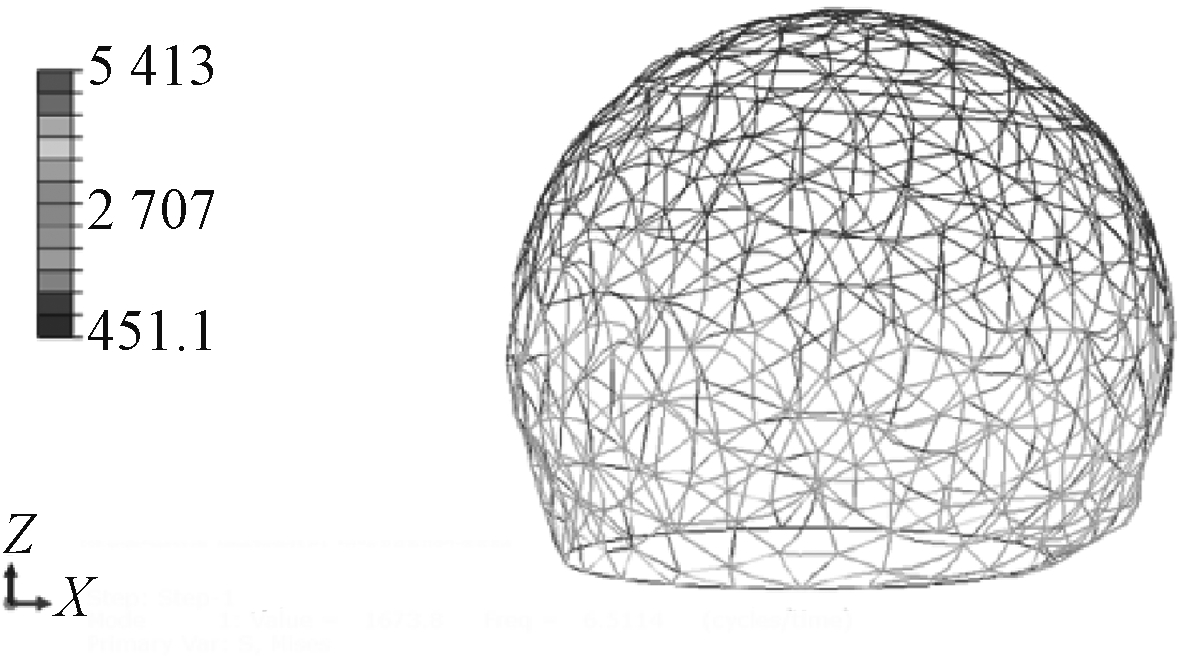
图8 结构一阶振型模态 MPa
Fig.8 The first order mode of the structure
根据JGJ 7—2010《空间网格结构技术规程》的规定:对于基本自振周期大于0.25 s的空间网格结构,宜进行风振计算。从结构动力特性分析可知,钢骨架的自振周期为0.154 s,故可不进行风振计算。
2.7 骨架非线性屈曲分析
天线罩骨架属于典型的单层网壳结构,其结构整体稳定性是结构安全设计中重点关注的问题。稳定性分析是一种用于确定结构开始变得不稳定时荷载与屈曲模态的技术,主要包含线性(特征值)屈曲和非线性全过程分析两种方法,其中特征值屈曲一般用于预测理想弹性结构的理论屈曲强度,往往可以作为非线性全过程分析的临界荷载上限,因为非线性全过程分析所获得的极限荷载与屈曲模态等特征相应更加接近真实情况。
非线性全过程分析的迭代方程一般采用以下方程:
(4)
式中:[Kt]为t时刻结构的切线刚度矩阵;{ΔU(i)}为当前位移的迭代增量;{Ft+Δt}为t+Δt时刻外部所施加的节点荷载向量;![]() 为t+Δt时刻相应的杆件节点内力向量。
为t+Δt时刻相应的杆件节点内力向量。
不考虑钢膜协同作用,仅考虑桁架自身承载,采用弹性全过程分析方法进行天线罩整体稳定性,其结构位移云图和荷载-位移曲线如图9及图10所示;从结构整体来看,非线性屈曲荷载因子(安全系数)为4.32,满足JGJ 7—2010中安全系数K应大于4.2的规定。

图9 弹性全过程分析天线罩位移云图 mm
Fig.9 Displacement nephogram of radome based on elastic analysis
为进一步探索分析结构的破坏模式,对结构进行了弹塑性稳定分析,其荷载-位移曲线如图10所示。从图中对比可以看出,两种情况下的全过程曲线大体一致,但弹塑性分析曲线在2.0~2.5的系数之间出现了明显拐点。经分析,此时有一根杆件因侧向失稳而进入塑性,但结构仍然有继续承载的能力。

图10 荷载-位移曲线
Fig.10 Load-displacement curves
从计算模型中提取2倍荷载系数时的结构应力云图如图11所示,可知,已有杆件最大应力为345 MPa(即达到屈服强度),但结构仍然可以继续承载,直至破坏。由此可见,结构稳定性满足JGJ 7—2010弹塑性全过程分析时安全系数为2.0的规定。

图11 天线罩应力云图 MPa
Fig.11 Stress nephogram of radome
3 柔性蒙皮分块金属桁架天线罩蒙皮效应研究
3.1 天线罩蒙皮效应概述
当围护体系与主体框架结构具有可靠连接时,围护体系与主体框架结构协同承担荷载,可以有效增强结构整体刚度,这种效应称之为蒙皮效应。传统建筑行业的设计中,一般不考虑膜结构对整体结构刚度和内力的影响。但是,天线罩由于同时兼具雷达防护和透波窗口的双重功用,考虑蒙皮效应的设计方法不仅可以使天线罩的设计状态和实际工作状态更加一致,同时在保证相同结构安全性的前提下,可降低天线罩金属桁架结构尺寸的要求,从而提高天线罩的电性能指标,并且节约成本,因而具有重要的理论和工程研究价值。
3.2 蒙皮效应试验研究
为研究膜材对天线罩整体稳定性的影响,分别采用两块无膜和两块有膜的三角形单元块拼装后进行轴向压缩失稳试验,以确定失稳临界荷载和屈曲模态。试验方法如图12所示,两个三角单元块拼装完成后,B点通过法兰和固定板固定在反力墙上,并安装有力传感器测量荷载,A点采用液压千斤顶进行加载。为了保证在试验过程中的荷载沿拼接杆轴线施加,模拟端头固支条件,设计了V形导向块和导轨,安装时导轨在一条直线上,两端的V型导向块卡在被试工件上。导向块和加载千斤顶之间有圆柱形压头,保证自动对心,如图13所示。在中间杆安装了5个位移传感器测量杆的变形,在加载端和对面的固定端安装了千分表测量V形块和工件之间的相对转角及面外的位移,在金属骨架的杆上安装了应变片,用来监测杆件的应力、应变,如图14所示。安装好试验装置后进行分级加载,直到发生结构破坏,具体试验步骤为:1)试验前检查各种仪器设备,仪器设备均需调零;2)正式试验前,用千斤顶加载20 kN的力,卸载,再进行试验,消除系统间隙;3)正式试验时按照10 kN的加载步进行加载,每一个加载步保压,采集数据;4)一直加载到杆件失稳,观察现象,拍照留存。根据三角单元块有膜和无膜状态,分两组进行试验。
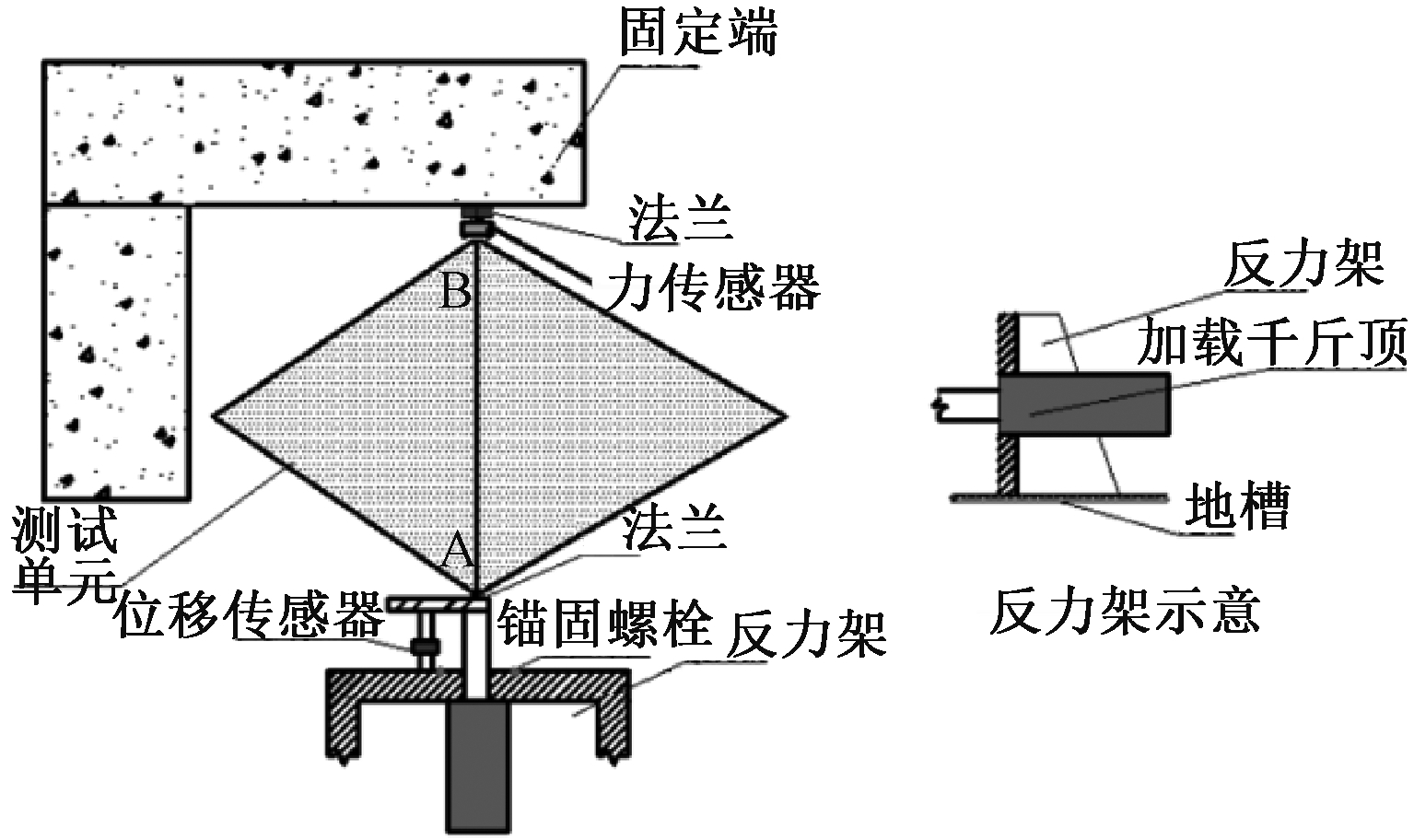
图12 三角单元块加载测试示意(水平放置)
Fig.12 Schematic diagram of loading test of radome triangle unit block (horizontal placement)

图13 试验装置局部实物
Fig.13 Diagram of partial experimental installation
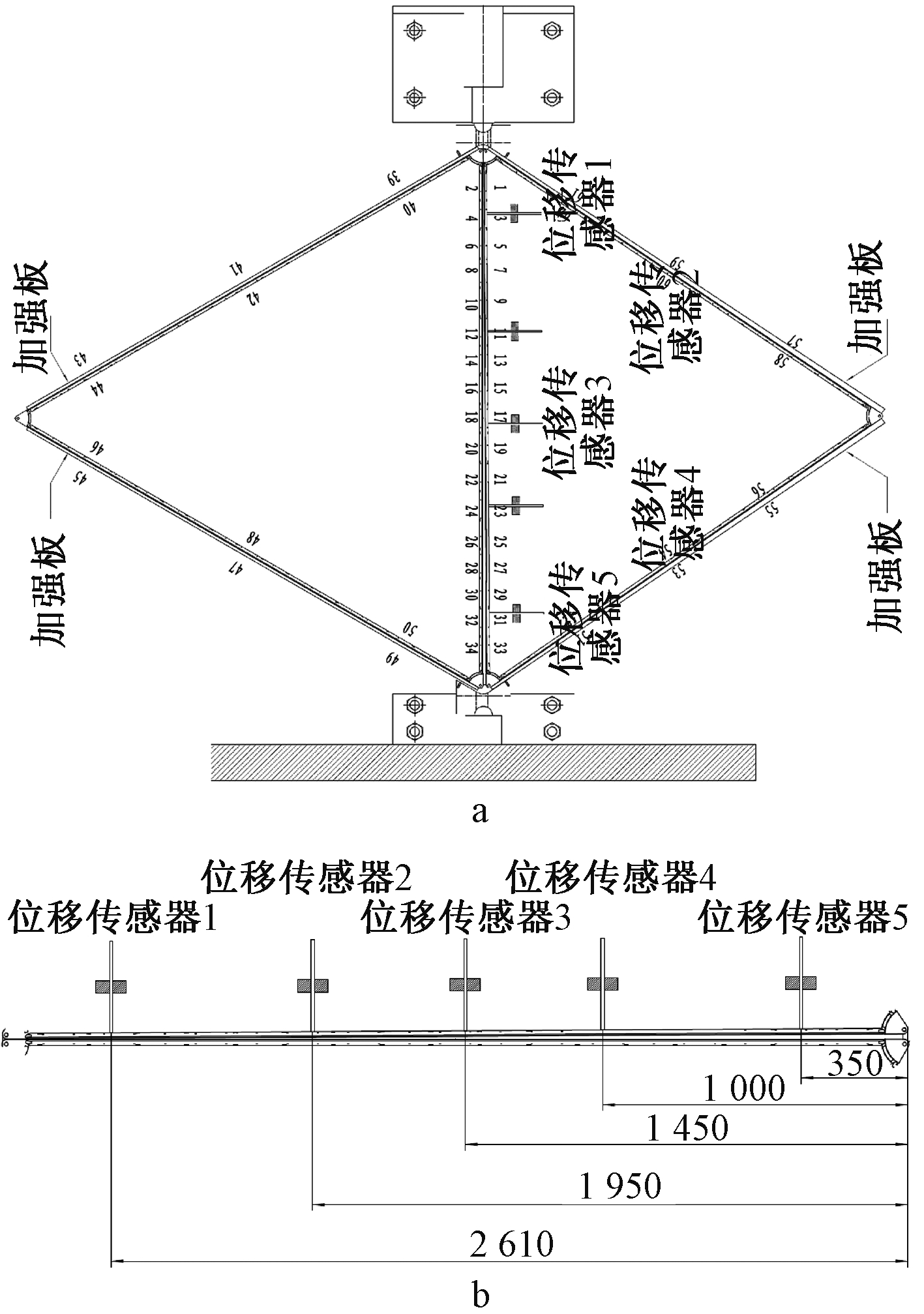
a—整体布置; b—中间杆传感器布置。
图14 传感器布置
Fig.14 Sensor arrangement
3.2.1 无膜三角单元块
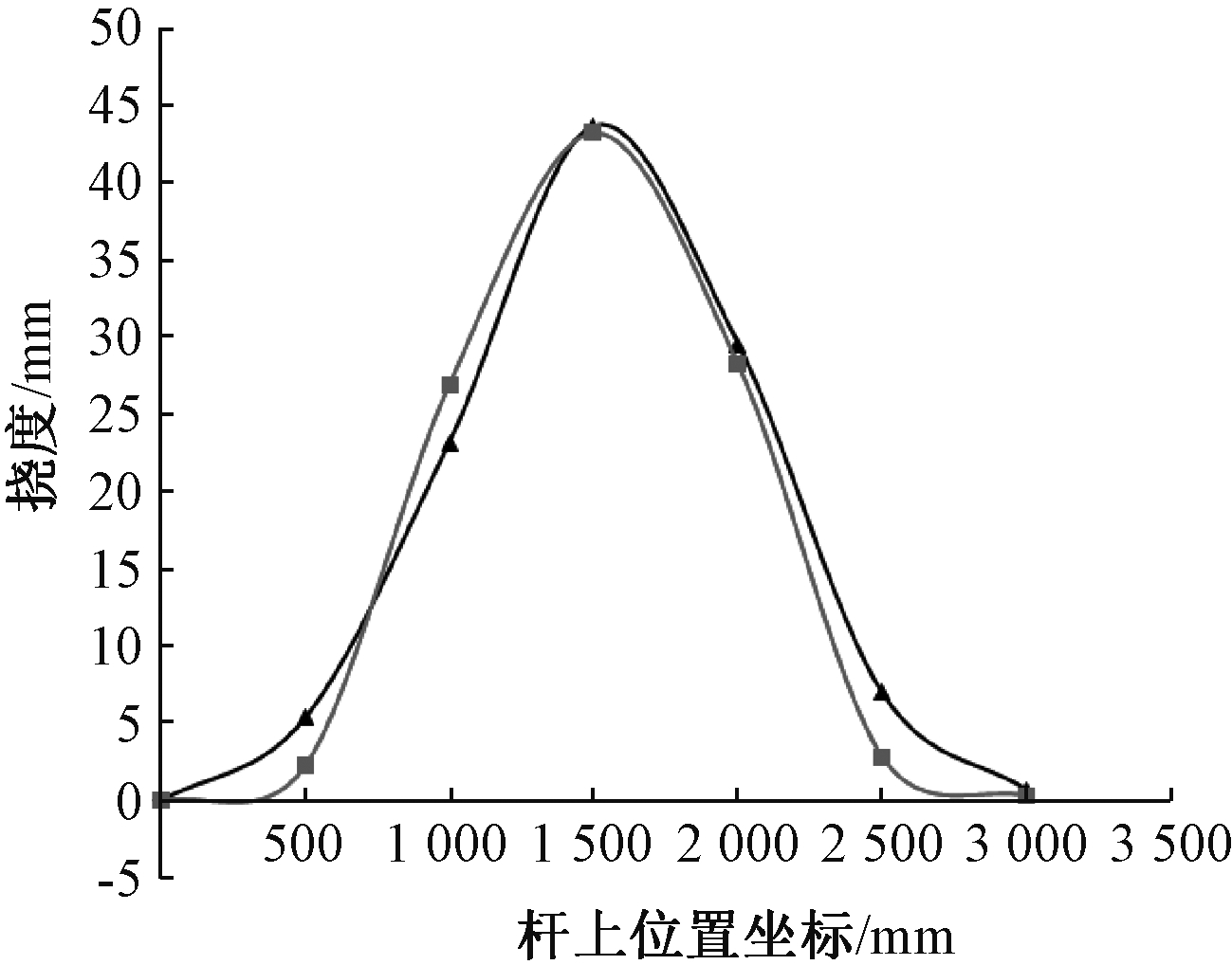
图15a为无膜三角单元块压缩失稳试验的照片,可以看出,两骨架对拼的杆件中间已经出现了明显的侧向弯曲。表1为无膜三角单元块压缩失稳试验的试验数据,试验过程中,杆件的变形随着荷载的增加而增加,前期基本呈线性增长趋势,但是从10 kN加载到120 kN的过程中,杆的变形突然急剧增加,并且加载到120 kN以后荷载便无法继续提升,说明杆件已经失去了承载能力。图16为三角单元块失稳时的变形曲线,图17为杆件中点的荷载-挠度曲线。从图中可以看出,无膜金属骨架拼接杆的实际承载能力为110 kN。在110 kN后,该杆虽然还能承受荷载,但是侧向变形很大,结构上认为已经失效。在失稳时,骨架上的应力值为91.56 MPa,应力水平远远小于材料的强度极限,因此,该杆件在弹性范围内失稳。

a—无膜三角单元块失稳时; b—有膜三角单元块失稳时。
图15 三角单元块稳定性试验
Fig.15 Stability experiment photo of radome triangle unit block
表1 无膜三角单元块的试验数据
Table 1 Experimental data of triangle unit block without membrane
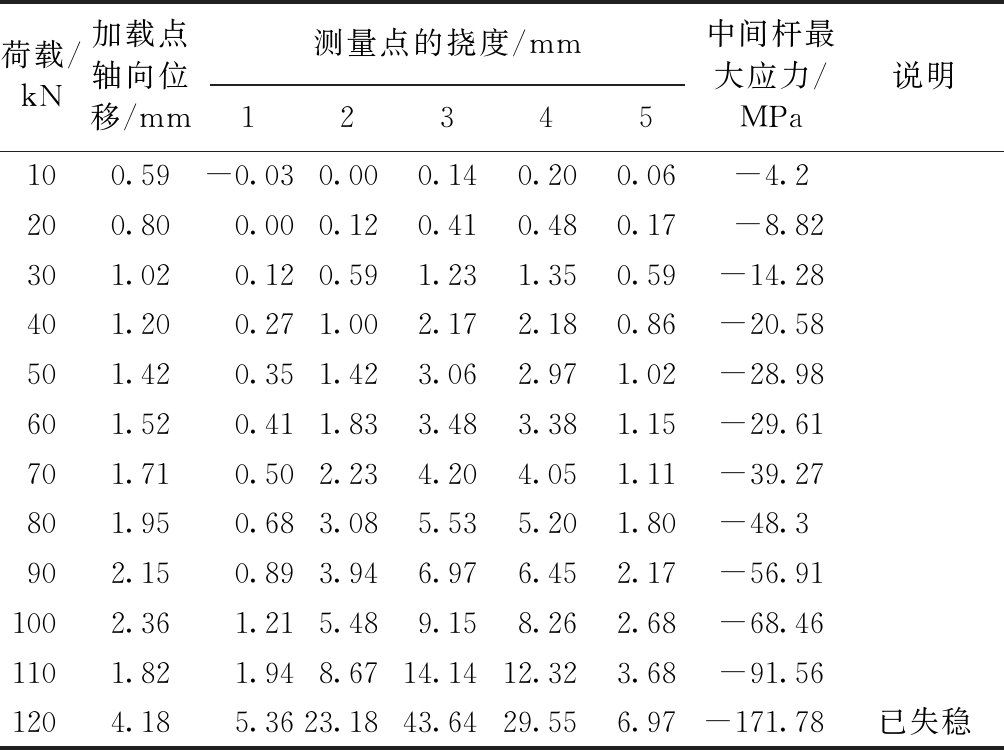
荷载/kN加载点轴向位移/mm测量点的挠度/mm12345中间杆最大应力/MPa说明100.59-0.030.000.140.200.06-4.2200.800.000.120.410.480.17-8.82301.020.120.591.231.350.59-14.28401.200.271.002.172.180.86-20.58501.420.351.423.062.971.02-28.98601.520.411.833.483.381.15-29.61701.710.502.234.204.051.11-39.27801.950.683.085.535.201.80-48.3902.150.893.946.976.452.17-56.911002.361.215.489.158.262.68-68.461101.821.948.6714.1412.323.68-91.561204.185.3623.1843.6429.556.97-171.78已失稳
![]() — 无膜三角单元块;
— 无膜三角单元块; ![]() — 有膜三角单元块。
— 有膜三角单元块。
图16 三角单元块中间杆件失稳时的位移曲线
Fig.16 Displacement curves of the middle bar of triangle unit block in the case of instability
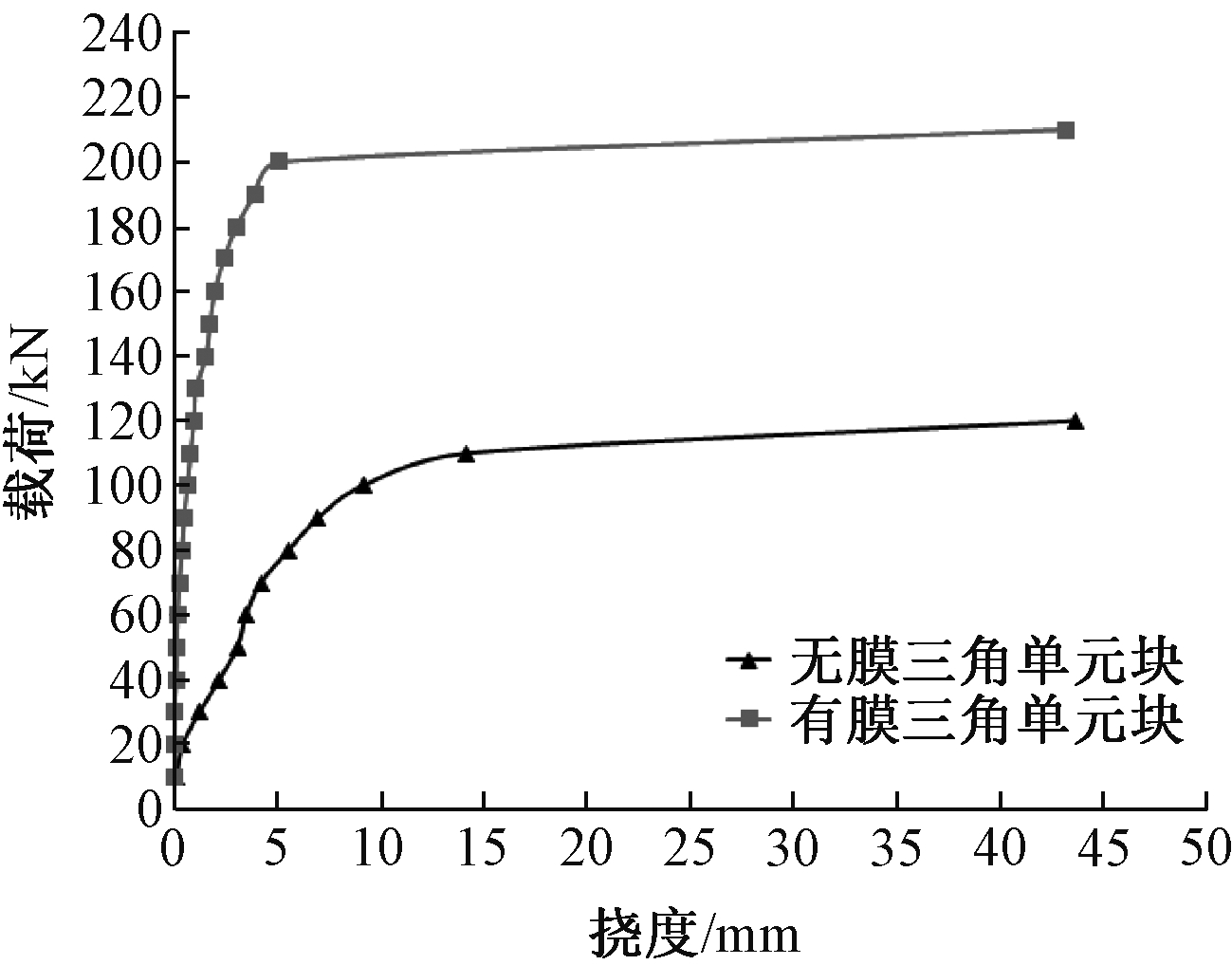
图17 三角单元块中间杆件中点荷载-挠度曲线
Fig.17 Load-deflection curves at the midpoint of the middle bar of triangle unit block
3.2.2 有膜三角单元块
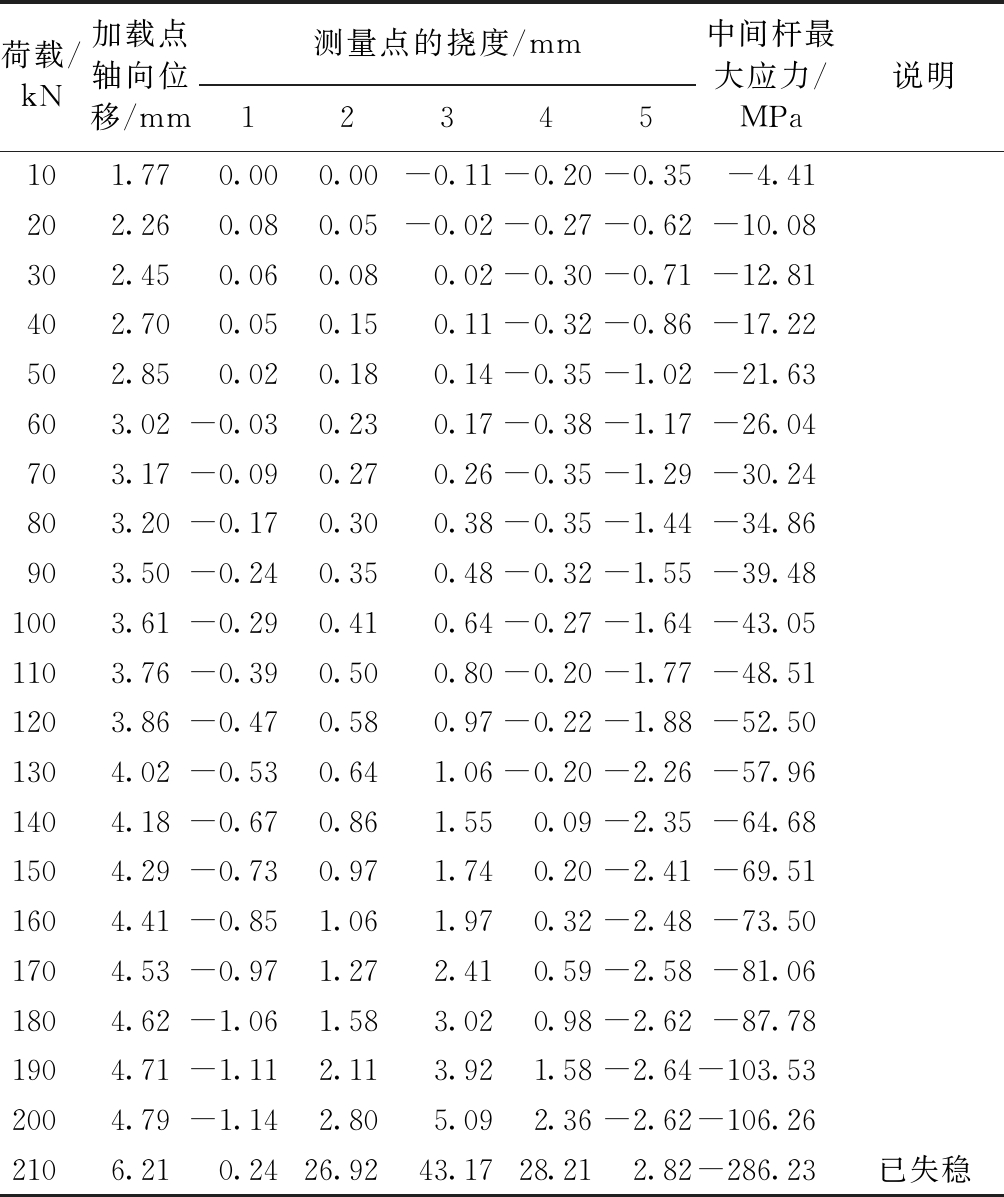
图15b为有膜三角单元块压缩失稳的试验情况,与无膜状态一样是杆件中部发生侧向变形。表2为有膜三角单元块压缩失稳试验的试验数据,试验前期,杆件的变形随着荷载的增加而呈线性增长趋势,并且承载能力明显比无膜状态要强,一直加载到210 kN才出现杆件急剧变形的情况,并且加载到210 kN以后荷载便无法继续提升,说明杆件已经失去了承载能力。从图16、图17中可以看到,有膜框架拼接杆的实际承载能力约为200 kN。在200 kN后该杆虽然还能承受荷载,但是侧向变形很大,结构上认为已经失效。在失稳时,框架上的应力值为106.26 MPa,应力水平也小于材料强度极限,属于在弹性范围内失稳。有膜框架与无膜框架相比,由于有膜的侧向拉结作用,其极限稳定承载能力有较大的提高,是无膜的1.8倍左右。
表2 有膜三角单元块的试验数据
Table 2 Experimental data of triangle unit block with membrane
荷载/kN加载点轴向位移/mm测量点的挠度/mm12345中间杆最大应力/MPa说明101.770.000.00-0.11-0.20-0.35-4.41202.260.080.05-0.02-0.27-0.62-10.08302.450.060.080.02-0.30-0.71-12.81402.700.050.150.11-0.32-0.86-17.22502.850.020.180.14-0.35-1.02-21.63603.02-0.030.230.17-0.38-1.17-26.04703.17-0.090.270.26-0.35-1.29-30.24803.20-0.170.300.38-0.35-1.44-34.86903.50-0.240.350.48-0.32-1.55-39.481003.61-0.290.410.64-0.27-1.64-43.051103.76-0.390.500.80-0.20-1.77-48.511203.86-0.470.580.97-0.22-1.88-52.501304.02-0.530.641.06-0.20-2.26-57.961404.18-0.670.861.550.09-2.35-64.681504.29-0.730.971.740.20-2.41-69.511604.41-0.851.061.970.32-2.48-73.501704.53-0.971.272.410.59-2.58-81.061804.62-1.061.583.020.98-2.62-87.781904.71-1.112.113.921.58-2.64-103.532004.79-1.142.805.092.36-2.62-106.262106.210.2426.9243.1728.212.82-286.23已失稳
4 结束语
本文介绍了柔性蒙皮分块金属桁架天线罩的力学性能分析流程,并对某28.5 m天线罩从结构静力、动力和稳定性等多个方面进行了仿真计算和校核,分析结果表明,该天线罩能够满足严苛自然环境对天线罩结构性能的要求。同时开展了天线罩蒙皮效应的试验研究,试验结果表明:柔性蒙皮金属桁架天线罩的蒙皮效应十分显著,按照试验中的状态膜对金属杆件稳定性的贡献系数达到了1.8倍左右,在天线罩桁架结构中膜结构的真实贡献可能和试验状态有所差异,但是对于天线罩整体刚度的提升肯定有很大作用,使得雷达安全性有了更高的保障。
[1]杜耀惟. 天线罩电信设计方法[M]. 北京: 国防工业出版社, 1993.
[2]张强. 天线罩理论与设计方法[M]. 北京: 国防工业出版社, 2014.
[3]唐守柱, 何炳发, 王仁德. 金属空间桁架天线罩分析与研究[J]. 现代雷达, 2006, 28(4):62-64.
[4]唐守柱, 刘兴贵, 何炳发. 球型毫米波金属桁架天线罩研究[J]. 现代雷达, 2015, 37(9): 55-59.
[5]夏邵华, 钱若军. 网壳结构非线性分析力学模型研究[J]. 河海大学学报, 1994, 22(6): 65-70.
[6]沈世钊, 陈昕, 林有军,等. 单层球面网壳的稳定性[J]. 空间结构, 1997, 3(3): 3-12.
[7]沈世钊. 网壳结构的稳定性[J]. 土木工程学报, 1999, 2(6):11-25.
[8]曾银枝. 单层球面网壳结构的稳定性能研究[D]. 上海:同济大学, 2001.
[9]曹正罡,范峰,沈世钊. 单层球面网壳的弹塑性稳定[J].土木工程学报, 2006(10): 9-12.
[10]顾磊, 王鹏, 武芳. ETFE气枕力学性能分析及其蒙皮效应研究[J]. 建筑结构学报, 2012, 33(5): 38-45.
[11]罗加智, 郑卫国, 吴乃森. 钢框架结构蒙皮效应的研究[J].工业建筑, 2005, 35(增刊): 306-309.
[12]郑谨, 张其林. 开洞压型板蒙皮效应的参数研究[J]. 建筑结构, 2006, 36(增刊): 104-106.
[13]中华人民共和国住房和城乡建设部. 建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012.
[14]董石麟, 钱若军. 空间网格结构分析理论与计算方法[M]. 北京: 中国建筑工业出版社, 2000.