建筑结构由于长期受到自然环境和使用环境的双重侵害,比如结构长期使用或功能改变,又或是设计时未严格遵照规范以及遭遇地震、海啸等偶然因素,造成结构承载力不足、变形过大,因此亟需进行维修、加固[1]。目前工程上常用到的混凝土结构加固补强措施有体外预应力技术、加大截面法、聚合物砂浆面层加固法、外粘钢板法、增设支点法等[2-3]。但是这些方法在施工过程中都有一定的缺点,而碳纤维以其质量轻、强度大、不易腐蚀、施工简便等优点被广泛应用在建筑结构加固领域[4-6]。
CFRP是一种新型的结构加固材料,属于脆性材料,无屈服点,不会发生塑性变形,在达到抗拉极限之前一直处于弹性阶段[7-8]。CFRP加固技术的工作原理是将CFRP沿着构件受拉方向或垂直于裂缝方向粘贴在涂抹好环氧树脂黏结剂的构件上,使其与原结构形成一体共同承担外力。在力的作用下,CFRP和钢筋的共同约束可增大结构的抗剪能力,改善结构的强度、刚度和抗裂性能,即可达到加固混凝土结构的最终目标。
随着土木工程领域的发展,国内外众多科研者对CFRP加固技术进行了一系列的理论和试验分析:MORTEZAEI A[9]、王新玲等[10]对碳纤维布补强损伤后的钢筋混凝土梁和预应力梁施加竖向荷载,研究了补强后的钢筋混凝土梁的受弯性能及抗弯承载力;卢春玲等利用ANSYS对预应力碳纤维加固混凝土柱的约束机理作数值模拟,分析了碳纤维包裹方式、方柱倒角半径的对构件的加固效果[11]。近年来,关于CFRP加固技术的研究对象逐渐从梁柱构件转向节点,Parvin 等选用不同种类、不同厚度、不同缠绕方式的 CFRP加固梁柱节点,进行试验及有限元抗震分析[12];常正非在完好框架节点和受损框架节点上用碳纤维补强,并对其进行低周反复加载试验,阐述了直接加固和受损后加固时框架节点的破坏过程[13]。
现阶段关于碳纤维加固技术的研究在材料和构件层面已经逐渐成熟,但在整体结构方面尚处于刚刚起步的阶段,还需更加系统化和全面化的分析。为此,本文在结构层面上对CFRP加固技术作有限元模拟。结合某工程利用有限元软件对结构模拟静力弹塑性分析,分别对比不同加固方案的框架柱对整体结构的刚度、延性、楼层位移及层间位移角的影响,并评价结构在加固前后的抗震性能,分析CFRP加固对结构性能的影响,为今后利用CFRP加固和改造框架结构的案例提供参考。
1 工程概况
某8层钢筋混凝土框架结构,首层层高为3.9 m,混凝土强度等级为C35,2~8层层高为3.3 m,用C30混凝土。各层梁柱截面尺寸见表1,均采用现浇方式。轴网布置如图1所示。楼板恒载取其自重和附加荷载,结构楼面永久荷载和可变荷载分别为3.3 kN/m2和2.0 kN/m2,屋面永久荷载为4.96 kN/m2,可变荷载为2 kN/m2。该工程使用年限为50年,结构处于7度抗震设防烈度区,设计基本地震加速度为0.15g,抗震等级为二级,场地类别为Ⅱ类,设计地震分组第一组,罕遇地震下αmax为0.72g,结构阻尼比ζ为0.05。
表1 梁柱截面尺寸
Table 1 Beam and column section sizes mm

楼层横梁(b×h)边跨中跨纵梁(b×h)次梁(b×h)柱(b×h)2~8300×500300×400300×600300×450700×7001350×500350×400350×600300×450700×700
图1 轴网布置
Fig.1 Arrangement of axis net
该框架结构为8层的综合办公楼,拟将该办公楼改为医院,而医院需要放置大型医疗器械、病床等,楼面活载增大。由于现有结构建成时间较久且不能承受新的活荷载,为了避免结构发生事故,现提出利用CFRP对结构进行抗震加固,以增强结构的整体刚度,改善其抗震性能。
2 碳纤维加固方法
为了实现对既有建筑的补强目标,改善结构的抗震性能,主要从两个方面考虑:一是对结构局部抗震加固,通过对结构中的薄弱构件予以加固来提高结构的延性,用此方法加固时,结构的刚度几乎没有变化;二是对结构进行整体抗震加固,利用加固抗侧力构件来提高整体刚度、改善结构的抗震性能,而有时需将两种方法结合起来对结构加固[14]。框架柱既是主要的抗侧力构件,又是承重构件,在水平地震作用下会发生弯曲破坏和剪切破坏。本文针对此工程提出两种加固方案:方案1,由于框架结构的底层柱为薄弱层,因此对首层框架柱进行加固;方案2,对该结构全部抗侧力构件加固以提高结构的整体刚度。
框架柱加固的具体做法是先对混凝土表面进行简单清理并打磨使构件表面尽量平顺,然后在构件表面均匀涂刷胶结剂,将宽300 mm,厚0.167 mm的碳纤维布沿柱受拉方向粘贴在其侧面,用来增加柱的抗弯承载力;并在柱端环包一层宽为100 mm的碳纤维布,作用与箍筋类似,用来约束框架柱的横向变形,提高其延性,两箍之间的净距为100 mm。具体加固详图见图2,采用的碳纤维力学性能见表2。

图2 混凝土柱加固详图
Fig.2 Strengthening details of concrete column
表2 碳纤维的力学性能
Table 2 Mechanical properties of CFRP
纤维种类纤维厚度/mm抗拉强度/MPa弹性模量/MPaCFRP0.1671 600230 000
混凝土柱经CFRP加固后的抗弯承载力计算公式如式(1),取一层框架柱KZ-1为算例,计算该构件的极限承载力:
Mu=fyAs(h0-0.5ξcfbh)+
Ecf[εcf]Acfh(1-0.5ξcfb)
(1)
式中:fy为受拉钢筋的抗拉强度设计值;As为普通受拉钢筋面积;h0为截面有效高度;εcfb为受弯构件加固后的相对界限受压区高度;Ecf为碳纤维片材的弹性模量,取Ecf=230 GPa;Acf为碳纤维片材的横截面积,取Acf=50.1 mm2;[εcf]为碳纤维布片材的允许拉应变,取Kmεcfu,其值不能超过碳纤维布片材的极限拉应变的2/3和0.01二者中的较小值;Km为碳纤维布片材厚度折减系数,取Km=0.90时;εcfu为碳纤维布材的极限压应变εcfu=0.01;有:
(2)
εcu=0.01
其中 ![]()
ξcfb=0.264
式中:εcu为混凝土的极限压应变,取0.003 3。
利用式(2)计算得到Mu=1 142.1 kN·m,是加固前抗弯承载力的1.3倍,满足GB 50367—2006《混凝土结构加固设计规范》中提出的补强后抗弯承载力增长幅度控制在40%以内,因此该加固方法可以提高框架柱的静力承载力。
3 有限元模型分析
3.1 模型建立
依据工程概况将现有结构及两加固结构的模型建立在有限元软件中,如图3所示。对三者分别作模态分析和静力弹塑性分析,在分析多自由度体系的地震响应时,应对模型进行简化,其基本假定为:
1)依据结构振型的正交性质,将其视为单自由度体系,结构的第一振型起主要作用;
2)在地震反应过程中,结构随高度的变形形状是固定不变的。

图3 有限元模型
Fig.3 The finite element model
3.2 模态分析
模态分析用来确定结构的固有特性,是进行结构分析的前提。对3个模型进行模态分析,选取结构前6阶振型的分析结果,见表3。可知:前三阶主振型符合结构自振规律,且符合质量参与系数大于90%的规定要求。原结构的频率最小,经CFRP加固后,自振频率增大,说明CFRP的加入增大了结构的抗侧刚度,改善了结构抵抗变形的能力,但前三阶振型增量不足5%,主要体现在对高阶振型的影响。
表3 结构前6阶自振频率
Table 3 First six natural frequency of frame structure

振型阶数f/Hz较未加固的增量/%未加固方案1方案2方案1方案211.2381.2641.2722.102.7521.3231.3351.3420.911.4431.3821.4251.4273.113.2643.8794.0984.0985.655.6554.1404.3864.5665.9410.2964.2684.6434.7398.7911.04
4 Pushover分析
Pushover分析可以识别出结构是否构成倒塌机制,检验其是否超出某一性能水平下的允许变形,能有效地评估结构的整体性能,为结构设计工作提供有效的理论支撑。本文建立了三个有限元模型,由于此结构的Y向刚度比X向刚度小,因此仅对其Y向进行抗震分析,采用均布加载模式,该模式适用于结构刚度和质量分布较平均且底层为薄弱层的结构,其提供的水平侧向力见式(3),并在此基础上考虑材料非线性,初始工况为结构自重,然后对结构施加水平力,用位移控制的方法进行静力弹塑性分析,来检验成果和方案选择的准确性。
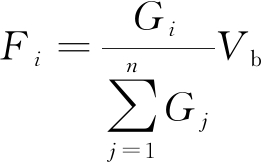
(3)
式中:Fi为第i层水平荷载;n为结构总层数;Gj为第j层的重力荷载代表值;Vb为基底总剪力。
4.1 塑性铰的定义和设置
模拟Pushover分析前,针对框架结构需在梁柱构件上设置塑性铰,将塑性铰的本构关系曲线分为4段:AB、BC、CD、DE,其依次对应弹性阶段、强化阶段、卸载阶段及塑性阶段,如图4所示。B点表示构件达到屈服,此时可确定构件的屈服点坐标;C点表示构件达到极限强度,结构发生倒塌;C点后构件的抵抗能力逐渐下降。美国规范ATC-40[15] 将构件弹塑性 BC段分成直接使用极限状态IO、安全极限状态LS、坍塌防止极限状态CP三个性能水平。
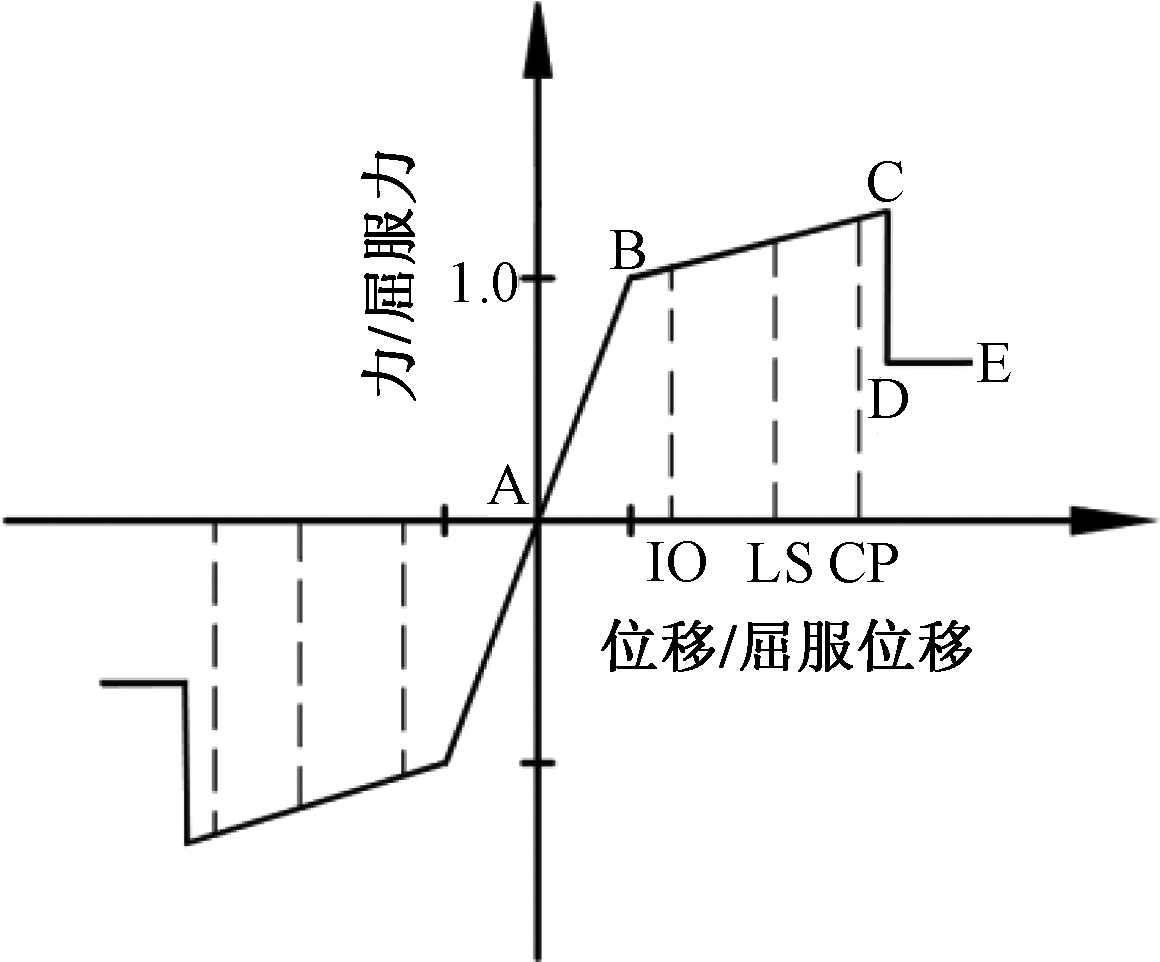
图4 塑性铰的本构关系
Fig.4 The constitutive relationship of the plastic hinge
原结构采用默认的方式设置构件的塑性铰,混凝土柱两端设置PMM耦合铰,梁端设置 M3铰,且设置点为杆件单元相对位置的0.1和0.9[16],塑性铰类型均选择FEMA型。
CFRP加固混凝土柱中包括钢筋、混凝土及碳纤维,由于该组合结构由多种不同的材料组合而成,因此需要根据材料及截面特性自定义塑性铰,在该类柱的两端设置PMM耦合铰。文献[17]中提出此类柱截面弯矩-曲率关系曲线大体上可以分成三个部分,分别为弹性段、屈服段和下降段,利用文中作者提出的无量纲特征参数的回归公式,通过计算得到CFRP加固柱的弯矩-曲率关系曲线。框架柱用CFRP加固后,其受力过程可分成两个阶段:第一阶段,混凝土横向变形较小,同时CFRP 受力也较小;第二阶段,随着荷载逐渐增加,CFRP 环向应力明显增大,直到CFRP 达到极限应变发生断裂。
4.2 Pushover曲线以及性能点分析
对三个模型进行Pushover分析,得到抗侧力曲线如图5所示:当结构顶点位移在0~22.7 mm之间时,推覆曲线保持直线,处于线弹性阶段;顶点位移在22.7 mm后,曲线斜率略有降低,此时第一批塑性铰开始出现;随着推覆分析的持续进行,曲线的斜率显著下降,逐渐趋于平缓,表现出结构的弹塑性性能。

![]() — 未加固;
— 未加固; ![]() — 方案1; ·
— 方案1; ·![]() ·· 方案2。
·· 方案2。
图5 基底剪力-顶点位移曲线
Fig.5 The relationship between base shear and top displacement
结构加固前后几乎同时达到屈服,CFRP的加固对初始刚度没有影响,结构进入弹塑性阶段后,在相同的位移处两个方案的基底剪力相较加固前都有了明显的增大,方案1的基底剪力较未加固结构增加了24.5%,方案2对应的基底剪力增加了30.4%,表明加固后结构在地震作用下承受更大的变形,CFRP改善了框架的延性且方案2结构的延性提升更多。
利用能力谱法分析结构的抗震性能时,将ATC-40规定的反应谱与中国规范反应谱对比,并进行等效转换,即通过式(4)进行地震参数转化。Pushover曲线等效得到的能力谱曲线与需求谱曲线的交点为结构性能点,通过该点的位移与位移允许值相比,来判定结构是否符合GB 50011—2010《建筑抗震设计规范》。表4列出了三种模型在罕遇地震下的性能点。CFRP加固后的结构在各自的性能点处,其顶点位移远远大于谱位移d,且小于要求控制点位移允许值,符合GB 50011—2010要求。由此可知,加固后结构符合罕遇地震的最大变形条件。
η2αmax=2.5Ca
(4a)
Tg=Cv/(2.5Ca)
(4b)
式中:Tg为特征周期;η2为阻尼调整系数;Ca为有效尖峰加速度;Cv为阻尼比是5%的结构系统反应谱。
表4 性能点坐标
Table 4 Coordinates of performance points
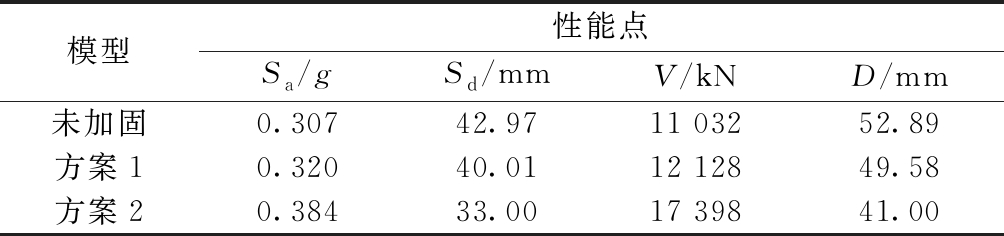
模型性能点Sa/gSd/mmV/kND/mm未加固0.30742.9711 03252.89方案10.32040.0112 12849.58方案20.38433.0017 39841.00
4.3 结构楼层位移和层间位移角分析
楼层位移和层间位移角通过对结构侧移的限制来保证结构足以抵抗水平荷载,避免产生过大位移而影响它的承载力和稳定性。图6和图7为各模型的楼层位移及层间位移角曲线。三个模型的楼层位移均呈现出理想的剪切变形,随着楼层增加,各层位移响应增大,加固后的楼层位移均小于未加固结构。结构加固前后的最大层间位移角均处于第3层,层间位移角分别为1/76,1/79,1/95,均超过弹性层间位移角限值,说明结构已经进入弹塑性阶段,而方案1最大层间位移角较加固前减小3.8%,方案2的最大层间位移角减小了20%;相较于初始结构,楼层越高,方案1对整体结构的加固效果越不明显,容易造成结构抗侧刚度不均,将导致薄弱层的出现,在地震作用下率先发生破坏,而方案2对结构各层的侧向刚度都有很大的提高,说明CFRP的加入增加了结构的侧向刚度,减小了结构地震反应,同时表明对结构整体加固更能有效增大结构的抗震性能。
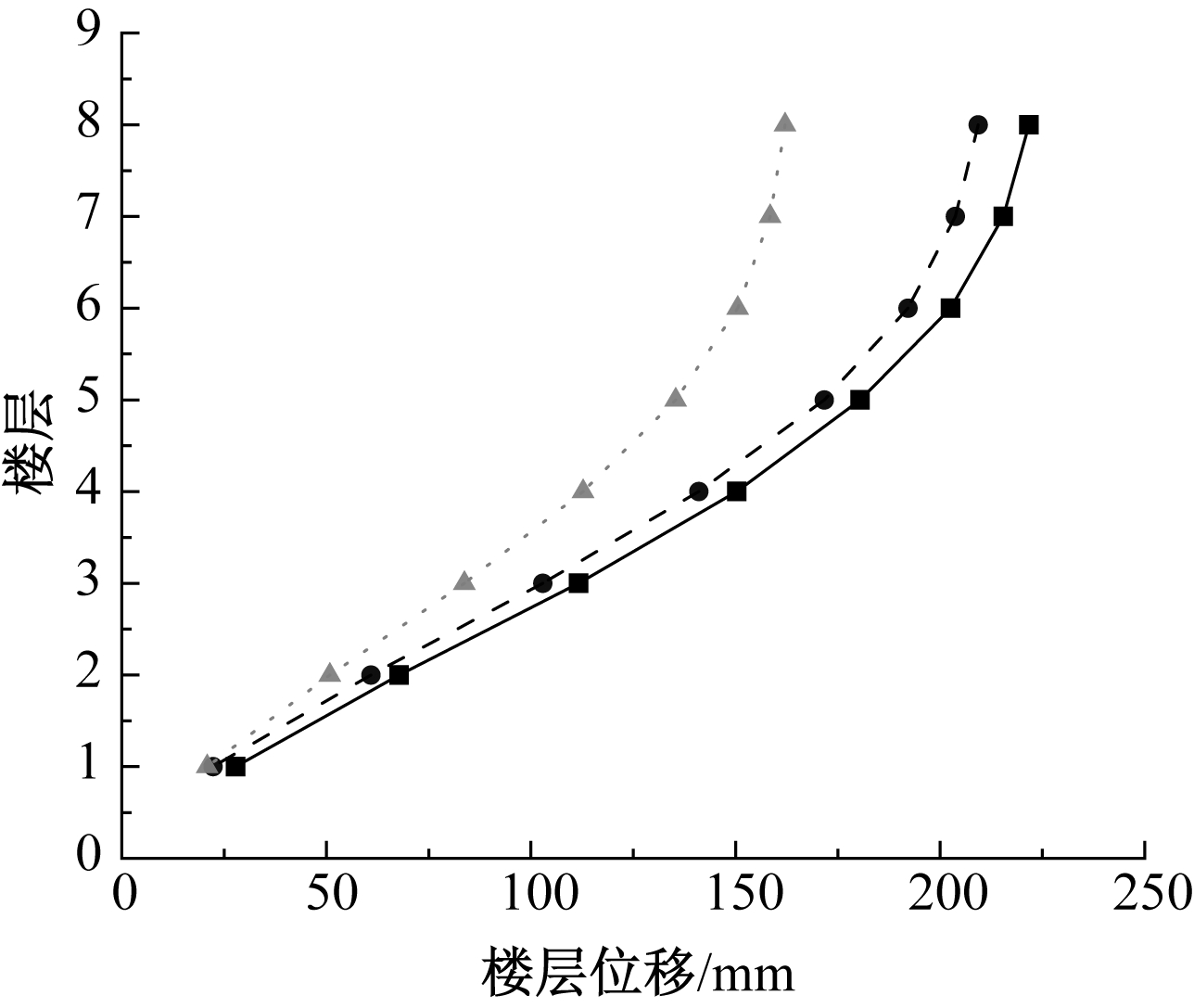
![]() — 未加固;
— 未加固; ![]() — 方案1; ·
— 方案1; ·![]() ·· 方案2。
·· 方案2。
图6 楼层位移曲线
Fig.6 Floor displacement curves

![]() — 未加固;
— 未加固; ![]() — 方案1; ·
— 方案1; ·![]() ·· 方案2。
·· 方案2。
图7 层间位移角曲线
Fig.7 Story drift angle curves
5 结束语
通过对三个模型进行模态分析和静力弹塑性分析,研究了在罕遇地震下原结构和两种不同加固方案下结构的刚度、延性、楼层位移及层间位移角的变化规律,对比分析得到以下结论:
1)加固后结构自振频率增大、周期减小,表明CFRP使得结构刚度有一定增强,但对前三阶主振型影响较小。
2)对比Pushover曲线得到结构顶点位移相同时,仅对首层柱加固结构的基底剪力较未加固结构增加了24.5%,整体加固结构的基底剪力增加了30.4%,表明加固后两个结构的延性有明显提高,CFRP的加入使得结构在水平推覆作用下可承受的塑性变形增大,有一定的安全储备。
3)对首层柱加固后最大层间位移角较未加固结构减小3.8%,整体结构加固的最大层间位移角减小了20%,且加固结构的各楼层侧移均小于未加固结构,说明CFRP的加入提高了结构的抗侧能力,且对整体结构加固后的刚度增强效果更好。
4)从影响程度来看,CFRP的加入对结构延性的影响最为显著;从追求安全系数更高的角度来看,方案1仅对CFRP加固层及相邻层有效,且造成结构各层刚度不均匀,而方案2加固效果更佳,因此可选择方案2,即CFRP加固整体结构的方案。
[1]赵彤,谢剑. 碳纤维布补強加固混凝土结构新技术[M]. 天津: 天津大学出版社, 2001: 32-40.
[2]李进卫. 碳纤维增强复合材料性能特点及其应用领域[J].化学工业,2015,33(8):13-18.
[3]张敬书.我国抗震鉴定和加固技术的发展[J]. 工程抗震与加固改造, 2004(5): 33-39.
[4]WEN H M. Penetration and Perforation of Thick FRP Laminates [J].Composites Science and Technology, 2001,61(8):1163-1172.
[5]HIROSHI F.FRP Composites in Japan[J].Concrete International,1999,21(10):29-32.
[6]LUC R T,STIJN MATTHYS.FRP for Construction: Activities in Europe[J].Concrete International, 1999,21(10): 33-66.
[7]张鑫, 李安起, 赵考重. 建筑结构鉴定与加固改造技术的进展[J]. 工程力学, 2011, 28(1):1-11,25.
[8]张荣国, 刘沐宇, 刘其卓. 碳纤维材料加固技术的研究现状[J].武汉理工大学学报, 2004(8):71-73.
[9]MORTEZAEI A, RONAGH H R, KHEYRODDIN A. Seismic Evaluation of FRP Strengthened RC Buildings Subjected to Near-fault Ground Motions Having Fling Step[J].Composite Structures, 2010, 92(5):1200-1211.
[10]王新玲,苏会晓,钱辉.碳纤维加固材料加固受损混凝土梁受弯性能试验及设计方法研究[J].工业建筑,2015,45(9):68-71,92.
[11]卢春玲,李中洋,黄博,等.预应力碳纤维复材布加固钢筋混凝土方柱轴压性能分析[J].工业建筑,2018,48(7):173-179.
[12]PARVIN A, GRANATA P. Investigation on the Effects of Fiber Composites at Concrete Joints[J]. Composites Part B: Engineering, 2000,31(6): 499-509.
[13]常正非,杨志勇,李书进.碳纤维加固受损混凝土框架节点的试验研究[J].华中科技大学学报(自然科学版),2016,44(12):64-69,75.
[14]胡孔国, 陈小兵, 岳清瑞.基于性能的碳纤维抗震加固设计[J].地震工程与工程振动,2004,24(5):159-166.
[15]ATC. ATC 40: Recommend Methodology for Seismic Evaluation And Retrofit of Existing Concrete Buildings[S]. Applied Technology Council,1996.
[16]北京金土木软件技术有限公司,中国建筑标准设计研究院.SAP2000中文版使用指南[M].2版. 北京:人民交通出版社, 2012: 466-476.
[17]吴波,王维俊,王帆.碳纤维布加固钢筋混凝土柱的弯矩-曲率关系分析[J].华南理工大学学报(自然科学版),2005(1):10-15.