不锈钢芯板结构是由远大可建科技有限公司独创、湖南大学配合远大可建参与研究的一种新型建筑结构体系,其结构类似于常见的蜂窝板夹层结构[1-2]。不锈钢芯板结构结合了不锈钢材料与蜂窝板结构两者的优点,通过独创的铜钎焊技术把以不锈钢为材料的面板及密布的芯管连接在一起,拥有非常优秀的各项性能。为顺利将不锈钢芯板结构投入实际应用,远大可建以不锈钢芯板结构为基础设计制作了芯板梁、芯板墙、芯板等受力构件。
目前对不锈钢芯板结构小构件的研究已比较完备,但是大型受力构件的研究还处于初步阶段,大构件研究是建筑结构推广与应用的第一步,对不锈钢芯板大构件的研究具有重要的意义。
本研究主要通过有限元分析对一字形墙压弯性能进行研究,首先利用ABAQUS软件在有限元建模方式的基础上建立3组共9个不锈钢芯板一字墙压弯的有限元模型[3],对不锈钢芯板结构一字形墙的压弯受力过程与破坏机理进行详细的分析,绘制构件压弯过程的荷载-位移曲线。先后建立共145组有限元模型,把得到的数据进行汇总、参数分析,结合各向异性板板壳理论,推导出不锈钢芯板一字形墙的压弯稳定承载力计算式,进而为不锈钢芯板结构一字形墙的设计与应用提供可靠的依据。
1 建立有限元模型
1.1 不锈钢材料与力学性能
1.1.1 材料的本构关系
不锈钢材料是一种非线性材料,其应力-应变曲线上没有明显的屈服点,也没有屈服平台,对于这种材料,通常是取塑性应变为0.2%时对应的应力作为材料的屈服强度f0.2。普通的奥氏体型不锈钢,断裂时的应变是碳素钢的1~2倍,达到了40%~60%,具有优异的塑性变形能力。
不锈钢材料实际上是一种高合金钢材,合金化元素影响着它的性能。不同于普通碳素钢的双线性模型(弹性-理想塑性模型),不锈钢材料应用连续本构关系模型是修正后的Ramberg-Osgood式,该式由Ramberg和Osgood提出,Hill进行第一次修正,Rasmussen等进行第二次修正[4]:
(1a)
(1b)
其中 f0.2<σ≤fu
m=1+3.5f0.2/fu
εu=1-f0.2/fu
式中:f0.2为名义屈服强度标准值;E0为初始弹性模量;n为应变强化系数;fu为抗拉强度标准值;m为计算系数;E0.2为f0.2时对应的切线弹性模量;εu为对应于极限强度fu的极限应变。
1.1.2 材料选择
S30408奥氏体不锈钢相比其他牌号的不锈钢,拥有更强的抗腐蚀能力,能够适应更多复杂的环境。它也是最常用的奥氏体不锈钢,耐腐蚀性强,塑性、韧性和冷加工性能良好[5],冲压、弯曲等热加工性能好,且价格经济实惠。所以不锈钢芯板结构采用S30408牌号不锈钢作为母材。S30408奥氏体不锈钢材料的应力-应变曲线如图1所示。各项材料力学参数取值见表1[6]。后续全部有限元计算将以S30408不锈钢的材性为主。

图1 S30408奥氏体不锈钢的应力-应变曲线
Fig.1 Stress-strain curve of S30408 austenitic stainless steel
表1 S30408奥氏体不锈钢的材料强度指标
Table 1 Material strength index of S30408 austenitic stainless steel

材料νE0/MPaE0.2/MPaσ0.2/MPaσ1.0/MPaσu/MPaS304080.3193 94921 201328379703
1.2 建立模型
采用有限元分析软件ABAQUS来研究不锈钢芯板一字形墙的压弯性能。本研究建立的有限元模型与文献[6-7]相同,在一字形墙轴压性能与芯板试件剪切[7]、侧压[8]研究中,研究有限元计算结果和破坏形态与试验结果都吻合得很好,故本文的有限元建模方法有可靠的参考价值。
由于芯管的管壁非常薄,属于圆柱壳结构,故可忽略其厚度方向即切向的应力。另外,因为面板相对于整个构件也很薄,受力面积和承载力都比较大,所以面板也采用壳单元进行模拟。在有限元模型中,面板和芯管均采用S4R四结点壳单元。一字形墙面板和芯管的材料均为奥氏体S30408不锈钢,其本构关系根据材料的力学性能试验确定,泊松比取0.3,弹性模量取1.93×105 MPa。
建立有限元模型时,均采用位移控制的方式进行单调加载,将墙顶与墙底平面分别耦合在RP1与RP2两个参考点上,把墙顶与墙底的边界条件施加在RP1与RP2上,加载点位于一字形墙端板上的参考点RP1处,上端约束了y、z两个方向的平移以及绕y轴的转动,下端铰接,约束三个方向上的平动以及绕y、z轴的转动。模型的边界条件与有限元模型的网格划分情况如图2、图3所示。

图2 不锈钢芯板一字形墙的荷载与边界条件
Fig.2 Load and boundary conditions of a in-line wall of stainless steel sandwich panel
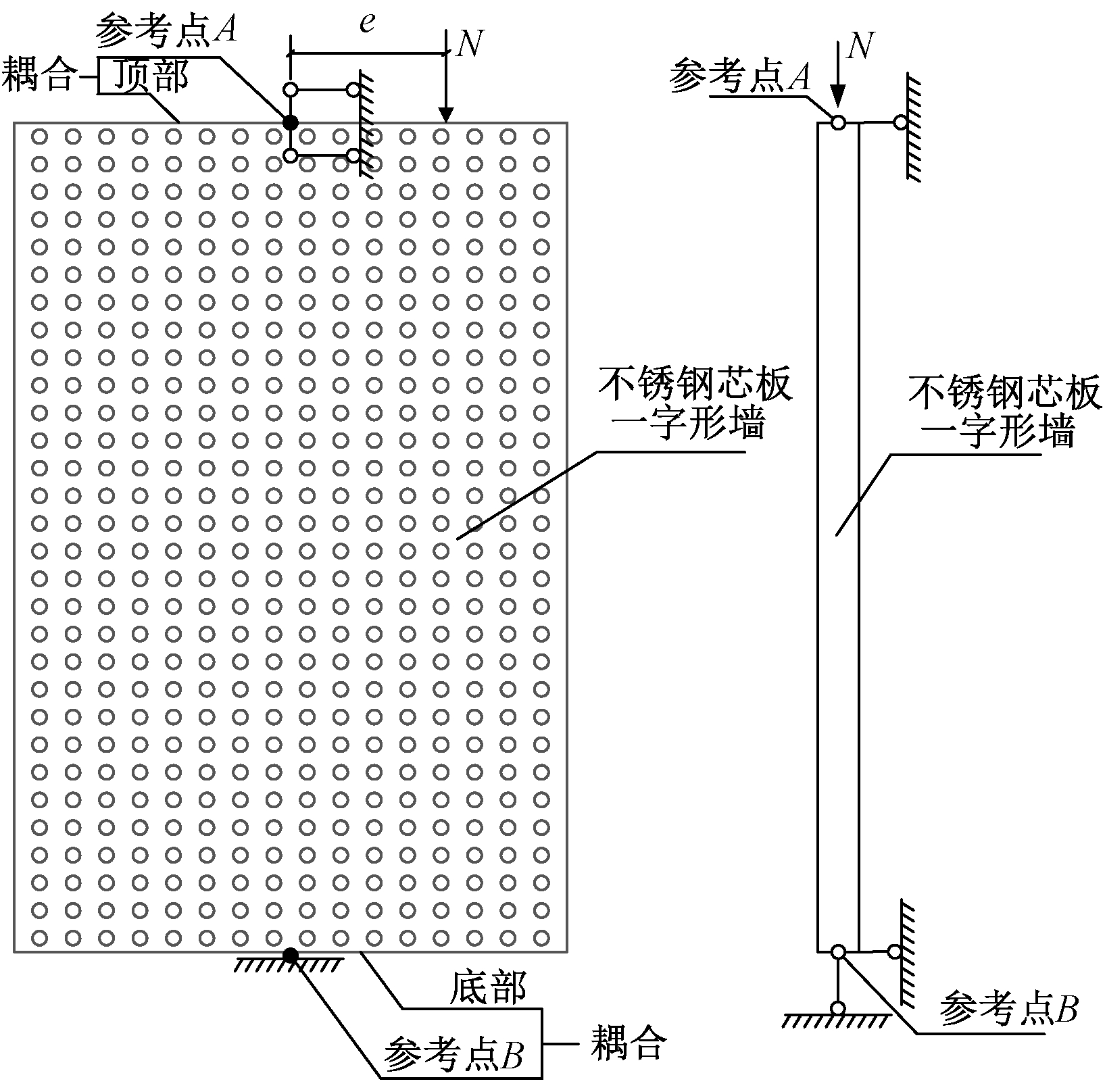
图3 构件有限元模型网格划分
Fig.3 Meshing of the finite element model of component
1.3 初始缺陷
由于构件上初始的几何缺陷会显著影响不锈钢芯板一字墙的压弯性能,所以采用有限元研究时必须考虑初始几何缺陷对整个结构的影响。故在对同一个试件进行有限元模拟时,先后建立两个有限元模型,在第1个模型中对结构的弹性屈曲进行分析,得到相应的特征值屈曲模态,再将第一阶屈曲模态(弹性屈曲荷载最小对应模态)按L/1 000(L为墙高)的比例施加于第2个模型上;利用第2个模型对结构进行非线性屈曲分析,以此来模拟实际试验的过程。图4为两组模型的一阶弹性屈曲模态。

a—第1个模型; b—第2个模型。
图4 不锈钢芯板一字形墙有限元弹性屈曲模态
Fig.4 The finite element elastic buckling mode of the in-line wall of the structure of stainless steel sandwich panel
2 有限元模拟分析
本文共建立了9个不锈钢芯板一字形墙的有限元模型,分别编号为ISWB2.5-1~ISWB6-3,试件对应规格见表2。
表2 构件分组及规格参数
Table 2 Component grouping and specifications

试件编号试件分组试件规格(长×宽×厚)/mm面板厚tf/mm芯管规格(外径×壁厚×管高)/mm芯管间距/mm横向lmz纵向lnx偏心距e/mm构件数/个ISWB2.5-1第1组3 000×2 000×1522.5ϕ51×0.5×1471001003001ISWB2.5-2第2组3 000×2 000×1522.5ϕ51×0.5×1471001005001ISWB2.5-3第3组3 000×2 000×1522.5ϕ51×0.5×1471001007001ISWB4-1第4组3 000×2 000×1554.0ϕ51×0.5×1471001003001ISWB4-2第5组3 000×2 000×1554.0ϕ51×0.5×1471001005001ISWB4-3第6组3 000×2 000×1554.0ϕ51×0.5×1471001007001ISWB6-1第7组3 000×2 000×1596.0ϕ51×0.5×1471001003001ISWB6-2第8组3 000×2 000×1596.0ϕ51×0.5×1471001005001ISWB6-3第9组3 000×2 000×1596.0ϕ51×0.5×1471001007001
2.1 破坏形态
9个构件的破坏形态十分一致,均为受压区面板与侧板的局部屈曲破坏,图5为3个典型构件的破坏形态。
从图5可以看出,不锈钢芯板一字形墙在压弯稳定承载力达到极限时,受压区一侧的面板出现了明显的屈曲,两块面板向同一个方向屈曲,与面板屈曲部分相连的芯管根部没有出现明显的屈曲,侧板上也由面板的带动出现了屈曲。
从9个有限元模型最终的破坏形态可以看出:不锈钢芯板一字形墙在压弯作用下最终的破坏均表现为受压区一侧的局部屈曲破坏,两块面板夹带一排芯管向同一个方向屈曲,受拉区没有发生屈曲,没有明显的偏心受压破坏。

a—ISWB2.5-1; b—ISWB4-1; c—ISWB6-1。
图5 构件最终破坏形态
Fig.5 Final failure mode of component
2.2 荷载-位移曲线
选取每个计算模型结果参考点上的竖向荷载与竖向位移,绘制构件受力过程中的荷载-位移曲线,如图6所示。9个模型受力过程中都经历了弹性受力、弹塑性受力以及塑性破坏等3个阶段[9]。典型试件ISWB2.5-2受力过程中的受力云图如图7所示。
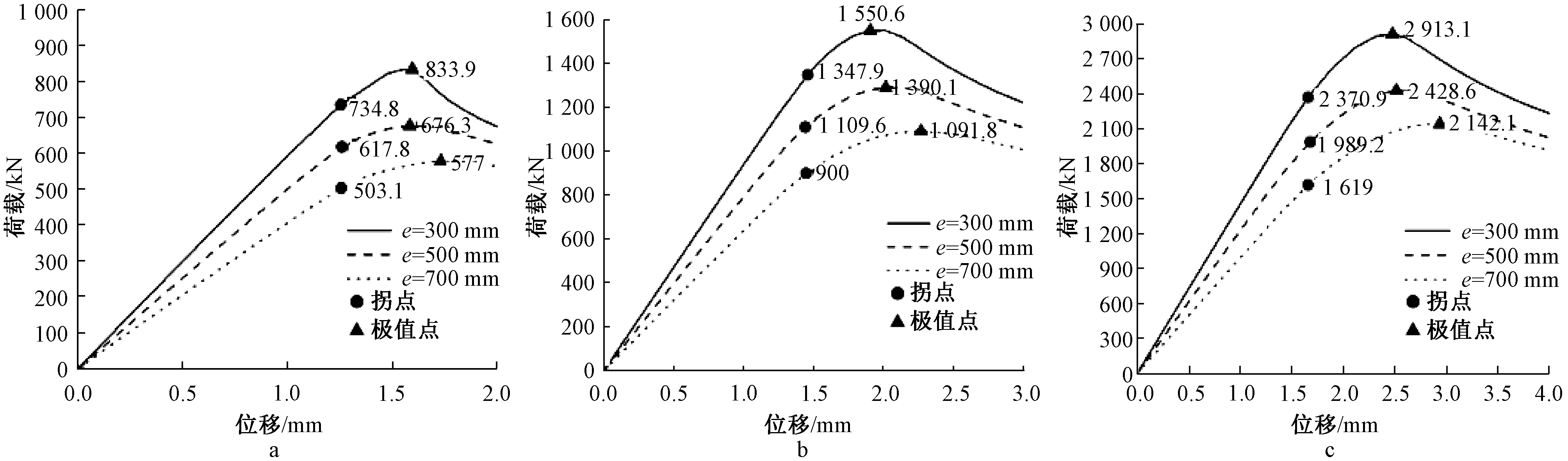
a—ISWB2.5-1~3; b—ISWB4-1~3; c—ISWB6-1~3。
图6 荷载-位移曲线
Fig.6 Load-displacement curves
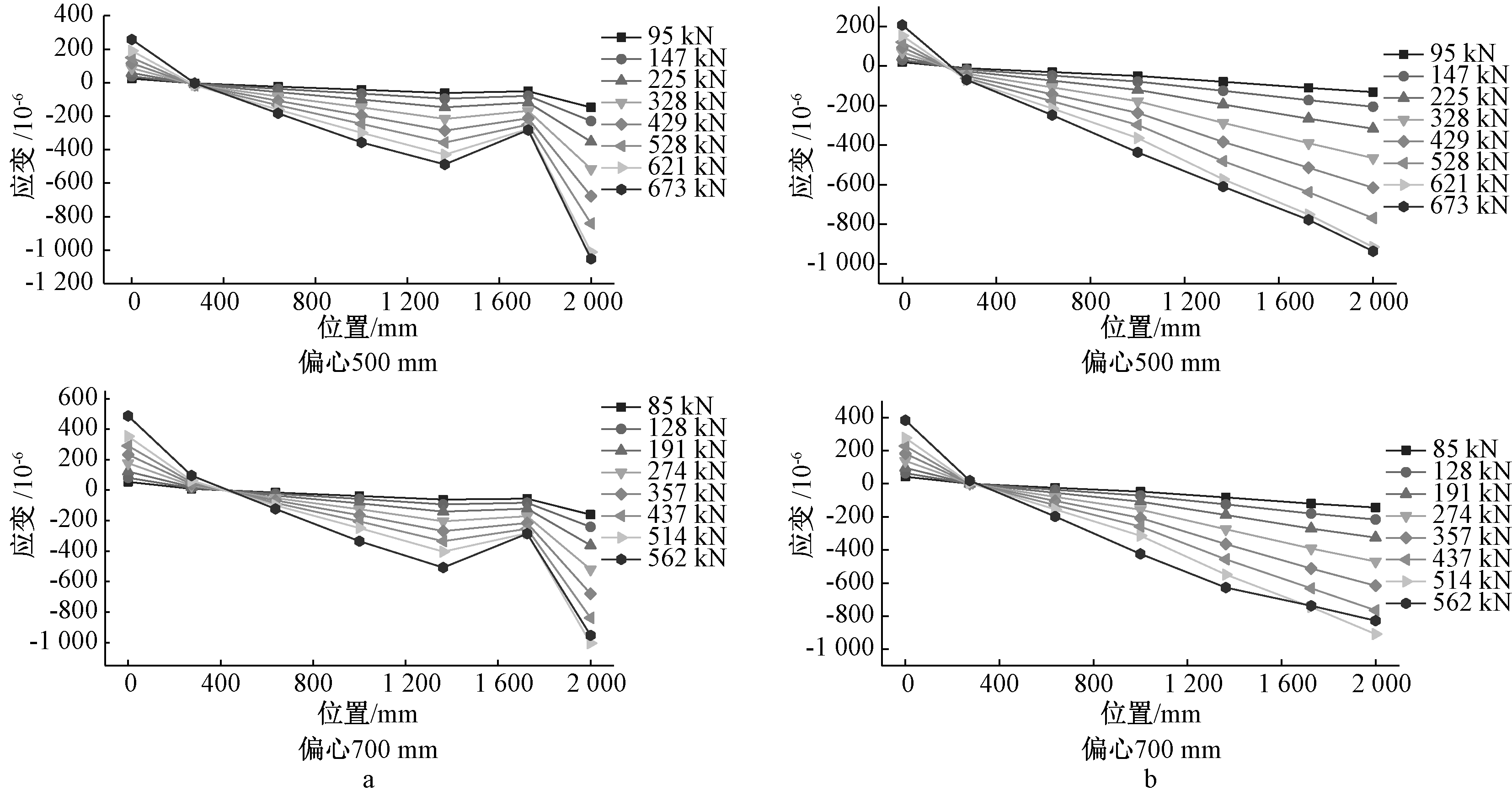
a—端板截面; b—破坏截面。
图7 一字形墙端板截面和破坏截面的应变分布(tf=2.5 mm)
Fig.7 Strain distribution of end-plate section and failure seation of in-line wall (tf=2.5 mm)
弹性受力阶段:荷载与位移基本呈线性增长的关系,整个阶段,构件面板、芯管与侧面板应力均小于328 MPa,均没有产生明显的屈曲,受压区上端相较于其他区域有更大的应力。随着竖向荷载的提高,此时荷载-位移曲线达到了直线段末端,即为拐点。到达拐点时,面板应力达到332 MPa,大于不锈钢的屈服强度,此时面板开始产生屈曲。
弹塑性受力阶段:过拐点后,竖向荷载与竖向位移已不再呈线性关系,荷载-位移曲线的斜率越来越小,荷载增加速度变慢,位移增大速度加快,此时达到弹塑性受力阶段。受压区一侧面板的应力大于不锈钢屈服强度328 MPa,开始以较慢的速度屈曲,芯管端部的应力小于屈服强度328 MPa,但是在面板的带动下开始小幅度的屈曲,此时芯管对面板仍有支撑作用,减缓了面板的屈曲速度。
塑性破坏阶段:竖向荷载达到极值点,即一字形墙压弯达到稳定极限承载力,此时受压区一侧面板上的应力已达到404.8 MPa,芯管端部应力已达到350 MPa,远大于不锈钢屈服强度328 MPa,芯管产生很大的屈曲并丧失对面板的支撑作用。失去芯管支撑作用后,面板瞬间产生了非常明显的屈曲,构件破坏。之后,竖向荷载开始缓慢下降,竖向位移仍继续增大,不锈钢芯板一字形墙丧失承载能力。
破坏本质:结构进入弹塑性破坏阶段后,受压区上端面板的应力超过不锈钢的屈服强度,导致面板开始产生屈曲变形,由于芯管面板有支撑作用,所以面板屈曲速度仍较慢,直到芯管端部应力超过不锈钢屈服强度,进而使与面板相连的芯管端部产生比较大的屈曲变形,芯管丧失对面板的支撑作用,受压区面板失去支撑,瞬间产生巨大屈曲,最终导致构件破坏。
2.3 截面内的应变分布
由前两节可以看到:不同规格的不锈钢芯板一字形墙在压弯作用下的破坏形态与受力过程基本相同,故为了研究不锈钢芯板一字形墙截面内的应变分布,本文取面板为2.5 mm厚、芯管外径为51 mm、芯管壁厚为0.5 mm、芯管排布为121 mm×100 mm的芯板为研究对象,建立有限元模型,计算偏心距为500,700 mm两种情况。在墙顶端板上与破坏截面上设立参考点,从截面最左端即0 mm处开始,在0,274,637,1 000,1 363,1 726,2 000 mm处设置参考点,输出这7个参考点在每一阶段上的应变,并作出应变图,观察截面整体的变化。
图8a、8c两个模型的端板应变在1 726 mm处发生了突变,这是由于该参考点处于芯管上方,芯管的存在使该点局部屈曲减小。由图8可以看出,不锈钢芯板一字形墙在压弯受力过程中基本截面符合平截面假定,与实际情况比较符合,截面的整体性很好,偏心一侧为受压区,另一侧则为受拉区。

a—荷载到达拐点时的应力云图; b—荷载到达极值点时面板的应力云图; c—荷载到达极限承载力时的应力云图。 1—受压区面板上的应力大于不锈钢屈服强度,面板开始出现屈曲,构件进入弹塑性阶段;2—受压区一侧的芯管端部应力较大,但小于不锈钢 的屈服强度,没有明显改变;3—受压区面板应力远大于屈服强度,屈曲越来越明显,屈曲位置的周围面板应力开始增大,构件失去承载能力; 4—由于面板屈曲,与面板相连的芯管端部应力大于不锈钢屈服应力,开始发生明显屈曲,对面板的支撑作用明显减弱; 5—受压区面板完全屈服,一侧发生非常明显的鼓曲,另一侧凹曲,构件完全破坏,失去承载能力; 6—受压区部分芯管端部完全屈曲,完全丧失对面板的支撑作用。
图8 典型试件ISWB2.5-2受力过程中的受力云图 MPa
Fig.8 Stress nephogram of typial specimen ISWB2.5-2 under loading
3 不锈钢芯板一字形墙压弯稳定承载力参数分析
3.1 设计参数
本文所研究的不锈钢芯板一字形墙的设计参数(图9、图10)如下:a为不锈钢芯板一字形墙的高度;b为不锈钢芯板一字形墙的宽度;h(h=hw+2tf)为芯板截面高度;tf为芯板面板厚度;tw为芯管壁厚; hw为芯管长度(或高度);d为芯管外径;dn为沿芯板宽度(y轴)方向芯管净距;lny(lny=d+dn)为沿芯板宽度(y轴)方向芯管中到中距离;dm为沿芯板长度(x轴)方向芯管净距;lmz(lmz=d+dm)为沿芯板长度(x轴)方向芯管中到中距离。
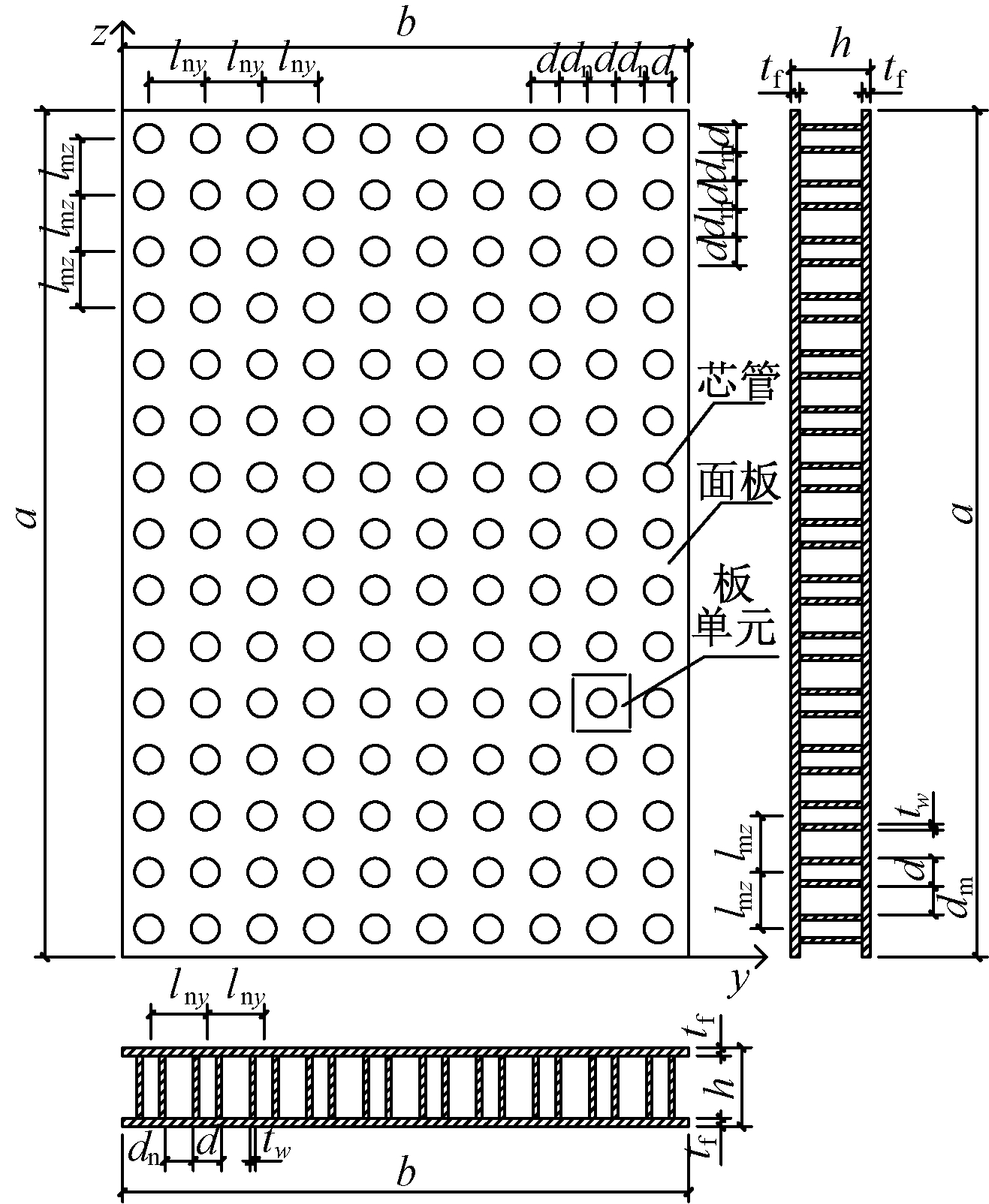
图9 不锈钢芯板一字形墙腹板墙肢设计参数
Fig.9 Schematic diagram of design parameters of the in-line wall of stainless steel sandwich panel

a—沿长度(z轴)方向截面单元; b—沿宽度(y轴)方向截面单元。
图10 计算板单元示意
Fig.10 Schematic diagram of calculation board unit
3.2 参数分析
为了研究偏心距、构件高宽比、面板厚度、芯管壁厚、芯管排布以及芯管管径对不锈钢芯板一字形墙压弯能力的影响[10],本文建立了各类不同规格的共92组有限元模型进行计算,从大量有限元计算结果中总结各因素对不锈钢芯板一字形墙压弯性能的影响。
3.2.1 高宽比
保持芯管壁厚为0.5 mm,芯管外径为51 mm,芯管纵间距为100 mm不变,取面板厚度为2.5,4,6 mm,柱高分别取3,3.6,4.2,4.5 m,即1.5、1.8、2.1、2.25的高宽比,偏心距均为500 mm,建立有限元模型进行计算,整理计算结果并绘出曲线如图11所示。

![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=4 mm;
— tf=4 mm; ![]() — tf=6 mm。
— tf=6 mm。
图11 构件宽高比与压弯承载力关系
Fig.11 Relationship between aspect ratio and compression-bending bearing capacity of member
可以看出:构件高宽比对其压弯稳定承载力的影响不大,高宽比的提高会使不锈钢芯板一字形墙的压弯稳定承载力提高,四种高宽比的有限元模型最终均为受压区面板的局部屈曲破坏。
3.2.2 面板厚度
保持芯管间距为121 mm×100 mm、芯管壁厚为0.5 mm、芯管外径51 mm不变,取面板厚度为1.5,2.5,4,6 mm、偏心距300~700 mm的一字形墙进行压弯计算,将计算结果整理并汇总为曲线(图12)。可以看出,随着面板厚度的增大,不锈钢芯板一字形墙的压弯承载力随之提高,四种面板厚度的构件在各偏心距压弯作用下,最终均表现为受压区面板的局部屈曲破坏。

![]() — e=700 mm;
— e=700 mm; ![]() — e=500 mm;
— e=500 mm; ![]() — e=400 mm;
— e=400 mm; ![]() — e=300 mm。
— e=300 mm。
图12 面板厚度与压弯承载力关系
Fig.12 Relationship between panel thickness and compression-bending bearing capacity
3.2.3 芯管外径

![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=4 mm;
— tf=4 mm; ![]() — tf=6 mm。
— tf=6 mm。
图13 芯管外径与压弯承载力关系
Fig.13 Relationship between outer diameter of core tube and compression-bending bearing capacity
保持芯管间距为121 mm×100 mm不变,芯管厚度为0.5 mm不变,取面板厚度为2.5,4,6 mm、偏心距为500 mm的一字形墙,分别以41,51,61 mm的芯管外径建立有限元模型进行计算,将计算结果整理并汇总为曲线,如图13所示。可以看到:随着芯管外径的增大,三种面板厚度的一字形墙压弯承载力都有所提高,这是由于芯管直径增加使得芯管与面板接触面积增大,对面板的支撑作用变强,使承载力得到提高。三种芯管外径与面板厚度的一字形墙的破坏形态都表现为受压区面板的局部屈曲破坏。
3.2.4 芯管壁厚
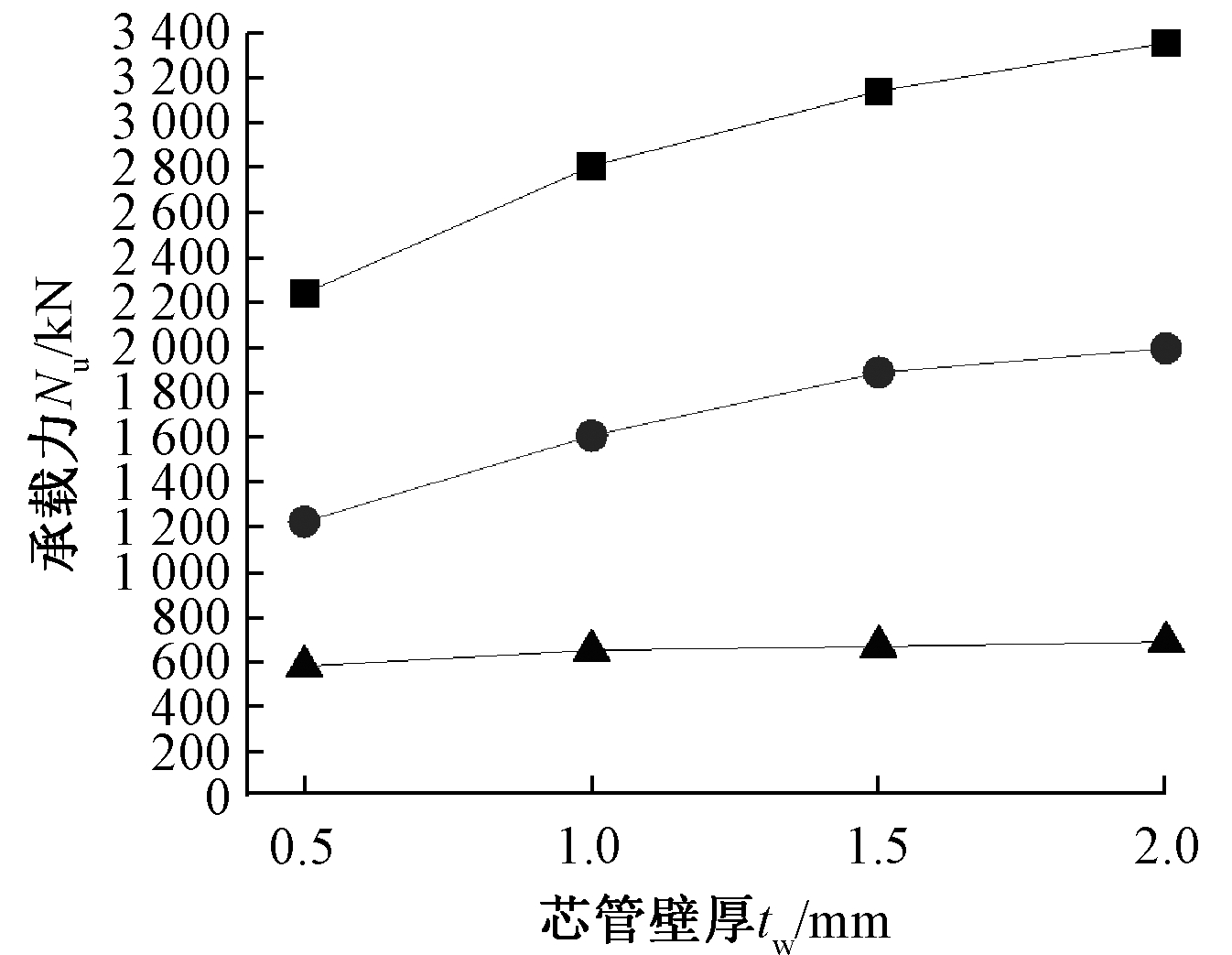
保持芯管间距为121 mm×100 mm不变、芯管外径为51 mm、面板厚度为2.5 mm不变时,分别以0.5,1,2 mm三种芯管壁厚建立模型,并分别在300,400,500 mm的偏心距下进行计算,将计算结果汇总并绘成曲线(图14)。可以看到,随着芯管厚度的增大,不锈钢芯板一字形墙的压弯稳定承载力也在增大。但面板厚度较薄时,芯管壁厚的影响会很小,这是因为当面板比较薄而芯管较厚时,芯管截面刚度更大,导致面板上不通过芯管的截面先发生局部屈曲,在芯管厚度较大时,破坏几乎全部由面板控制,使构件的压弯承载力不会随芯管壁厚而发生明显的改变。说明芯管壁厚与面板厚度应当有一定的匹配度,在一定面板厚度下,应配置合理的芯管构造厚度,避免浪费。3种芯管壁厚以及4种面板厚度的一字形墙的破坏形态均表现为受压区面板的局部破坏。
![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=4 mm;
— tf=4 mm; ![]() — tf=6 mm。
— tf=6 mm。
图14 芯管壁厚与压弯承载力关系
Fig.14 Relationship between wall thickness of core tube and compression-bending bearing capacity
3.2.5 芯管纵间距
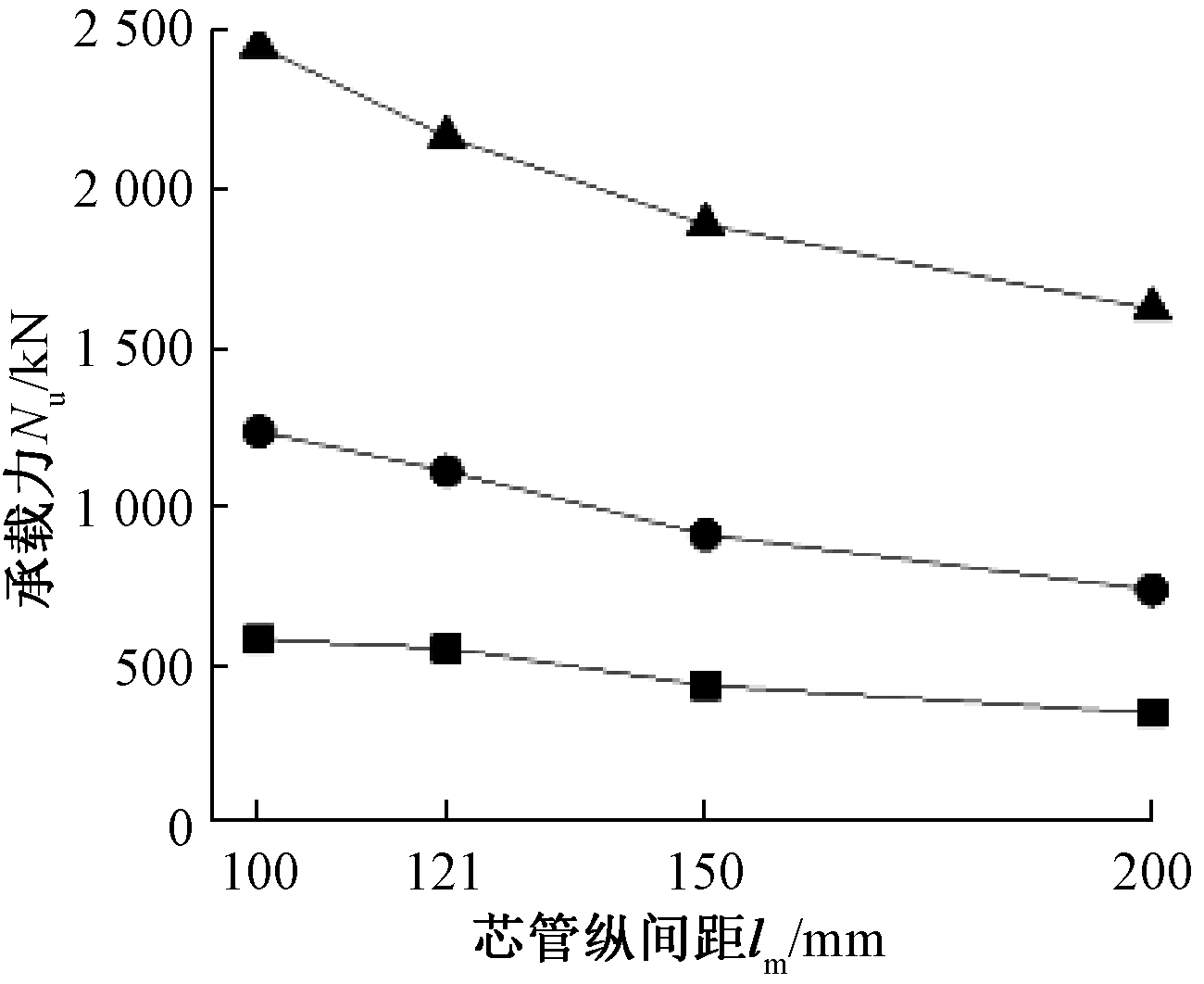
保持芯管壁厚为0.5 mm,芯管外径为51 mm,芯管横间距为121 mm不变,取面板厚度为2.5,4,6 mm,芯管纵间距分别为100,121,150,200 mm,偏心距为500 mm,建立有限元模型进行计算,将计算结果汇总为曲线(图15)。可以看出:随着芯管纵间距的变大,三种面板厚度的不锈钢芯板一字形墙的压弯承载力都逐渐下降。三种芯管纵间距下的一字形墙的破坏形态都表现为受压区面板屈曲的局部破坏。
![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=4 mm;
— tf=4 mm; ![]() — tf=6 mm。
— tf=6 mm。
图15 芯管纵间距与压弯承载力关系
Fig.15 Relationship between longitudinal spacing of core tube and compression-bending bearing capacity
3.2.6 芯管横间距
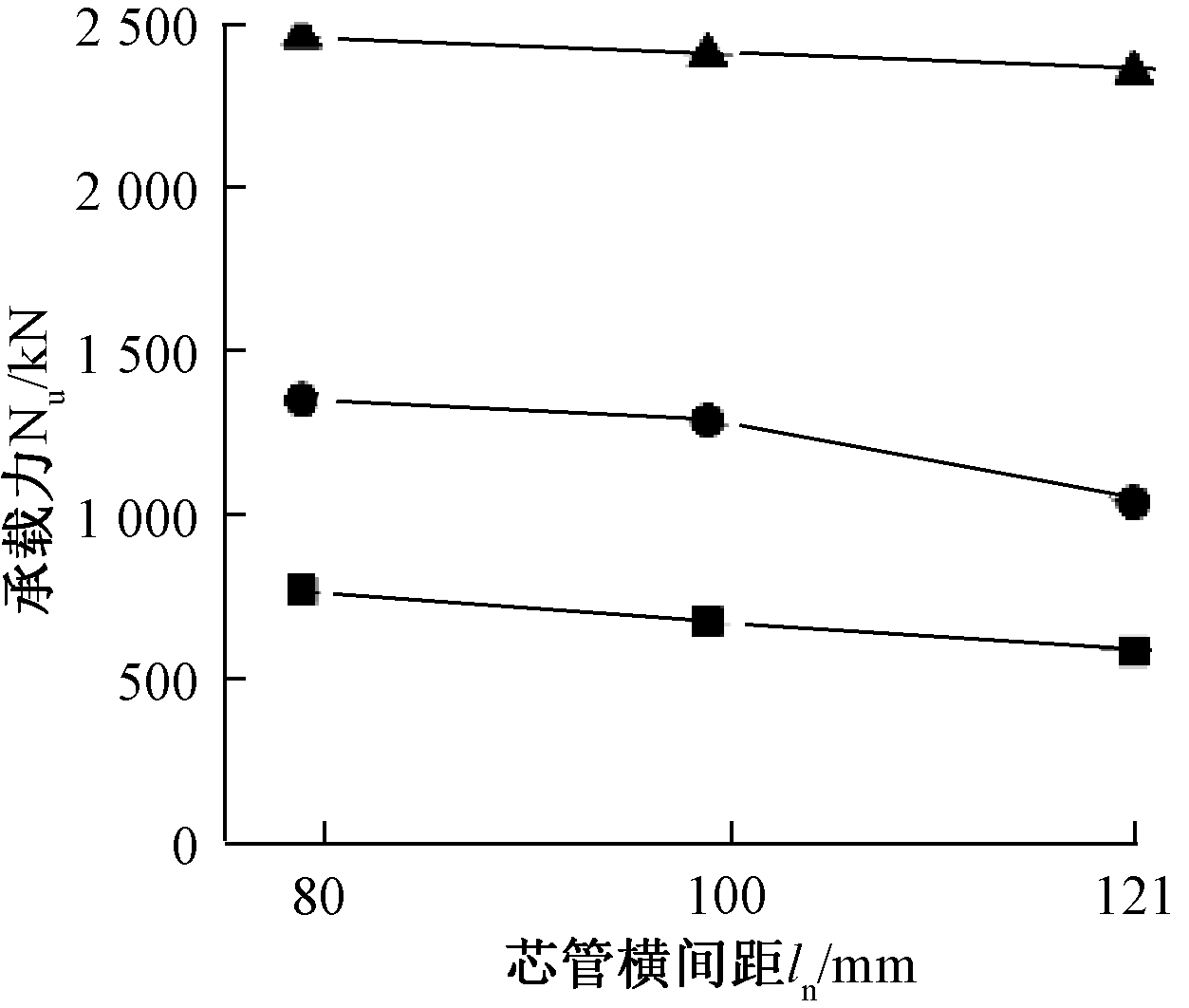
保持芯管壁厚为0.5 mm、芯管外径为51 mm、芯管纵间距为100 mm不变,取面板厚度为2.5,4,6 mm,芯管横间距分别为80,100,121 mm,建立有限元模型进行偏心距为500 mm的压弯计算,整理计算结果并汇总为曲线(图16)。
可以看出,随着芯管横间距的变大,三种面板的一字形墙的压弯承载力都有所降低,在一定范围内,芯管横间距对压弯承载力的影响不大,以上计算的各模型中一字形墙的破坏形态均体现为受压区的面板屈曲的局部破坏。
![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=4 mm;
— tf=4 mm; ![]() — tf=6 mm。
— tf=6 mm。
图16 横间距与压弯承载力关系
Fig.16 Relationship between lateral spacing and compression-bending bearing capacity
3.2.7 偏心距
建立面板厚度为1.5,2.5,4,6 mm,芯管间距均为121 mm×100 mm,芯管外径均为51 mm的有限元模型,分别以300,400,500,700 mm四个偏心距进行计算,将计算得到的结果整理并汇总为曲线(图17)。可以看出,随着加载偏心距的增大,四种面板厚度的一字形墙的压弯承载力都在逐渐变小,且偏心距对四种面板厚度的一字形墙压弯承载力的影响程度都是相近的。在所有偏心距和面板厚度的模型计算中,一字形墙的破坏形态均表现为受压区面板的局部屈曲破坏。

![]() — tf=1.5 mm;
— tf=1.5 mm; ![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=4 mm;
— tf=4 mm; ![]() — tf=6 mm。
— tf=6 mm。
图17 偏心距与压弯承载力关系
Fig.17 Relationship between eccentricity and compression-bending bearing capacity
3.3 不锈钢芯板一字形墙压弯稳定承载力计算理论
传统的钢板墙在各个方向上的刚度差距不大甚至非常一致,一般可以通过各向同性的板壳理论进行比较精确的描述。但是对于某些材料特殊或者结构特殊的墙体,各向同性板壳理论对其的描述会显得比较粗糙、不太精确,比如:木材由于其纤维分布的特点,使得木材构件在沿纤维方向与垂直纤维方向的受力性能完全不同;常见的波形钢板墙,由于其面板上的波折构造,导致其在两正交方向上的受力性能有非常大的区别。本文所研究的不锈钢芯板结构,由于其芯管排布的不同,使得不锈钢芯板在两个正交方向上的受力性能也不尽相同,故本文将借鉴前人的经验,采用正交各向异性板壳理论[11]以及参考清华大学对正交各向异性波形钢板剪力墙的相关研究[12-15]来描述不锈钢芯板一字形墙的压弯稳定承载力。利用大量的轴压与纯弯的有限元计算结果,进行整理、拟合总结出一字形墙压弯的稳定承载力计算公式。
3.3.1 轴心受压以及纯弯稳定承载力设计公式
参照GB 50017—2017《钢结构设计标准》不锈钢芯板一字形墙的轴心受压稳定承载力与纯弯作用稳定承载力按式(2)计算:
Nu≤φNNy
(2a)
Mu≤φMMy
(2b)
式中:Nu为不锈钢芯板一字形墙的轴心受压稳定承载力;Mu为不锈钢芯板一字形墙的纯弯稳定承载力;Ny为不锈钢芯板一字形墙全截面塑性承载力标准值;My为不锈钢芯板全截面塑性弯矩承载力标准值;φN为不锈钢芯板一字形墙轴心受压稳定系数;φM为不锈钢芯板一字形墙纯弯稳定系数。φN与φM的计算按下式:
φN=Nu/Ny
(3a)
φM=Mu/My
(3b)
Ny与My按下式进行计算:
Ny=2tfbfy
(4a)
(4b)
为研究轴心受压稳定系数与纯弯稳定系数的表达式,引入不锈钢芯板一字形墙在轴压作用下的正则化高宽比λnN,以及在纯弯作用下的正则化高宽比λnM,其表达式为:
(5a)
(5b)
3.3.2 弹性屈曲分析
1)弹性屈曲模态。
利用ABAQUS软件,按照前文所建立有限元的方法,共建立50组模型,分析了不锈钢芯板一字形墙在压弯作用下的弹性屈曲模态,在多个不同参数规格的有限元弹性屈曲分析中,一阶模态均只出现了受压区面板的局部弹性屈曲,具体如图18所示,图8a,b为不同规格模型在同种荷载下的模态。
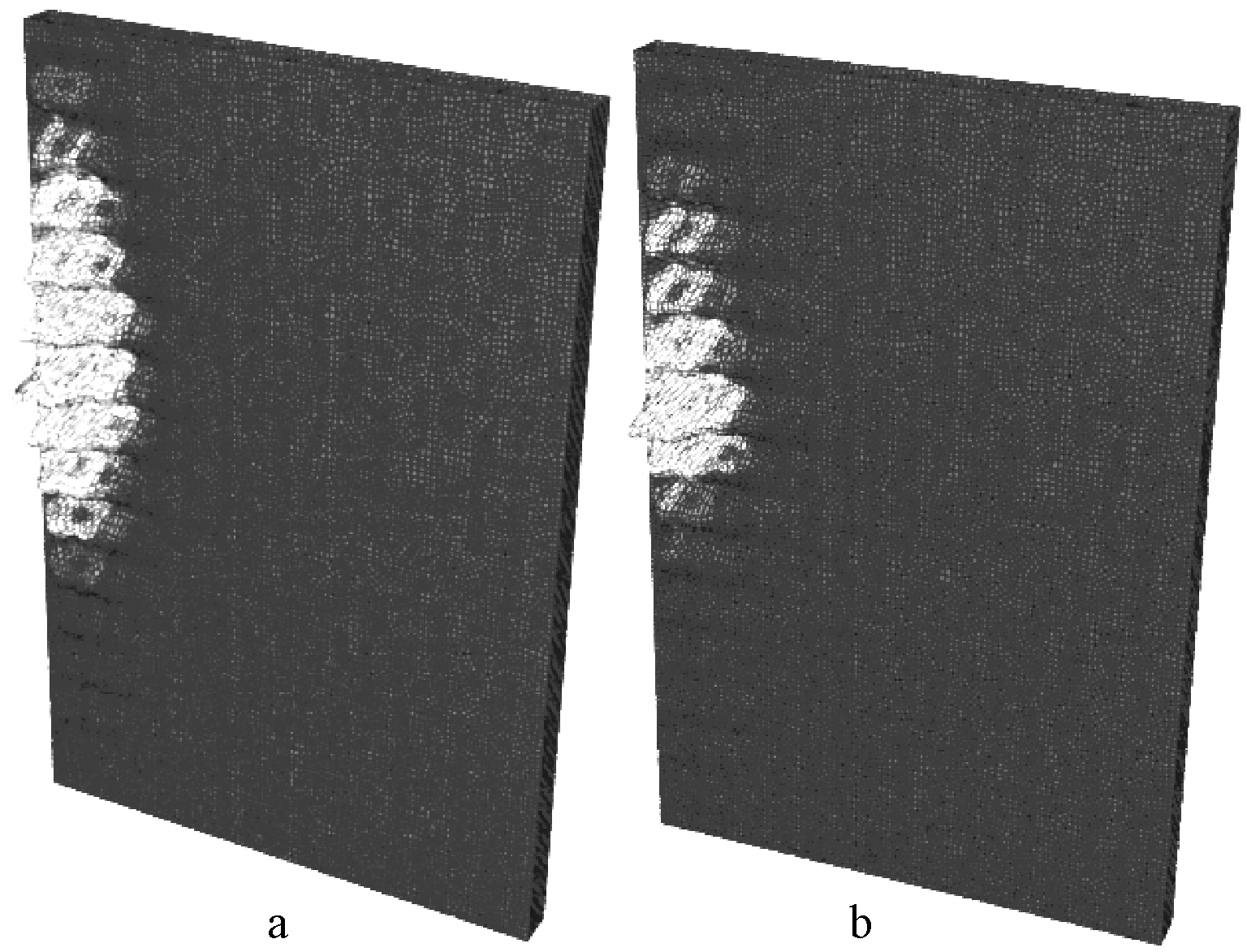
图18 不锈钢芯板一字形墙纯弯弹性屈曲一阶模态
Fig.18 The bending elastic buckling first-order mode of the in-line wall of the structure of stainless steel sondwich panel
2)弹性屈曲荷载算式拟合。
借鉴各向异性板壳理论[16],结合大量的有限元分析计算结果推导弹性屈曲荷载的计算式。参照单向均匀受压的弹性荷载理论与不锈钢芯板的各向异性,不锈钢一字形墙轴心受压弹性屈曲荷载与不锈钢芯板一字形墙的纯弯弹性屈曲荷载可表示为:
(6a)
(6b)
式中:kIN为芯板一字形墙的轴心受压弹性屈曲系数;kIM为芯板一字形墙纯弯弹性屈曲系数;引用两个只与芯板自身规格有关的参数θ与β对kIN与kIM进行拟合计算;θ为一字形墙的刚度常数比;β为一字形墙的等效高宽比;Dz、Dy分别为芯板一字形墙在强轴与弱轴方向上的弯曲刚度常数。
由各向异性板理论,取构件中的一个单元,计算芯板一字形墙在强轴与弱轴方向上的弯曲刚度常数与扭转刚度常数[10],表达式如下:
(7a)
(7b)
H=(Hz+Hy)/2
(8a)
(8b)
(8c)
式中:G为不锈钢剪变模量。
θ与β的表示式如下:
β=a/b
(9a)
(9b)
根据大量有限元特征值屈曲分析的结果,把θ、β与kIN和kIM的关系进行数值上的拟合计算,得到kIN与kIM的表达式:
kIN=0.063β+3 157.3θ-0.007 6β2-
1 079 250θ2+385βθ
(10a)
kIM=0.054β+534.13θ-0.002 9β2+
134 020.72θ2-48.12βθ
(10b)
以参数kIM为例,将kIM的有限元结果与拟合情况绘制于图19中,点代表有限元计算结果,面为最终拟合方程的空间图像。从图像上可以看出,计算结果的拟合情况很好,拟合方程能够比较好地描述kIM,误差控制在实际工程所允许的范围内。
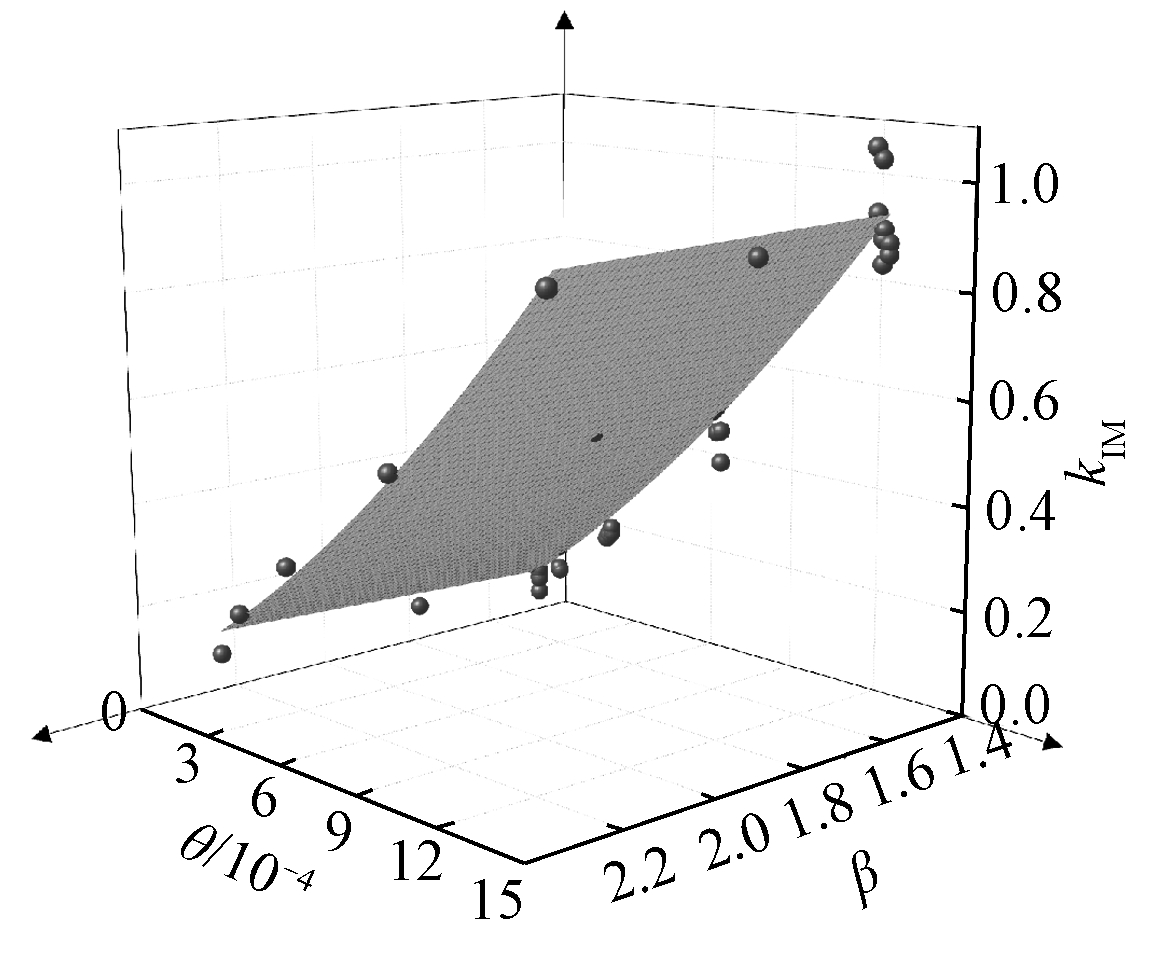
图19 kIM、θ、β有限元结果与拟合面
Fig.19 kIM、θ、β finite element results and fitting surface
3)稳定系数与正则化长细比拟合。
通过结合式(2a)~式(5a)以及大量的不锈钢一字形墙的轴压以及纯弯有限元分析结果,得到稳定系数φN与φM与正则化长细比λnN与λnM的关系式:
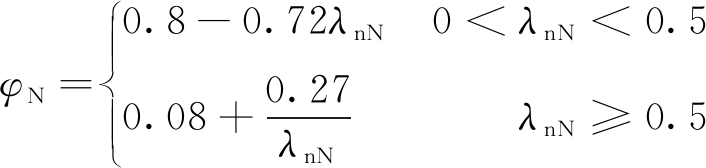
(11a)

(11b)
以φM为例,将纯弯稳定承载力的有限元分析得到的φM-λnM相关曲线绘制于图中,并在点集下方进行曲线拟合。通过拟合曲线图20可以看到,拟合公式偏安全地描述了稳定系数与正则化长细比的关系,能够安全地计算不锈钢一字形墙的纯弯稳定承载力。
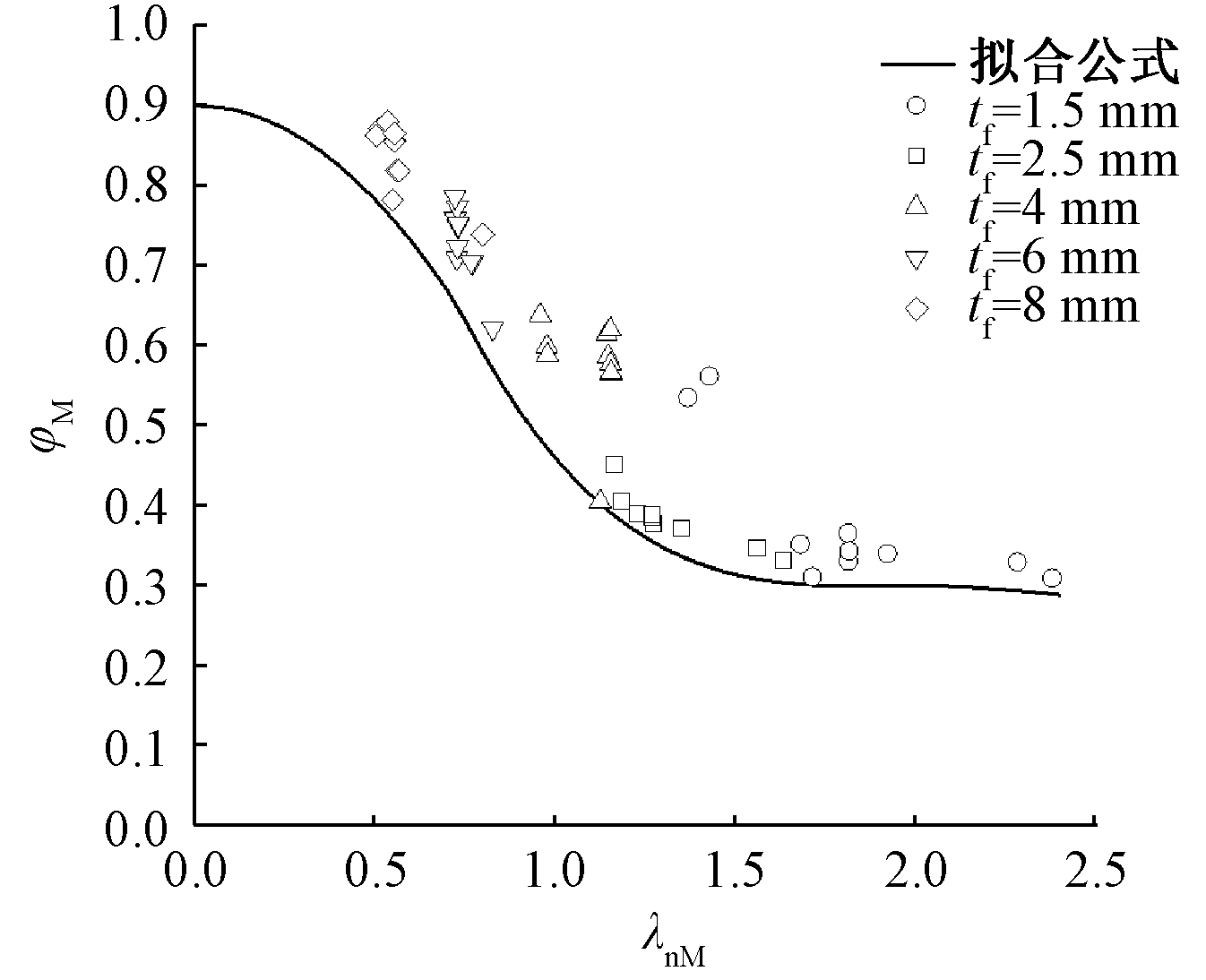
图20 φM-λnM计算结果与拟合曲线
Fig.20 φM-λnM calculation results and fitting curve
4)压弯稳定承载力设计公式拟合。
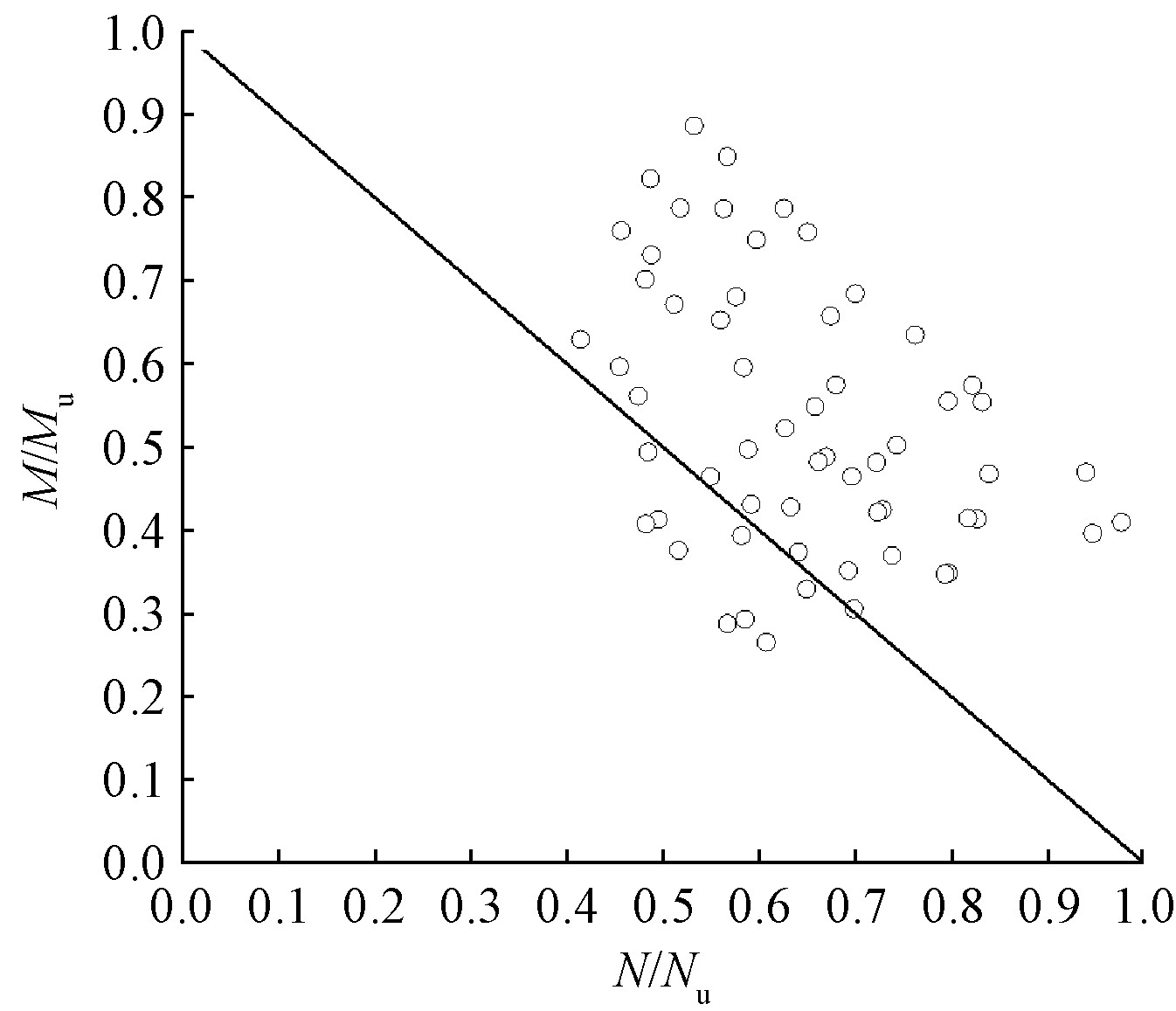
图21 N/Nu计算结果与拟合曲线
Fig.21 N/Nu and M/Mu calculation results and fitting curves
实际应用中的一字形墙所受的压弯作用可以看作轴力与弯矩的共同作用,本文中通过进行不锈钢芯板一字形柱的偏压计算来模拟压弯作用,可以得到其偏压作用下的轴力与弯矩,整合结果将每一组模型的N/Nu与M/Mu绘制在图21中,并进行拟合,得到最终不锈钢芯板一字形墙压弯稳定承载力公式:
(12)
由图21可以看出,拟合公式偏安全地描述了不锈钢芯板结构一字形墙的压弯承载力。计算了多组有限元模型,得到对应各参数下一字形墙的压弯承载力,并用多组数据对公式进行验证,大部分计算结果均保持在实际工程所允许的范围内,证明本文推出的设计公式对实际工程有较高的参考价值。
4 结束语
本文针对不锈钢芯板结构一字形墙的压弯性能进行了研究,建立有限元模型并分析了其在压弯作用下的受力特征、工作过程与破坏形态;利用多组有限元计算结果进行了参数分析;理论推导了一字形墙的压弯稳定承载力计算公式。结论如下:
1)通过有限元分析模拟了3组共9个构件的压弯受力过程,得到了对应的荷载-位移曲线,通过观察模型的变形云图,得知不锈钢芯板结构一字形墙在压弯受力时,没有明显的大小偏心破坏之分,破坏形态均体现为受压区一侧的面板与侧板的局部屈曲破坏。
2)在可靠的有限元基础上对不锈钢芯板结构一字形墙的压弯受力过程以及破坏机理进行了分析,结果表明,一字形墙在压弯过程中共经历三个受力过程,先后为弹性受力阶段、弹塑性受力阶段以及塑性破坏阶段,受力过程中截面符合平截面假定。
3)利用大量的有限元模型,对不锈钢芯板结构一字形墙进行了参数分析,结果表明,在单一参数作用下,高宽比、面板厚度、芯管管径、芯管壁厚越大,构件的压弯承载力越大;芯管的纵间距与横间距越大,构件的承载力会越小。这几个参数中,面板厚度、芯管管径与纵间距对一字形墙压弯承载力的影响比较大,横间距与芯管壁厚的影响较小。
4)参考各向异性板壳理论,结合大量的有限元计算数据,推导出不锈钢芯板一字形柱压弯稳定承载力设计公式,该设计公式能够偏安全地计算不锈钢芯板一字形墙的压弯稳定承载力,经验算,设计公式对进一步实际工程的研究有可靠的参考作用。
本研究得到了远大可建科技有限公司的资助和大力支持,在此表示衷心感谢。
[1]刘杰,郝巍,孟江燕.蜂窝夹层结构复合材料应用研究进展[J].宇航材料工艺,2013,43(3):25-29.
[2]许潮华,张小珍,宋桂枝.“Nomex”蜂窝芯材的研制及应用[J].玻璃钢/复合材料,1986(2):22-24.
[3]陈大川,蒋玉春,舒兴平,等.不锈钢芯板一字形墙轴心受压承载力研究[J].工业建筑,2020,50(2):51-58.
[4]RASMUSSEN K J R. Full-Range Stress-Strain Curves for Stainless Steel Alloys[J]. Journal of Constructional Steel Research, 2003, 59(1):47-61
[5]史勤益, 颜余仁, 赵先锐,等. 304奥氏体不锈钢的热处理工艺研究[J]. 科学技术与工程, 2011, 11(24):5910-5913.
[6]中国工程建设标准化协会.不锈钢结构技术规程:CECS 410∶2015[S].北京:中国计划出版社,2015.
[7]董雨辰. 不锈钢芯板结构芯管剪切性能试验研究与有限元分析[D].长沙:湖南大学,2018.
[8]黄牧兴. 不锈钢芯板结构侧压性能试验研究与有限元分析[D].长沙:湖南大学,2018.
[9]彭明军,孙勇,段永华,等.钎焊蜂窝铝板侧压变形模式分析研究[J].材料导报,2010,24(6):75-77.
[10]於忠华,王静峰,沈奇罕.椭圆钢管混凝土长柱偏压受力性能研究[J].建筑钢结构进展,2018,20(2):103-109.
[11]TIMOSHENKO S P, GERE J M. Theory of Elastic Stability[M]. New York: McGraw-Hill, 1961.
[12]GUO T. Shear Resistance of Stiffened Steel Corrugated Shear Walls[J]. Thin-Walled Structures, 2018,127: 76-89.
[13]GUO Y, ZHU J, WANG M, et al. Overall Instability Performance of Concrete-Infilled Double Steel Corrugated-Plate Wall[J]. Thin-Walled Structures, 2018, 130:372-394.
[14]WANG M Z, GUO Y L, ZHU J S, et al. Strength Design of Concrete-Infilled Double Steel Corrugated-Plate Walls with T-Section Under Combined Axial Compression and Bending Moment[J]. J. of Constructional Steel Research, 2019, 160:23-44.
[15]ZHU J S, GUO Y L, ZHU B L, et al. Strength Design of Concrete-Infilled Double Steel Corrugated-Plate Walls Under Uniform Compressions[J]. Thin-Walled Structures, 2019, 141:153-174.
[16]TIMOSHENKO S P, WOINOWSKY-KRIEGER S. Theory of Plates and Shells[M]. New York: McGraw-Hill, 1959.