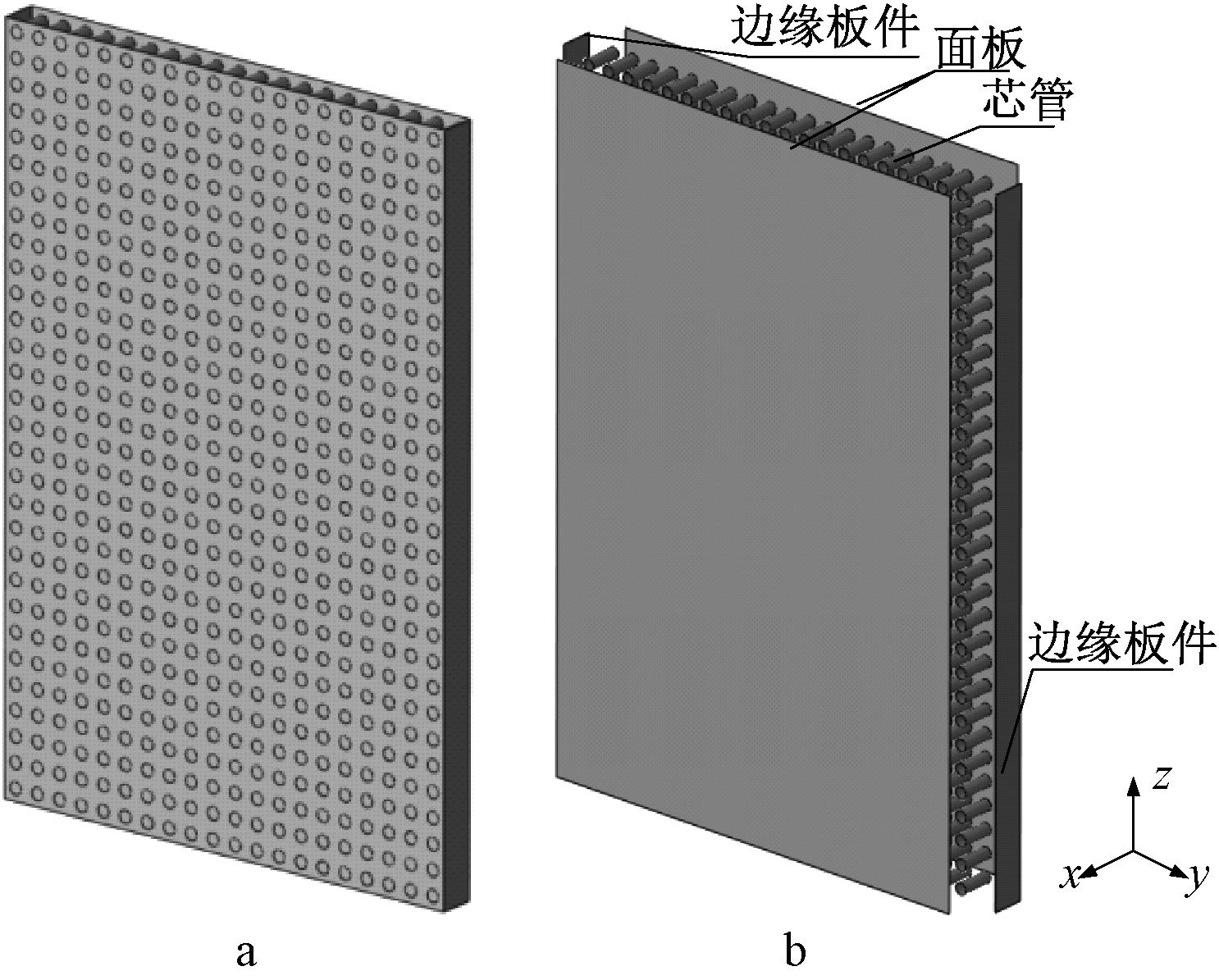
不锈钢不仅耐腐蚀性和耐久性良好,还能很好地适应高低温环境,其良好的力学性能更是使得它在未来有良好的应用前景,夹芯结构拥有很高的比强度和比刚度。为将蜂窝夹层结构这种受力性能良好的结构与不锈钢的优质材性很好地结合在一起,不锈钢芯板应运而生,它是一种新型的夹层构件,采用S304不锈钢材料薄板作为面板,以按照一定间距排列的S304不锈钢材料薄壁圆管作为夹芯,面板与薄壁芯管用铜钎焊焊接而成,薄壁圆管作为芯子,面板和薄壁芯管采用铜钎焊焊接。
这种新型夹层构件能够用作建筑的梁、板、墙等承重部位,在不锈钢芯板用作墙柱时,其轴向的承载能力是其作为结构设计时的最重要参数,本文就一字形墙的轴压力学性能进行研究。
目前许多国内外学者对蜂窝夹层板的力学性能做过研究,他们通常都是采用试验方法和有限元两种方法来研究[1-6],不锈钢芯板一字形墙轴压主要是由面板承受,组成形式上与钢板组合墙相似,因此参照对组合剪力墙轴压的研究方法[7-9]。本文对多组不锈钢芯板一字形墙进行了轴压承载力试验研究,并建立了相应的有限元模型,通过有限元非线性分析对比了试验结果和有限元分析结果来验证有限元分析模型的准确性。在此基础上,对不锈钢芯板一字形墙的受力特征和破坏形态进行理论分析,并通过大量有限元模拟,对影响不锈钢一字形墙轴压承载力的各项参数进行分析,提出一字形墙轴压承载力计算公式。
1 不锈钢芯板一字形墙轴压试验
1.1 试件设计参数
试验共设计了3组不锈钢芯板试件,每组2个试件,共6个试件,该试件由远大可建科技有限公司研发生产。试件编号及基本参数详见表1。试件模型示意见图1。
表1 试件分组及规格参数
Table 1 Specimen grouping and specifications

试件分组试件编号试件数/个试件尺寸(高h×宽b×厚d)/mm面板厚tf/mm侧面板厚tf/mm芯管规格(外径D×壁厚tc×管高hc)/mm芯管间矩(纵向d1×横向d2)/mm第一组YZ1-1、YZ1-223 000×2 000×1501.52.5ϕ51×0.5×147100×121第二组YZ2-1、YZ2-223 000×2 000×1522.52.5ϕ51×0.5×147100×121第三组YZ3-1、YZ3-223 000×2 000×1554.02.5ϕ51×0.5×147100×121
a—组合; b—拆分。
图1 不锈钢芯板一字形墙示意
Fig.1 Schematic diagram of the in-line wall of the structure of stainless steel sandwich panel
1.2 加载和量测装置
1.2.1 加载装置设计
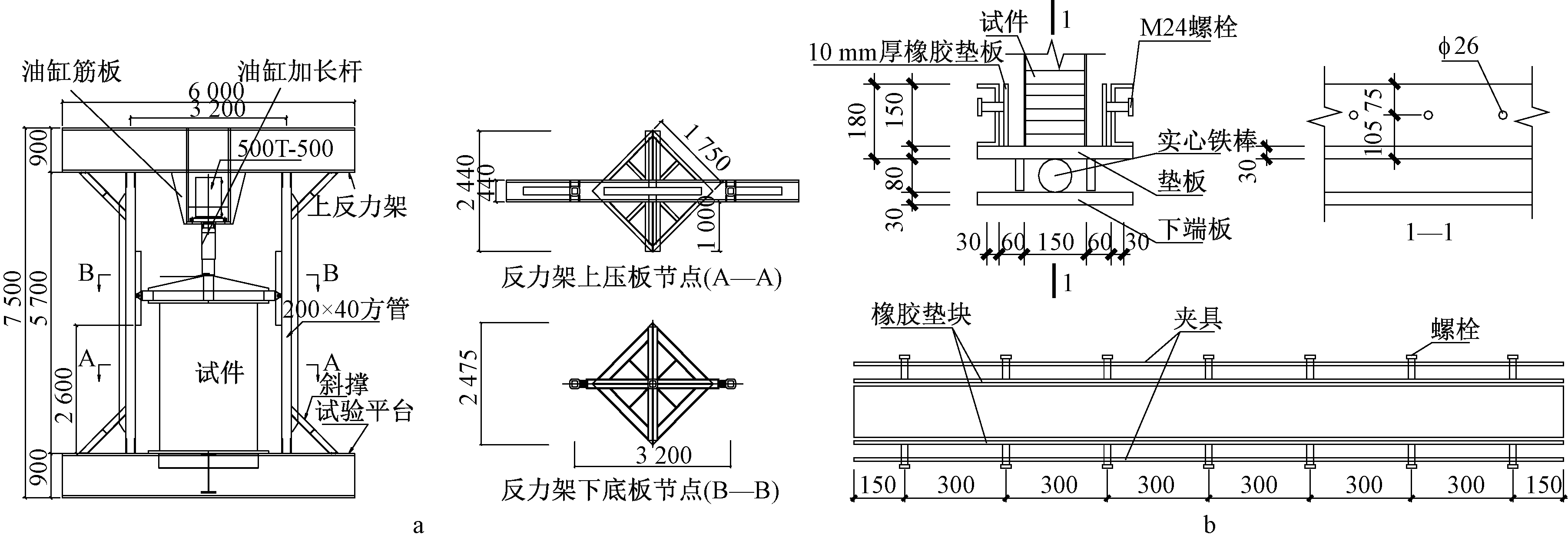
试验加载按GB/T 1454—2005《夹层结构侧压性能试验方法》[10]的规定进行。采用5 000 kN液压千斤顶在反力架上对试件加载,荷载传感器读取施加的荷载值,位移计读取试件轴压竖向位移值。为保证试件轴心受压,使液压千斤顶施加的力作用于上截面形心处,用全站仪垂直放置试件并用线锤检查是否垂直,同时在试件上下端设计了刚性垫板。加载装置的上端采用球铰将加载板和传感器的底部相连,为最大程度上保证试件试验过程中不产生侧向位移,在其顶部加侧向支撑,下端在试验平台和夹具中间加入实心铁棒让下端可以产生平面外的弯曲,同时在下端实心铁棒两侧的垫板上焊上钢片,但是钢片没有和实心铁棒接触。为防止上下夹具对试件端部的加强与破坏,夹具与试件的接触采用橡胶垫块隔开,夹具螺栓采用M24并纯手工拧紧,只起固定试件位置的作用。加载装置见图2。
a—加载装置; b—下夹具。
图2 加载装置及下夹具示意
Fig.2 Load device and lower fixture
1.2.2 加载方式及测量布置
采用单调分级加载,直至试件破坏,在每级荷载加载结束后等待5 min左右,待荷载传感器和位移计读数稳定后,再读取试验数据。加载初期,当荷载小于理论承载力的80%时,每级施加荷载大小不超过极限荷载的10%;大于极限荷载的80%时,每级施加荷载大小不超过极限荷载的5%。
在正式加载前,首先要对试件进行预加载,以检查位移计和加载设备的工作状态以及试件的对中情况,消除加载设备与试件之间的缝隙对试验产生的不利影响。
为测得试件在轴压过程中发生的竖向和横向的变形与位移,在试件上下端部和面板上布置位移计,在试件一边的面板和侧面封板上布置应变片,位移计布置如图3所示。

图3 位移计布置示意
Fig.3 Schematic diagram of displacement meter arrangement
1.3 试验结果及现象
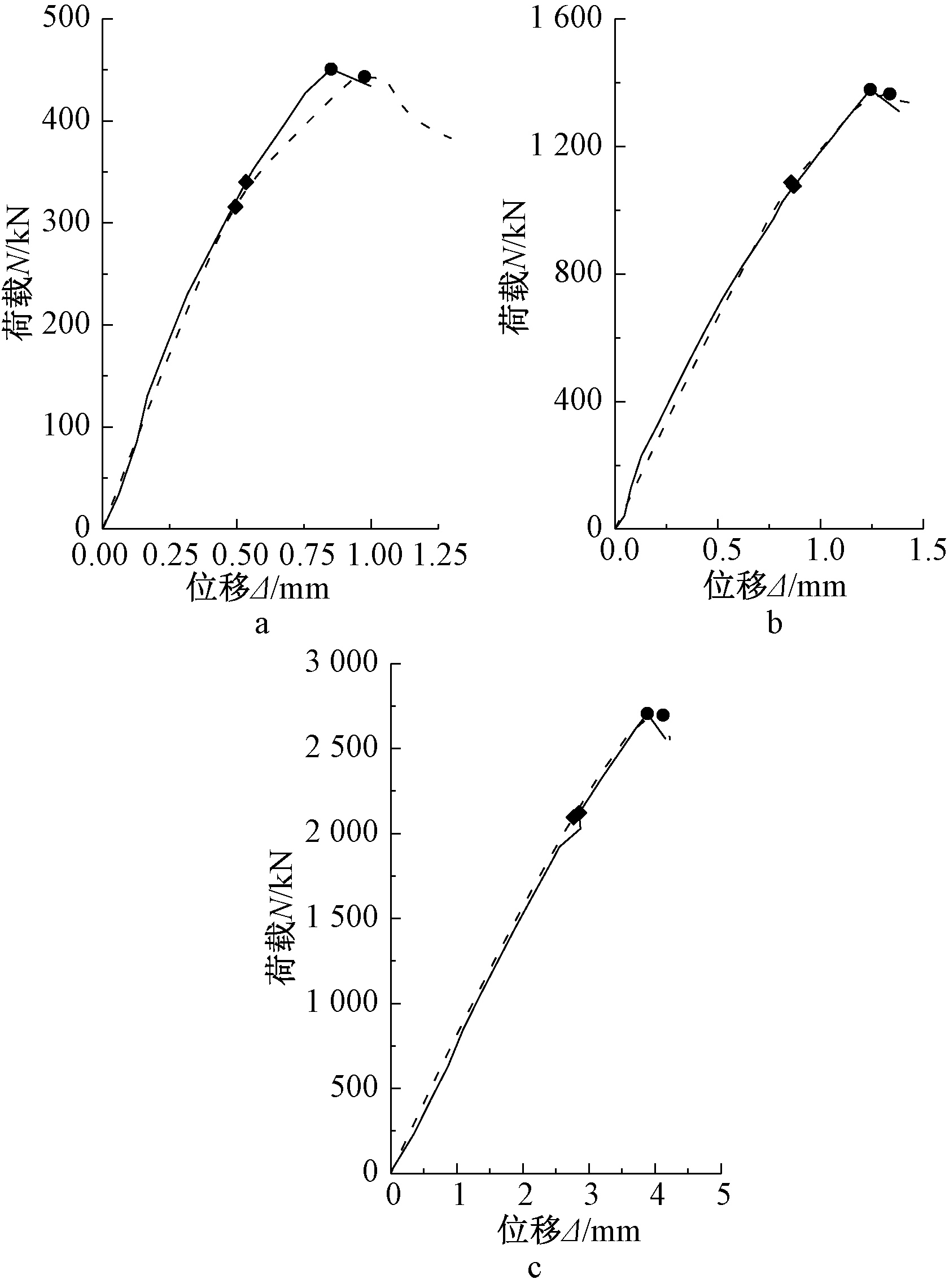
图4为试验得到的各组试件的荷载-位移曲线。纵坐标为试件所受到的竖向荷载,横坐标为试件在竖向荷载作用下产生的竖向位移,竖向位移为左右两侧测量结果的平均值,将荷载-位移曲线中由直线变为曲线的点称为拐点,将荷载达到最大值时对应的点称为极值点。可以看出:试件的拐点出现在极限荷载的75%左右。在拐点之前,位移随着荷载的增加呈线性增长;拐点之后,位移增加的幅度大于荷载增加的幅度,荷载-位移曲线的斜率逐渐减小,过了极限荷载后位移迅速增大,荷载也跟着急剧下降。
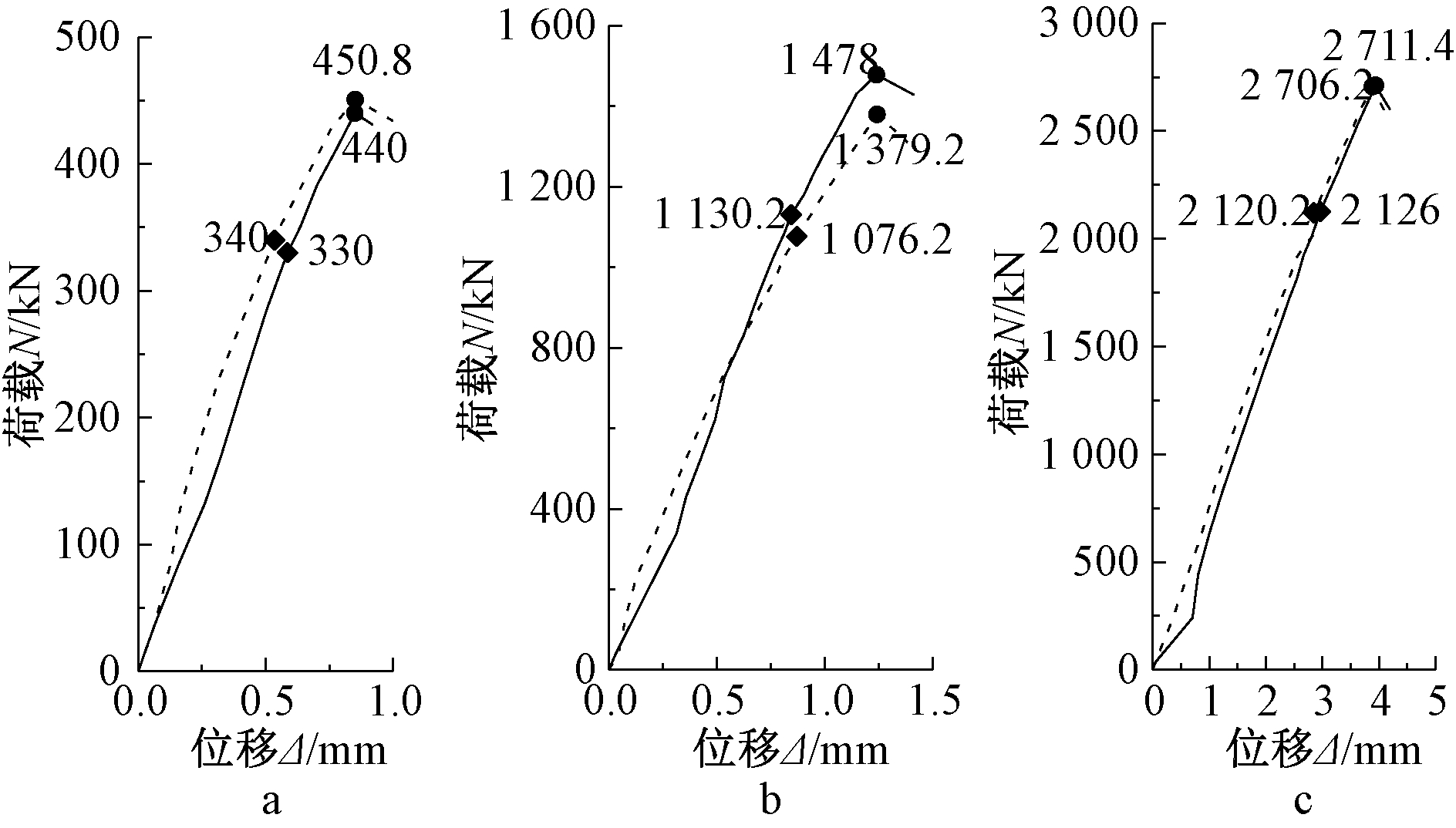
a—第一组; b—第二组; c—第三组。 ![]() YZ3-1; ----YZ3-2;
YZ3-1; ----YZ3-2;![]() 拐点;
拐点;![]() 极值点。
极值点。
图4 各组荷载-位移曲线
Fig.4 Load-displacement curve of each group
图5为各组试件的破坏形态及破坏处局部放大图。观察试件在竖向荷载作用过程中的试验现象以及3组试件的荷载-位移曲线可以看出:在试验开始时荷载和位移基本保持线性关系递增,此时的面板和芯管都没有明显的变形,每级加载结束后荷载传感器与位移计的读数能够很快稳定下来。当荷载达到极限荷载的75%左右时,荷载-位移曲线由线性变为非线性,荷载传感器的读数在加载结束后出现些微的下降,且很快就能稳定下来,越接近极限荷载,稳定所需的时间变长,这个过程面板依然没有明显的变化,到了极限荷载的90%左右时,第三组开始从内部偶尔传来清脆的“滋滋”响声。当荷载达到极限峰值荷载时,所有试件发出“砰”的一声巨响,位移计读数突然变大,上部位移计由于巨大压力释放产生的振动而不能继续工作,腹板面板出现非常明显的局部屈曲现象。此时千斤顶已不能继续增加荷载,荷载传感器的读数持续下降,而变形仍在继续增加,试件失去了承载能力。继续加载,试件的变形足够大时终止试验。

a—YZ1-2破坏形态; b—YZ1-2破坏局部; c—YZ2-2破坏形态; d—YZ2-2破坏局部; e—YZ3-1破坏形态; f—YZ3-1破坏局部。
图5 试件破坏形态
Fig.5 Failure modes of specimens
试件的局部屈曲均发生在没有芯管的截面,其余截面均没有明显的变化。仅第三组试件局部屈曲附近芯管出现了轻微的压曲变形。
比较三组的数据可以发现,面板的厚度对试件的轴压承载能力有特别大的提升。
2 有限元分析
2.1 建立有限元模型
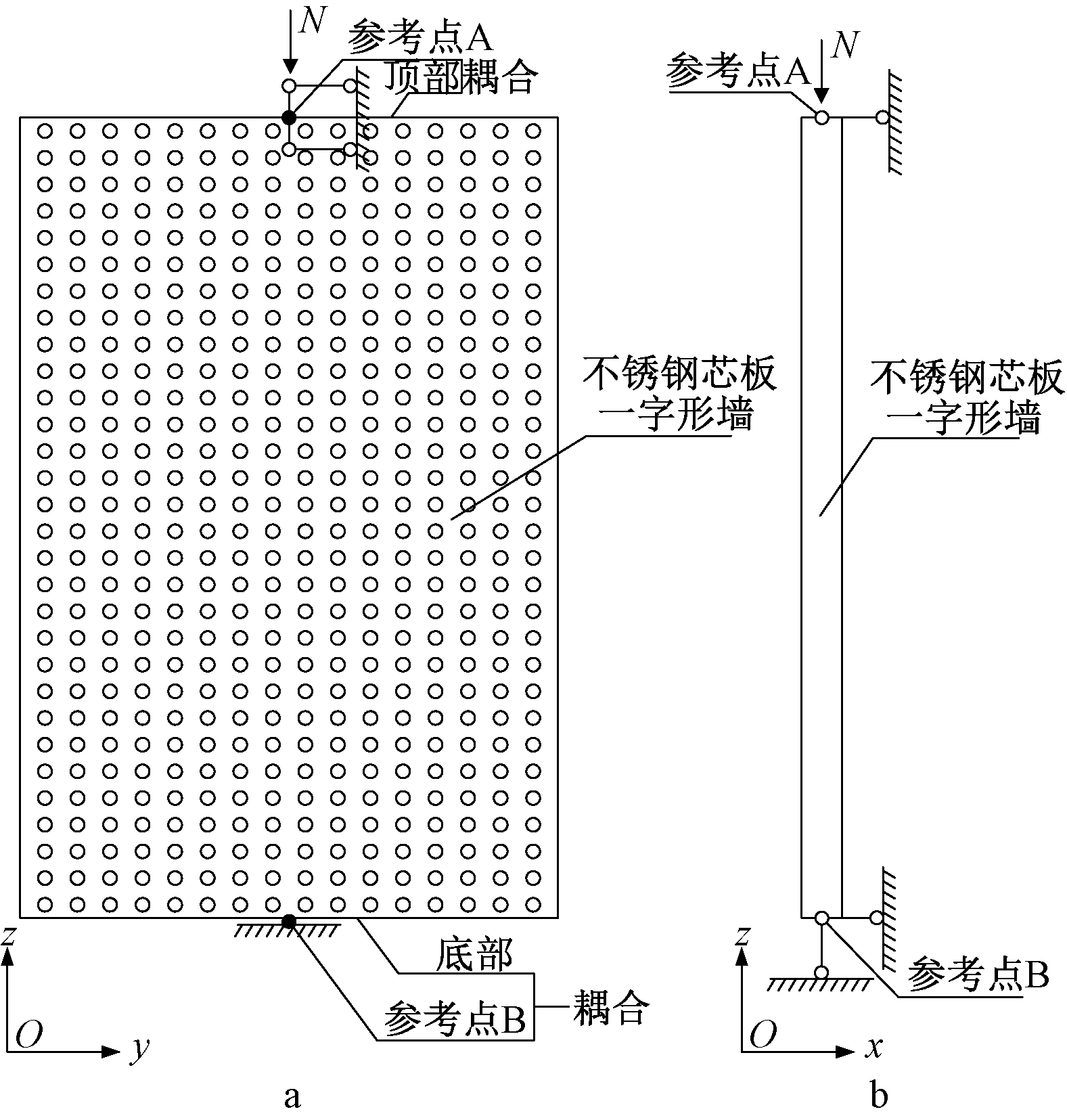
通过ABAQUS有限元分析软件建立有限元模型,模型中的面板和芯管都采用S4R四结点壳单元模拟,面板和芯管的材料都为奥氏体S30408不锈钢,其本构关系根据材料的力学性能试验确定,泊松比取0.3,弹性模量取1.93×105 MPa,模型的上下端分别于参考点A、B耦合,点A、B位于一字形墙上下截面的形心处,参考点A沿y、z方向的水平自由度被限制,参考点B沿x、y、z方向的水平自由度都被限制。边界条件如图6所示。轴力N为模型计算时参考点B所受的反力。
a—正视图; b—侧视图。
图6 模型边界条件
Fig.6 Boundary conditions of the model
通过有限元模型对不锈钢芯板一字形墙进行了弹性屈曲分析和非线性分析,分析了不锈钢芯板一字形墙在轴压作用下的极限承载能力和失效机理。模型的计算分为两步,先用弹性屈曲分析,对模型施加单位轴向压力得到结构的屈曲模态;再根据屈曲模态为结构添加初始几何缺陷,然后用静态Riks分析计算。
2.2 弹性屈曲分析
通常结构的一阶屈曲模态是其最可能发生的破坏模态,不锈钢芯板一字形墙的一阶屈曲模式均为局部屈曲,屈曲模式主要有两种,如图7所示。分析过程中,在轴压作用下,当面板厚度较薄时类似屈曲模态1,当面板厚度较厚时类似屈曲模态2。在此输出轴压作用下一阶屈曲模态对应的弹性屈曲荷载Ncr。

a—局部屈曲模态1; a—局部屈曲模态2。
图7 一阶弹性屈曲模态
Fig.7 First-order elastic buckling modes
2.3 非线性屈曲分析
按照墙高1/1 000的比例将一阶屈曲模态的变形施加在试件上,以此来模拟试件的初始几何缺陷。本文根据试件规格共建立了三个有限元模型,分别与试验的三组试件相对应,尺寸规格以及各种几何参数均与试件相同。
将三个有限元模型计算所得到的荷载-位移曲线和对应的各组试验的典型荷载-位移曲线作对比,得到图8。表2对比了有限元模拟计算和试验得到的拐点荷载值、极值点荷载值,两者误差都较小。
a—第一组; b—第二组; c—第三组。 ![]() 试验; ---有限元;
试验; ---有限元;![]() 拐点;
拐点;![]() 极值点。
极值点。
图8 荷载-位移曲线对比
Fig.8 Comparison of load-displacement curves
表2 有限元模拟与试验所得的拐点荷载值对比
Table 2 Comparisons of inflection point loads from finite element simulation and test
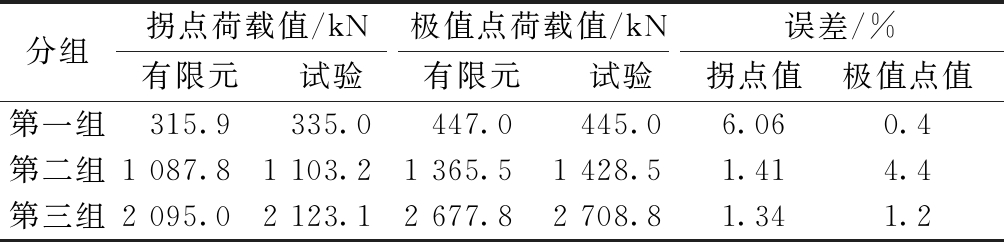
分组拐点荷载值/kN极值点荷载值/kN误差/%有限元试验有限元试验拐点值极值点值第一组315.9335.0447.0445.06.060.4第二组1 087.81 103.21 365.51 428.51.414.4第三组2 095.02 123.12 677.82 708.81.341.2
通过有限元模拟得到的结果,所有模型的破坏均为局部屈曲破坏,与试验现象基本一致。但局部屈曲的位置有所不同,这是因为有限元数值模拟过程中对于初始几何缺陷的模拟采用的是其一阶屈曲模态,而试件的实际缺陷具有随机性,有缺陷的位置比较容易先发生屈曲,故二者屈曲的位置可能不同。
对比以上分析可以知道:有限元模拟的结果与试验的结果吻合良好,验证了在有限元模拟中所选取的参数合理,表明本文所建立的有限元模型能够准确地模拟试验过程。
2.4 参数分析
图9给出了不锈钢芯板一字形墙的详细设计示意图的参数编号。其中,tw为芯管壁厚;hw为芯管长度(或高度);d为芯管外径;dn为沿芯板宽度(y轴)方向芯管净距;dm为沿芯板长度(z轴)方向芯管净距;tf为芯板面板厚度;lny(lny=d+dn)为沿芯板宽度(y轴)方向芯管中到中距离;lmz(lmz=d+dm)为沿芯板长度(z轴)方向芯管中到中距离;h(h=hw+2tf)为芯板截面高度;a为芯板一字形墙的高度;b为芯板一字形墙的宽度。
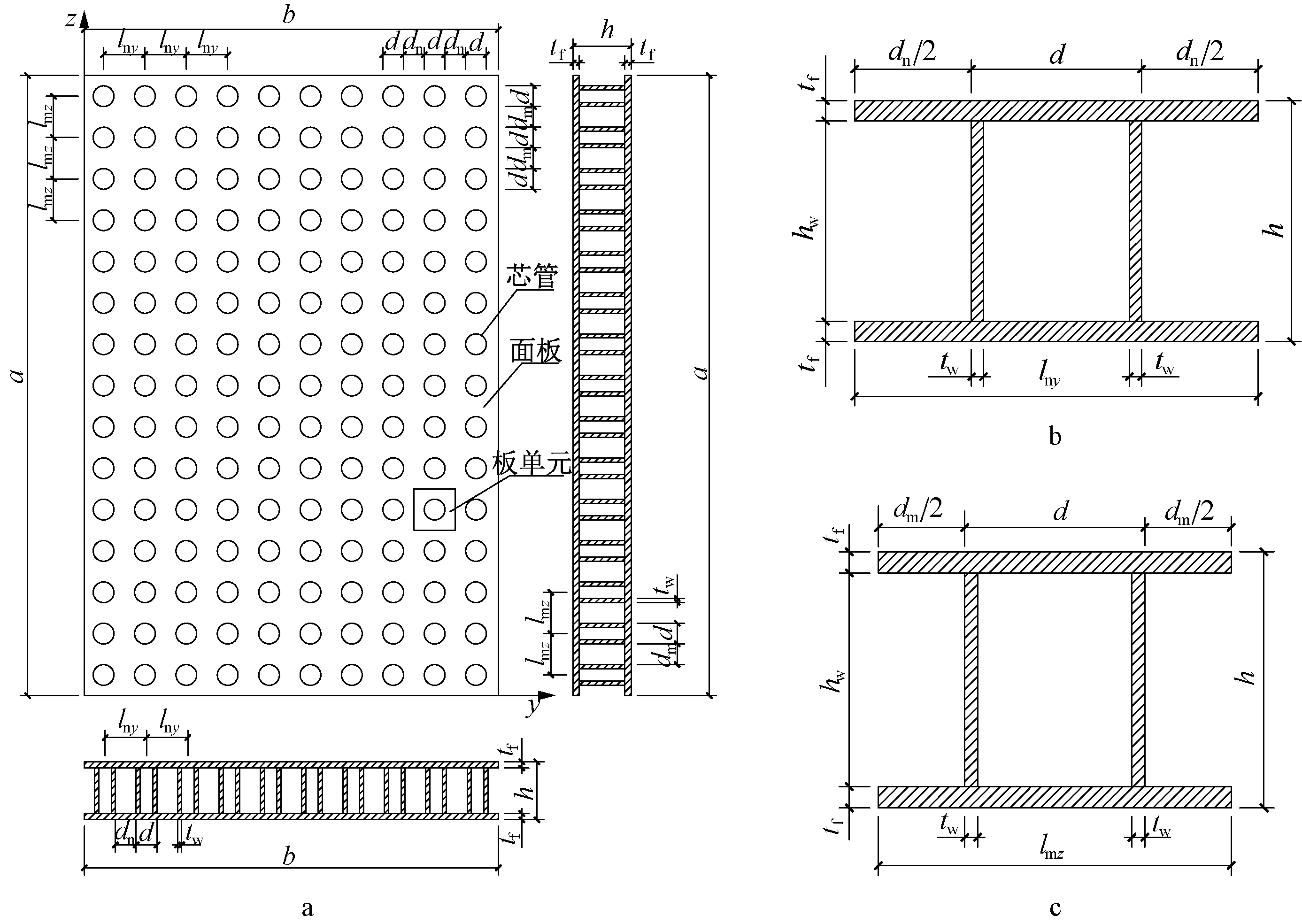
a—不锈钢芯板一字形墙腹板墙肢设计参数示意; b—沿长度(z轴)方向截面单元; c—沿宽度(y轴)方向截面单元。
图9 不锈钢芯板一字形墙设计参数
Fig.9 Design parameters of the in-line wall of the structure of stainless steel sandwich panel
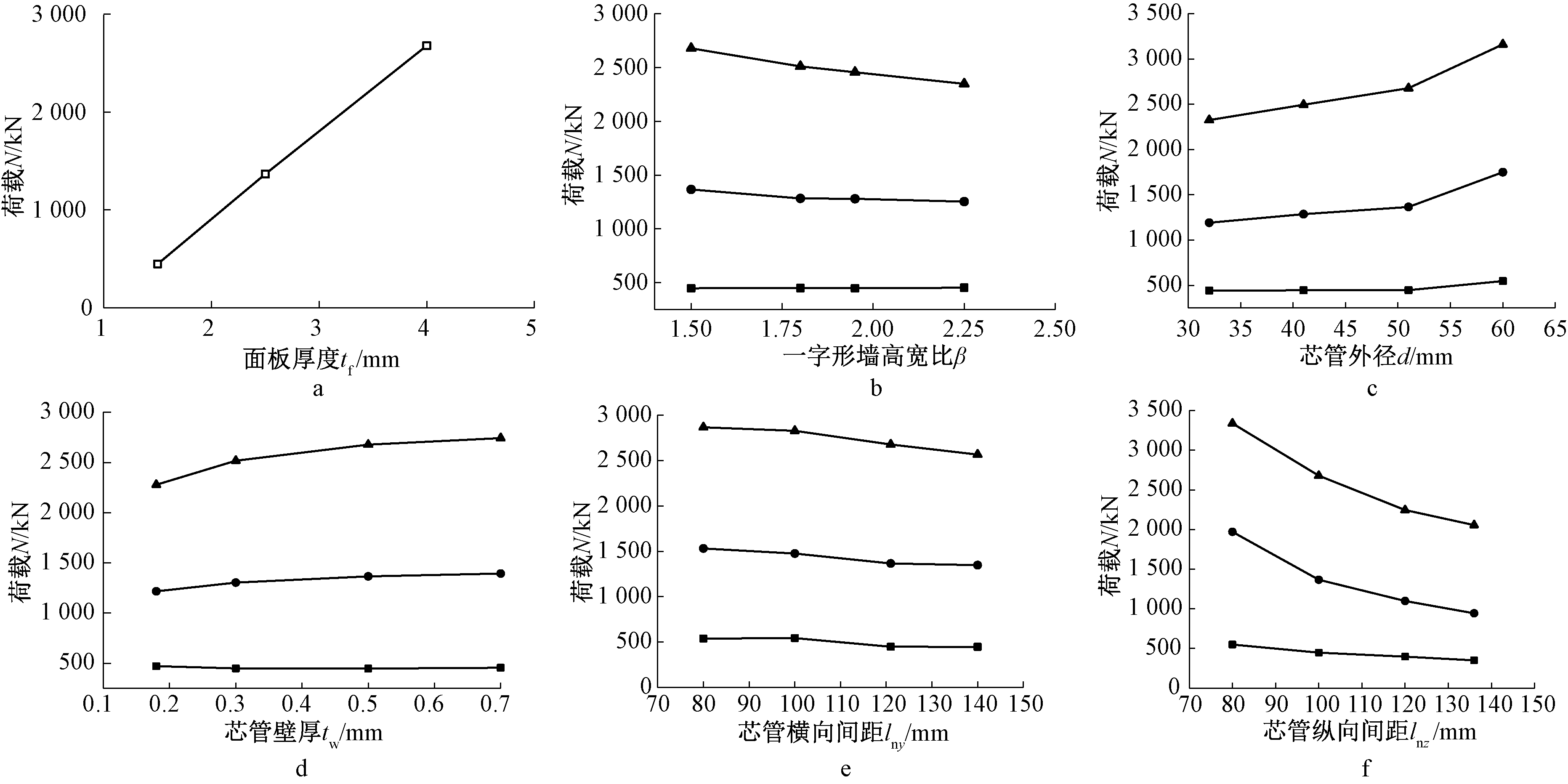
通过有限元建模,对影响不锈钢芯板一字形墙的轴压承载力的墙肢高宽比、面板厚度、芯管外径、芯管壁厚以及芯管分布间距等因素进行了参数分析,结果如图10所示。
作为不锈钢芯板一字形墙的主要承力部分,面板厚度的变化对轴压承载能力的影响最为明显。如图10a可以看出:在芯管厚度一定时,一字形墙的轴压极限承载力随面板的增厚按比例增加。
如图10b所示:当保持墙宽为2 000 mm时,提高其高宽比对一字形墙的轴压承载力并没有明显的影响,这是由于在轴压作用下一字形墙发生局部屈曲破坏,但随着面板厚度变大,墙高的影响变大。
如图10c所示:芯管外径的增加有利于一字形墙极限荷载的提升,同时芯管外径的影响随着面板厚度的增加而变大,芯管间距不变,芯管外径变小时会导致芯管与芯管的净间距增大,这使没有被芯管约束的芯板变宽,与增大芯管间距有着类似的效果。
如图10d所示:芯管壁厚的增加也有利于一字形墙极限荷载的提升,芯管厚度的影响随着面板厚度的增加而变大。面板厚度为1.5 mm时,芯管壁厚基本没有影响,但在面板厚度为2.5 mm时,芯管壁厚的影响在其达到0.3 mm后变得不明显了,而当面板厚度达到4 mm时,芯管壁厚的影响在芯管壁厚小于0.5 mm时比较明显,在大于0.5 mm时就变得不明显,说明芯管壁厚的影响不是单纯地随着面板的变厚而变大,而是每种面板厚度都对应有一种芯管壁厚,在某一面板厚度时,当芯管壁厚小于面板厚度所对应的芯管壁厚时,芯管壁厚的影响明显,而大于对应的厚度时,芯管壁厚的影响将变得很小。
a—面板厚度的影响; b—墙肢高宽比的影响; c—芯管外径的影响; d—芯管壁厚的影响; e—芯管横向间距的影响; f—芯管纵向间距的影响。 ![]() — tf=1.5 mm;
— tf=1.5 mm; ![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=4.0 mm。
— tf=4.0 mm。
图10 参数分析
Fig.10 Parameter analysis
如图10e和图10f所示:芯管间距有纵向间距和横向间距,可以看出,在其他参数不变时,纵、横向间距增大会大大降低面板的极限荷载。芯管的纵、横向间距增大使得芯管对面板的约束作用减弱,在相同的荷载下面板更容易发生变形。同时纵向间距的变化对极限荷载的影响要比横向间距的影响大。
3 轴压承载力设计式
轴压承载力的计算式参考GB 50017—2017《钢结构设计标准》,不锈钢芯板一字形墙考虑局部屈曲的轴压承载力按式(1)计算。
N≤Nu=φNy
(1)
式中:Nu为不锈钢芯板一字形墙考虑局部屈曲的轴压承载力;N为不锈钢芯板一字形墙考虑局部屈曲的轴压承载力设计值;φ为不锈钢芯板一字形墙考虑局部屈曲的轴压稳定系数,按式(2)计算;Ny为不锈钢芯板一字形墙全截面(不包括芯管与边缘板件截面,仅为面板)塑性承载力标准值,按照式(3)计算。
(2)
Ny=2tfbfy
(3)
为了更好地了解不锈钢芯板一字形墙弹性屈曲行为,定义其正则化高宽比为:
(4)
式中:Ncr为不锈钢芯板一字形墙轴心受压弹性屈曲荷载。
3.1 弹性屈曲荷载公式
参照单向均匀受压正交异性板的弹性屈曲荷载理论[11-12]以及清华大学对正交各向异性波形钢板剪力墙研究的相关论文[13-16],考虑不锈钢芯板芯管排布的各向异性,其轴心受压弹性屈曲荷载可按式(5)计算。
(5)
式中:kI为不锈钢芯板一字形墙轴心受压弹性屈曲系数;Dz、Dy分别为计算板单元在强轴与弱轴方向的平均弯曲刚度常数,其计算式如下:
(6)
(7)
为拟合kI表达式,引入计算板单元的刚度常数比θ与一字形墙的高宽比β:
(8a)
(8b)
其中 H=(Hz+Hy)/2
式中:H为扭转刚度常数;Hz、Hy分别为计算板单元在强轴与弱轴方向的扭转刚度常数,按下式计算:
(9a)
(9b)
通过多组包括面板厚度tf为1.5,2.5,4.0 mm、芯管壁厚tw为0.18,0.3,0.5,0.7 mm、芯管间距lmz×lny为100 mm×100 mm,100 mm×121 mm和121 mm×121 mm、高宽比β为1.5,1.8和2.25等参数反算出相对应的kI,并将kI、β、θ绘于三维坐标系中,如图11所示。
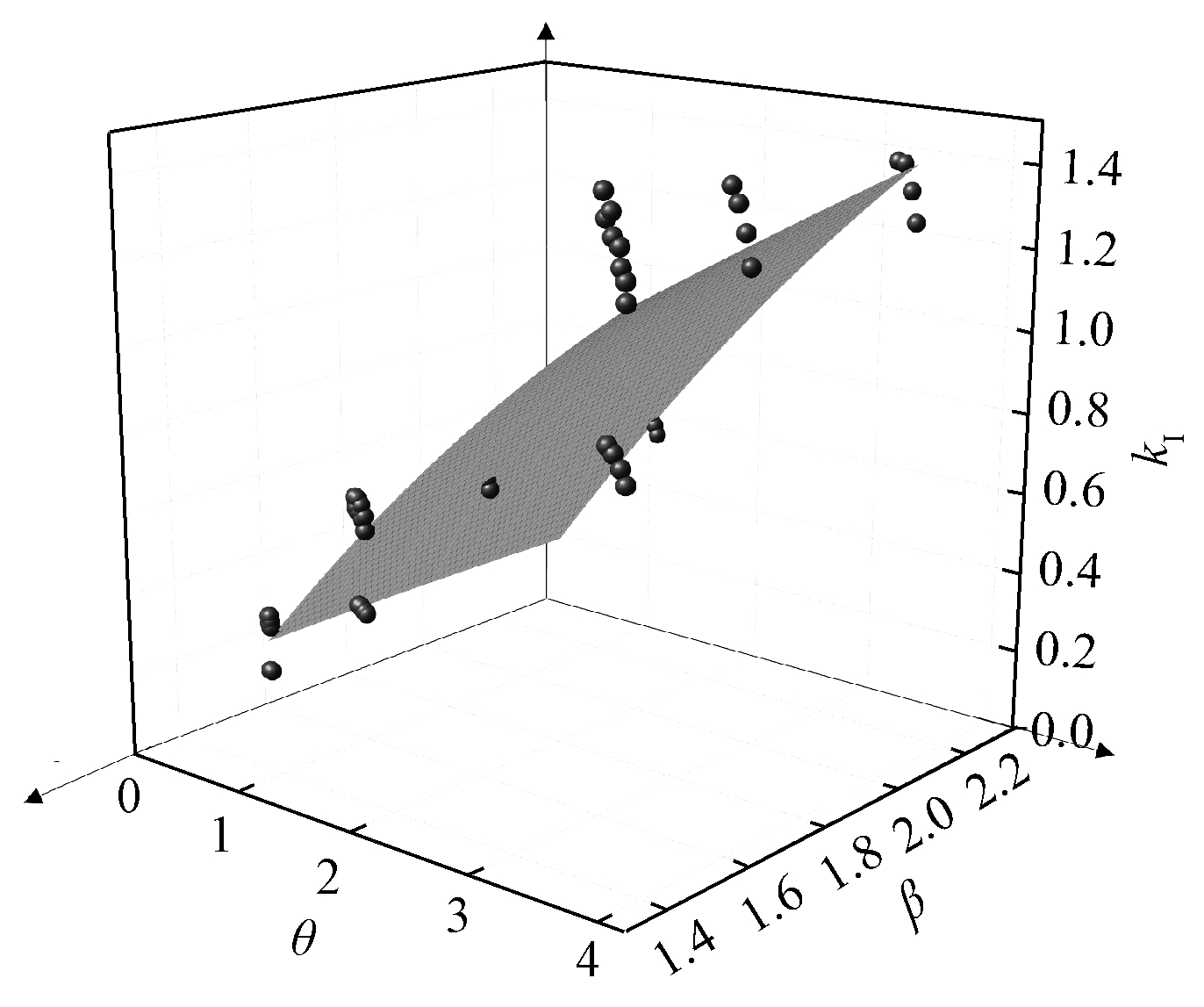
图11 弹性屈曲系数kI拟合公式的有限元验证
Fig.11 Finite element verification of fitting formula for elastic buckling coefficient kI
通过对kI、β、θ面进行的拟合可得三者之间的关系式。
kI=f(β,θ)=0.080 4β+3 197θ-0.030 84β2-
2 555 700θ2+701βθ
(10)
3.2 φ-λn相关曲线
通过对大量芯板一字形墙轴压承载性能有限元分析,得到各模型的稳定系数,将有限元计算得到的φ-λn数值绘制在图12中。因不锈钢芯板的结构特点为薄壁夹层结构,面板厚度不宜过厚,在受压时无芯管支撑的弱截面发生局部破坏,难以全截面屈服,故偏安全考虑,取局部屈曲的轴压稳定系数φ=0.6。
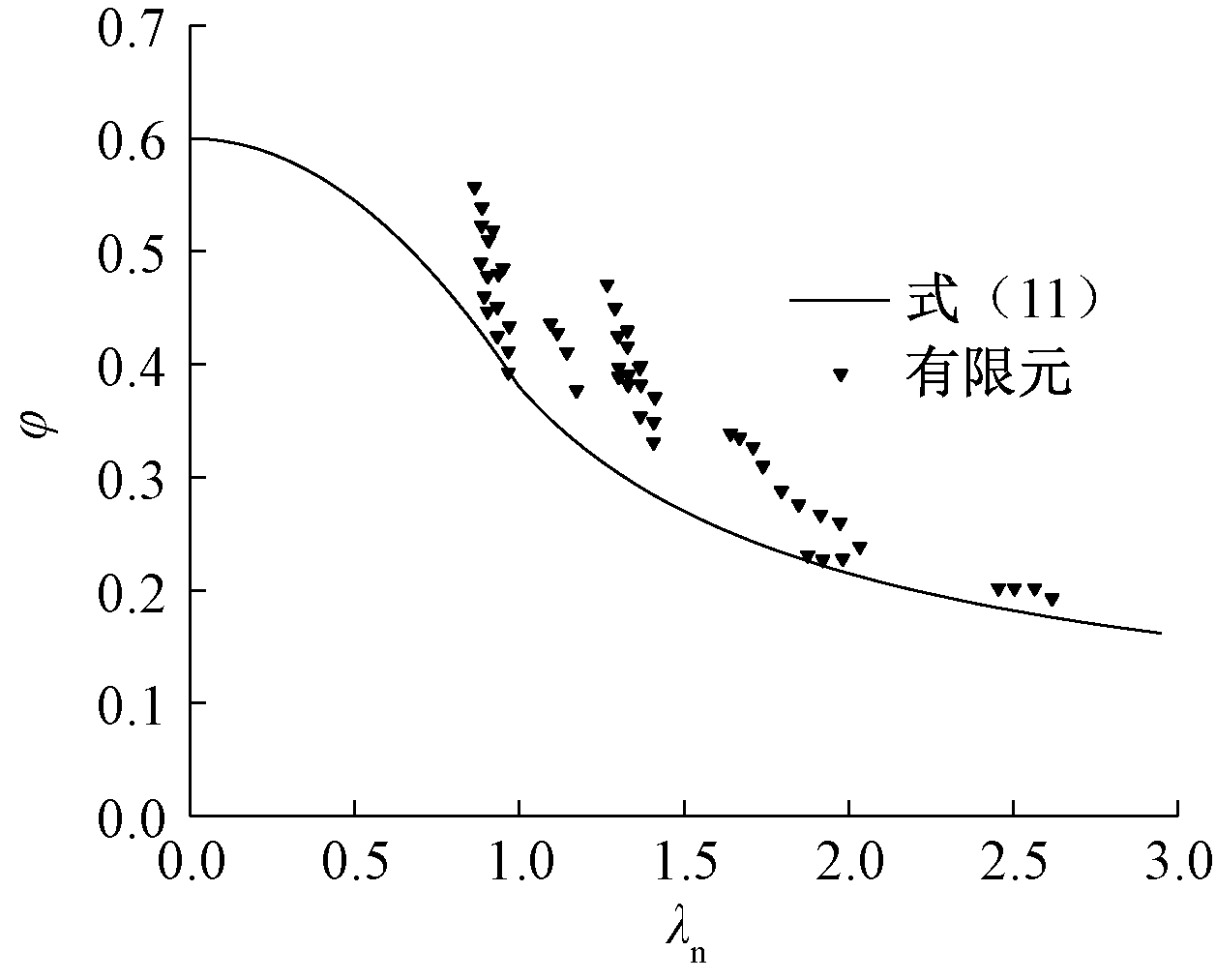
图12 φ-λn相关曲线
Fig.12 Correlation curve of φ-λn
将所有φ-λn点拟合成两段曲线,获得的稳定系数φ与正则化高宽比λn之间的相关曲线如图12所示,其关系式由式(11)给出。
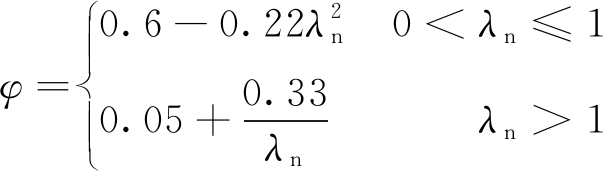
(11)
3.3 轴压承载力计算结果对比
利用上述计算公式对试验试件进行计算,并与试验结果进行比较,结果见表3。
由表3可见:试验结果均大于计算结果,且基本吻合,验证了算式的可靠性。
表3 不锈钢芯板一字形墙轴压承载力结果对比
Table 3 Comparisons of axial compressive bearing capacity of the in-line wall of the structure of stainless steel sandwhich panel
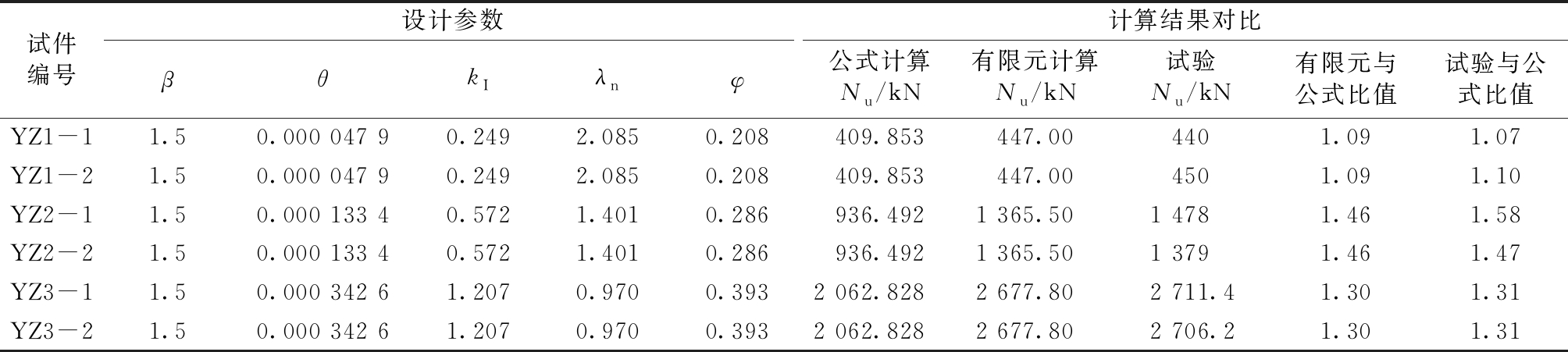
试件编号设计参数计算结果对比βθkIλnφ公式计算Nu/kN有限元计算Nu/kN试验Nu/kN有限元与公式比值试验与公式比值YZ1-11.50.000 047 90.2492.0850.208409.853447.004401.091.07 YZ1-21.50.000 047 90.2492.0850.208409.853447.004501.091.10 YZ2-11.50.000 133 40.5721.4010.286936.4921 365.501 4781.461.58 YZ2-21.50.000 133 40.5721.4010.286936.4921 365.501 3791.461.47 YZ3-11.50.000 342 61.2070.9700.3932 062.8282 677.802 711.41.301.31 YZ3-21.50.000 342 61.2070.9700.3932 062.8282 677.802 706.21.301.31
4 结束语
本文针对不锈钢芯板一字形墙的轴压性能进行了试验研究,建立了有限元计算模型,并将有限元模拟计算结果与试验结果进行了对比,验证了有限元模型的准确性,通过分析得出以下结论:
1)通过轴压试验得到三组荷载-位移曲线,并通过观察分析试验现象发现,不锈钢芯板一字形墙在层高3 m、面板厚度不大于4 mm的情况下,破坏形式均为芯板发生局部屈曲。
2)有限元模拟结果与试验结果吻合良好,验证了有限元模型的准确性,模型能够较好地模拟试验过程。
3)通过大量有限元模型对影响一字形墙轴压极限荷载的因素作进一步分析,明确了面板厚度、芯管壁厚、芯管间距、芯管外径对极限荷载的影响。
4)通过试验和有限元模拟对不锈钢芯板一字形墙轴压承载力计算方法进行研究,分析拟合了不锈钢芯板一字形墙轴压承载力计算公式。
本研究得到了远大可建科技有限公司的资助和大力支持,在此表示衷心感谢。
[1]王海忠,何保康,陶忠.建筑夹芯板结构性能分析[J].钢结构, 1999,15(4):41-45.
[2]王海忠,赵天宇.夹芯板结构设计与破坏模式分析[J].工业建筑,2005,35(8):97-99,120.
[3]彭明军. 钎焊蜂窝铝板力学性能研究[D]. 昆明:昆明理工大学, 2013.
[4]POKHAREL N, MAHENDRAN M. Finite Element Analysis and Design of Sandwich Panels Subject to Local Buckling Effects[J]. Thin-Walled Structures, 2004, 42(4):589-611.
[5]PAIK J K, THAYAMBALLI A K, KIM G S. The Strength Charac-teristics of Aluminum Honeycomb Sandwich Panels[J]. Thin-Walled Structures, 1999, 35(3):205-231.
[6]周祝林. 蜂窝夹层板的极限强度[J].力学学报,1993(1): 62-69.
[7]韦芳芳,郑泽军,喻君,等.基于钢板屈曲分析的双钢板-混凝土组合剪力墙轴压承载力计算方法[J].工程力学,2019, 36(2):154-164.
[8]朱梓健,李俞瑜,魏木旺,等.新型装配式钢板组合剪力墙轴压受力性能分析[J].钢结构,2018,33(11):87-91.
[9]郝婷玥,曹万林,张建伟,等.内置加劲肋钢板-混凝土组合剪力墙轴压性能研究[J].建筑结构学报,2017,38(增刊1):90-97.
[10]中国国家标准化管理委员会. 夹层结构侧压性能试验方法:GB/T 1454—2005[S]. 北京:中国标准出版社,2005.
[11]TIMOSHENKO S P, WOINOWSKY-KRIEGER S. Theory of Plates and Shells[M]. New York: McGraw-Hill, 1959.
[12]TIMOSHENKO S P, GERE J M. Theory of Elastic Stability[M]. New York: McGraw-Hill, 1961
[13]TONG J Z, GUO Y L. Shear Resistance of Stiffened Steel Corrugated Shear Walls[J]. Thin-Walled Structures, 2018,127: 76-89.
[14]GUO Y, ZHU J, WANG M, et al. Overall Instability Performance of Concrete-Infilled Double Steel Corrugated-Plate Wall[J].Thin-Walled Structures, 2018, 130: 372-394.
[15]ZHU J S, GUO Y L, ZHU B L, et al. Strength Design of Concrete-Infilled Double Steel Corrugated-Plate Walls Under Uniform Compressions[J]. Thin-Walled Structure, 2019,141:153-174.
[16]WANG M Z, GUO Y L, ZHU J S, et al. Strength Design of Concrete-Infilled Double Steel Corrugated-Plate Walls with T-Section Under Combined Axial Compression and Bending Moment[J]. J. of Constructional Steel Research, 2019, 160:23-44.