0 引 言
与传统钢结构相比,不锈钢芯板结构由两块钢板夹薄壁芯管组成,面板有芯管支持不易失稳。面板和芯管都可以很薄,与碳素钢相比要轻得多且刚度大,在不影响使用的前提下,减重效果非常明显,可工业化、规模化加工生产,减少基础造价,且避免传统钢结构易腐蚀缺点。
鉴于不锈钢芯板结构的诸多优点,这种结构形式可能具有广泛的应用前景。目前,国内外的学者对夹芯板结构做了大量的研究工作,但主要内容偏重材料学科,例如蜂巢夹芯板在船舶车辆、航空航天方面的应用,对不锈钢芯板结构受力性能分析具有一定的理论意义。
经过多年的理论研究和工程实践,我国在不锈钢结构领域的设计和施工技术取得了长足的进步,相关标准也不断完善。但是,不锈钢芯板结构作为一种全新的结构体系,目前仍存在大量空白需要进一步研究。
通过有限元分析的方法,对图1所示不锈钢芯板结构T形柱轴压性能进行研究,并根据有限元计算得到的应力、应变等数据深入分析试件的破坏机理;通过建立多组有限元分析模型,探究肢长、面板厚度和芯管壁厚等因素对不锈钢芯板结构T形柱轴压性能的影响,为全面研究T形柱的力学性能提供参考。

图1 不锈钢芯板结构T形柱
Fig.1 A T-shaped column made of the stainless steel sandwich panel with core tubes
1 不锈钢材料的力学性能
1.1 材料本构关系
不锈钢材料是一种非线性材料,其应力- 应变曲线没有明显的屈服点,也没有屈服平台,对于这种材料,通常是取塑性应变为0.2%时对应的应力作为材料的屈服强度f0.2。普通的奥氏体不锈钢断裂时的应变是碳素钢的1~2倍,达到了40%~60%,具有优异的塑性变形能力。
不锈钢材料实际上是一种高合金钢材,合金元素影响着它的性能。不同于普通碳素钢的双线性模型(弹性-理想塑性模型),不锈钢材料应用的连续本构关系模型是修正后的Ramberg-Osgood算式,该式由Ramberg和Osgood提出,后经Hill以及Rasmussen等的修正,其表达式[1-2]为:
σ≤f0.2 (1a)
f0.2<σ≤fu (1b)
其中 m=1+3.5f0.2/fu
E0.2=E0/(1+0.002E0/f0.2)
εu=1-f0.2/fu
式中:f0.2为名义屈服强度标准值;E0为初始弹性模量;n为应变强化系数;fu为抗拉强度标准值;m为计算系数;E0.2为应力为f0.2时对应的切线模量;εu为对应于抗拉强度标准值fu时的极限应变。
1.2 材料选择
S30408奥氏体不锈钢相比其他牌号不锈钢,抗腐蚀能力更强,能够适应大多数环境。它也是最常用的奥氏体不锈钢,耐腐蚀性强,塑性、韧性和冷加工性能良好[3-4],冲压、弯曲等热加工性能好,价格经济实惠,故采用S30408牌号的不锈钢作为母材。S30408奥氏体不锈钢材料的应力-应变曲线如图2所示,材料各项力学指标见表1[5]。
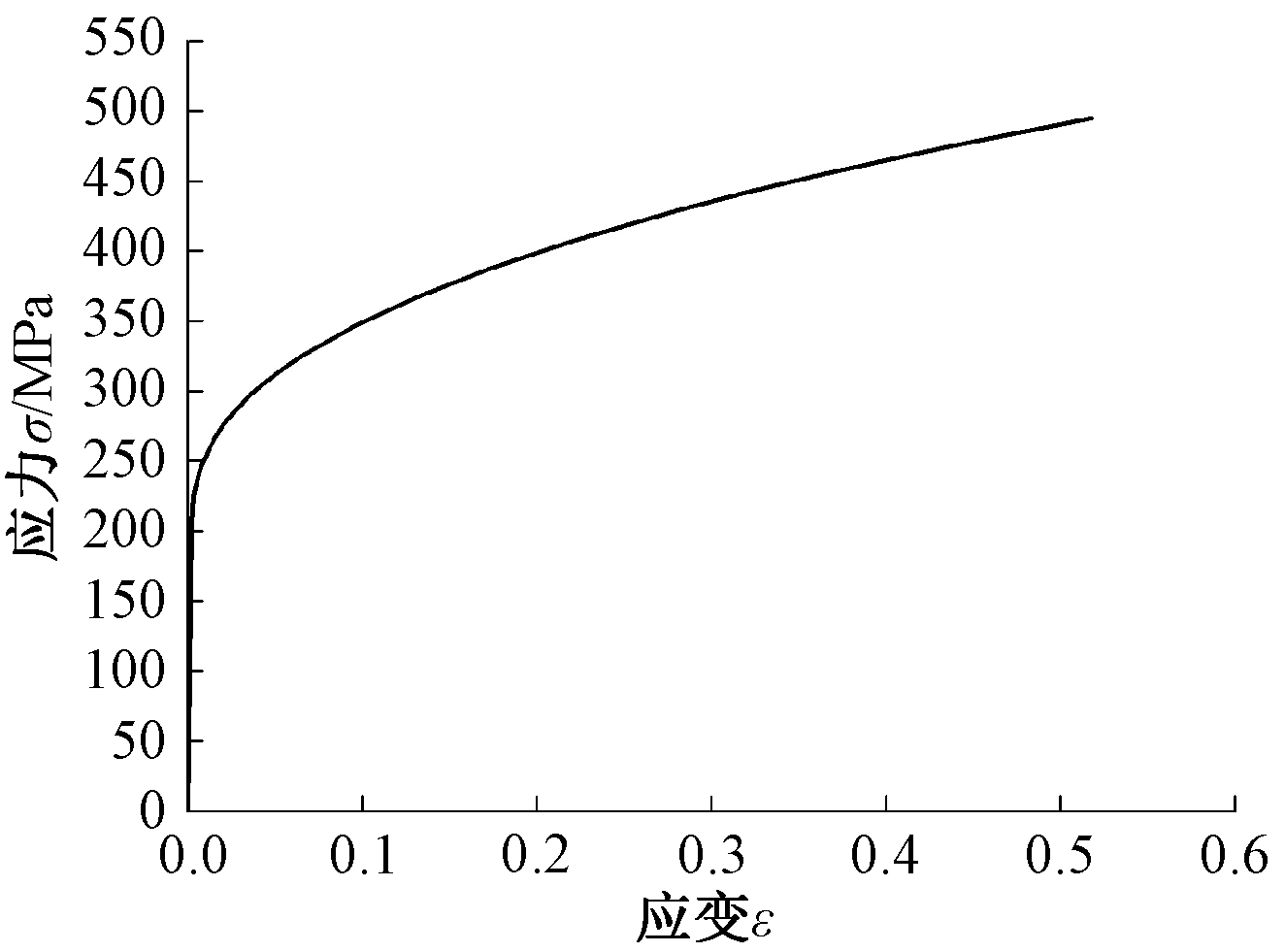
图2 S30408奥氏体不锈钢的应力-应变曲线
Fig.2 The stress-strain relationship of Austenitic stainless steel S30408
表1 S30408奥氏体不锈钢的材料强度指标
Table 1 The strength indexes of Austenitic stainless steel MPa

名义屈服强度f0.2抗拉强度标准值fu抗拉、抗压和抗弯强度设计值f抗剪强度设计值fv断面承压强度设计值fce205515175100450
2 有限元模型和计算方法
2.1 计算模型
采用有限元计算软件ABAQUS来研究不锈钢芯板T形柱的力学性能。计算简图如图3所示。
图3 模型计算简图
Fig.3 Schematic diagram for calculation
由于模型部件为三维结构,故采用自由划分网格技术划分模型部件,网格形状主要以四边形单元(S4R单元)为主,在模型圆孔位置处适当采用三角形单元调节网格的数量。初始网格大小:支座取默认值20 mm,其他部分13 mm。材料的本构关系根据材料的力学性能试验确定,泊松比取0.3,弹性模量取1.93×105 MPa。
不锈钢板结构T形柱由面板和芯管组成,由于厚度方向尺寸远小于其他两个方向的尺寸,故采用壳单元来模拟其变形和受力。综合考虑以上因素对有限元分析模型进行网格划分,统一将网格密度设置为10 mm。
模型的坐标系和加载方式如图4所示。约束条件为构件的上端约束X、Z方向的平动,放开Y向平动和三个方向的转动;构件的下端为刚接,即约束所有方向的运动。将柱顶和底面所有点耦合在所在面形心处,将边界条件施加在耦合点上。加载方式为在模型上端形心处施加轴压力。
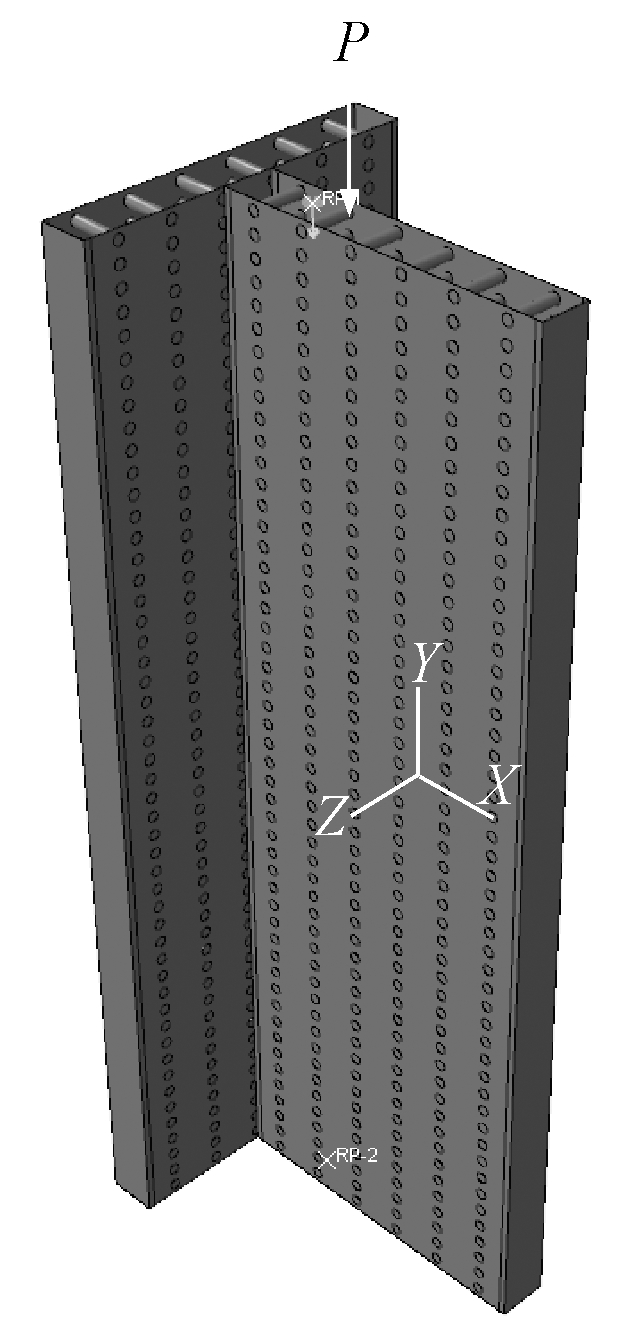
图4 模型坐标及加载方式
Fig.4 The coordinate axis of models and loading pattern
这种模拟方式在前期的不锈钢芯板侧压试验[6]中被证明是可靠的。
2.2 计算方法
由于不锈钢强度较高,而T形柱高度较高、面板和芯管厚度薄,比较容易发生整体失稳或局部失稳,为了更好了解T形柱的工作性能,采用ABAQUS对模型进行屈曲分析。屈曲分析是一种用于确定结构失稳时的临界屈曲荷载和确定结构屈曲时的模态形状的方法,ABAQUS提供了两种屈曲模态的分析方法——特征值屈曲分析和非线性屈曲分析。
本文首先进行特征值屈曲分析,得到初始弯曲、扭转和临界力,以此为参考进行非线性屈曲分析。
3 不锈钢芯板结构T形柱轴压性能研究
共建立了10个有限元模型,编号为1~10(表3)。具体尺寸包括肢长、面板厚和芯管管壁厚,其中1号为标准模型。
第1组:1~4号计算模型,主要研究肢长对T形柱轴压性能的影响。
第2组:1、5~7号计算模型,主要研究板厚对T形柱轴压性能的影响。
第3组:1、8~10号计算模型,主要研究芯管壁厚对T形柱轴压性能的影响。
构件详细规格和相应数据取值见图5及表3。
表3 不锈钢芯板结构T形柱构件尺寸
Table 3 Demensions of T-shaped column made of stainless steel sandwich panel with core tubes mm
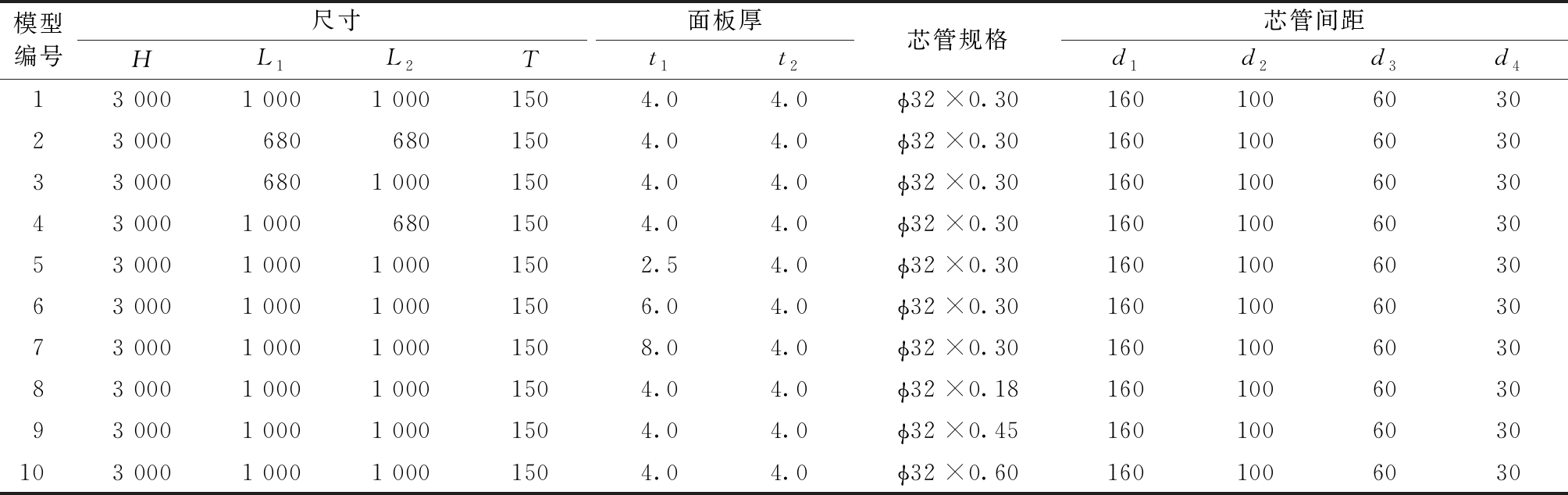
模型编号尺寸面板厚HL1L2Tt1t2芯管规格芯管间距d1d2d3d413 0001 0001 0001504.04.0ϕ32×0.30160100603023 0006806801504.04.0ϕ32×0.30160100603033 0006801 0001504.04.0ϕ32×0.30160100603043 0001 0006801504.04.0ϕ32×0.30160100603053 0001 0001 0001502.54.0ϕ32×0.30160100603063 0001 0001 0001506.04.0ϕ32×0.30160100603073 0001 0001 0001508.04.0ϕ32×0.30160100603083 0001 0001 0001504.04.0ϕ32×0.18160100603093 0001 0001 0001504.04.0ϕ32×0.451601006030103 0001 0001 0001504.04.0ϕ32×0.601601006030

图5 不锈钢芯板结构T形柱规格
Fig.5 The specifications of T-shaped column made of stainless steel sandwich panel with core tubes
如图6所示,在前期进行的不锈钢芯板结构侧压试验[6],取单块不锈钢芯管夹层结构试验构件进行非线性屈曲分析,截面参数为h=480 mm,b=380 mm,d=150 mm,面板厚度分别为t=1.5,4,4 mm,芯管规格为φ32×0.18、φ32×0.30、φ32×0.30,芯管间距为60 mm×80 mm、60 mm×80 mm、60 mm×160 mm,共三个试件,编号分别为试件1、试件2、试件3,临界荷载试验结果与ABAQUS非线性屈曲分析对比如表4所示。
分析结果显示,短柱以弯曲屈曲为主,并有局部屈曲发生。3种构件其屈曲计算结果均高于试验值。这是因为在实际结构中,有残余应力和本构关系差异的影响。试验结果低于非线性屈曲分析的结果符合规律,所以非线性分析的结果是可信的。

a—试验前; b—试验后。
图6 不锈钢芯板结构侧压试验
Fig.6 The lateral compressive test for the structure of stainless steel sandwich panel with core tubes
表4 ABAQUS分析与试验结果对比
Table 4 The comparisons between ABAQUS analysis and the test results

试件编号ABAQUS值/kN试验值/kN误差/%1206.2198.53.92762.1729.34.53715.1697.72.6
3.1 特征值屈曲分析
根据上述的计算方法,利用ABAQUS对1~10号不同尺寸的不锈钢芯板结构T形柱进行了特征值屈曲分析,具体结果如表5所示。
表5 特征值屈曲计算结果
Table 5 The eigenvalue buckling analysis results kN
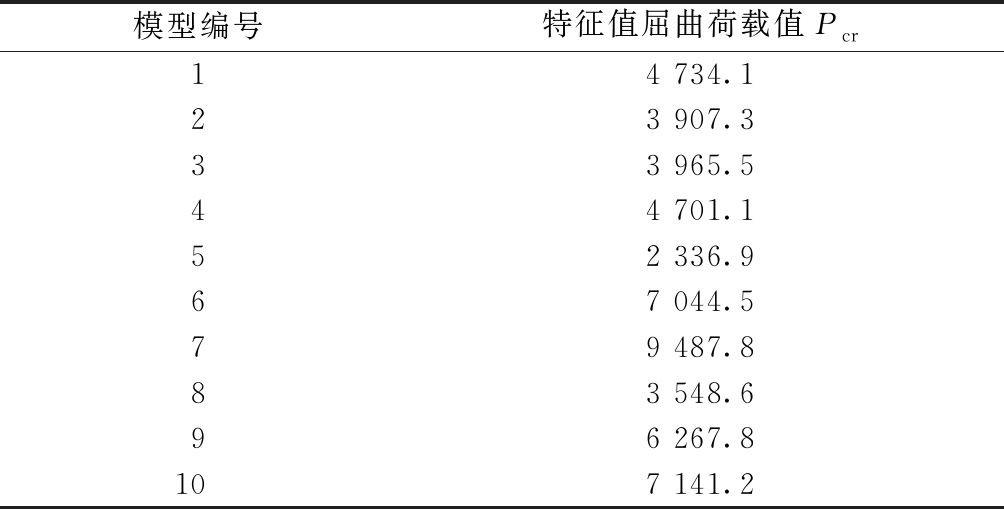
模型编号特征值屈曲荷载值Pcr14 734.123 907.333 965.544 701.152 336.967 044.579 487.883 548.696 267.8107 141.2
3.2 非线性屈曲分析
异形柱的屈曲荷载临界力的理论解为[7]:
(2)
式中:λxyω为柱换算长细比;Pxyω为特征值屈曲荷载值;E为柱材料的弹性模量;A为柱横断面的面积。
由式(2)可知换算长细比为:
(3)
稳定系数φ计算式为:
(4)
式中:Pu为非线性屈曲临界荷载;fy为材料的屈服强度。
在特征值屈曲分析的基础上,利用ABAQUS中的Riks算法,并采用位移加载的方式进行加载,缺陷值采用1%柱长,对1~10号不同尺寸的不锈钢芯板结构T形柱进行非线性屈曲分析,根据式(3)、(4)计算换算长细比与稳定系数,相关数据如表6所示。
表6 非线性屈曲的相关数据
Table 6 Nonlinear buckling analysis results
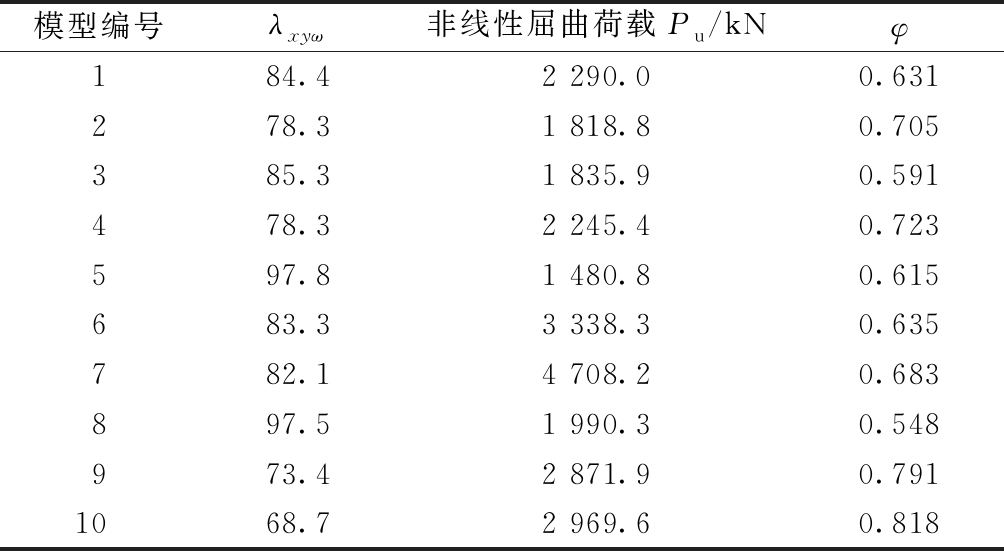
模型编号λxyω非线性屈曲荷载Pu/kNφ184.42 290.00.631278.31 818.80.705385.31 835.90.591478.32 245.40.723597.81 480.80.615683.33 338.30.635782.14 708.20.683897.51 990.30.548973.42 871.90.7911068.72 969.60.818
3.3 计算结果分析
1号标准模型的荷载-位移曲线如图7所示,开始加载时,荷载迅速增大并与位移基本保持线性关系,大部分区域的应力值很低。随着荷载的不断增大,某些区域达到屈服极限,进入了塑性阶段,荷载增长滞后于位移增长,两者不再保持线性的关系。荷载-位移曲线的顶点实质上是面板开始发生失稳时的状态。随着位移继续增大,构件的承载力开始下降,且曲线变得平缓,这是由于有限元模拟时,模型的荷载与位移的关系是按照定义的应力-应变关系来计算,当材料的应变达到定义的最大应变后,荷载就趋于水平线,而位移继续增加。
图7还给出了第1组、第2组和第3组试件的荷载-位移曲线。由图7可以看出:肢长对T形柱的临界屈曲荷载有很大的影响,增加翼缘长度对提高T形柱极限荷载值有显著作用,翼缘为腹板提供了必要的侧向支撑;而增加腹板长度对极限荷载值几乎没有作用,反而会减少极限荷载值,因为面板的皱曲是绕T形柱对称轴的,提高腹板长度相当于减少了侧向支撑。
根据表6的数据,图8、图9分别给出了随肢长、面板厚度和芯管壁厚的变化,稳定系数的变化情况。
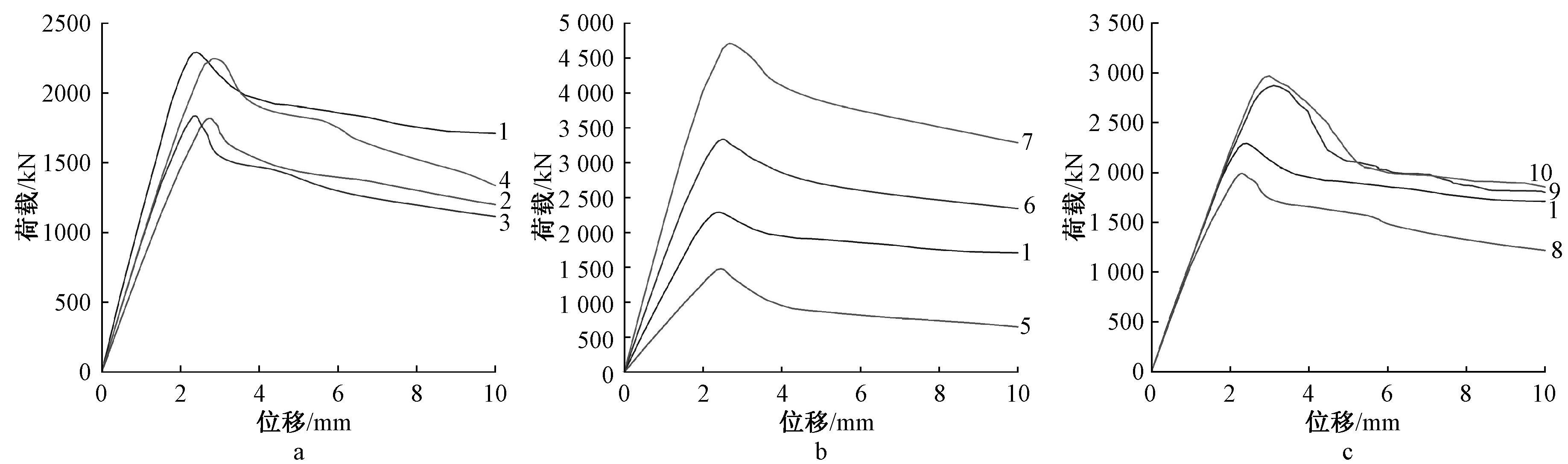
a—第1组; b—第2组; c—第3组。
注:图中曲线1~10编号对应试件模型1~10。
图7 构件的荷载-位移曲线
Fig.7 The load-displacement curves of the specimens
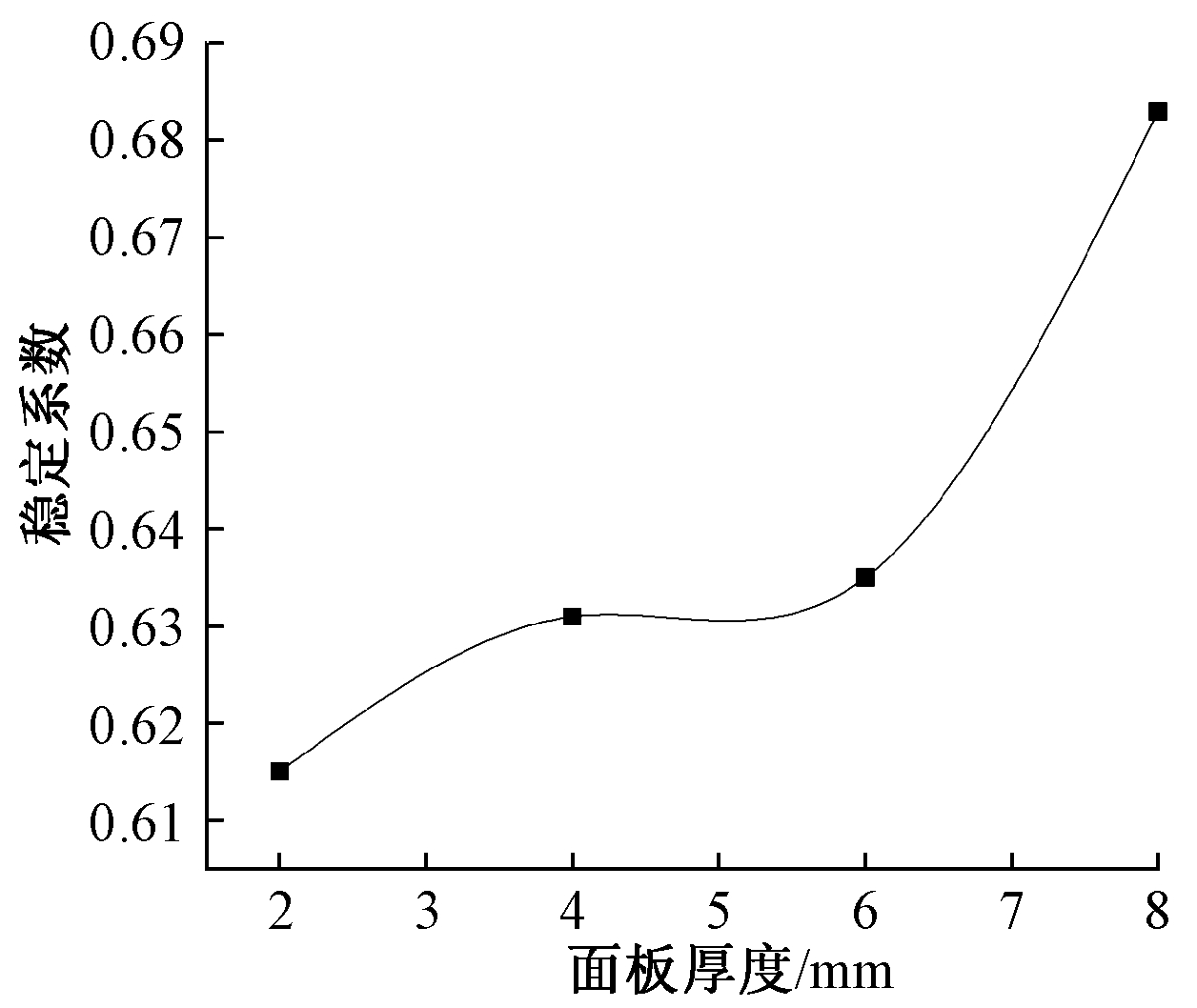
图8 稳定系数φ与面板厚度的关系
Fig.8 The relationship between the stability coefficient and the thickness of panel
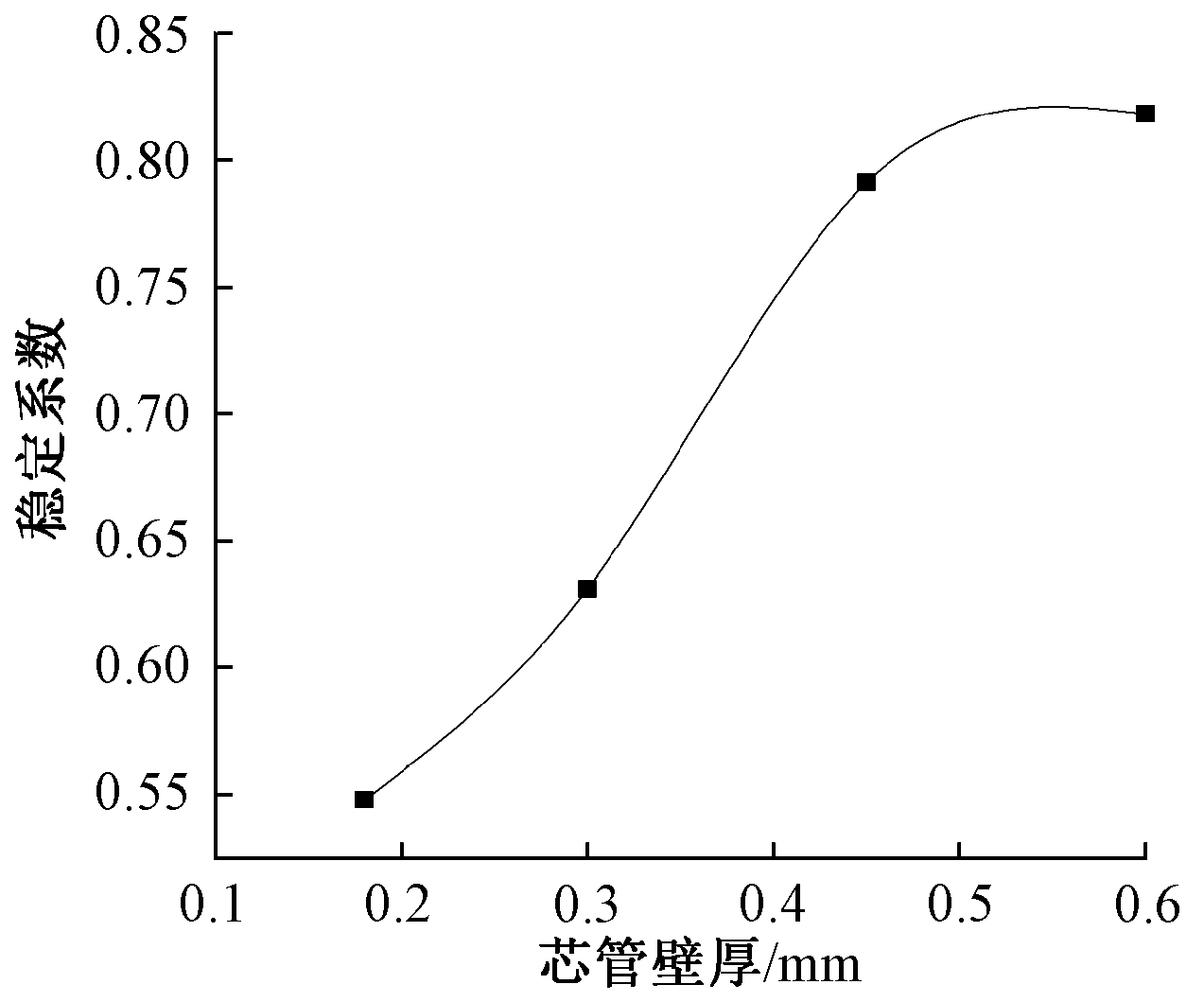
图9 稳定系数φ与芯管壁厚的关系
Fig.9 The relationship between the stability coefficient and the wall thickness of core tube
由表6可知:截面面积较小的试件模型2、4的稳定系数反而比截面较大的试件模型1大,而试件模型1、2的临界荷载值相差并不大。这说明一味地提高肢长可能不经济,需要找到性价比较高的肢长组合。
随着板厚度的增加,T形柱的临界屈曲荷载和稳定系数均有明显增加(图7a、图8),较厚的面板更难以屈曲,不易失稳。
当面板厚度为4.0 mm时,随着芯管壁厚的增加,芯管对面板的局部约束变强。但厚度到达一定程度后,临界屈曲荷载值和稳定系数增长不大(图7b、图9)。这是由于面板厚度过薄,容易产生大变形,从而将轴向压力转化为水平力施加在芯管上,导致芯管局部屈曲,最终引起T形柱破坏。
图10是用非线性曲线拟合的φ-λxyw曲线,两者关系基本符合规律。事实上,不锈钢芯板结构T形柱的φ与λxyw关系应与面板厚度、肢长,芯管壁厚、直径和排布有关。当面板较薄而芯管壁厚较厚时,与本文所研究构件的破坏形态不同,可能发生的破坏是面板的屈曲,导致 φ - λxyw曲线规律也不相同。因此,要研究不锈钢芯板结构T形柱φ与λxyw的关系,尚需进行大量的试验和分析。
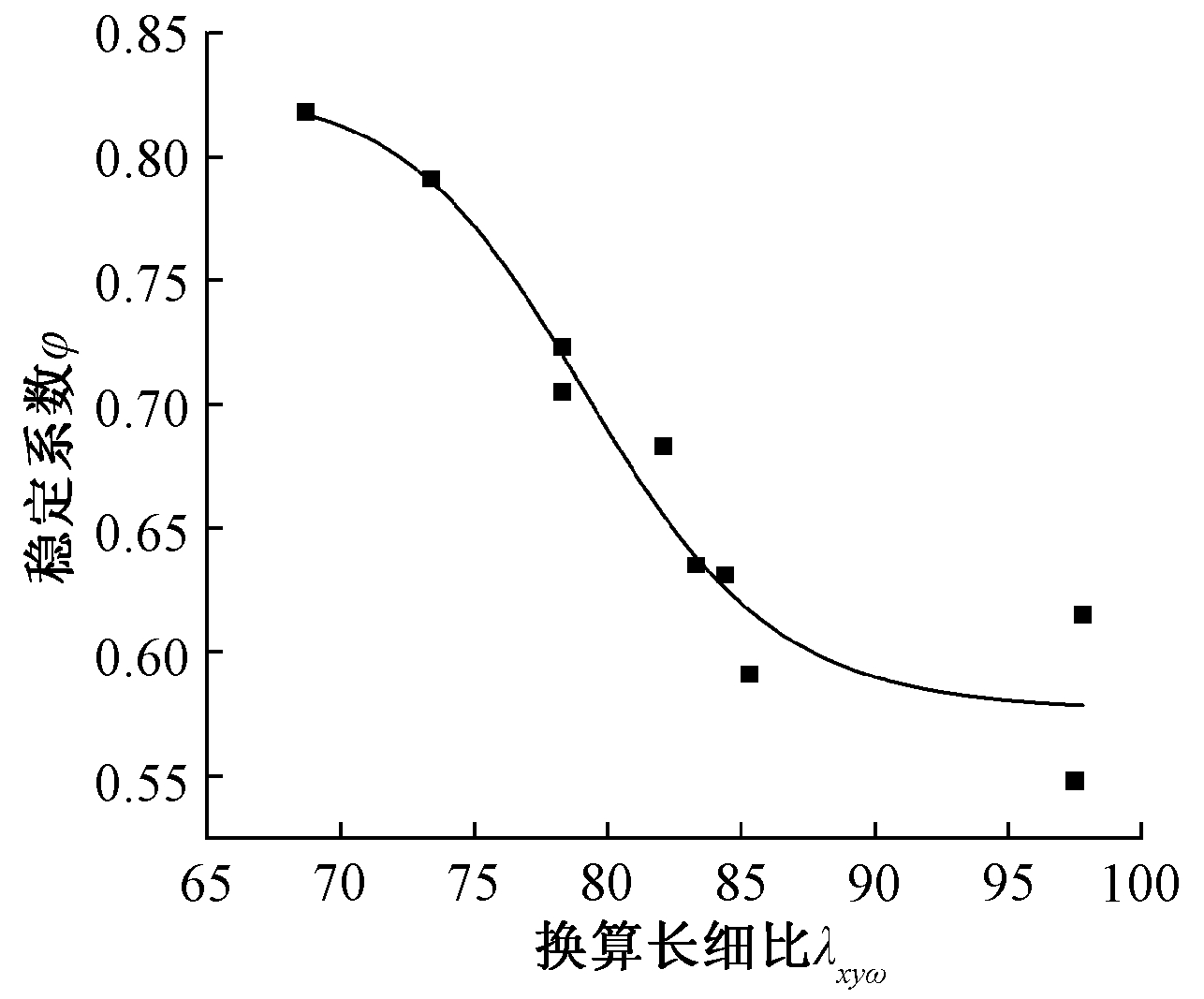
图10 稳定系数φ与换算长细比λxyω的关系
Fig.10 The relationship between φ and λxyω
4 结束语
在考虑材料非线性和初始缺陷的基础上,利用ABAQUS对不锈钢芯板结构T形柱的稳定承载力进行分析,得到如下结论:
1)不锈钢芯板结构T形柱的稳定承载能力受截面肢长比的影响较大,在一定范围内增加翼缘长度能有效阻止柱的失稳。
2)T形柱的破坏属于局部屈曲破坏,增加厚度能够有效阻止芯管因面板皱曲而破坏,较大提升该T形柱的稳定承载力。
3)芯管能给面板提供一定的支撑,但在面板厚度恒定的情况下,芯管厚度到达一定程度后,厚度的增加对稳定承载力的提升作用不大。
[1]舒赣平, 王元清, 袁焕鑫,等. 《不锈钢结构技术规程》编制及内容简介[J]. 工业建筑, 2015,45(12):1-6.
[2]王元清, 袁焕鑫, 石永久,等. 不锈钢结构的应用和研究现状[J]. 钢结构, 2010, 25(2):1-12.
[3]吴耀华. 不锈钢结构的材料选用及防腐蚀设计[J]. 工业建筑, 2015,45(12):7-12.
[4]史勤益, 颜余仁, 赵先锐,等. 304奥氏体不锈钢的热处理工艺研究[J]. 科学技术与工程, 2011, 11(24):5910-5913.
[5]中国工程建设标准化协会. 不锈钢结构技术规程:CECS 410:2015[S].北京:中国计划出版社,2015.
[6]舒兴平,黄牧兴,项梦洁. 不锈钢芯板结构侧压性能试验研究[J].工业建筑, 2020,50(2):17-23.
[7]王明贵, 王晓瑜, 陈章华. 钢异形柱轴心受压承载力实用计算研究[J]. 钢结构, 2007,22(6):44-47.