随着人民生活水平的提高,人们对居住空间的要求也越来越高,不仅要求使用面积大,而且要求建筑结构内部空间利用率高。普通框架结构因具有露梁露柱等缺点,给室内装饰和家具布置带来极大不便,已不能满足人们对住宅平面和空间的要求。采用异形截面框架柱可以有效地解决这些问题,因此受到广泛欢迎[1]。
不锈钢芯板结构L形柱是一种新型的异形柱结构形式,是用不锈钢夹层结构作为材料焊接而成的一种预制不锈钢构件。 不锈钢芯板结构L形柱由于能够在工厂预制,拓宽了异形柱的使用空间,使该课题的研究显得有意义。
1 新型不锈钢芯板结构L形柱的提出
我国的不锈钢产量近年来迅速提高,不锈钢材料的应用范围逐渐扩大,在建筑行业中由传统的装饰构件逐渐扩大到结构承重构件。一方面由于不锈钢构件外形光滑易加工,再加上其所具有的诸如耐腐蚀性强、环境适应性强以及在很宽温度范围内都能够保持高强度、高韧性等特点,使其在建筑业中拥有广阔的适用性。另一方面,经济的飞速发展使得目前社会不仅仅对建筑物的安全性能和使用性能有较高要求,对环保性和美观性也提出了更高的需求。综合以上因素,不锈钢材料有着很广阔的应用和发展空间。
蜂窝夹层结构材料与传统的建筑材料相比具有许多明显的优点,如高强、轻质、隔热、隔声性能较好,所以被广泛应用于社会生活的各个方面[2]。但由于蜂窝夹层结构的造价过高,这种结构形式在建筑领域直接用于承重构件的并不多见。远大可建集团改进的铜钎焊技术使得这种夹层结构的制作实现了流水化,大大降低了造价,使得这种结构形式在建筑领域直接作为承重构件成为了可能。
为了充分发挥两者的优点,将其有机结合在一起,提出了不锈钢芯板结构L形柱,如图1所示。本研究依助有限元软件ABAQUS,采用有限元非线性屈曲分析的方法,对不同面板厚度、芯管厚度以及芯管间距的不锈钢芯板结构L形异形柱进行轴压屈曲性能的数值分析研究,以期得到不锈钢芯板结构L形异形柱在轴向压缩荷载作用下的稳定性能。同时通过对单一参数变化条件下这种新型L形柱的屈曲模式、变形过程、荷载-位移曲线等方面的分析,为后续全面研究力学性能和工程实践提供参考。
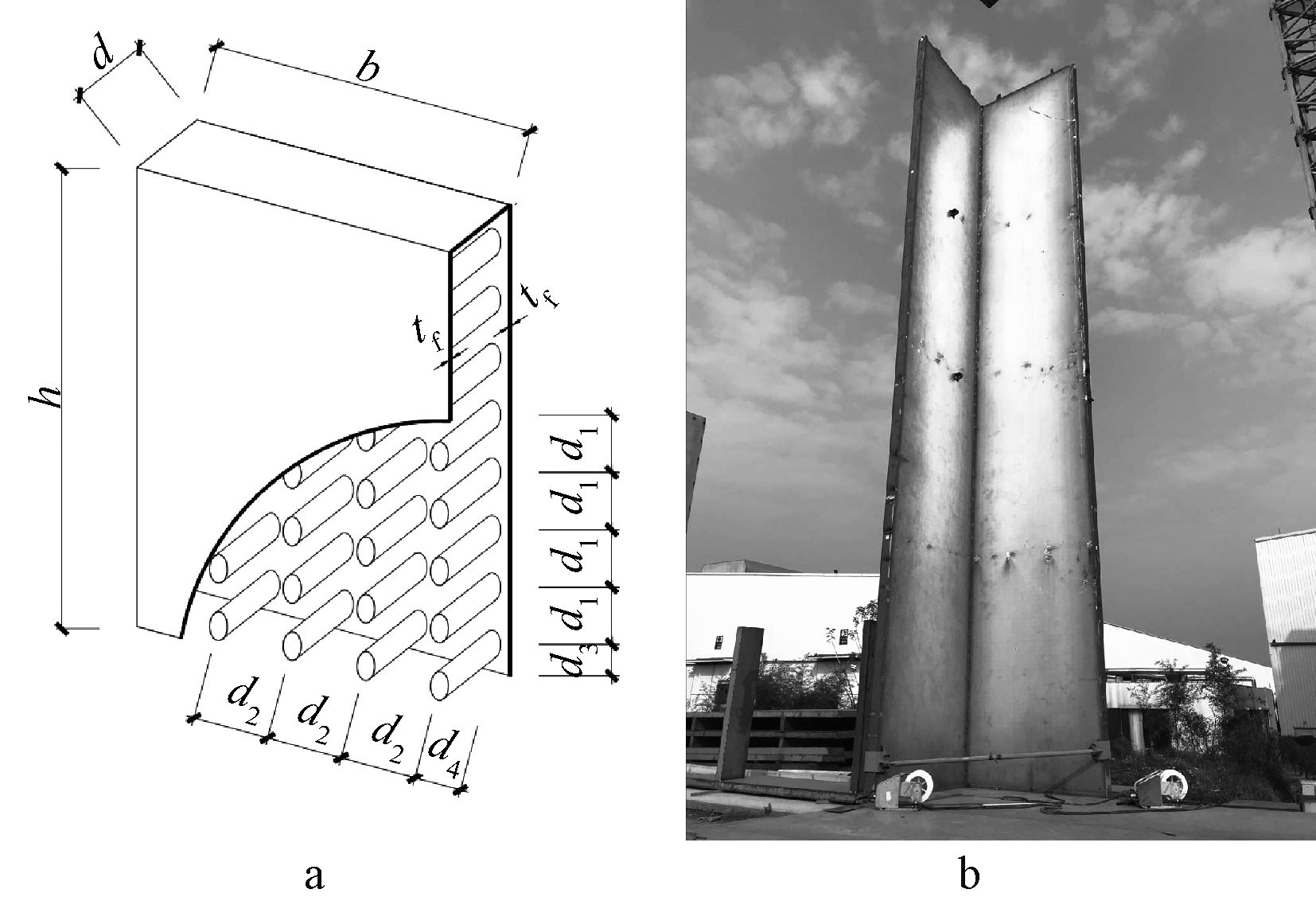
图1 不锈钢夹层结构L形柱示意
Fig.1 Schematic diagram of L-shaped column made of stainless steel sandwich panel with core tubes
2 有限元模型和计算方法的确定
2.1 材料本构关系的选取
不锈钢材料实际上是一种高合金钢材,不同于普通碳素钢的双线性模型,不锈钢材料使用的本构关系模型[3]是修正后Ramberg-Osgood算式,该算式由Ramberg和Osgood提出,经过Hill的第一次修正和Rasmussen等的第二次修正,其表达式如式(1)所示:
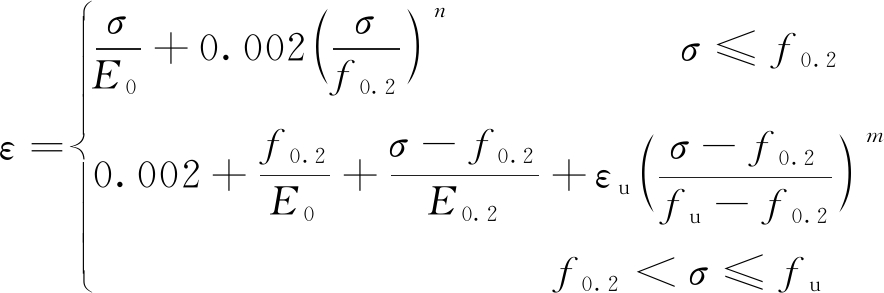
(1)
其中 ![]()
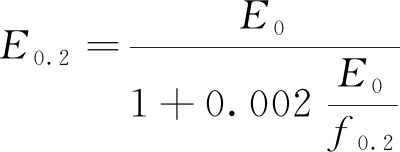
式中:f0.2为不锈钢名义屈服强度;E0为初始弹性模量;n为应变强化系数;fu为抗拉极限强度。
对于不锈钢芯板结构常采用S30408型号的不锈钢面板,其本构关系如图2所示。
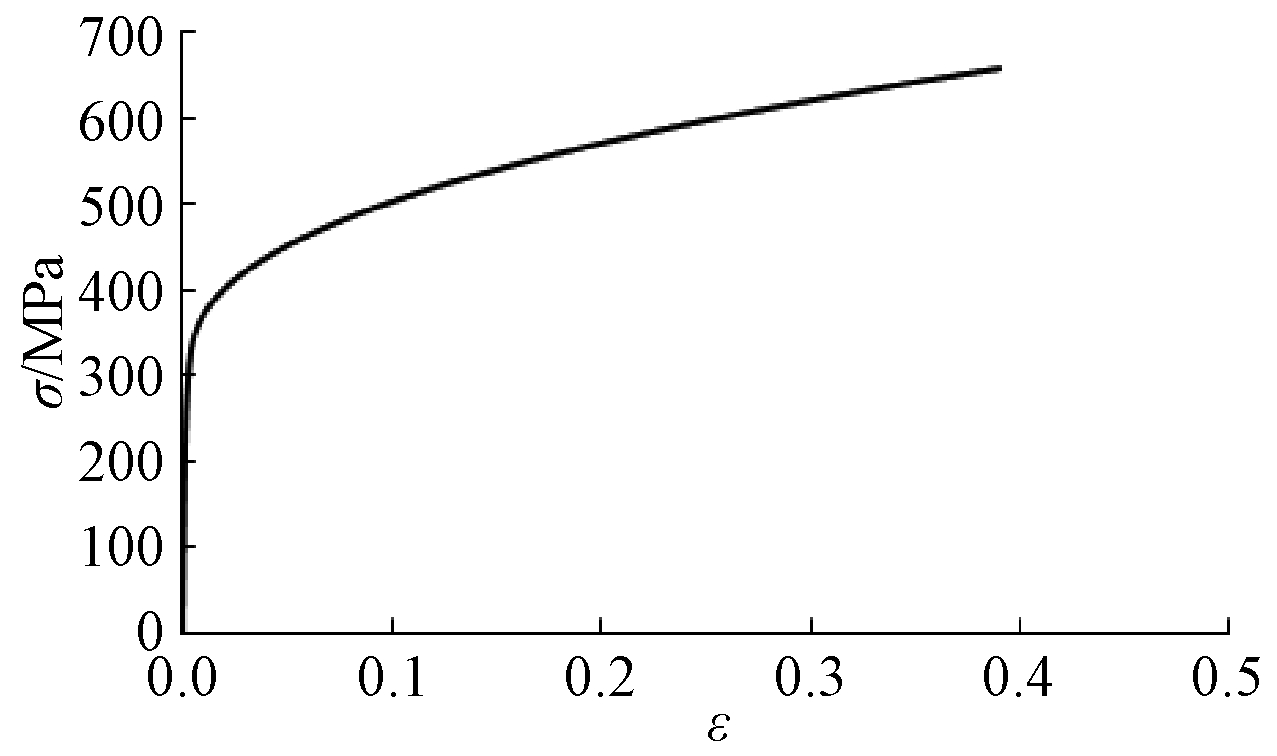
图2 不锈钢S30408本构关系曲线
Fig.2 The constitutive relation of stainless steel S30408
在有限元数值模拟中需要采用材料的真实应力-应变关系曲线(σt-εt),而试验得到的是名义应力-应变关系曲线(σn-εn),因此需要将材料名义应力-应变关系曲线(σn-εn)转化为真实应力-应变关系曲线(σt-εt),可用式(2)进行转换:
(2)
式中:εn、σn分别为名义应变、应力;εt、σt分别为实际应变、应力。
2.2 建立有限元模型
采用大型有限元通用程序ABAQUS进行力学性能的研究,单元选用壳单元。模型的坐标系、边界条件以及加载方式如图3所示。模型的约束条件:构件一端约束X、Z方向的平动,释放Y向平动和三个方向的转动;对称端为固定端,加载方式采用位移加载。
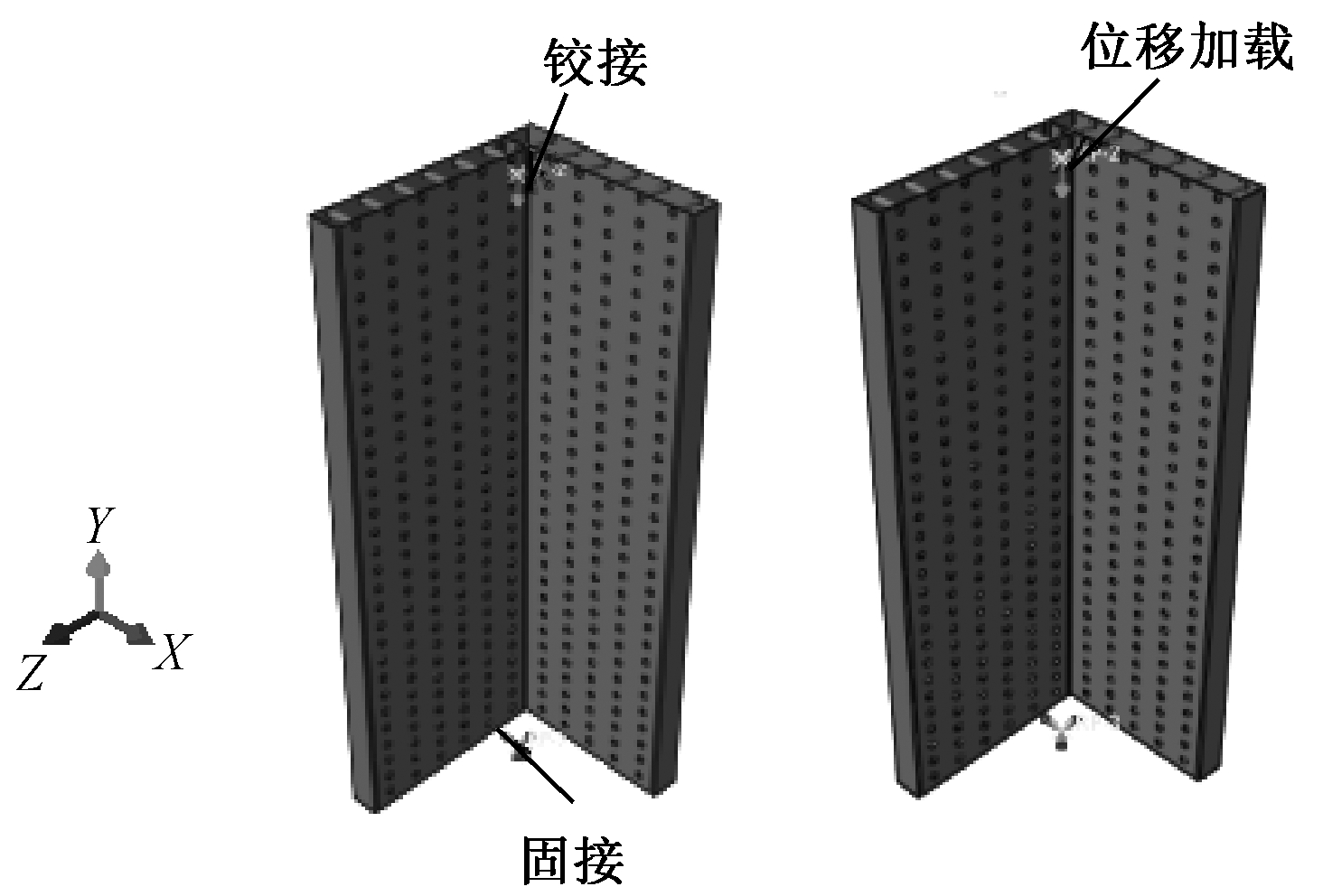
图3 模型坐标系、边界条件及加载方式
Fig.3 The coordinate system, boundary condition and loading mode of the model
为了更加真实地模拟实际加载方式,建模前首先计算好异形柱的形心,建模时在柱顶和柱底形心点处分别设置一个参考点,并将它们分别与柱顶和柱底的一排单元绑定。建立边界条件时直接施加在参考点上即可。有限元模拟试件的基本参数如表1所示。
表1 有限元模拟试件的基本参数
Table 1 Basic parameters for the numerical simulation mm
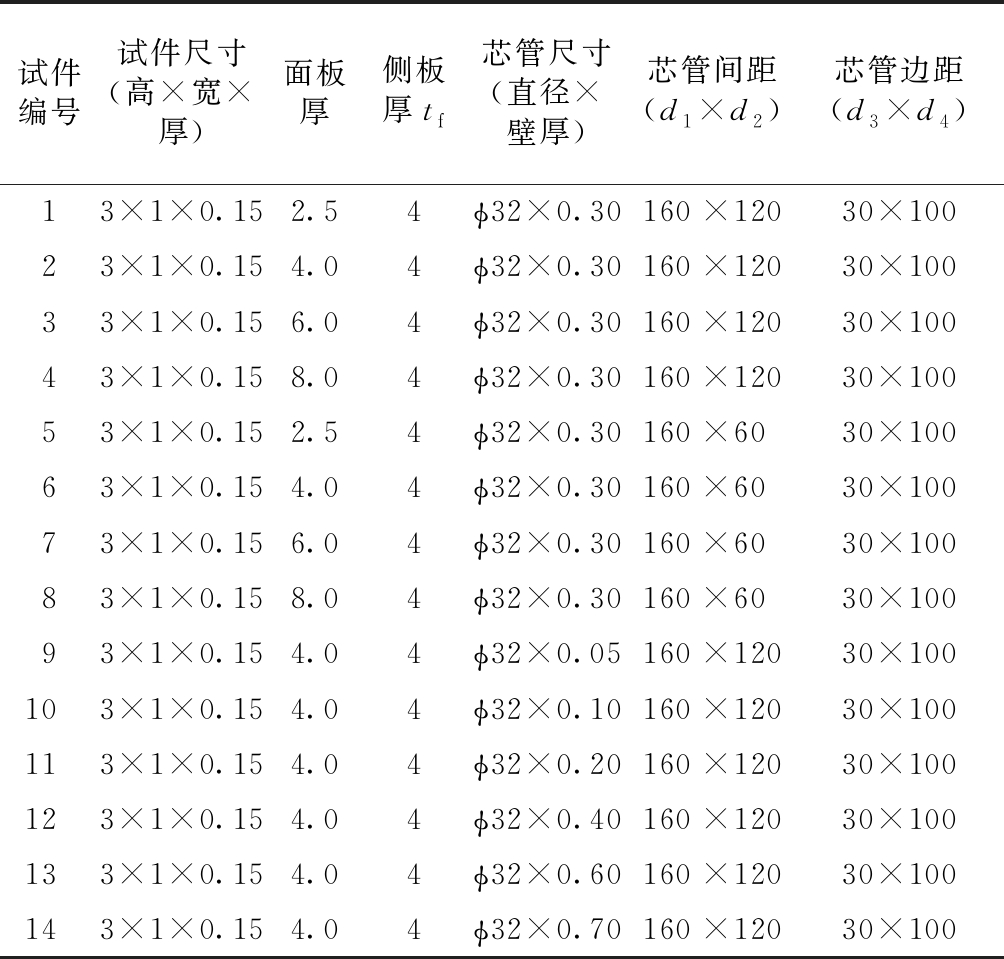
试件编号试件尺寸(高×宽×厚)面板厚侧板厚tf芯管尺寸(直径×壁厚)芯管间距(d1×d2)芯管边距(d3×d4)13×1×0.152.54ϕ32×0.30160×12030×10023×1×0.154.04ϕ32×0.30160×12030×10033×1×0.156.04ϕ32×0.30160×12030×10043×1×0.158.04ϕ32×0.30160×12030×10053×1×0.152.54ϕ32×0.30160×6030×10063×1×0.154.04ϕ32×0.30160×6030×10073×1×0.156.04ϕ32×0.30160×6030×10083×1×0.158.04ϕ32×0.30160×6030×10093×1×0.154.04ϕ32×0.05160×12030×100103×1×0.154.04ϕ32×0.10160×12030×100113×1×0.154.04ϕ32×0.20160×12030×100123×1×0.154.04ϕ32×0.40160×12030×100133×1×0.154.04ϕ32×0.60160×12030×100143×1×0.154.04ϕ32×0.70160×12030×100
2.3 计算方法的确定
由于不锈钢强度较高,而L形柱高度高、面板和芯管厚度薄,比较容易发生整体失稳或局部失稳,为了更好了解L形柱的工作性能,采用ABAQUS对模型进行屈曲分析。屈曲分析[4]是一种用于确定结构失稳时的临界屈曲荷载和确定结构屈曲时的模态形状的方法,ABAQUS提供了特征值屈曲分析和非线性屈曲分析两种方法。
首先在特征值屈曲分析的基础上,得到初始弯曲、扭转和临界力,以此为基础进行非线性屈曲分析。
进行特征值屈曲分析的目的有:1)获取试件的屈曲模态,为后续非线性屈曲分析时结构初始缺陷的施加提供一种方法;2)通常线性屈曲的特征值往往高于非线性屈曲的极限荷载,所以线性屈曲分析得到的极限承载力可以作为非线性屈曲分析时外荷载选取的参考。
由于初弯曲和初偏心对轴心受压构件的影响都使得试件出现极值点失稳现象,使构件的承载力有所降低,两种影响在本质上并无差别,因此在研究实际构件时,通常把它们的影响一并考虑。计算中,初始缺陷通过特征值屈曲分析的屈曲模态的扩展实现,调整至壳厚的20%。
采用ABAQUS的自动荷载增量和弧长迭代法技术进行几何非线性和材料非线性分析,求得轴向极限荷载。
3 屈曲分析
3.1 计算方法的验证
取单块不锈钢芯板结构试验构件进行非线性屈曲分析,截面参数为h=480 mm,b=380 mm,d=150 mm,面板厚度分别为t1=1.5,4.0,4.0 mm,芯管规格分别为φ32×0.18,φ32×0.18,φ32×0.3,芯管间距分别为60 mm×80 mm,60 mm×80 mm,60 mm×80 mm共三个试件,编号分别为试件1、试件2、试件3,计算结果如表2所示。
表2 ABAQUS分析与试验结果对比
Table 2 The comparisons between ABAQUS and experimental result[5]

试件ABAQUS值/kN试验值/kN误差/%试件11401362.90试件27367290.96试件37617422.60
分析结果显示:短柱以弯曲屈曲为主,并有局部屈曲发生。3种构件其屈曲计算结果均高于试验值。这是因为在实际结构中,由于残余应力和本构关系差异的影响,试验结果低于非线性屈曲分析的结果符合规律,所以此非线性分析的结果是可取的。
3.2 特征值屈曲分析
研究不同面板厚度对L形柱屈曲承载力的影响,对表1的试件编号1~4的构件进行ABAQUS有限元特征值屈曲分析,分析结果如表3所示。
表3 特征值屈曲分析结果
Table 3 The analytical results for eigenvalue buckling
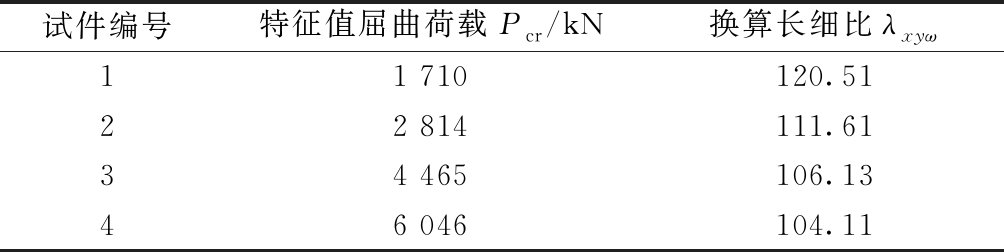
试件编号特征值屈曲荷载Pcr/kN换算长细比λxyω11 710120.5122 814111.6134 465106.1346 046104.11
3.3 非线性屈曲分析
采用以上分析方法,取试件编号1~4的构件,进行ABAQUS有限元非线性屈曲分析,可以得出每个构件的荷载-位移全过程曲线如图4所示。
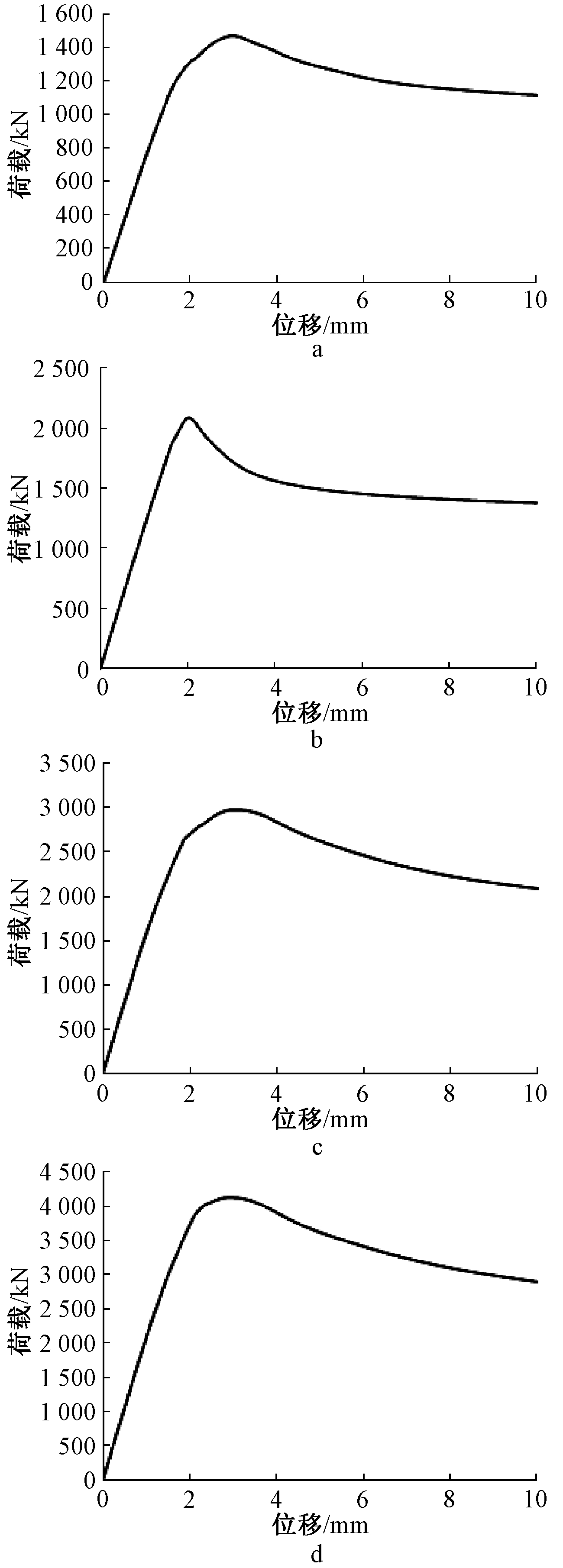
a—2.5 mm; b—4.0 mm; c—6.0 mm; d—8.0 mm。
图4 不同板厚荷载-位移曲线
Fig.4 The loading-displacement curves for different panel thicknesses
4 计算结果分析
4.1 荷载-纵向位移曲线分析
从4个试件的轴压荷载-纵向位移曲线可知:在加载的初期,试件处于弹性工作阶段,随着荷载的增大,位移与之保持线性关系;此阶段由于施加的荷载较小,相应的变形很小,从外观上看无明显特征,模型大部分区域的应力值也很低。随着荷载不断增加,材料屈服进入塑性阶段,此时结构的荷载增量明显比位移增量小很多,两者呈现非线性的关系。当4个试件达到极限荷载后,荷载-位移曲线表现为位移继续增加而承载力却不断减小,最终趋于一个恒值,在荷载-位移曲线上表现为曲线逐渐趋于水平。通常情况下,在试验中当承载力下降到极限承载力的70%~80%时,试件已经发生破坏。然而有限元软件在进行数值模拟时,其受力和变形会严格遵循定义的材料本构关系,当到达极限承载力后,应力不再增加,应变还在继续变大,表现为承载力最后趋于一个恒值。
4.2 破坏形态分析
图5分别给出了试件1~4的最终破坏形态以及von Mises应力云图,从截取的应力云图中可以看出:当试件达到极限承载力时,试件的von Mises应力达到了380 MPa左右,远远没有达到不锈钢的极限强度,试件表现为局部屈曲破坏,从而使得整个构件丧失承载能力。

a—试件1; b—试件2; c—试件3; d—试件4。
图5 破坏形态和von Mises应力云图
Fig.5 The failure mode and von Mises stress contour
4.3 稳定极限承载力分析
根据钢结构稳定的相关理论[5-7],异形截面柱的稳定临界承载力Pcr为:
(3)
式中:λxyω为柱换算长细比;E为材料的弹性模量;A为受压构件横断面的面积。
由式(3)可以得到换算长细比:
(4)
稳定系数φ计算式为:
(5)
式中:Pu为非线性屈曲分析时的极限荷载;fy为材料的屈服强度,不锈钢S30408可取205 MPa。
在充分考虑材料非线性和几何非线性的情况下,根据式(3)~(5),非线性屈曲的相关数据如表4所示。
表4 非线性屈曲的相关数据
Table 4 The relevant data for the nonlinear yield

试件编号λxyωPcr/kNPu/kNφ1120.511 7101 4680.5772111.612 8142 0960.5563106.134 4652 9790.5514104.116 0464 1250.585596.772 5222 0050.794682.165 1922 6720.708785.126 9393 5090.648887.378 5834 6670.6629151.651 5241 8400.48810119.462 4561 9420.5151193.743 9892 2540.598282.165 1922 6720.7081271.596 8392 8850.7651368.897 3852 9910.7931466.967 8163 0550.810
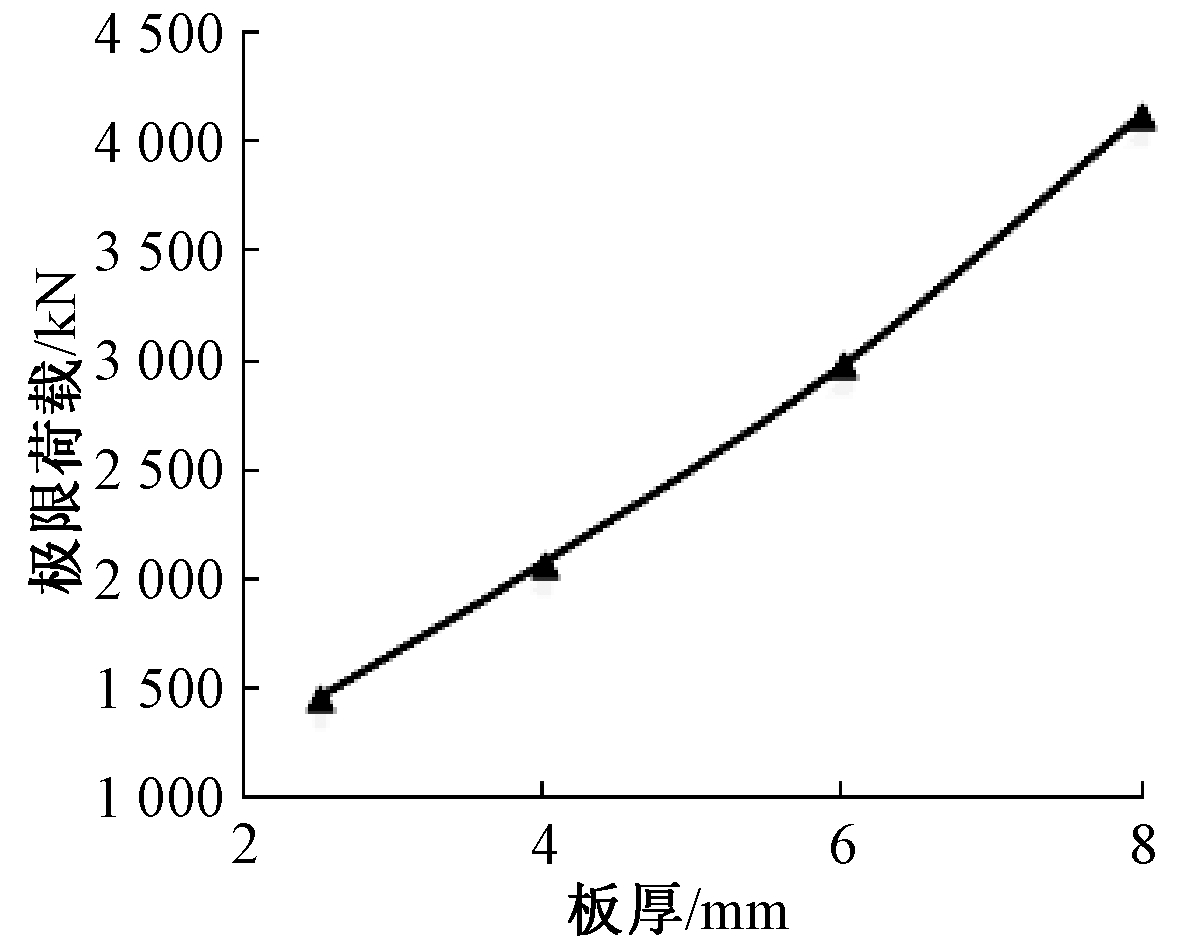
图6 不同板厚下的稳定极限荷载曲线(试件1~4)
Fig.6 The stable ultimate load curve for the panel with different thicknesses (specimen 1 to 4)
由表4和图6可以看出:1)随着面板厚度的增加,L形柱的极限荷载逐渐增加;2)随着面板厚度的增加,其稳定系数并没有明显的变化,其原因可能是随着面板厚度的增大,芯管对面板的约束逐渐减弱,对L形柱稳定极限承载力的贡献越来越小,从而使得构件整体的稳定系数没有明显提高。
5 研究芯管参数变化对稳定系数的影响
5.1 芯管间距对稳定性的影响
以4 mm板厚的构件(试件5~8)为研究对象,当芯管厚度和板厚不变的情况下,分析芯管间距对L形柱稳定极限承载力的影响,分析结果如表4和图7所示。
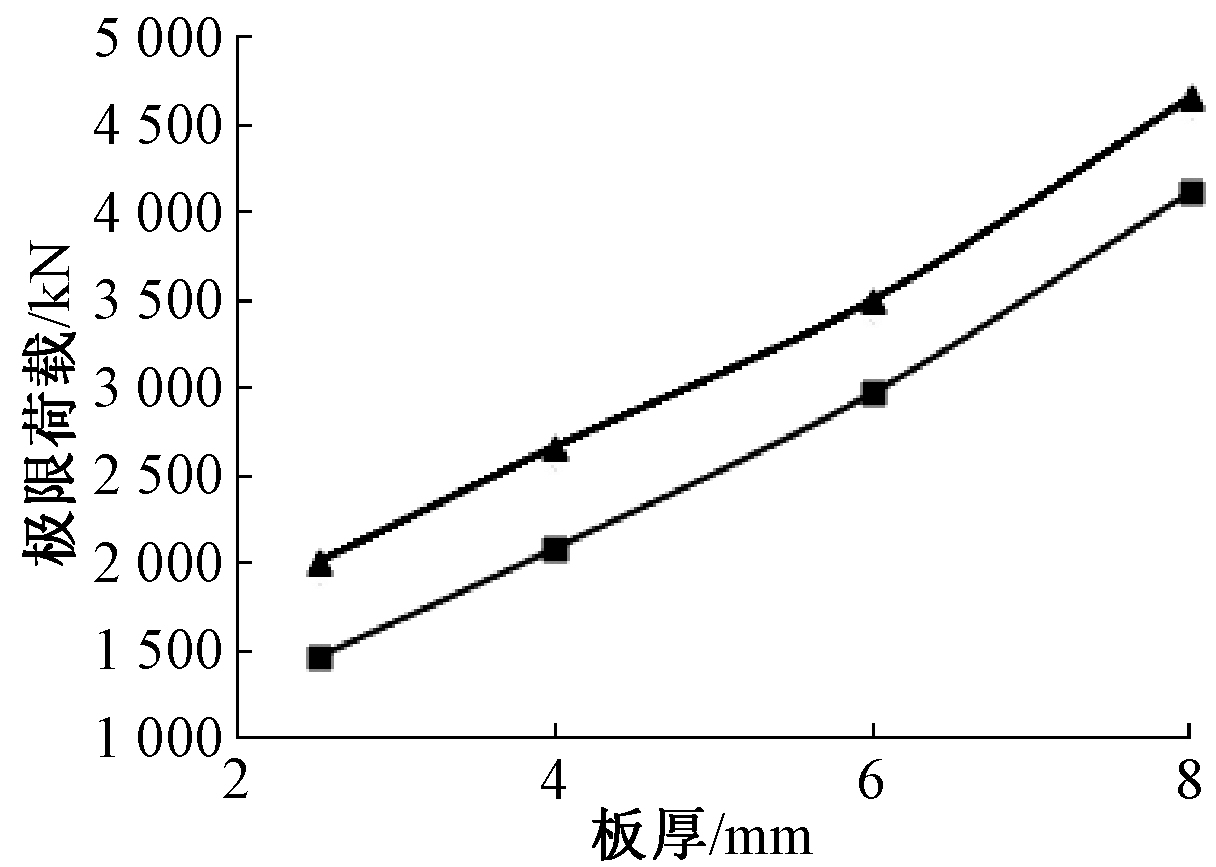
![]() — 160 mm×60 mm;
— 160 mm×60 mm; ![]() — 160 mm×120 mm。
— 160 mm×120 mm。
图7 不同芯管间距下的稳定极限荷载曲线(试件5~8)
Fig.7 The stable ultimate load curves for the panel with different spacings of core tube (specimen 5 to 8)
由表4和图7可以看出:试件的极限承载力在一定范围内随着芯管间距的减小而增大,其稳定系数也是随着芯管间距的减小而增大。
5.2 芯管厚度对稳定极限承载力的影响
以4 mm厚构件(试件9~14)为研究对象,分析当面板厚度一定的情况下,芯管厚度对L形柱稳定承载力的影响,相关数据如表4所示。
由图8~9可见:当面板厚度一定时,随着芯管厚度变大,芯管对面板的约束逐渐增强,L形柱的稳定极限荷载逐渐变大,同时其换算长细比逐渐减小,稳定系数逐渐变大。
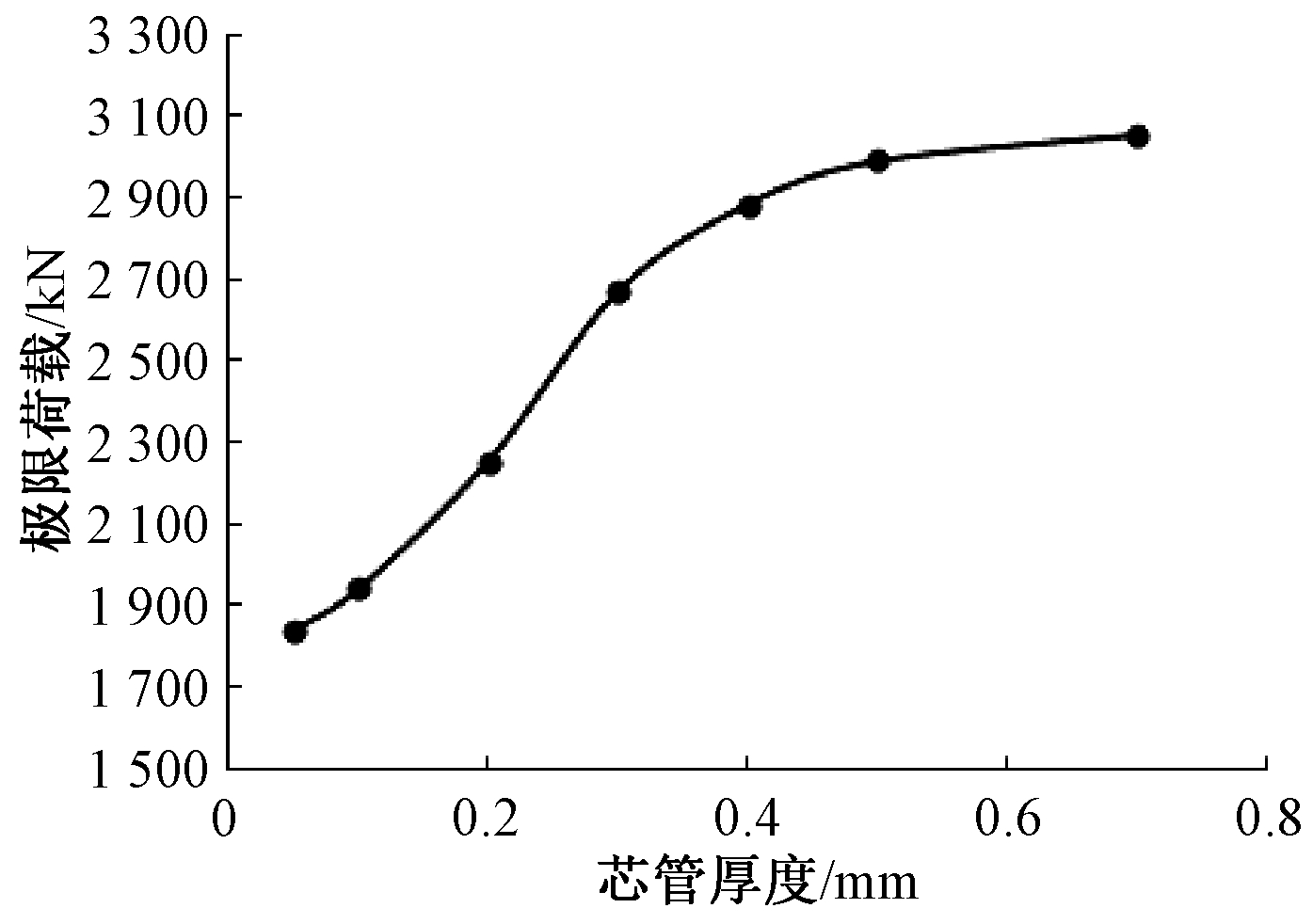
图8 不同芯管厚度下稳定极限荷载曲线(试件9~14)
Fig.8 The stable ultimate load curve for the core tube with different wall thicknesses(specimen 9 to 14)

图9 不同芯管厚度下的φ-λ曲线(试件9~14)
Fig.9 The φ-λ curve of the core tubes with different wall thicknesses (specimen 9 to 14)
6 结束语
在考虑了材料非线性、几何非线性和初始几何缺陷的基础上,利用ABAQUS有限元软件对实际无对称轴截面不锈钢夹层结构L形柱轴心受压构件的稳定承载力进行了分析,得到以下结论:
1)不锈钢芯板结构L形柱破坏形态主要是局部屈曲破坏。短柱试件的工作阶段可分为弹性、弹塑性和破坏三个阶段,并表现出一定的弹塑性性能。
2)试件的稳定极限承载力随着芯管间距减小而增大,达极限荷载后,稳定极限承载力随纵向位移的增加而降低,间距越小,下降越平缓,试件延性越好;试件的稳定极限承载力随着芯管厚度增大而增大,达极限荷载后,稳定极限承载力随纵向位移增大呈减小趋势,芯管厚度越大,下降越平缓,延性越好。
3)由于芯管的存在,芯管承担部分荷载,芯管和钢板两者相互作用,改善了结构的力学性能,有效延缓了钢板局部屈曲的发生。
4)构件的稳定系数随着换算长细比的增大而减小。
[1]杨滇平.异形柱的研究进展现状[J].山西科技,2011(4):98-99.
[2]刘杰, 郝巍, 孟江燕. 蜂窝夹层结构复合材料应用研究进展[J]. 宇航材料工艺, 2013, 43(3):25-29.
[3]段文峰, 邓泽鹏, 刘文渊,等. 不锈钢S30408材料本构模型试验研究[J]. 钢结构, 2016, 31(5):37-40.
[4]屠永清, 杨明, 刘林林. 基于有限元法的L形轴压钢柱屈曲分析[J]. 钢结构, 2009, 24(6):40-43.
[5]陈骥. 钢结构稳定理论与设计[M]. 北京:科学出版社, 2014.
[6]王明贵, 王晓瑜, 陈章华. 钢异形柱轴心受压承载力实用计算研究[J]. 钢结构, 2007, 22(6):44-47.
[7]中国建设工程标准化协会.不锈钢结构技术规程:CECS 410∶2015[S].北京:中国计划出版社,2015.