不锈钢因具有优良的耐腐蚀、耐高温以及耐磨性能等优点,在土木工程等领域中得到了广泛的应用[1-2]。蜂窝夹层板有强度高,刚度大,减振性好以及隔声、隔热性能好等传统结构板不具备的众多优点,具有很大的工程潜力[3-4]。不锈钢芯板是将性能优越的蜂窝夹层板结构与不锈钢材料有机结合形成的一种新型的夹层板,是由不锈钢面板与不锈钢薄壁芯管采用铜钎焊连接组成,空隙处填充岩棉隔热、隔声。
抗弯性能是夹层板的主要性能指标,弯曲强度和剪切强度是夹层板的两个重要参数,是选用和设计夹层板的重要依据。目前,国内外学者对蜂窝夹层板的抗弯性能研究较多[5-12]:Abbadi等通过试验得到了等效密度以及芯子的取向对结构弯曲性能的影响[5];Ogasawara等采用有限元法对蜂窝夹层板进行结构分析,发现板的刚度由蜂孔尺寸和孔壁厚度等参数决定[6];彭明军等研究了钎焊蜂窝铝板三点弯曲的力学行为,发现蜂窝芯厚度与面板厚度之比在10%~15%时蜂窝板弯曲最为合理[7-8];周丽英等采用有限元软件对蜂窝夹芯板进行三点弯曲仿真模拟,解决了仿真中网格划分的关键问题,得到抗弯刚度随着壁厚增大而增大的结论[9]。但关于不锈钢芯板在建筑结构中的研究还处于起步阶段,国内外尚鲜有研究,仍有大量的工作需要进行。因此,本文采用ABAQUS有限元软件对不锈钢芯板三点弯曲力学行为和破坏模式进行模拟,探究不锈钢芯板的弯曲强度与面板厚度、芯管壁厚及芯管直径之间的关系。
1 弯曲性能研究方法的确定
弯曲加载是构件最为常见的外力加载形式,而三点弯曲法则是评判构件受弯强度、受弯刚度最常见的方法[13]。因此,采用三点弯曲法对不锈钢芯板弯曲性能进行分析,其加载示意如图1所示,支承方式为简支。
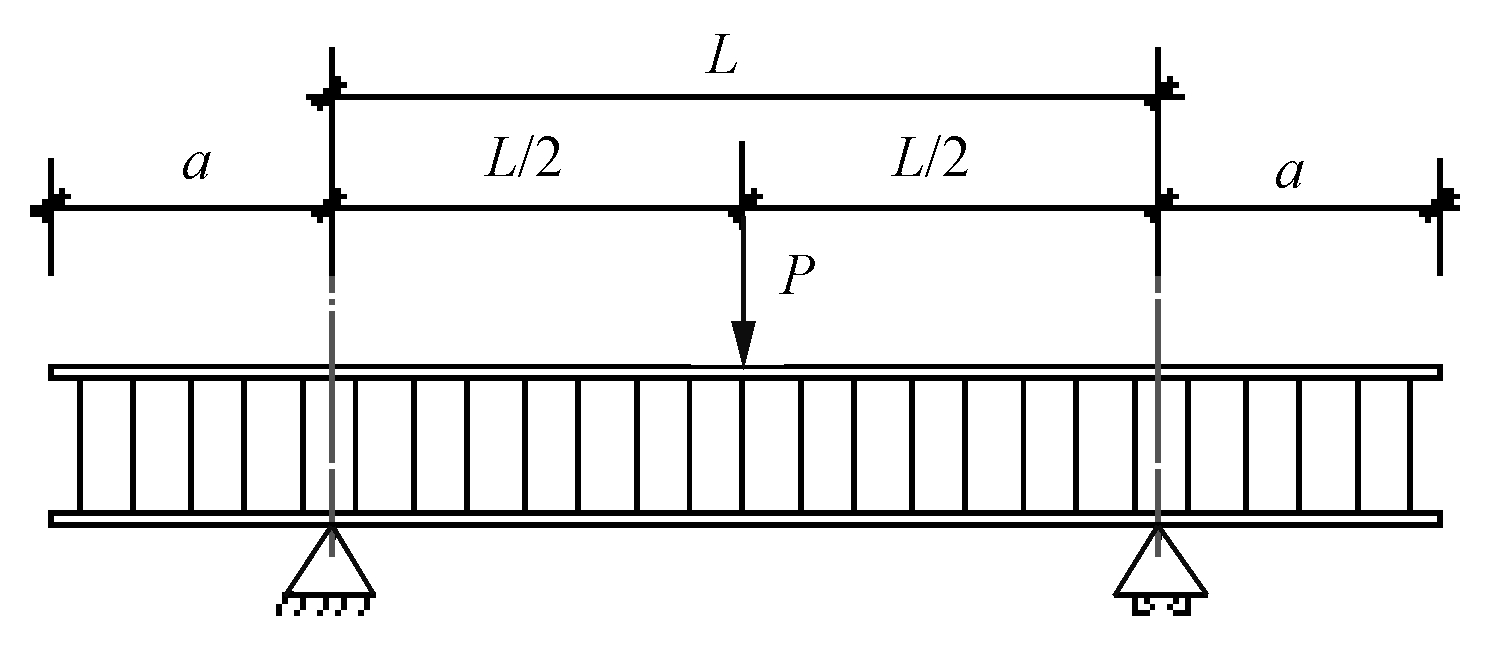
注:P为跨中集中荷载;L为跨度;a为外伸臂长度。
图1 三点弯曲法加载示意
Fig.1 Schematic diagram of three-point bending loading
依据GB/T 1456—2005《夹层结构弯曲性能试验方法》[14],并结合文献[15]介绍的刚度分离法进行有限元模拟,可以得到当a=L/3时,模型在跨中载荷P作用下的弯曲刚度Ui及剪切刚度DQ,i的计算式为:
(1a)
(1b)
其中 ws=wc-wb
式中:wb、ws、wc分别为对应P的外伸点挠度值、跨中剪切挠度值和总挠度值,mm。
根据GB/T 1456—2005,夹层板芯子剪切应力和面板应力分别为:
(2a)
(2b)
式中:τc为芯子剪切应力;tf为面板厚度;σf为面板应力。
当P为破坏载荷,不锈钢芯板发生芯子屈曲等破坏现象时,式(2a)的计算结果为剪切强度。当P为破坏载荷,不锈钢芯板发生面板拉断或压缩皱褶等破坏现象时,式(2b)的计算结果为弯曲强度。
2 有限元模型的建立
参照GB/T 1456—2005,有限元模型采用的基本尺寸见表1和图2所示。
表1 不锈钢芯板尺寸
Table 1 Demensions of the stainless steel panel

模型尺寸/mm(长×宽×高)面板厚度tf/mm芯管壁厚tc/mm芯管外径D/mm芯管间距/mm1 500×400×1501.50.183280×60

a—整体模型; b—加载区域; c—铰支座。
图2 有限元模型
Fig.2 Finite element model
材料参数:把同批次不锈钢材料和不锈钢芯管试件一起放入钎焊炉,经过升温和降温的过程,再将不锈钢板按GB/T 1456—2005规定的规格进行材性试验,将得到的结果取平均值列于表2,其中ν为泊松比,σ0.2和 σ1.0分别为残余应变为0.2%和1.0%时对应的应力,一般取0.2%为不锈钢材料的名义屈服强度,σu为极限抗拉强度,n为材料的应变硬化指数,E0为初始弹性模量,E0.2为残余应变为0.2%处应力-应变曲线的切线模量。
施加荷载:在有限元模拟中,为了实现模拟的真实性,采用位移加载方式,取加载宽度为60 mm,加载跨距为900 mm,支座距离板边300 mm。建模中为方便加载,在垫块上建立了参考点,将参考点与垫块上表面进行运动耦合后只需要在参考点上施加位移荷载,如图2b所示。
约束条件:支座边界条件为两端铰接。另外,下面板与钢垫块之间采用绑定约束,可以将两者永久地捆绑在一起,如图2c所示的支座处。模型不考虑不锈钢芯板铜钎焊残余应力和焊接差异对最终计算结果的影响,因为焊接工艺、残余应力和变形可以通过加工技术消除。
3 结果和分析
3.1 有限元模拟结果分析
选用了参数如表1的有限元模型进行数值模拟,为了有良好的单元形状和适当的网络密度,通过反复对比后统一将网格种子密度尺寸设置为4 mm,以保证模型在满足较高计算效率的情况下拥有较高的精度,网格单元类型为四结点曲面薄壳S4R。在ABAQUS后处理模块中,可得不锈钢芯板跨中加载面的荷载-位移曲线及曲线上的特征值,如图3。同时,通过有限元结果还计算出了芯板的弯曲刚度和剪切刚度值,如表3所示。
表2 不锈钢板材S30408的材料拉伸力学性能
Table 2 Tensile mechanical properties of stainless steel sheet S30408
νE0/MPaE0.2/MPaσ0.2/MPaσ1.0/MPaσu/MPan0.3193 94921 2013287037035.9
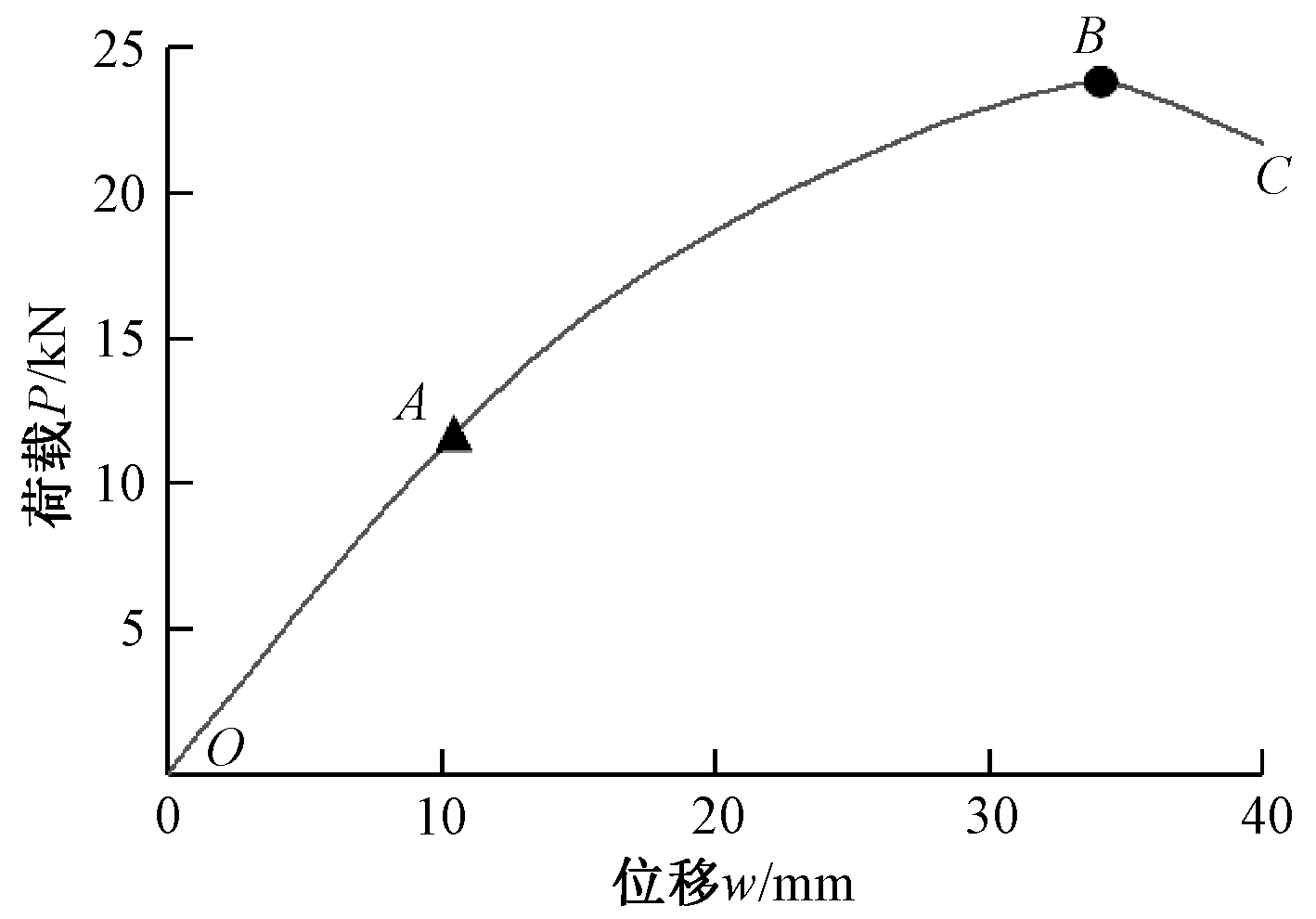
![]() 拐点;
拐点;![]() 极值点。
极值点。
图3 不锈钢芯板三点弯曲典型的荷载-位移曲线
Fig.3 Typical loading-displacement curve of stainless steel sandwich panel with core tube under three-point bending
表3 荷载-位移曲线的特征点
Table 3 Characteristic points of load-displacement curve
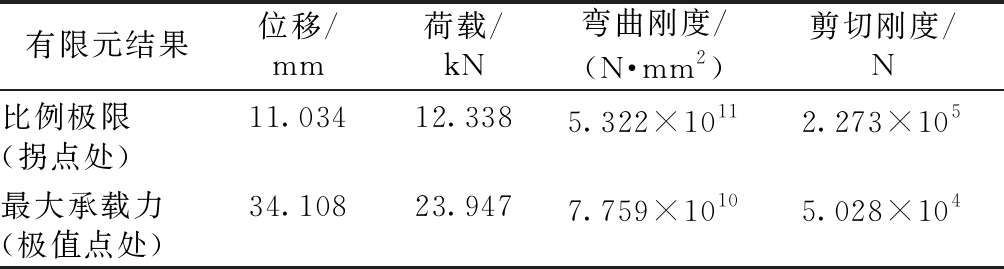
有限元结果位移/mm荷载/kN弯曲刚度/(N·mm2)剪切刚度/N比例极限(拐点处)11.03412.3385.322×10112.273×105最大承载力(极值点处)34.10823.9477.759×10105.028×104
3.2 不锈钢芯板受弯破坏机理研究
从ABAQUS后处理中导出受弯破坏的荷载-位移曲线(图3)可以看出不锈钢芯板从开始加载到最终破坏可分为三个阶段。
1)弹性阶段,即OA段。在这个阶段内,荷载-位移曲线为一条斜直线。荷载与位移基本保持线性关系,荷载迅速增加,直到曲线出现拐点。图4为曲线拐点A处的等效应力云图,可以看出芯管两端与面板连接处的应力较大,部分区域的应力已经超过了不锈钢的屈服强度;芯管其余大部分区域的应力都比较小,应力分布较为均匀。不难看出,荷载-位移曲线的拐点处实际上对应了芯管根部发生屈服时的状态。这一阶段芯管的变形很小,几乎保持加载前的形状。

图4 荷载-位移曲线拐点处模型的von Mises应力云 MPa
Fig.4 The von Mises stress contour of the model at the inflection point on the loading-displacement curve
2)弹塑性阶段,即AB段。弹性阶段结束后,荷载-位移曲线由线性变成非线性,荷载增加缓慢而位移增长较快,曲线的斜率越来越小,一直持续到极值点处。在此过程中,芯管的上、下根部均出现略微鼓曲的现象,且随着荷载的增大,鼓曲现象越来越明显。图5为极值点B处的等效应力云图,可以看出芯管根部与面板连接处的应力很大,已达到临界屈曲应力值,且芯管上、下根部发生了明显的鼓曲现象。

图5 荷载-位移曲线极值点处模型的von Mises应力云 MPa
Fig.5 The von Mises stress contour of the model at the ultimate point on the load-displacement curve
3)破坏阶段,即BC段。过极值点后,荷载-位移曲线出现下降段,表明不锈钢芯板承受的荷载不再增大,而变形仍然在继续增加,此时不锈钢芯板已丧失了承载能力。
3.3 不锈钢芯板三点弯曲失效模式研究
不锈钢芯板结构是一种典型的工字梁结构。当芯板在荷载作用下受弯挠曲时,上面板承受压应力,下面板承受拉应力,中间芯管主要承受剪切应力[16]。受中间芯管尺寸及面板厚度的影响,不锈钢芯板构成不同的失效模式。
选取tf=2.5 mm,芯管直径为32 mm,芯管壁厚tc为分别为0.25,0.30,0.35,0.40 mm的芯板作为代表,以其最终形变结果的云图来分析不锈钢芯板三点弯曲的失效模式,如图6所示。
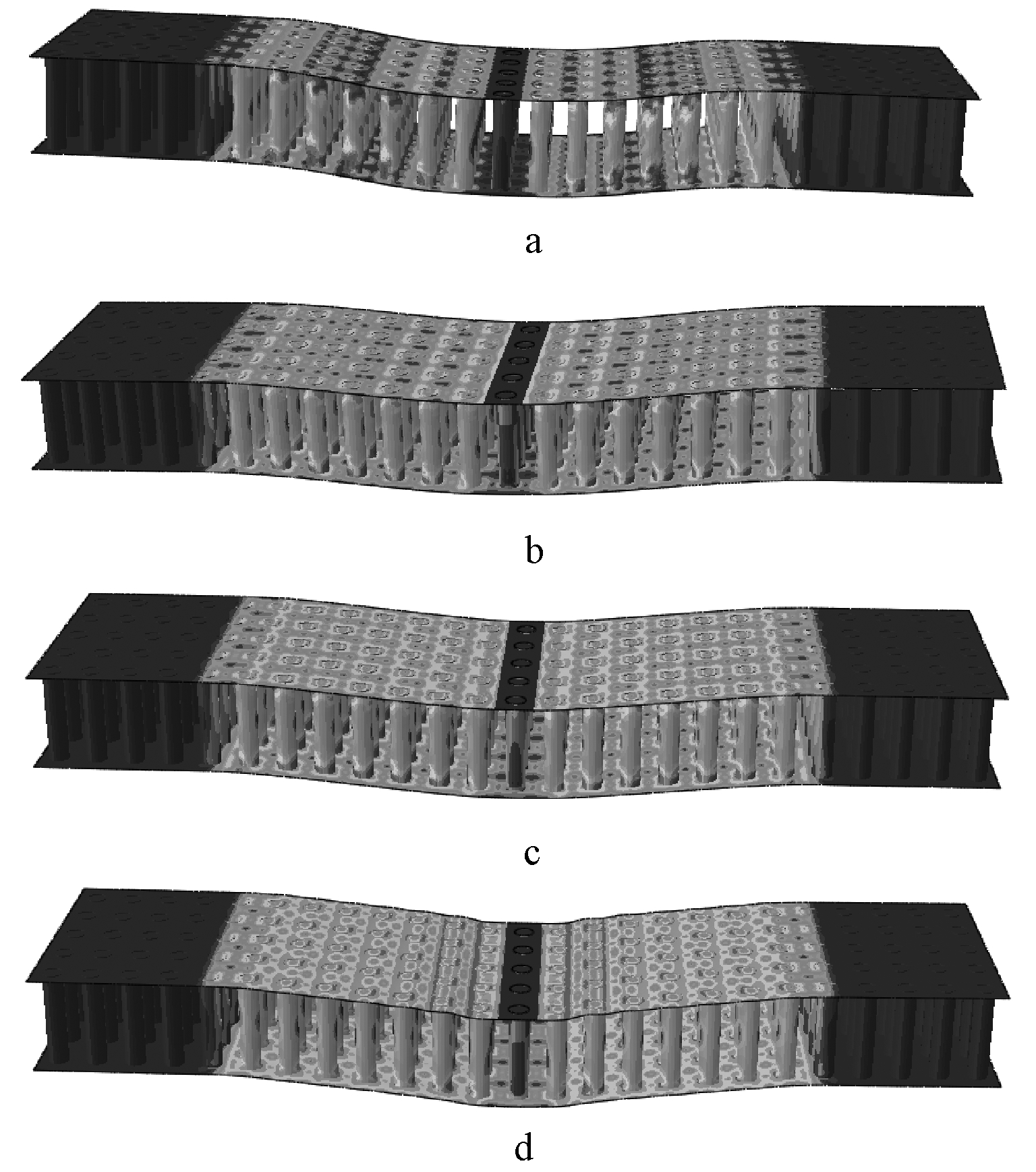
a—tc=0.25 mm; b—tc=0.30 mm; c—tc=0.35 mm; d—tc=0.40 mm。
图6 不锈钢芯板三点弯曲最终形变结果
Fig.6 Final deformation results contour of stainless steel sandwich panel with core tubes under the three-point bending
从图6观察到不锈钢芯板受弯时呈现出三种典型的失效模式:芯管端部局部剪切失效(图6a)、整体弯曲失效(图6b和图6c)和面板剪切失效(图6d)。
3.3.1 芯管端部局部剪切失效
加载处和固定支承之间的区域中芯管屈曲,且有明显的褶皱。当tf=2.5 mm,tc<0.25 mm时,芯管剪切强度相对面板抗弯强度较小,不锈钢芯板在承受外界跨中弯曲荷载时发生中间芯管两端局部剪切失效。
3.3.2 整体弯曲失效
中间芯管整体均匀出现剪切性皱褶。tf=2.5 mm,芯管壁厚tc介于0.30~0.35 mm时,芯管剪切强度与面板抗弯强度之间相互匹配,不锈钢芯板发生整体弯曲失效,芯管和面板均处于最佳状态。
3.3.3 面板剪切失效
不锈钢芯板中间加载处发生剪切失稳,加载区域两端出现最大应力。但在加载过程中,芯管未出现剪切性皱褶。当tf=2.5 mm,tc<0.40 mm时,面板抗弯强度不变,但芯管的剪切强度会越来越大,两者之间越来越不匹配,不锈钢芯板发生面板剪切失效。
可见,当芯管壁厚与面板厚度相匹配时,不锈钢芯板发生整体失效,此时,材料的受力均处于最佳状态,能充分发挥芯管剪切和面板抗拉或压的各自优点。
4 不锈钢芯板三点弯曲破坏荷载影响因素分析
当不锈钢芯板的板厚相同时,影响其力学性能的三大因素为:面板厚度、芯管壁厚、芯管直径。通过建立75个模型来分析这三大因素对不锈钢芯板三点弯曲破坏荷载的影响。
4.1 芯管直径对破坏荷载的影响
选取芯管直径分别为28,32,36 mm的不锈钢芯板进行三点弯曲仿真研究,以约束结点上的反作用力作为不锈钢芯板三点弯曲破坏荷载。图7为上、下面板厚度相同时,芯管直径与不锈钢芯板三点弯曲破坏荷载关系曲线。
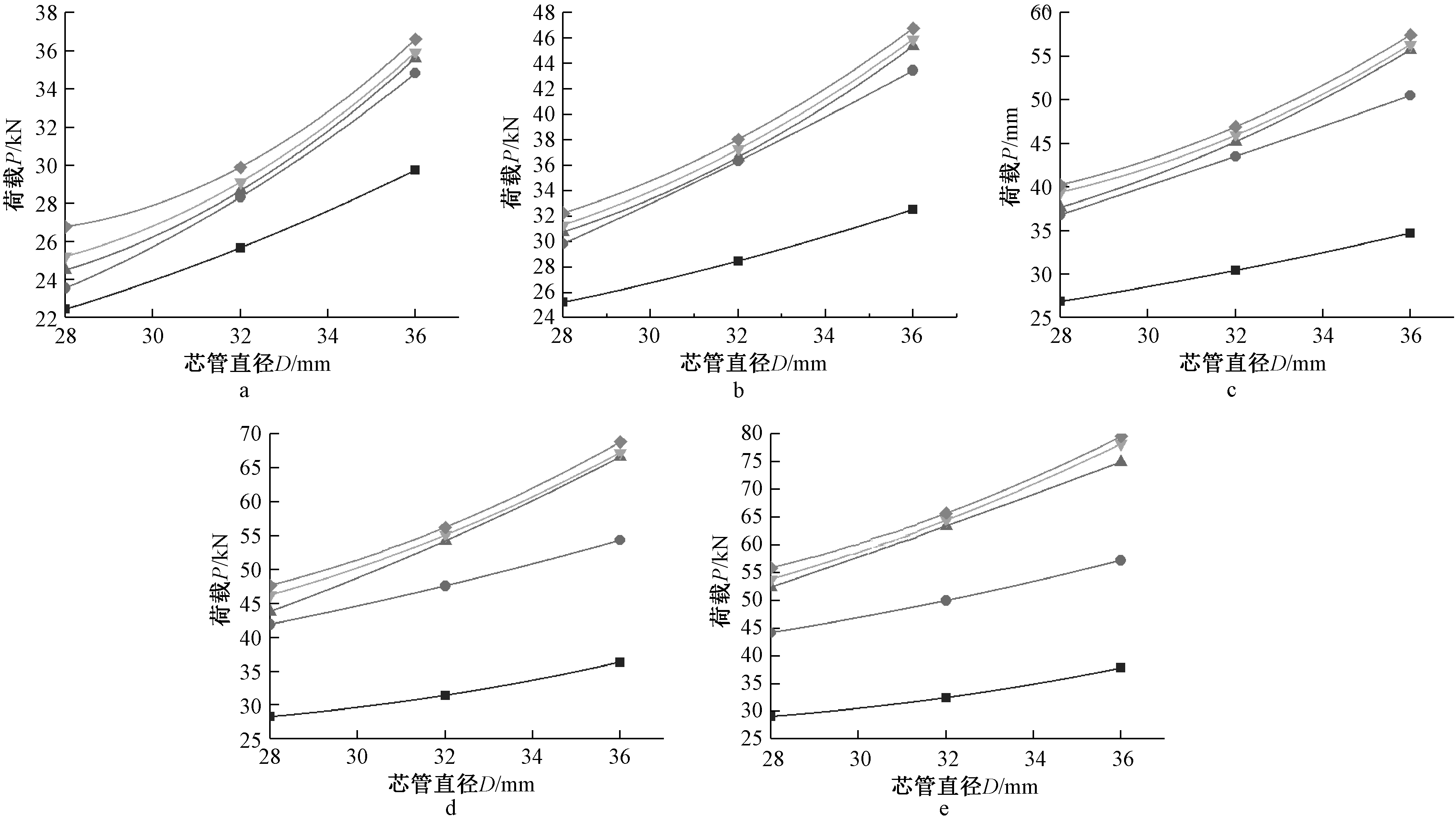
a—tc=0.20 mm; b—tc=0.25 mm; c—tc=0.30 mm; d—tc=0.35 mm; e—tc=0.40 mm。 ![]() — tf=1.5 mm;
— tf=1.5 mm; ![]() — tf=2.0 mm;
— tf=2.0 mm; ![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=3.0 mm;
— tf=3.0 mm; ![]() — tf=3.5 mm。
— tf=3.5 mm。
图7 芯管直径与三点弯曲破坏荷载的关系曲线
Fig.7 Relationship curves between core tube diameter and failure load under three-point bending
从图7中可知:不锈钢芯板的抗弯能力随着芯管直径的增大逐渐增强。在本文研究的范围内,芯板抗弯破坏荷载与芯管直径的关系以面板2.5 mm厚时为分界线。当tf>2.5 mm时,芯管直径对破坏荷载的影响较大;tf<2.5 mm时,芯管直径对破坏荷载的影响越来越小。从图7可以发现:当芯管剪切强度相对于面板抗弯强度来说较小时,不锈钢芯板发生芯管局部剪切失效。因此面板厚度较大的情况下,芯管直径的减小导致不锈钢芯板整体抗剪强度明显下降,芯管直径对破坏荷载的影响较为明显;当tf<2.5 mm时,上、下面板抗拉压强度降低,不锈钢芯板的弯曲性能主要靠上、下面板的强度来体现,故芯管直径对不锈钢芯板抗弯能力影响越来越小。
因此,当面板厚度较小时,芯管直径的增大对不锈钢芯板整体抗剪能力的影响较小;当面板较厚时,芯管直径的增大对不锈钢芯板的抗弯能力的影响明显增大。
4.2 芯管壁厚对破坏荷载的影响
选取芯管壁厚tc分别为0.20,0.25,0.30,0.35,0.40 mm的不锈钢芯板进行三点弯曲仿真研究。图8为面板厚度相同时,芯管壁厚对不锈钢芯板三点弯曲破坏荷载影响的关系曲线。
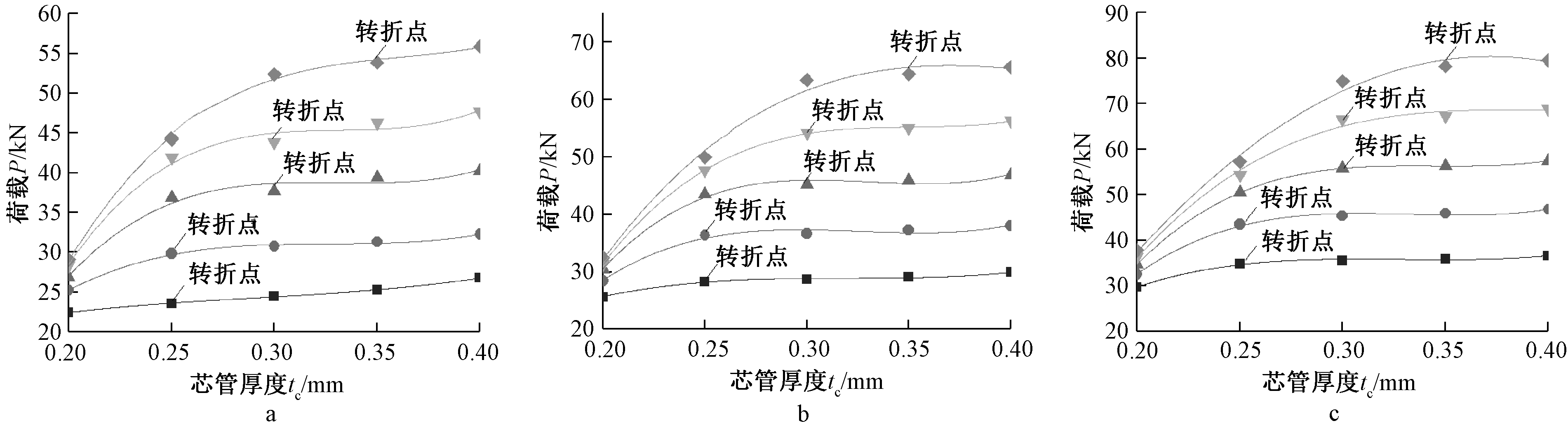
a—D=28 mm; b—D=32 mm; c—D=36 mm。 ![]() — tf=1.5 mm;
— tf=1.5 mm; ![]() — tf=2.0 mm;
— tf=2.0 mm; ![]() — tf=2.5 mm;
— tf=2.5 mm; ![]() — tf=3.0 mm;
— tf=3.0 mm; ![]() — tf=3.5 mm。
— tf=3.5 mm。
图8 芯管壁厚与三点弯曲破坏荷载的关系曲线
Fig.8 Relationship curve between core tube of wall thickness and failure load under three-point bending
由图8可知:tf<2.5 mm时,以tc=0.25 mm为转折点。其中,当tc<0.25 mm时,破坏荷载随着芯管壁厚的增加而快速增大,tc>0.25 mm时,破坏荷载增大的趋势有所减缓,此时芯管壁厚增加对板抗弯能力的提升作用不太明显。当2.5 mm<tf<3 mm时,以tc=0.3 mm为转折点。其中,当tc<0.3 mm时,破坏荷载随着芯管壁厚增加而快速增大,tc>0.3 mm时,破坏荷载随着芯管壁厚增加而增大的趋势有所减缓。同理,当tf>3 mm时,以tc=0.35 mm为转折点。
表4 拐点处芯管壁厚值
Table 4 Core tube wall thickness value at the inflection mm
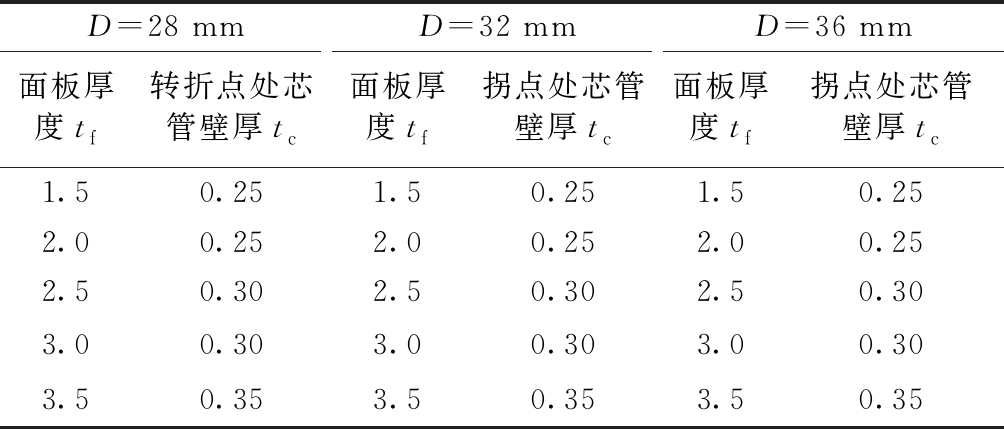
D=28 mmD=32 mmD=36 mm面板厚度tf转折点处芯管壁厚tc面板厚度tf拐点处芯管壁厚tc面板厚度tf拐点处芯管壁厚tc1.50.251.50.251.50.252.00.252.00.252.00.252.50.302.50.302.50.303.00.303.00.303.00.303.50.353.50.353.50.35
可见,当上、下面板厚度不变的情况下,增加芯管壁厚能使破坏荷载有所增大,但不会一直增加。芯管壁厚对整体影响的转折点会随着面板厚度的增加而逐渐外移。
4.3 面板厚度对不锈钢芯板纵向三点弯曲破坏荷载的影响
选取面板厚度tf分别为1.5,2.0,2.5,3.0,3.5 mm的不锈钢芯板进行三点弯曲仿真研究。以约束结点上的反作用力作为不锈钢芯板三点弯曲仿真破坏荷载。图9为面板厚度与不锈钢芯板三点弯曲破坏荷载的关系曲线。从图9中可以看出:当芯管直径与芯管壁厚相同时,破坏荷载均随着面板厚度的增加而增大。
当芯管壁厚较小时(tc<0.3 mm),三点弯曲破坏荷载与面板厚度呈正比,但相比芯管壁厚较大时(tc>0.3 mm)的增长速度较弱,由此说明当芯管壁厚较小时,不锈钢芯板整体抗剪能力与面板抗弯之间不匹配。此时,芯管抗剪能力较弱,面板厚度的增加使整体抗弯能力增长有限。当芯管壁厚较大时,整体破坏荷载随着面板厚度的增加而呈线性增加。说明芯管壁厚较大时,不锈钢芯板整体抗剪刚度提升较为明显,芯管能更好地支撑隔离面板,使整体获得较好的抗弯性能。

a—D=28 mm; b—D=32 mm; c—D=36 mm。 ![]() — tc=0.20 mm;
— tc=0.20 mm; ![]() — tc=0.25 mm;
— tc=0.25 mm; ![]() — tc=0.30 mm;
— tc=0.30 mm; ![]() — tc=0.35 mm;
— tc=0.35 mm; ![]() — tc=0.40 mm。
— tc=0.40 mm。
图9 面板厚度与三点弯曲破坏荷载的关系曲线
Fig.9 Relationship curves between panel thickness and failure load under three-point bending
5 结束语
1)不锈钢芯板三点弯曲的荷载-位移曲线可分为弹性阶段、弹塑性阶段和破坏阶段。
2)变形云图显示:构件在三点弯曲时,在荷载作用下,依照面板抗拉压强度和芯管抗剪切刚度的协调性,不锈钢芯板呈现三种典型的失效模式——芯管局部剪切失效、整体弯曲失效和面板剪切失效。
3)当芯管壁厚与面板厚度相匹配时,不锈钢芯板发生整体失效。在此失效模式下,材料的受力状态均处于最佳状态,能充分发挥出面板抗拉压和芯管剪切各自的优点。在实际应用中,要合理选择不锈钢芯管的壁厚和面板的厚度,实现结构性能的最优化。
4)面板厚度、芯管壁厚、芯管直径的增大均使不锈钢芯板在三点弯曲时的破坏荷载有不同程度的增大。合理调节不锈钢芯板的截面参数能得到良好的抗弯性能。
[1]王元清, 袁焕鑫, 石永久, 等. 不锈钢结构的应用和研究现状[J]. 钢结构, 2010, 25(2):1-12.
[2]朱浩川, 姚谏. 不锈钢材料的应力-应变模型[J]. 空间结构, 2011, 17(1):62-69.
[3]张铁亮, 丁运亮, 金海波. 蜂窝夹层板结构等效模型比较分析[J]. 应用力学学报, 2011, 28(3):275-282.
[4]郝景新. 蜂窝夹层木质复合材横向承载力学特性研究[D]. 长沙:中南林业科技大学, 2017.
[5]ABBADI A, KOUTSAW Y, CARMASOL A, et al. Experimental and Numerical Characterization of Honeycomb Sandwich Composite Panels[J]. Simulation Modelling Practice & Theory, 2009, 17(10):1533-1547.
[6]OGASAWARA N, SHIRATORI M, YU Q, et al. Elastic-Plastic Analysis of Honeycomb Sandwich Panel by Using Honeycomb Element[J]. JSME International Journal, 2008, 42(3):381-387.
[7]彭明军. 钎焊蜂窝铝板力学性能研究[D]. 昆明:昆明理工大学, 2013.
[8]PENG M J, SUN Y, YAO J, et al. Finite Element Simulation on Three-Point Bending of Brazed Aluminum Honeycomb Panel[J]. Advanced Materials Research, 2011(168/169/170):1046-1050.
[9]周丽英, 吴明春, 何和智. 正六边形蜂窝结构塑料板抗弯性能有限元分析[J]. 塑料, 2016(3):78-80.
[10]赵金森. 铝蜂窝夹层板的力学性能等效模型研究[D].南京: 南京航空航天大学, 2006.
[11]KOBAYASHI H, DAIMARUYA M, OKUTO K. Elasto-Plastic Bending Deformation of Welded Honeycomb Sandwich Panel[J]. Transactions of the Japan Society of Mechanical Engineers Part A, 1994, 60(572):1011-1016.
[12]李谏. 解读蜂窝板的弯曲刚度及弯曲面板强度[J]. 中国建材科技, 2010(5):58-62.
[13]孙小曼. 车用波纹夹芯板弯曲性能研究[D]. 大连:大连理工大学, 2013.
[14]中华人民共和国国家技术监督局. 夹层结构弯曲性能试验方法:GB/T 1456—2005[S]. 北京:中华人民共和国国家技术监督局,2005.
[15]李家驹, 曾汉民. 复合材料蜂窝夹层板刚度分离实验法研究与应用[J]. 中山大学学报, 1994(3):67-72.
[16]CARLSSON L A, KARDOMATEAS G A. Structural and Failure Mechanics of Sandwich Composites[M]. Springer, Borlin; Germany: 2011.