0 引 言
不锈钢芯板夹层结构是由远大可建科技有限公司研发、湖南大学参与研究的一种新型夹层结构,采用不锈钢材料薄板作为面板,按照一定间距排列的不锈钢材料薄壁圆管作为芯子,面板与薄壁芯管采用铜钎焊焊接,如图1所示。其结构形式类似于工字型钢材,面板对应型钢的翼缘,芯管对应型钢的腹板。相比于工字型钢,不锈钢芯板夹层结构的面板更宽、更薄、也更轻质,这些优点使得这种结构可以用作建筑结构中梁、柱、墙、板等承重及围护构件。当此种结构用作建筑结构中墙、柱时,主要承受沿面板方向的作用力。因此,作为新型的夹层结构,需要了解其侧压的力学性能。

图1 不锈钢芯板夹层结构
Fig.1 The stainless steel sandwich panel structure
国内外不少学者对夹层板的力学性能做过研究。王海忠对夹层板进行了弯曲试验研究,发现试验测得的弯曲变形和正应力与理论值吻合很好[1]。周祝林对碳纤维复合材料夹层结构的极限强度进行了理论计算,并对胶黏蜂窝板侧压试验的 6 种破坏形式进行了研究,建立了相应的纵向承载能力理论计算式[2-3]。计宏伟等通过试验研究了蜂窝纸板的侧压强度,分析了试验过程中的温度、湿度、加载速率等因素对蜂窝纸板侧压强度的影响[4]。彭明军等通过对钎焊蜂窝铝板的侧压试验,研究了侧压方向对承载能力和变形模式的影响[5]。夏明凯研究了蜂窝芯子脱焊尺寸等缺陷对蜂窝夹层结构整体侧压性能的影响[6]。Pokharel等通过一系列的试验测试及有限元分析研究了蜂窝夹层结构的局部屈曲行为[7]。Paik等对铝蜂窝夹层板进行了试验研究,分析了蜂窝芯的壁厚、高度对其侧压强度的影响[8]。
这些研究集中讨论了面板为铝或碳纤维板材、芯子为正六边形的蜂窝芯的情况,对本文这种新型不锈钢芯板夹层结构特点的研究较少。为此,通过对不锈钢芯板夹层结构试件进行侧压性能试验,分析各种因素对结构受力特点、破坏模式的影响,并对优化不锈钢芯板夹层结构的参数设计提出建议。
1 试验概况
1.1 试件设计和制作
共设计了6组不锈钢芯板试件,每组3件,共18件。试件高度均为480 mm,宽度为380,460 mm,面板厚度为1.5,4.0 mm。芯管直径均为32 mm,厚度为0.18,0.30 mm,芯管纵向间距为60,80 mm,芯管横向间距为60,80,160 mm。试件示意见图2,试件编号及基本信息见表1。
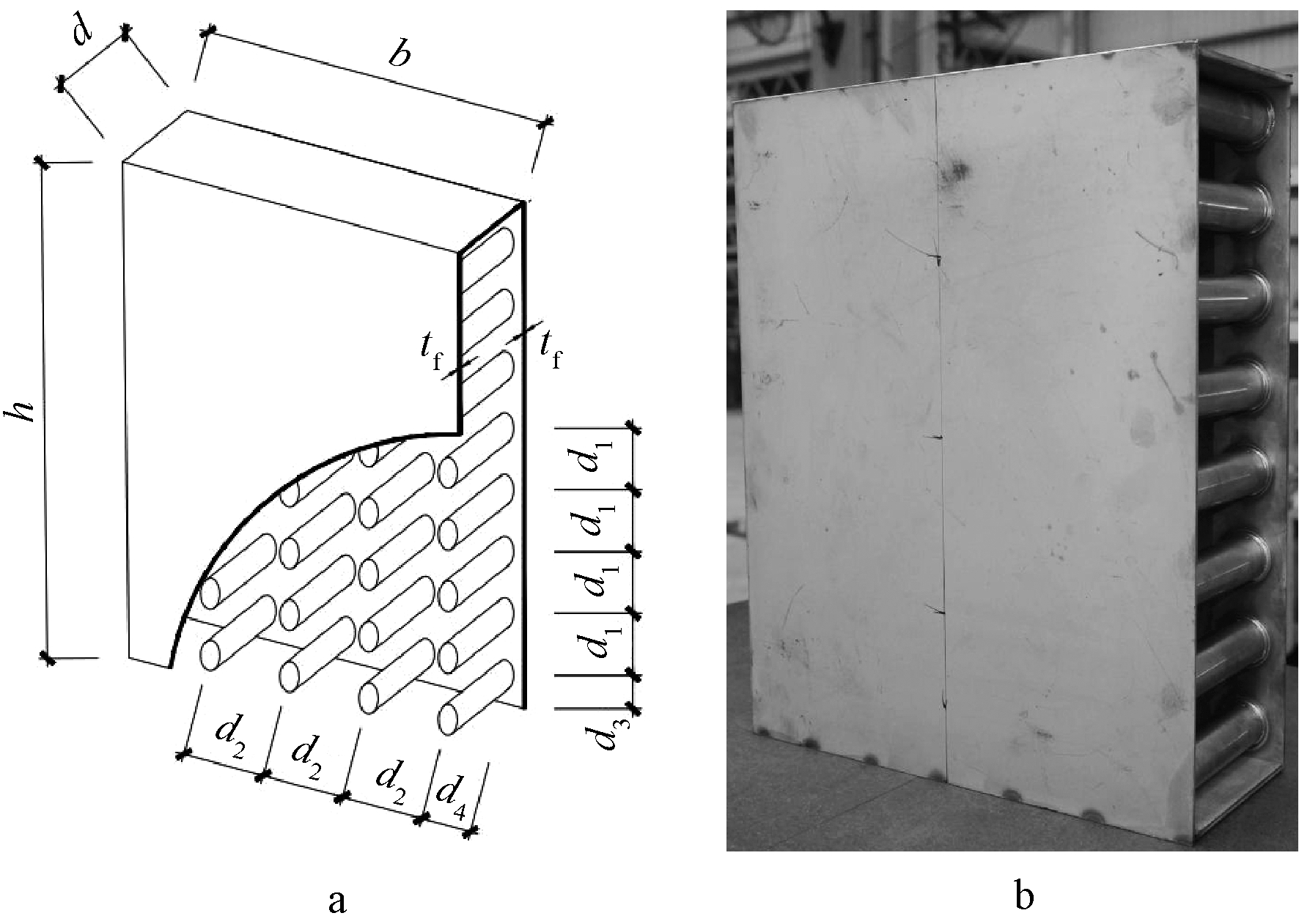
a—芯管间距; b—实物。
图2 试件示意
Fig.2 Schematic diagram of the specimen
表1 试件编号及基本尺寸
Table 1 The grouping and basic information of specimens

试件分组试件尺寸/mm(高×宽×厚)面板厚tf/mm芯管尺寸/mm(外径×壁厚)芯管间距/mm(d1×d2)芯管间距/mm纵向d3横向d4试件编号试件/个第一组480×380×1501.532×0.1860×803030CY01-1~CY01-33第二组480×380×1504.032×0.1860×803030CY02-1~CY02-33第三组480×380×1504.032×0.3060×803030CY03-1~CY03-33第四组480×460×1504.032×0.3060×803030CY04-1~CY04-33第五组480×380×1504.032×0.3080×808030CY05-1~CY05-33第六组480×380×1504.032×0.3060×1603030CY06-1~CY06-33
1.2 加载装置及加载制度
试验加载按GB/T 1454—2005《夹层结构侧压性能试验方法》[9]的规定进行。采用3 000 kN液压千斤顶在反力架上对试件加载,荷载传感器读取施加的荷载值,位移表读取试件侧压竖向位移值。为最大程度上保证试件试验过程中不产生侧向位移,在其顶部加侧向支撑,同时在传感器的底部加球铰以保证试验过程中轴心受压。加载装置见图3。
试验前利用有限元软件模拟试验过程,通过模拟得到荷载-位移曲线上的极值点确定试件预估极限荷载。试验采用单调分级加载,直至试件破坏。在施加的荷载小于预估极限荷载15%前,每级增加荷载大小为预估极限荷载的5%;在预估极限荷载的15%~80%时,每级增加荷载大小为预估极限荷载的10%;大于预估极限荷载的80%时,每级增加荷载大小为预估极限荷载的5%。
正式加载前,首先进行预加载,以检查仪器及加载设备的工作状态和试件的对中情况,消除加载设备与试件之间的缝隙对试验产生的不利影响。在每级荷载加载结束后等待3~5 min,待荷载传感器和位移表读数基本稳定后,读取试验数据。
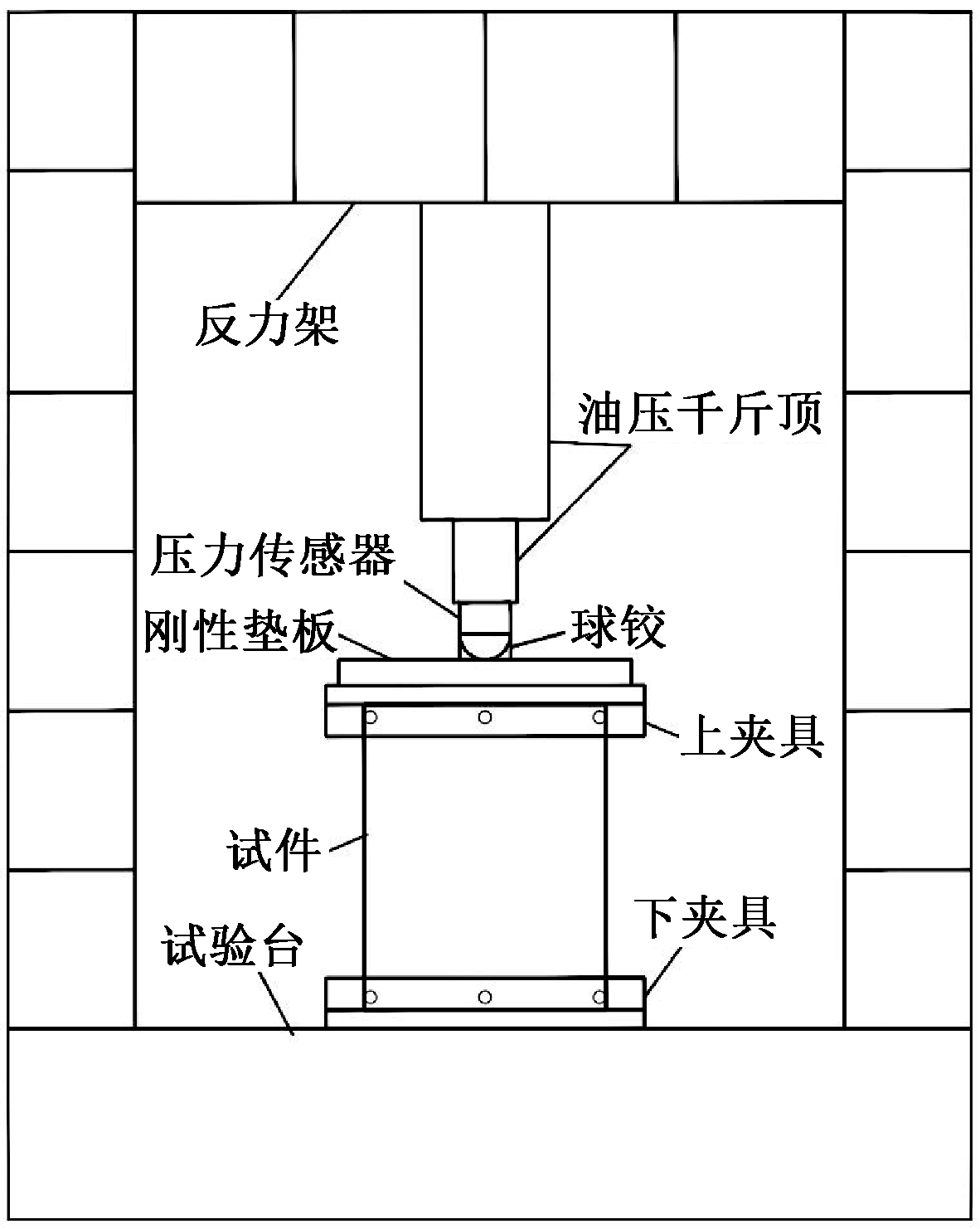
图3 试验加载装置示意
Fig.3 Loading device schematic diagram
1.3 测点布置
为测量试件在侧压过程中发生的竖向和横向的位移,在试件上、下端部和侧面布置位移计,测点布置如图4所示。
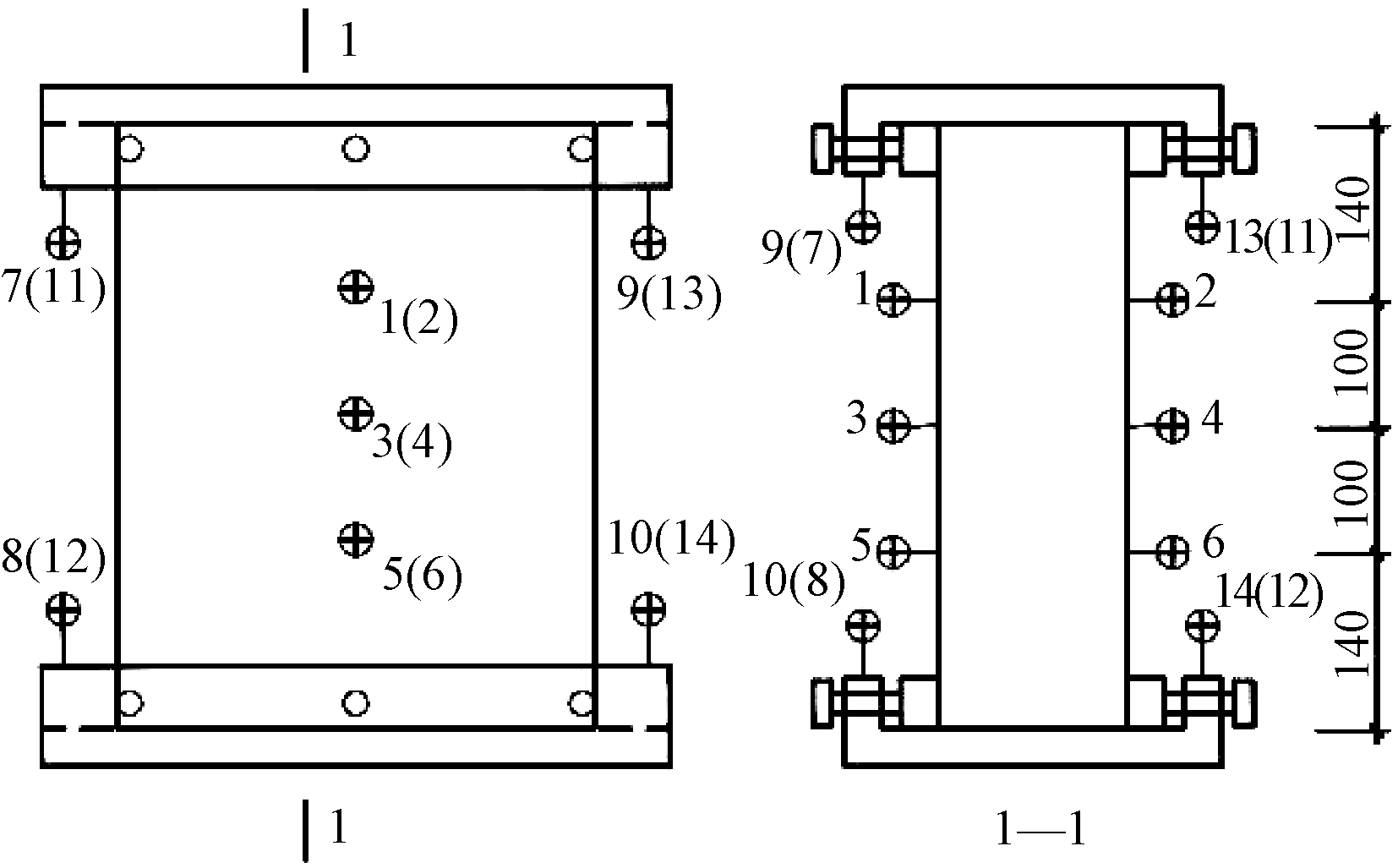
图4 位移计布置
Fig.4 Arrangement of displacement meter
2 试验结果
2.1 荷载-位移曲线
图5给出了试验得到各组试件的荷载-位移曲线。纵坐标为施加的竖向荷载,横坐标为试件在竖向荷载作用下产生的竖向位移,取4个角部测量结果的均值。
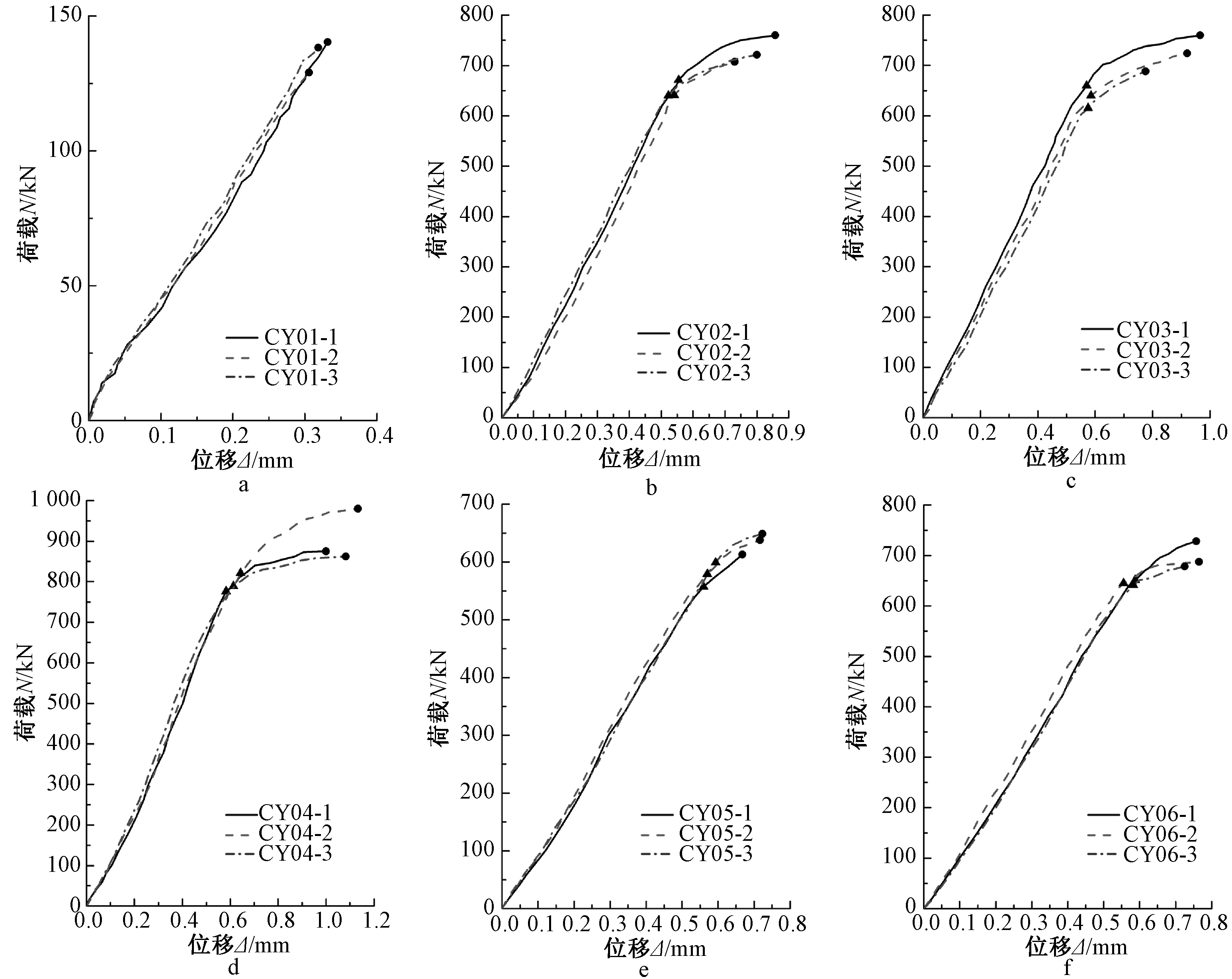
a—第一组; b—第二组; c—第三组; d—第四组; e—第五组; f—第六组。
注:![]() 为拐点;
为拐点;![]() 为极值点。
为极值点。
图5 荷载-位移曲线
Fig.5 Loading-displacement curves
由图5可以看出:第一组试件荷载-位移曲线上没有出现拐点,位移随着荷载增加始终呈线性增长。第二~六组试件的荷载-位移曲线上,拐点出现在极限荷载的85%附近。在拐点之前,位移随着荷载的增加呈线性增长;拐点之后,位移增加的幅度大于荷载增加的幅度,荷载-位移曲线的斜率逐渐减小。因此,可以把荷载-位移曲线上拐点之前的阶段,看作试件的弹性阶段;拐点之后的阶段,看作试件的弹塑性阶段。
2.2 试验现象及破坏形态
各组试件在破坏前,面板和芯管均无明显变形。第一组试件试验过程中,当施加的荷载小于极限荷载时,每级加载结束后位移计和荷载传感器读数能够保持稳定,无明显卸载;当施加的荷载达到极限荷载时,试件的竖向变形瞬间增大,试件破坏。面板局部范围出现皱折,芯管根部无明显变形,荷载传感器读数下降到试件极限荷载的20%附近。
第二~六组试件试验过程中,在施加的荷载小于极限荷载的85%时,每级加载结束后位移计和荷载传感器读数能够保持稳定,无明显卸载。大于极限荷载的85%但小于极限荷载时,每级加载结束后出现卸载现象,位移计和荷载传感器的读数缓慢减小并逐渐稳定。加载越接近试件的极限荷载,稳定读数需要的时间越长,变化的幅度越大。达到极限荷载时,第二、六组试件的竖向变形瞬间增大并伴随有较大的响声,试件破坏。面板整体弯曲成弧形,全部芯管根部明显皱曲,荷载传感器的读数下降到极限荷载的20%附近。第三~五组试件变形缓慢增大,面板局部出现弯曲,与面板弯曲部位相连的芯管根部皱曲明显,荷载传感器的读数下降并稳定在极限荷载的40%附近,试件破坏。
试件的破坏形态可以分为局部皱折破坏、整体屈曲破坏、局部屈曲破坏三类,分别对应着局部皱折失稳、整体屈曲失稳、局部屈曲失稳三种失稳模式。局部皱折破坏表现为面板局部发生皱折变形,芯管根部无明显变形,如图6a;整体屈曲破坏表现为面板整体发生弯曲变形,全部芯管根部皱曲明显,如图6b;局部屈曲破坏表现为面板局部发生弯曲变形,与面板弯曲部位相连的芯管根部皱曲明显,其他部位的芯管变形不明显,如图6c。图6d~6f为各组试件的破坏形态,表2为试件的主要试验结果和破坏特征,表中的面板拐点应力值、面板极限应力值由拐点荷载值、极值点荷载值分别除以试件的两块面板截面积所得。
由试验现象和表2可知:试件发生局部皱折失稳和整体屈曲失稳时,试件的变形瞬间增大,其极限位移相对于局部屈曲失稳时的极限位移明显偏小,呈现出明显的脆性特征,而发生局部屈曲失稳时则表现出一定的延性。

a—第一组; b—第二组; c—第三组; d—第四组; e—第五组; f—第六组。
图6 试件破坏形态
Fig.6 Failure modes of specimers
3 理论分析
试验现象和结果初步表明不同参数设计的试件失稳破坏形式不同。本部分对各种失稳破坏形式进行理论分析,研究试件失稳破坏形式、面板临界应力的影响因素。
3.1 局部皱折失稳分析
局部皱折失稳的破坏特征表现为试件局部和面板局部发生皱折,芯管根部均无明显变形,试件破坏是由面板局部皱折屈曲造成的。取两横排芯管间的面板进行分析,可以建立图7的分析模型,图中a为芯管的纵向间距,b为试件面板的宽度。因为芯管根部未见明显的变形,可以假设面板的上、下边界的约束为定向滑动支座,左、右边界为自由端,此分析问题可进一步简化为压杆的稳定分析问题。根据欧拉失稳临界荷载计算式可得试件局部皱折失稳时面板临界应力计算表达式为:
表2 试验结果和破坏特征
Table 2 Test results and failure characteristics
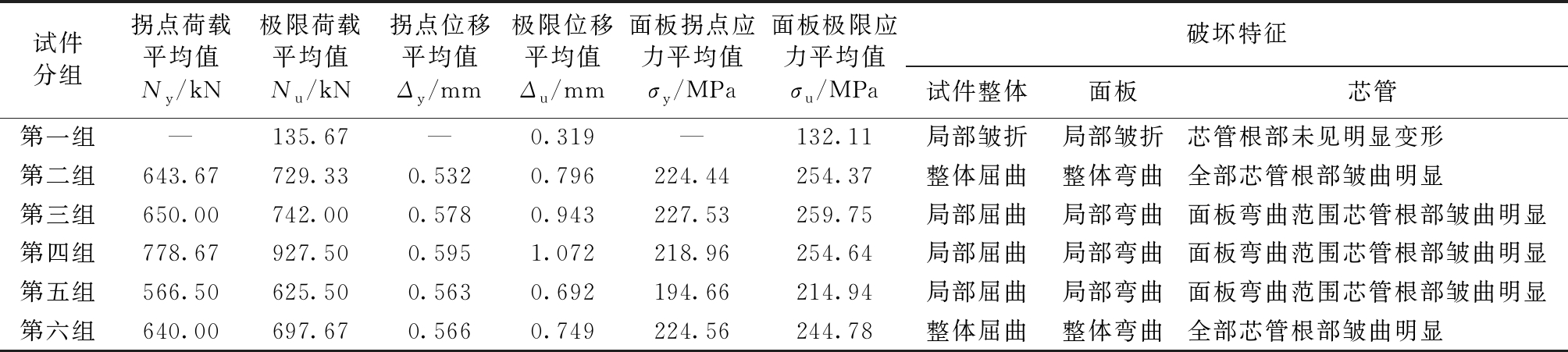
试件分组拐点荷载平均值N y/kN极限荷载平均值Nu/kN拐点位移平均值Δy/mm极限位移平均值Δu/mm面板拐点应力平均值σy/MPa面板极限应力平均值σu/MPa破坏特征试件整体面板芯管第一组—135.67—0.319—132.11局部皱折局部皱折芯管根部未见明显变形第二组643.67729.330.5320.796224.44254.37整体屈曲整体弯曲全部芯管根部皱曲明显第三组650.00742.000.5780.943227.53259.75局部屈曲局部弯曲面板弯曲范围芯管根部皱曲明显第四组778.67927.500.5951.072218.96254.64局部屈曲局部弯曲面板弯曲范围芯管根部皱曲明显第五组566.50625.500.5630.692194.66214.94局部屈曲局部弯曲面板弯曲范围芯管根部皱曲明显第六组640.00697.670.5660.749224.56244.78整体屈曲整体弯曲全部芯管根部皱曲明显
(1)
式中:σcr1为局部皱折失稳时面板临界应力;E为面板材料弹性模量;I为单块面板截面惯性矩;b为面板的宽度;tf试件面板的厚度;a为芯管的纵向间距;μ为长度因数。
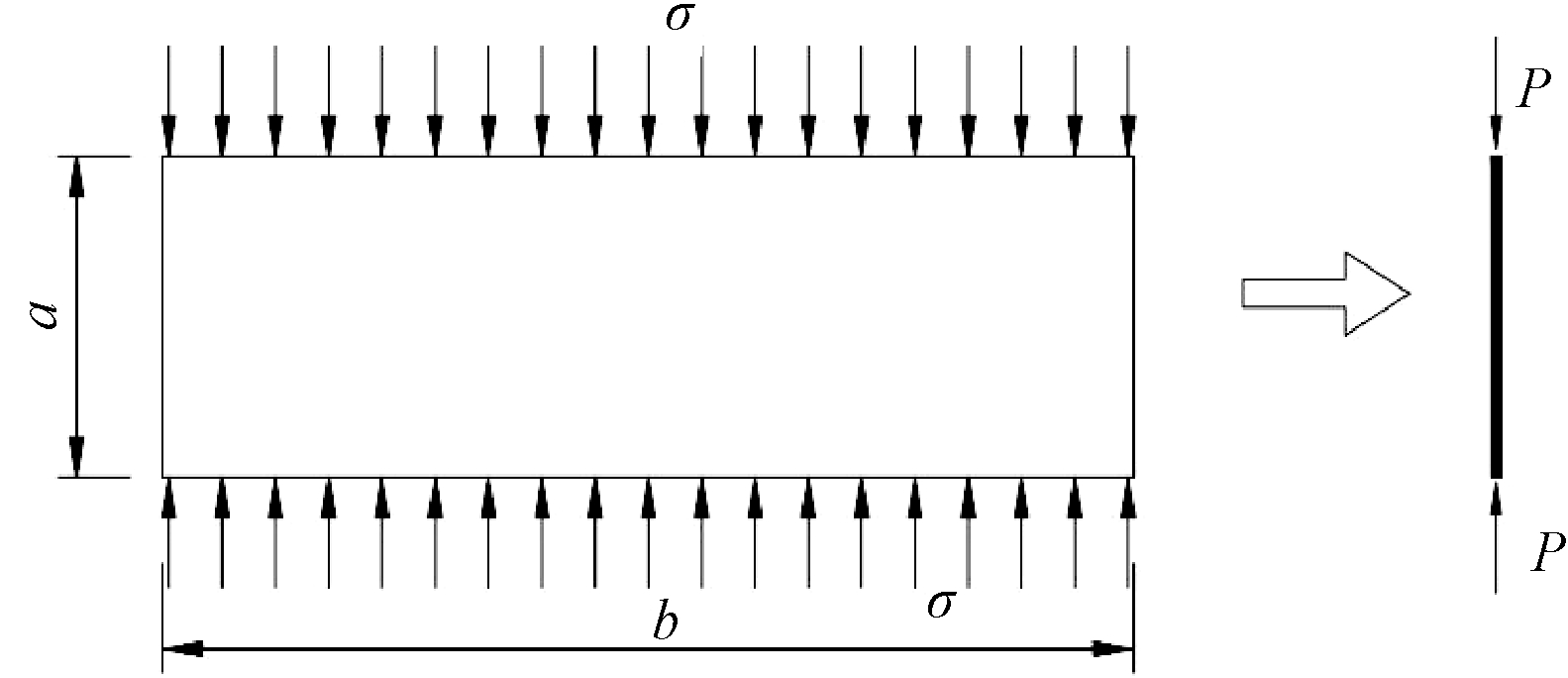
图7 面板受力示意
Fig.7 Diagram of schematic forced panel
由式(1)可以看出不锈钢夹层结构侧压抗局部皱折失稳能力与面板厚度、芯管纵向间距有关。增加面板的厚度tf、减小芯管的纵向间距a,可以提高其侧压时抗局部皱折失稳的能力。增加芯管的厚度、减小芯管的横向间距,对提高不锈钢芯板结构侧压时抗局部皱折失稳的能力作用不明显。
3.2 整体屈曲失稳分析
整体屈曲失稳的破坏特征表现为结构和面板整体发生弯曲变形,所有芯管根部皱曲明显,试件的破坏与整体抗弯能力以及芯管抗剪能力有关。文献[2]介绍了对碳纤维复合材料蜂窝夹层柱的整体稳定性研究,认为夹层柱的弯曲变形包含两个方面:一是普通柱的弯曲变形;二是由芯层剪切变形产生的附加弯曲变形。通过建立受力平衡微分方程,计算得到夹层结构整体稳定的临界荷载式[2]:
(2)
其中 ![]()
Fc=b(h-tf)
式中:Pcr为整体屈曲的临界荷载;P∂为普通柱的欧拉失稳临界荷载;FcGc为芯子的剪切刚度;Gc为芯子的剪切模量;E为面板材料的弹性模量;I为试件横截面惯性矩;b为试件的宽度;h为试件的厚度;tf为面板的厚度。
由式(2)可以看出:当芯子剪切模量Gc很大时,夹层结构整体的临界荷载接近欧拉临界荷载;当Gc很小时,接近于FcGc。由于本文研究的不锈钢芯板夹层结构试件高度较小、厚度较大,计算欧拉失稳临界荷载P∂远大于FcGc,因此不锈钢芯板夹层结构侧压整体屈曲的临界荷载近似等于FcGc。式(3)为结构整体屈曲失稳时面板临界应力σcr2计算式:
(3)
由式(3)可以看出不锈钢芯板夹层结构侧压抗整体屈曲失稳能力与芯层的剪切模量、芯板厚度及面板厚度有关。在不改变不锈钢芯板结构整体尺寸的情况下,通过提高芯层的材料剪切模量可以提高其侧压整体失稳极限承载力。但增加面板的厚度,会降低整体屈曲失稳时面板临界应力,不利于充分发挥材料的性能。
3.3 局部屈曲失稳分析
局部屈曲失稳的破坏特征表现为结构和面板局部发生弯曲变形,与面板弯曲部位相连芯管根部皱曲明显,其他部位的芯管无明显变形。试件破坏是由面板局部弯曲造成的,此种失稳模式属于面板的皱曲失稳的问题。文献[3]中对面板皱曲型失稳的蜂窝夹层板的极限强度进行理论研究,认为失稳的半波长很短,与芯子的高度同量级,可以把板当作支承在弹性基础上的杆(或板),芯子当作弹性基础,建立如图8所示的分析模型,图中l为面板失稳半波长,tf为面板的厚度。建立受力平衡微分方程,计算得到夹层结构局部失稳时面板临界半波长和临界应力计算表达式[3]:
(4a)
(4b)
式中:σcr3为局部屈曲失稳时面板临界应力;Ef为面板材料的弹性模量;tf为试件面板的厚度;Ec为芯层的平压模量;hc为芯层的高度;lcr为局部屈曲时面板临界半波长。
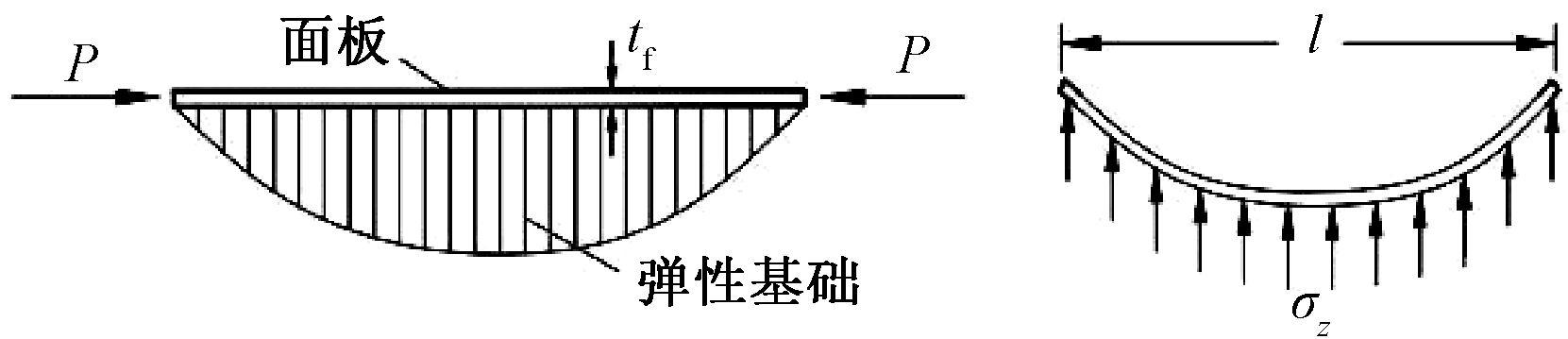
图8 局部屈曲破坏时面板受力示意
Fig.8 The forced state of the panel in local buckling
由式(4)可以看出:不锈钢芯板夹层结构侧压抗局部屈曲失稳能力与芯层的平压模量、面板厚度,以及芯层高度有关,在不改变结构整体尺寸的情况下,可以通过提高芯层的平压模量、面板的厚度以提高其侧压时抗局部屈曲失稳的能力。同时,提高芯层的平压模量,会减小结构局部屈曲的临界半波长;增加面板的厚度,会增大结构局部屈曲失稳时面板临界半波长[3]。
4 不锈钢芯板夹层结构侧压性能的影响因素
4.1 面板厚度的影响
由表2可知:第一、二组试件面板厚度分别为1.5,4.0 mm,试验得到面板极限应力平均值分别为132.11,254.37 MPa,试件破坏形态分别为局部皱折破坏和整体屈曲破坏。说明在试件面板很薄时,通过增加试件面板的厚度,可以提高试件失稳时的面板临界应力,改变试件的破坏形态。
第三~五组面板厚度为4.0 mm,试件的破坏形态均为局部皱曲破坏。结合理论分析结果可以说明:当面板厚度适中、芯层剪切强度较高时,试件发生局部屈曲破坏;继续提高面板的厚度,会增大面板局部屈曲时的临界半波长,结构的破坏形态可能由局部屈曲转变为整体屈曲。
4.2 芯管厚度的影响
由表2可知:第二、三组试件芯管厚度分别为0.18,0.30 mm,试验得到面板极限应力平均值分别为254.37,259.75 MPa,试件破坏形态分别为局部皱折破坏和整体屈曲破坏。结合理论分析的结果表明:增加芯管的厚度,可以增大芯层材料的剪切模量,结构的破坏形态会由整体屈曲转变为局部屈曲,面板的临界应力也会提高。但试验得到的极限面板应力平均值相差不大,这主要是由于试件破坏时,面板进入了弹塑性变形阶段,较小的荷载增量引起结构较大的竖向变形,进而导致结构破坏。
增加芯管的厚度也会提高芯层的平压模量,根据局部屈曲失稳分析结果,可以提高试件失稳时面板的临界应力,减小面板屈曲的临界半波长。
4.3 芯管间距的影响
芯管间距对不锈钢芯板夹层结构侧压性能的影响可分为两个方面讨论:纵向间距的影响和横向间距的影响。由表2可知:第三、五组试件芯管的纵向间距分别为60,80 mm,试验得到面板极限应力平均值分别为259.75,214.94 MPa,试件破坏形态均为局部屈曲破坏。结合理论分析结果可以说明,结构发生局部屈曲破坏时,增大纵向芯管的间距,会降低芯层的平压模量,从而减小试件失稳时的面板临界应力,增大面板局部屈曲的半波长。当结构发生局部皱折破坏时,减小芯管的纵向间距,可以提高面板的临界应力,结构的破坏形态也可能由局部皱折破坏,转变为局部皱曲破坏。
由表2可知:第三、六组试件芯管的横向间距分别为80,160 mm,试验得到的极限面板应力平均值分别为259.75,244.78 MPa,试件破坏形态分别为局部皱曲破坏和整体屈曲破坏。结合理论分析的结果可以说明:当结构发生局部屈曲破坏时,增加芯管的纵向间距,会减小芯层的平压模量,降低面板的临界应力。同时,面板局部屈曲的半波长也会增大,试件破坏形态可能由局部屈曲转变为整体屈曲。
4.4 不锈钢芯板夹层结构设计参数优化建议
从试验和理论分析的结果可以得知:不同设计参数的不锈钢芯板夹层结构试件,具有不同的失稳模式。试件发生局部皱折失稳、整体屈曲失稳时都表现出明显的脆性,其中局部皱折失稳时,试件仍处于弹性阶段,没有充分发挥材料的力学性能;整体屈曲失稳时,虽然试件处于弹塑性阶段,但试件的极限位移较小,结构的延性较差。
因此在不锈钢芯板夹层结构参数设计时,应当避免结构侧压时发生局部皱折失稳和整体屈曲失稳。通过缩小芯管的纵向间距,增加芯子的剪切模量使结构发生局部屈曲失稳,并适当地增加芯子的平压模量以减小面板局部屈曲的临界半波长,增加结构在破坏前的塑性变形以提高结构的延性。
针对试验情况,第一组可以考虑减小芯管的纵向间距使结构不发生局部皱折破坏,提高面板的临界应力;第二、六组试可以考虑减小芯管的间距、增加芯管的厚度来提高芯子的剪切强度,使结构不发生整体屈曲破坏;第三~五组试件可以考虑减小芯管的间距、增加芯管的厚度来减小面板局部屈曲的临界半波长,增加结构在破坏前的塑性变形以提高结构的延性。
5 结束语
通过对6组18个不锈钢芯板夹层结构试件进行侧压试验,对不同的设计参数试件的失稳破坏模式、面板极限应力进行分析,得到以下结论:
1)不同参数设计的不锈钢芯板夹层结构试件有三种失稳破坏模式——局部皱折失稳、整体屈曲失稳、局部屈曲失稳。
2)试件发生局部皱折失稳、整体屈曲失稳时,面板极限应力和试件极限位移小,表现出脆性破坏;局部屈曲失稳时,面板的极限应力和试件极限位移大,表现出一定的延性。
3)不锈钢芯板夹层结构侧压抗局部皱折失稳能力与面板厚度、芯管纵向间距有关,抗整体屈曲失稳能力与芯层剪切模量、芯板厚度及面板厚度有关,抗局部屈曲失稳能力与芯层平压模量、面板厚度以及芯层高度有关。
4)参数设计时,应当避免结构侧压发生局部皱折失稳和整体屈曲失稳。应通过缩小芯管的纵向间距,增加芯层的剪切模量使结构发生局部屈曲失稳,并适当地增加芯层的平压模量以减小面板局部屈曲的临界半波长,增加结构在破坏前的塑性变形以提高结构的延性。
[1]王海忠, 何保康. 建筑夹芯板结构性能试验研究[J]. 钢结构, 2001, 16(5):54-56.
[2]周祝林. 蜂窝夹层板的极限强度[J]. 力学学报, 1983,19(1):64-71.
[3]周祝林. 纤维复合材料蜂窝夹层柱的极限强度[J]. 纤维复合材料, 1993(1):38-44.
[4]计宏伟, 徐革玲, 李俊超,等. 蜂窝纸板侧压强度实验研究[J]. 包装工程, 2006, 27(6):90-91.
[5]彭明军, 孙勇, 段永华,等. 钎焊蜂窝铝板侧压变形模式分析研究[J]. 材料导报, 2010, 24(6):75-77.
[6]夏明凯. 芯子缺失对蜂窝板侧压力学性能的影响研究[J]. 河南科技, 2013(12):74-74.
[7]POKHAREL N, MAHENDRAN M. Finite Element Analysis and Design of Sandwich Panels Subject to Local Buckling Effects[J]. Thin-Walled Structures, 2004, 42(4):589-611.
[8]PAIK J K, THAYAMBALLI A K, KIM G S. The Strength Charac-teristics of Aluminum Honeycomb Sandwich Panels[J]. Steel Construction, 2008, 35(3):205-231.
[9]国家标准化管理委员会. 夹层结构侧压性能试验方法:GB/T 1454—2005[S]. 北京:中国标准出版社,2005.