0 引 言
不锈钢芯板结构是一种类似于蜂窝夹层结构的新型建筑结构体系。不锈钢芯板由不锈钢面板与中间密布的不锈钢薄壁芯管组成,采用铜钎焊将芯管与面板焊接成一个牢固的整体。不锈钢芯板结构将蜂窝夹层结构的优点与不锈钢材料有机结合,通过对不锈钢芯板标准件的拼接和组合,可制成建筑结构中的梁、柱、墙、板等构件,用于建筑结构的安装和施工。不锈钢芯板标准件示意见图1、图2。
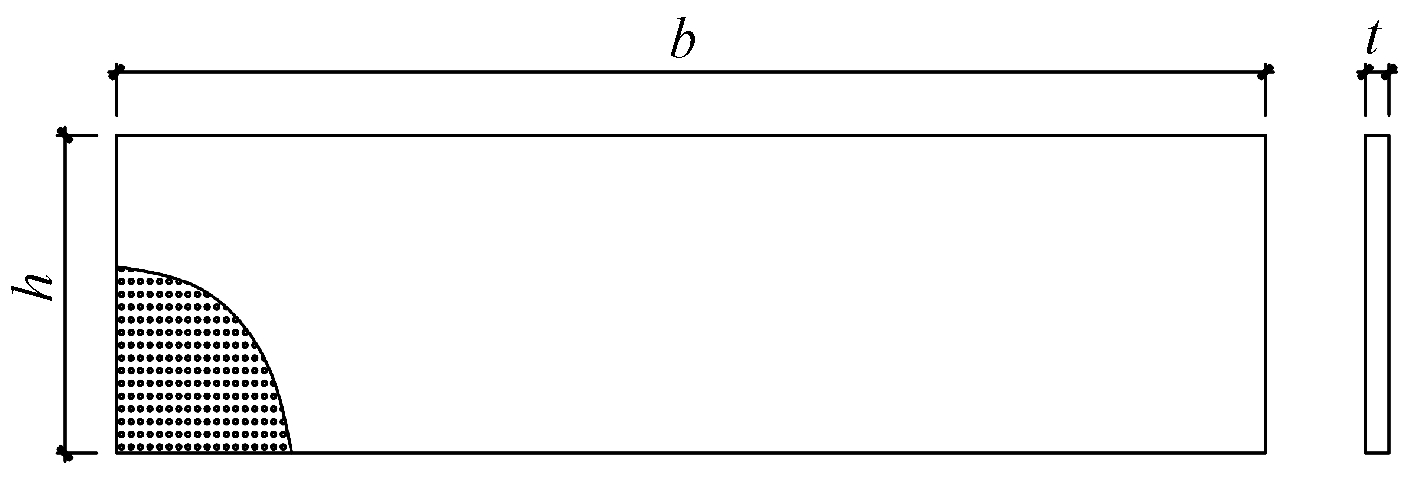
图1 不锈钢芯板标准件大样
Fig.1 Schematic diagram of standard specimen for stainless steel sandwich panel
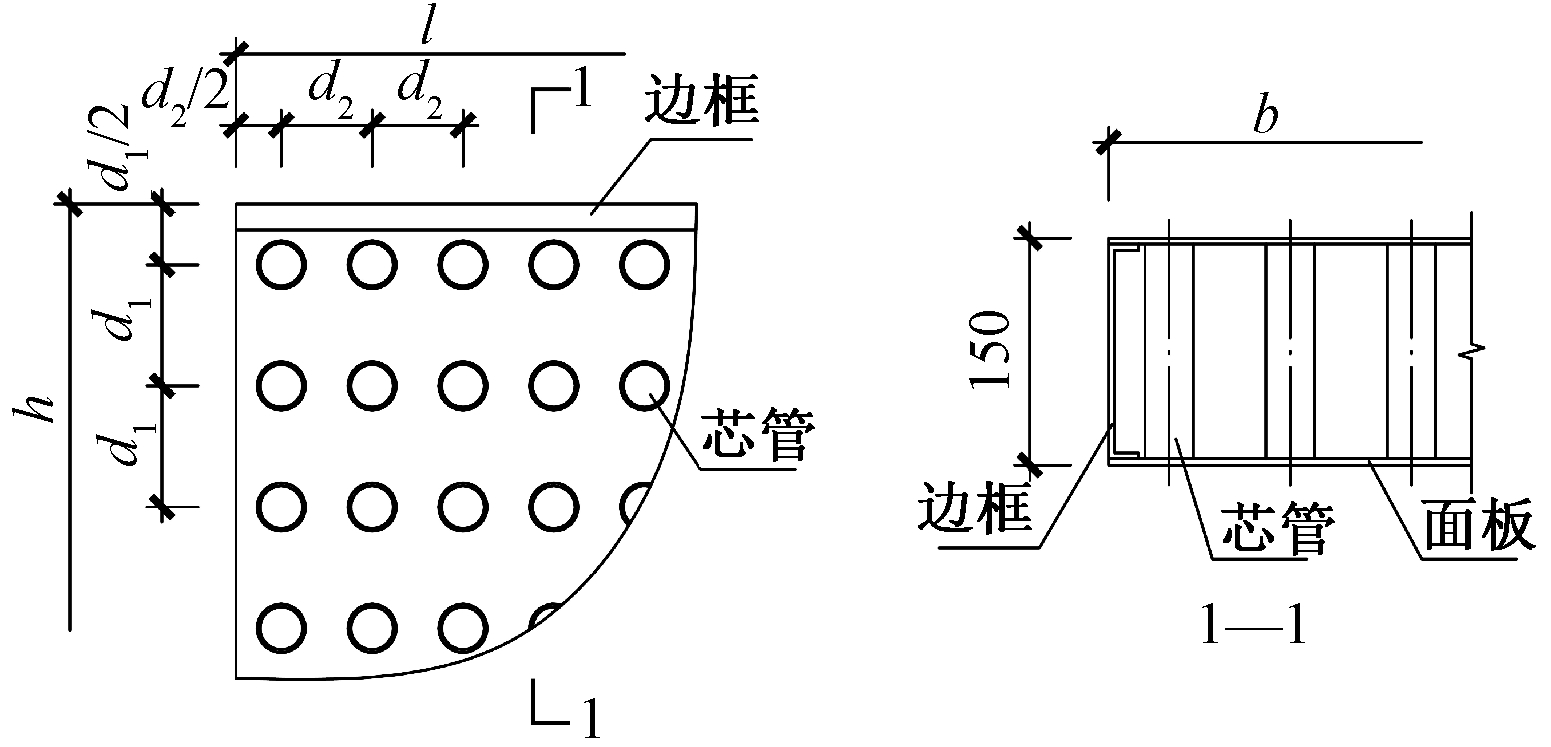
图2 不锈钢芯板标准件内部构造
Fig.2 The internal structure diagram of standard specimen for stainless steel sandwich panel
目前对于不锈钢芯板结构的研究还处于起步阶段,有大量的工作需要进行,特别是对不锈钢芯板结构基本力学性能的研究。不锈钢芯板结构的受力机理与蜂窝夹层结构的十分相似,在蜂窝夹层结构中,剪力主要由两块面板之间的芯子承受,而不锈钢芯板结构中的芯管就相当于蜂窝夹层结构中的芯子,因此有必要对不锈钢芯板结构芯管的剪切性能进行研究。
对不锈钢芯板结构的研究可以参照蜂窝夹层结构的研究方法,国内外学者对蜂窝夹层结构通常采用试验[1-6]和有限元分析[7-9]两种手段进行研究。课题组在对多组不锈钢芯板试件进行拉剪作用试验的基础上,采用有限元方法进行模拟,并对模拟结果与试验结果进行比较。在验证有限元模型的准确性的基础上,对不锈钢芯板结构芯管的剪切受力过程和破坏机理进行分析,为不锈钢芯板结构的设计提供参考。
1 试验研究
1.1 试验概况
参考GB/T 1455—2005《夹层结构或芯子剪切性能试验方法》[10]和ASTM C273/C273-16《夹芯层材料剪切材料标准试验方法》[11]对6组试件进行拉剪试验,并对试验结果进行计算和分析。
1.2 试件设计
试验以规格为480 mm×480 mm×150 mm的不锈钢芯板剪切试件为研究对象,试件面板和芯管的材料均为奥氏体S30408不锈钢。试件的面板厚度为1.5,4.0,10.0 mm,芯管厚度为0.18,0.30 mm,芯管排布间距有80 mm×60 mm和160 mm×60 mm两种,考虑X向和Y向两种加载方向(X向和Y向所指方向见图3)。经组合后共制作6组试件,每组3个,共18个试件。试件制备完成后,需要将两块加载钢板分别与试件的上、下面板用环氧树脂胶黏剂胶接,使两块加载钢板与试件形成一个整体。加载钢板的材质选用Q345钢,长、宽、厚分别为510,480,30 mm。在加载钢板的加载端焊接一铰支座,在其中插入一根钢棒形成一个固定铰支座。试件具体规格、参数以及分组见表1,试件大样见图3,加载钢板大样见图4,图5为加载钢板与剪切试件的黏接组合件。
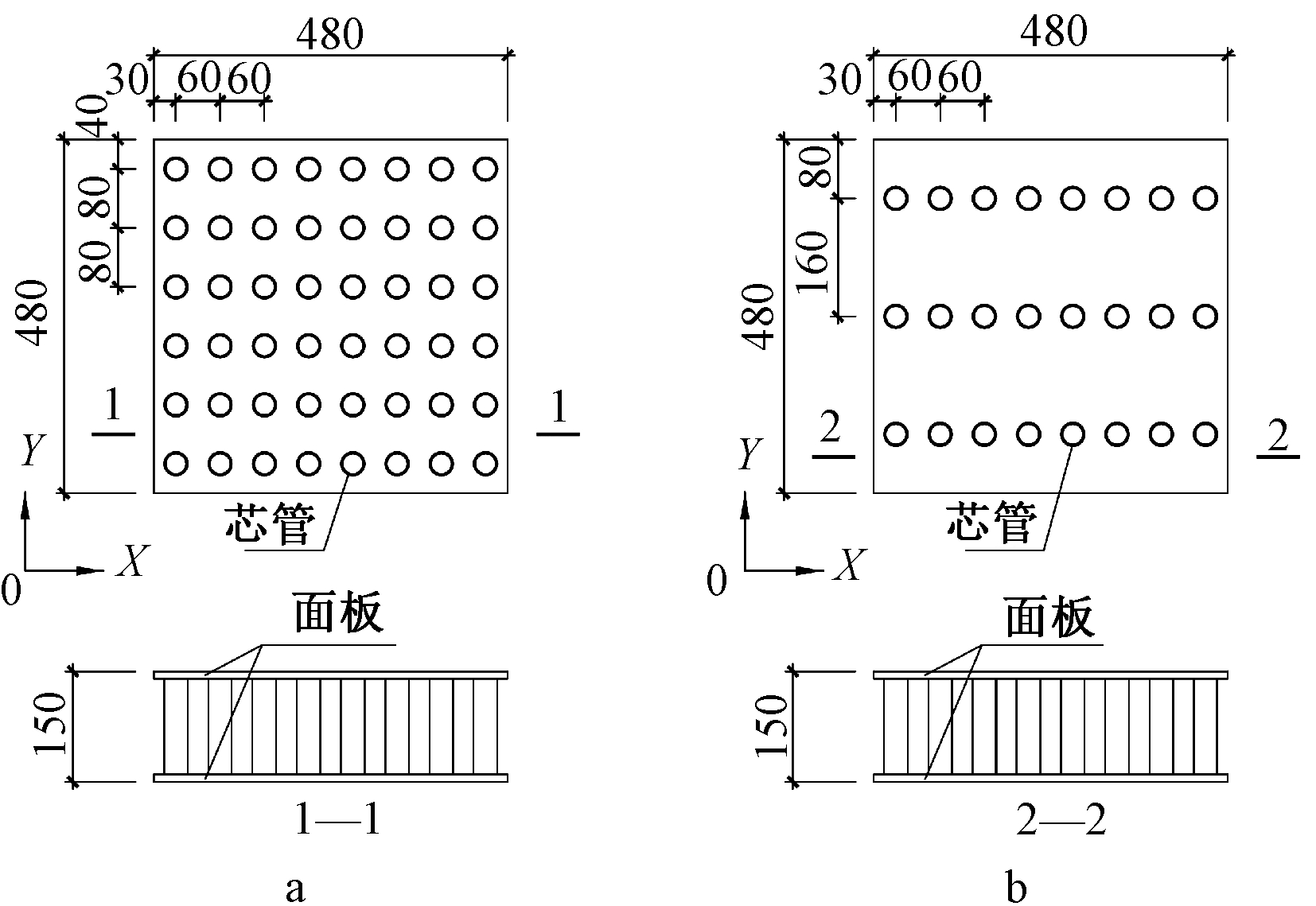
图3 试件大样
Fig.3 Schematic diagram of specimens
表1 试件分组及规格参数
Table 1 Specimen grouping and specifications
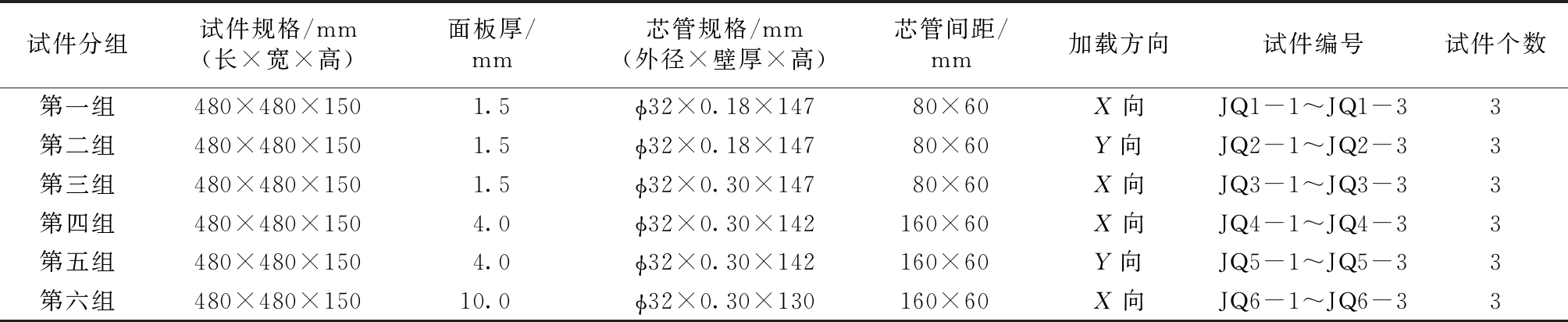
试件分组试件规格/mm(长×宽×高)面板厚/mm芯管规格/mm(外径×壁厚×高)芯管间距/mm加载方向试件编号试件个数第一组480×480×1501.5ϕ32×0.18×14780×60X向JQ1-1~JQ1-33第二组480×480×1501.5ϕ32×0.18×14780×60Y向JQ2-1~JQ2-33第三组480×480×1501.5ϕ32×0.30×14780×60X向JQ3-1~JQ3-33第四组480×480×1504.0ϕ32×0.30×142160×60X向JQ4-1~JQ4-33第五组480×480×1504.0ϕ32×0.30×142160×60Y向JQ5-1~JQ5-33第六组480×480×15010.0ϕ32×0.30×130160×60X向JQ6-1~JQ6-33
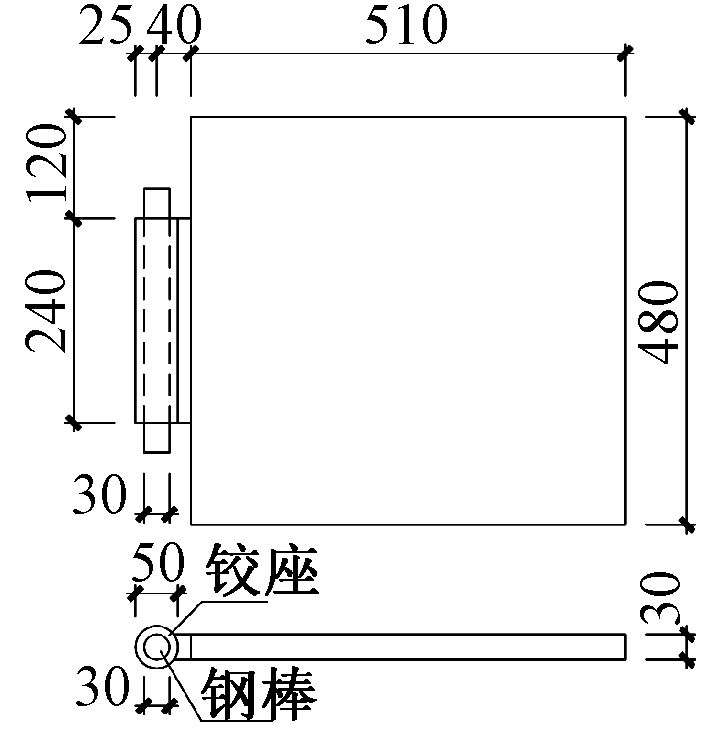
图4 加载钢板大样
Fig.4 Schematic diagram of loading plates

图5 加载钢板与试件的黏接组合件
Fig.5 Bonding assembly of loading plate and specimen
1.3 加载和量测装置
试验采用320 kN级立式油压千斤顶作为加载设备,加载方式为分级加载,加载装置如图6。
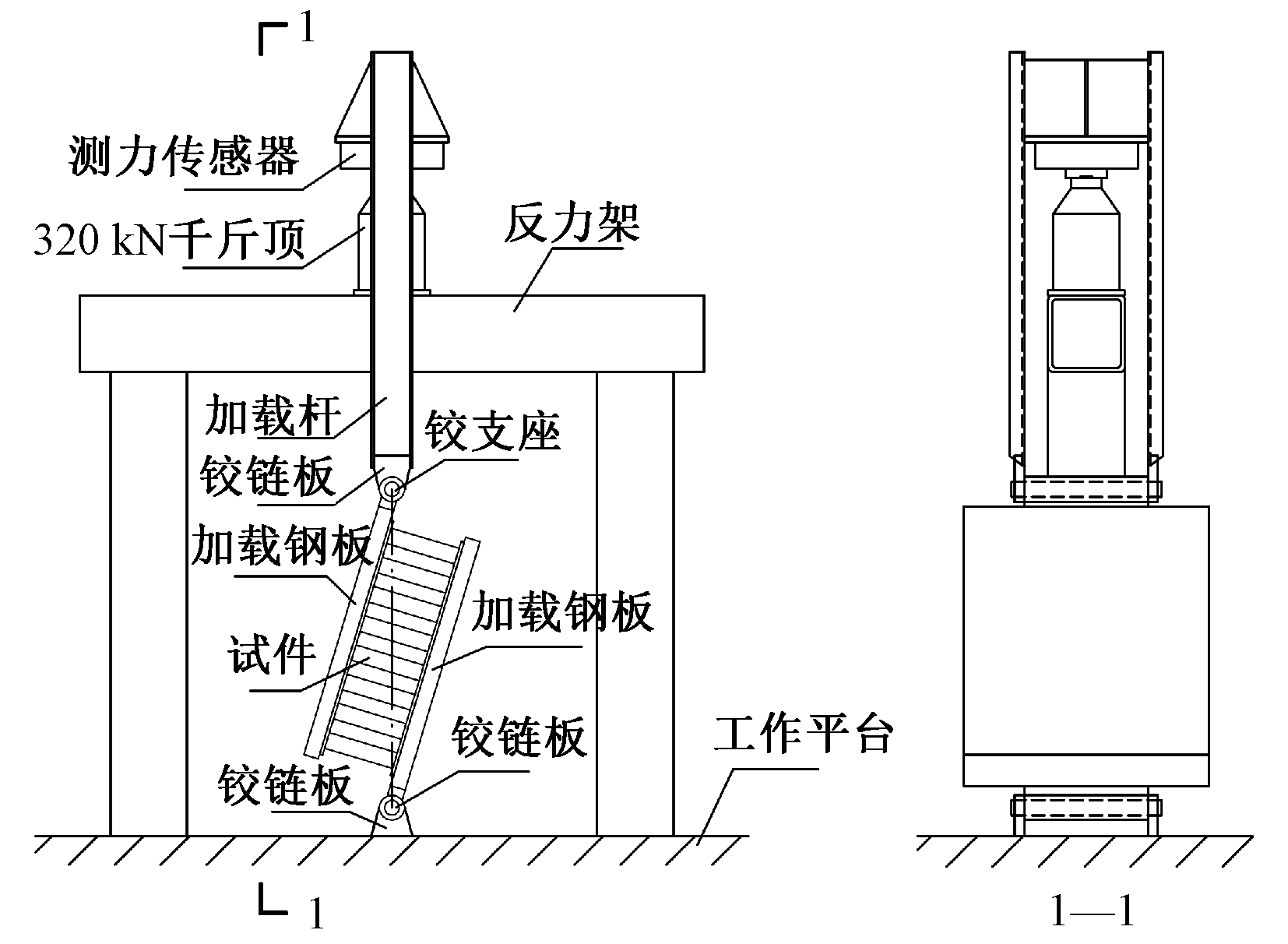
图6 加载装置示意
Fig.6 Loading device schematic diagram
试验前通过有限元模拟对试件的破坏荷载进行预估,通过有限元模拟得到试件的荷载-位移曲线,并以曲线的极值点所对应的荷载作为预估破坏荷载。
正式加载前先进行预加载,预加载时对试件施加15%~20%的拉伸破坏荷载,检查设备和仪表的运行状况,并调整试件的位置,使荷载作用线不超过并尽量接近试件的对角线。
正式加载时,先采用预估破坏荷载的5%作为级差对试件施加拉力,当达到破坏荷载值的70%时,改为用预估破坏荷载的2%作为级差对试件施加荷载,加载至试件破坏。
试验主要测量设备和仪表为测力传感器和百分表。测力传感器安装在千斤顶压头处,两块加载钢板上各安装一个百分表,百分表安装位置尽量靠近加载钢板中部,且百分表的测杆与加载钢板平行。
1.4 试验结果及现象
以各级荷载平行于试件面板方向的分力N为纵坐标,两个百分表测出的两块加载钢板之间的相对位移平均值Δ为横坐标,绘制各组试件的荷载-位移曲线(图7),其中试件JQ6-1由于在试验过程中百分表损坏,导致位移读数不准确,因此未将该试件的试验曲线体现出来。
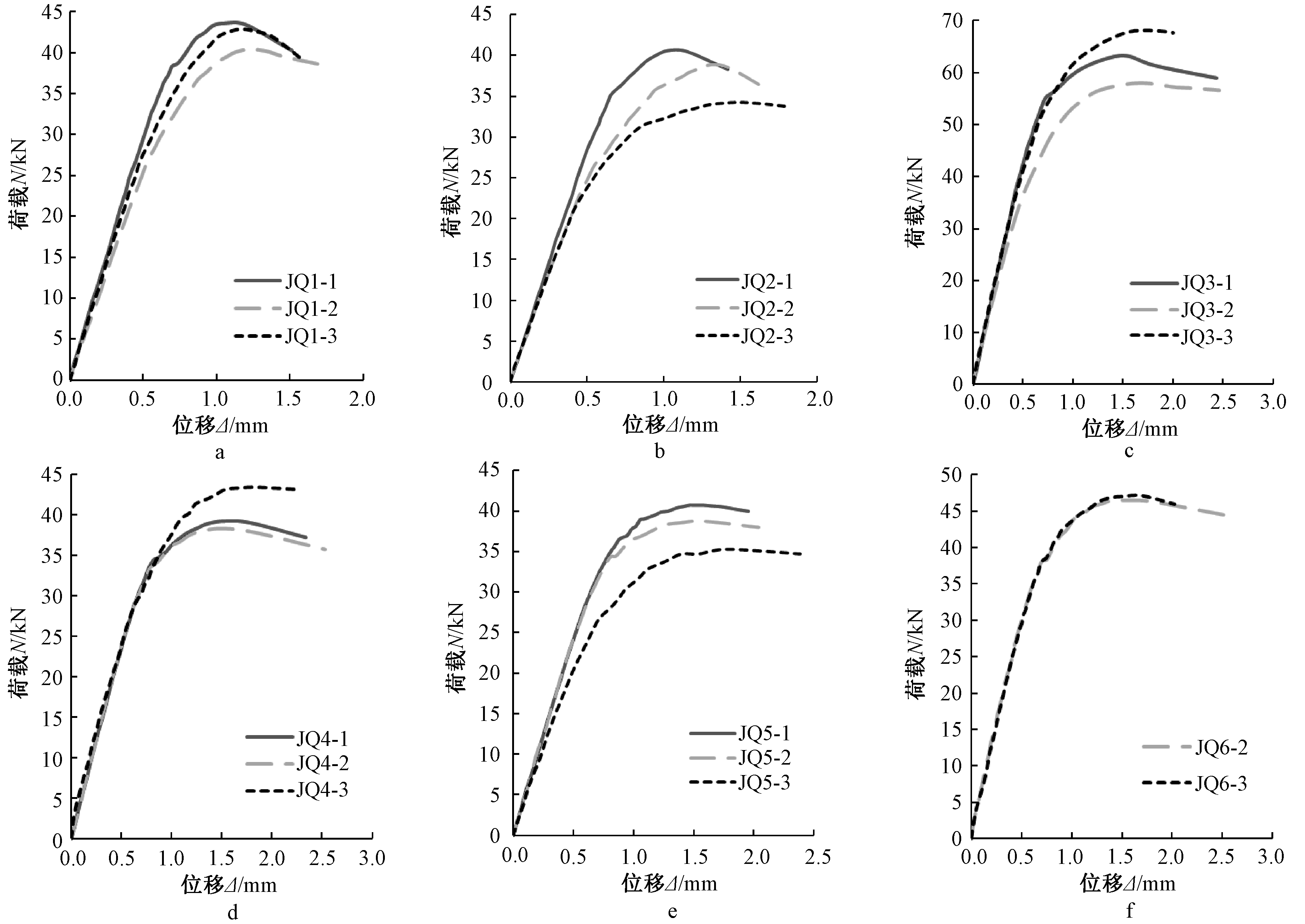
a—第一组; b—第二组; c—第三组; d—第四组; e—第五组; f—第六组。
图7 荷载-位移曲线
Fig.7 Load-displacement curves
将荷载-位移曲线中直线段的终点称为拐点,将荷载达到最大值时对应的点称为极值点。表2列出了各组试件的拐点荷载平均值、极值点荷载平均值和直线段斜率平均值,按照文献[10]给出的计算方法可以进一步计算出各组试件的拐点剪切强度平均值、极值点剪切强度平均值和剪切模量平均值,见表3。
观察剪切试验过程中的试验现象以及六组试件的荷载-位移曲线可以看出:开始时荷载与位移呈线性关系增长,此时芯管无明显变形,与试验开始未受荷载时的情况相同。当荷载继续增大越过荷载-位移曲线的拐点时,荷载-位移曲线由线性变为非线性,且当荷载接近极值点荷载值时,芯管的上、下端部受压区均出现略微鼓曲的现象。当荷载越过荷载-位移曲线的极值点时,千斤顶无法继续加力,而百分表读数仍在增大,表明试件承受的荷载不再增大,而变形仍在继续增加,试件已经失去了承载能力,此时芯管的鼓曲现象较为明显。继续加载至试件完全破坏,芯管端部受压区的鼓曲现象越来越明显,最终发展为芯管端部严重褶皱变形,且芯管明显倾斜,上、下加载钢板发生明显错动。整个试验过程中,芯管与面板之间的铜钎焊连接处始终未出现开裂脱焊的现象。从试验现象可以看出:试件在拉剪作用下最终的破坏模式是芯管端部受弯发生局部屈曲破坏。图8展示了试件从开始加载到完全破坏的变形过程。
表2 试验结果数据
Table 2 Test results data

试件分组拐点荷载平均值/kN极值点荷载平均值/kN直线段斜率平均值/(kN·mm-1)第一组29.442.354.9第二组27.037.953.4第三组45.263.179.9第四组26.240.346.1第五组26.138.244.8第六组30.646.864.4
表3 试件芯子剪切强度和剪切模量
Table 3 Specimen shear strengths and shear moduli
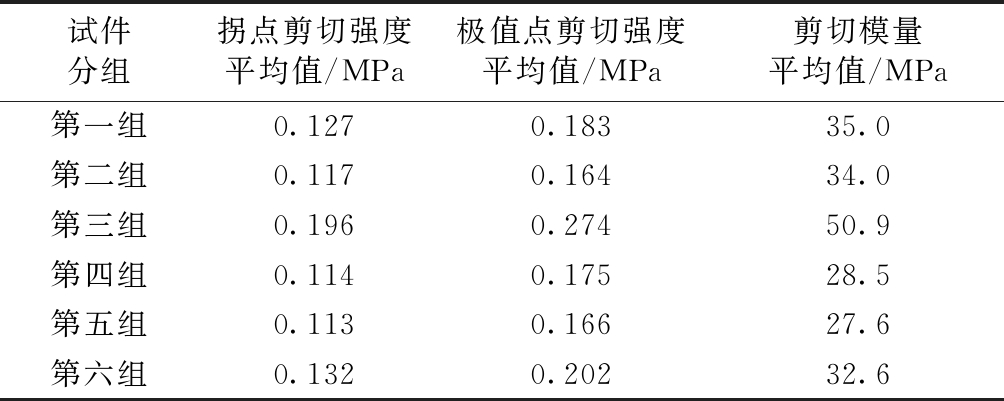
试件分组拐点剪切强度平均值/MPa极值点剪切强度平均值/MPa剪切模量平均值/MPa第一组0.1270.18335.0第二组0.1170.16434.0第三组0.1960.27450.9第四组0.1140.17528.5第五组0.1130.16627.6第六组0.1320.20232.6

a—芯管未发生变形; b—芯管端部受压区略微鼓曲; c—芯管端部受压区明显鼓曲; d—芯管端部严重褶皱变形。
图8 试件变形过程
Fig.8 Specimen deformation process
2 有限元模拟
通过ABAQUS有限元分析软件建立有限元模型对上述试验过程进行模拟,并将有限元模拟结果与试验结果进行对比,以验证有限元模型的准确性。
2.1 建立模型
共建立了6个有限元模型,编号为1~6,分别与试验的六组试件相对应,尺寸规格以及各种几何参数均与试件相同。
模型中的面板和芯管采用S4R四结点壳单元模拟,加载钢板采用C3D8R八结点六面体单元模拟。模型涉及两种材料:面板和芯管的材料为奥氏体S30408不锈钢,其本构关系采用Gardner-Nethercot两段线模型[12]确定,泊松比取0.3,弹性模量取1.93×105 MPa;加载钢板的材料为Q345钢,由于加载钢板并非本文的研究对象,因此其本构关系简单采用理想弹塑性模型,泊松比取0.3,弹性模量取2.06×105 MPa,有限元塑性分析采用von Mises屈服准则、相关联流动性法则、各向同性硬化法则。
模型采用位移控制的加载方式进行单调加载,荷载及边界条件的设置见图9,有限元模型网格划分见图10。
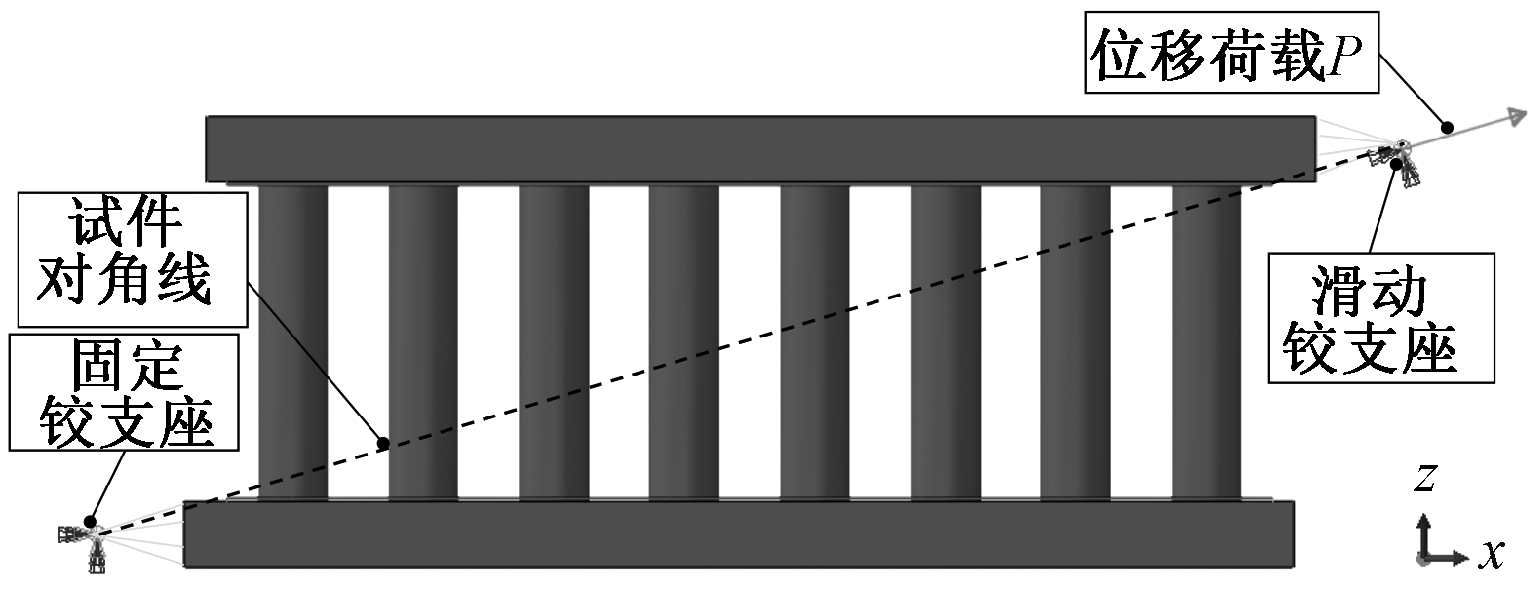
图9 荷载及边界条件
Fig.9 Load and boundary conditions

图10 整体模型网格划分
Fig.10 Meshing of the overall model
2.2 有限元模拟结果与试验结果对比
将六个有限元模型计算得到的荷载-位移曲线与相对应的各组试验的典型荷载-位移曲线进行对比,结果见图11。
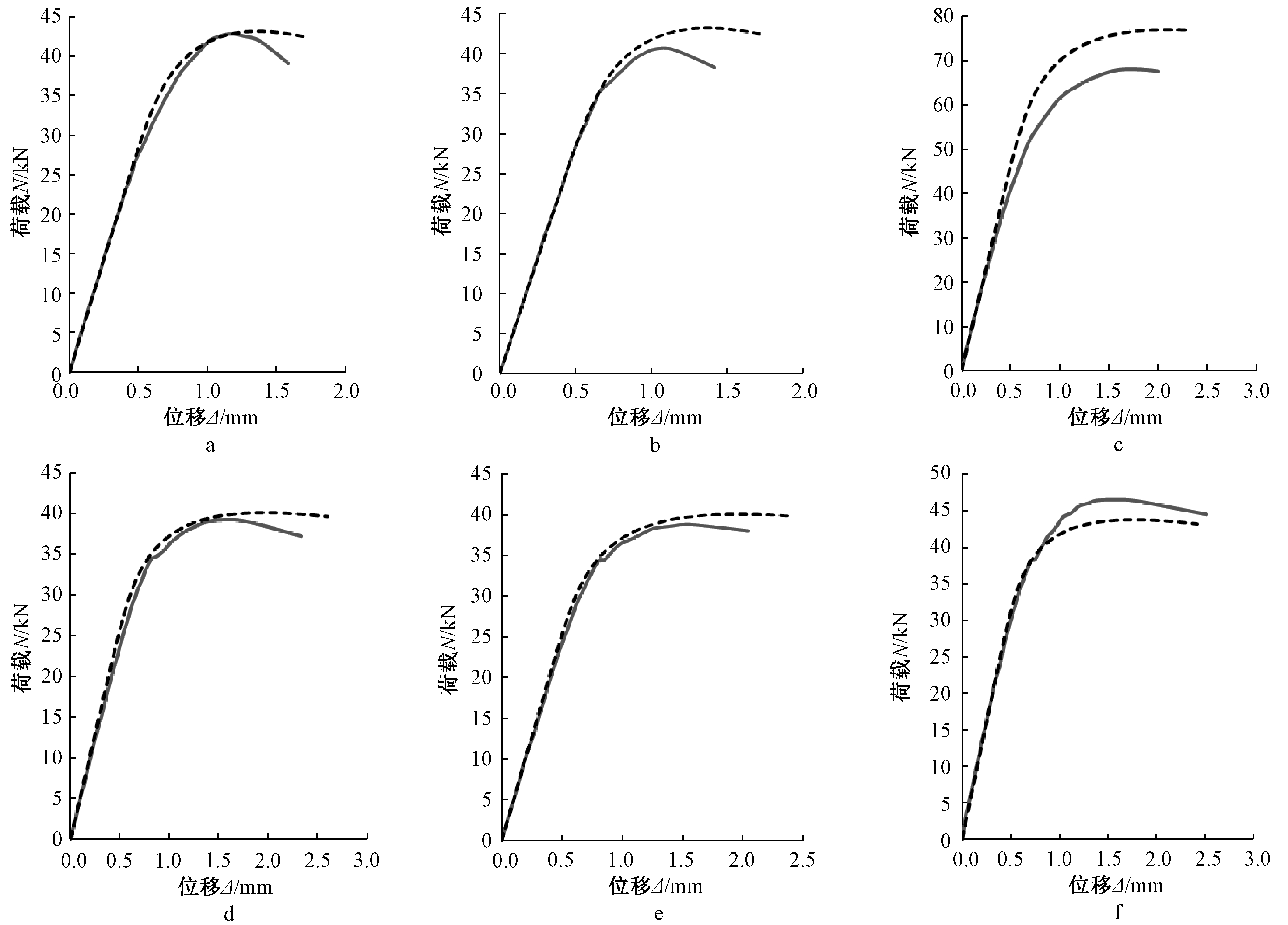
a—第一组; b—第二组; c—第三组; d—第四组; e—第五组; f—第六组。 ![]() 试验; -----有限元。
试验; -----有限元。
图11 模型验证
Fig.11 The verification for the models
从以上对比中可以看出:有限元模拟计算得到的荷载-位移曲线与试验得到的荷载-位移曲线吻合良好。表4~6对比了有限元模拟计算与试验得到的拐点荷载值、极值点荷载值和直线段斜率,除了第三组差距偏大,其余各组误差均在15%以内。这是由于第三组试验的预估破坏荷载值比其他各组大许多,而试件的面板较薄,容易发生变形,环氧树脂胶黏剂的胶接效果不够理想,当加载至较大的荷载时,面板与加载钢板之间局部发生脱胶,导致加载不均匀,试件所承受的力没有被每根芯管均匀分担,提前破坏。
表4 有限元模拟与试验所得的拐点荷载值对比
Table 4 Comparisons of inflection point load values obtained by finite element simulations and experiments
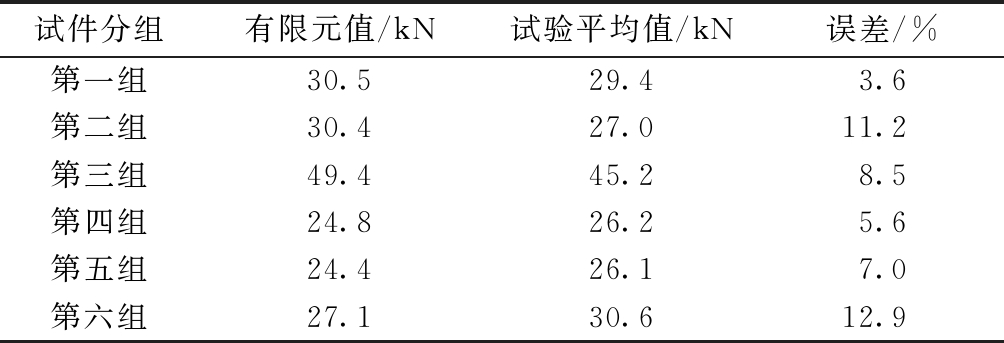
试件分组有限元值/kN试验平均值/kN误差/%第一组30.529.43.6第二组30.427.011.2第三组49.445.28.5第四组24.826.25.6第五组24.426.17.0第六组27.130.612.9
在有限元模拟中,所有模型的破坏位置均为芯管端部,与试验现象一致。图12为有限元模型与试件的变形模式对比,可以看出:无论是芯管端部受压区鼓曲还是最终发展为芯管端部严重褶皱变形,有限元模型与试验的结果十分吻合。
表5 有限元模拟与试验所得的极值点荷载值对比
Table 5 Comparisons of ultimate extreme point load values obtained by finite element simulations and experiments
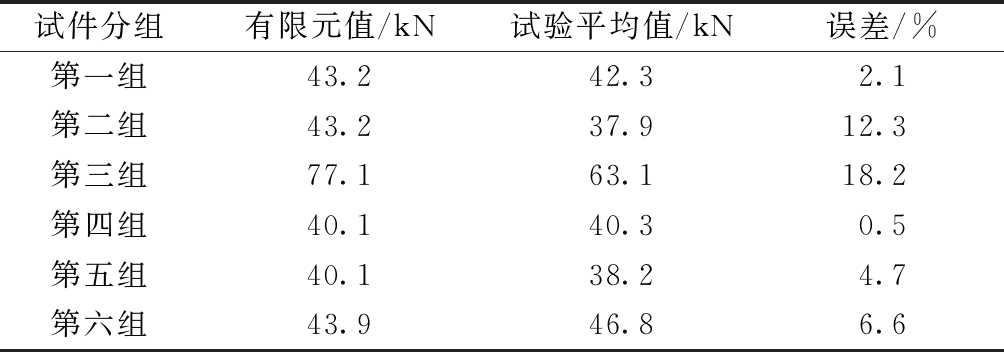
试件分组有限元值/kN试验平均值/kN误差/%第一组43.242.32.1第二组43.237.912.3第三组77.163.118.2第四组40.140.30.5第五组40.138.24.7第六组43.946.86.6
表6 有限元模拟与试验所得的直线段斜率对比
Table 6 Comparisons of straight line segment gradient obtained by finite element simulations and experiments

试件分组有限元值/(kN·mm-1)试验平均值/(kN·mm-1)误差/%第一组57.354.94.2第二组57.253.46.6第三组93.879.914.8第四组51.846.111.0第五组51.244.812.5第六组64.464.40

图12 有限元模型与试件变形模式对比
Fig.27 Deformation mode comparisons between finite element model and specimen
可见,有限元模拟结果与试验结果吻合良好,验证了有限元模拟中所选取的参数的合理性,表明本文所建立的有限元模型能够准确地模拟试验过程,具有较高的参考价值。
3 受力过程与破坏机理分析
以第一组模型为例,分析不锈钢芯板结构芯管在剪切作用下的受力过程和破坏机理。如图13所示,不锈钢芯板结构芯管在剪切作用下的受力过程可以分为三个阶段:弹性阶段、弹塑性阶段和塑性破坏阶段。
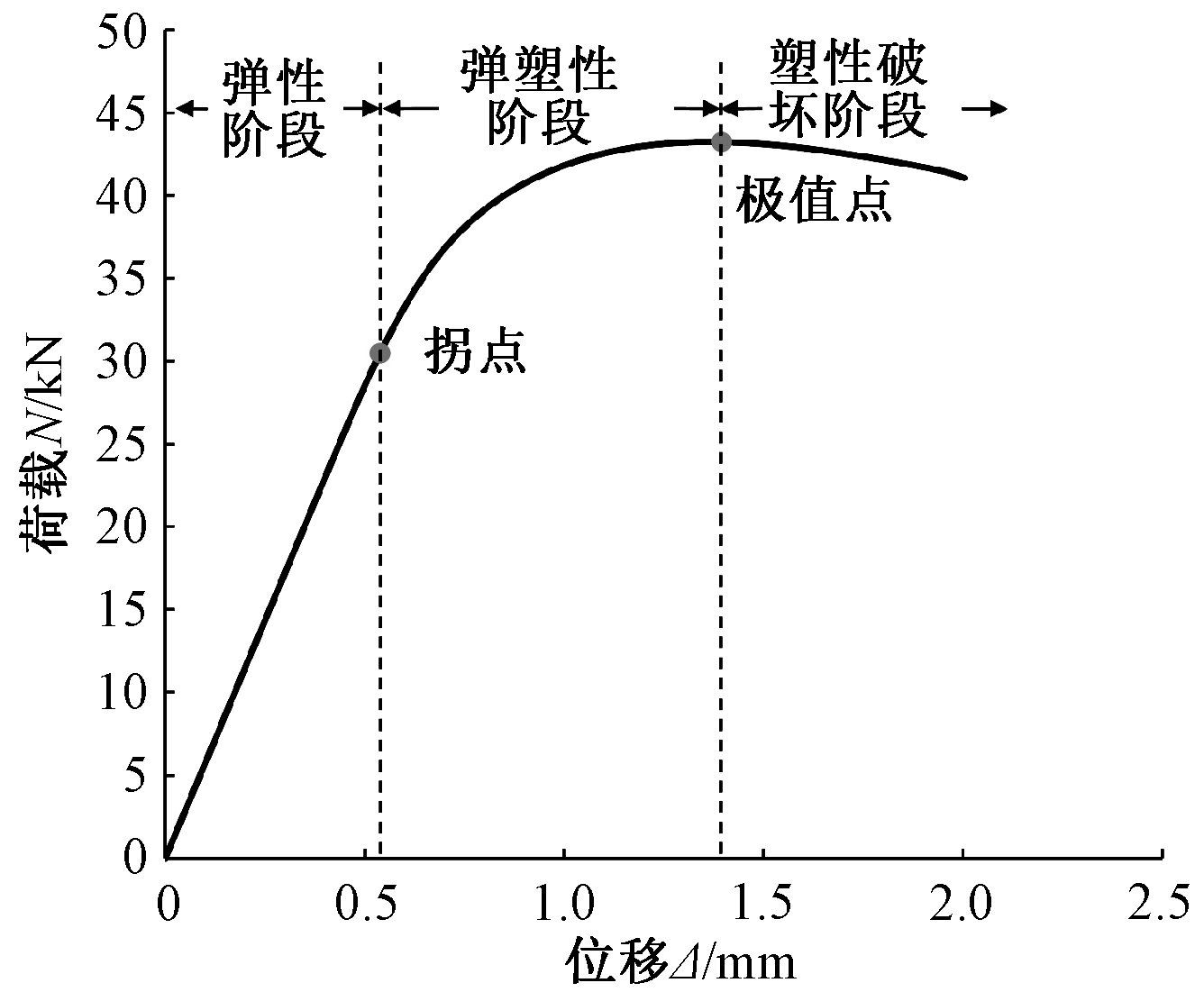
图13 芯管受力阶段变形
Fig.13 The load-deformation curve
3.1 弹性受力阶段

图14 弹性阶段结束时有限元模型的von Mises应力云
Fig.14 The von Mises stress contour of model at the end of elastic stage
在弹性阶段,荷载与位移呈线性关系,且荷载增长较快,直到芯管端部受压区的部分点发生屈服,曲线的斜率降低出现拐点,弹性受力阶段结束。从图14所示的荷载-位移曲线拐点处有限元模型的等效应力云图可以看出:芯管端部的应力分布较为集中,且应力较大,部分点的应力已经超过了材性试验实测的S30408不锈钢的屈服强度276 MPa;芯管其余部分的应力分布较为均匀,应力大小基本都在200 MPa以下。
3.2 弹塑性受力阶段
弹性阶段结束后,芯管进入弹塑性阶段,荷载增长越来越缓慢,而位移增长加快,荷载-位移曲线逐渐趋于平缓。这一阶段中芯管端部越来越多的点发生屈服,且应力迅速增大,端部受压区出现鼓曲的现象,发生局部屈曲,此时曲线达到极值点,不再上升,弹塑性阶段结束。图15为荷载-位移曲线极值点处有限元模型的等效应力云图,从中可见:芯管端部受压区出现鼓曲,并随之发生应力重分布,鼓曲部分的应力很大,而端部受压区其余范围的应力相对较小。

图15 弹塑性阶段结束时有限元模型的von Mises应力云图
Fig.15 The von Mises stress contour of model at the end of elastic-plastic stage
3.3 塑性破坏阶段
越过极值点以后,荷载-位移曲线出现下降段,位移仍在继续增长,而荷载则缓慢下降,此时芯管已经丧失了承载能力。随着位移的增加,芯管端部受压区的鼓曲现象越来越明显,局部屈曲的范围不断扩大,鼓曲变形逐渐转变为褶皱变形。从图15的位移-荷载曲线可以看出:不锈钢芯板结构芯管失效时,承载力是缓慢下降的,表现出塑性破坏的特征。
从以上分析表明:不锈钢芯板结构芯管在剪切作用下的破坏本质是芯管端部受弯,受压区纤维屈服导致局部屈曲破坏。荷载-位移曲线的拐点实质上对应于芯管端部受压区部分点开始发生屈服时的状态,拐点处的荷载值是芯管在弹性阶段的抗剪承载力,称之为芯管弹性抗剪承载力Ne;荷载-位移曲线极值点处的荷载值是芯管的极限抗剪承载力,称之为芯管极限抗剪承载力Nu。取试验平均值与有限元模拟计算值中的较小值作为各组试件的芯管弹性抗剪承载力或芯管极限抗剪承载力的取值,汇总于表7。
表7 各组试件的芯管弹性抗剪承载力和极限抗剪承载力
Table 7 Core tube elastic shear capacity and ultimate shear capacity of each group specimens
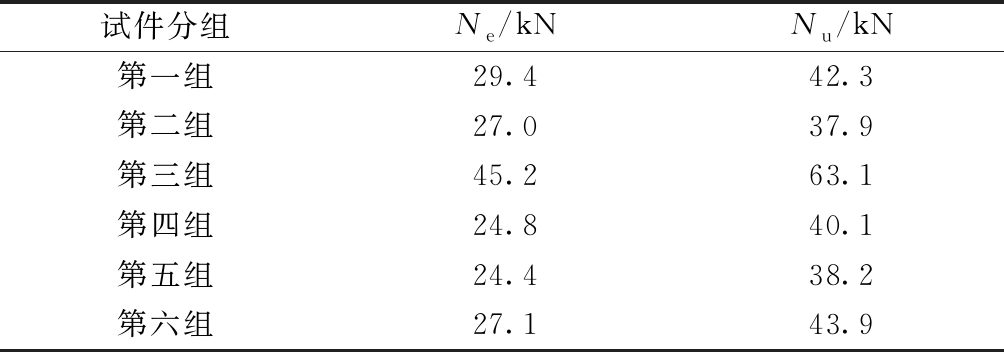
试件分组Ne/kNNu/kN第一组29.442.3第二组27.037.9第三组45.263.1第四组24.840.1第五组24.438.2第六组27.143.9
进入弹塑性阶段之后,芯管开始发生塑性变形,荷载-位移曲线趋于平缓,变形较大,已经不适宜继续承载,出于对控制变形和强度储备等因素的考虑,应以芯管弹性抗剪承载力Ne作为不锈钢芯板结构芯管设计计算时所采用的抗剪承载力标准值。
4 结束语
针对不锈钢芯板结构芯管的剪切性能进行了试验研究,建立了有限元计算模型并将有限元模拟计算结果与试验结果进行对比,通过分析得出以下结论:
1)通过拉剪试验得到了六组试件的荷载-位移曲线,计算出了各组试件的剪切强度和剪切模量。通过观察试验现象可知,不锈钢芯板结构芯管的破坏发生在芯管端部受压区。
2)有限元模拟结果与试验结果吻合良好,说明有限元模型所采用的单元类型、材料特性、边界条件和屈服准则等是合理的。
3)在试验和有限元对照的基础上对不锈钢芯板结构芯管的剪切受力过程和破坏机理进行了分析,明确了不锈钢芯板结构芯管在剪切作用下的受力过程可以分为弹性、弹塑性和塑性破坏三个阶段,芯管破坏的本质是芯管端部受弯,受压区纤维屈服后发生局部屈曲破坏。
4)通过试验和有限元模拟计算得到了六组试件的芯管弹性抗剪承载力和芯管极限抗剪承载力。
[1]王海忠, 何保康. 建筑夹芯板结构性能试验研究[J]. 钢结构, 2001, 16(5):54-56.
[2]弓晓芸, 陈晓明. 新型夹芯板的研究及应用[J]. 钢结构, 2000, 15(2):51-52.
[3]徐永君, 李敏, 战颂,等. 蜂窝结构抗剪性能实验研究及其数值模拟[J]. 实验室研究与探索, 2007(10):241-242,259.
[4]彭明军, 孙勇, 段永华,等. 钎焊蜂窝铝板侧压变形模式分析研究[J]. 材料导报, 2010, 24(6):75-77.
[5]辛亚军, 李慧剑, 赵旭亚,等. 环氧树脂/泡沫铝一体型复合夹层板压缩及弯曲试验研究[J]. 实验力学, 2015, 30(4):421-428.
[6]王迎春, 谷秀娥, 权高峰,等. 镁合金蜂窝板的制备及力学性能研究[J]. 科技创新导报, 2009(15):4.
[7]周金翠, 盛美萍, 张安付. 基于有限元模型的蜂窝芯层面内等效弹性模量仿真[J]. 机械强度, 2015, 37(3):488-492.
[8]GREDIAC M. A Finite Element Study of the Transverse Shear in Honeycomb Cores[J]. International Journal of Solids & Structures, 1993, 30(13):1777-1788.
[9]PENG M J, SUN Y, YAO J, et al. Finite Element Simulation on Three-Point Bending of Brazed Aluminum Honeycomb Panel[J]. Advanced Materials Research, 2010(168/169/170):1046-1050.
[10]中华人民共和国质量监督检验检疫总局.夹层结构或芯子剪切性能试验方法:GB/T 1455—2005 [S]. 北京:中国标准出版社,2005.
[11]AMERICAN SOCIETY OF TESTING MATERIALS (ASIM) INTERNATIONAL. Standard Test Method for Shear Properties of Sandwich Core Materials:ASTM C273/C273M-16[S]. West Conshohocken, PA, USA:ASTM, 2005.
[12]袁焕鑫. 焊接不锈钢轴心受压构件局部稳定和相关稳定性能研究[D]. 北京:清华大学, 2014:64-94.