不锈钢芯板结构是一种新的建筑结构体系,类似于蜂窝夹层结构,由不锈钢面板与面板间密布的不锈钢薄壁芯管组成,芯管与面板通过铜钎焊焊接成一个牢固的整体,空隙处填充岩棉以隔热隔声。不锈钢芯板结构将蜂窝夹层结构的优良特性与不锈钢材料有机结合,通过对不锈钢芯板标准件的拼接和组合制作成建筑结构中的梁、柱、墙、板等构件,进而用于建筑结构的安装和施工。不锈钢芯板标准件不锈钢芯板结构芯管的平压性能、剪切性能和芯板的侧压性能是该结构的主要基本力学性能,采用不锈钢芯板设计梁、柱、墙、板等构件时,这些基本力学性能指标是设计的基本参数,本研究主要针对不锈钢芯板结构芯管的平压性能。
由于不锈钢芯板结构和蜂窝夹层结构在结构组成上类似,因此研究不锈钢芯板结构可以参照蜂窝夹层结构的研究方法,国内外学者对蜂窝夹层结构通常采用试验和有限元分析两种手段进行研究[1-4]。不锈钢芯板结构芯管平压性能主要反映不锈钢薄壁圆筒芯管的承载性能,因此参照国内外学者对薄壁圆筒结构的研究方法[5-7]。
本研究以多组不锈钢芯板试件平压试验为基础,通过对相应有限元模型的分析,并与试验结果进行比较,在验证有限元分析可靠性的基础上,对不锈钢芯板结构芯管的平压性能进行数值分析,为不锈钢芯板结构的设计和应用提供参考。
1 试验研究
1.1 试验概况
参照GB/T 1453—2005《夹层结构或芯子平压性能试验方法》[1]和ASTM C365/C365M-11a《夹芯板的抗平压性能的标准试验方法》[2]通过压缩试验机沿垂直芯板结构面板方向施加压缩荷载,使芯管破坏,测出平压强度,同时安装测量变形仪表测出压缩变形,测定平压模量,并绘制试件的荷载-位移曲线。
1.2 试件设计
鉴于文献[3]指出试样尺寸对试验结果有一定的影响,因此对此种新型夹层结构设计了三种试件规格:分别为80 mm×60 mm(单管试验)、160 mm×120 mm(四管试验)、480 mm×480 mm(大板试验),见图1;同时考虑试件的面板厚度有1.5,4.0,10.0 mm三种,芯管厚度有0.18,0.30 mm两种,芯管排布间距有80 mm×60 mm和160 mm×60 mm两种,共组合出12组试件;其中单管试验4组,每组40个试件;四管试验4组,每组10个试件;大板试验4组,每组3个试件,总212个试件。试件面板和芯管的材料均为奥氏体S30408不锈钢。试件具体规格、参数以及分组见表1,试件实物见图2。
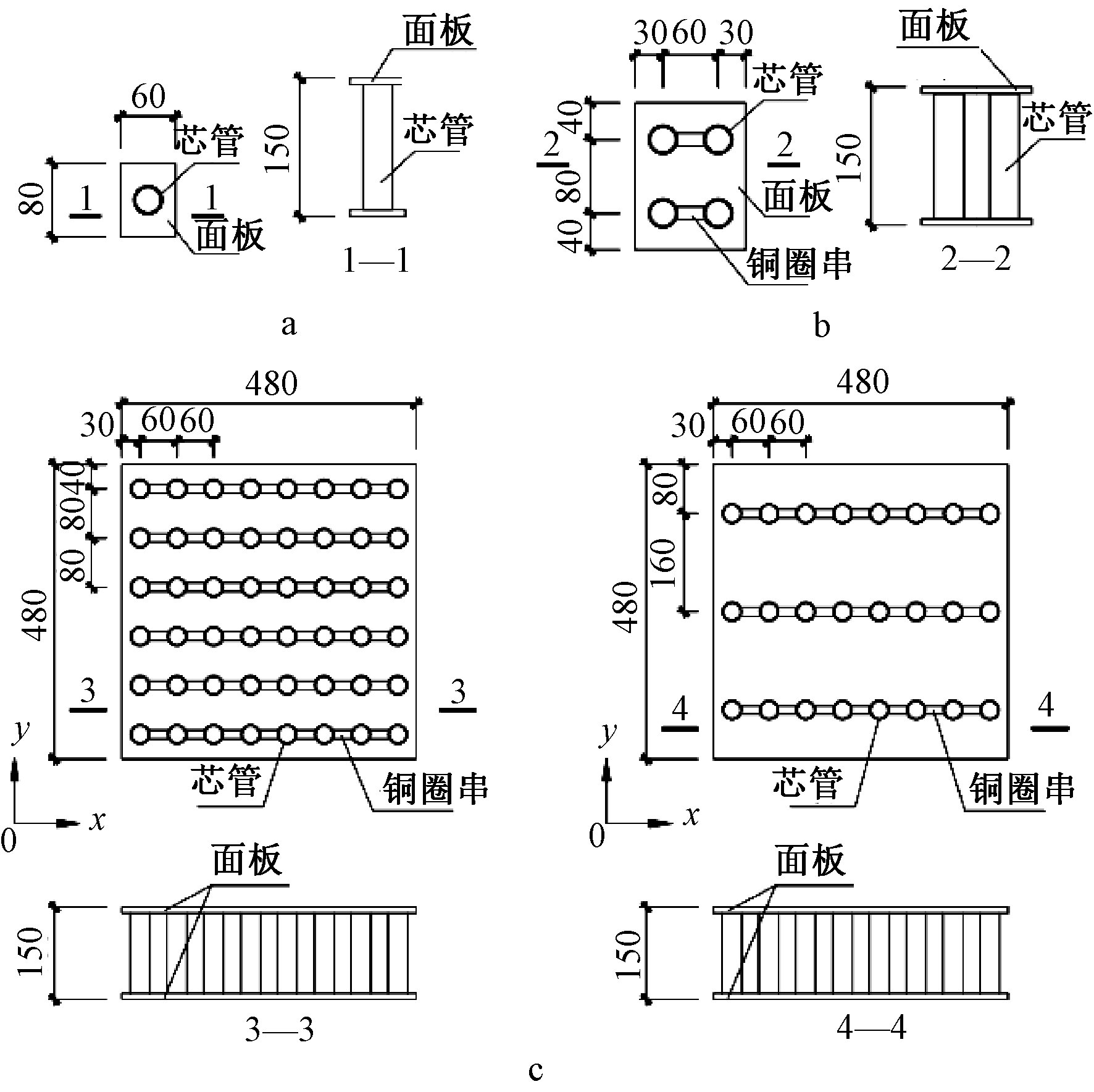
a—单管; b—四管; c—大板。
图1 试件大样
Fig.1 Schematic diagram of specimens
表1 试件分组及规格参数
Table 1 Specimen grouping and specifications
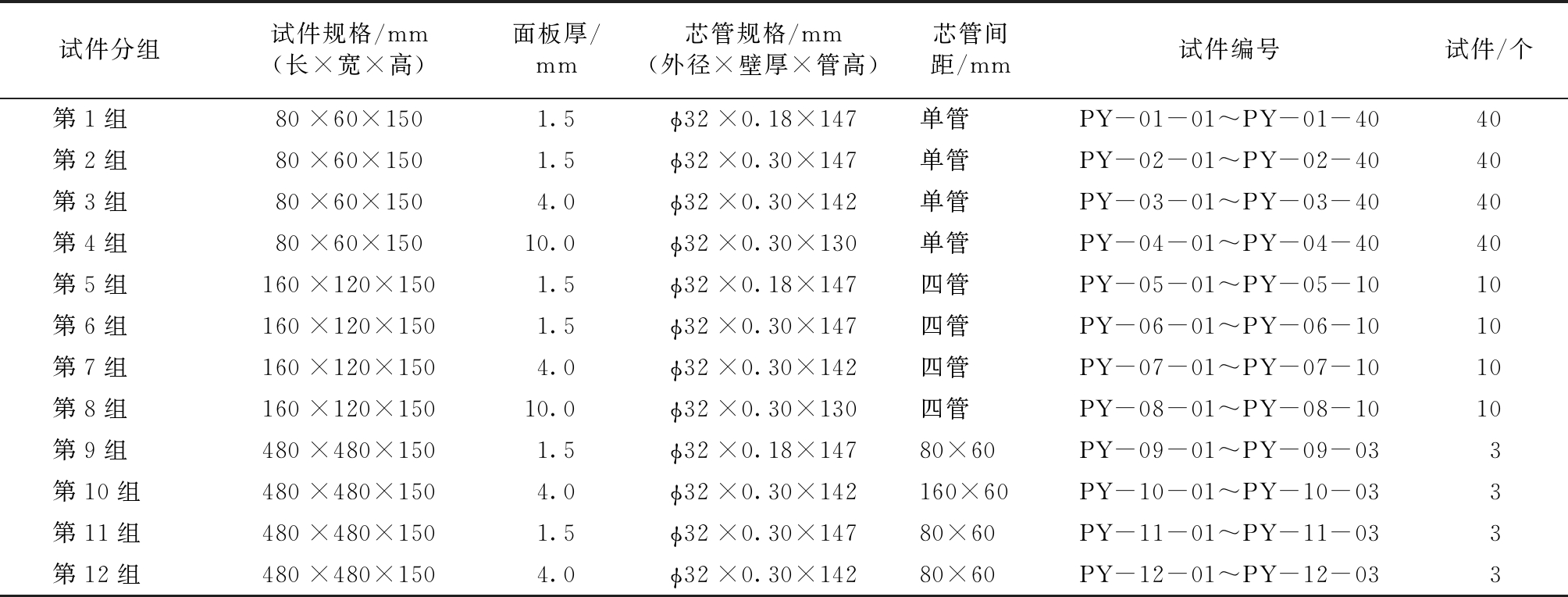
试件分组试件规格/mm(长×宽×高)面板厚/mm芯管规格/mm(外径×壁厚×管高)芯管间距/mm试件编号试件/个第1组80×60×1501.5ϕ32×0.18×147单管PY-01-01~PY-01-4040第2组80×60×1501.5ϕ32×0.30×147单管PY-02-01~PY-02-4040第3组80×60×1504.0ϕ32×0.30×142单管PY-03-01~PY-03-4040第4组80×60×15010.0ϕ32×0.30×130单管PY-04-01~PY-04-4040第5组160×120×1501.5ϕ32×0.18×147四管PY-05-01~PY-05-1010第6组160×120×1501.5ϕ32×0.30×147四管PY-06-01~PY-06-1010第7组160×120×1504.0ϕ32×0.30×142四管PY-07-01~PY-07-1010第8组160×120×15010.0ϕ32×0.30×130四管PY-08-01~PY-08-1010第9组480×480×1501.5ϕ32×0.18×14780×60PY-09-01~PY-09-033第10组480×480×1504.0ϕ32×0.30×142160×60PY-10-01~PY-10-033第11组480×480×1501.5ϕ32×0.30×14780×60PY-11-01~PY-11-033第12组480×480×1504.0ϕ32×0.30×14280×60PY-12-01~PY-12-033

a—单管; b—四管; c—大板。
图2 试件实物
Fig.2 The photos of the specimens
1.3 加载和量测装置
加载装置采用万能试验机,单管和四管试件采用55 kN电子万能试验机,在上、下加载平面用螺栓连接200 mm×200 mm×20 mm钢板,要求保证钢板平整。大板试件在600 kN液压万能试验机上加载,在试验机上、下加载平面各固定一块480 mm×480 mm×20 mm的钢板并设置加劲板,要求保证钢板平整。试验采用分级加载方式,预加载破坏荷载(采用有限元法模拟预估值)的15%,观察百分表的读数,若不对称,重新调整试件的位置,待试件两侧仪表读数一致后,卸至初载,然后以破坏荷载的5%为级差,按照0.5 mm/min的加载速度,分级加载至破坏为止,记录各级载荷和相应的变形值;达到破坏荷载之后,试验机连续加载,从而得到试件清晰明显的破坏形态。试件加载简图如图3所示。

图3 试件加载
Fig.3 Loaded specimens
试验的主要测试仪表为百分表。荷载由万能试验机直接读出,变形则用百分表来测量上、下面板位移的差值,以消除上、下面板与加载板之间的间隙。对于单管试件和四管试件,在上、下面板各焊接两个角钢,用百分表来测量角钢的位移值;在大板结构的上、下面板各焊接四个角钢,同样用百分表来测量角钢的位移,从而得到上、下面板的相对变形。测点布置见图4。
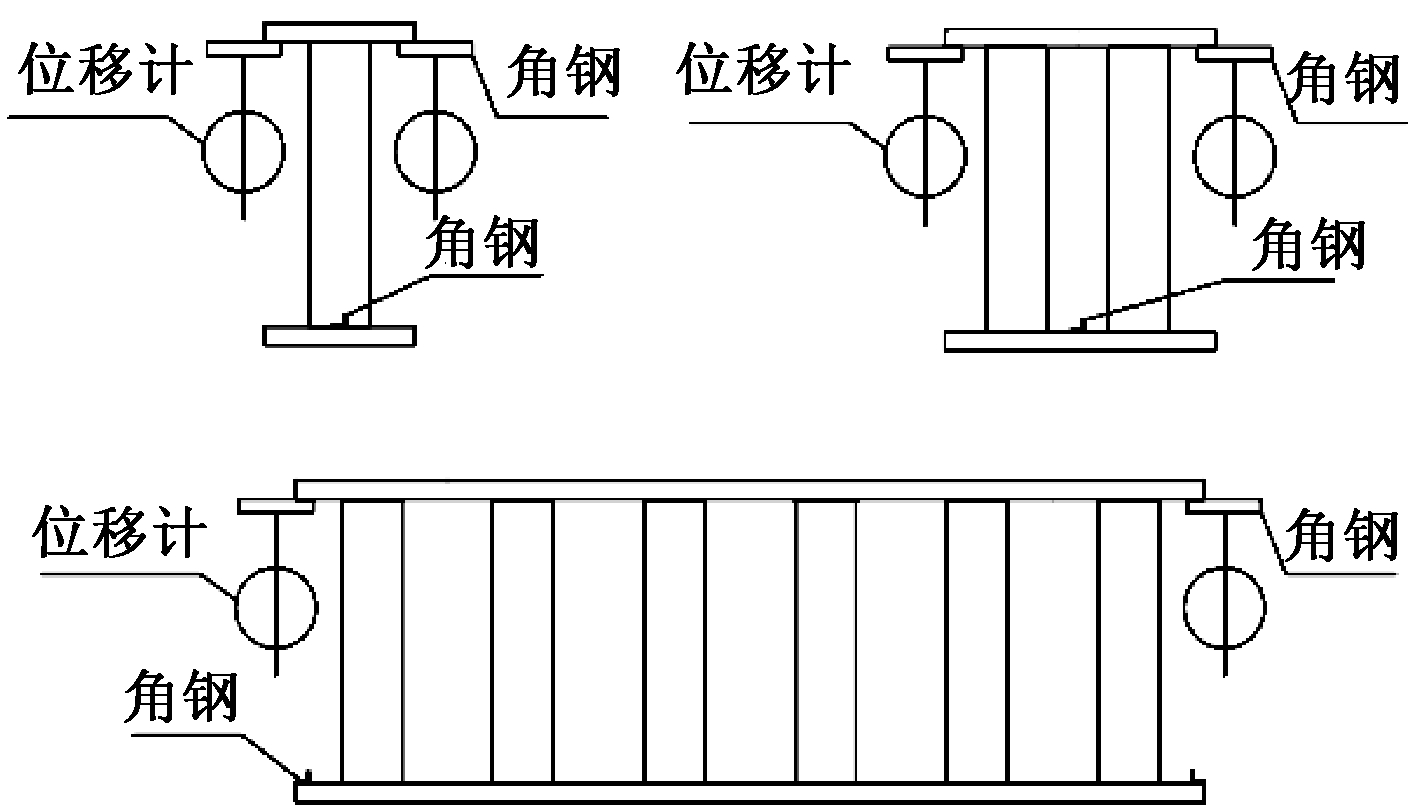
图4 测点布置示意
Fig.4 Schematic diagrams of measuring points arrangement
1.4 试验结果及现象
以各级荷载N为纵坐标,百分表测出的上、下面板间的相对位移平均值Δ为横坐标,绘制各组试件的荷载-位移曲线,每组典型的荷载-位移曲线,如图5、图6所示。
将荷载-位移曲线中直线段的终点称为拐点,将荷载达到最大值时对应的点称为极值点。表2列出了各组试件的拐点荷载平均值、极值点荷载平均值,并按照文献[11]给出的计算方法进一步计算出各组试件的拐点平压强度平均值、极值点平压强度平均值和平压模量平均值。
观察试验过程中芯管的变化和荷载-位移曲线的走势,试验加载可分为四个阶段:第一阶段为试件的接触阶段,由于试件上、下面板与加载板之间不可避免地存在间隙,此段加载过程为试件压紧过程(图7a),荷载-位移曲线较为平缓;第二阶段为试件的弹性阶段(图7b),此段曲线的斜率较为陡峭,试件本身没有肉眼可见的变形;第三阶段为弹塑性阶段,此阶段试件的芯管端部会出现少许的局部鼓曲(图7c),此段曲线的斜率会逐渐转为平缓;第四阶段为破坏阶段,当达到破坏荷载即荷载值不能继续增大时,芯管端部的局部鼓曲已较大,继续加载,鼓曲越来越大(图7d),荷载值逐渐减小。

a—第1组;b—第2组;c—第3组;d—第4组;e—第5组;f—第6组。
图5 第1~6组荷载-位移曲线
Fig.5 The load-displacement curves of test set 1 to 6
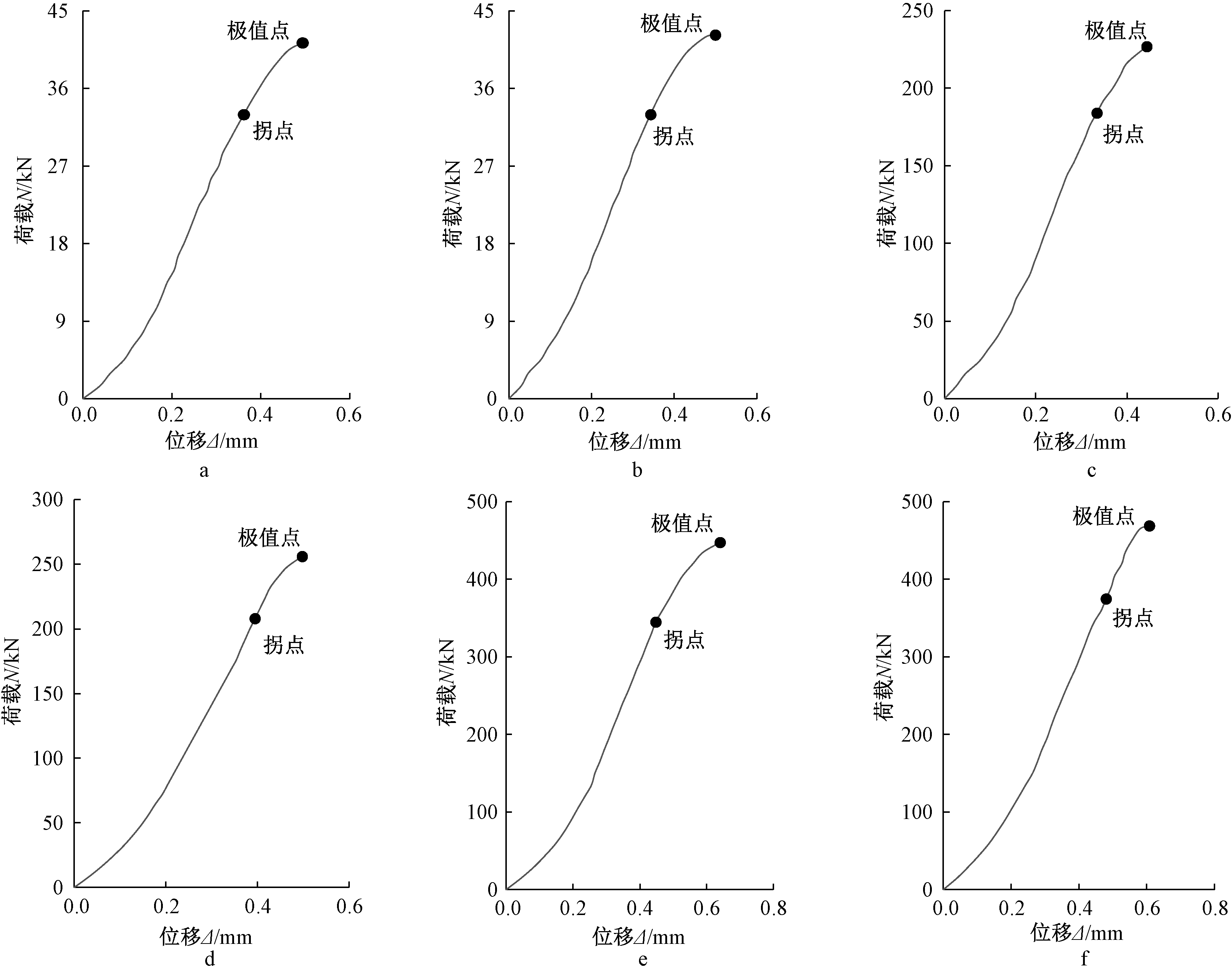
a—第7组;b—第8组;c—第9组;d—第10组;e—第11组;f—第12组。
图6 第7~12组荷载-位移曲线
Fig.6 The load-displacement curves of test set 7 to 12
表2 试验结果数据
Table 2 Test data
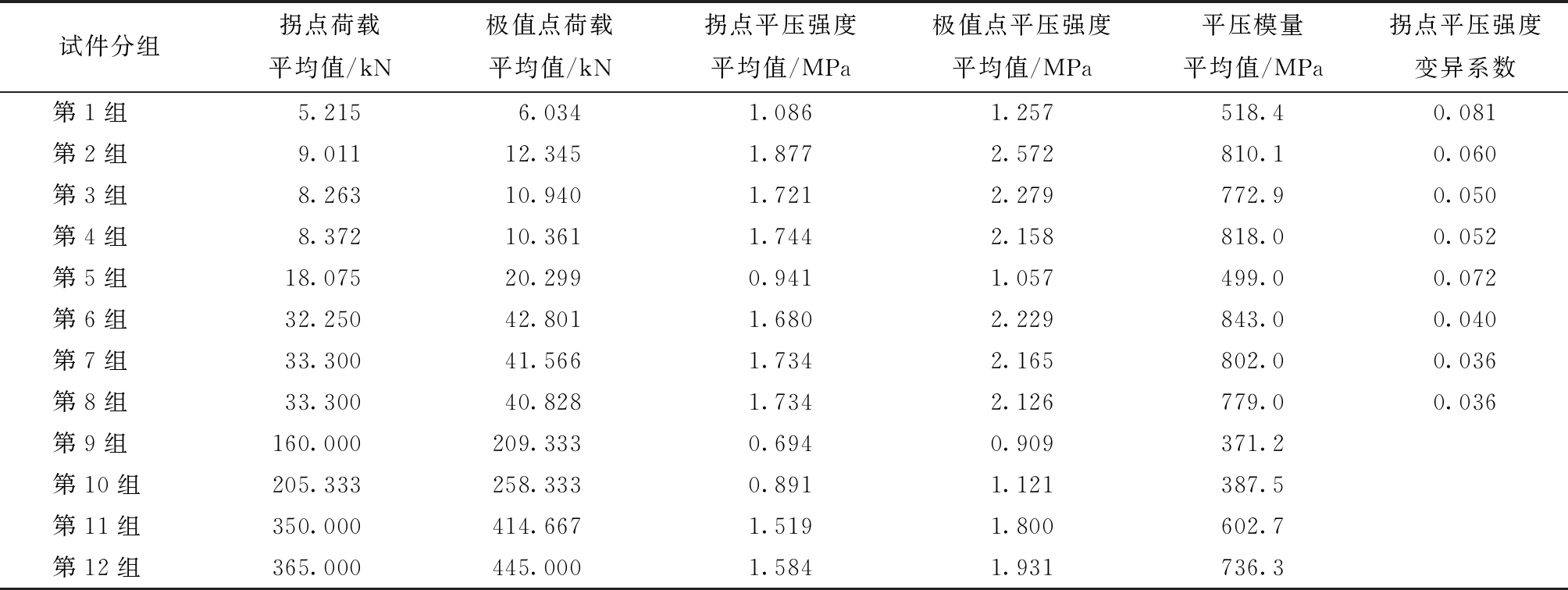
试件分组拐点荷载平均值/kN极值点荷载平均值/kN拐点平压强度平均值/MPa极值点平压强度平均值/MPa平压模量平均值/MPa拐点平压强度变异系数第1组5.2156.0341.0861.257518.40.081第2组9.01112.3451.8772.572810.10.060第3组8.26310.9401.7212.279772.90.050第4组8.37210.3611.7442.158818.00.052第5组18.07520.2990.9411.057499.00.072第6组32.25042.8011.6802.229843.00.040第7组33.30041.5661.7342.165802.00.036第8组33.30040.8281.7342.126779.00.036第9组160.000209.3330.6940.909371.2第10组205.333258.3330.8911.121387.5第11组350.000414.6671.5191.800602.7第12组365.000445.0001.5841.931736.3

a—芯管未发生变形; b—芯管无明显变形; c—芯管发生局部鼓曲; d—芯管发生较大鼓曲。
图7 试件变形过程
Fig.7 Specimens deformation process
1.5 试验结果分析
从试验现象可知:试件的破坏位置为芯管端部局部屈曲,这是由于试件制作过程中是通过挤压的方式将芯管管壁扩口并缩短至焊接长度,这样势必会使芯管端部存在较大的几何缺陷,使得芯管在受压的过程中容易发生端部的屈曲破坏。
比较第1、2组试件,两组试件的规格、面板厚度等参数完全相同,仅芯管的厚度不同。对比两组试件的试验结果,可得到增加芯管的厚度可以明显增加芯管的平压强度和平压模量。
比较第1、5组试件,两组试件的芯管厚度、面板厚度等参数完全相同,仅面板的面积即芯管个数不同。对比两组试件的试验结果,可得到第5组试件的试验结果偏小,这是由于试件在焊接过程中存在一定的偶然性,具有一定的离散性。第5组拐点平压强度平均值比第1组试验结果小13%,在可接受的范围之内。
比较第2~8组试验结果可以发现:第2组试验结果偏大,这是由于试验中存在着个别特例以及试件焊接过程中可能焊接时间过长等原因造成的;其余5组试验结果相差较小,可得到在试件高度150 mm不变的情况下,面板厚度从1.5 mm变到10.0 mm时,对芯管的平压强度和平压模量的影响较小,可以忽略不计。
对比单管试件与四管试件的试验结果可以发现:在面板厚度、芯管规格、芯管的间距等参数都一致的情况下,单管和四管试件的平压强度和平压模量基本一致,但是单管试件得到的平压强度和平压模量的离散性较大,而四管试件的离散性较小。
对比四管试件与大板试件的试验结果可以发现:在面板厚度、芯管规格、芯管间距等参数都一致的情况下,大板试件中第9~12组试件的平压强度和平压模量都比四管试件的平压强度和平压模量小,这是由于大板试件的芯管根数较多,芯管高度的不均匀以及面板的不均匀,都会导致加载过程中存在不均匀的现象,因此大板试件中第9~12组试验结果都偏小;而大板试件中第10组试件,在其他参数都不变的情况下,与芯管间距80 mm×60 mm的四管试件中第7组比较可以发现:第10组试件的平压强度和平压模量是第7组的一半,说明第10组的试验结果较准确;通过以上分析,可知大板试件中第10组结果较准确,这是由于第10组芯管的根数是第9~12组芯管根数的一半,会更容易做到均匀受压,所以结果比较准确。
通过以上分析可知:单管试件的离散性较大,大板试件很难做到均匀受压,因此选择四管试件的结果来计算平压强度和平压模量较为合理且稳定;芯管受压过程中,端部破坏是由于芯管制作过程中导致的初始几何缺陷所致;改变芯管壁厚和芯管间距对不锈钢芯管结构平压强度和平压模量有显著影响,增大芯管壁厚和减小芯管间距对提高不锈钢芯板结构平压性能具有良好的效果。
2 有限元分析
通过ABAQUS有限元分析软件建立有限元模型对上述试验过程进行模拟,并将有限元分析结果与试验结果进行对比,验证其准确性。
2.1 建立模型
根据试验结果,大板试件实测的平压强度和平压模量普遍偏小,因此建立了8个有限元模型,编号为1~8,分别与试验的前8组试件相对应,尺寸规格以及各种几何参数均与试件相同。
模型中的面板和芯管采用S4R四结点壳单元模拟;面板和芯管的材料为奥氏体S30408不锈钢,不锈钢芯管是通过冷轧工艺得到,冷轧会提高不锈钢屈服强度[10],芯管厂家提供的材料屈服强度为276 MPa,泊松比为0.3,弹性模量为1.93×105 MPa。根据文献[11]在有限元模型中采用Gardner-Nethercot两段线模型来模拟不锈钢材料的应力-应变曲线,如图8。有限元分析采用相同的拉压本构模型。
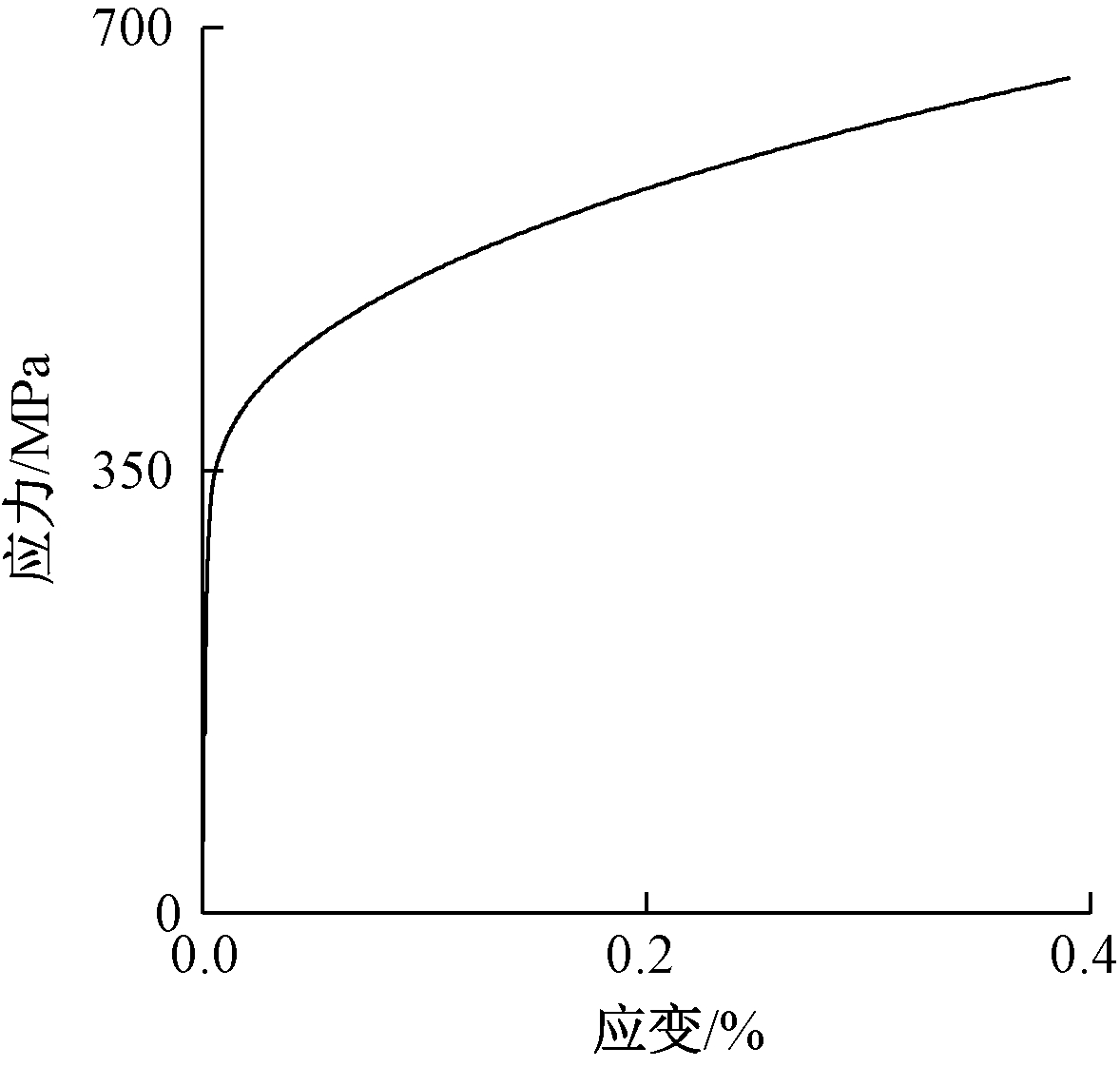
图8 不锈钢材料应力-应变简化模型
Fig.8 Stainless steel material stress-strain simplified model
模型计算分为两个环节,首先采用特征值屈曲分析,得到结构的屈曲模态;然后再根据得到的屈曲模态,为结构添加初始几何缺陷,采用riks分析计算,得到结构的荷载-位移曲线。有限元塑性分析采用von Mises屈服准则,采用关联流动法则,硬化法则为各向同性。荷载及边界条件的设置见图9,有限元模型网格划分见图10。
图9 荷载及边界条件
Fig.9 Load and boundary conditions

图10 整体模型网格划分
Fig.10 Meshing of the overall model
2.2 有限元分析结果与试验结果对比
将8个有限元模型计算得到的荷载-位移曲线与相对应的各组试验的典型荷载-位移曲线进行对比,结果见图11,表3~5。
在有限元结果中,所有模型的破坏位置均为芯管端部局部屈曲破坏,与试验现象较为吻合。图12为有限元模型与试验中试件的变形模式对比,可以看出:无论是拐点时芯管端部稍许的局部鼓曲还是破坏阶段芯管端部较大的屈曲破坏形态,有限元模型与试验中试件的变形模式都十分吻合。
从上一节的分析可知:试验曲线的第一阶段为试件的接触阶段,此阶段不会在有限元模型中出现,因此将试验曲线去掉第一阶段,然后将第二阶段即弹性阶段的曲线向下延伸至x轴,并将曲线平移至坐标原点;然后就可以得出第1~8组的试验曲线与有限元曲线吻合良好。从上一节可知:第2组试验结果偏大,第5组试验结果偏小,因此从对比曲线可以看出:第2组的试验曲线比有限元曲线要高,第5组的试验曲线比有限元曲线要矮;因此从整体上看,有限元模型非常准确地反映了试验结果,从而验证了有限元结果的准确性。
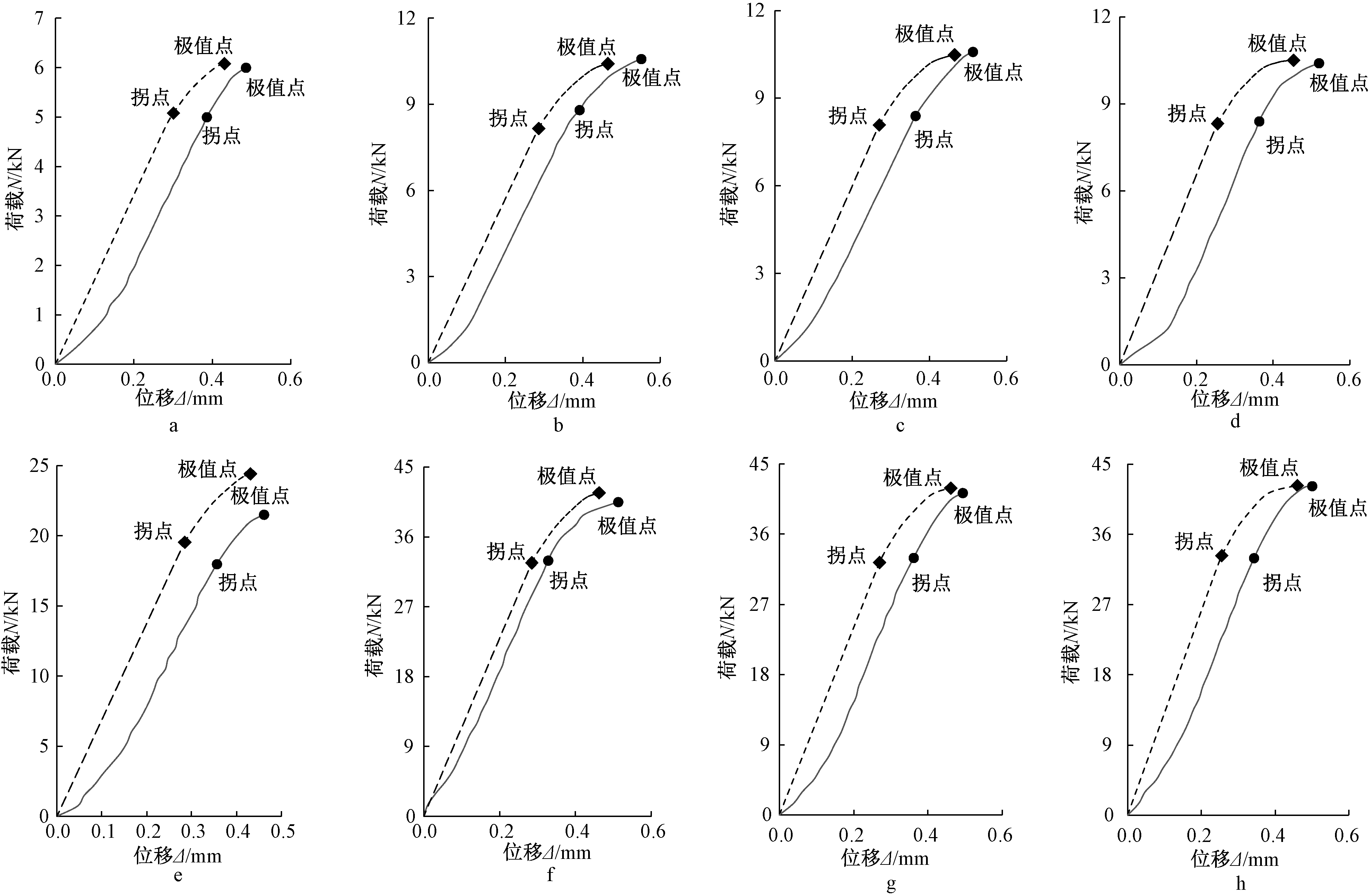
a— 第1组; b—第2组; c—第3组; d—第4组; e—第5组; f—第6组;g—第7组;h—第8组。
图11 第1~8组模型有限元模型计算对比曲线
Fig.11 The comparisons of FEM calculation curves of set 1 to 8
表3 有限元分析与试验所得的拐点荷载值对比
Table 3 Comparisons of inflection point load values obtained by finite element analysis and experiment
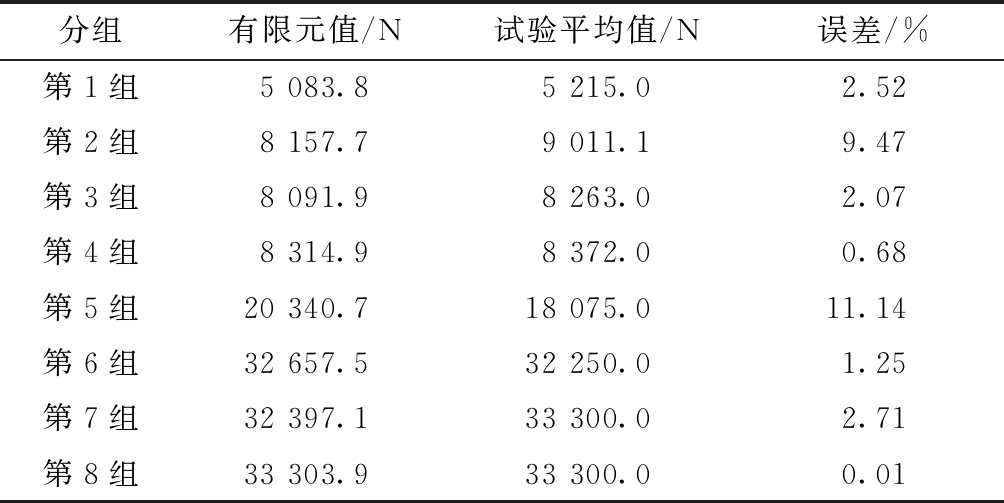
分组有限元值/N试验平均值/N误差/%第1组5 083.85 215.02.52第2组8 157.79 011.19.47第3组8 091.98 263.02.07第4组8 314.98 372.00.68第5组20 340.718 075.011.14第6组32 657.532 250.01.25第7组32 397.133 300.02.71第8组33 303.933 300.00.01
表4 有限元分析与试验所得的极值点荷载值对比
Table 4 Comparisons of ultimate point load values obtained by finite element analysis and experiment
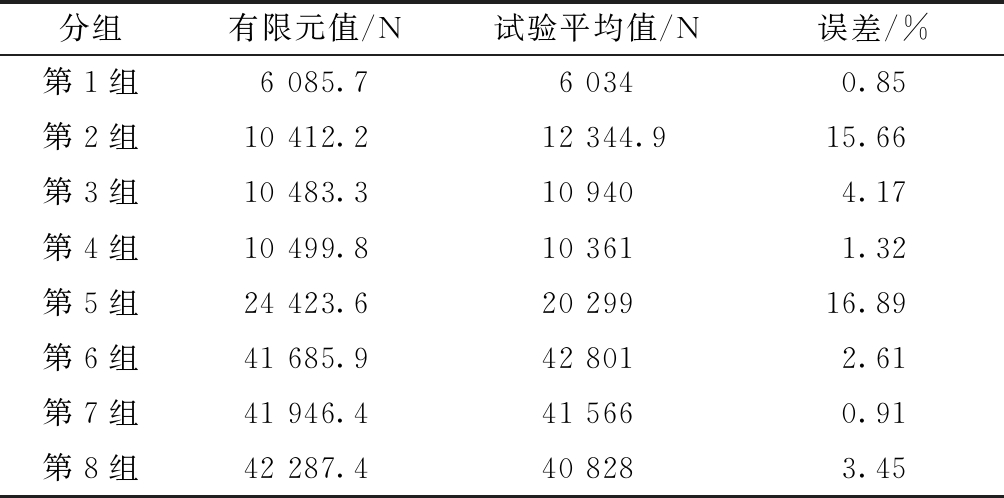
分组有限元值/N试验平均值/N误差/%第1组6 085.76 0340.85第2组10 412.212 344.915.66第3组10 483.310 9404.17第4组10 499.810 3611.32第5组24 423.620 29916.89第6组41 685.942 8012.61第7组41 946.441 5660.91第8组42 287.440 8283.45
表5 有限元分析与试验所得的平压模量对比
Table 5 Comparisons of compression moduli obtained by finite element analysis and experiment
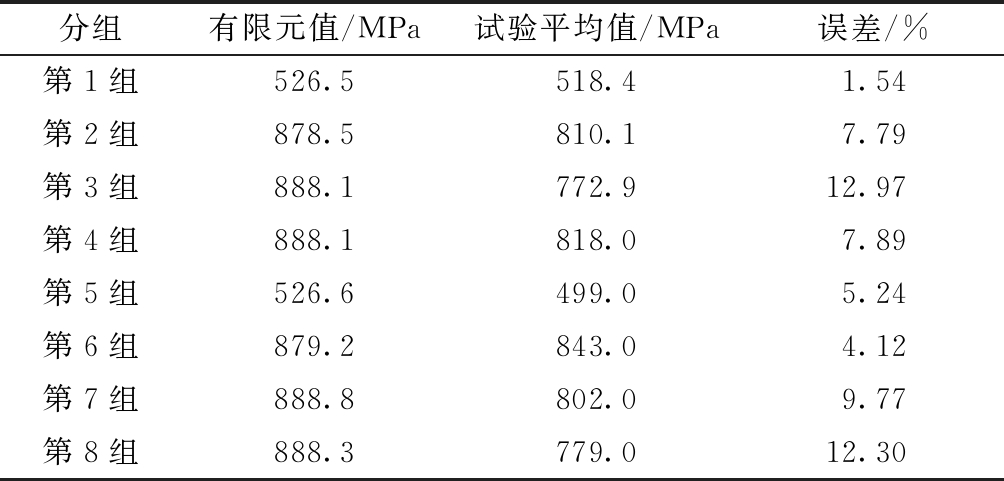
分组有限元值/MPa试验平均值/MPa误差/%第1组526.5518.41.54第2组878.5810.17.79第3组888.1772.912.97第4组888.1818.07.89第5组526.6499.05.24第6组879.2843.04.12第7组888.8802.09.77第8组888.3779.012.30
由此可见,有限元分析结果与试验结果吻合良好,本文的有限元模型能够准确地模拟试验过程,具有参考价值。
3 理论分析
3.1 受力过程及破坏机理分析
以第5组模型为例,深入分析不锈钢芯板结构芯管在平压作用下的受力过程和破坏机理。如图13所示,不锈钢芯板结构芯管在平压作用下的受力过程可以分为三个阶段:弹性阶段、弹塑性阶段和破坏阶段。

图12 有限元模型与试件变形模式对比
Fig.12 Deformation mode comparisons between finite element models and specimens
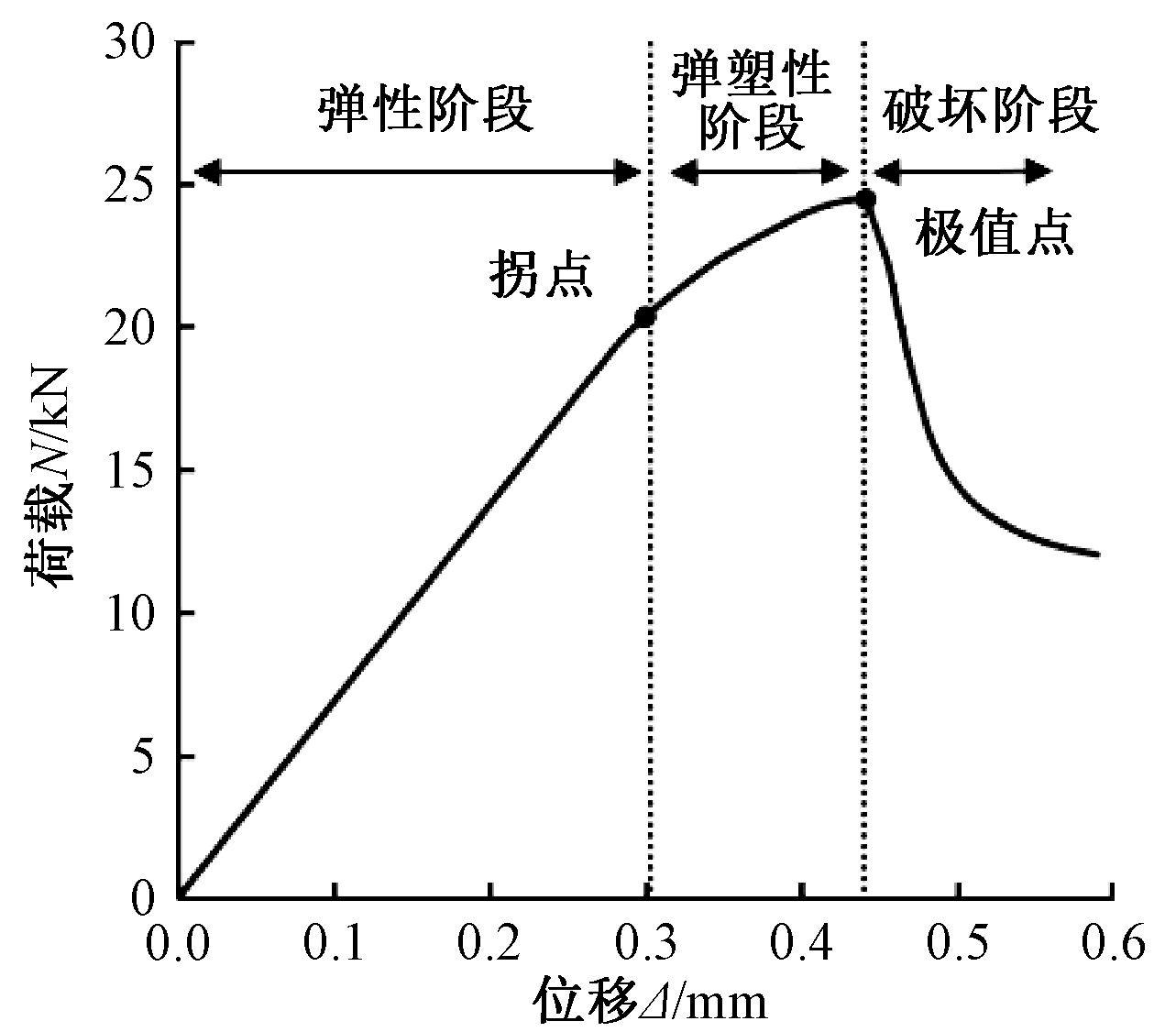
图13 芯管受力阶段示意
Fig.13 Schematic diagram of core tube at stress stage
3.1.1 弹性阶段
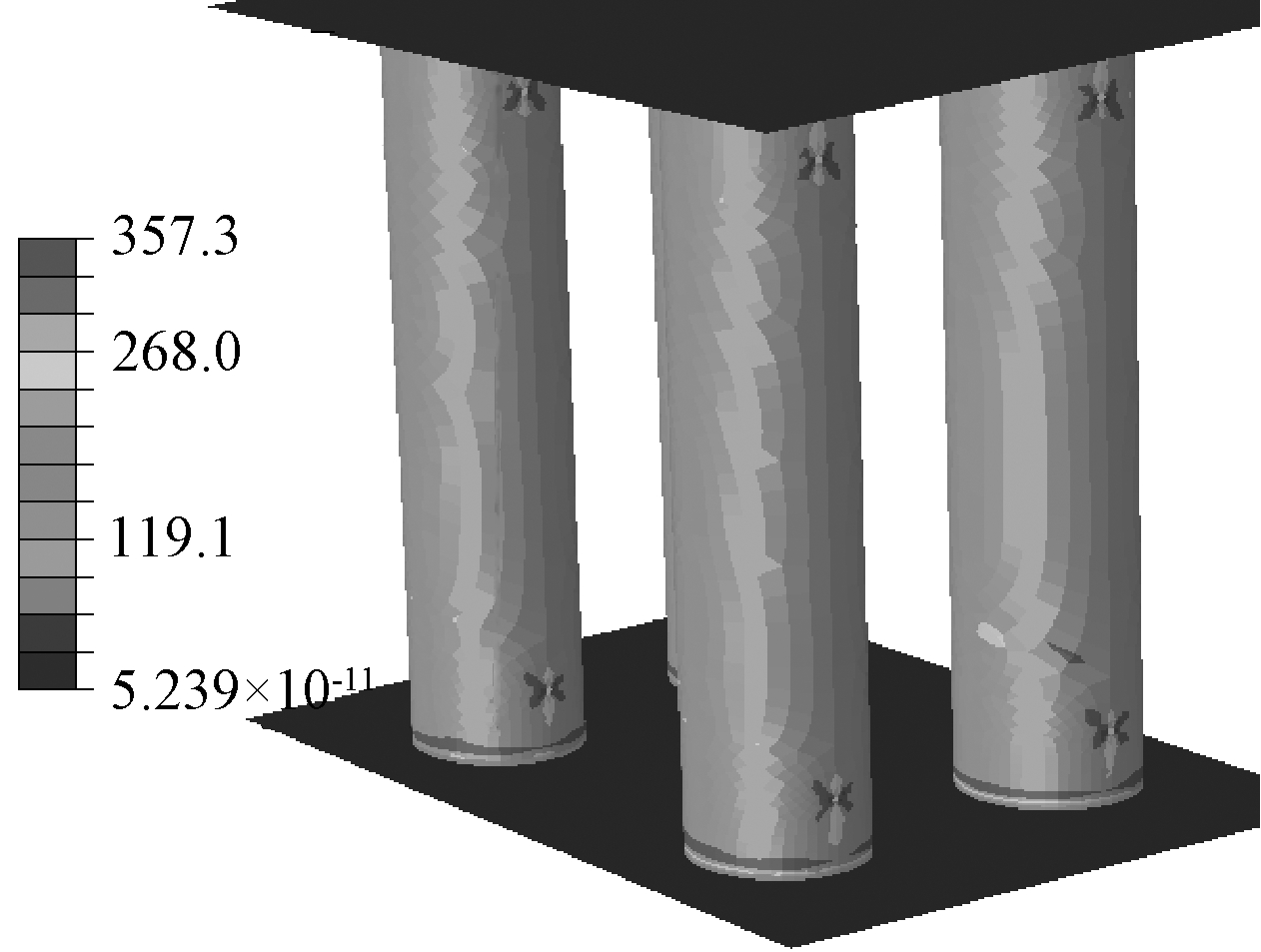
图14 弹性阶段结束时的von Mises应力云图 MPa
Fig.14 The von Mises stress contour at the end of elastic stage
在弹性阶段,荷载与位移呈线性关系,且曲线的斜率较大,直到芯管的部分截面屈服,曲线的斜率降低出现拐点,弹性阶段结束。从图14所示的荷载-位移曲线拐点处有限元模型的等效应力云图可见:芯管中部大部分的全截面应力分布非常均匀;而芯管端部的部分截面已经进入塑性阶段,此块区域部分点的应力已经超过了材性试验实测的芯管的屈服强度276 MPa。
3.1.2 弹塑性阶段
弹性阶段结束后,芯管进入弹塑性阶段,此阶段曲线斜率越来越小,荷载-位移曲线逐渐趋于平缓,直到出现荷载极值点。在此阶段过程中,芯管端部区域应力值逐渐增大,直到应力达到临界屈曲应力值时,芯管端部出现少许鼓曲的现象,发生局部屈曲,此时曲线达到极值点,不再上升,弹塑性阶段结束。由图15所示的荷载-位移曲线极值点处有限元模型的等效应力云图可见:芯管端部出现少许鼓曲,整个截面达到临界屈曲应力值;而芯管中部截面部分区域达到临界屈曲应力值。

图15 弹塑性阶段结束时的von Mises应力云图 MPa
Fig.15 The von Mises stress contour at the end of elastic-plastic stage
3.1.3 塑性破坏阶段
越过极值点以后,荷载-位移曲线出现下降段,位移仍在继续增长,而荷载则突然下降,此时芯管已经丧失了承载能力。
从以上分析可知:不锈钢芯板结构芯管在平压荷载作用下的破坏本质是芯管端部全截面达到临界屈曲应力值,此时芯管端部出现稍许鼓曲的现象,发生局部屈曲破坏。荷载-位移曲线的拐点实质上对应于芯管端部部分截面达到屈服点时的状态,拐点处的荷载值就是芯管在弹性阶段的平压承载力,称之为芯管弹性平压承载力Ny;荷载-位移曲线极值点处的荷载值就是芯管的极限平压承载力,称之为芯管极限平压承载力Nu。从上一节分析可知:有限元值与试验值吻合良好,因此取有限元分析值作为各组试件的芯管弹性平压承载力和芯管极限平压承载力,见表6。
进入弹塑性阶段之后,芯管开始发生塑性变形,荷载-位移曲线趋于平缓,变形较大,已经不适宜继续承载,出于对控制变形和强度储备等因素的考虑,以芯管弹性平压承载力Ny作为不锈钢芯板结构芯管设计计算时所采用的平压承载力标准值,用Nyk来表示。
表6 各组试件的芯管弹性平压承载力和芯管极限 平压承载力
Table 6 Elastic compression bearing capacity and ultimate compression bearing capacity for the core tube of specimen in each group N
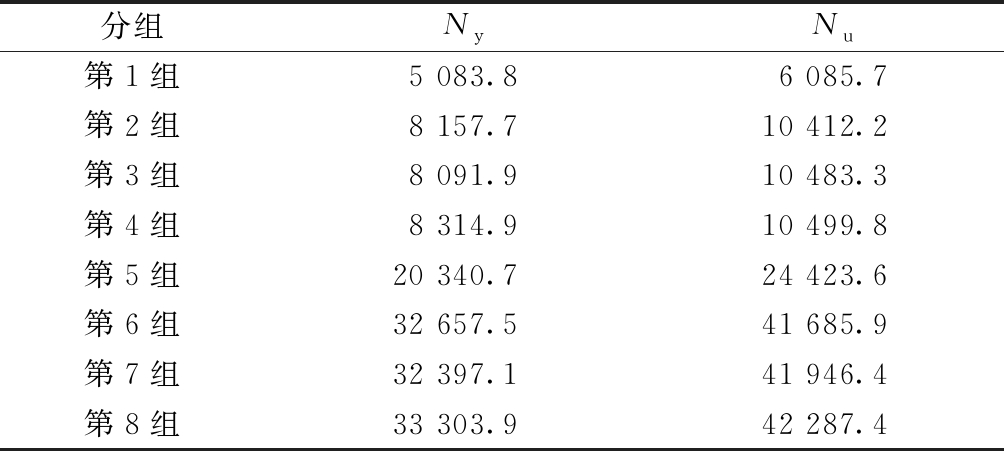
分组NyNu第1组5 083.86 085.7第2组8 157.710 412.2第3组8 091.910 483.3第4组8 314.910 499.8第5组20 340.724 423.6第6组32 657.541 685.9第7组32 397.141 946.4第8组33 303.942 287.4
3.2 芯管平压承载力计算式
由于芯管处于拐点处时,芯管中部全截面应力都比较均匀,而此时芯管的变形很小,肉眼几乎无法察觉,此时芯管平压承载力标准值Nyk为:
Nyk=λfy A
(1)
式中:fy为S30408不锈钢的屈服强度,取276 MPa;A为芯管横截面面积;λ为固定参数。
用表6中的芯管弹性平压承载力来确定式(1)中的λ值,fy取276 MPa,λ值的计算值见表7。
表7 参数λ的计算
Table 7 Calculation of the parameter λ
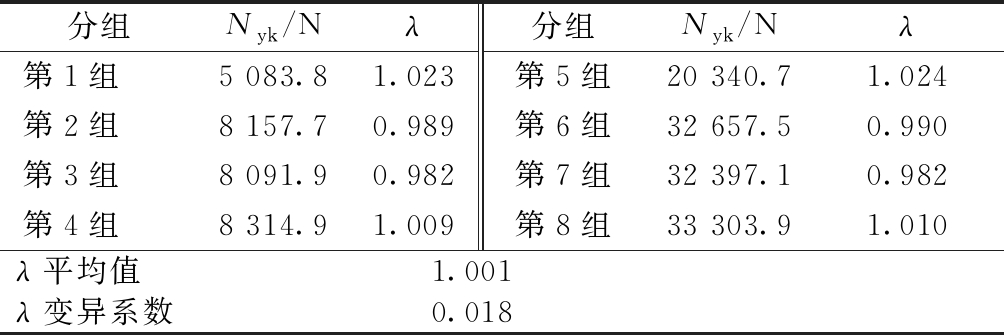
分组Nyk/Nλ分组Nyk/Nλ第1组5 083.81.023第5组20 340.71.024第2组8 157.70.989第6组32 657.50.990第3组8 091.90.982第7组32 397.10.982第4组8 314.91.009第8组33 303.91.010λ平均值1.001λ变异系数0.018
从表7可以得知:λ的变异系数非常小,因此λ值的变化范围很小,为了在实际应用中简化计算,可近似取λ平均值为一定值,并将十分位以后的数字都略掉,就有λ=1.0。因此有:
Nyk=0.8fy A
(2)
在结构设计时可以偏于安全地取CECS 410∶2015《不锈钢结构技术规程》[12]中的S30408不锈钢的抗拉、抗压和抗弯强度设计值f作为材料强度,从而得到此种不锈钢芯板结构芯管的平压承载力设计值Ny的计算式:
Ny=0.8fA
(3)
根据式(3),结合文献[11]的计算方法,可以计算出不锈钢芯板结构芯管平压强度设计值:
(4)
式中:S为不锈钢芯板结构芯板面积。
4 结束语
针对不锈钢芯板结构芯管的平压性能进行了试验研究和有限元分析,通过分析得出以下结论:
1)不锈钢芯板结构芯管的破坏发生在芯管端部靠近面板的部位,是由于在芯管制作和加工过程中对芯管端部的几何缺陷较大。
2)单管试验与四管试验得到的平压强度和平压模量大致相同,但单管试验的试验结果离散性较大;而大板试验的平压强度和平压模量普遍偏小,这是由于试验过程中加载不均匀造成的;因此选择四管试验的试验结果较为稳定。
3)不锈钢芯板结构,当高度为150 mm,面板厚度在1.5~10.0 mm变化时,结构的平压强度和平压模量变化很小,因此可以忽略面板厚度对平压强度和平压模量的影响;另一方面,改变芯管壁厚和芯管间距对不锈钢芯管结构平压强度和平压模量有显著影响,增大芯管壁厚和减小芯管间距对提高不锈钢芯板结构平压性能具有良好的效果。
4)通过理论分析确定了不锈钢芯板结构芯管在平压荷载作用下的受力过程可以分为弹性、弹塑性和破坏三个阶段,芯管破坏的本质是芯管端部发生局部屈曲破坏。
5)得到了各组试件的芯管弹性平压承载力和芯管极限平压承载力,并以弹性平压承载力来作为平压承载力标准值,然后给出了此种不锈钢芯板结构芯管平压承载力设计值的理论计算式。
6)建议对不锈钢芯板结构进行结构设计时,不锈钢芯板结构芯管的平压模量取值为四管试验的平压模量平均值,而平压强度偏于安全地按照文中给出的平压强度设计值进行计算。
[1]中华人民共和国质量监督检验检疫总局. 夹层结构或芯子平压性能试验方法:GB/T 1453—2005[S]. 北京:中华人民共和国质量监督检验检疫总局,2005.
[2]AMERICAN SOCIETY OF TESTING MATERIALS(ASTM) INTERNATIONAL. Standard Test Method for Flatwise Compressive Properties of Sandwich Cores: C365/C365M-11a[S]. West Conshohocken, PA, USA:ASTM,2011.
[3]王俊, 樊喜刚. 轻质蜂窝结构压缩性能的测试[J]. 理化检验:物理分册, 2014, 50(4):261-265.
[4]王塞北. 焊接蜂窝铝板平压力学性能数值模拟研究[D]. 昆明:昆明理工大学, 2010.
[5]彭明军. 钎焊蜂窝铝板力学性能研究[D]. 昆明:昆明理工大学, 2013.
[6]彭明军, 孙勇, 沈黎,等. 面板对钎焊蜂窝铝板平压性能的影响[J]. 材料导报, 2006, 20(11):471-472.
[7]王登峰, 曹平周. 考虑焊缝几何缺陷影响时整体与局部轴向压力共同作用下薄壁圆柱壳稳定性分析[J]. 工程力学, 2009, 26(8):65-73.
[8]MILADI S, RAZZAGHI M S. A Parametric Study on Inelastic Buckling in Steel Cylindrical Shells with Circular Cutouts[J]. International Journal of Advanced Structural Engineering, 2014, 6(1):47.
[9]UMBARKAR K R, PATTON L M, SINGH K D. Effect of Single Circular Performation in Lean Duplex Stainless Steel (LDSS) Hollow Circular Stub Columns Under Pure Axial Compression[J]. Thin-Walled Structures, 2013, 68(10):18-25.
[10]周翠兰, 刘红梅, 白晋钢, 等. 冷轧变形量对304不锈钢力学性能的影响[J]. 钢铁, 2012, 47(10):70-75.
[11]袁焕鑫. 焊接不锈钢轴心受压构件局部稳定和相关稳定性能研究[D]. 北京:清华大学, 2014.
[12]中国工程建设协会标准.不锈钢结构技术规程:CECS 410∶2015[S].北京:中国计划出版社,2015.