拆装式箱型房屋是一种以轻钢为骨架、以夹芯板为围护材料的环保经济型活动房屋,该房屋以标准模数进行空间组合,构件采用螺栓连接,具有易拆装重组、使用寿命长、周转次数多的特点。现在可拆装式箱型房屋已经在一些建筑工地、商店、展厅、办公室等建筑中得到应用。目前,国内外学者对箱型房屋的研究主要集中在集装箱式房屋上[1-4],而对拆装式箱型房屋的理论和试验研究较少。陈世云对拆装式箱型房屋做了优化设计[5]。尹静等对拆装式房屋的压缩单元进行了刚性试验,分析了在运输过程中压缩单元能否满足刚性要求[6]。张俊峰等对拆装式箱型房屋进行了底框结构竖向分级加载试验,分析了拆装式箱型房屋整体抗弯刚度和立柱与顶底框连接处的半刚性性能[7]。拆装式箱型房屋立柱与顶底框采用螺栓连接,梁柱截面均为冷弯薄壁型非对称开口截面、结构受力复杂,相较于集装箱式房屋竖向抗弯刚度小,而这方面的理论和试验研究很少。
在对拆装式箱型房屋进行的足尺寸模型竖向分级加载试验[7]的基础上,采用有限元分析软件ABAQUS 6.10对试验进行了模拟分析,对比了底框梁1/4截面、跨中以及底框中心处的荷载-位移曲线,验证有限元模拟分析的可靠性,最后基于有限元模拟,分析了底框硅酸钙板楼板、角件开孔、立柱与顶底框的螺栓连接刚度、角件角部约束4个因素对底框抗弯刚度的影响。
1 试 验
采用1∶1足尺寸模型进行了试验,拆装式箱型房屋全箱长6 055 mm,宽3 000 mm,高2 790 mm,如图1所示。顶框梁、底框梁分别与角件焊接形成顶框和底框,顶框、底框角件和立柱通过螺栓连接,如图2所示。底框横向设有卷边C型钢构成的次梁,次梁上按照实际铺设15 mm厚的硅酸钙盖板,以便于施加荷载。试验箱型房屋直接放置于0.5 mm高的刚性支座上,类似于铰接。底框梁和立柱截面均为冷弯薄壁型非对称开口截面,其截面的公称几何尺寸和实测尺寸见图3和表1、表2,底框梁按正立面和背立面分为LA、LB,4个立柱按逆时针顺序分别命名为ZA、ZB、ZC、ZD,如图1b所示。
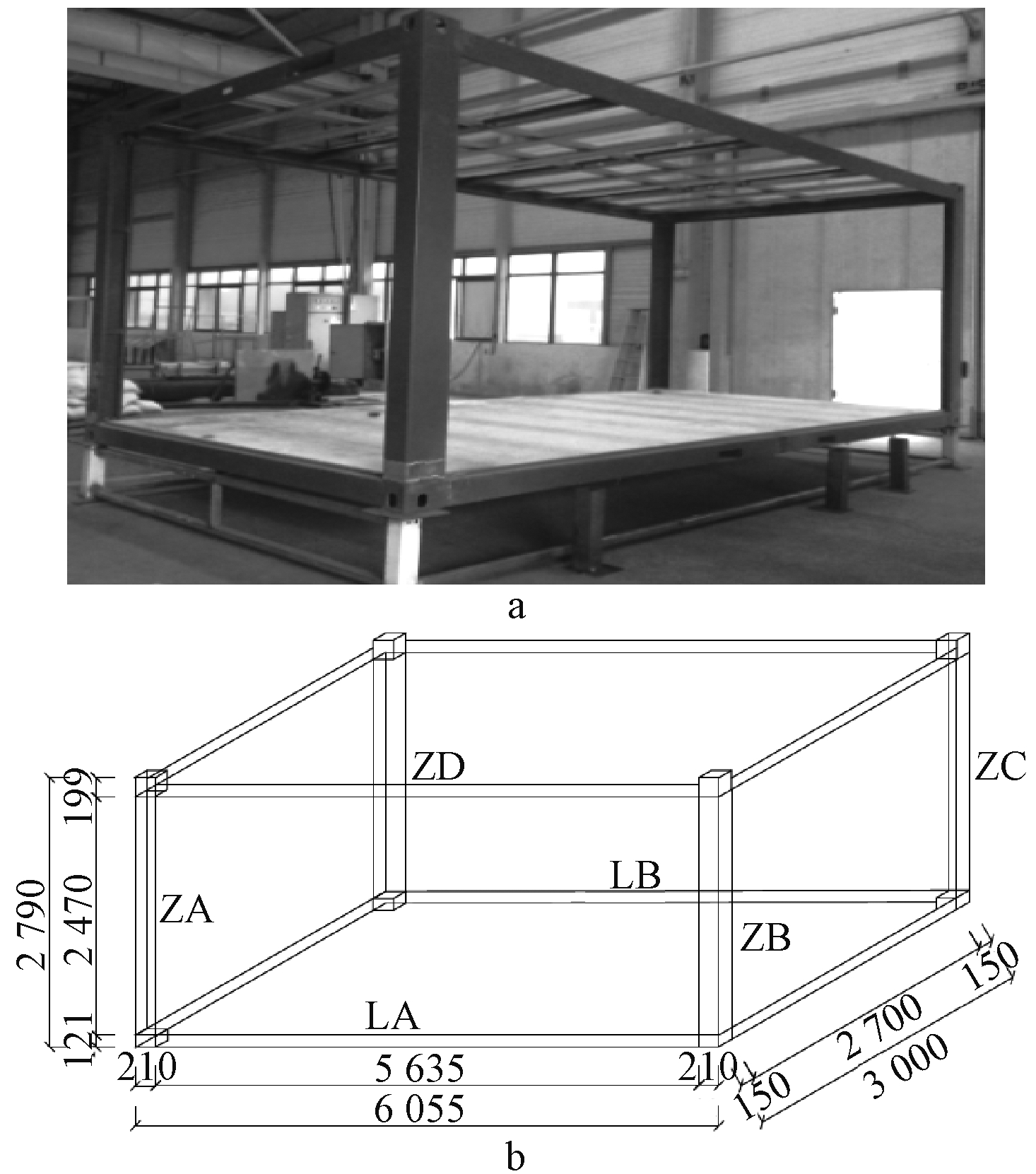
a—试验模型; b—试验模型尺寸。
图1 拆装式箱型房屋试验模型
Fig.1 Removable box house test model
主梁和立柱均采用3 mm厚的Q345钢,屈服强度为365 MPa,抗拉强度为518 MPa,断后伸长率为32.5%,弹性模量为E=2.08×105 MPa;梁柱连接板采用20 mm的Q345钢,材性试验平均屈服强度为360 MPa,平均抗拉强度为510 MPa,断后伸长率为34%,弹性模量为E=2.08×105 MPa。螺栓采用8.8级高强螺栓,直径为12 mm,平均屈服强度为640 MPa,平均抗拉强度为800 MPa,弹性模量为E=2.06×105 MPa。
试验采用了竖向分级加载试验方案,每级荷载持荷时间为5 min,试验加载方案见图4。
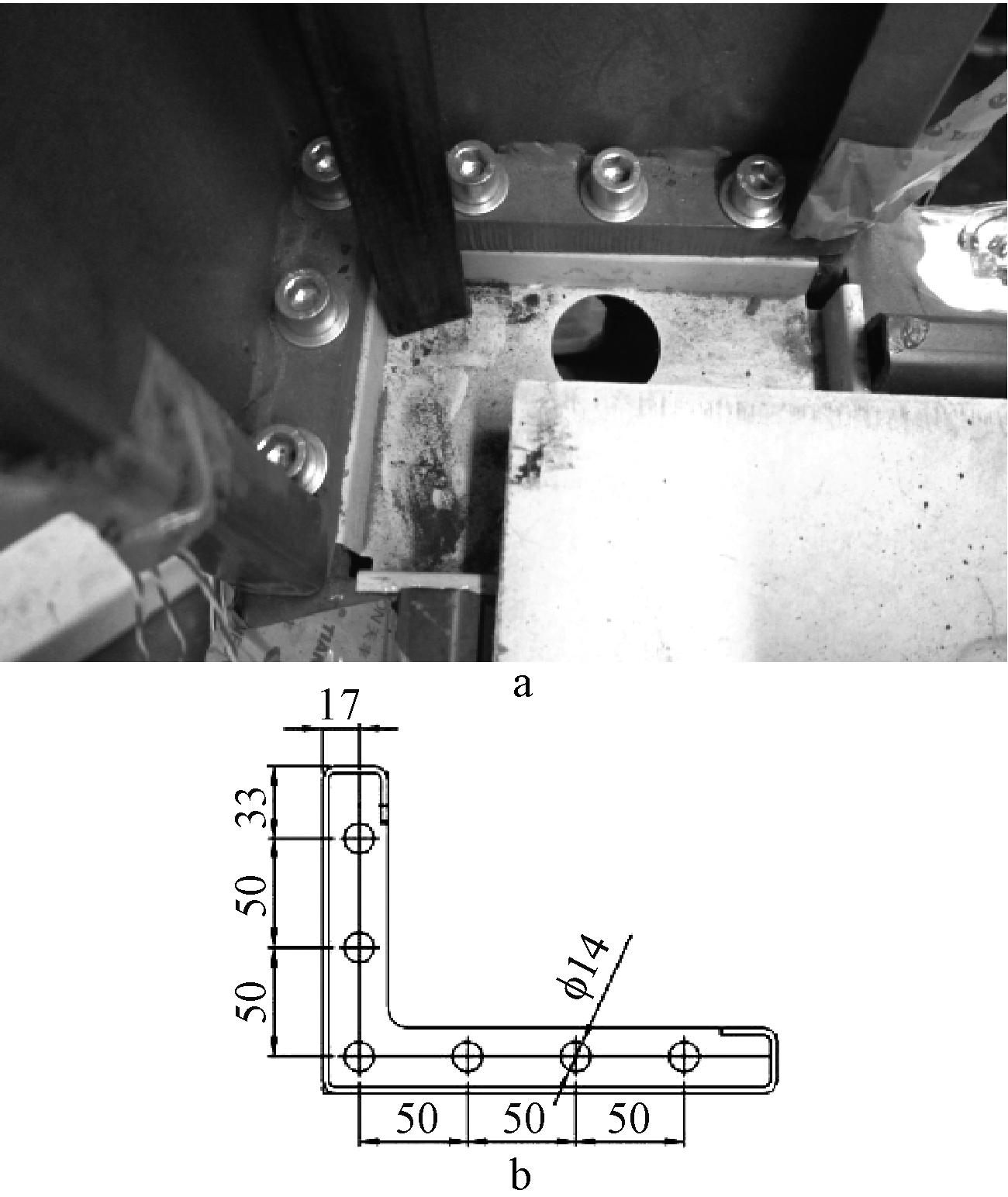
a—照片; b—截面尺寸。
图2 立柱与顶底框角件连接节点
Fig.2 Connection column and the top of bottom frame corner
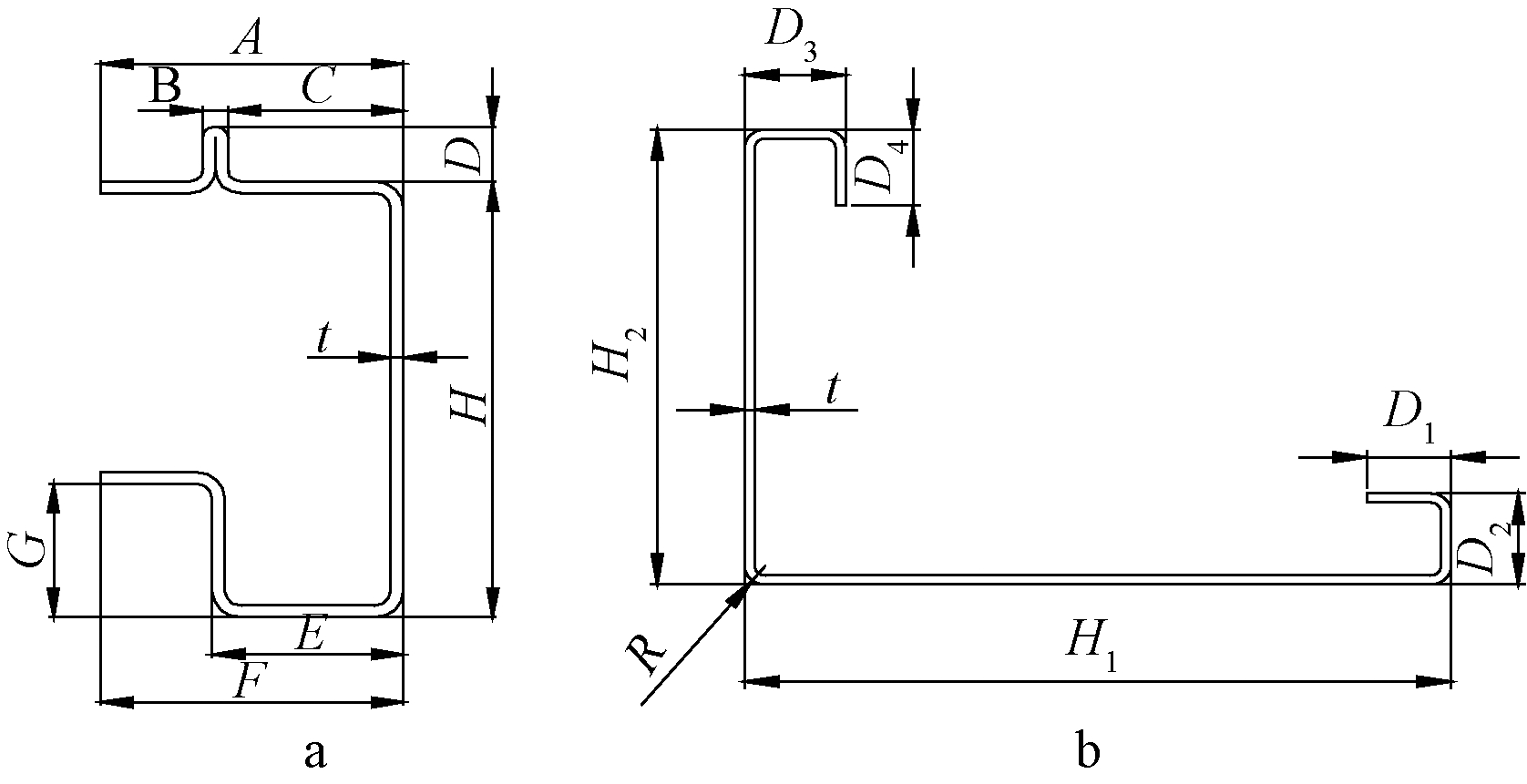
a—底框梁; b—立柱。
图3 底框梁和立柱截面几何尺寸
Fig.3 Geometric sizes of bottom frame beam and column section
表1 底框梁公称尺寸和实际尺寸
Table 1 Nominal size and actual size of bottom frame beam
mm

尺寸公称实际LALBt3.002.882.87H121.00120.50120.50A90.2089.7089.50B8.208.158.17C55.0054.5054.70D20.0019.8019.70E50.0049.5049.70G92.0091.8091.70
表2 立柱公称尺寸和实际尺寸
Table 2 Nominal size and actual size of column mm
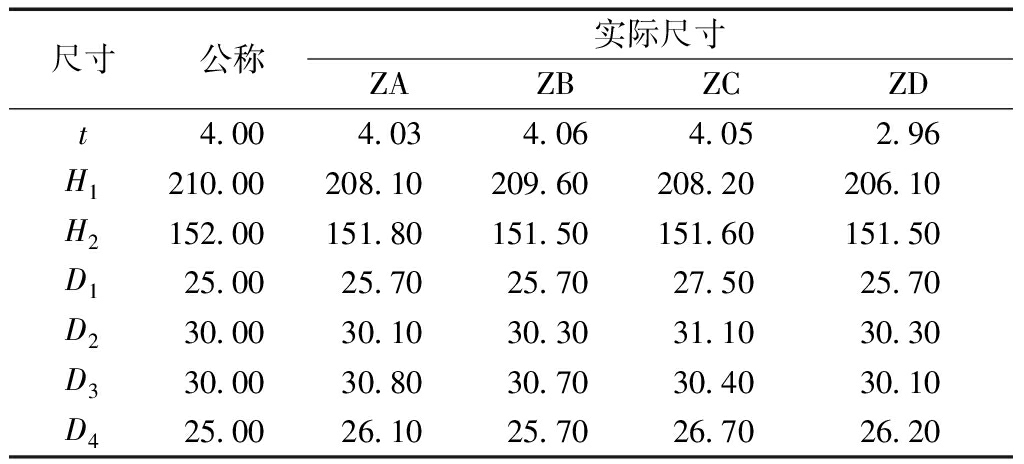
尺寸公称实际尺寸ZAZBZCZDt4.004.034.064.052.96H1210.00208.10209.60208.20206.10H2152.00151.80151.50151.60151.50D125.0025.7025.7027.5025.70D230.0030.1030.3031.1030.30D330.0030.8030.7030.4030.10D425.0026.1025.7026.7026.20
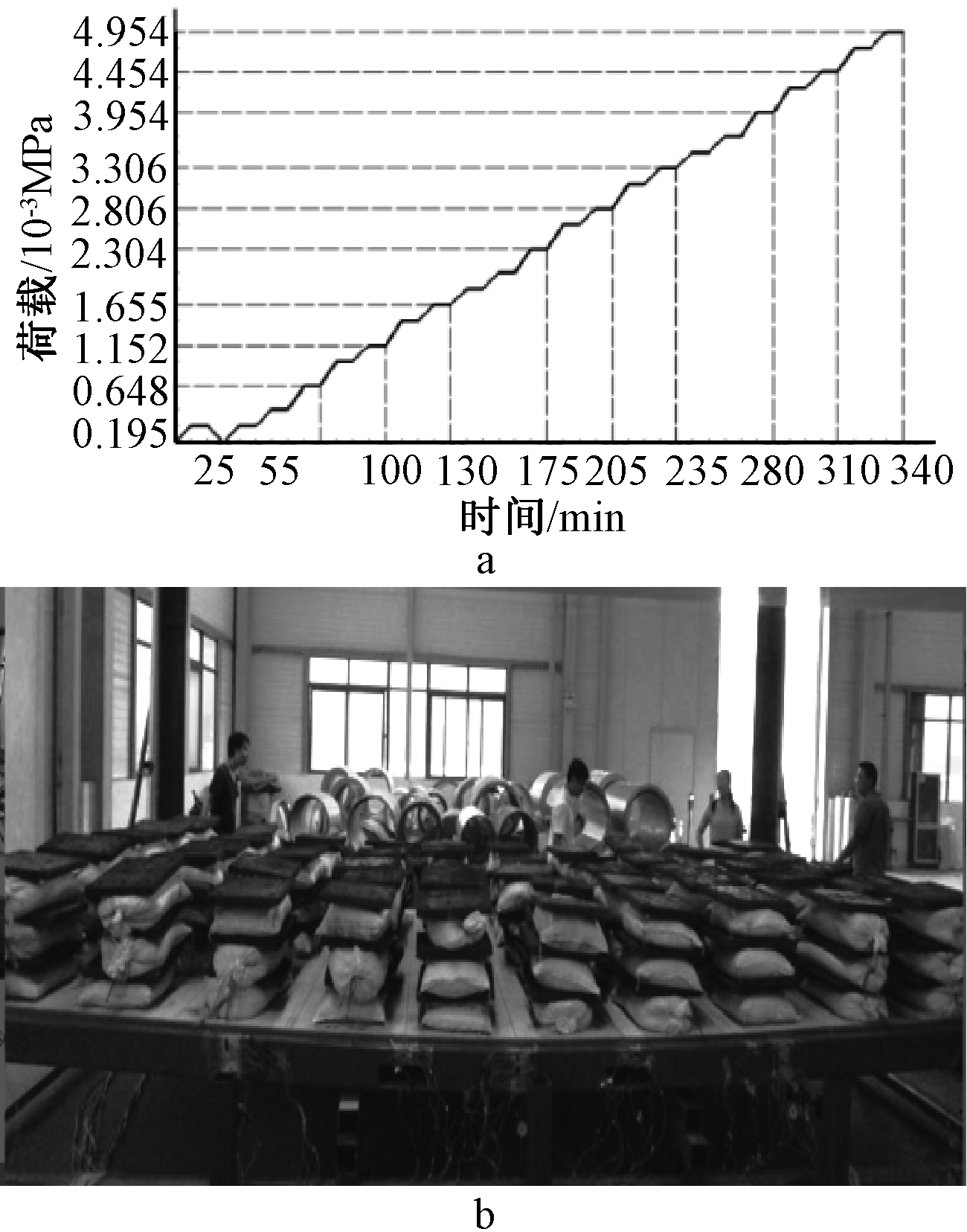
a—试验荷载加载方案; b—试验加载。
图4 试验加载方案
Fig.4 Test loading scheme
图5a为底框梁LA和LB的1/4截面处LA1、LA5、LB1及LB3的荷载-位移曲线,由图5a可知:当荷载小于2.30 kPa时,荷载-位移曲线处于线性阶段。图5b为底框梁跨中LA3、LB2和底框中心的荷载-位移曲线,当荷载达到1.07 kPa时,LA3位移为12.1 mm,为底框梁长度的1/500。当荷载达到2.06 kPa时,跨中LA3位移为24.22 mm,为底框梁长度的1/250。当荷载达到2.806 kPa时,立柱与顶底框开口变形增大,已能发现螺栓被拔出,见图6a。当荷载达到4.954 kPa,正立面跨中位移达到90.37 mm,变形特别明显,见图6b。试验加载完毕,卸除荷载,梁的变形有一定恢复,但存在明显的塑形变形。由于构件在加工中存在误差,致使4个立柱与顶底框梁的螺栓连接存在不同的安装偏差,这就造成1/4截面处荷载-位移曲线LA1、LA5、LB1及LB3存在一定的离散性。
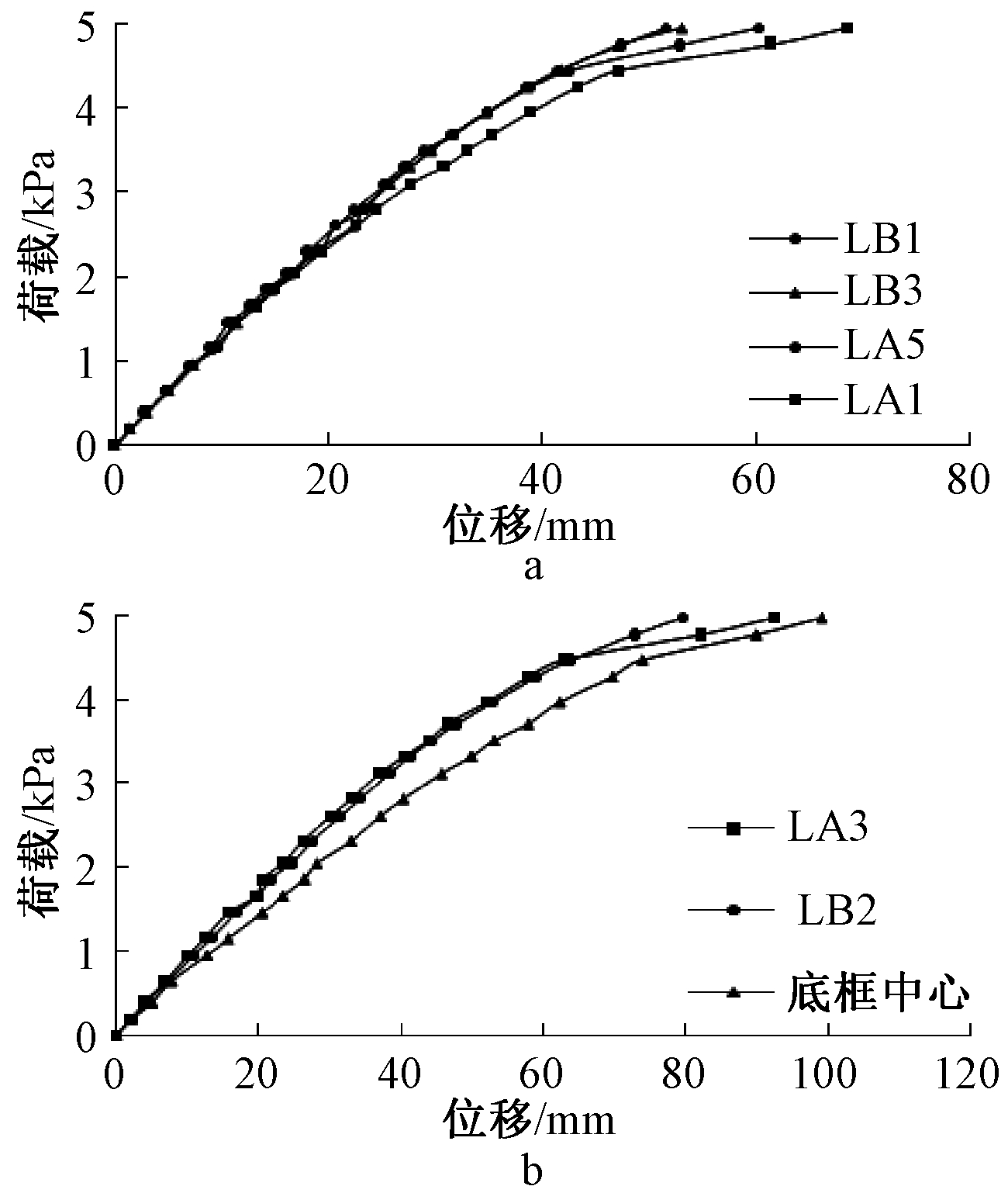
a—1/4截面处; b—跨中及底框中心处。
图5 底框梁荷载-位移曲线
Fig.5 Load-displacement curves of bottom frame beam

a—立柱与顶底框开口; b—底框梁整体变形。
图6 试验变形
Fig.6 Test deformation diagram

a—整体模型; b—角件与立柱弹簧连接模拟。
图7 ABAQUS模型
Fig.7 The ABAQUS model
由以上试验现象分析可知:由于底框梁均为冷弯薄壁异型开口截面,底框竖向抗弯刚度较弱,在荷载作用下变形较大。在试验中,由于螺栓被拔出、螺栓孔发生破坏,引起立柱与顶底框连接处的刚度退化,增大了结构的变形。
2 有限元模拟
采用有限元软件ABAQUS 6.10建立了拆装式箱型房屋1∶1模型,梁、板、柱、角件均采用S4R壳单元,梁柱构件采用的材性与试验相同,底框硅酸钙板的弹性模量为8 874 MPa,泊松比为0.24[8]。由于梁柱构件截面公称几何尺寸和实测尺寸相差较小,有限元模拟采用公称几何尺寸,顶底框主梁与角件之间采用绑定约束,硅酸盖板楼面与底框梁采用绑定约束并释放转动自由度以模拟试验中硅酸钙板与底框梁之间采用的单排自攻螺钉连接方式。柱上下两端与顶底框角件螺栓连接的位置采用Spring2的线性弹簧单元连接[9],在X、Z向设置较大的弹簧刚度,以限制角件与立柱在X、Z向的相对位移;在Y向设置合理的弹簧刚度模拟螺栓的拉拔性能,其弹簧刚度假定为1.5×105 kN/mm[7]。试验过程中,立柱端部和角件之间存在相对滑动和挤压,做接触处理,端板间法向接触采用硬接触,切向采用无摩擦接触,见图6。荷载的施加采用均布荷载直接作用在硅酸钙盖板面上,采用U1=U2=U3=0铰接约束方式约束底部角件的底板内孔边缘来模拟试验时箱房底部的铰接约束。所有角件的网格大小为15 mm×15 mm,其余部件的网格大小均为50 mm×50 mm。采用静力-通用分析步并打开几何非线性对模型进行分析。
经有限元分析,分别对底框梁跨中、1/4截面处以及底框中心的模拟值与试验值进行对比,得到底框结构不同部位的荷载-位移曲线如图8~图10所示,由于对称,1/4截面和底框梁跨中仅选取一个模拟值参与对比。
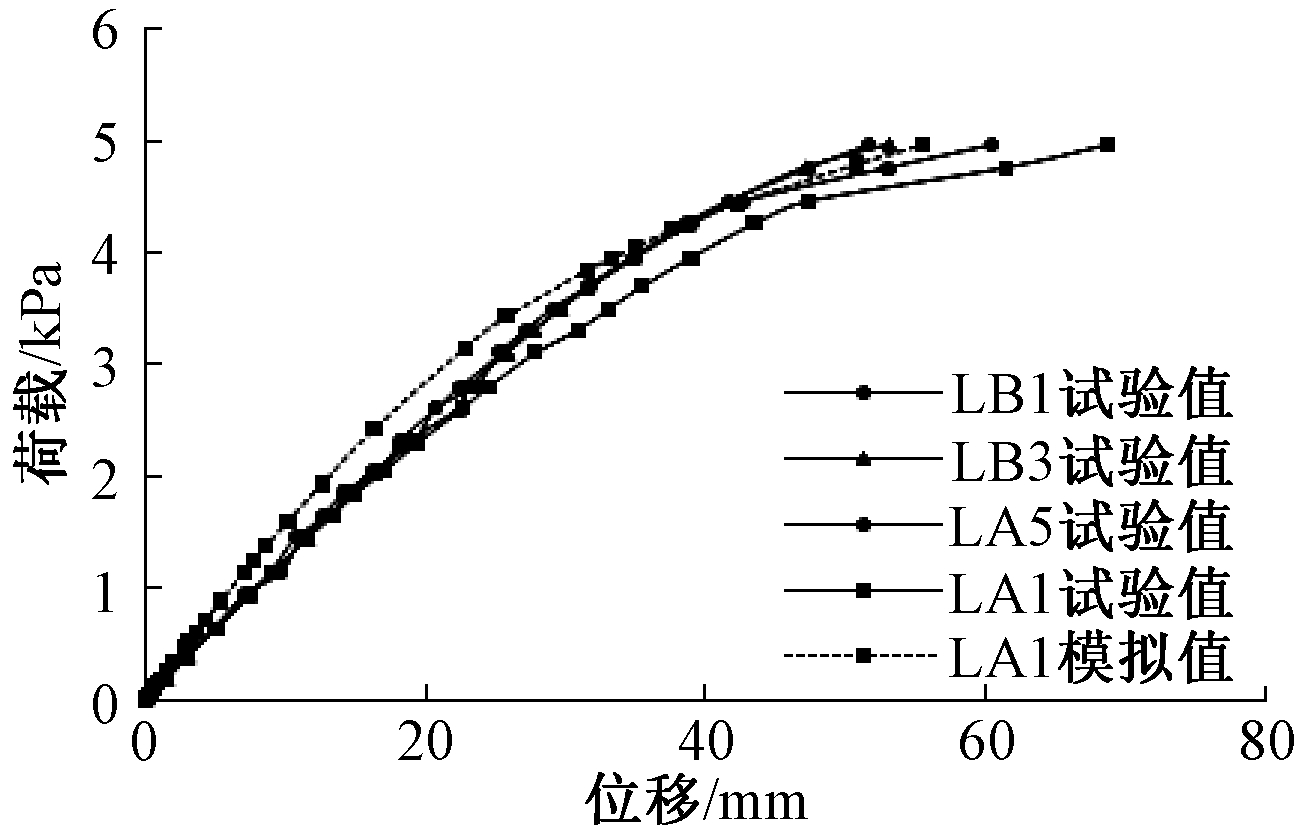
图8 底框梁1/4截面处荷载-位移曲线对比
Fig.8 Comparison of load-displacement curves at 1/4
section of bottom frame beam
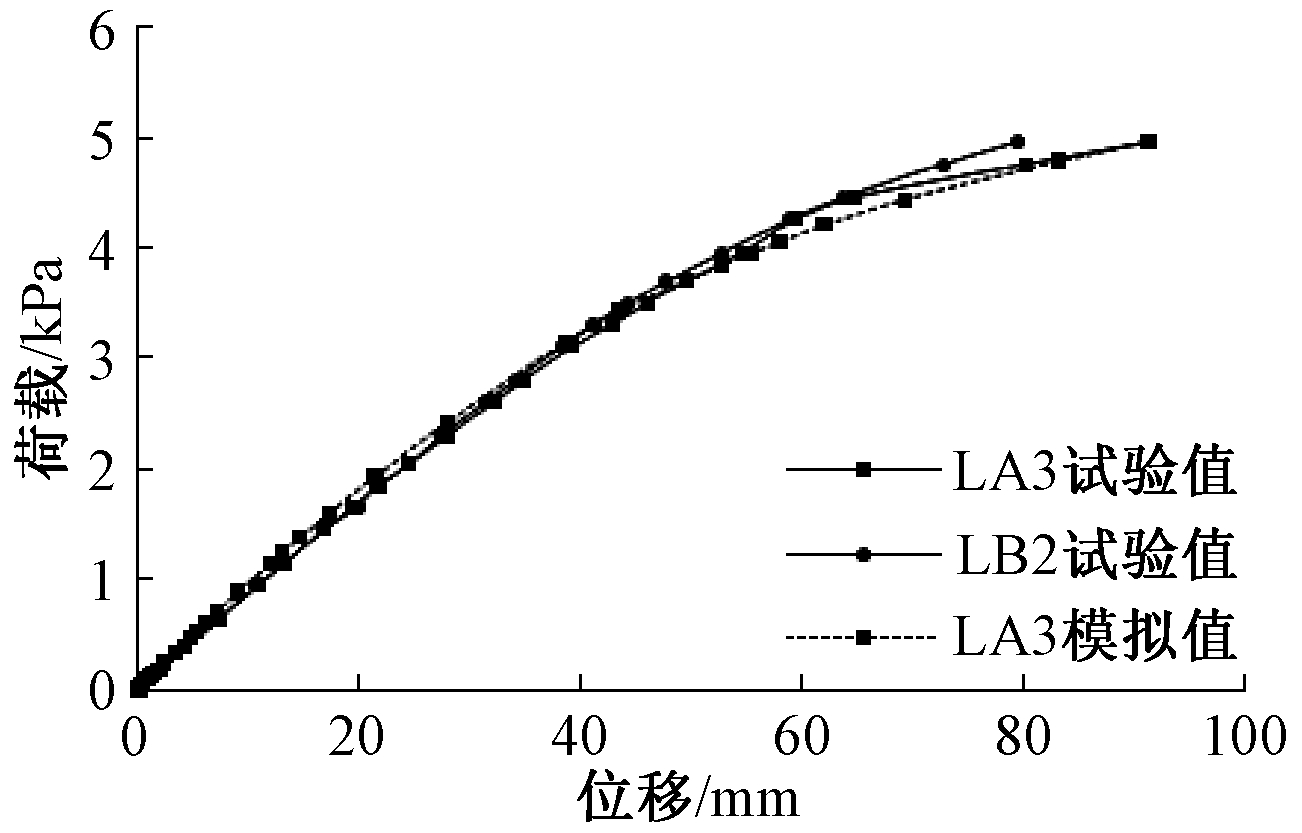
图9 底框跨中荷载-位移曲线对比
Fig.9 Comparison of the mid-span load-displacement
curve of bottom frame beam
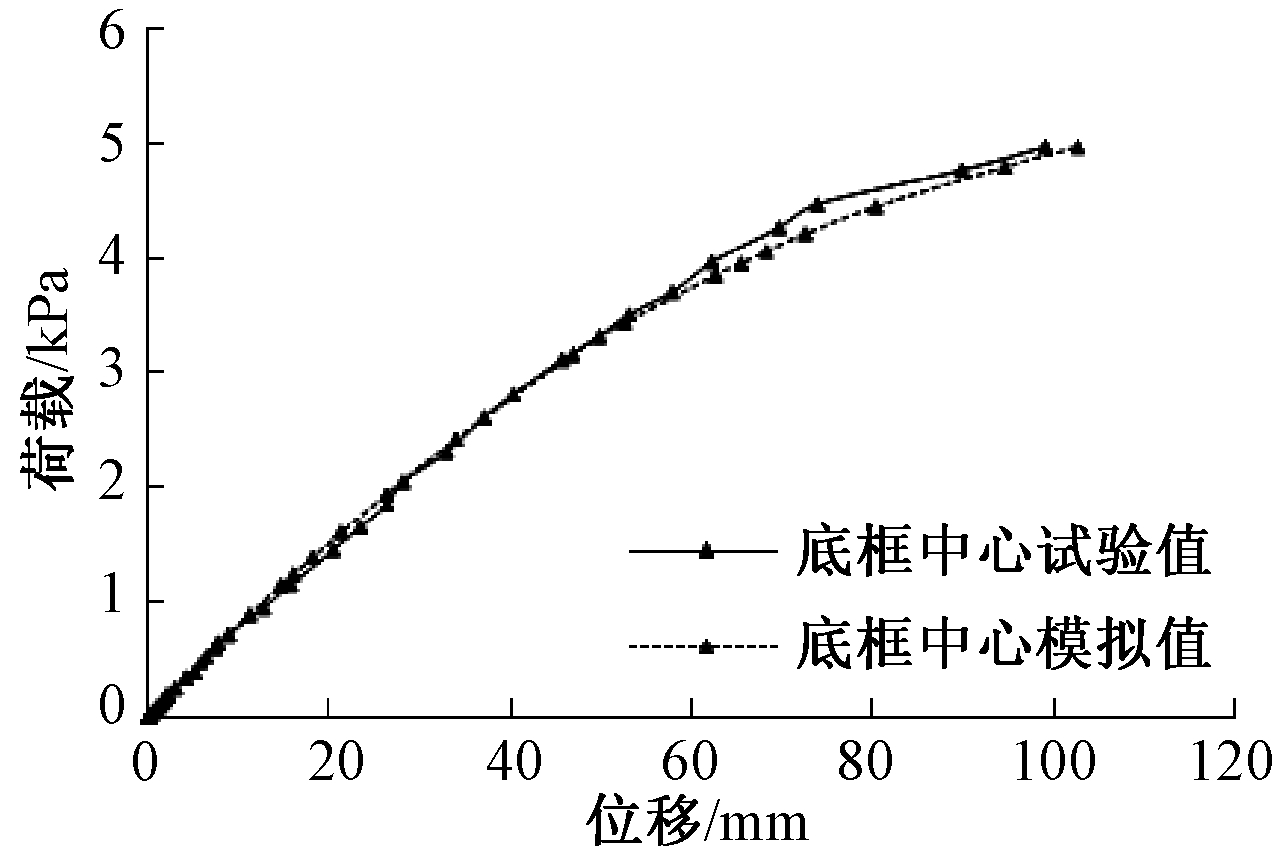
图10 底框中心荷载-位移曲线对比
Fig.10 Comparison of the mid-span load versus displacement
curves of bottom frame center
图8为底框梁1/4截面处荷载-位移曲线对比。从图中可以看出线性阶段模拟值略小于试验值,当荷载加载到4.02 kPa时,模拟值与试验值趋于吻合。图9为底框梁跨中LA3荷载-位移曲线对比,可以看出开始时模拟值略高于试验值,当荷载加载到3.84 kPa时,荷载值与试验值基本吻合。图10为跨中截面的底框中心荷载-位移曲线对比,底框中心为底框中部次梁中心,试验值与模拟值基本吻合。
楼面恒荷载约为0.5 kN/m2、假定楼面活荷载分别取2.0 kN/m2(宿舍、办公楼)和3.5 kN/m2(商店、展览厅)[10],对比底框梁1/4截面处LA1、跨中LA3及底框中心在荷载标准组合值为2.5 kN/m2和4.0 kN/m2时的位移值,如表3和表4所示。由表3可知,拆装式箱型房屋底框梁1/4截面处竖向位移相对误差小于18%,底框梁跨中和底框中心相对误差最大不超过7.5%,平均相对误差不超过10%,有限元模拟结果与试验结果比较吻合,由此可以说明采用弹簧模拟螺栓以及假设的Y向弹簧刚度是合理的,基于ABAQUS采用本文的方法对拆装式箱型房屋的底框抗弯分析是可靠的。
表3 荷载标准组合值2.5 kN/m2下的各截面位移值对比
Table 3 Comparison of the displacement values of each section under standard combination of load of 2.5 kN/m2
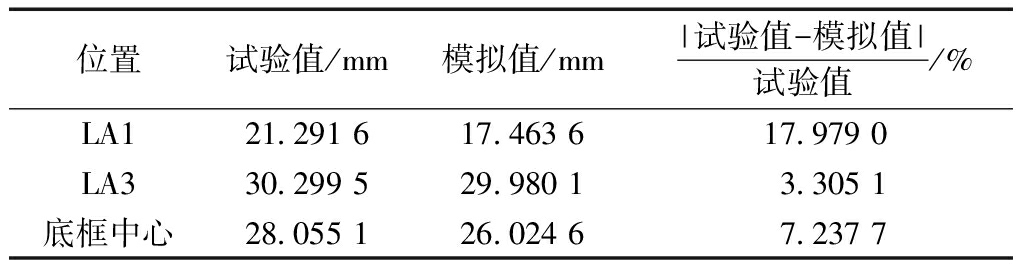
位置试验值/mm模拟值/mm|试验值-模拟值|试验值/%LA121.291 617.463 617.979 0LA330.299 529.980 13.305 1底框中心28.055 126.024 67.237 7
表4 荷载标准组合值4.0 kN/m2下的各截面位移值对比
Table 4 Comparison of the displacement values of each section under standard combination of load of 4.0 kN/m2
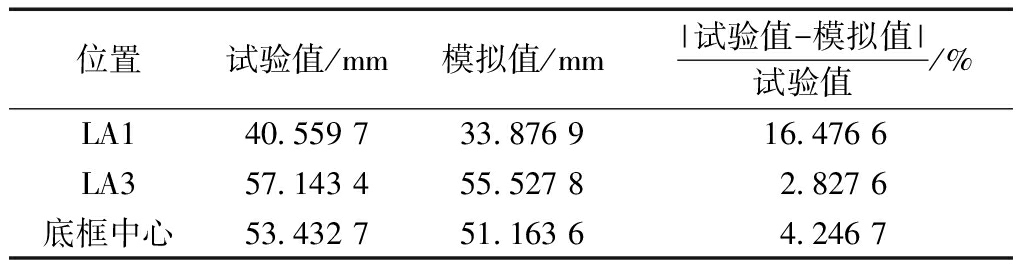
位置试验值/mm模拟值/mm|试验值-模拟值|试验值/%LA140.559 733.876 916.476 6LA357.143 455.527 82.827 6底框中心53.432 751.163 64.246 7
3 影响因素分析
基于验证了的ABAQUS模型和分析方法,对底框硅酸钙板楼板、角件开孔、立柱与顶底框的螺栓连接刚度、角件角部约束对底框抗弯刚度的影响进行分析。
3.1 硅酸钙板楼板
在实际工程中,由于硅酸钙板楼板采用自攻钉与底框梁和底框次梁连接,硅酸钙板楼板将部分参与底框楼板的竖向抗弯,图11为基于ABAQUS有限元分析,考虑和不考虑硅酸钙板楼板的底框梁跨中的荷载位移-曲线对比。
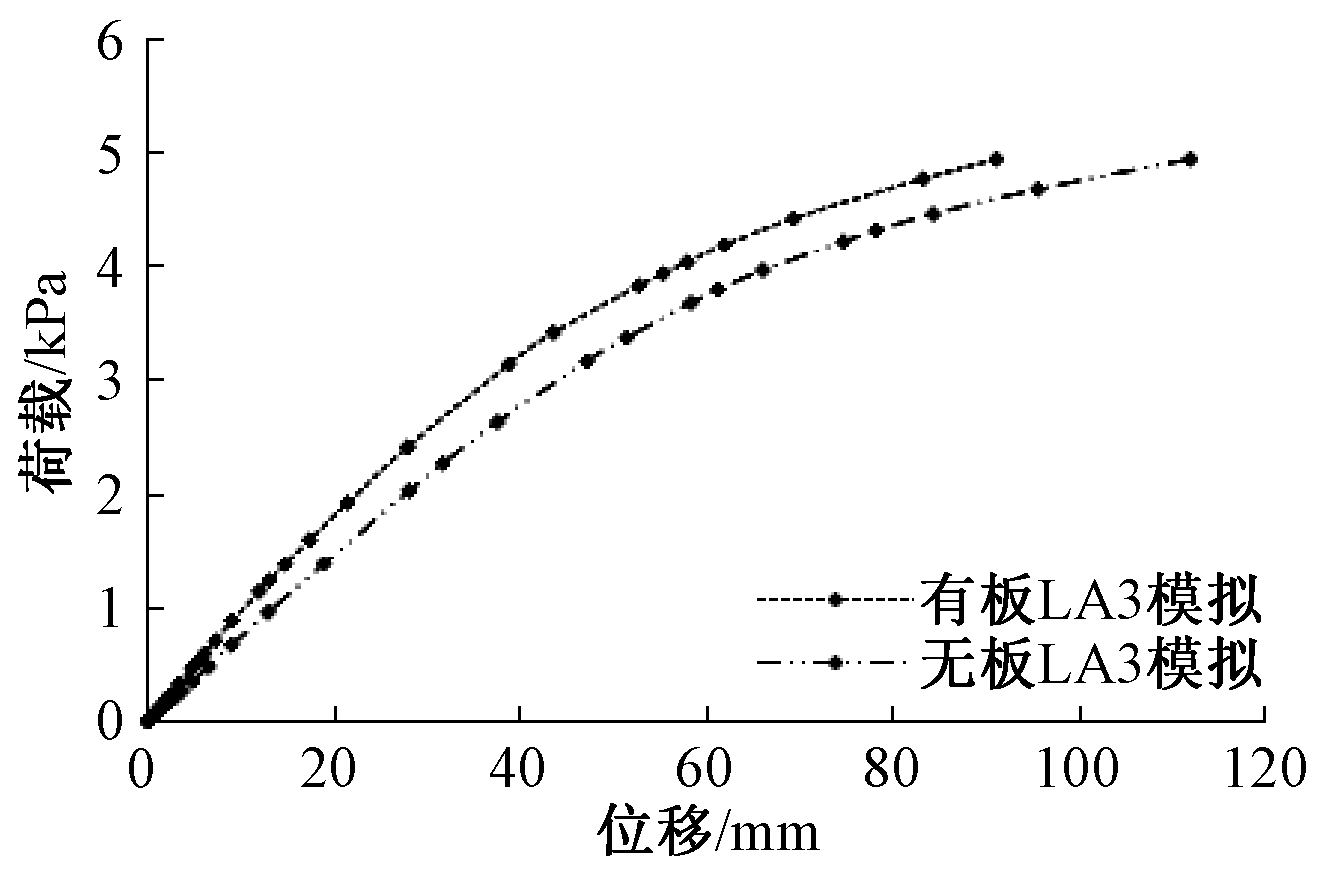
图11 硅酸钙板对底框梁跨中荷载-位移曲线的影响
Fig.11 Effects of calcium silicate board on the mid-span
load-versus displacement curves of bottom frame beam
表5 不同荷载标准组合下无板与有板模拟值对比
Table 5 Comparison of the simulation values of the floor
and no floor under different standard combinations of loads
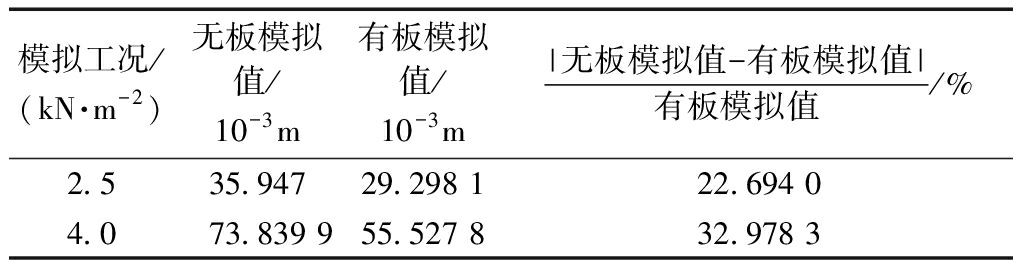
模拟工况/(kN·m-2)无板模拟值/10-3m有板模拟值/10-3m|无板模拟值-有板模拟值|有板模拟值/%2.535.94729.298 122.694 04.073.839 955.527 832.978 3
由图11及表5可以看出:荷载标准组合值为2.5 kN/m2时,采用无硅酸钙楼板模型进行分析得到的底框梁跨中荷载-位移曲线模拟值与有板模型的模拟值相比,相对误差为22.694%,荷载标准组合值为4.0 kN/m2时,无板模型的模拟相对误差为32.978 3%。可以看出分析时不考虑硅酸钙板楼板的影响对底框刚度影响较大,且随着荷载的增大无板模型的分析误差随之增大。
3.2 角件开孔
拆装式箱型房屋角件的两个外侧面上开有50 mm×75 mm的孔口,方便吊装等,角件侧板厚度为4 mm,开洞处向里卷进10 mm,如图12所示,由于角件侧板较薄,开孔较大,是否对底框抗弯刚度有影响还不确定,且底板开洞给有限元分析带来不便,基于试验试件,建立了角件是否开洞的两个有限元模型,图13为角件开孔对底框梁跨中荷载-位移的影响。
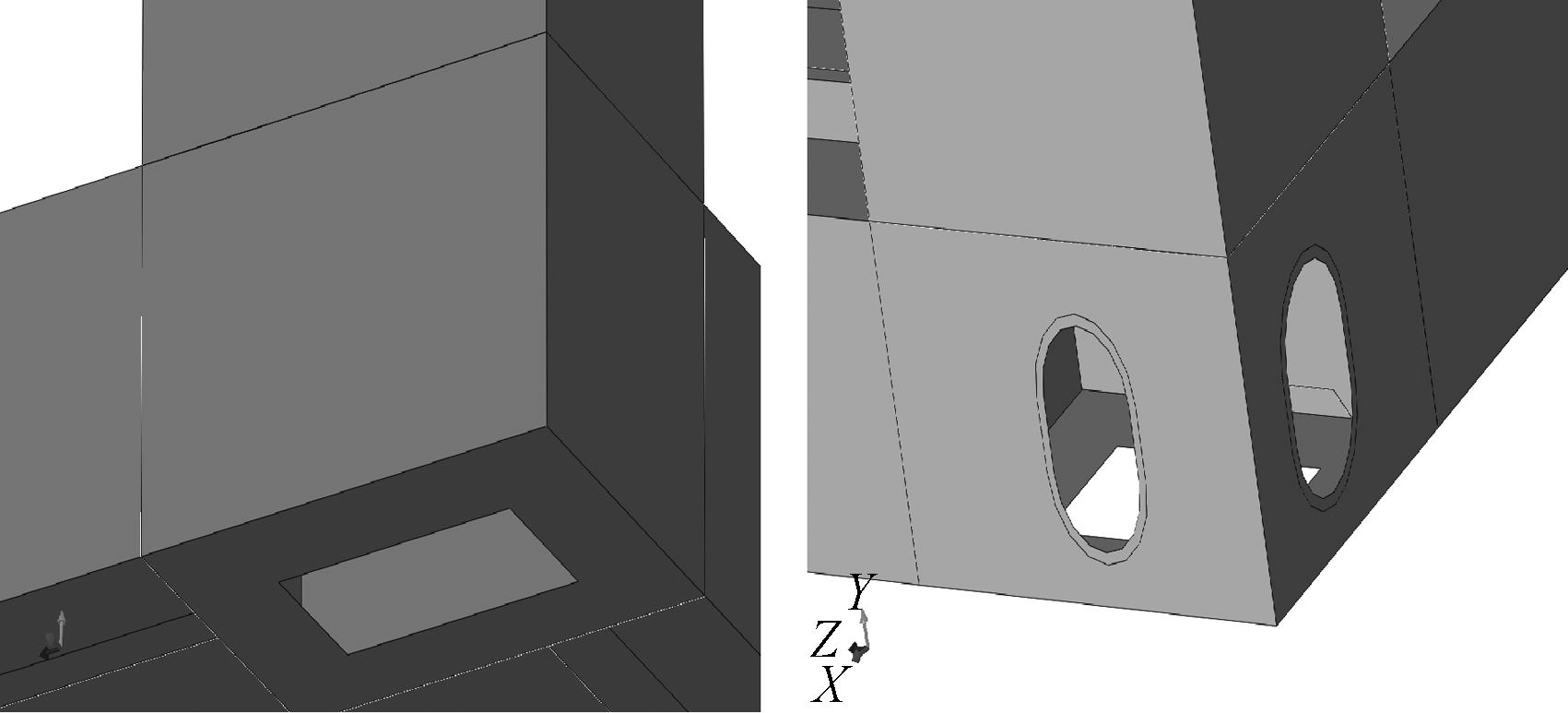
图12 无孔角件与有孔角件模型
Fig.12 Non-opening and opening corner models
由图13可知:在荷载标准组合值为2.5 kN/m2和4.0 kN/m2时角件无孔与有孔的跨中荷载-位移曲线的模拟结果基本吻合,可以得出角件侧面板开孔并加强的做法对底框梁跨中荷载-位移的影响不大,因此在建立有限元模型时可以采用无孔角件进行模拟分析。

图13 角件开孔对底框梁跨中荷载-位移曲线的影响
Fig.13 Effects of corner opening on the mid-span load-versus
displacement curves of bottom frame beam
3.3 螺栓连接刚度
采用弹簧单元模拟立柱与顶底框角件的螺栓连接,试验模拟分析时假设X、Z向的弹簧刚度设置为3×1015 kN/mm,以限制角件与立柱在X、Z向的相对位移;在Y向设置合理的弹簧刚度模拟螺栓的拉拔性能,为了考虑不同弹簧刚度对底框抗弯刚度的影响,Y向弹簧刚度分别取K1=1.5×103 kN/mm、K2=1.5×105 kN/mm、K3=1.5×107 kN/mm以及角件与立柱之间采用绑定模拟完全刚接,来确定不同连接刚度对底框梁抗弯刚度的影响,结果如图14所示。
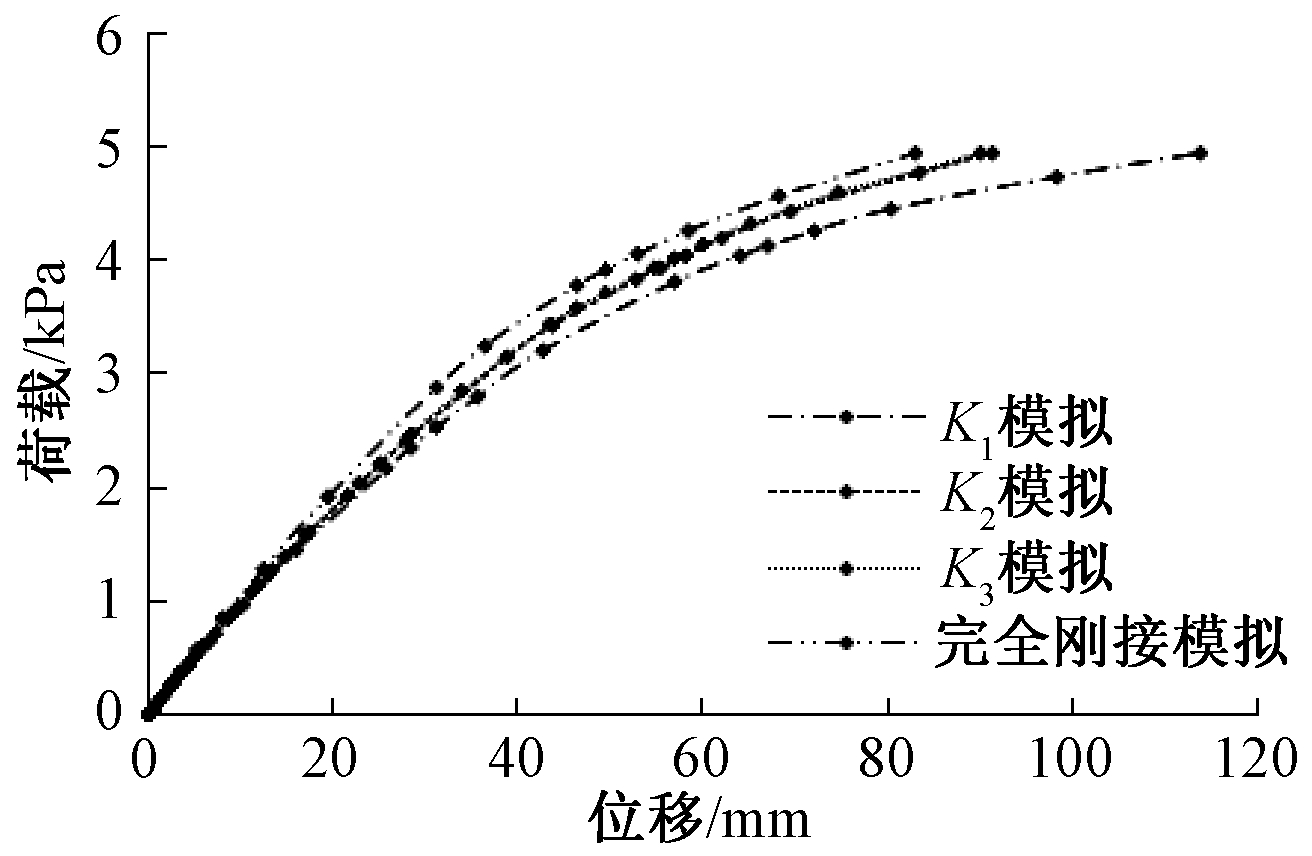
图14 不同弹簧刚度对底框梁跨中荷载-位移曲线的影响
Fig.14 Effects of different spring stiffness on the mid-span
load-versus displacement curves of bottom frame beam
从图14和表6可以看出:荷载标准组合值为2.5 kN/m2时,弹簧刚度为1.5×103 kN/mm、1.5×107kN/mm以及完全刚接对应跨中LA3模拟值相对误差分别为6.740 4%、3.422 7%和9.778 8%,而当荷载标准组合值为4.0 kN/m2时LA3模拟值的相对误差分别为15.373 2%、2.169 7%和10.537 4%。当Y向弹簧刚度等于与大于1.5×105 kN/mm时,跨中荷载-位移曲线的模拟值十分接近,而当Y向弹簧刚度小于1.5×105 kN/mm或完全刚接时得到的模拟值相对误差较大,因此可以验证采用弹簧单元模拟螺栓半刚性连接时,Y向弹簧刚度取1.5×105 kN/mm比较合理。
表6 荷载标准组合值下不同弹簧刚度模拟值对比
Table 6 Comparison of the simulation values of different spring stiffnesses under different standard combinations of loads

模拟工况/(kN·m-2)不同刚度下的挠度值/mmK1K2K3完全刚接|K1-K2|K2/% |K3-K2|K2/%|完全刚接-K2|K2/%2.531.193 829.298 128.295 326.433 16.740 43.422 79.778 84.064.064 255.527 854.323 049.676 615.373 22.169 710.537 4
3.4 角部约束
不同的边界约束条件对结构的受力性能有很大影响,因此探究角部不同约束方式对拆装式箱型房屋抗弯刚度的影响很有必要性。分别从约束底部角件内孔边缘、约束角件底板外边缘及约束整个角件底板来探究不同约束方式对跨中荷载-位移曲线的影响,如图15所示。
从图15可以看出:当角件底部采用约束底板外边缘与约束整个底板所得到到跨中荷载-位移曲线模拟结果完全吻合,因此以下分析仅分析约束底板模型,由表7可知:当荷载标准组合值为2.5 kN/m2时,采用约束底板模型进行分析得到的底框梁跨中荷载-位移曲线模拟值与约束底板内孔边缘模型的相对误差为17.973 5%;当荷载标准组合值为4.0 kN/m2时模拟值的相对误差为14.671 6%,由此可知采用约束底部角件内孔边缘可以很好地模拟试验时拆装式箱房抗弯的铰接约束。
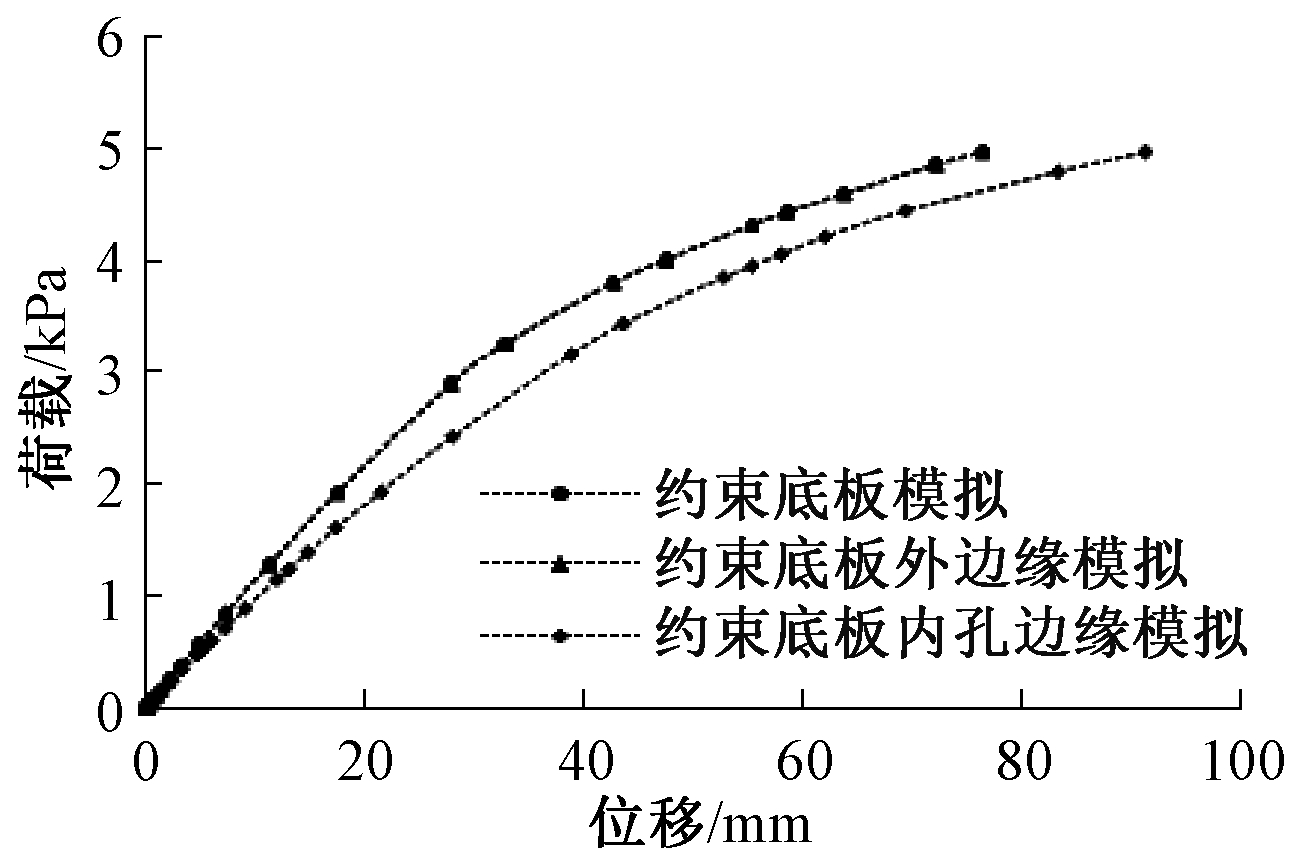
图15 不同约束方式对底框梁跨中荷载-位移曲线的影响
Fig.15 Effects of different restraint modes on the mid-span
load-versus displacement curves of bottom frame beam
表7 荷载标准组合值下不同约束方式模拟值对比
Table 7 Comparison of the simulation values of different constraint modes under standard combinations of loads

模拟工况/(kN·m-2)约束底板和约束底板外边缘的挠度/mm约束底板内孔边缘的挠度值/mm|约束底板-约束底板内孔边缘|约束底板内孔边缘/%2.524.032 229.298 117.973 54.047.381 055.527 814.671 6
4 结束语
通过对拆装式箱型房屋整体抗弯刚度的试验和有限元模拟分析,并对影响底框抗弯刚度的底框硅酸钙板楼板、角件开孔、立柱与顶底框角件的螺栓连接刚度、角件角部约束的因素分析,得到如下结论:
1)有限元模拟结果与试验结果比较吻合,验证了采用本文的基于ABAQUS对拆装式箱型房屋底框抗弯刚度的研究分析是可靠的。
2)在有限元分析中,采用硅酸钙板与底框梁边线进行绑定连接得到的底框梁位移的模拟值与试验值相比,平均相对误差小于10%,说明此连接方式与试验时硅酸钙楼板与底框梁之间的铆钉连接比较符合。
3)立柱与顶底框的螺栓连接属于半刚性连接,相比刚接底框梁跨中挠度增大约10%,采用弹簧单元代替角件与立柱的连接螺栓进行有限元分析时,选取X、Z向刚度为3×1015 kN/mm、Y向刚度为1.5×105 kN/mm的弹簧单元可以很好地模拟该半刚性连接性能。
4)由于底部角件开孔对底框梁跨中荷载-位移曲线的影响不大,因此建议在运用有限元软件进行模拟时可以简化角件模型,对侧面板不进行开孔处理。
5)不同的角件约束方式对底框梁跨中荷载-位移曲线的影响较大,采用约束角件底板内孔边缘模拟箱房底部的铰接约束时,与试验值相比平均相对误差不大于10%,因此该约束方式与试验情况比较符合。约束角件整个底板相比约束角件底板内孔边缘,底框梁跨中位移减小约14%~18%,实际工程中应区别考虑。
[1] BORVIK T, HANSSEN A G, DEY S, et al. On the Ballistic and Blast Load Response of a 20ft ISO Container Protected with Aluminum Panels Filled with a Local Mass-Phase: Design of Protective System [J]. Engineering Structures, 2008, 30(6): 1605-1620.
[2] KEVIN GIRIUNAS, HALILSEZEN, REBECCA B DUPAIX. Evaluation, Modeling, and Analysis of Shipping Container Building Structures [J]. Engineering Structures, 2012, (43): 48-57.
[3] 杨建江,刘叶,李苏盐,等. 集装箱组合房屋墙板抗风及抗剪性能试验研究[J].工业建筑,2015,45(7):164-169.
[4] 杨柳. 拓展集装箱式活动房非线性静力分析[D]. 天津:天津大学,2007.
[5] 陈世云. 箱式集成房构件和整体的优化设计研究[D]. 深圳:哈尔滨工业大学, 2009.
[6] 尹静,查晓雄. 箱式集成房屋折叠单元刚性试验及有限元分析[J]. 工业建筑, 2010, 40(4):446-448.
[7] 张俊峰,杨大雍,胡文悌,等. 拆装式箱型房屋整体抗弯研究[J].钢结构,2016,31(12):28-32.
[8] 赵梦圆. 冷弯薄壁型钢连接件力学性能研究[D].南京:东南大学,2015.
[9] 马晓峰.ABAQUS6.11中文版有限元分析从入门到精通[M]. 北京:清华大学出版社,2013.
[10] 中华人民共和国住房和城乡建设部. 建筑结构荷载规范:GB 50009—2012[S].北京:中国建筑工业出版社,2012.