随着城市现代化的发展,城市交通变得尤为重要,门式桥墩在城市交通运输中应用较为广泛。在桥梁设计中,桥墩对全桥的抗震性能起控制作用,是保证桥梁安全的重要组成部分。在地震作用下,门式桥墩的破坏一般发生在墩柱根部区域。目前,在地震频发的国家及地区,已逐步采用钢结构墩柱作为门式桥墩的下部支撑结构。
在钢墩柱的各种结构形式中,箱形钢墩柱在两个主轴方向均有较好的抗弯性能,使得箱形钢墩柱得到广泛应用。但在地震作用下,箱形钢墩柱的壁板易发生局部屈曲变形、角部竖向焊缝开裂等破坏,如1995年日本阪神大地震[1-2]中大量箱形钢墩柱发生此类破坏。因此,采取有效措施阻止或延缓钢墩柱壁板产生局部屈曲已成为桥梁抗震研究中关注度较高的课题。
国内外学者对钢墩柱的抗震性能进行了各方面的深入研究。Dang等以方钢管桥墩为研究对象,共进行了15个方钢管桥墩试验,且探讨了单向地震加载与双向地震加载下结构抗震性能的区别[3]。高圣彬等研究了影响内填混凝土箱形截面桥墩局部屈曲位置的因素[4-5],结果表明:当混凝土较少时,钢板局部屈曲的位置位于其上部;当填充量较多时,发生局部屈曲的部位为桥墩底部。Shimizu采用数值模拟方法,分别研究部分内填混凝土箱形钢桥墩在不同地震波输入模式下和多向地震耦合作用下的抗震性能[6-7]。Yuan等以部分填充混凝土方钢管桥墩为研究对象,探讨了静力加载、单向加载及双向加载等模式下结构受力性能的区别[8]。王占飞等研究了水平往复荷载作用下部分填充混凝土圆形钢桥墩柱的力学性能[9]。Aoki等采用试验研究方法,探究了设置纵向加劲肋的箱形截面门式钢桥墩的抗震性能[10]。试验结果表明,采用纵向异形板的门式钢桥墩底部和顶部的强度和延性得到了增加,并提出了针对采用纵向异形板的箱形截面门式钢桥墩的设计建议。张建东等对薄壁加劲箱形钢桥墩的抗震性能进行数值分析,验证了选择简单双线性随动强化模型作为模型的材料本构关系,与试验结果吻合较好[11]。Ge等对箱形钢桥墩的超低周疲劳破坏机理进行了系统的试验研究[12]。Wang等采用拟静力试验研究方法,研究了Q460高强钢箱形柱的抗震性能[13]。王占飞等对偏心常轴力作用下的圆形钢桥墩进行数值分析,研究表明,当偏心率增大时,钢桥墩的滞回性能不对称性越明显,抗震性能随之变差[14]。Shi等采用试验研究与数值分析,探究了4个Q460高强钢箱形轴压柱的受力性能[15]。
桥梁结构的整体延性能力一般是通过桥墩塑性铰区的转动能力获得;对于工程中常用的上部结构放置在支座上的门式桥墩,塑性铰区可能出现在墩柱根部区域。基于损伤控制理论,在门式钢桥墩根部区域设置特定的可更换耗能区,进而研发出可恢复功能的新型门式钢桥墩。根部墩柱设置低屈服点钢板和约束钢板为可更换耗能部件,如图1所示。在中等强度地震后可快速更换受损的低屈服点钢板和约束钢板;而在罕遇地震后整个耗能区也可以整体更换,进而快速修复门式钢桥墩的抗震能力,确保桥梁生命线工程畅通,提升城市抗震救灾能力。

图1 根部设置可更换耗能墩柱的新型门式钢桥墩示意
Fig.1 Schematic diagram of the new portal steel column with renewable
energy-consuming piers at the root
为研究根部新型耗能墩柱的屈曲机理和耗能性能,通过对比验证轴压下的试验结果和数值模拟结果,进一步对根部耗能墩柱进行反复拉压下受力性能的数值分析。探讨低屈服点耗能钢板的高度、宽度及厚度等因素对新型箱形钢墩柱骨架曲线、延性系数及耗能能力的影响规律,获得一系列规律性结论,为门式钢桥墩在实际工程中应用提供理论依据。
1 对比试验概况
轴压试验采用华侨大学10 000 kN电液伺服压剪试验机进行加载,试验的加载控制方式为力-位移混合控制加载,具体为在弹性阶段用力加载进行控制,之后用位移加载进行控制。轴压试验试件的具体构造为:在四面壁板上开一矩形洞口,将低屈服点钢板置于洞中与壁板焊接,并在低屈服点钢板内外两侧分别设置一块矩形夹板,采用高强螺栓栓接,如图2所示。

a—正立面; b—横截面。
图2 试件示意
Fig.2 Schematic diagram of specimen
试验中,4个试件的低屈服点钢板均为Q160材料,箱形钢墩柱四面壁板及低屈服点钢板的两侧夹板均为Q345材料。
轴压试验试件根据实际以1∶4缩尺比例制作,共有4个试件,试件的详细参数如表1所示。
表1 试件的设计参数
Table 1 Design parameters of specimens mm

组样Lhbh1b1twtftpT-050037537530018788—T-1500375375187187888T-2500375375300187888T-3500375375420187888
注:L为钢墩柱的立面高度;h为柱截面的高度;b为柱截面的宽度;h1为低屈服点钢板的高度;b1为低屈服点钢板的宽度;tw为低屈服点钢板的厚度;tf为箱形钢墩柱四面壁板的厚度;tp为低屈服点钢板内外两侧夹板的厚度。
2 轴压有限元模型
采用ANSYS软件,根据轴压试验试件的几何尺寸建立相应的计算模型。有限元模型采用板壳单元Shell 181,柱底刚性连接,柱顶约束X、Y两个水平方向,并对柱顶Z方向进行竖向位移控制。钢材的本构关系采用多线性随动强化模型KINH,并在材性试验的基础上确定钢材的应力σ-应变ε曲线,如图3和图4所示。
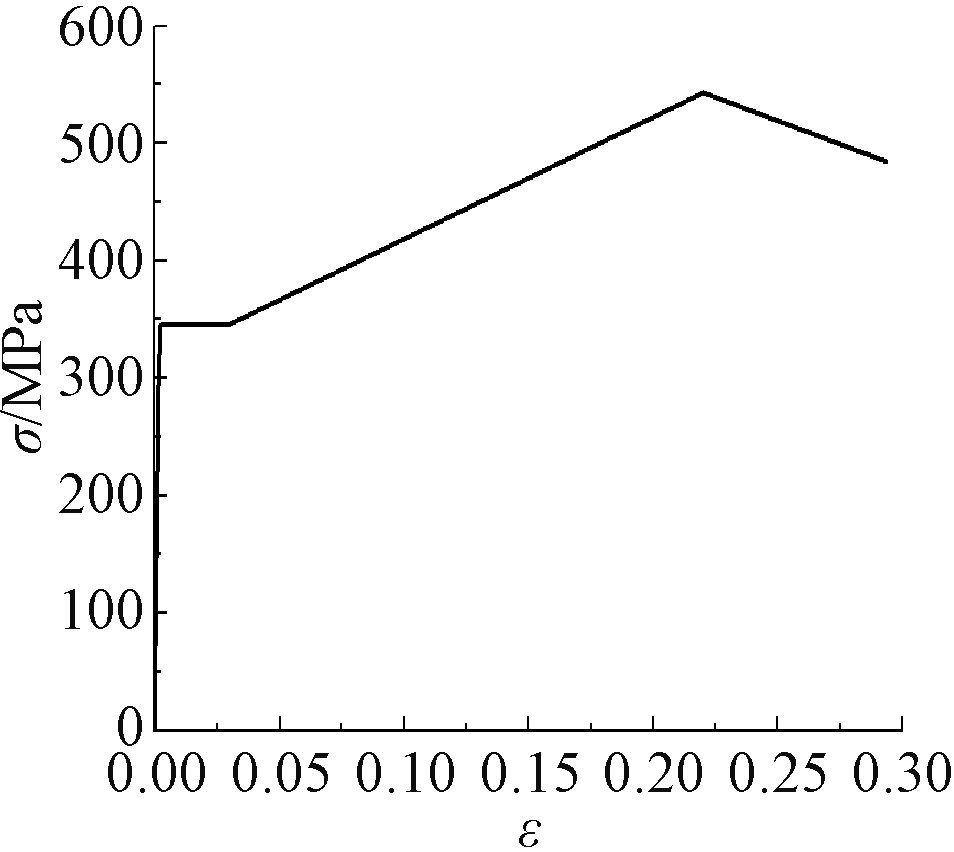
图3 Q345钢材应力-应变曲线
Fig.3 Stress-strain curve of steel Q345

图4 Q160钢材应力-应变曲线
Fig.4 Stress-strain curve of steel Q160
有限元模型的初始几何缺陷依据与试验破坏形态相似变形的屈曲模态来确定。最大变形取值为L/1 000(L为试件高度)。有限元模型的网格划分取单位大小15 mm为控制参数,如图5所示。

图5 有限元模型
Fig.5 The finite element model
箱形钢墩柱的有限元模型中,普通钢材为Q345,低屈服点钢材为Q160,材料弹性模量取206 GPa,泊松比取0.3。试件的低屈服点钢板与内外两侧夹板采用高强螺栓连接,在有限元模型中通过耦合各个板件对应结点UX、UY、UZ三个方向的自由度进行模拟。
3 试验与有限元结果对比
提取数值分析所得荷载-位移曲线与轴压试验结果进行对比,如图6所示。图中,P为作用在箱形钢墩柱柱顶的竖向荷载;δ为对应的柱顶竖向位移。
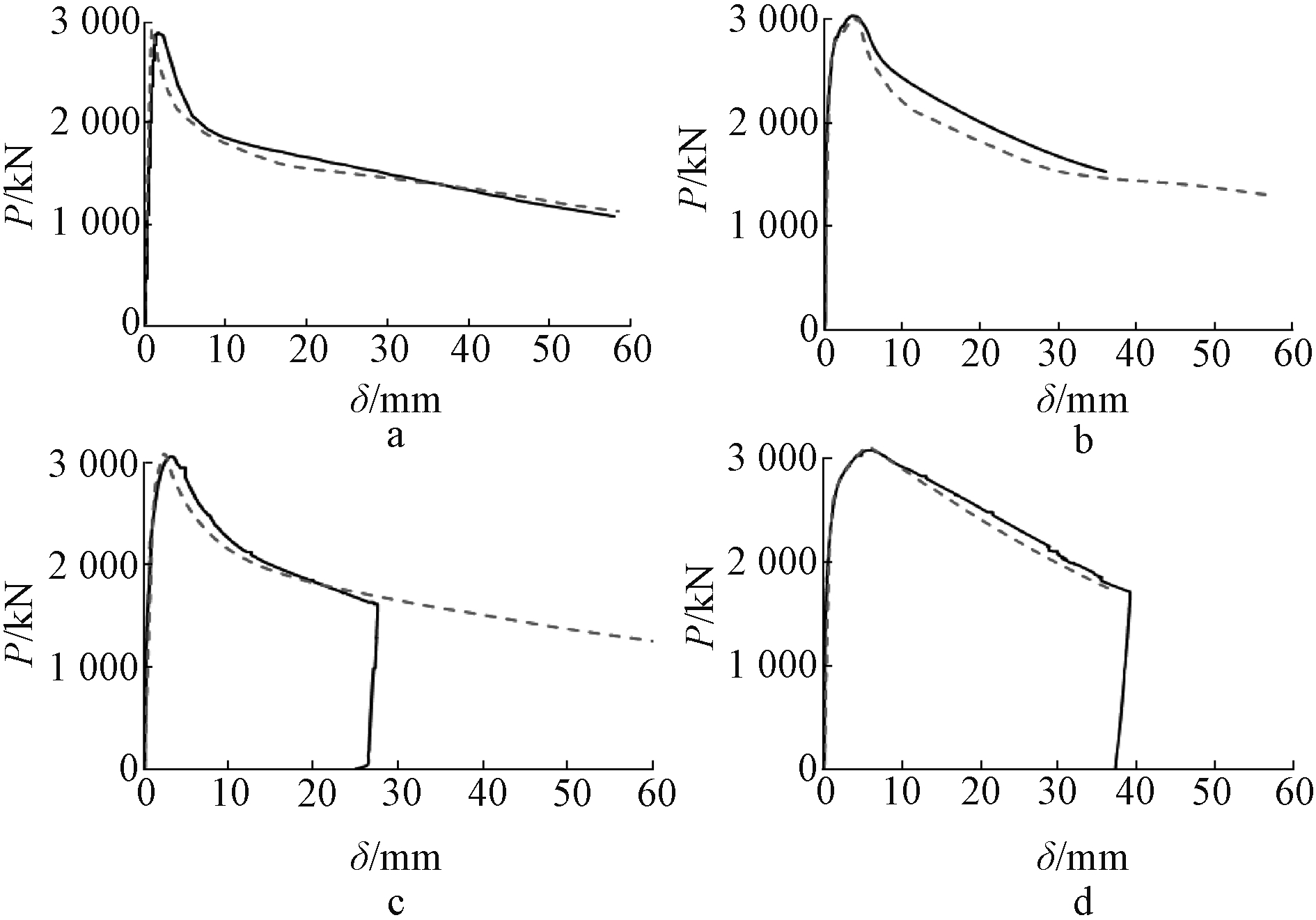
a—试件T-0; b—试件T-1; c—试件T-2; d—试件T-3。![]() 试验曲线;
试验曲线;![]() 有限元曲线。
有限元曲线。
图6 试验与有限元荷载-位移曲线对比
Fig.6 Comparison of load-deformation curves between
experimental data and numerical results
数值分析所得试件破坏形态与轴压试验结果进行对比,如图7所示。

a—试件T-0; b—试件T-1; c—试件T-2; d—试件T-3。
图7 试件破坏形态对比
Fig.7 Comparison of failure modes of specimens
由图6和图7可知:有限元分析结果与试验结果基本吻合,能较好反映竖向荷载作用下箱形钢墩柱的受压屈曲塑性变形过程。由于此类新型钢墩柱数值仿真的难点在于受压状态下墩柱壁板及耗能板的相关屈曲机理,而受拉状态下受拉性能为常规模拟方法,因而采用本文数值仿真方法可以进一步模拟反复轴向拉压作用下此类新型钢墩柱的受力机理。基于此,本文第4部分采用上述有限元仿真技术进一步研究在反复轴向拉压作用下,低屈服点钢板的高度、宽度、厚度等因素对箱形钢墩柱受力性能的影响规律。
4 反复轴向拉压数值分析
采用ANSYS有限元软件进行模拟分析,为使模拟结果更接近于工程实际,按照实际几何尺寸建立有限元足尺模型。有限元模型加载模式采取先压后拉为1圈循环,并将0.5,0.7,1,2倍屈服位移等作为各级位移加载控制的位移值。其中,第1级和第2级循环2圈,之后每级循环3圈。材料参数和本构关系与轴压有限元模型相同。
4.1 数值分析试件设计
数值分析中,箱形钢墩柱试件的高度为2 000 mm,柱横截面的高度为1 500 mm,宽度也为1 500 mm。设置耗能壁板的箱形钢墩柱有限元模型的设计参数如表2所示,探讨了低屈服点钢板的高度、宽度及厚度等参数对箱形钢墩柱受力性能的影响。其中,L为箱形钢墩柱的高度;h1为低屈服点钢的高度;b1为低屈服点钢的宽度;tw为低屈服点钢的厚度;tf为箱形钢墩柱壁板的厚度;tp为低屈服点钢板内外两侧夹板的厚度;δs为低屈服点钢板的强度;δs,f为箱形钢墩柱壁板的强度;δs,p为低屈服点钢内外两侧夹板的强度。
表2 数值分析试件的设计参数
Table 2 Design parameters of specimens
in numerical analysis
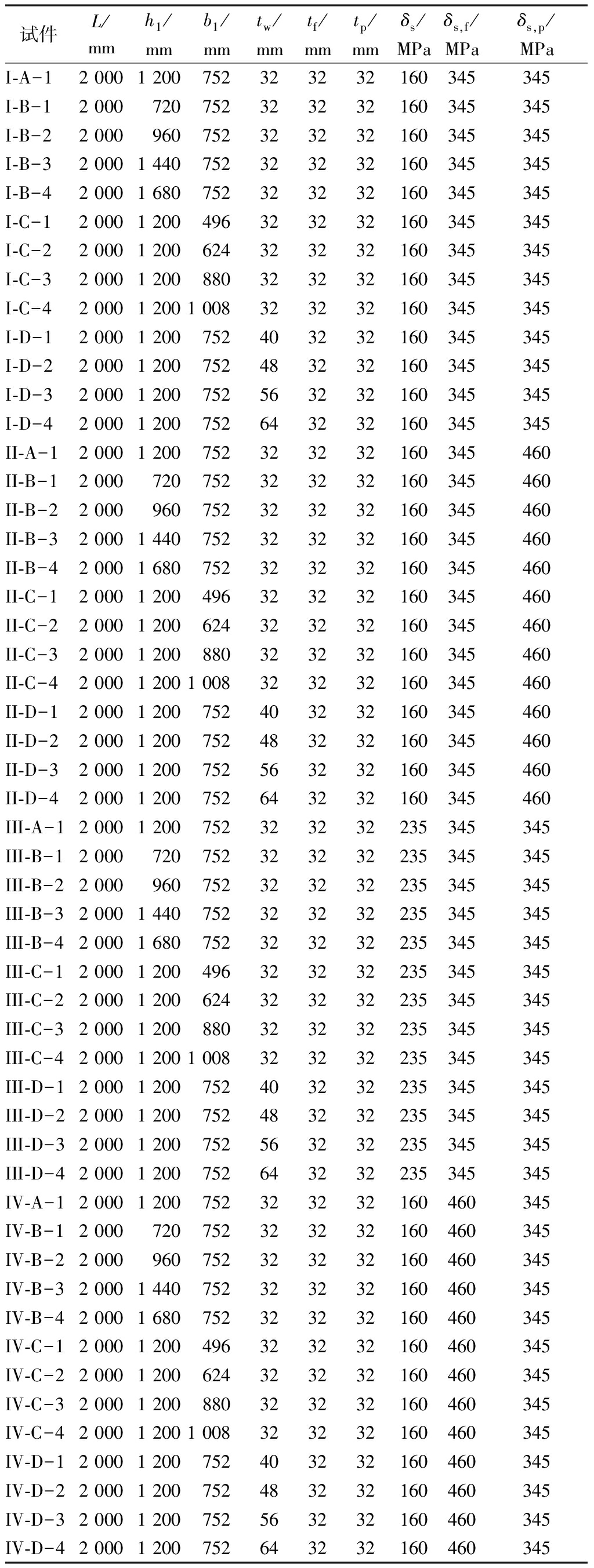
试件L/mmh1/mmb1/mmtw/mmtf/mmtp/mmδs/MPaδs,f/MPaδs,p/MPaI-A-12 0001 200752323232160345345I-B-12 000720752323232160345345I-B-22 000960752323232160345345I-B-32 0001 440752323232160345345I-B-42 0001 680752323232160345345I-C-12 0001 200496323232160345345I-C-22 0001 200624323232160345345I-C-32 0001 200880323232160345345I-C-42 0001 2001 008323232160345345I-D-12 0001 200752403232160345345I-D-22 0001 200752483232160345345I-D-32 0001 200752563232160345345I-D-42 0001 200752643232160345345II-A-12 0001 200752323232160345460II-B-12 000720752323232160345460II-B-22 000960752323232160345460II-B-32 0001 440752323232160345460II-B-42 0001 680752323232160345460II-C-12 0001 200496323232160345460II-C-22 0001 200624323232160345460II-C-32 0001 200880323232160345460II-C-42 0001 2001 008323232160345460II-D-12 0001 200752403232160345460II-D-22 0001 200752483232160345460II-D-32 0001 200752563232160345460II-D-42 0001 200752643232160345460III-A-12 0001 200752323232235345345III-B-12 000720752323232235345345III-B-22 000960752323232235345345III-B-32 0001 440752323232235345345III-B-42 0001 680752323232235345345III-C-12 0001 200496323232235345345III-C-22 0001 200624323232235345345III-C-32 0001 200880323232235345345III-C-42 0001 2001 008323232235345345III-D-12 0001 200752403232235345345III-D-22 0001 200752483232235345345III-D-32 0001 200752563232235345345III-D-42 0001 200752643232235345345IV-A-12 0001 200752323232160460345IV-B-12 000720752323232160460345IV-B-22 000960752323232160460345IV-B-32 0001 440752323232160460345IV-B-42 0001 680752323232160460345IV-C-12 0001 200496323232160460345IV-C-22 0001 200624323232160460345IV-C-32 0001 200880323232160460345IV-C-42 0001 2001 008323232160460345IV-D-12 0001 200752403232160460345IV-D-22 0001 200752483232160460345IV-D-32 0001 200752563232160460345IV-D-42 0001 200752643232160460345
表2中,第I组组件的低屈服板强度为160 MPa,壁板强度为345 MPa,夹板强度为345 MPa。其中,I-A-1为对比件,I-B组试件的变化参数为耗能壁板的高度,I-C组试件的变化参数为耗能壁板的宽度,I-D组试件的变化参数为耗能壁板的厚度。
第II组组件的低屈服板强度为160 MPa,壁板强度为345 MPa,夹板强度为460 MPa。其中,II-A-1为对比件,II-B组试件的变化参数为耗能壁板的高度,II-C组试件的变化参数为耗能壁板的宽度,II-D组试件的变化参数为耗能壁板的厚度。
第III组组件的低屈服板强度为235 MPa,壁板强度为345 MPa,夹板强度为345 MPa。其中,III-A-1为对比件,III-B组试件的变化参数为耗能壁板的高度,III-C组试件的变化参数为耗能壁板的宽度,III-D组试件的变化参数为耗能壁板的厚度。
第IV组组件的低屈服板强度为160 MPa,壁板强度为460 MPa,夹板强度为345 MPa。其中,IV-A-1为对比件,IV-B组试件的变化参数为耗能壁板的高度,IV-C组试件的变化参数为耗能壁板的宽度,IV-D组试件的变化参数为耗能壁板的厚度。
有限元分析中,部分试件的荷载-位移滞回曲线如图8所示。
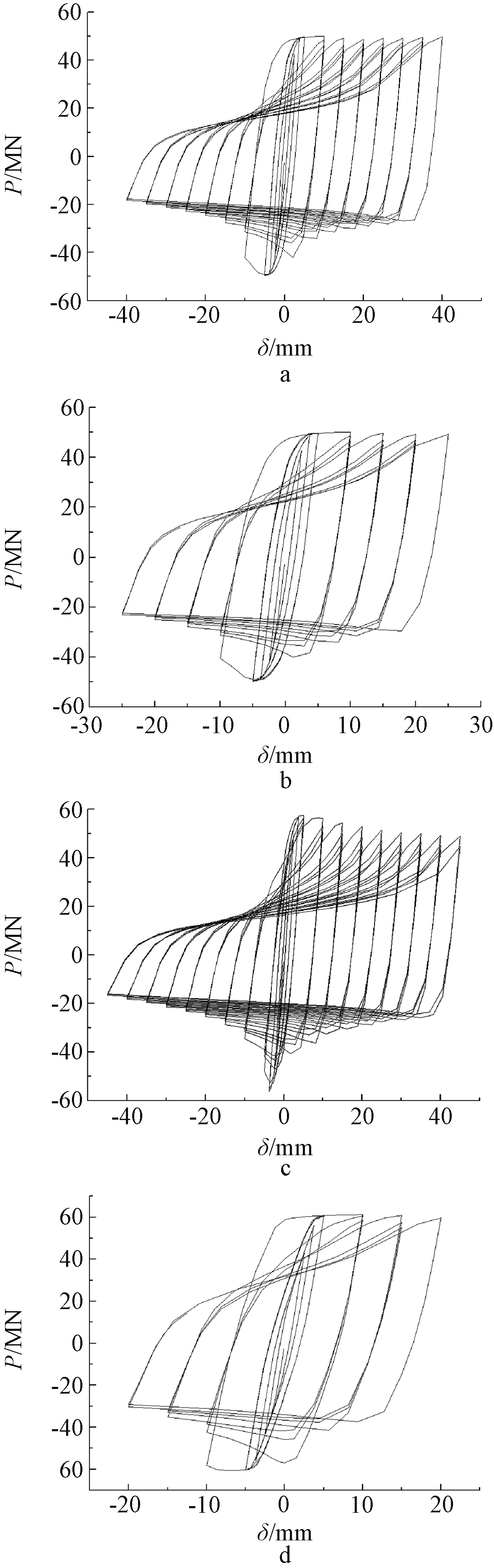
a—试件I-A-1; b—试件II-A-1; c—试件III-A-1; d—试件IV-A-1。
图8 有限元分析荷载-位移滞回曲线
Fig.8 Load-displacement hysteretic curves in finite element analysis
4.2 影响参数分析
结构在往复荷载加载作用下,得到荷载-位移曲线,将荷载峰值点依次相连,得到的曲线即为试件的骨架曲线。它既能反映结构在受力与变形的各个不同阶段的强度、刚度、延性、耗能等特性,也是确定恢复力模型中特征点的重要依据。骨架曲线中正向位移加载为轴向受拉,反向位移加载为轴向受压。
4.2.1 低屈服点钢板高度
为研究低屈服点钢板高度对箱形钢墩柱受力性能的影响,每组数值分析试件中低屈服点钢板高度设计为720,960,1 200,1 440,1 680 mm。将每组的对比件A-1与B组试件的骨架曲线进行对比,如图9所示。
分析图9可知:随着低屈服点钢板高度h1的改变,试件在正向及反向加载中的极限破坏位移变化较大,低屈服点钢板高度在(1/2~5/7)试件高度范围内,正、反向极限破坏位移最大值均达到50 mm;试件在正向加载过程中曲线基本重合,低屈服点钢板高度h1对受拉加载时的承载力及刚度影响较小。
4.2.2 低屈服点钢板宽度
为研究低屈服点钢板宽度对箱形钢墩柱受力性能的影响,每组数值分析试件中低屈服点钢板宽度设计为496,624,752,880,1 008 mm。将每组的对比件A-1与C组试件的骨架曲线进行对比,如图10所示。
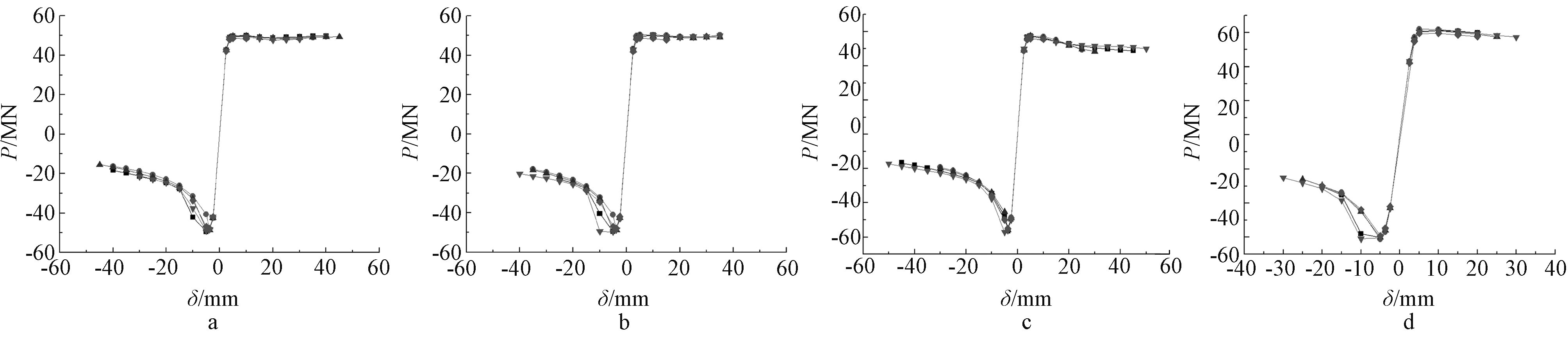
a—I-B组骨架曲线; b—II-B组骨架曲线; c—III-B组骨架曲线; d—IV-B组骨架曲线。![]() —A-1;
—A-1; ![]() —B-1;
—B-1; ![]() —B-2;
—B-2; ![]() —B-3;
—B-3; ![]() —B-4。
—B-4。
图9 低屈服点钢板高度对试件受力性能的影响
Fig.9 Influence of the height of low-yield point steel plates on the mechanical properties of specimens
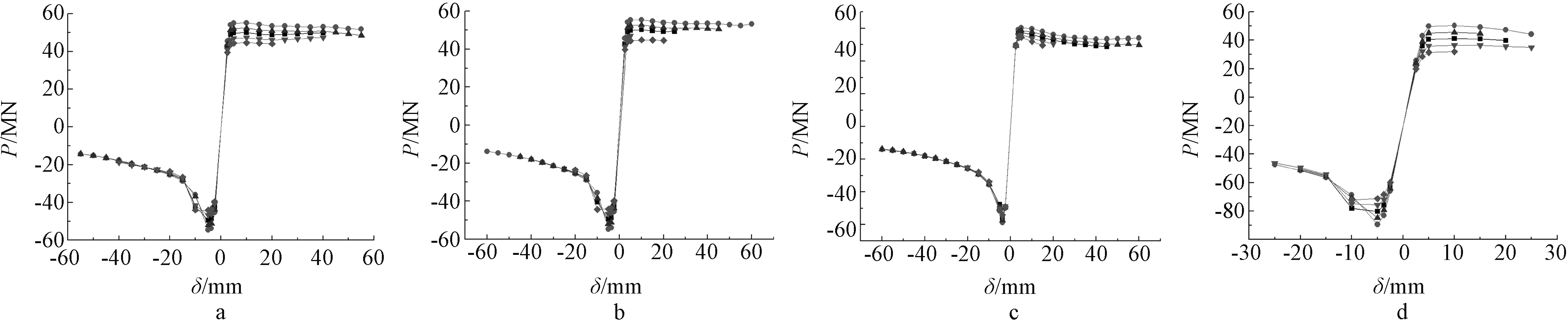
a—I-C组骨架曲线; b—II-C组骨架曲线; c—III-C组骨架曲线; d—IV-C组骨架曲线。![]() —A-1;
—A-1; ![]() —C-1;
—C-1; ![]() —C-2;
—C-2; ![]() —C-3;
—C-3; ![]() —C-4。
—C-4。
图10 低屈服点钢板宽度对试件受力性能的影响
Fig.10 Influence of the width of low-yield point steel plates on the mechanical properties of specimens
分析图10可知,随着低屈服点钢板宽度b1的增大,试件的正、反向最大承载力逐渐减小,其正、反向初始刚度也均有所减小;随着低屈服点钢板宽度b1的改变,试件的正、反向极限破坏位移变化较大,低屈服点钢板宽度在(2/5~1/2)试件横截面宽度范围内,试件正、反向极限破坏位移最大值均达到60 mm。
4.2.3 低屈服点钢板厚度
为研究低屈服点钢板厚度对箱形钢墩柱受力性能的影响,每组数值分析试件中低屈服点钢板厚度设计为32,40,48,56,64 mm。将每组的对比件A-1与D组试件的骨架曲线进行对比,如图11所示。

a—I-D组骨架曲线; b—II-D组骨架曲线; c—III-D组骨架曲线; d—IV-D组骨架曲线。![]() —A-1;
—A-1; ![]() —D-1;
—D-1; ![]() —D-2;
—D-2; ![]() —D-3;
—D-3; ![]() —D-4。
—D-4。
图11 低屈服点钢板厚度对试件受力性能的影响
Fig.11 Influence of the thickness of low-yield point steel plates on the mechanical properties of specimens
分析图11可知:随着低屈服点钢板厚度tw的增大,试件的正、反向最大承载力逐渐增大,其正、反向初始刚度也逐渐增大;改变低屈服点钢板的厚度,试件的正、反向极限破坏位移随之改变,低屈服点钢板厚度在(1.25~1.75)壁板厚度范围内,试件正、反向极限破坏位移最大值均达到60 mm。表明增加低屈服点钢板厚度对试件拉压下承载力和刚度均有有利影响。
4.3 延性系数与耗能能力
延性是指结构在达到最大承载力后,仍具有一定的变形能力,且能继续吸收一定的能量。一般可通过直接比较各试件位移延性系数的大小来定量判断结构的抗震性能。位移延性系数的计算式为:
μ=δu/δy
(1)
其中 δy=Lεy
式中:δu代表构件的极限位移,取骨架曲线上试件最大承载力80%时对应的位移值;δy为有限元分析试件名义屈服点位移;εy为钢材应力-应变曲线上的屈服应变。计算可得 Q345钢材名义屈服点位移为4.4 mm,Q460钢材名义屈服点位移为5.8 mm。
由于所有试件的骨架曲线在正向位移加载过程中的承载力下降均不明显,故位移延性系数的计算取试件反向位移加载过程部分的骨架曲线。同时,为更明确地反映试件的耗能能力,采取计算试件的荷载-位移滞回曲线的包络总面积来衡量试件的耗能能力E。
在不同的影响参数下,各试件的名义屈服点、峰值点、极限点的柱顶位移δ和位移角θ,以及试件的延性系数μ和耗能能力E如表3~表5所示。
表3 耗能壁板高度对试件延性系数及耗能能力的影响
Table 3 The influence of energy-dissipating wallboard
height on the ductility coefficient and energy
dissipation capacity of specimens
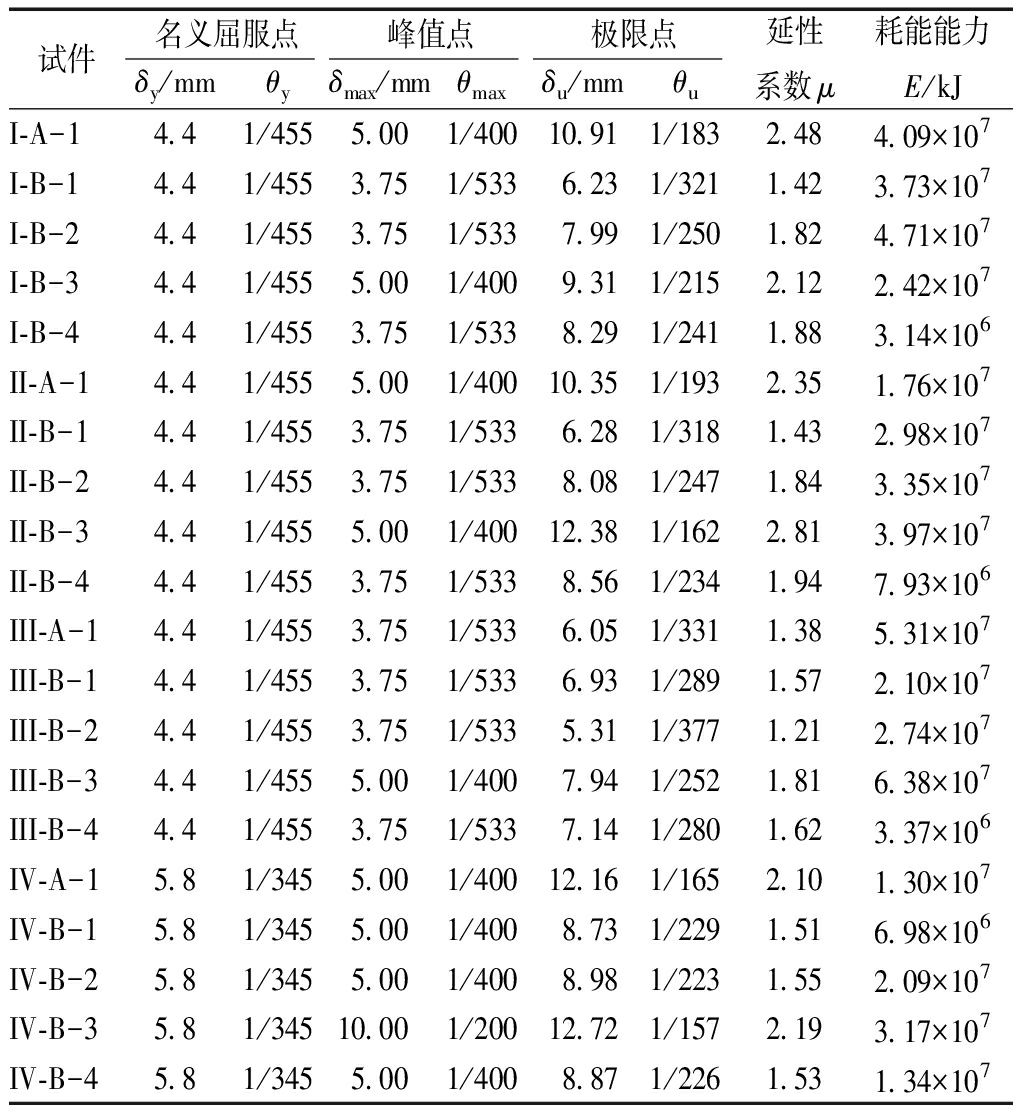
试件名义屈服点峰值点极限点δy/mmθyδmax/mmθmaxδu/mmθu延性系数μ耗能能力E/kJI-A-14.41/4555.001/40010.911/1832.484.09×107I-B-14.41/4553.751/5336.231/3211.423.73×107I-B-24.41/4553.751/5337.991/2501.824.71×107I-B-34.41/4555.001/4009.311/2152.122.42×107I-B-44.41/4553.751/5338.291/2411.883.14×106II-A-14.41/4555.001/40010.351/1932.351.76×107II-B-14.41/4553.751/5336.281/3181.432.98×107II-B-24.41/4553.751/5338.081/2471.843.35×107II-B-34.41/4555.001/40012.381/1622.813.97×107II-B-44.41/4553.751/5338.561/2341.947.93×106III-A-14.41/4553.751/5336.051/3311.385.31×107III-B-14.41/4553.751/5336.931/2891.572.10×107III-B-24.41/4553.751/5335.311/3771.212.74×107III-B-34.41/4555.001/4007.941/2521.816.38×107III-B-44.41/4553.751/5337.141/2801.623.37×106IV-A-15.81/3455.001/40012.161/1652.101.30×107IV-B-15.81/3455.001/4008.731/2291.516.98×106IV-B-25.81/3455.001/4008.981/2231.552.09×107IV-B-35.81/34510.001/20012.721/1572.193.17×107IV-B-45.81/3455.001/4008.871/2261.531.34×107
分析表3~表5可知:随着低屈服点钢板高度的改变,试件的峰值点对应的位移角介于1/533~1/200之间,极限点对应的位移角介于1/331~1/157之间;随着低屈服点钢板高度的增加,试件的延性系数先增大后减小,低屈服点钢板高度在(1/2~5/7)试件高度范围内,延性系数有明显的最大值;低屈服点钢板高度在(1/3~5/7)试件高度范围内,增大低屈服点钢板高度,试件耗能能力随之增加,低屈服点钢板高度在(5/7~4/5)试件高度范围内,增大低屈服点钢板高度,试件耗能能力随之减小。随着低屈服点钢板宽度的改变,试件的峰值点对应的位移角介于1/533~1/200之间,极限点对应的位移角介于1/331~1/156之间;增大低屈服点钢板的宽度,其耗能能力逐渐减小。随着低屈服点钢板厚度的改变,试件的峰值点对应的位移角介于1/533~1/400之间,极限点对应的位移角介于1/409~1/165之间;随着低屈服点钢板厚度的增加,试件的延性系数随其减小,低屈服点钢板厚度在(1.25~1.75)壁板厚度范围内,增大低屈服点钢板厚度,试件的耗能能力随其提高。
表4 耗能壁板宽度对试件延性系数及耗能能力的影响
Table 4 The influence of energy-dissipating wallboard
width on the ductility coefficient and energy
dissipation capacity of specimens
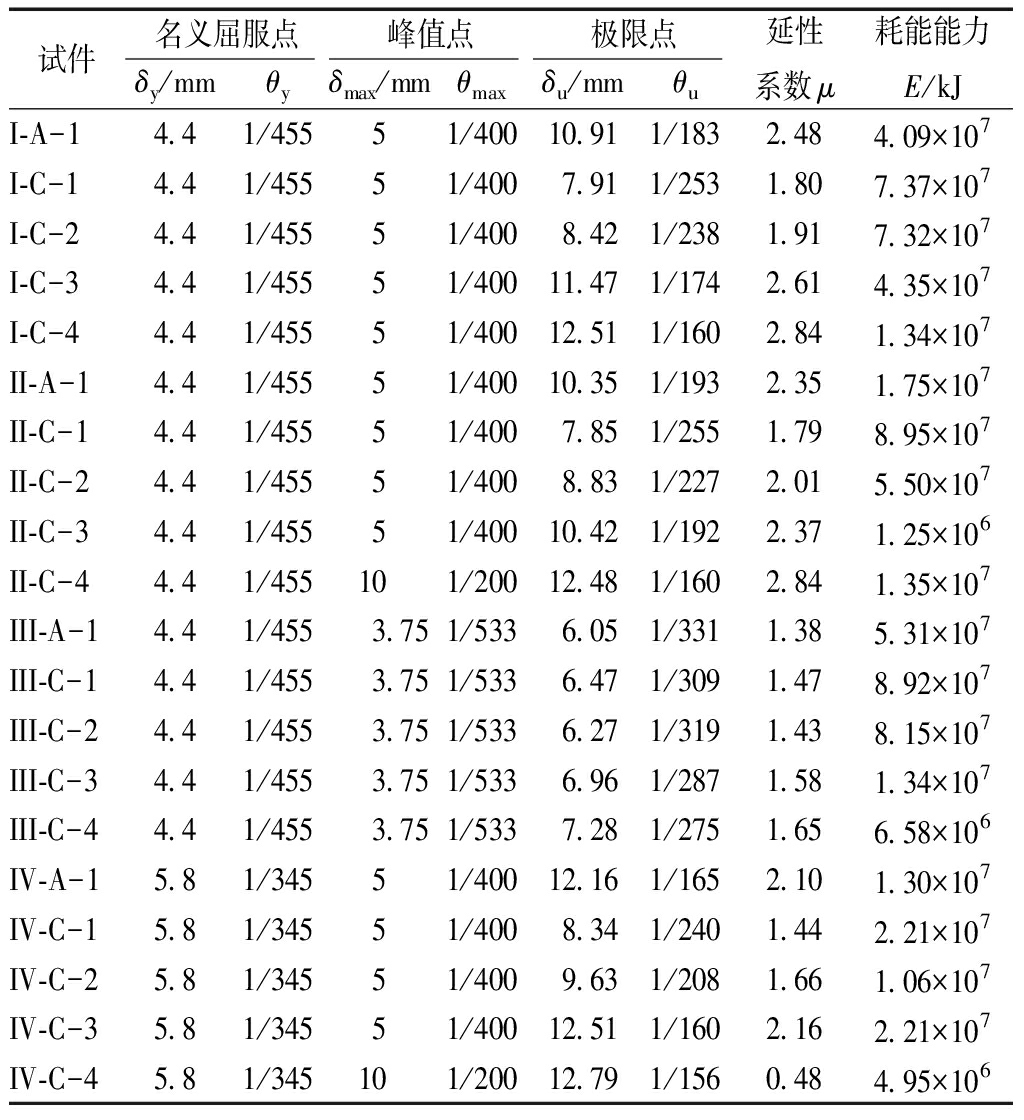
试件名义屈服点峰值点极限点δy/mmθyδmax/mmθmaxδu/mmθu延性系数μ耗能能力E/kJI-A-14.41/45551/40010.911/1832.484.09×107I-C-14.41/45551/4007.911/2531.807.37×107I-C-24.41/45551/4008.421/2381.917.32×107I-C-34.41/45551/40011.471/1742.614.35×107I-C-44.41/45551/40012.511/1602.841.34×107II-A-14.41/45551/40010.351/1932.351.75×107II-C-14.41/45551/4007.851/2551.798.95×107II-C-24.41/45551/4008.831/2272.015.50×107II-C-34.41/45551/40010.421/1922.371.25×106II-C-44.41/455101/20012.481/1602.841.35×107III-A-14.41/4553.751/5336.051/3311.385.31×107III-C-14.41/4553.751/5336.471/3091.478.92×107III-C-24.41/4553.751/5336.271/3191.438.15×107III-C-34.41/4553.751/5336.961/2871.581.34×107III-C-44.41/4553.751/5337.281/2751.656.58×106IV-A-15.81/34551/40012.161/1652.101.30×107IV-C-15.81/34551/4008.341/2401.442.21×107IV-C-25.81/34551/4009.631/2081.661.06×107IV-C-35.81/34551/40012.511/1602.162.21×107IV-C-45.81/345101/20012.791/1560.484.95×106
表5 耗能壁板厚度对试件延性系数及耗能能力的影响
Table 5 The influence of energy-dissipating wallboard
thickness on the ductility coefficient and energy
dissipation capacity of specimens
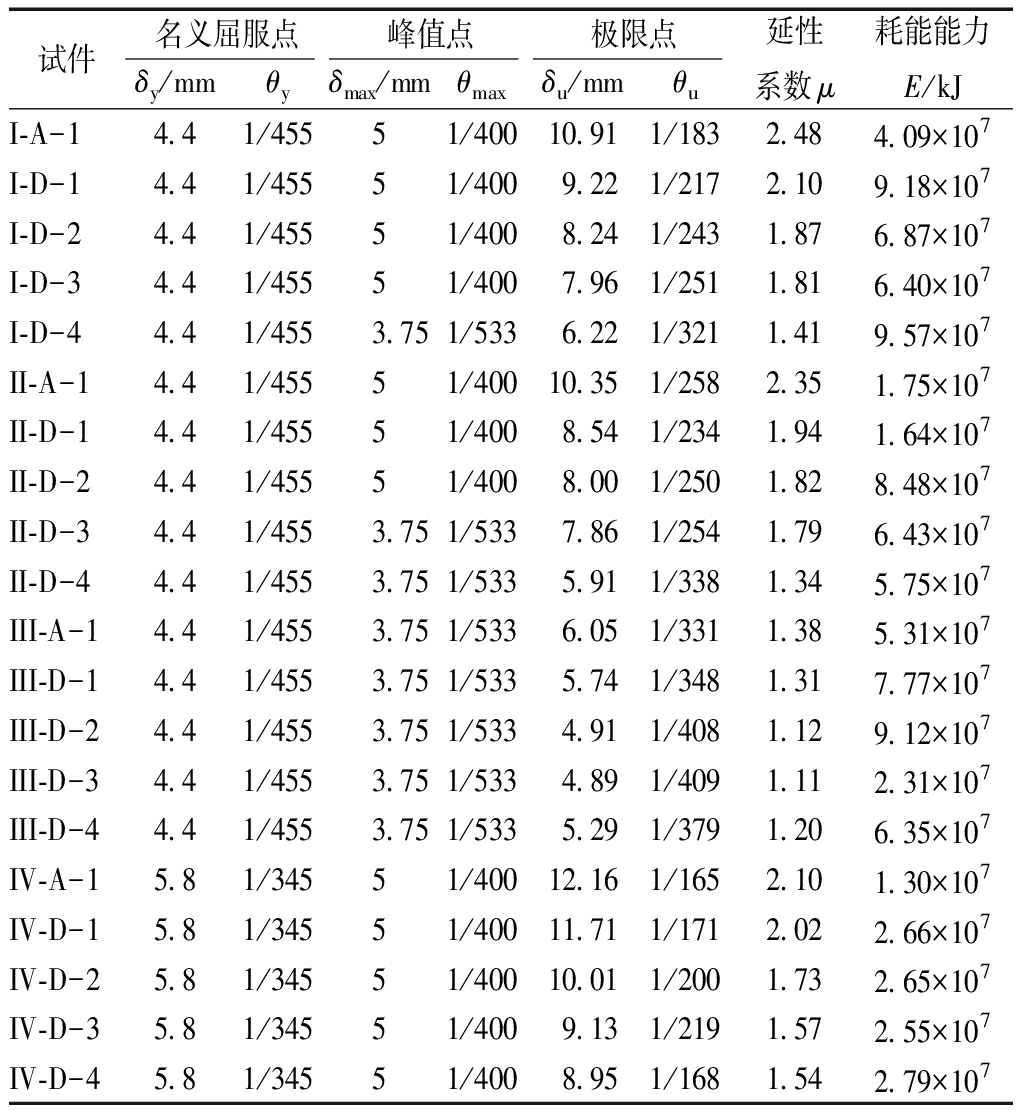
试件名义屈服点峰值点极限点δy/mmθyδmax/mmθmaxδu/mmθu延性系数μ耗能能力E/kJI-A-14.41/45551/40010.911/1832.484.09×107I-D-14.41/45551/4009.221/2172.109.18×107I-D-24.41/45551/4008.241/2431.876.87×107I-D-34.41/45551/4007.961/2511.816.40×107I-D-44.41/4553.751/5336.221/3211.419.57×107II-A-14.41/45551/40010.351/2582.351.75×107II-D-14.41/45551/4008.541/2341.941.64×107II-D-24.41/45551/4008.001/2501.828.48×107II-D-34.41/4553.751/5337.861/2541.796.43×107II-D-44.41/4553.751/5335.911/3381.345.75×107III-A-14.41/4553.751/5336.051/3311.385.31×107III-D-14.41/4553.751/5335.741/3481.317.77×107III-D-24.41/4553.751/5334.911/4081.129.12×107III-D-34.41/4553.751/5334.891/4091.112.31×107III-D-44.41/4553.751/5335.291/3791.206.35×107IV-A-15.81/34551/40012.161/1652.101.30×107IV-D-15.81/34551/40011.711/1712.022.66×107IV-D-25.81/34551/40010.011/2001.732.65×107IV-D-35.81/34551/4009.131/2191.572.55×107IV-D-45.81/34551/4008.951/1681.542.79×107
5 结束语
1)低屈服点耗能钢板的宽度和厚度对箱形钢墩柱的承载能力和初始刚度影响较大。随着低屈服点钢板宽度的增加,箱形钢墩柱的最大承载力及初始刚度逐渐减小;随着低屈服点钢板厚度的增加,箱形钢墩柱的最大承载力及初始刚度逐渐增大;低屈服点钢板的高度对箱型钢墩柱的承载能力和初始刚度影响相对较小。
2)箱形钢墩柱试件峰值点的位移角介于1/533~1/200之间,箱形钢墩柱试件极限点的位移角介于1/409~1/166之间。
3)低屈服点耗能钢板的高度、宽度及厚度均对箱形钢墩柱延性有影响。增大低屈服点钢板厚度或高度,箱形钢墩柱的延性系数先增大后减小;低屈服点钢板高度在(1/2~5/7)试件高度范围内,延性系数最大值为2.81;低屈服点钢板厚度在(1.25~1.75)壁板厚度范围内,延性系数最大值为2.84。
4)改变低屈服点耗能钢板高度、宽度及厚度,对箱形钢墩柱的耗能能力均有影响。低屈服点钢板高度在(1/3~5/7)试件高度范围内,增大低屈服点钢板高度,箱形钢墩柱耗能能力随其提高;低屈服点钢板厚度在(1~1.5)壁板厚度范围内,增大低屈服点钢板厚度,箱形钢墩柱耗能能力随其提高;增加低屈服点钢板宽度,箱形钢墩柱耗能能力下降。
[1] WATANABE E, SUGIURA K, NAGATA K, et al. Performances and Damages to Steel Structures During the 1995 Hyogoken-Nanbu Earthquake[J]. Engineering Structures, 1998, 20(4/5/6): 282-290.
[2] BRUNEAU M. Performance of Steel Bridges During the 1995 Hyogoken-Nanbu (Kobe, Japan) Earthquake-a North American Perspective[J]. Engineering Structures, 1998, 20(12): 1063-1078.
[3] DANG J, AOKI T. Bidirectional Loading Hybrid Tests of Square Cross-Sections of Steel Bridge Piers[J]. Earthquake Engineering Structural Dynamics, 2013, 42(8): 1111-1130.
[4] 高圣彬, 徐旻洋, 张大旭. 内填部分混凝土箱形截面钢桥墩的延性影响参数[J]. 哈尔滨工业大学学报, 2014, 346(12):89-95.
[5] 徐旻洋, 高圣彬. 内填部分混凝土钢桥墩延性性能简化计算方法[J]. 河北工程大学学报(自然科学版), 2014, 31(3): 9-14.
[6] SHIMIZU S, WATANABE T. Behaviour of Concrete-Filled Steel Columns Under the Seismic Loading[J]. Thin-Walled Structures, 2007, 45: 921-926
[7] SHIMIZU S. Behaviour of Steel Columns Under 3-D Seismic Load[J]. Thin-Walled Structures, 2011,49: 544-553.
[8] YUAN H H, JI D, AOKI T. Behavior of Partially Concrete-Filled Steel Tube Bridge Piers Under Bidirectional Seismic Excitations[J]. Earthquake Engineering Structural Dynamics, 2013,42: 2197-2216.
[9] 王占飞, 隋伟宁, 李帼昌, 等. 水平往复荷载作用下部分填充混凝土圆形钢桥墩柱的力学性能[J]. 中国公路学报, 2015, 28(1):62-70.
[10] AOKI T, TAKAKU T, FUKUMOTO Y, et al. Experimental Investigation for Seismic Performance of Framed Structures Having Longitudinally Profiled Plates[J]. Journal of Constructional Steel Research, 2008,64: 875-881.
[11] 张建东, 葛汉彬, 王春林. 薄壁加劲箱形钢桥墩简化抗震评估方法[J]. 中国公路学报, 2013,26(1): 113-120.
[12] GE HB, LAN K. Ductile Crack Initiation and Propagation in Steel Bridge Piers Subjected to Random Cyclic Loading[J]. Engineering Structures, 2014,59: 809-820.
[13] WANG Y B, LI G Q, CUI W, et al. Seismic Behavior of High Strength Steel Welded Beam-Column Members[J]. Journal of Constructional Steel Research, 2014,102: 245-255.
[14] 王占飞, 邱国强, 高彬, 等. 平面内往复荷载作用下竖向偏心圆形钢桥墩的弹塑性能有限元分析[J]. 地震工程与工程振动, 2014, 34:611-615.
[15] SHI G, ZHOU WJ, YU B, et al. Local Buckling of 460 MPa High Strength Steel Welded Section Stub Columns Under Axial Compression[J]. Journal of Constructional Steel Research, 2014,100: 60-70.