随着我国经济发展方式的转变和产业结构战略性调整,建筑行业将转向尊重经济规律、重质量、重效益、重可持续发展之路。装配式建筑具有施工速度快、劳动效率高、现场环境污染小、建筑质量高等优点,它将在各行业得到更加广泛的应用,同时,近年来,城市建设用地规模不断扩大,土地资源锐减,人均土地资源将越来越匮乏,因此城市地下工程建设项目越来越多,地下结构的研究也越来越受到关注。现将预制装配式结构体系应用于地下工程建设,既体现了预制装配式的高效率、高质量、低成本、速度快的优势,又符合国家对装配式结构建设的规划。
综合国内外研究成果,预应力混凝土结构在抗冲击领域的研究开展得较少。美国夏威夷大学将轻质夏威夷骨料混凝土制成预应力混凝土梁[1],并对其在周期性冲击荷载作用下的动力性能进行试验分析。美国德克萨斯大学土木工程系以界面的粗糙度和钢筋强度为参数对预应力混凝土叠合梁的动力特性和抗力进行了试验研究[2],试验分别包括:3根叠合梁的静载试验以及9根简支预应力叠合梁的动载试验。王新武等对3根带覆土无黏结部分预应力混凝土梁采用跨中施加落锤冲击荷载的方法,研究其抗冲击性能,得出实测波形曲线,得到无黏结部分预应力混凝土试验梁的动力特性和极限承载能力,结果表明:带少量覆土无黏结部分预应力混凝土试验梁具有很好的抗冲击性能,不会发生脆性破坏,可用于大跨度地下结构[3]。李砚召等利用平面装药爆炸模拟核爆炸的加载技术,进行了分配层分层结构对核爆炸荷载防护效果的大比尺相似模拟野外爆炸试验,通过4个不同分层结构的平面装药加载试验,证明了分配层分层结构对核爆炸的防护效果明显优于单层结构,分配层分层设置的人防工程结构对核爆炸冲击波具有弥散效应,分层材料相同且各种材料的总厚度也相同时,采用周期循环布置时弥散效应明显加强,利用这一特性可显著降低核爆炸空气冲击波感生地冲击对脆性材料的破坏作用[4]。宗周红等结合不同截面形式、长细比、混凝土类型、箍筋形式、轴压比等参数,研究了爆炸冲击荷载作用下钢筋混凝土墩柱的动力响应特性、损伤破坏模式及破坏机理[5],研究结果表明:在非接触爆炸作用下,随着柱截面面积增大以及螺旋箍筋等措施,墩柱的抗爆性能得到增强;在接触爆炸作用下,构件在炸药接触位置发生冲切破坏,局部损伤严重。
用于停车库的大跨装配式预应力屋面结构常见的有双T板结构和槽型板结构,其中双T板构件两侧翼板为悬臂受力结构,因此其受力极限值和动力延性较差,不适于在竖向恒载较大的地下车库顶板上使用。槽型板结构是在双T板结构基础上演变而来的,因此槽型板结构具有与双T板结构类似的受力特性和优点。它将双T板两侧翼板取消,提高了槽型板的抗力水平和动力延性,因此槽型板结构适合作为竖向恒载较大的地下车库顶板使用。
目前针对装配式结构体系在人防荷载作用下的抗爆性能的模拟研究较少,因此,本文对装配式预应力槽型板结构体系在人防荷载作用下的抗爆性能模拟及设计方法进行研究,为其在有人防功能要求的地下工程的研究和应用提供参考。
1 试验分析
针对先张预应力混凝土槽型板设计了缩尺比为1∶3的先张预应力混凝土槽型板平面装药爆炸模拟试验,以检验预应力混凝土槽型板的抗爆性能。根据GB 50038—2005《人民防空地下室设计规范》[6]、2009JSCS-6《全国民用建筑工程设计技术措施——防空地下室》[7]、《预应力工程设计施工手册》[8]、GB 50010—2010《混凝土结构设计规范》[9]对装配式预应力(先张法)槽型板结构进行设计(图1)。
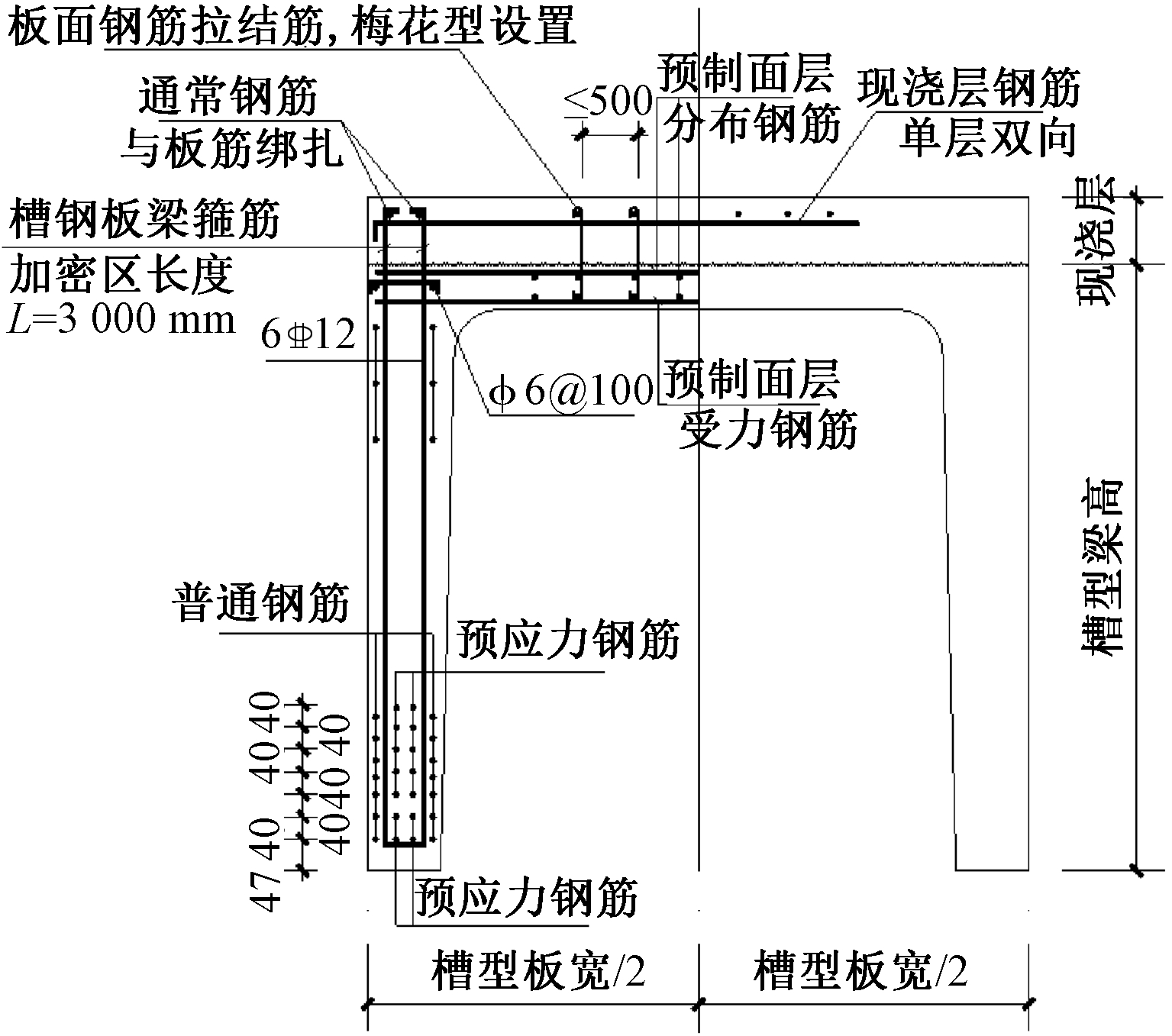
图1 模型形式
Fig.1 Model form
然后依据GJBz 20129—93《平面装药爆炸模拟核爆炸空气冲击波试验规程》[10],对构件采用平面装药爆炸模拟方式,即在覆土的上表面产生竖直向下的平面波,用来模拟核爆炸冲击波均布荷载对构件整体结构的作用。地面入射超压峰值取0.06,0.10,0.2,0.4 MPa,正压作用时间不小于260 ms,并依次进行爆炸试验。

图2 混凝土槽型板
Fig.2 Concrete channel slab
如图3所示,结构跨中位移随时间变化,结构在4级爆炸等级作用下的挠度最大,试验值为41.644 mm。
图4、图5分别表示跨中应变随时间的变化和峰值混凝土应变与空压关系。板跨中上表面的峰值应变的绝对值随空气冲击波超压峰值的增加而增加,所测到的最大混凝土应变为-2 833×10-6,仍未达到混凝土的极限压应变,因而预应力混凝土槽型板达到破坏时所能承受的最大空气冲击值超压波峰大于0.465 MPa。
试验结果表明:该试件在0.467 MPa空气冲击波荷载作用下裂纹很小,塑性变形小,具有抵抗更大荷载的能力;考虑到缩尺构件的承载能力要稍小一点,因此原型预应力混凝土槽型板完全可以承受4级人防工程的荷载而不会发生破坏。
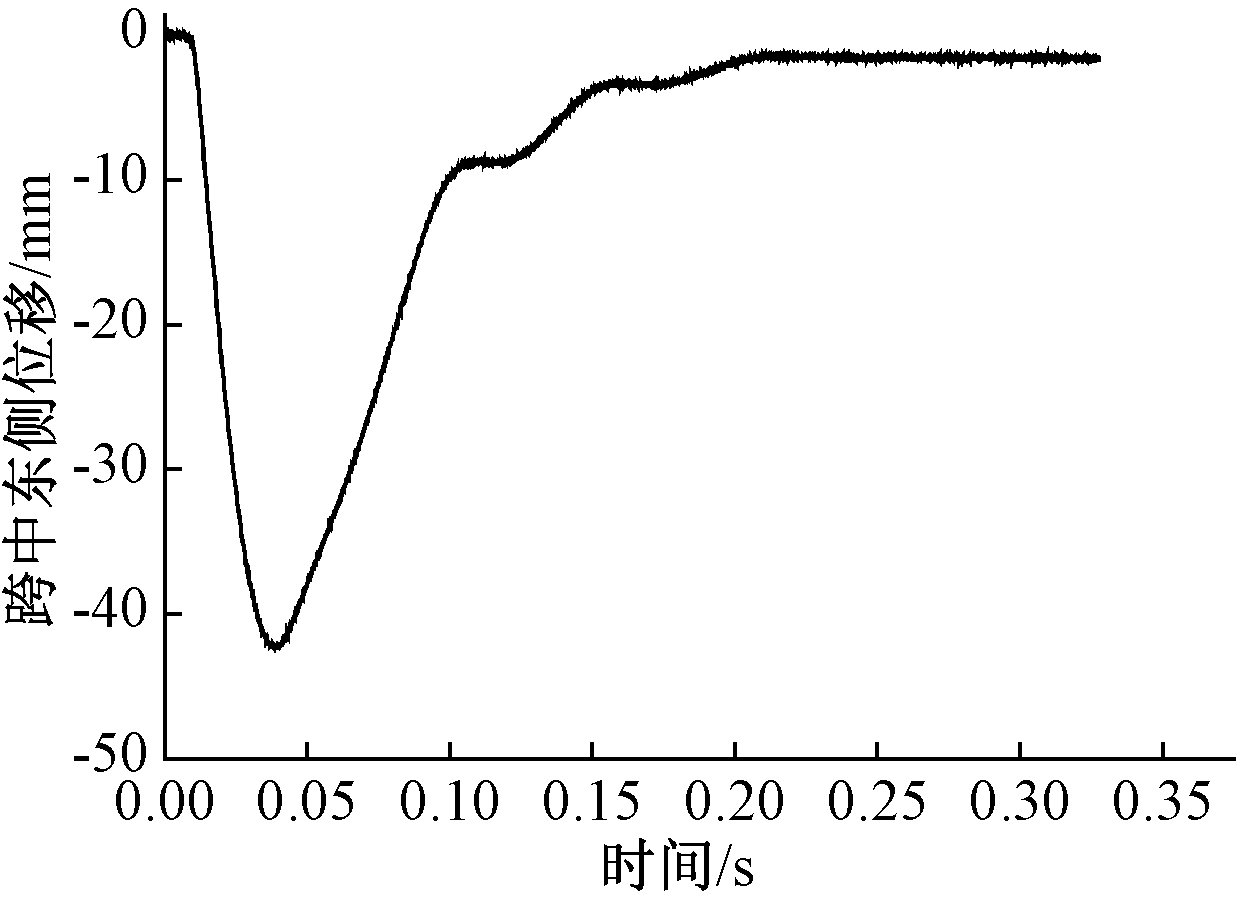
图3 跨中东侧位移
Fig.3 Mid-span displacement in east
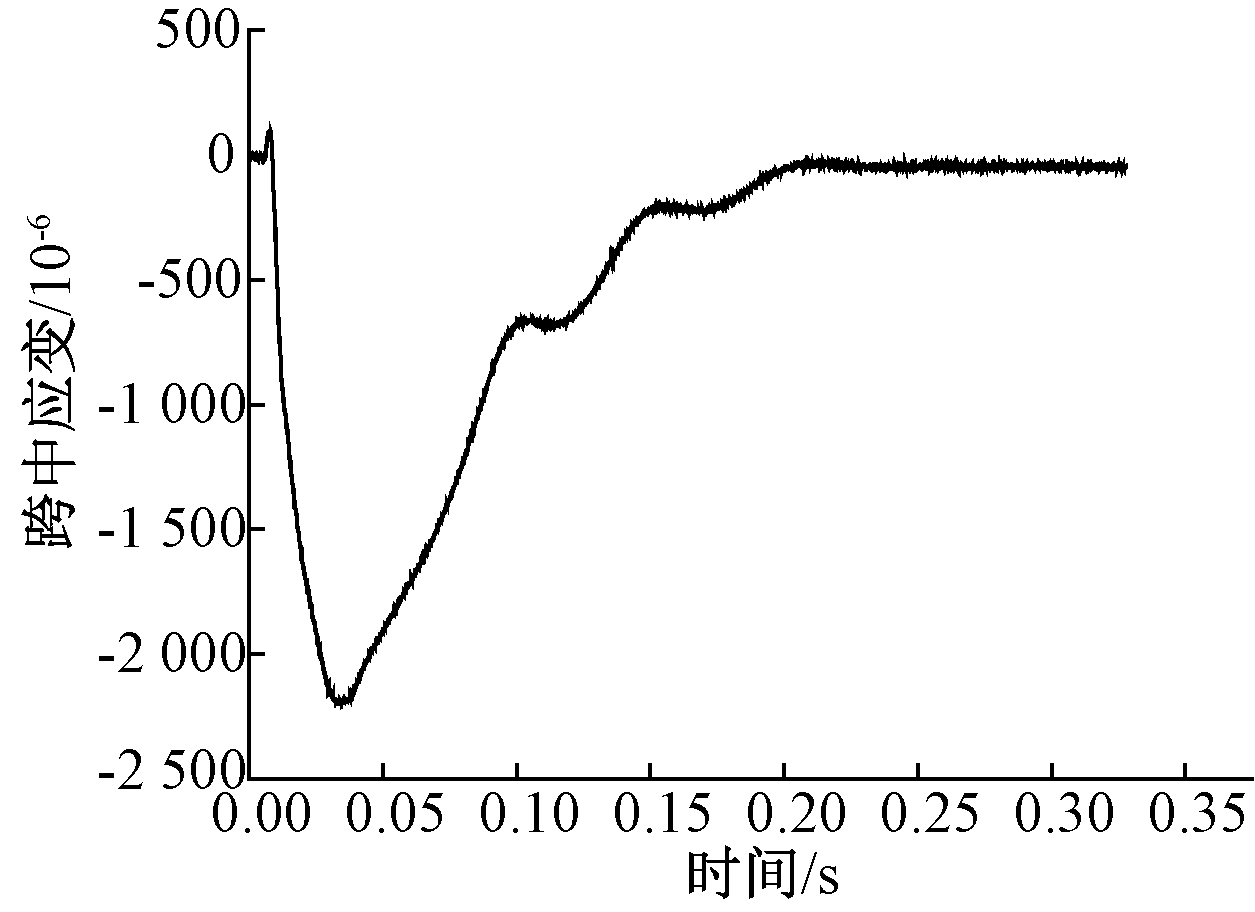
图4 跨中应变
Fig.4 Mid-span structural strain
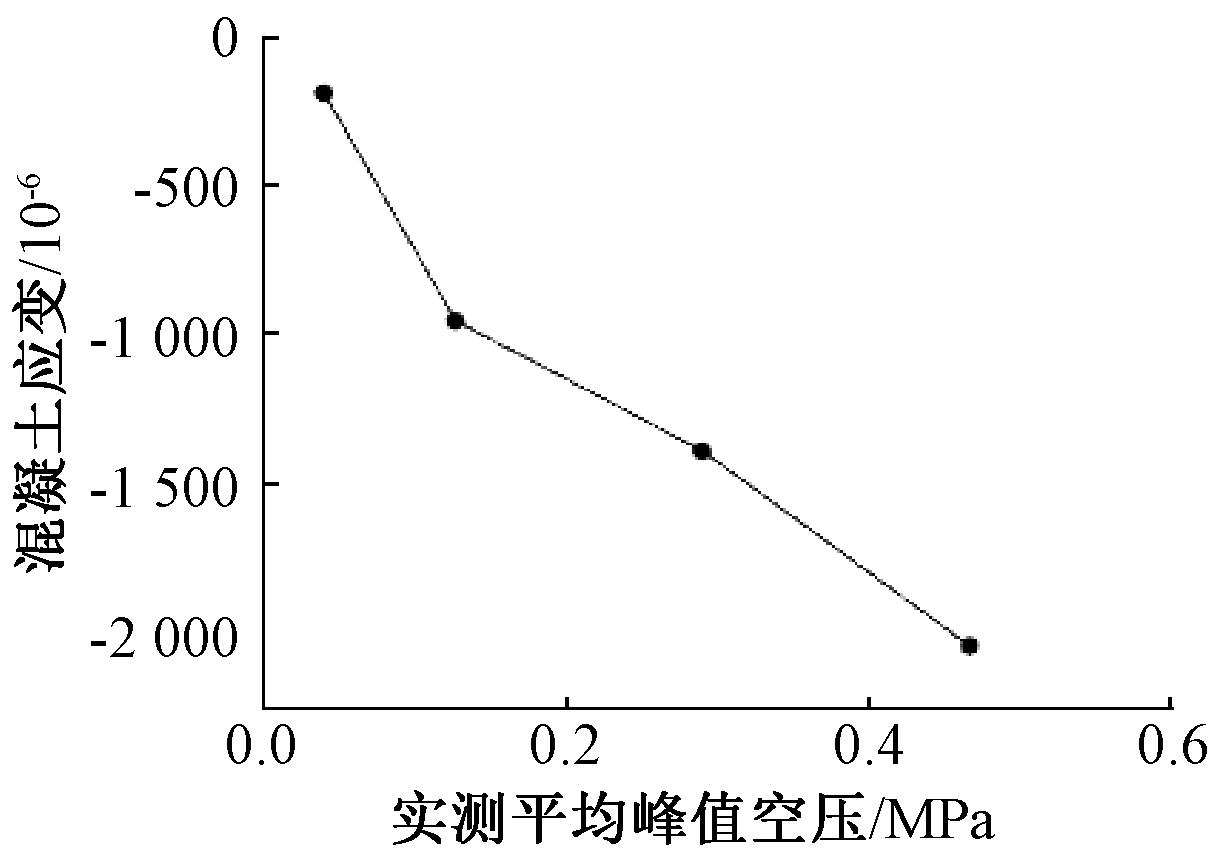
图5 混凝土应变与峰值空压关系曲线
Fig.5 Relationship between peak strain and peak
air pressure of concrere
2 有限元模型
2.1 本构模型
本文对钢筋应力-应变关系曲线采用五段式二次塑流模型,分为弹性阶段、弹塑性阶段、塑性阶段、强化阶段和二次塑流阶段五个阶段,其数学表达式见式(1)。本文建立有限元模型时,钢筋弹性模量根据GB 50010—2010取不同钢筋对应的弹性模量,弹性阶段泊松比取0.30。结构进行弹塑性分析时,材料的性能指标宜取用平均值。

(1)
其中 ![]()
式中:Es为钢材弹性模量;εe为比例极限应变;εe1为弹性极限应变;εe2为屈服时应变;εe3为峰值荷载时的应变;fym为屈服强度。
钢绞线本构采用理想弹塑性模型,其应力-应变关系采用GB 50010—2010推荐的模型,认为钢绞线只承受轴向拉力,不受横向剪切力。
在动力荷载作用下,许多金属材料的屈服极限有明显的提高,而屈服的出现有滞后现象,此种现象称为材料的应变率效应。因此本文中对钢筋和钢绞线的模拟采用ABAQUS中提供的经典金属性模型,该模型的等效塑性应变率由动态屈服应力与静态屈服应力比值R给出,其中D与n为材料常数,在本模型中取D=40,n=5。
混凝土材料的轴心抗压强度标准值、轴心抗拉强度标准值以及单轴受压和受拉应力-应变关系曲线均按GB 50010—2010附录C取用。混凝土材料的单轴受压应力-应变关系曲线按式(2)采用。
普通混凝土单轴受压应力-应变关系:
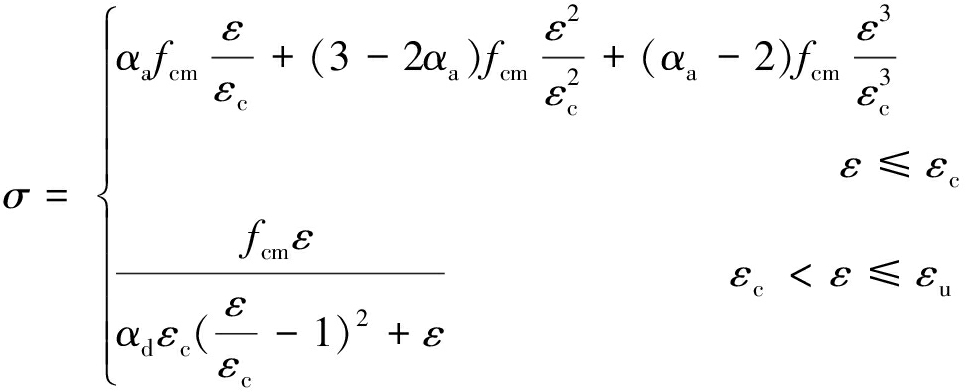
(2)
式中:αa、αd分别为单轴受压应力-应变关系曲线的上升段与下降段参数;εc为混凝土峰值压应变;fcm为混凝土抗压强度平均值。
混凝土材料的单轴受拉应力-应变关系曲线按式(3)采用。
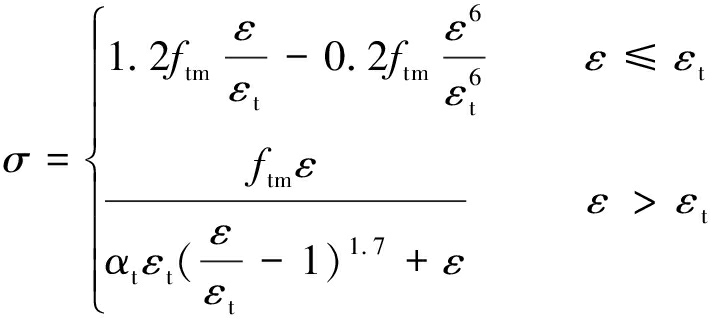
(3)
式中:αt为单轴受拉应力-应变关系曲线的下降段参数;εt为混凝土峰值拉应变;ftm为混凝土抗拉强度平均值。
结构材料在爆炸和冲击荷载作用下会发生毫秒级的快速变形,且随应变速率的提高,材料内部发生了一系列物理和化学变化,其力学特性主要表现为一些关于应力-应变的特征参数,例如强度、延性、弹性模量、阻尼比和内聚力均发生不同程度的改变。因此在ABAQUS中依据文献[11-12]的建议,建立损伤塑性模型,用于模拟混凝土、砂浆等准脆性材料的行为。
混凝土动态抗压强度fcd与准静态抗压强度fc之间的关系如下:
fcd/fc=0.022ln(ε/ε0)+0.997 3
(4)
式中:ε和ε0分别为当前应变率和准静态应变率,取ε0为3.0×10-5/s。
混凝土动态抗拉强度ftd与准静态抗拉强度ft之间的关系如下:
ftd/ft=0.071 4ln(ε/ε0)+0.988 3
(5)
式中:ftd和ft分别为当前应变率和准静态应变率下的抗拉强度。
2.2 单元类型
混凝土的单元类型采用三维8结点减缩积分实体单元C3D8R,每结点具有3个平动自由度。钢筋的单元类型则采用三维线性桁架单元T3D2进行模拟,该单元只能承受轴力,不能承受弯矩和剪力作用。
2.3 网格划分及有限元模型
建立几何模型和选择单元类型后,应基于几何模型划分网格。本模型形状十分规则,因此采用结构优化网格及中性轴算法来进行网格划分。建立的ABAQUS模型如图6所示。
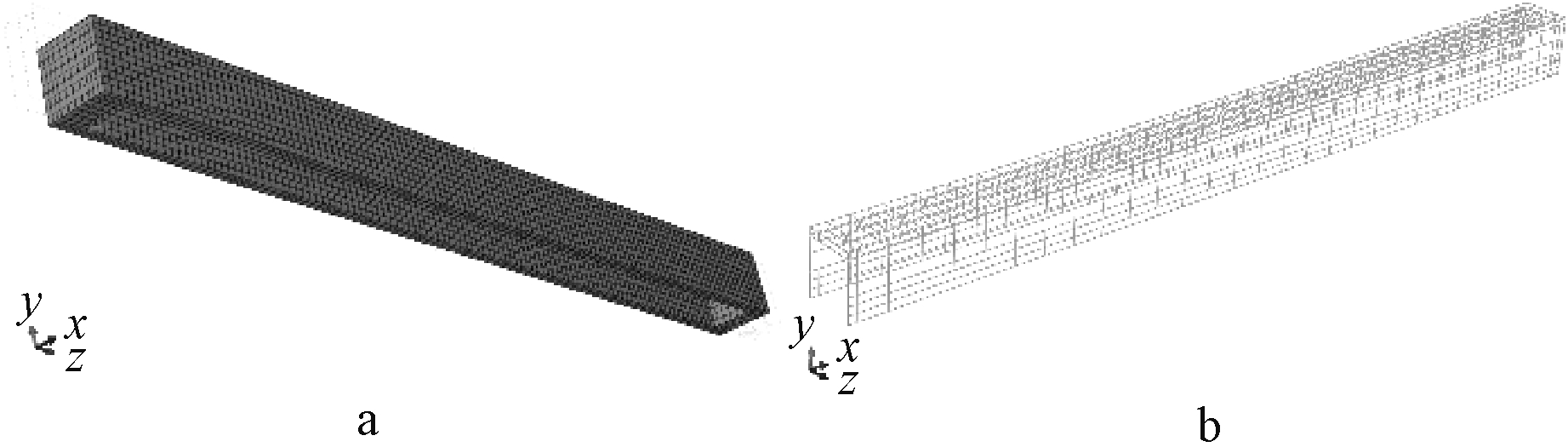
a—混凝土模型网格划分; b—钢筋有限元模型。
图6 ABAQUS有限元模型
Fig.6 ABAQUS finite-element model
2.4 相互作用
将两种材料视为独立个体,分别建立混凝土部分模型和钢筋部分模型,再通过相互作用中Embed命令将钢筋部分嵌入到混凝土部分中,使其成为整体。使用这种方式建模,等于认为钢筋与混凝土的应变是相互协调的。
2.5 加载方式与边界条件
在ABAQUS中建立了2个分析步,第1个分析步施加温度荷载,即为钢绞线施加预应力。第2个分析步施加均布荷载,即为试验爆炸荷载,如图7所示。分析步类型均采用显示动力分析。
图7 试验爆炸荷载
Fig.7 Experimental explosion load
根据现场试验实际情况,板两端按简支条件设置。在ABAQUS软件中的LOAD模块里,将构件的一端释放UR3,另一端释放UR3、U1,既允许构件沿构件长边方向转动。
3 缩尺模型模拟结果
3.1 位移分析
现对槽型板试验进行有限元模拟。通过有限元分析结果与试验结果的对比来验证有限元模拟的真实性以及分析结果的可靠性。根据试验槽型板尺寸建立4个有限元模型,对应4种工况,即分析在不同爆炸等级作用下的槽型板的受力性能和破坏模式。表1说明不同爆炸工况对应的试验荷载以及抗力等级。
表1 槽形极上表面结构峰值压力统计
Table 1 Peak structural pressure on upper
surface of channel plates

爆炸工况防核武器抗力级别试验爆炸峰值空压/MPa16级0.04025级0.12734B级0.29044级0.467

a—工况1; b—工况2; c—工况3; d—工况4。
——试验数据; ----模拟数据。
图8 试验数据与有限元模拟值对比
Fig.8 Comparison of experimental data and finite element simulation
对模型进行分析,对比试验数据与有限元分析出的跨中点位移,详见表2。4种荷载工况下关于位移的试验数据与有限元模拟对比见图8。通过对比发现,有限元模拟所得曲线和试验曲线基本吻合,最大位移相差小于9%,说明跨中极限位移有限元模拟结果与试验结果接近,表明有限元模拟结果真实可靠。
表2 最大位移与试验结果对比
Table 2 Comparison of maximum
displacement and test results
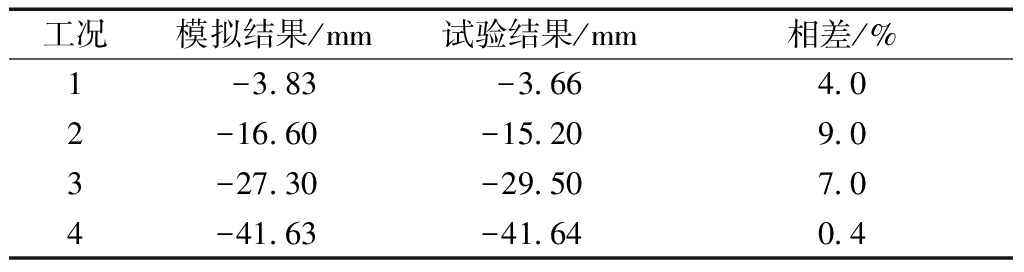
工况模拟结果/mm试验结果/mm相差/%1-3.83-3.664.02-16.60-15.209.03-27.30-29.507.04-41.63-41.640.4
3.2 Mises应力云图
图9列出了在核爆荷载作用下混凝土、钢筋和预应力筋的应力云图,混凝土结构在0.04 s达到核爆荷载的压力峰值,同时混凝土Mises应力达到峰值为46.99 MPa,由于爆心的竖直投影落在构件的中心点, 因而顶板的中心点及其周边区域在爆炸初始阶段处于高应力状态, 随着时间的增加,应力向四周传递,强度逐渐降低,构件处于弹塑性阶段。由图9可知:普通钢筋应力峰值749 MPa,达到屈服强度。预应力钢绞线应力峰值为1 852 MPa,接近钢绞线抗拉极限强度,但仍具有一定的富裕度。

a—混凝土; b—普通钢筋应力峰值;
c—预应力钢绞线应力峰值。
图9 Mises应力云图 MPa
Fig.9 Mises stress nephogram
通过分别比较4种工况下混凝土、钢筋、钢绞线的最大应力(表3),得出随着防核武器抗力级别的提升,爆炸峰值压力增大,构件的峰值应力逐渐增大。
表3 4种工况下构件最大应力
Table 3 Maximum stress of members MPa

工况混凝土钢筋钢绞线14.189.2 8.3214.3195.2894.0322.5264.51 196.0447.0749.11 852.0
3.3 混凝土损伤云图
由于工况4的动力荷载数值最大,因而该工况的混凝土损伤程度最大,图10给出了爆炸工况4荷载作用下槽型板混凝土损伤云图,分别反映了有限元模拟槽型板结构的受压和受拉损伤程度。且混凝土受压损伤最大值为0.165,受拉损伤最大值为0.158。由图10a可知:跨中及其附近截面处靠近上表面的区域出现了一定程度受压损伤,但损伤状态较轻。从图10b可知:构件下表面的大部分区域出现较为严重的受拉损伤,跨中底部大片混凝土受拉损伤,裂缝将在跨中底部处开始发展。这种现象与试验观察的结果一致。
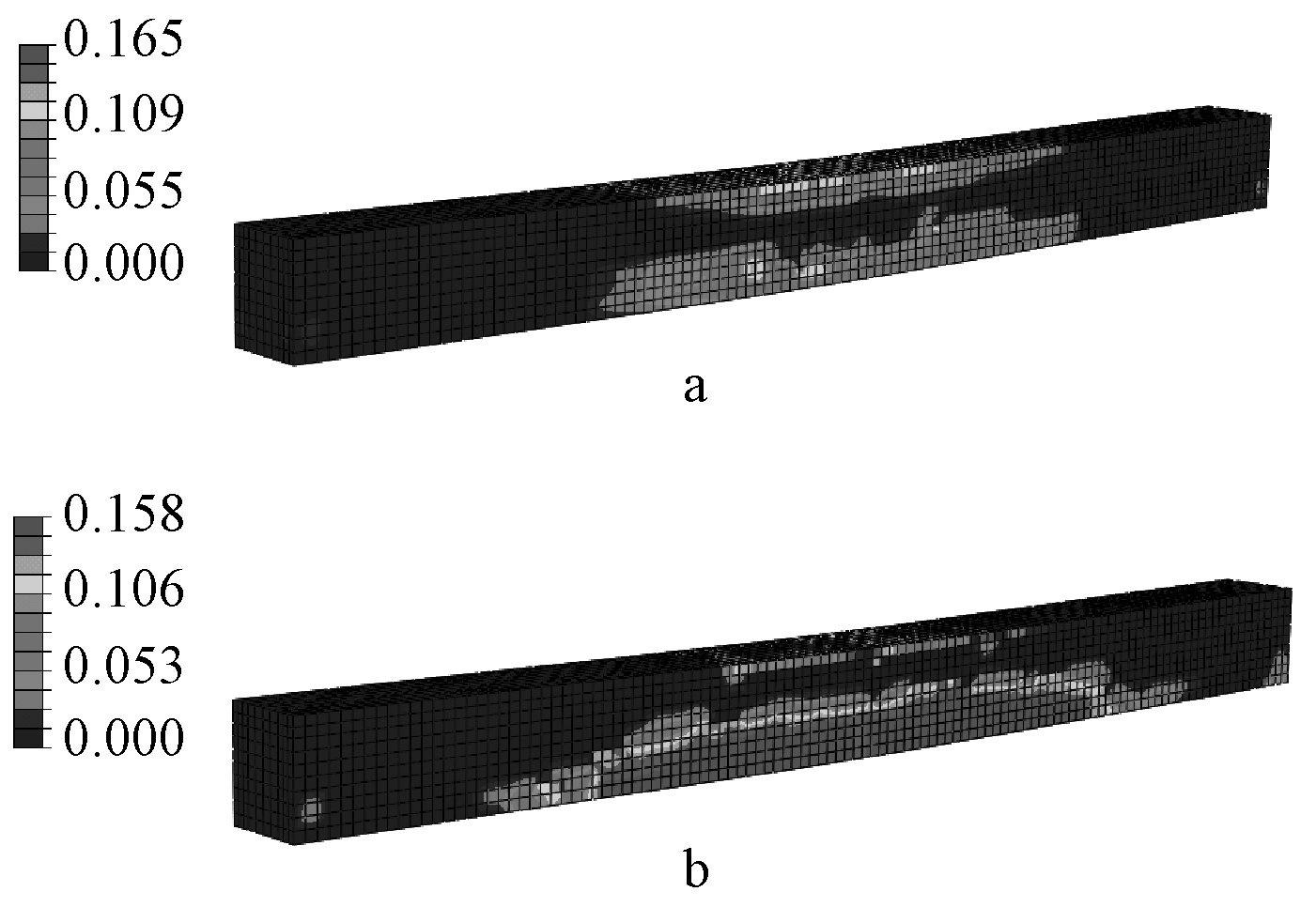
a—最终混凝土受压损伤; b—最终混凝土受拉损伤。
图10 混凝土损伤云图
Fig.10 Concrete damage rephogram
表4 正压作用时间统计
Table 4 Statistical table of positive pressure action time
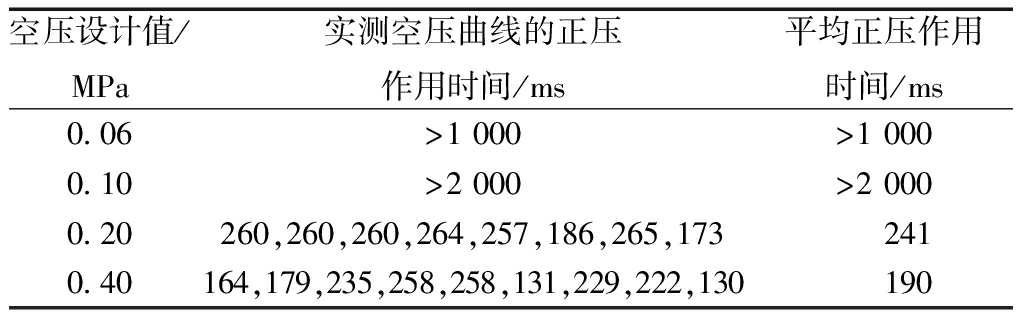
空压设计值/MPa实测空压曲线的正压作用时间/ms 平均正压作用时间/ms0.06>1 000>1 0000.10>2 000>2 0000.20260,260,260,264,257,186,265,1732410.40164,179,235,258,258,131,229,222,130190
3.4 应力流
图11给出了4个爆炸工况荷载作用下槽型板内部的应力流,从数值上看,压应力流变化不大,且压应力分布较均匀;而构件拉应力较为集中,随着爆炸荷载的增大而增大,其变化率高于受压应力。
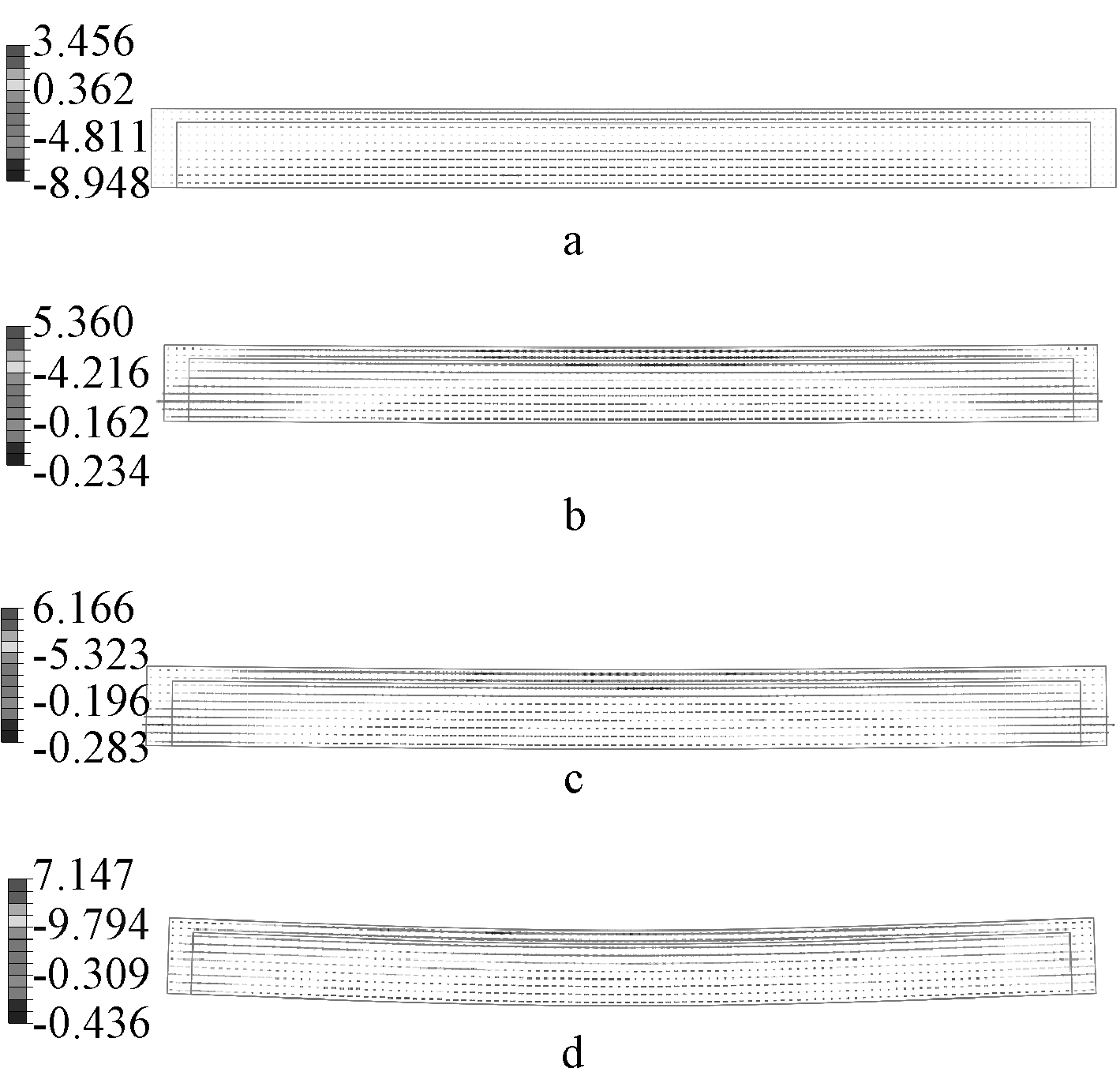
a—工况1; b—工况2; c—工况3; d—工况4。
图11 应力流
Fig.11 Stress flow
3.5 延性分析
为了判断结构的延性比,需要对槽型板进行静力荷载下的模拟,分析槽型板在静力作用的位移,如图12所示,以支座反力和跨中位移为坐标绘制荷载-位移曲线,得出结构的弹性极限位移为1.946 mm,屈服荷载为16.622 kN。
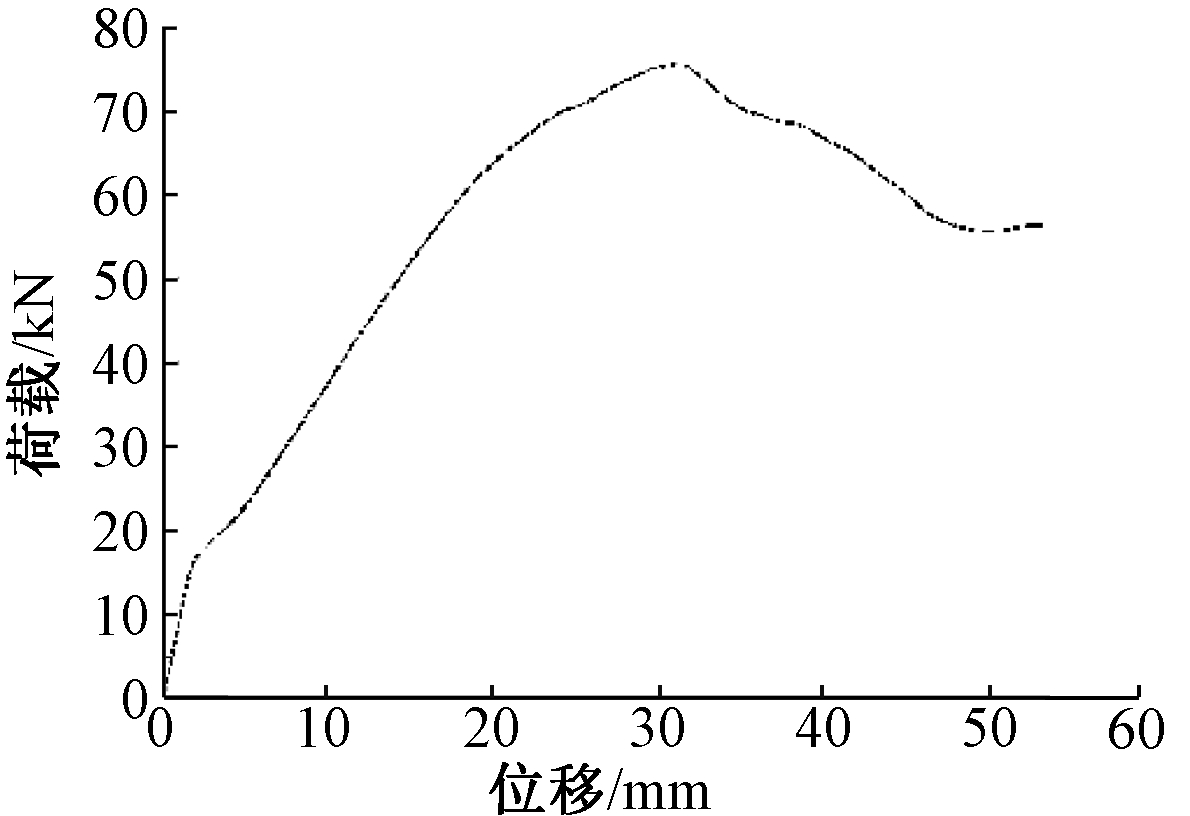
图12 荷载-位移曲线
Fig.12 Load-displacement curve
缩尺槽型板在对应防核爆抗力等级5级时对应荷载作用的构件最大位移为15.486 mm,有限元模拟得到的跨中最大位移为17.639 mm,在静力荷载作用下弹性极限位移为6.946 mm,故计算得到槽型板结构的延性比为7.958,而对应有限元模拟最大位移计算得到的延性比为9.064。证明有限元模拟真实可靠。
4 足尺模型模拟结果
通过有限元模拟分析与试验结果的对比,充分验证了有限元模拟的真实性和结果的可靠性。为了深入研究槽型板的受力性能、破坏模式以及抗爆能力,现利用ABAQUS软件对足尺寸的槽型板在不同工况下进行动力以及静力加载模拟。工况5对应防核武器抗力级别为6级,工况6对应防核武器抗力级别为5级。
4.1 动力荷载作用下槽型板响应分析
根据GB 50038—2005计算得到简单的爆炸荷载曲线如图13所示。
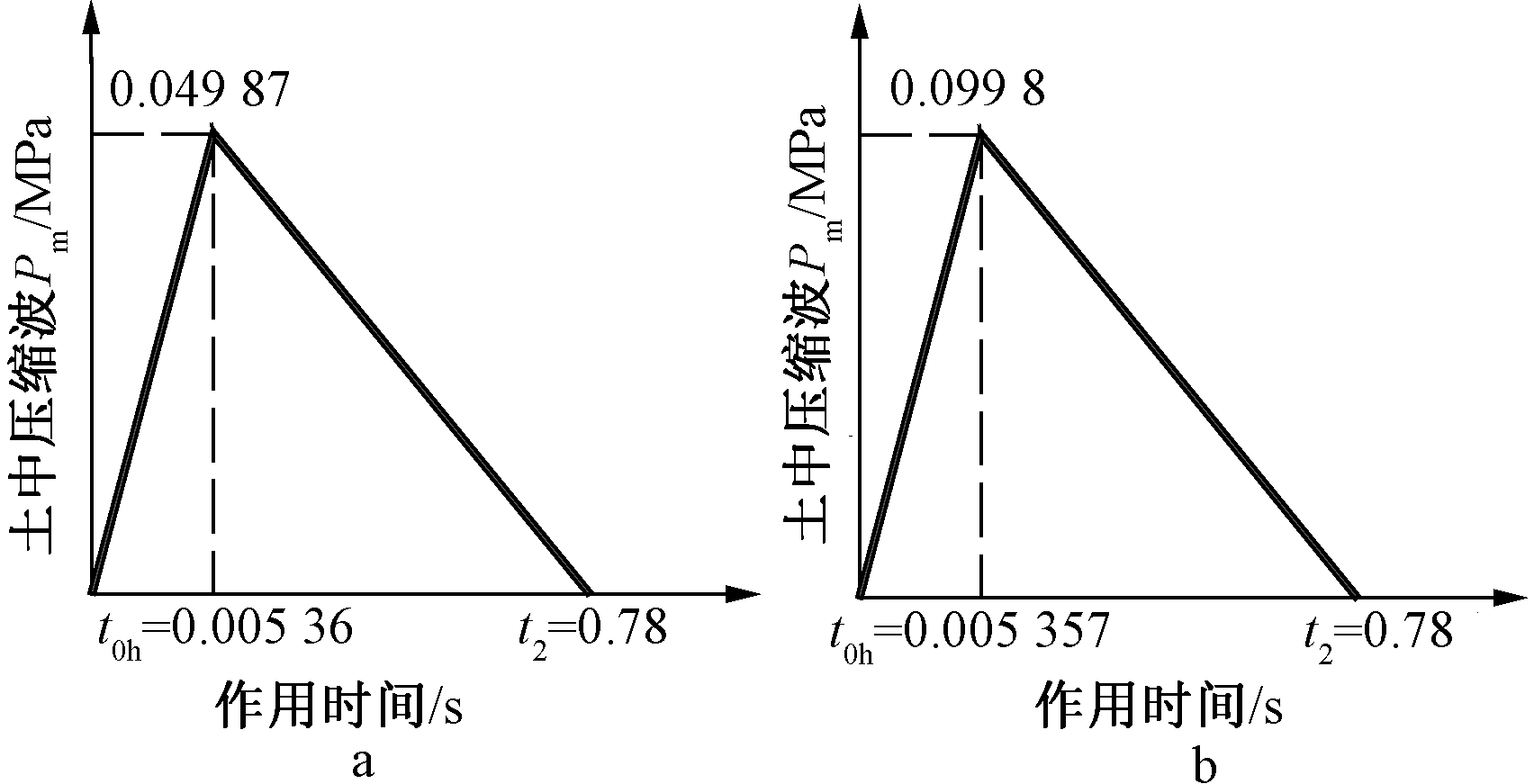
a—工况5; b—工况6。
图13 规范爆炸荷载曲线
Fig.13 Load curves of code
通过分析得到了槽型板在动力荷载作用下结构受力形态。如表5所示,除了工况6作用下受拉钢筋应力峰值为477 MPa(超过屈服强度),此时钢筋屈服。其他的混凝土、钢筋、预应力筋的Mises应力均处于弹性阶段。
表5 2种工况下构件最大应力
Table 5 Maximum stress of members under two conditions MPa

工况混凝土钢筋钢绞线58.74423298623.4477697
在动力荷载作用下,两个工况的混凝土损伤程度见表6,损伤均比较小,说明混凝土受力性能良好,裂缝从混凝土受拉损伤最大处开始发展。
表6 混凝土损伤
Table 6 Concrete damage

工况受压受拉50.2790.2560.4100.39
如图14所示为槽型板在动力荷载作用下结构内部应力流。从数值上看,随着爆炸荷载的增大,应力流的数值也越大,压应力流变化不大,且压应力分布较均匀;而构件拉应力面积较为集中。
a—工况5; b—工况6。
图14 构件最终变形
Fig.14 Final deformation of member
图15为跨中位移时程曲线。两个工况的最大极限位移分别为54.29,84.604 mm。
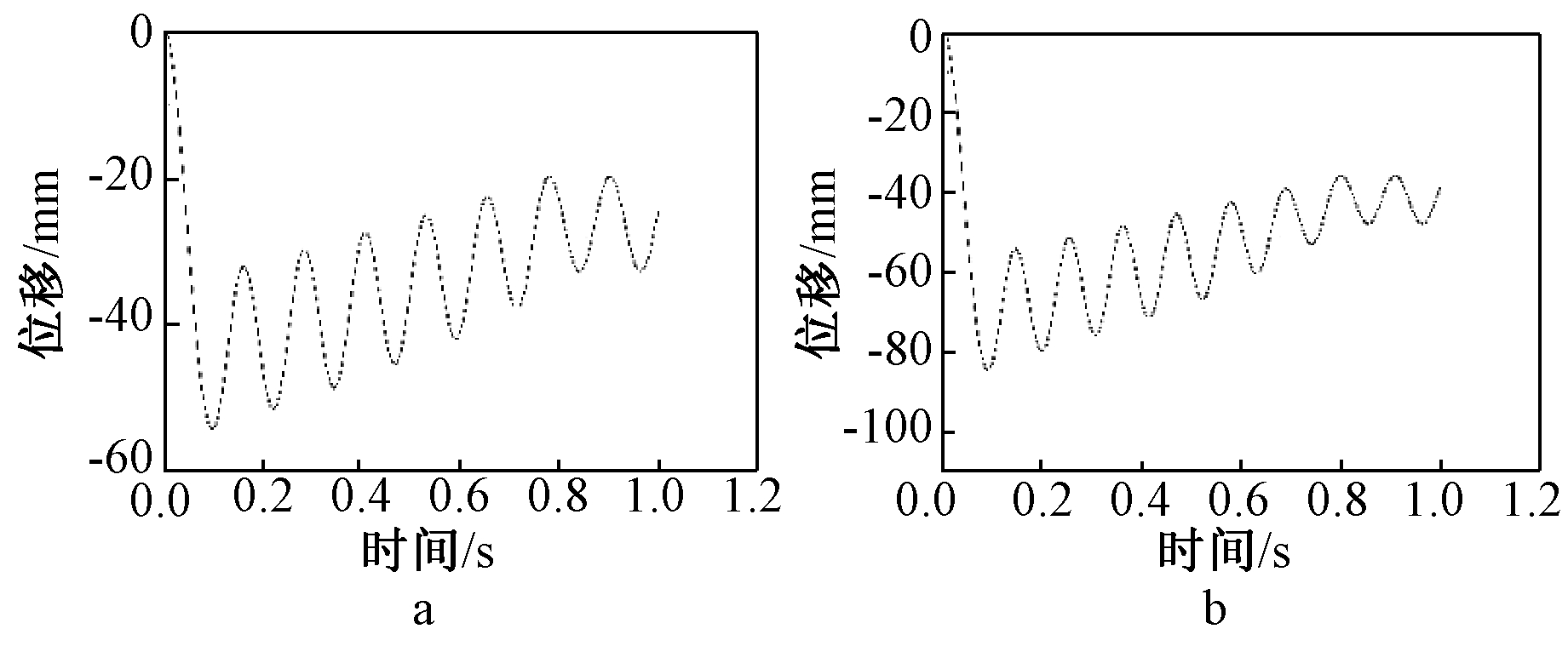
a—工况5; b—工况6。
图15 位移-时程曲线
Fig.15 Displacement time curves
4.2 静力荷载作用下槽型板响应分析
通过静力分析,得出槽型板在静力荷载作用下的最终破坏状态:普通钢筋下部受拉钢筋屈服,而预应力钢绞线仍处于弹性阶段,见图16。

a—工况5; b—工况6。
图16 不同工况作用下混凝土损伤
Fig.16 Concrete damage patterns under different conditions
研究混凝土的受力状态必须通过研究混凝土的损伤来判断混凝土的状态。由图16发现,混凝土跨中受拉损伤值随着爆炸荷载增大而逐渐增大,损伤范围也增大,受拉损伤的发展也表明裂缝的发展趋势。
以支座反力和跨中位移为坐标绘制荷载-位移曲线,以方便得出结构的屈服位移、极限位移等,如图17所示。
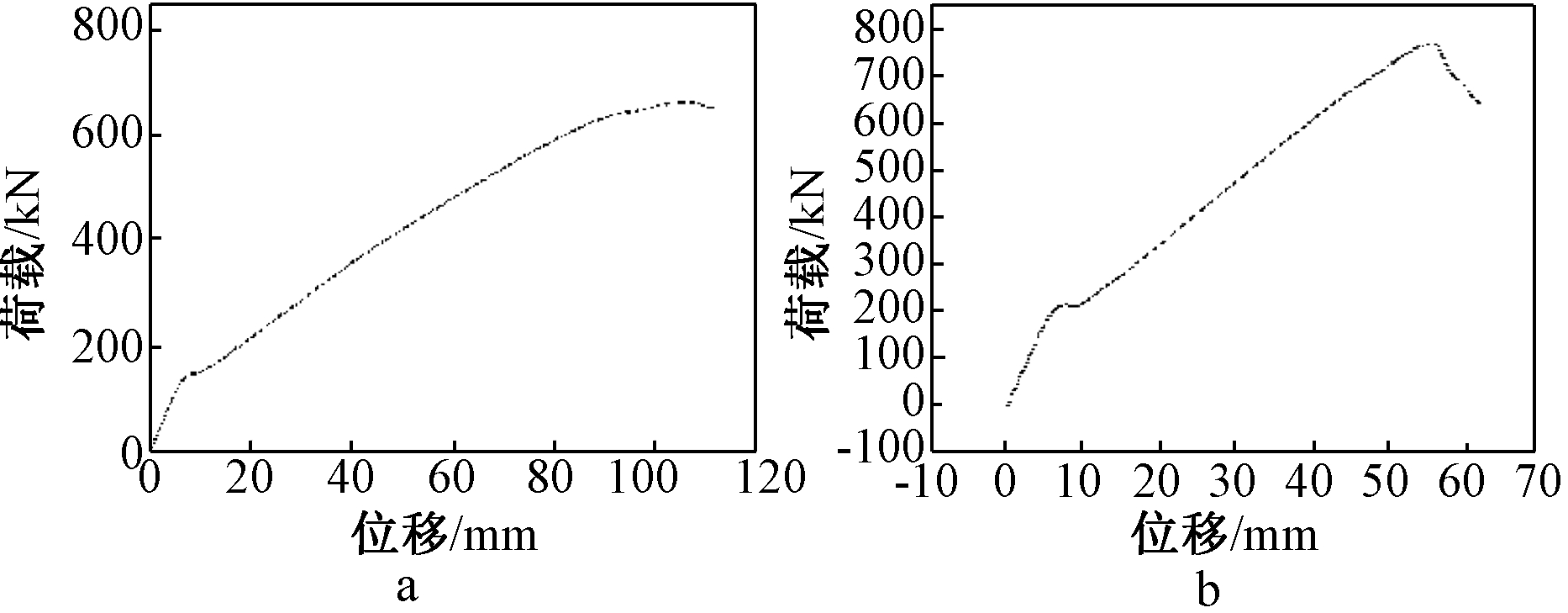
a—工况5; b—工况6。
图17 荷载-位移曲线
Fig.17 Load-displacement curves
由曲线得出结构的弹性极限位移为7.33 mm,屈服荷载为146.277 kN。
4.3 延性分析
人防设计中结构在动载作用下允许发生屈服后的塑性变形,虽然结构暂时处于机动状态,但由于荷载的短暂性,变形不会无限制地发展。只要求控制结构的最大变形不超过结构破坏的极限变形,当动荷载消失后结构又处于稳定状态,仅留下允许的残余变形,这样既满足安全,又充分利用材料的潜能,具有巨大的经济意义。人防设计中定义的允许延性β,系指结构构件允许出现的最大变位与弹性极限变位的比值。
槽型板在对应防核爆抗力等级6级时对应荷载作用的构件最大位移为54.29 mm,构件在静力荷载作用下弹性极限位移为7.33 mm,计算得到槽型板结构的延性比为7.406;槽型板在对应防核爆抗力等级5级时对应荷载作用的构件最大位移为84.604 mm,构件在静力荷载作用下弹性极限位移为9.717 mm,计算槽型板结构的延性比为8.706。
5 结束语
利用ABAQUS软件对槽型板试验对比分析,验证了有限元分析结果的合理性、真实性、可靠性。同时利用有限元软件对足尺截面的槽型板进行模拟,对比分析了静载和动载形式下结构的破坏形式和受力性能。综合分析试验现象以及有限元模拟的结果表明:
1)高应变速率的动态本构模型可以很好地模拟结构在爆炸荷载作用下的受力性能以及破坏模式。
2)装配式预应力槽型板在核6级、核5级、核4B级、核4级对应荷载作用下,混凝土受压与受拉损伤值均小于0.5。
3)预应力钢绞线在装配式预应力槽型板中起到重要的作用,不论在哪种工况模式下,预应力钢绞线均未达到其极限抗拉强度,始终处于弹性工作阶段,使结构在爆炸荷载峰值压力作用后处于相对稳定的状态。
4)装配式预应力槽型板在爆炸荷载作用下具有良好的抗爆性能,结构的整体延性比在7.5以上。
综上所述,装配式预应力槽型板具有良好的冲击韧性,有效地控制了结构在冲击波作用下的变形。由于预应力钢绞线的作用,整体结构在爆炸后均可以控制到一个相对稳定的状态,仅留少量的残余变形,充分利用了材料的性能。
[1] FONG, STEVEN K L. Dynamic Behavior of Pretensioned Hawaiian Aggregate Concrete Beams[J]. Honolulu:Hawaii Univ, 1976,6(6):30-36.
[2] BURNSNED H, RIPPERGER E A. Dynamic Behavior and Resistance of Prestressed Split Beams[J]. Texas Univ Austin Dept of Civil Engineering, 1997:42-47.
[3] 王新武,李砚召.带覆土预应力混凝土梁抗冲击试验[J].华中科技大学学报(自然科学版),2008,36(9): 113-116.
[4] 李砚召, 王肖钧, 吴祥云, 等. 分配层分层结构对核爆炸荷载的防护效果试验研究[J]. 中国科学技术大学学报, 2009, 39(9): 931-935.
[5] 宗周红,唐彪,高超,等.钢筋混凝土墩柱抗爆性能试验[J]. 中国公路学报, 2017, 30(9):51-60.
[6] 中华人民共和国建设部.人民防空地下室设计规范:GB 50038—2005[S].北京:中国建筑工业出版社,2005.
[7] 中华人民共和国住房和城乡建设部.全国民用建筑工程设计技术措施——防空地下室:2009JSCS-6[S]. 北京:中国计划出版社,2009.
[8] 熊学玉, 黄鼎业. 预应力工程设计施工手册[M]. 北京:中国建筑工业出版社, 2003.
[9] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S]. 北京:中国建筑工业出版社, 2011.
[10] 总参工程兵科研三所.平面装药爆炸模拟核爆炸空气冲击波试验规程:GJBz 20129—93[S].北京:总装备部军标出版社,2008.
[11] LEE J, FENVES G L. Plastic-Damage Model for Cyclic Loading of Concrete Structures[J].Journal of Engineering Mechanics,1998, 124(8):892-900.
[12] 李伟琛,韩小雷,崔济东.基于试验的ABAQUS混凝土塑性损伤参数取值方法[J].结构工程师,2016, 32(2):64-69.