螺旋筋对核心混凝土具有良好的约束效果,不仅可以提高其轴压承载力及抗震性能,同时变形能力和延性也得到了大幅的改善[1-4]。在构造上,因螺旋筋没有锚固弯钩,不会发生锚固弯钩提前错位的问题,同时可以节省大量钢材。因此,螺旋筋得到较为广泛的应用。
近年来,国内外学者对单重螺旋筋的研究较为系统、成熟。Mander等在试验的基础上,提出了螺旋筋的约束模型[5];尹衍樑成功地将螺旋箍筋应用于矩形柱中,结果表明螺旋箍筋对矩形柱起到较好约束效果[6];徐小君研究了配置矩形螺旋箍筋对混凝土梁抗剪承载力的影响,结果表明剪跨比对螺旋箍筋梁的抗剪承载力影响最显著[7];苏俊省等完成了3个高强度螺旋箍筋约束下混凝土圆柱的抗震性能试验,结果表明试件的滞回曲线饱满,具有良好的滞回性能、耗能能力、变形能力及位移延性[8]。但随建筑层数的增加,单层螺旋筋对构件的约束能力难以解决“胖柱肥梁”的问题。为此,有学者提出了多重螺旋筋约束钢筋混凝土的概念并展开了相关研究。文献[9-10]介绍了对双层箍筋约束混凝土柱采用ABAQUS有限元软件模拟的研究;张耀跃等分析了轴向荷载下双层箍筋混凝土柱的力学性能[11]。上述结果表明:双层箍筋混凝土柱的延性优于单层箍筋混凝土柱。
目前,国内外学者对多重螺旋筋约束钢筋混凝土柱的研究主要集中在两重螺旋筋,而三重螺旋筋约束形式的研究鲜见报道。基于此,本研究通过8个多重螺旋筋复合约束钢筋混凝土圆形截面短柱的轴心受压试验,其中包括3个两重螺旋筋柱和5个三重螺旋筋柱,从加载的破坏过程及形态、荷载-位移曲线等对其展开分析,并重点探讨轴压性能及参数分析,以期为该类组合构件的进一步研究和工程应用提供参考。
1 试验概况
1.1 试件设计及制作
以螺旋筋间距、钢筋笼间距以及螺旋筋重数等为变化参数,设计并制作了8个多重螺旋筋复合约束钢筋混凝土圆形截面短柱试件,其中3个两重螺旋筋试件和5个三重螺旋筋试件。试件的具体设计参数详见表1,横截面及应变片布置如图1所示。
表1 试件设计参数及力学性能
Table 1 Design parameters and mechanical properties of specimens

试件编号R/mmL/mm钢筋笼重数n纵筋螺旋箍筋D/mmρc/%ρt,1/%ρt,2/%ρt,3 /%ρt /%Np/kNΔ/mmE0/(103 kN·mm-1)μηC-2-40-504001 20021612ϕ6@4050 1.440.810.58—1.396 981.08.511.041.530.67C-2-60-504001 20021612ϕ6@6050 1.44 0.540.39—0.936 508.07.251.031.520.67C-2-80-504001 20021612ϕ6@8050 1.44 0.410.29—0.706 561.57.021.011.300.61C-3-40-504001 20031612ϕ6@4050 1.44 0.810.580.351.747 688.56.851.401.610.67C-3-60-504001 20031612ϕ6@6050 1.44 0.540.390.231.167 398.06.161.231.380.62C-3-80-504001 20031612ϕ6@8050 1.44 0.410.290.170.876 150.05.671.201.370.64C-3-40-404001 20031612ϕ6@4040 1.440.810.630.441.888 022.57.161.251.470.66C-3-40-604001 20031612ϕ6@4060 1.44 0.810.530.251.597 281.08.801.171.680.71
注:试件编号中第一个字母代表多重螺旋筋复合约束钢筋混凝土圆形柱,第二个符号表示螺旋筋重数,第三个符号表示螺旋筋间距,第四个符号表示钢筋笼间距;R为试件截面直径;L为试件长度;D为钢筋笼间距;ρc为纵筋率;ρt,i表示第i重箍筋相对于试件整体的体积配箍率;ρt为总体积配箍率,有:ρt=ρt,1+ρt,2+ρt,3;Np为试件峰值荷载;Δ为峰值荷载所对应的峰值变形;E0为试件初始压缩刚度;μ为延性系数;η为耗能系数。
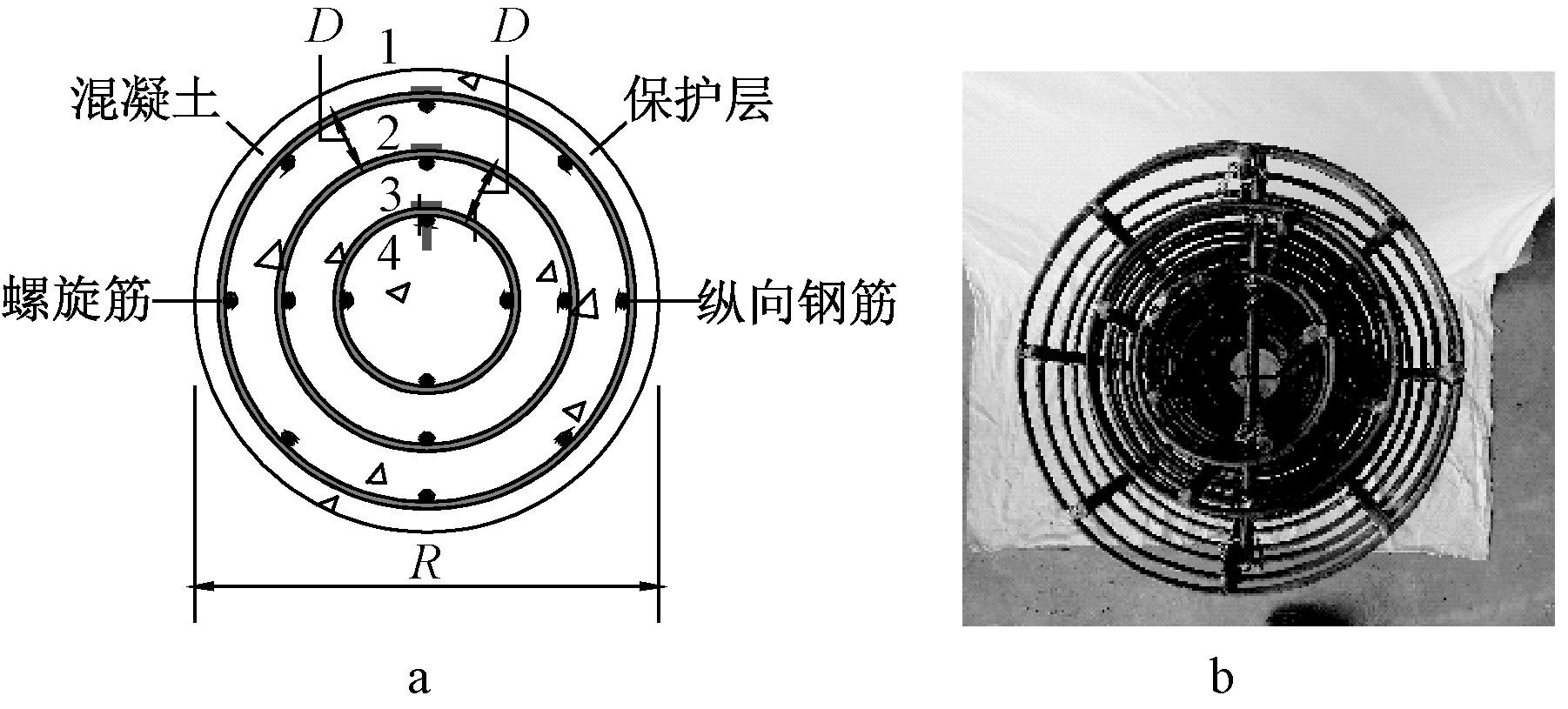
a—横截面示意; b—实物。
图1 试件截面及应变片布置示意
Fig.1 Schematic diagram of specimen dimensions
and layout of strain gauges
试件的制作分为以下几个过程:1)螺旋筋制作,根据试件设计的高度、外径以及间距在弹簧加工机床上加工成型;2)钢筋笼成型,控制纵筋的位置及螺旋筋间距,通过点焊将纵筋与螺旋筋固定成型,点焊程度在30%~40%之间;3)装配钢筋笼,将成型的钢筋笼依次套设,并固定钢筋笼之间的距离,最后将装配好的钢筋笼装入模中;4)混凝土浇筑与养护,采用分层法浇筑,试件与试块放在室外同条件养护,浇筑后的两个星期喷水养护。试件制作过程如图2所示。

图2 试件制作过程
Fig.2 Specimen production process
1.2 材料力学性能
纵筋采用HRB400螺纹钢筋,螺旋箍筋采用HPB300光圆钢筋。钢材的力学性能指标根据GB/T 228.1—2010《金属材料 拉伸试验 第1部分:室温试验方法》进行测试,结果见表2。
表2 钢材力学性能
Table 2 Mechanical properties of steel
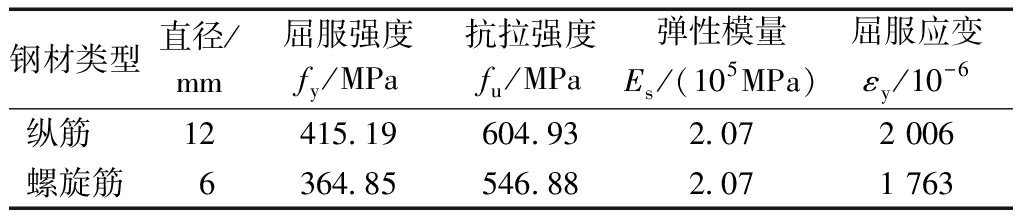
钢材类型直径/mm屈服强度fy/MPa抗拉强度fu/MPa弹性模量Es/(105MPa)屈服应变εy/10-6纵筋 12415.19604.932.072 006螺旋筋6364.85546.882.071 763
混凝土采用商品混凝土,试件浇筑时预留了边长为150 mm×150 mm×300 mm棱柱体试块,按GB/T 50081—2002《普通混凝土力学性能试验方法》进行混凝土轴心抗压强度测定。弹性模量按GB 50010—2010《混凝土结构设计规范》计算取值,其力学性能见表3。
表3 混凝土力学性能
Table 3 Mechanical properties of concrete

立方体抗压强度实测值/MPa立方体抗压强度均值fcu/MPa轴心抗压强度fc/MPa58.58,54.89,55.0256.1636.20
1.3 加载方案与测量方案
试验加载设备为YAW-10000J微机控制电液伺服压剪试验机。加载制度采用位移控制连续加载,加载速率为1 mm/min。正式加载前对试件预加载,预加载值为600 kN,检查试件、仪器是否正常工作。将预加荷载卸载至零后,开始正式加载,直至荷载下降到峰值荷载的75%时停止试验。为防止在加载过程中试件端部因局部受压提前破坏,本试验采用柱头两端粘贴碳纤维布的方式替代保护钢套,加载示意如图3所示。
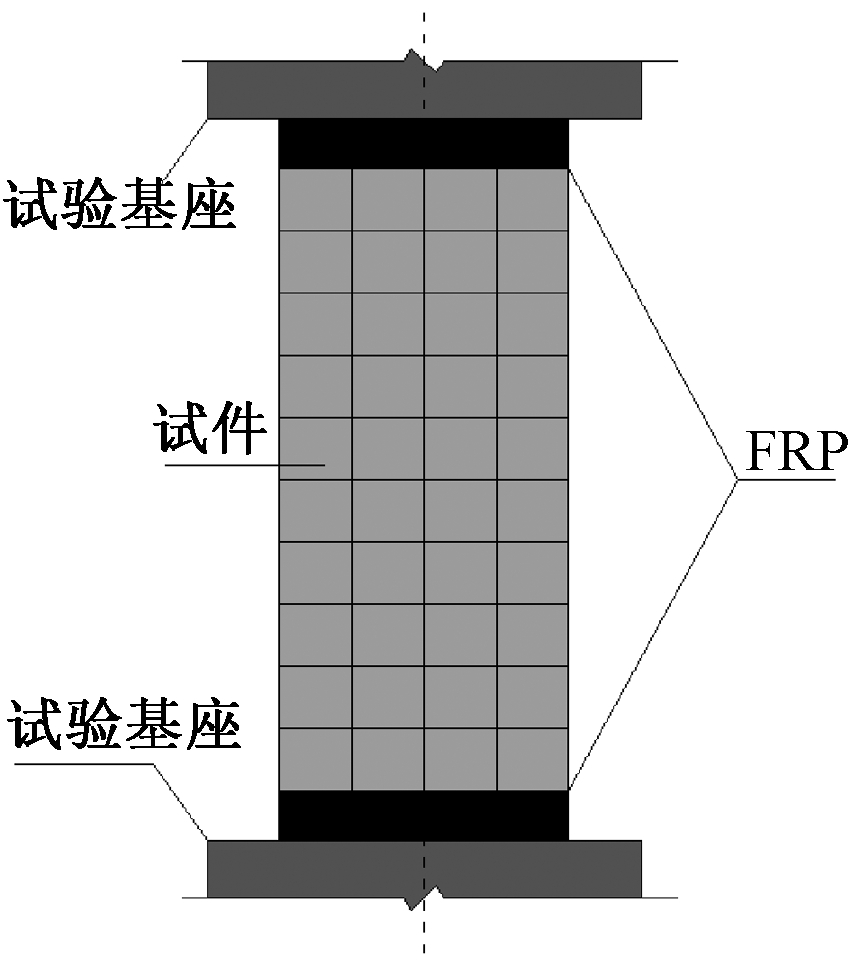
图3 加载装置示意
Fig.3 Schematic diagram of loading set-up
试验主要测量的内容有:1)轴向荷载及变形,由试验装置的传感系统测量;2)螺旋筋、纵筋以及混凝土应变,通过华东DH3821Net静态应变测试系统采集。
2 试验结果与分析
2.1 试件破坏形态
多重螺旋筋复合约束钢筋混凝土试件的破坏过程基本相同,本文以试件C-3-60-50的表观形态演变全过程来说明。由图4可见:加载初期,试件的外观没有发生明显的变化;当加载至0.8Np左右时,试件上部或者下部约1/3高度处开始出现短且比较竖直的细小裂缝;峰值荷载后,裂缝逐渐增多,剪切破坏面初显,随着裂缝的开展和相互贯通,剪切裂缝开裂严重,从裂缝处发现有少量混凝土细屑、渣片落下,此时试件中部呈现腰鼓状;当荷载降至0.75Np左右时,保护层混凝土剥落较严重,从鼓出部分剥落许多的混凝土细屑,此时剪切破坏面明显。

图4 试件的表观破损过程
Fig.4 Appearance damage process of specimens
加载结束后,将试件表面开裂的混凝土块轻轻敲掉,能清楚观察到混凝土剪切碎裂带,剪切破坏面与试件中轴线夹角在25°~45°之间,沿斜裂缝有碾碎的混凝土细屑。局部可观察到纵筋压屈的现象,剪切碎裂带上的混凝土在三轴压应力下发生挤压流动,螺旋筋受挤压流动的影响而发生错位甚至被拉断。试件的最终破坏形态如图5所示。
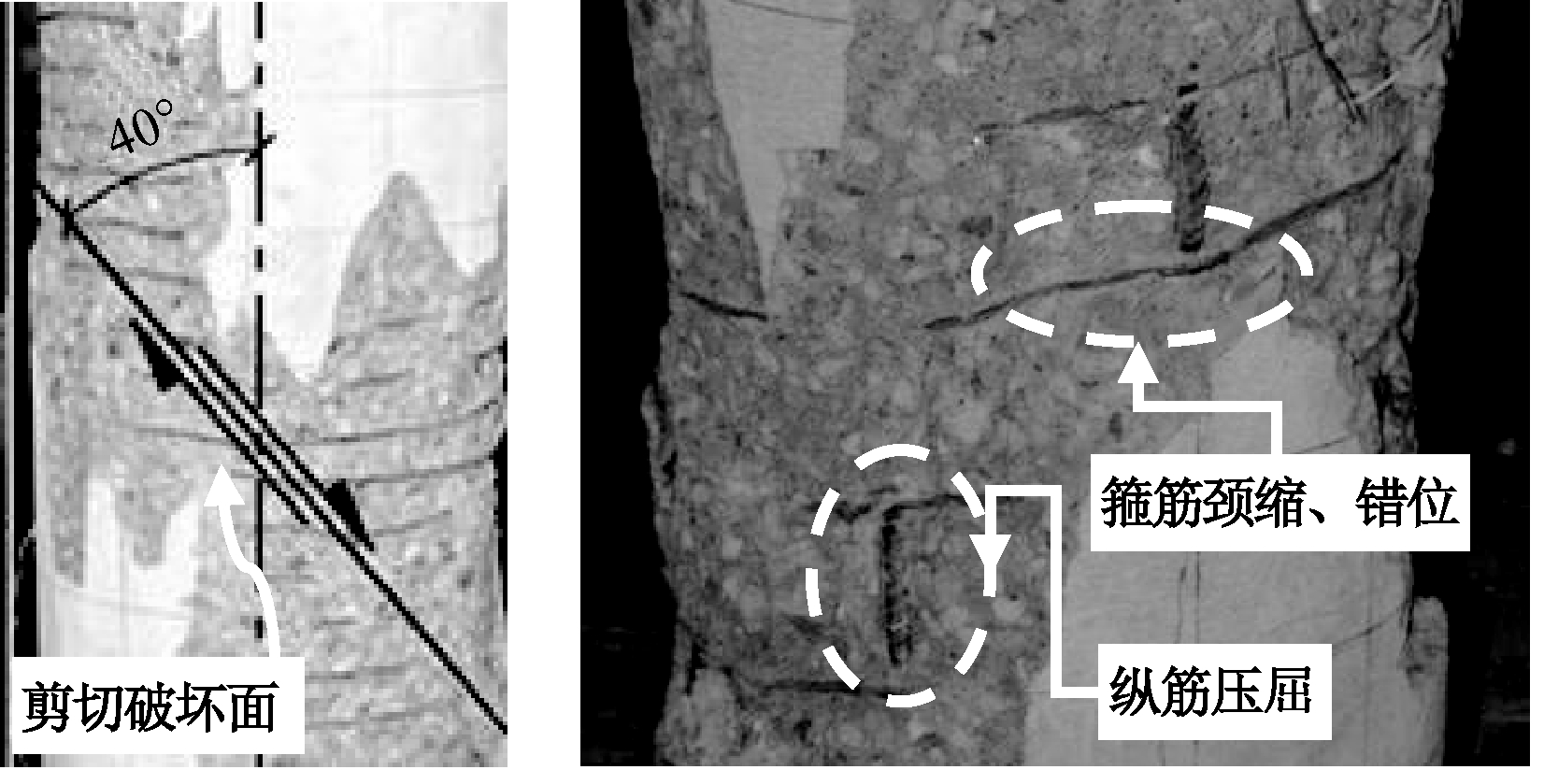
图5 试件破坏形态
Fig.5 Failure mode of specimens
2.2 轴向荷载-变形曲线
图6为试件实测的轴向荷载-变形曲线,其中纵坐标N为试件所受轴向压力,横坐标Δ为试件整体轴向变形。由图6可见,各试件的N-Δ曲线都经历快速增长、迅速下降以及缓慢下降三个阶段。
对比发现,配三重螺旋筋的试件,其N-Δ曲线的上升段较两重螺旋筋试件倾斜。峰值点过后,各试件的下降段曲线有所差异。对于螺旋筋间距越大的试件(如C-2-80-50和C-3-80-50),其N-Δ曲线过峰值荷载后形成明显的尖峰,同时试件C-2-80-50出现突然垂直下跌的现象(此现象对应箍筋被拉断);对于螺旋筋重数不同的试件(如C-2-60-50和C-3-60-50),螺旋筋重数越多,其N-Δ曲线在峰值点过后具有更明显的下降段;而对于钢筋笼间距不同的试件,其曲线的下降段没有明显的差异。
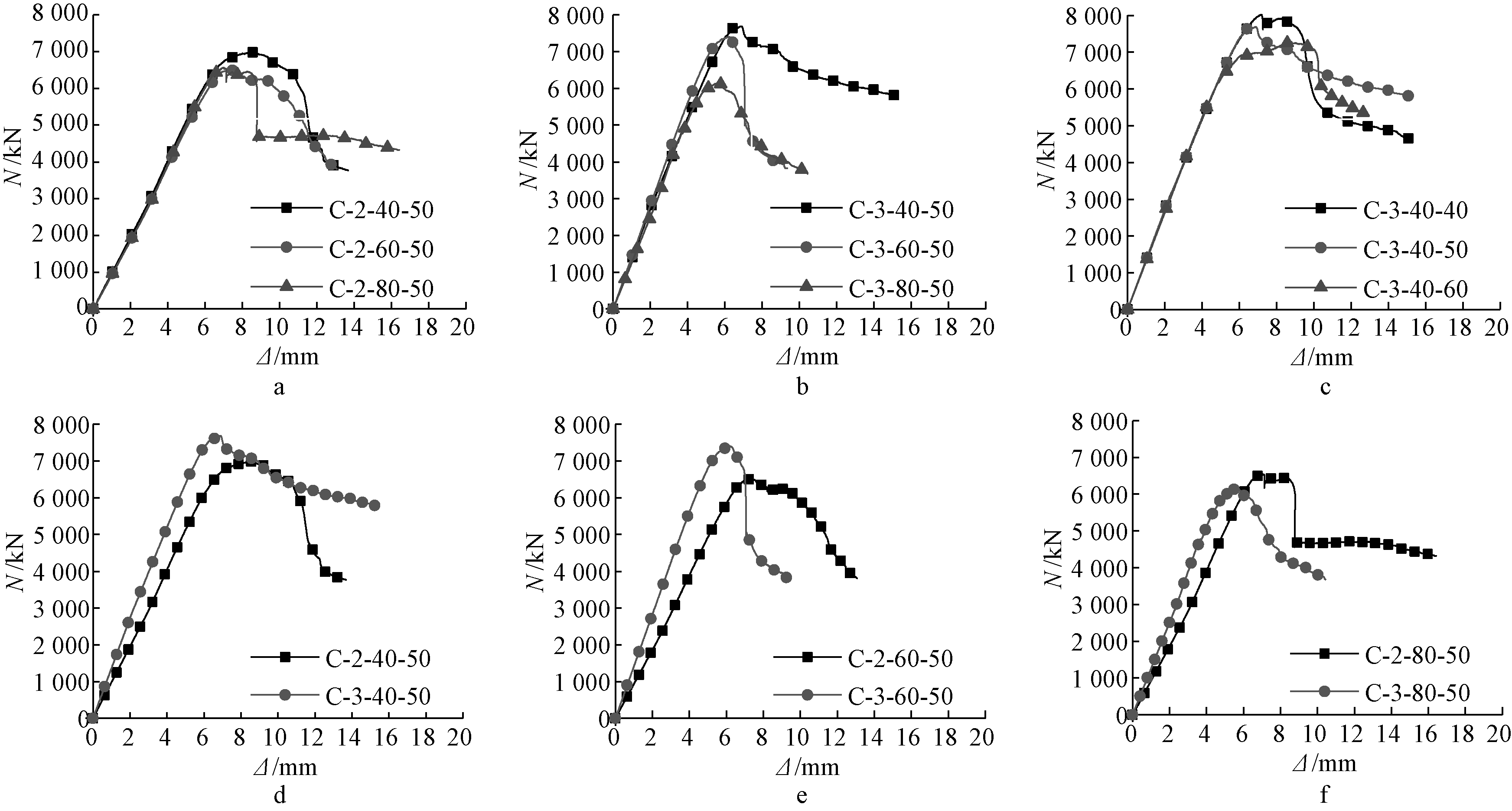
a—不同螺旋筋间距d(n=2); b—不同螺旋筋间距d(n=3); c—不同钢筋笼间距D; d—不同螺旋筋重数n(d=40 mm);
e—不同螺旋筋重数n (d=60 mm); f—不同螺旋筋重数n(d=80 mm)。
图6 荷载-变形曲线
Fig.6 Load-deformation curves
3 轴压性能及参数分析
3.1 峰值荷载
3.1.1 螺旋筋间距对峰值荷载的影响
为更好反映螺旋筋间距对试件峰值荷载的影响,结合配箍率来定量分析,如图7所示。图中纵坐标α表示相对峰值荷载,即对于两重螺旋筋试件的峰值荷载N2和三重螺旋筋试件的峰值荷载N3,以螺旋筋间距d=40 mm试件的峰值荷载为基准进行归一化处理。同理,以螺旋筋间距d=40 mm试件的配箍率ρ为基准进行归一化处理,得到相对配箍率β。
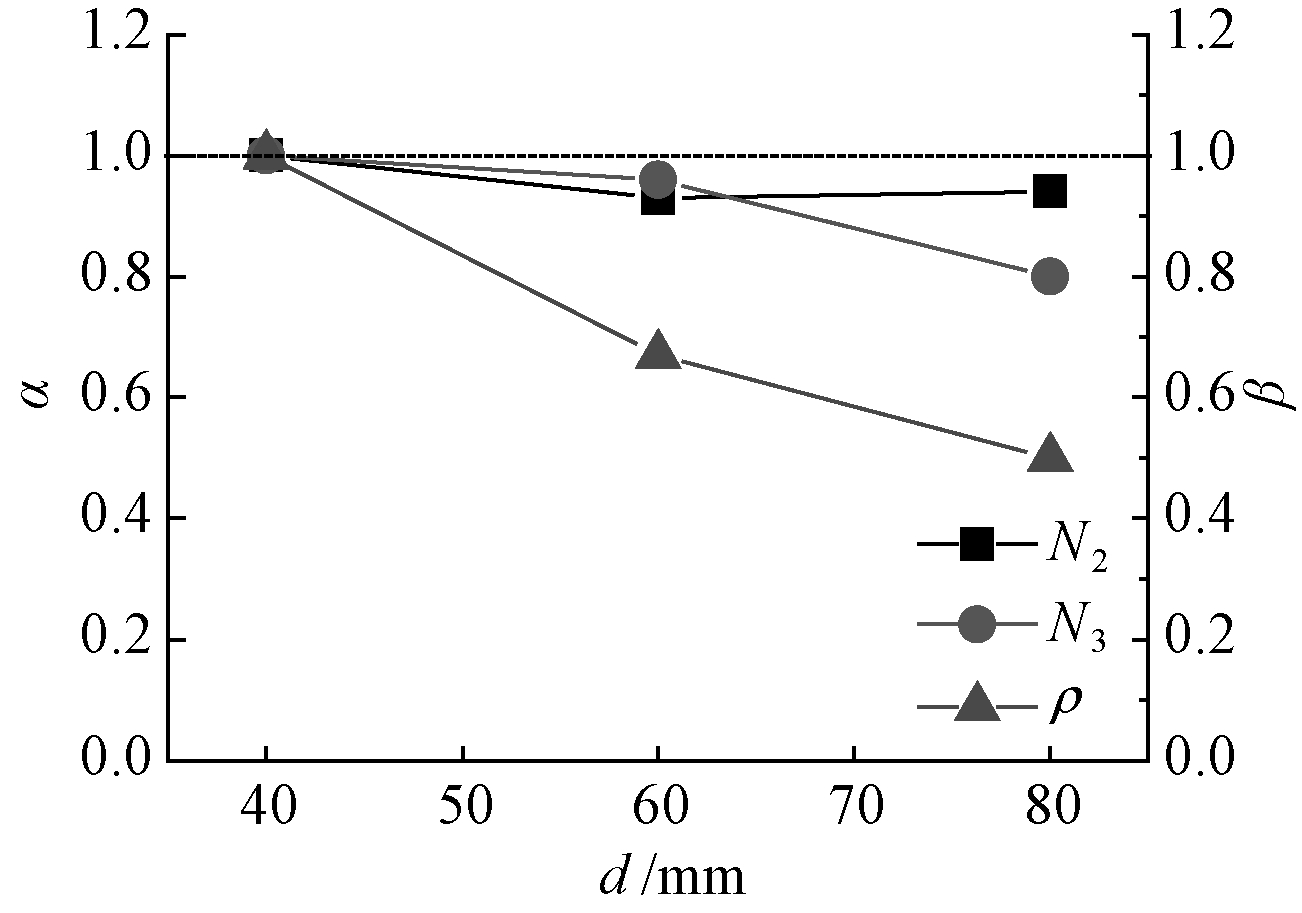
图7 螺旋筋间距对峰值荷载的影响
Fig.7 Effects of spiral stirrup spacing on peak load
由图7可见:试件的峰值荷载随着螺旋筋间距的增大整体上呈下降的趋势。相比d=40 mm的试件,当d=60 mm时,配箍率降低了33%,承载力下降了约5%;而当d=80 mm时,配箍率降低了50%,承载力下降了13%左右。可见,在配箍率显著减少的情况下,其承载力并没有明显的下降。
3.1.2 钢筋笼间距对峰值荷载的影响
图8为峰值荷载随钢筋笼间距和配箍率的变化相关曲线,其中α和β的定义与上一节相同。由图8可见,随着钢筋笼间距的增大(相应配箍率减少),峰值荷载具有小幅线性下降的趋势。与D=40 mm的试件相比,当D=50,70 mm时,其相对配箍率分别下降了7%和15%,峰值荷载仅分别降低了4%和9%。通过分析可知:增大钢筋笼间距,可以节省用钢量,同时不会显著降低承载力。
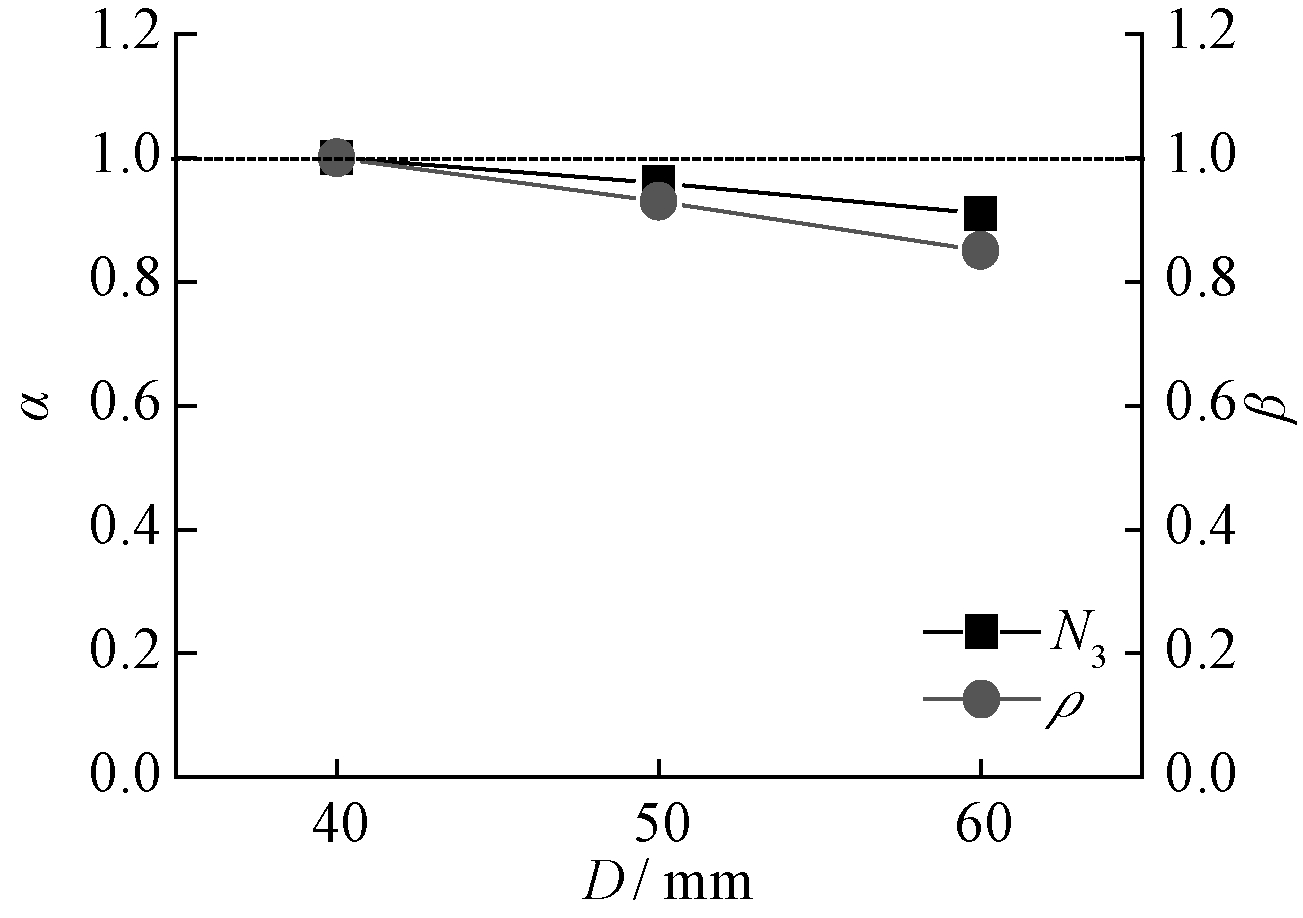
图8 钢筋笼间距对峰值荷载的影响
Fig.8 Effects of steel cage spacing on peak load
3.1.3 螺旋筋重数对峰值荷载的影响
为揭示螺旋筋重数对试件承载力的影响,在螺旋筋间距和钢筋笼间距相同的条件下,将三重螺旋筋试件的峰值荷载N3和两重螺旋筋试件的峰值荷载N2相比作为纵坐标,同时也将其配箍率ρ3/ρ2作为纵坐标绘制了图9所示的相关曲线。由图9可见:当仅改变螺旋筋重数时,三重螺旋筋的配箍率较两重螺旋筋的增大了25%。对比两者的峰值荷载发现,当d=40,60 mm时,配三重螺旋筋试件的峰值荷载分别较两重螺旋筋试件的增大了10%和14%;而当d=80 mm时,其峰值荷载反而下降了6%。这可能与试件浇筑质量有关,导致其承载力相比有所下降。总体上,增加螺旋筋重数,其用钢量明显增加但并没有显著提高承载力。
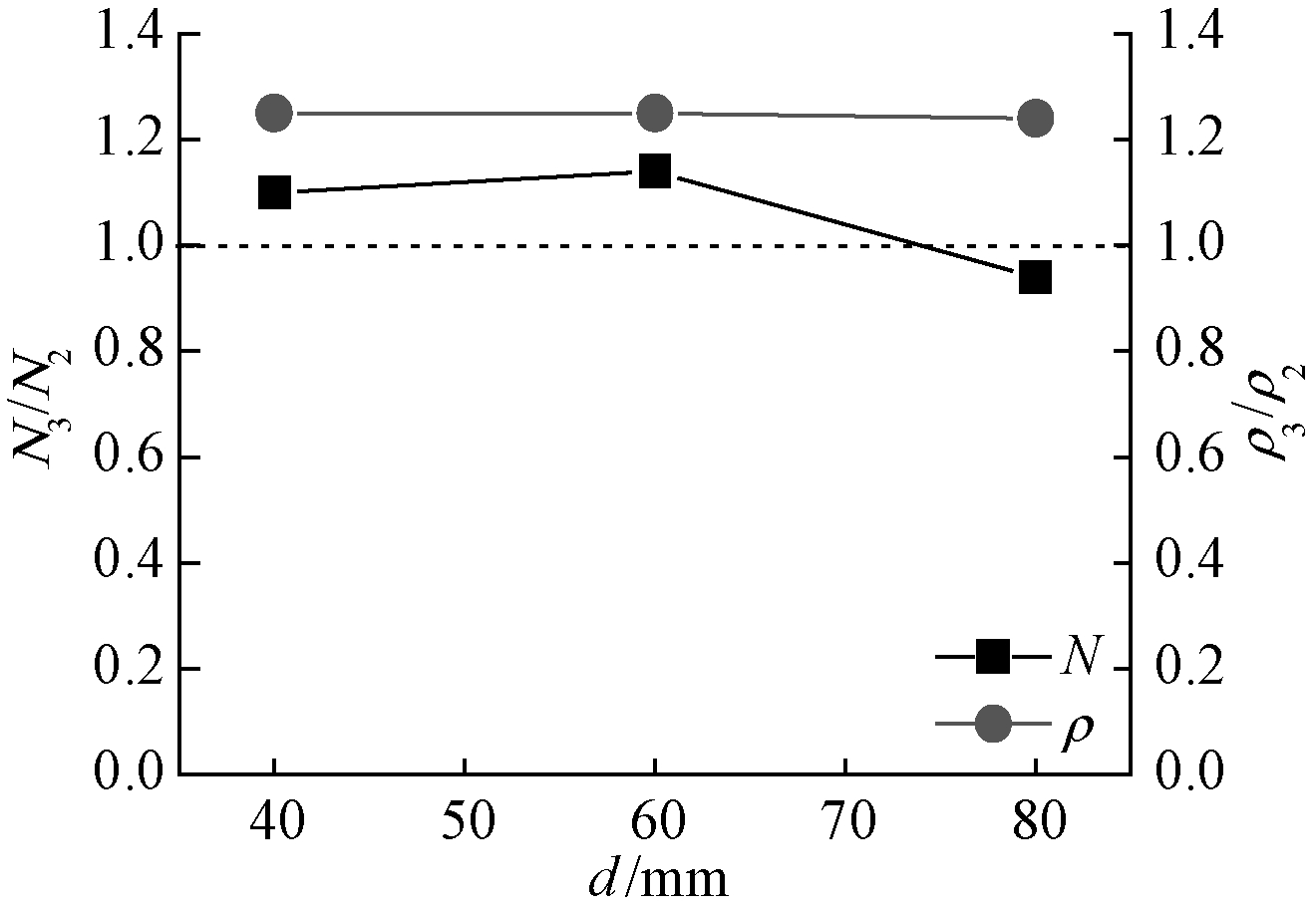
图9 螺旋筋重数对峰值荷载的影响
Fig.9 Effects of number of spiral stirrups on peak load
3.2 峰值变形
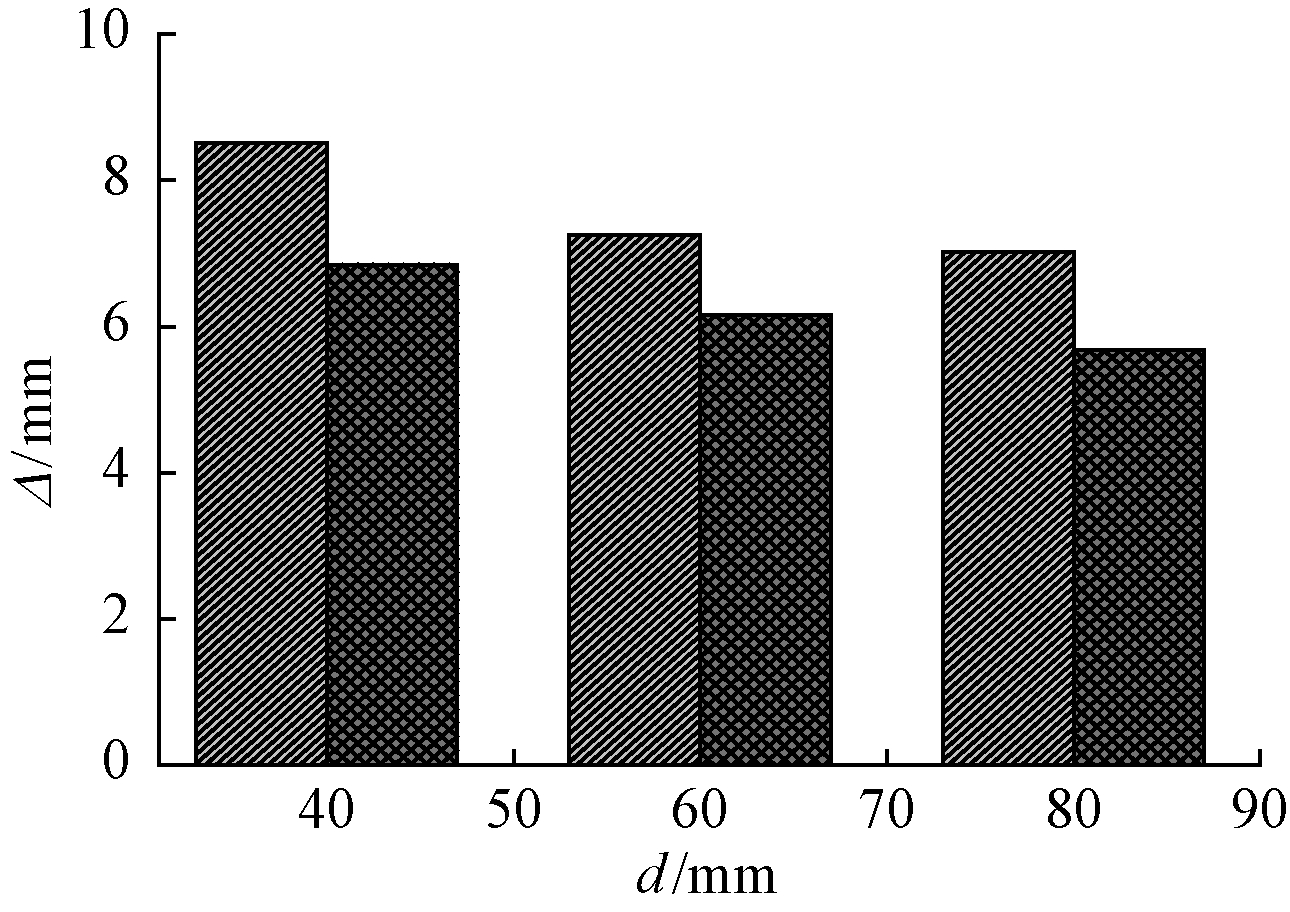
3.2.1 螺旋筋间距和重数对峰值变形的影响
图10为试件的峰值变形随螺旋筋间距和重数的变化关系。可见:1)随着螺旋筋间距的增大,试件的峰值变形逐渐下降,下降的幅度在10%~18%;2)对比配置不同螺旋筋重数的试件发现,两重螺旋筋试件较三重螺旋筋试件具有更好的变形能力,其位移变形值约大了22%。这可能是因为试件达到峰值荷载时,三重螺旋筋试件中的螺旋筋并没有屈服,仍有较大的富余。
![]() n=2;
n=2; ![]() n=3。
n=3。
图10 螺旋筋间距和重数对峰值变形的影响(D=50 mm)
Fig.10 Effects of spacing and number of spiral stirrups
on peak deflection(D=50 mm)
3.2.2 钢筋笼间距对峰值变形的影响
图11给出了钢筋笼间距对峰值变形的影响。可见:钢筋笼间距较大的试件,其峰值变形值更大,而钢筋笼间距较小的试件(如C-3-40-40和C-3-40-50),其峰值变形值相差不大;D=60 mm的试件,其峰值变形较D=40,50 mm的试件提高了23%和28%。可见,适当增加钢筋笼间距可以提高试件的变形能力。
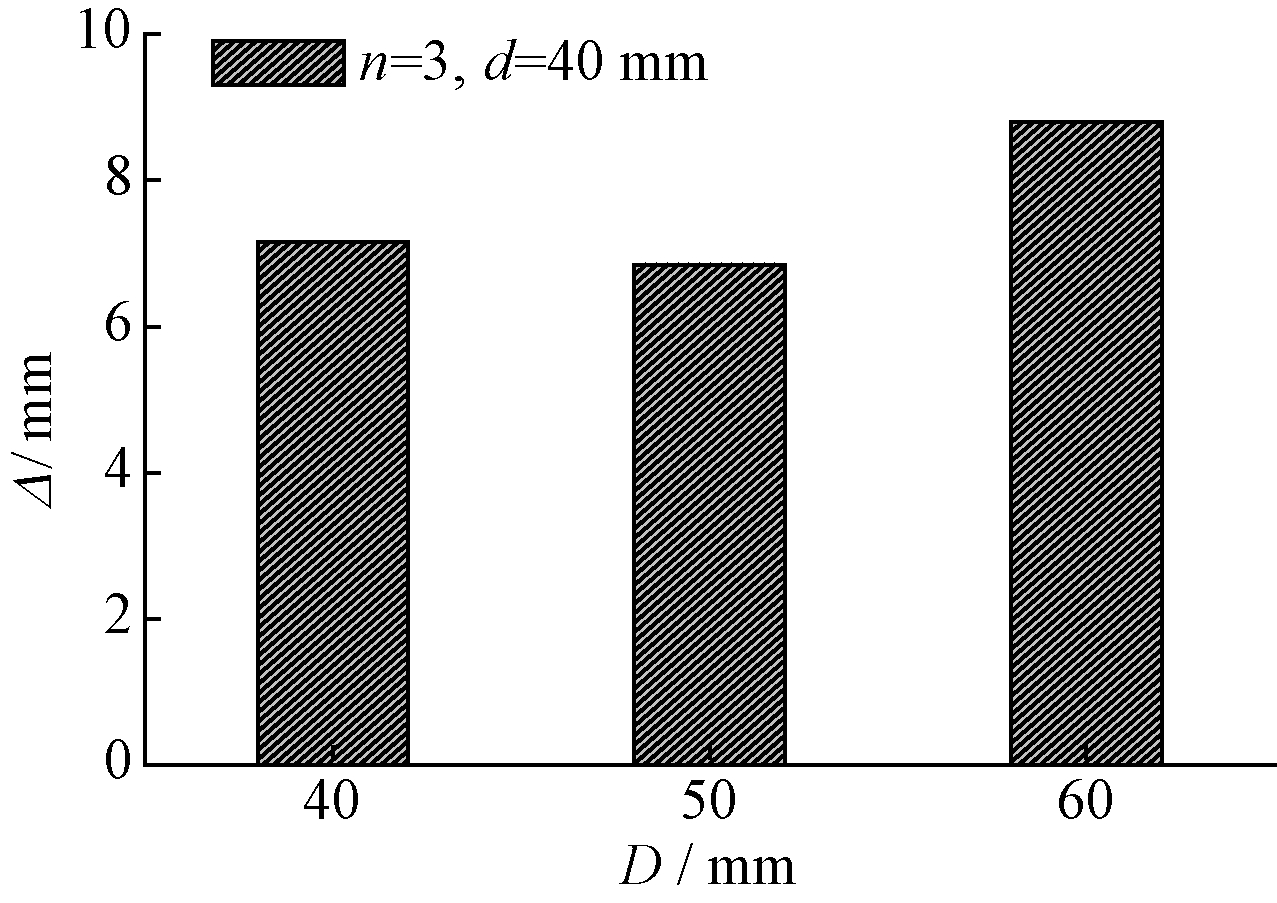
图11 钢筋笼间距对峰值变形的影响
Fig.11 Effects of steel cage spacing on peak deflection
3.3 初始压缩刚度
3.3.1 螺旋筋间距和重数对初始压缩刚度的影响
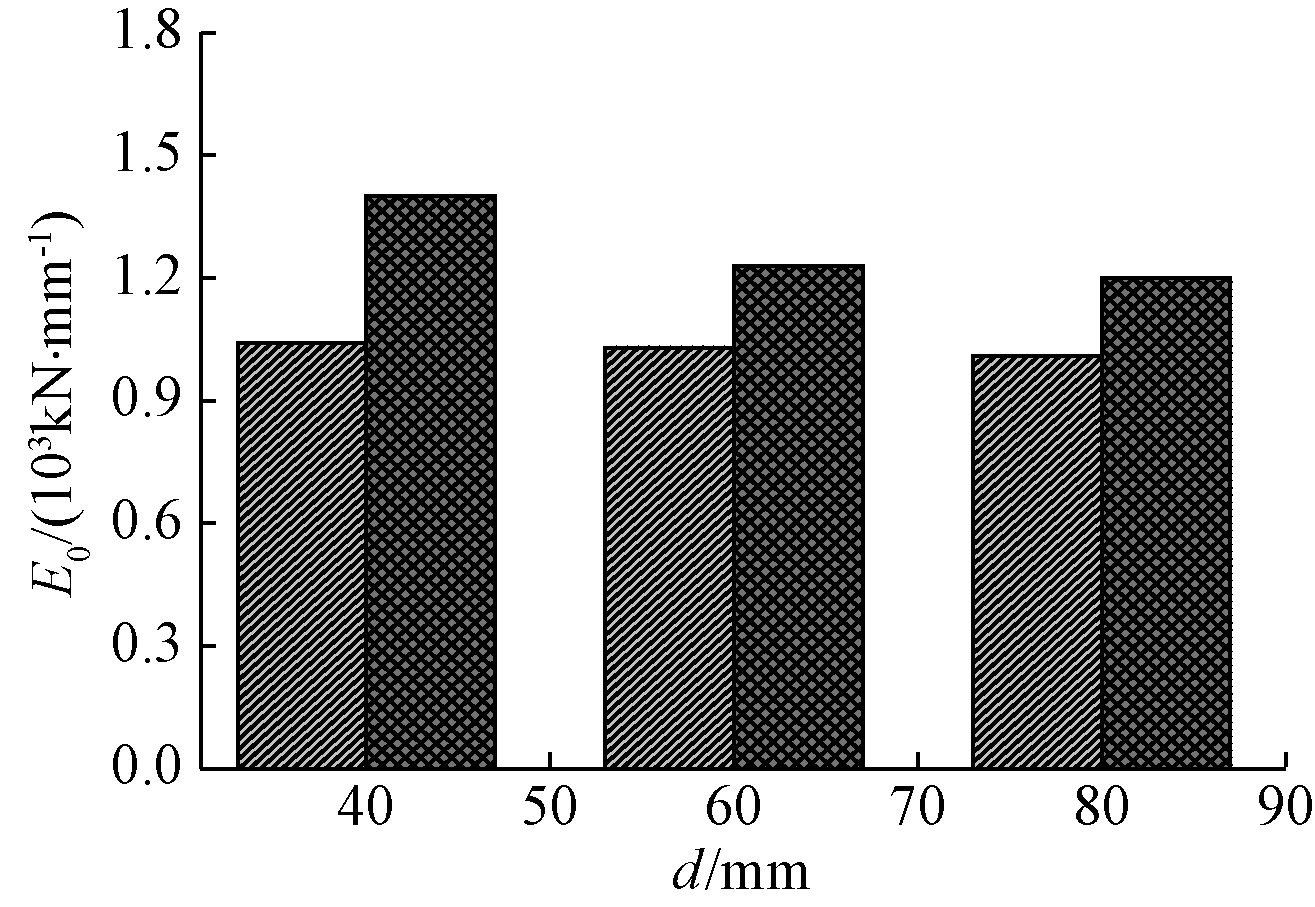
利用实测的荷载-位移曲线对应的弹性阶段求出各试件的初始压缩刚度,结果见表1。
图12给出了试件的初始压缩刚度随螺旋筋间距和重数的变化关系。可见:螺旋筋间距对初始压缩刚度的影响规律与对峰值荷载的影响规律相似,随着螺旋筋间距的增大,初始压缩刚度呈小幅下降的趋势;螺旋筋重数对试件的初始压缩刚度影响较大,相比两重螺旋筋的试件,三重螺旋筋试件的初始压缩刚度提高幅度在19%~34%之间。
![]() n=2;
n=2; ![]() n=3。
n=3。
图12 螺旋筋间距和重数对初始压缩刚度的影响(D=50 mm)
Fig.12 Effects of spacing and number of spiral
stirrups on initial stiffness(D=50 mm)
3.3.2 钢筋笼间距对初始压缩刚度的影响
图13为钢筋笼间距对初始压缩刚度的影响柱状图。可见:随着钢筋笼间距的增大,初始压缩刚度呈先增后减的变化趋势,D=50 mm时试件具有最大的初始压缩刚度;D=60 mm时初始压缩刚度最小,这与螺旋筋重数对峰值荷载的影响相似。

图13 钢筋笼间距对初始压缩刚度的影响(n=3, d=40 mm)
Fig.13 Effects of steel cage spacing on initial
stiffness(n=3, d=40 mm)
3.4 延 性
采用轴压位移延性系数反映试件的非弹性变形能力,并根据荷载-位移曲线,运用式(1)计算其延性系数μ,各试件的具体计算结果详见表1。
(1)
式中:Δu为极限位移,取荷载-位移曲线下降段85%峰值荷载对应的位移值;Δy为初始屈服位移,采用通用屈服弯矩法确定,如图14所示。其中Ny和0.85Np分别为Δy和Δu对应的荷载值。

图14 通用弯矩屈服法示意
Fig.14 Schematic diagram of universal bending yield method
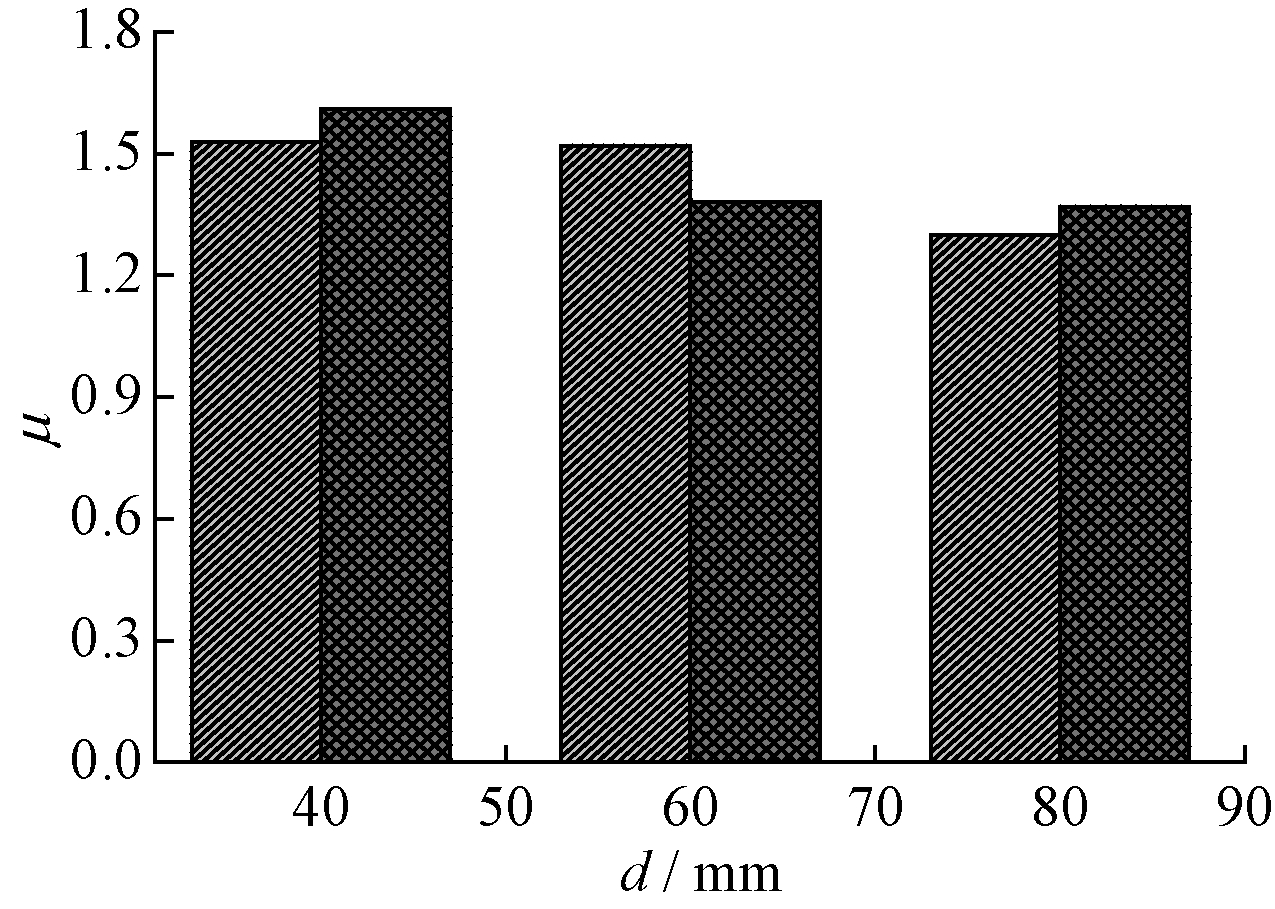
3.4.1 螺旋筋间距和重数对延性的影响
图15为试件的延性系数随螺旋筋间距和重数的变化关系。可见:试件的延性系数随螺旋筋间距的增大而减小,下降幅度为1%~15%;对比不同螺旋筋重数的试件发现,总体上,三重螺旋筋的试件具有更好的位移延性。
![]() n=2;
n=2; ![]() n=3。
n=3。
图15 螺旋筋间距和重数对位移延性的影响(D=50 mm)
Fig.15 Effects of spacing and number of spiral
stirrups on ductility(D=50 mm)
3.4.2 钢筋笼间距对延性的影响
图16为试件的延性系数随钢筋笼间距的变化关系。可见:钢筋笼间距对试件延性的影响较显著,随着钢筋笼间距的增大,延性系数具有逐渐增大的趋势;D=50,60 mm时,试件的延性系数较D=40 mm时分别提高了10%和14%。可见,增大钢筋笼间距有利于提高试件的非弹性变形能力。
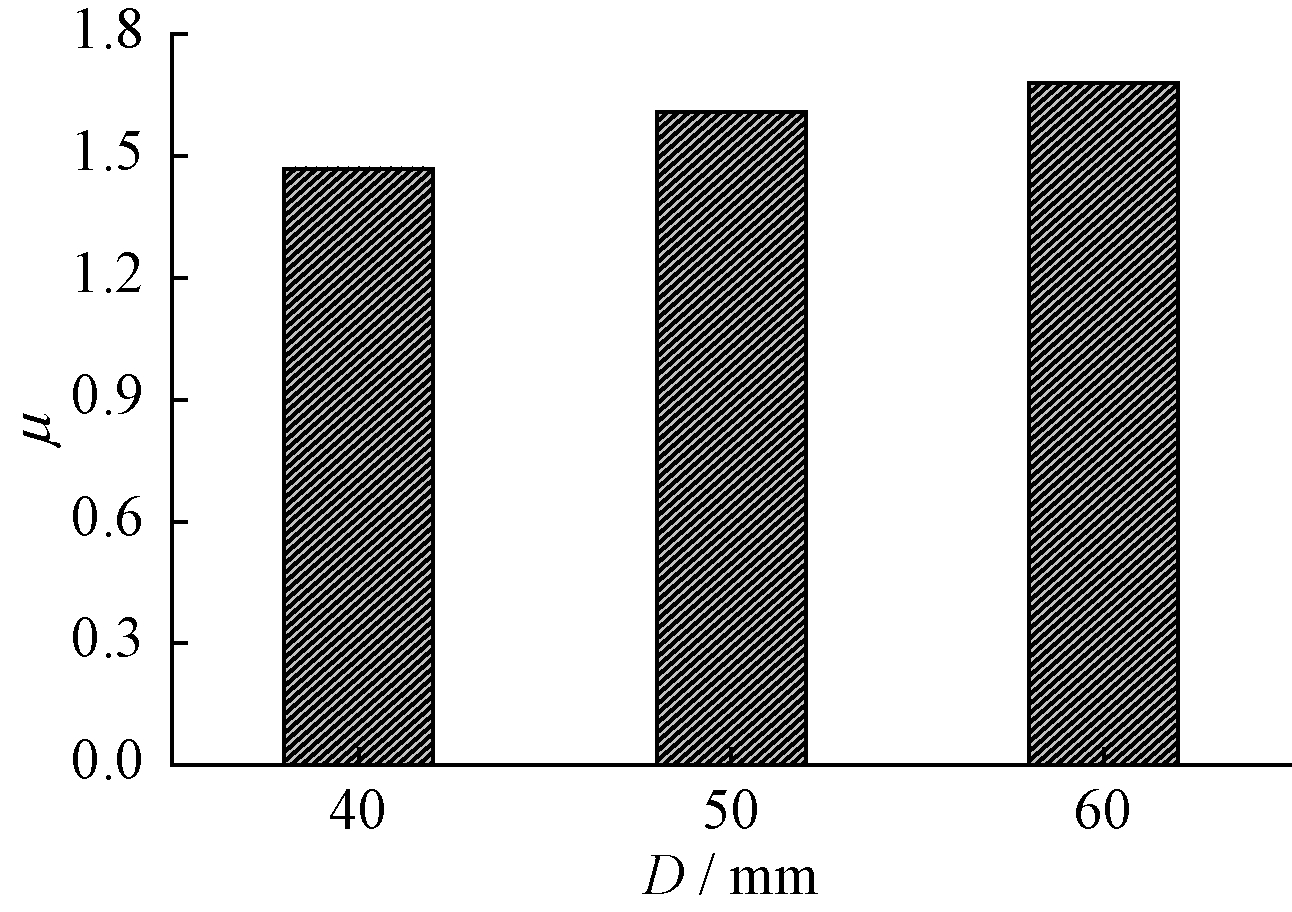
图16 钢筋笼间距对位移延性的影响(n=3, D=40 mm)
Fig.16 Effects of steel cage spacing on ductility(n=3, D=40 mm)
3.5 耗 能
采用耗能系数反映试件吸收和消耗能量的关系,并根据荷载-位移曲线,运用式(2)计算其耗能系数η,各试件的具体计算结果详见表1。
(2)
式中:W为实际耗能,取荷载-位移曲线上从坐标原点至下降段85%极限荷载时的曲线与水平轴所包围的面积。
3.5.1 螺旋筋间距和重数对耗能的影响
图17给出试件的耗能系数随螺旋筋间距和重数的变化关系。可知:总体上,螺旋筋间距对耗能系数的影响规律与对延性系数的影响规律相似,随着螺旋筋间距的增大,耗能系数具有小幅减小的趋势;而螺旋筋重数对试件的耗能系数影响不大。

![]() n=2;
n=2; ![]() n=3。
n=3。
图17 螺旋筋间距和重数对耗能的影响(D=50 mm)
Fig.17 Effects of spacing and number of spiral
stirrups on energy dissipation(D=50 mm)
3.5.2 钢筋笼间距对耗能的影响
钢筋笼间距对试件耗能系数的影响规律与对延性系数影响规律相似,如图18所示。可见:随着钢筋笼间距的增大,耗能系数具有小幅增大的趋势,增大幅度在2%~8%之间。可见,增加钢筋笼间距可以有效改善试件的耗能能力。
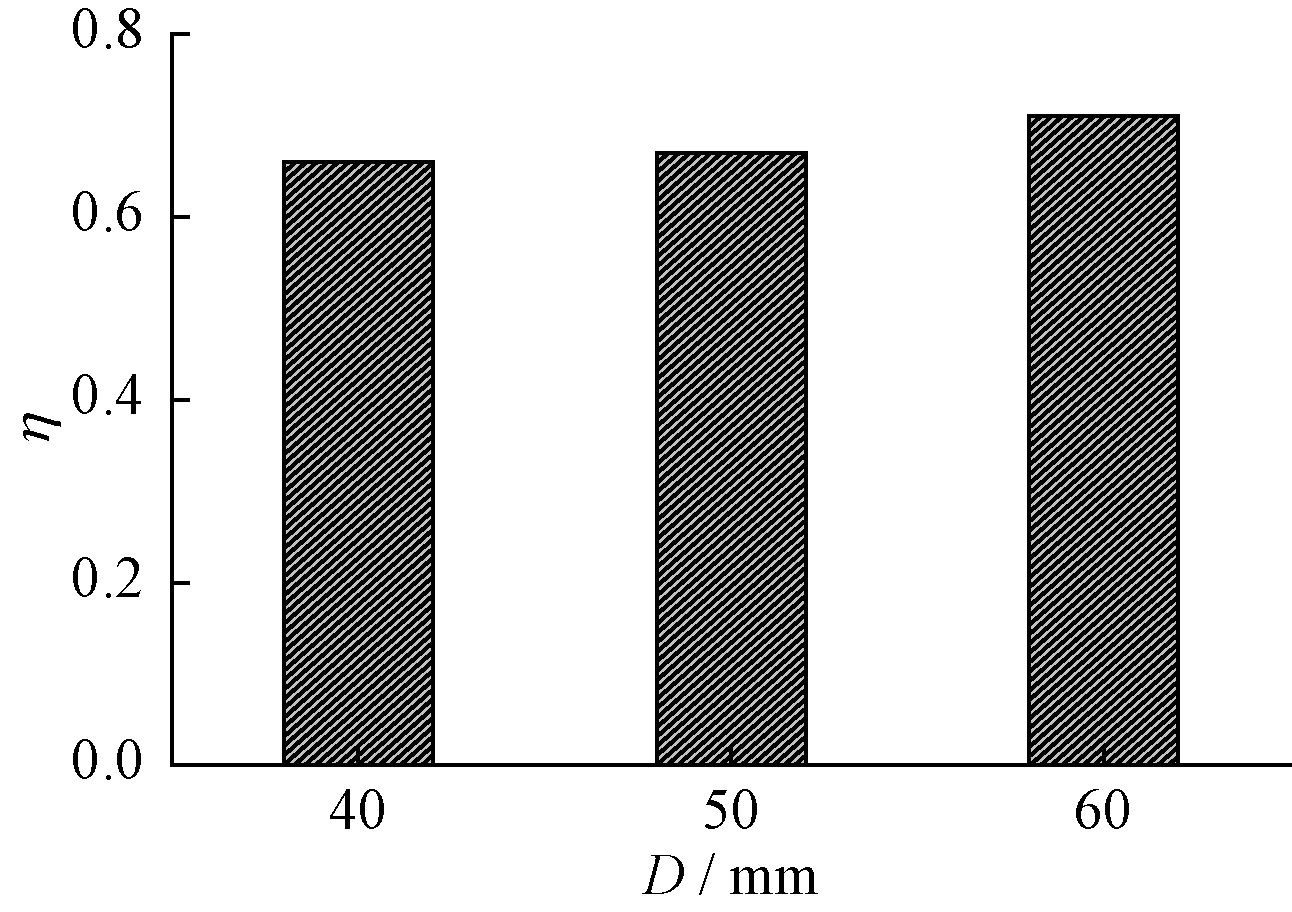
图18 钢筋笼间距对耗能的影响(n=3, d=40 mm)
Fig.18 Effects of steel cage spacing on energy
dissipation(n=3, d=40 mm)
4 结束语
1)三重螺旋筋复合约束钢筋混凝土圆形截面短柱的破坏过程及形态与两重螺旋筋试件的相似,表现为剪切破坏面的形成,箍筋的错位、拉断。
2)与二重螺旋筋的试件相比,三重螺旋筋的试件的荷载-变形曲线在弹性阶段的斜率更大,峰值点过后具有更明显的下降段。
3)增大螺旋筋间距,可以明显减少用钢量,同时不会显著降低承载力;而峰值变形、初始压缩刚度、延性及耗能系数随箍筋间距的增大逐渐减小。
4)增大钢筋笼间距,用钢量的减少幅度大于承载力的降低幅度;延性及耗能系数随钢筋笼间距的增大具有逐渐增大的趋势;而峰值变形和初始压缩刚度没有表现出明显的规律。
5)与两重螺旋筋试件相比,三重螺旋筋试件的用钢量明显增加但并没有有效提高其承载力;其具有更大的初始压缩刚度和更好的延性,但其峰值变形能力较差。
[1] BING L,PARK R,TANAKA H. Stress-Strain Behaviour of High Strength Concrete Confined by Ultra High and Normal Strength Transverse Reinforcements[J]. ACI Structural Journal,2001,98(3):395-406.
[2] SHEIKH S A,TOKLUCU M T. Reinforced Concrete Columns Confined by Circular Spirals and Hoops[J]. ACI Structural Journal,1993,90(5):542-553.
[3] 陈志华,杜颜胜,周婷. 配螺旋筋方钢管混凝土柱力学性能[J]. 建筑结构,2015,45(20):28-23.
[4] 张兴虎,郑晓龙,潘树宾,等. 高强螺旋筋约束混凝土柱抗震性能试验[J]. 建筑科学与工程学报,2013,30(2):21-27.
[5] MANDER J B,PRIESTLEY M J N,PARK R. Theoretical Stress-Strain Model for Confined Concrete[J]. Journal of Structural Engineering,1988,14(8):1804-1826.
[6] 尹衍樑. 矩形混凝土柱新的约束型式之研发(Ⅱ)外方内圆、组合螺箍及其衍生型式[J]. 土木工程学报, 2004,37(10):1-12.
[7] 徐小君. 配置矩形螺箍筋对混凝土梁抗剪承载力影响的研究[D]. 徐州:中国矿业大学,2015.
[8] 苏俊省,王君杰,王文彪,等. 高强度螺旋箍筋约束下混凝土圆柱的抗震性能试验研究[J]. 地震工程与工程振动,2014,34(4):206-211.
[9] 曾芳金,朱蓉芬,孙林柱,等. 方形混凝土柱在双层箍筋约束下的力学特性研究[J]. 江西理工大学学报,2013,34(3):23-31.
[10] 宋力,丁慧,王建平. 双层高强螺旋箍筋约束高强混凝土圆柱轴压受力性能分析[J]. 水利与建筑工程学报,2015,13(4):141-145.
[11] 张耀跃,孙林柱,李昀阳,等. 轴向荷载下双层箍筋混凝土柱的力学性能分析[J]. 建筑结构,2016,46(4):91-96,101.