随着基于性能抗震设计理念的提出和不断发展,如何在地震发生后使建筑物具有良好的恢复功能,引起了国际地震工程界的广泛关注。美国、日本和我国学者相继提出了“可恢复功能抗震结构”的概念[1-2]:即地震后不需修复或稍加修复即可快速恢复使用功能的结构,在“可恢复设计”中,美国和日本合作开展了“预制抗震结构体系(PRESSS)计划”,提出的预制混凝土框架基于后张预应力技术的“干连接”概念可以有效提高结构震后修复能力[3-5]。该体系中,框架梁与框架柱通过后张预应力筋(钢绞线)装配成整体,并在梁柱连接部位设置屈服或摩擦耗能部件。预应力不仅作为梁柱装配的可靠连接,同时在地震过程中为整体结构提供稳定的弹性恢复力,其预应力自复位机制与节点处的屈服或摩擦耗能机制有效融合,形成了典型的旗帜形滞回特征,因此这种框架结构体系也被称为预应力自复位混凝土(SCPC)框架。采用这些基于屈服或摩擦耗能的“干连接”节点的框架在震后残余位移小,主体结构损伤较低,相对于传统现浇混凝土框架具有良好的抗震性能,虽然结构整体初始抗侧刚度较大,但一旦耗能器屈服或摩擦启动,梁柱节点间隙张开,结构抗侧刚度主要靠预应力筋刚度提供,将会导致结构刚度明显降低。文献[6-7]介绍了对不同节点滞回特征SCPC框架的研究,成果表明:在强震作用下,层间刚度的较大削弱,易导致SCPC结构产生较明显的高阶模态效应,结构变形易于集中,局部楼层位移角增大,非结构构件损伤增加,结构的震后复位能力亦受到影响。所以提高结构在节点张开后的刚度、控制高阶模态效应是这类结构推广应用亟待解决的问题之一。而由大量关于框架-填充墙结构的震害分析及研究表明:填充墙与框架相互影响,强度和刚度设计合理的填充墙可以提高结构的耗能能力和刚度,降低结构地震作用下的高阶模态效应[8-9]。填充墙由于其良好的经济性、施工性能以及布置的灵活性,虽然已被广泛应用于现浇钢筋混凝土框架结构中[8-10],但目前在SCPC框架中的研究较少。SCPC框架结构作为一种新型的钢筋混凝土框架结构,必然会涉及填充墙的布置以及填充墙与结构整体的相互作用等问题。因此本文提出了在SCPC框架中布置可以提高结构刚度和耗能能力的填充墙,以研究其对SCPC框架节点张开后刚度,高阶模态效应明显的影响,分析框架中梁柱等主体构件和填充墙之间的相互关系,以期给出关于带填充墙SCPC框架抗震设计的相关建议。
基于《预制混凝土抗震结构体系设计指南》[11](PRESSS)构建了具有自复位摩擦耗能节点的5层和9层带填充墙的自复位预应力混凝土(SCPC)框架结构有限元模型。选取FEMA P695[12]地震集中的22条地震动记录,并调整至美国土木工程师学会颁布的ASCE 7-2010《建筑物最小设计荷载》[13]规定的设计基准地震(DBE)水平和罕遇地震(MCE)强度水平,对结构进行了非线性动力分析。
1 SCPC-IW框架结构设计实例
1.1 多层带填充墙SCPC框架算例
为研究填充墙对SCPC框架结构高阶模态等动力响应的影响,选取文献[6]中按PRESSS技术设计手册设计的SCPC原型结构(图1a)为设计算例,将其抗震框架的节点构造设置为图1b所示摩擦耗能型节点形式[14],建立了5层、9层带填充墙和不带填充墙(图1c~图1f)的有限元模型(5层带填充墙和不带填充墙的模型分别记作SCPC-IW5和SCPC-Bare5, 9层带填充墙和不带填充墙的模型分别记作SCPC-IW9和SCPC-Bare9)。SCPC框架各层预应力筋面积、初始预应力,节点耗能需求,梁柱设计弯矩、轴力及剪力等具体设计参数详见文献[6]。
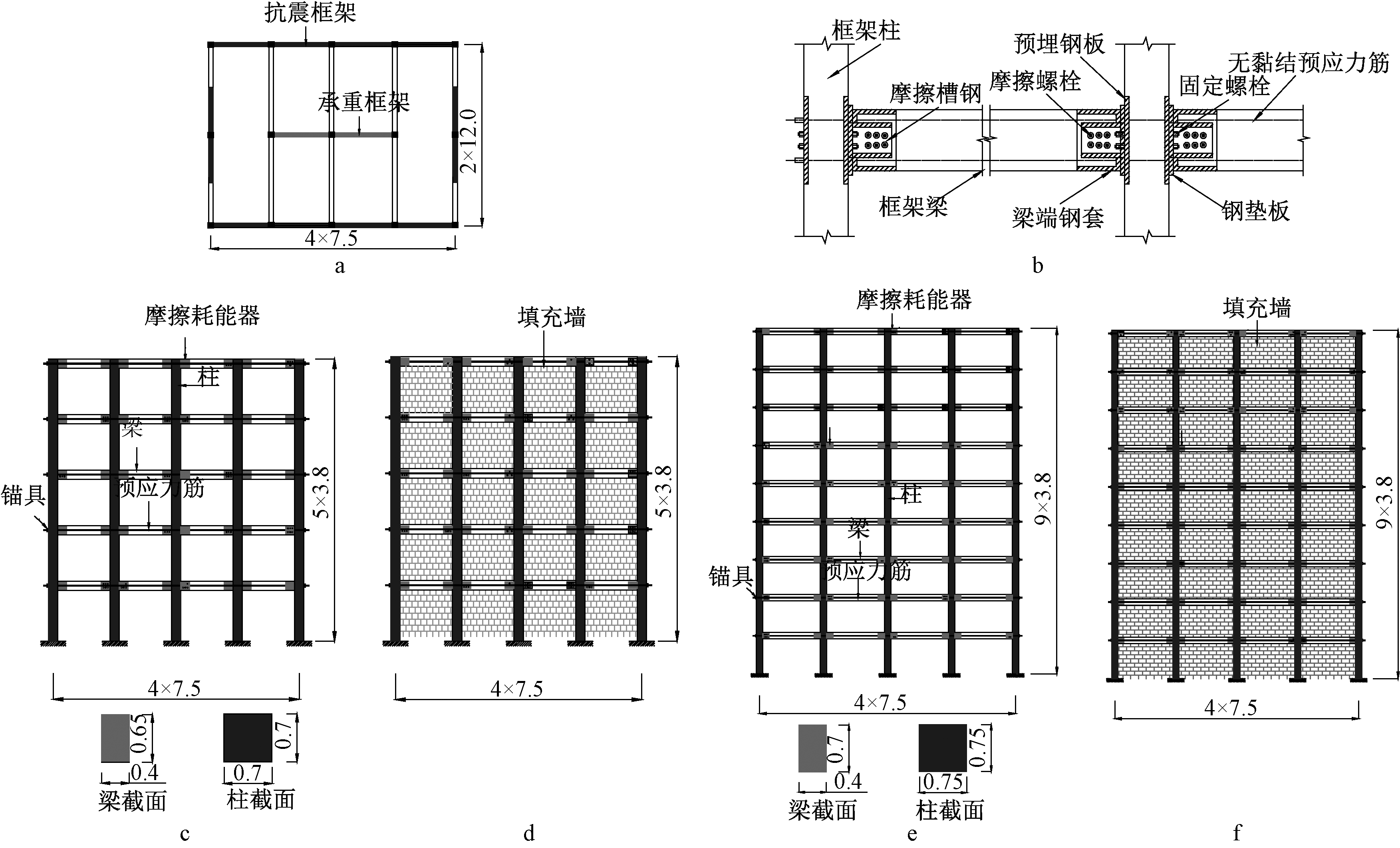
a—原型结构平面[6]; b—摩擦耗能型SCPC节点构造[14]; c—SCPC-Bare5; d—SCPC-IW5; e—SCPC-Bare9; f—SCPC-IW9。
注:图1d、图1f中砌体强度等级MU15; 砂浆强度等级Mb15; 墙体抗压强度设计值为4.61 MPa。
图1 SCPC原型结构及填充墙布置 m
Fig.1 Prototype SCPC frame and the arrangement of infill walls
1.2 多层SCPC框架有限元分析模型
采用OpenSees有限元分析平台进行建模分析,节点精细化建模方法如图2所示[8],梁柱均用纤维离散化的非线性梁柱单元。其中混凝土采用可以考虑受拉的Concrete 02本构模型,预制梁柱中为考虑核心区混凝土在箍筋约束作用下的增强效应,对核心区和保护层混凝土分别定义,钢筋采用可以考虑反复加载过程中的Bauschinger效应和等向强化效应的Steel 02本构模型。预应力筋采用Truss单元模拟,并赋予其Steel 02本构模型和初始预应力属性。零长度接触单元赋予只压材料本构模拟节点张开闭合,零长度截面单元赋予Steel 01本构模拟节点相互错动过程摩擦耗能器产生的摩擦力。刚性单元和弹性单元均采用弹性梁柱单元。

图2 SCPC梁柱节点数值模型
Fig.2 Analytical model of SCPC beam-column connections
介于梁柱框架之间的每片填充墙采用如图3a所示的两个只受压力的对角斜杆单元模拟,该斜杆单元的厚度与墙体的实际厚度相同,根据文献[4,9],该等效单元的宽度为:
a=0.175(λ1hcol)-0.4Ldiag
(1)
式中:hcol为以梁中心线间计算的柱高度;Ldiag为填充墙对角长度;λ1为用来确定填充墙斜杆等效宽度a的系数,其表达式[9-10]为:
(2)
式中:hinf为填充墙的高度;tinf为填充墙的厚度;Ef和Einf分别为框架材料和填充墙材料的弹性模量;Icol为柱截面惯性矩;θ的正切值表示填充墙高度和长度的比值,即tan θ=hinf/Linf,Linf为填充墙的长度。
两个对角等效杆单元用桁架单元模拟,材料采用Hysteretic本构模型,如图3b所示。
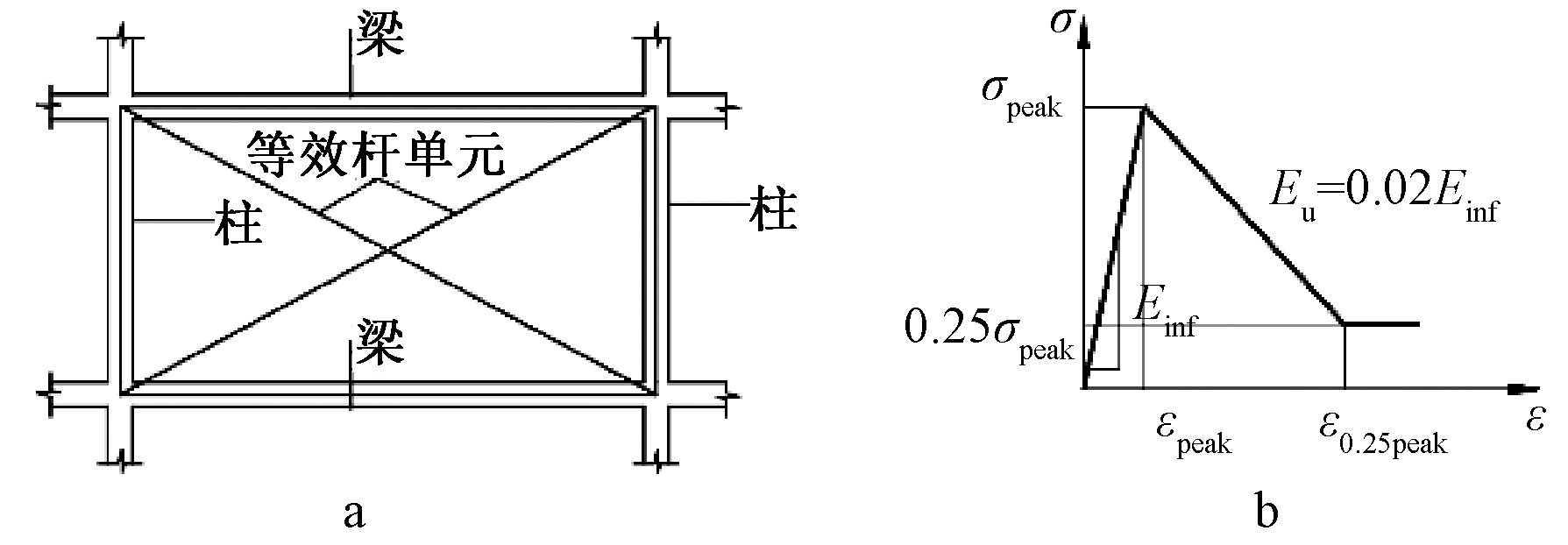
a—等效斜杆单元; b—本构模型。
图3 填充墙模型[10]
Fig.3 Infill wall model
对所有框架柱采用P-Delta转化考虑了重力二阶效应。在节点处采用这种多单元模拟的方式精确及全面地模拟了各单元在实际结构中的相互作用机理。在节点处利用转动弹簧模拟节点区剪切破坏的方式解决了基于塑性分布纤维单元不能考虑剪切的问题。已有研究中多使用单杆或多杆单元仅与梁或柱连接的方法,而该研究的建模方法中将填充墙考虑为一对斜杆与梁柱的节点相互连接而非与梁或柱单一主体构件相连,充分模拟了填充墙与梁柱单元的相互作用[5]。并且这种填充墙模型中参数的确定是基于填充墙模态作为结构模态一部分的假定,充分考虑了填充墙对结构的模态贡献[10]。
2 SCPC-IW框架结构的动力分析
2.1 地震动输入
将图4a所示的22条地震动记录以谱加速度Sa(T1,5%)为强度指标分别调整至ASCE 7-2010中规定的DBE和MCE两个烈度水平(图4b),对结构进行非线性动力时程分析。楼层的抗震质量平均分布于各楼层梁柱节点区的中心节点处。为了计算结构的残余变形,每条地震波作用后继续对结构进行持时30 s的自由振动分析。
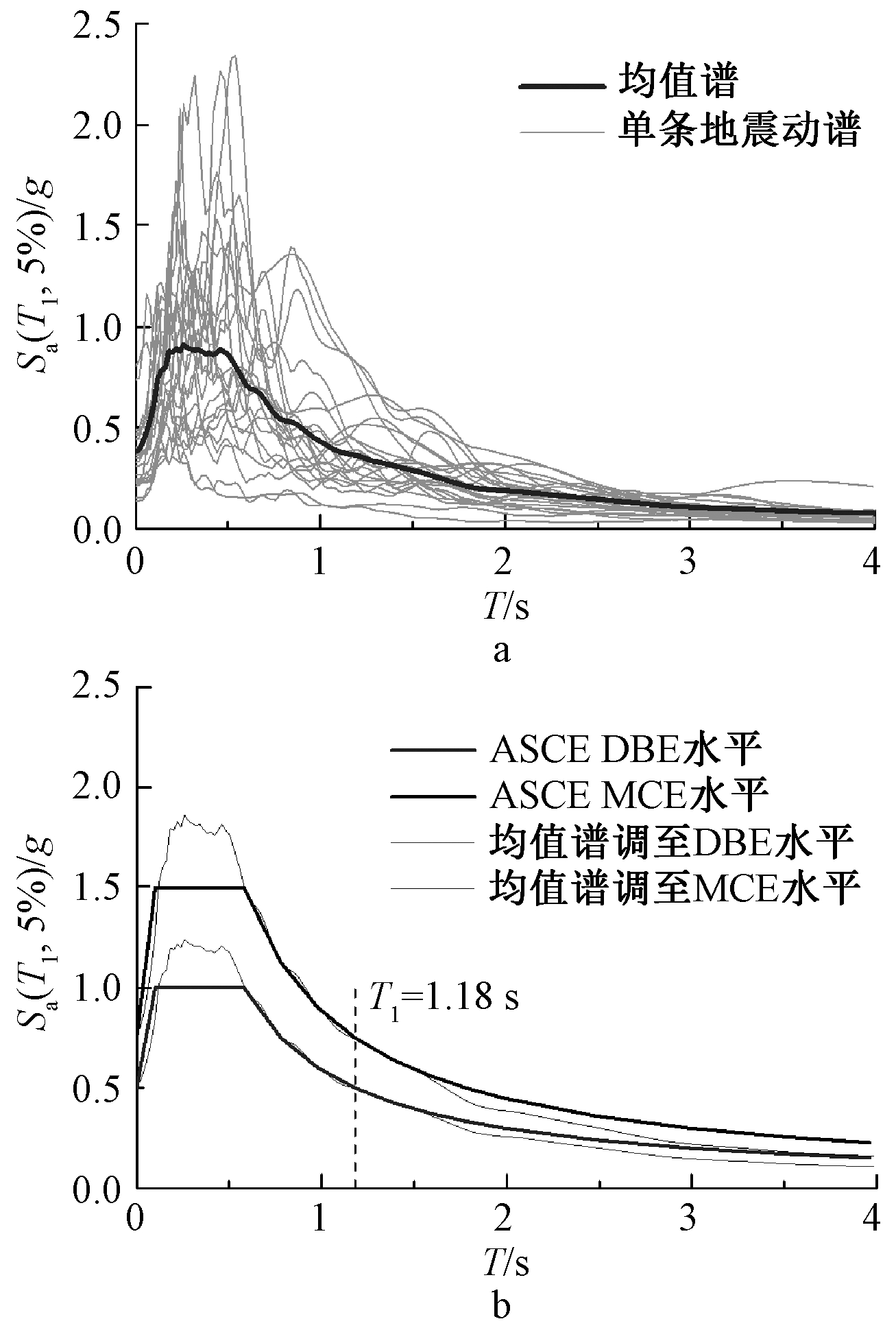
a—选取的22条地震动的加速度谱;
b—地震动调至DBE和MCE水平。
图4 选用地震动的拟加速度谱
Fig.4 Pseudo-acceleration spectra of selected ground motions
以DBE、MCE水平下结构的最大层间位移角θmax,最大残余位移角θr,max和损伤集中系数DCF3个指标评估结构的动力响应。其中,残余层间位移角θr,max可直接反映结构在地震作用下的自复位能力,Kam基于FEMA 356关于结构可恢复功能的相关规定,提出钢筋混凝土框架可修复状态的限值为θr,max=0.4%[6]。损伤集中系数DCF体现了结构的变形集中效应,其表达式为[15]:
(3)
式中:Δroof为结构顶层位移;hn为结构总高度。
2.2 结构最大层间位移角和最大残余层间位移角分析
图5、图6分别给出了5层和9层SCPC框架中布置填充墙后结构的θmax和θr,max,表1给出了结构在DBE水平和MCE水平22条地震动记录输入下θmax和θr,max的平均值。
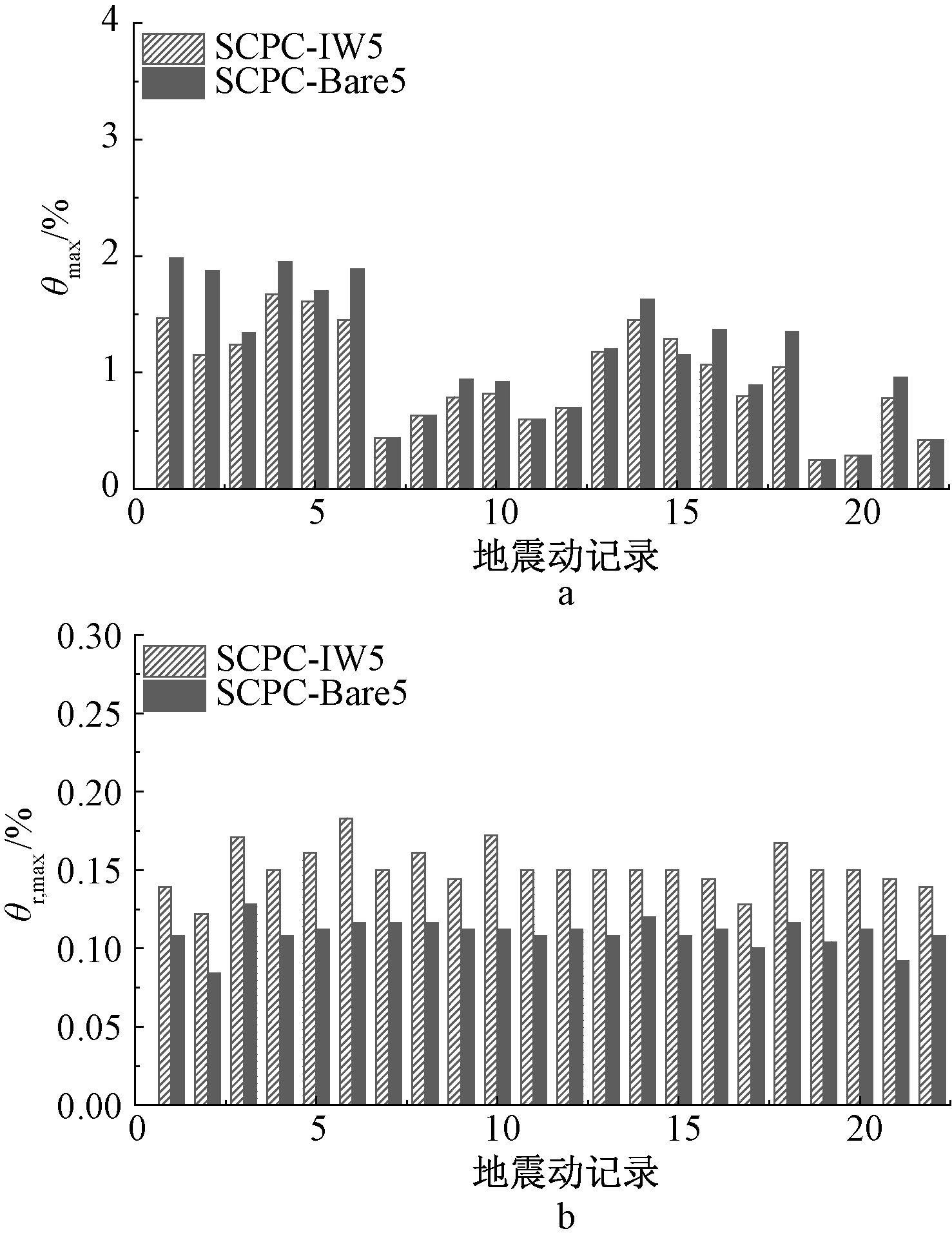
a—θmax的比较; b—θr,max的比较。
图5 5层结构DBE水平输入下最大层间位移角及残余层间位移角
Fig.5 Maximum inter-story drift ratio and residual drift ratio for
a five-story frame under DBE level
从图中可以看出:大多数地震动记录输入下,在DBE水平,由于布置填充墙,提高了结构刚度和耗能能力,从而导致5层和9层SCPC框架结构最大层间位移角均明显降低。SCPC-Bare9和SCPC-IW9中,有部分地震动记录输入下,结构层间位移角超过美国联邦应急管理署(FEMA)《HAZUS计划》[16]中规定的钢筋混凝土结构“中等破坏”的层间位移角限值2.0%。
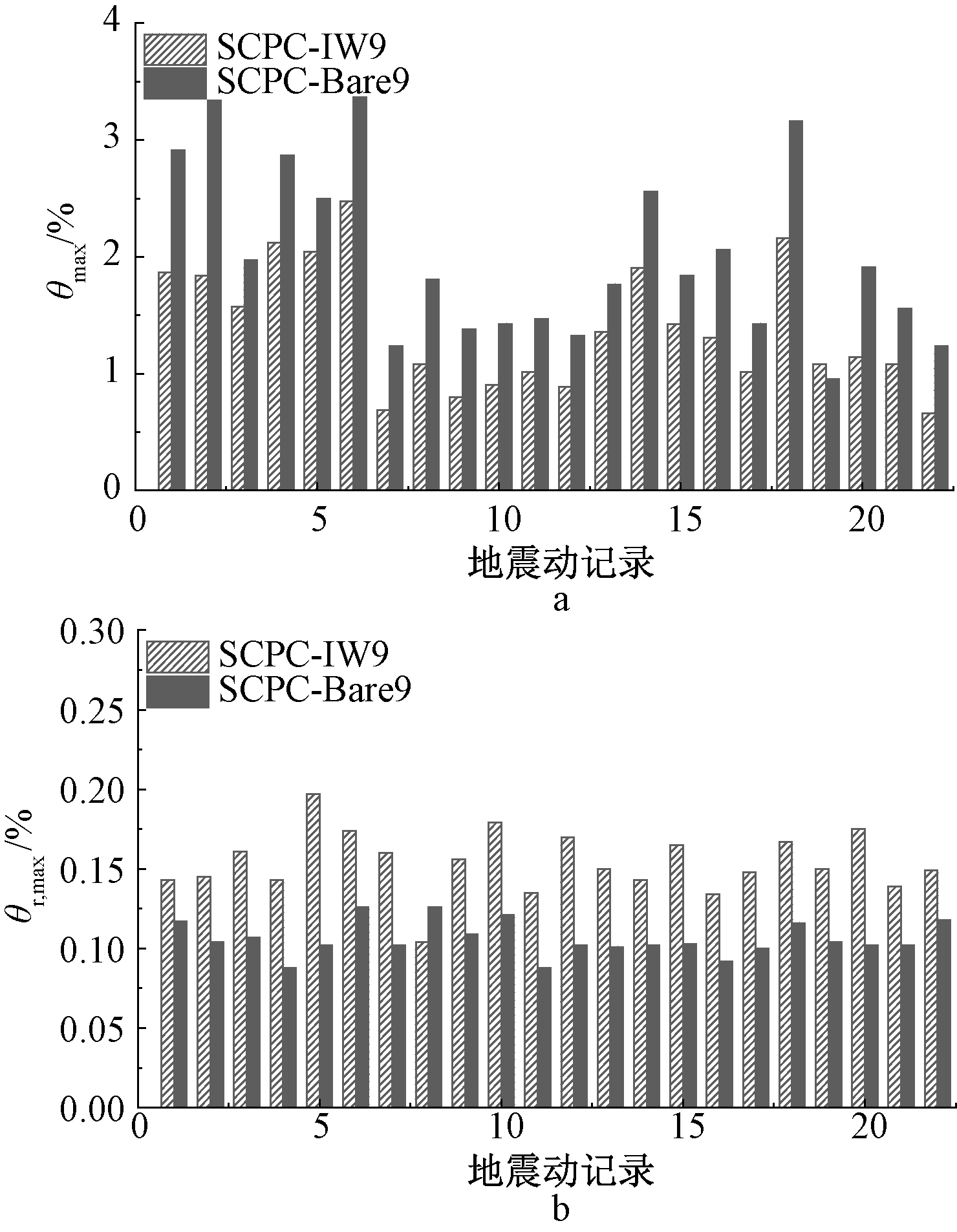
a—θmax的比较; b—θr,max的比较。
图6 9层结构DBE水平输入下最大层间位移角及
残余层间位移角
Fig.6 Maximum inter-story drift ratio and residual drift ratio for
a nine-story frame under DBE level
从表1可见:SCPC-Bare9对应θmax的均值也超过2.0%,而布置填充墙的SCPC-IW9对应θmax的均值仅为1.39%,远小于2.0%。虽然SCPC结构的位移需求较大,θmax超过2%不会造成梁柱等主体构件的严重破坏,但会导致结构中布置的附属构件发生较大变形,产生严重破坏,而布置填充墙后,可以有效将结构θmax控制在2%以内。
另一方面,无论DBE水平还是MCE水平,布置填充墙后,结构层间位移角的平均值均减小,而残余层间位移角均值增大(表1),由于填充墙产生了不可恢复的塑性变形,从而导致大多数地震动调至DBE强度水平输入下,结构的残余层间位移角呈现增大趋势,但并未超过Kam提出的结构可修复限值0.4%。
表1 结构动力响应
Table 1 Dynamic response of structures

模型DBEMCEθmax/%θr,max/%DCFλmaxθmax/%θr,max/%DCFλmaxSCPC-IW51.1080.1511.640.562.010.2181.720.80SCPC-Bare51.8700.1091.730.362.420.1791.820.56 SCPC-IW91.3900.1611.720.582.210.2321.840.82SCPC-Bare92.0400.1171.830.383.010.1841.920.60
2.3 结构高阶模态效应及变形集中效应分析
图7 所示为结构在22条地震动记录调至DBE和MCE 水平下层间位移角平均值沿楼层的分布规律。从图中可以看出,未布置填充墙的SCPC-Bare5, SCPC-Bare9均呈现出底层层间位移角小于上层层间位移角的规律。随着楼层的增高,结构上层的位移角逐步增大,即高阶模态的影响逐渐明显,有研究表明这种高阶模态效应使结构变形易于集中,导致局部楼层位移角较大,非结构构件损伤增加,结构的震后复位能力亦受到影响[9,17]。上层结构的较大变形会导致预应力松弛[9],一方面导致残余层间位移角过大,严重影响到结构震后的可修复能力;另一方面,预应力松弛势必会导致这种主要依靠梁柱界面预压摩擦抗剪的节点处抗剪能力严重不足。而布置填充墙以后,SCPC-IW5、SCPC-IW9中结构层间位移角沿楼层的分布发生显著改变,上层层间位移角明显减小。

a—5层结构; b—9层结构。
图7 最大层间位移角沿楼层分布
Fig.7 Maximum inter-story drift ratio along the building height
有研究表明高阶模态效应容易导致结构发生薄弱层破坏和损伤集中失效等破坏模式[17],故给出布置填充墙和未布置填充墙结构在DBE水平下各地震动记录所得损伤集中系数DCF,如图8所示。表1也给出了DBE和MCE水平下结构在22条地震动记录下的DCF平均值。
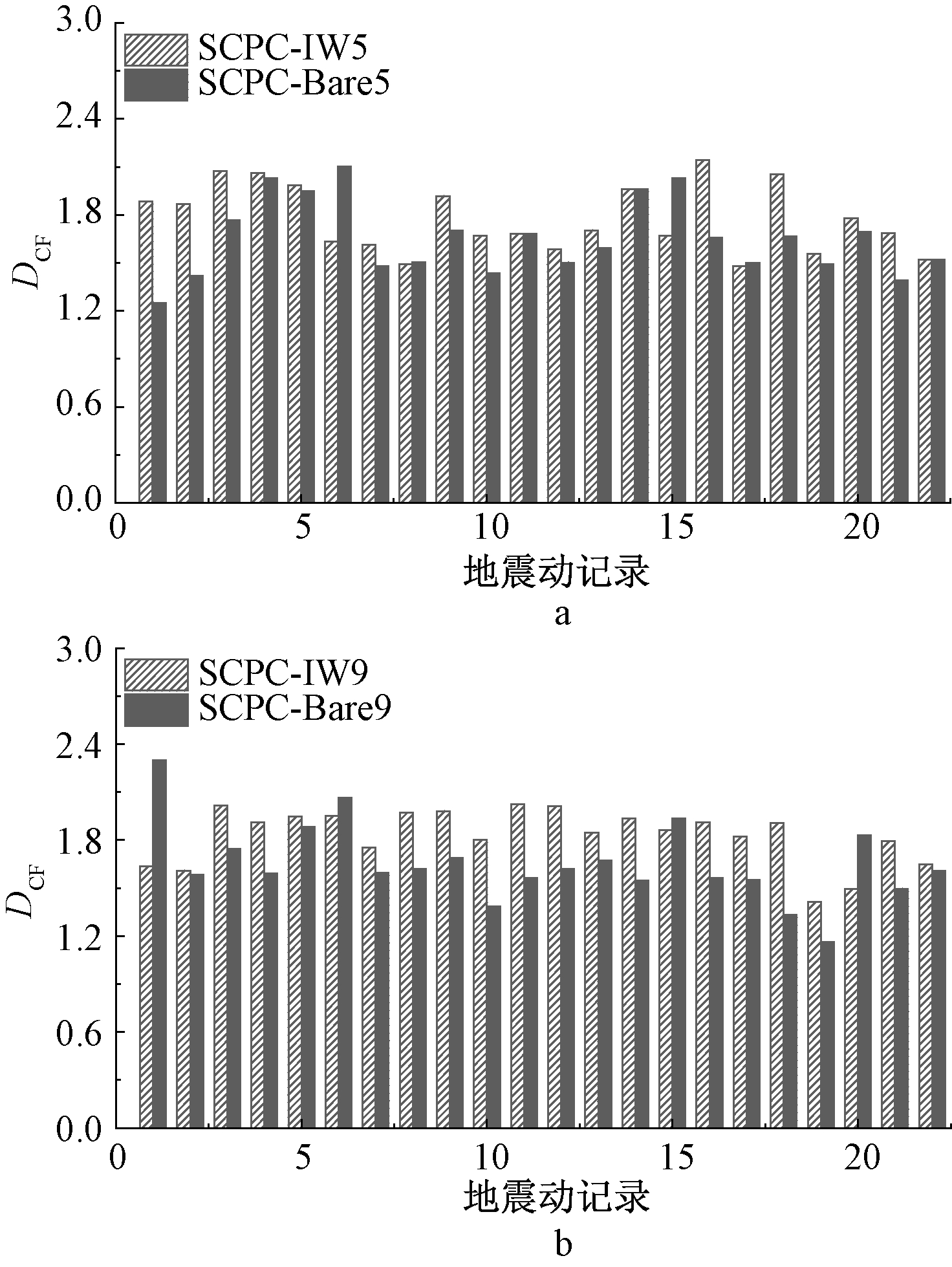
a—5层结构; b—9层结构。
图8 结构DBE水平输入下的DCF
Fig.8 The DCF of structures under DBE level
由表1可知:无论DBE水平还是MCE水平,9层结构的DCF均值均大于5层结构的DCF均值,即随着楼层的增高,结构表现出明显的变形集中效应和高阶模态效应,即结构楼层数越多,发生薄弱层破坏的可能性也越大。由图8可见:相对于DBE水平θmax和θr,max的计算结果,DCF在22条地震动记录作用下呈现出一定的离散性,但在绝大多数地震动记录作用下,布置填充墙后,DCF明显降低。
而SCPC结构中布置填充墙可以有效降低结构损伤集中破坏,这是由于填充墙会导致结构高阶模态效应降低从而使结构变形模式趋于合理。
2.4 地震作用下填充墙对框架柱的影响
为得到填充墙对主体构件的影响,统计出DBE和MCE下,框架柱的轴压比λmax(表1)。由表1可见:SCPC-IW框架柱的轴压比明显高于SCPC-Bare,如,SCPC-IW5轴压比高于SCPC-Bare5, SCPC-IW9的轴压比高于SCPC-Bare9,并且SCPC-IW5和SCPC-IW9中柱的最大轴压比均超过了GB 50011—2010《建筑抗震设计规范》[18]中关于二级框架中柱轴压比限值0.75的规定,这可能会造成柱的破坏。也即,过高强度填充墙会造成SCPC框架中柱的破坏。亦有研究表明随着填充墙强度的提高,轴压比逐渐增大。根据文献[19],为避免在SCPC-IW中框架柱轴压比过高而导致框架柱过早破坏,在SCPC-IW设计时,填充墙强度不应超过耗能器中摩擦力的33%。值得注意的是,SCPC-IW9柱截面面积相对于SCPC-IW5的提高了7.1%,而两者轴压比相差并不明显,这说明在SCPC-IW结构中可以通过提高柱截面面积来避免过高轴压比,进而避免结构构件的破坏。
3 结束语
1)SCPC结构受高阶模态的影响较大,随着楼层的增高,结构表现出更加明显的变形集中效应和高阶模态效应。
2)在SCPC框架结构中满布填充墙可以明显提高结构的刚度、耗能能力,同时又不会明显降低结构自复位能力。
3)在地震作用下,SCPC-IW框架结构中的填充墙作为非结构构件,参与承担地震耗能,可以明显降低结构的动力响应,降低结构高阶模态效应。
4)填充墙的布置会导致地震作用下柱的轴压力过高,进而增加其破坏的可能性,反而不利于结构震后修复。在结构设计时,填充墙的承载能力不宜超过摩擦耗能器设计摩擦力的33%。同时相对于裸框架应该适当提高柱的截面面积以避免过多结构构件的破坏。
建议在SCPC框架结构中布置承载能力不超过耗能器摩擦力33%的填充墙,有效减小结构地震响应,同时又可以保证在罕遇地震下主体结构实现“可修”的控制目标。
[1] DYKE S J, STOJADINOVIC B, ARDUINO P, et al. 2020 Vision for Earthquake Engineering Research: Report on an Openspace Technology Workshop on the Future of Earthquake Engineering [R]. St. Louis, MO, USA:Network for Earthquake Engineering Simulation (NEES), 2010:7-40.
[2] 周颖,吕西林. 摇摆结构及自复位结构研究综述[J]. 建筑结构学报, 2011, 32(9): 1-10.
[3] STANTON J F, HAWKINS N M, HICKS T R.PRESSS Project 1.3: Connection Classification and Evaluation [J]. PCI Journal, 1991, 36(6): 62-71.
[4] 黄林杰, 周臻. 带填充墙自复位预应力混凝土框架结构的抗震性能分析[J]. 工程力学, 2018, 35(10):162-171.
[5] PAMPANIN S, PRIESTLEY M J N, SRITHATAN S.Analytical Modeling of the Seismic Behavior of Precast Concrete Frames Designed with Ductile Connections [J].Journal of Earthquake Engineering, 2001, 5(3): 329-367.
[6] KAM W Y, PAMAPANIN S, CARR A J. Design Procedure and Behavior of Advanced Flag-Shape (AFS) MDOF Systems[C]//Proceedings of NZSEE 2008 Conference. Wairakei, NZ:2008.
[7] LI L M. Further Experiments on the Seismic Performance of Structural Concrete Beam-Column Joints Designed in Accordance with the Principles of Damage Avoidance [D]. Christchurch:University of Canterbury, 2006.
[8] CHEN X, LIU Y. Finite Element Study of the Effect of Interfacial Gaps on the In-Plane Behaviour of Masonry Infills Bounded by Steel Frames [J]. Structures, 2017(10): 1-12.
[9] LANDI L, TARDINI A, DIOTALLEVI P P. A Procedure for the Displacement-Based Seismic Assessment of Infilled RC Frames [J]. Journal of Earthquake Engineering, 2016, 20(7): 1077-1103.
[10] 韩建平,黄林杰,孙小云.考虑填充墙平面内外相互作用评估RC框架-填充墙结构抗整体性倒塌能力[J]. 工程力学, 2016, 33(9): 146-154.
[11] STANTON J F, NAKAKI S D. Design Guidelines for Precast Concrete Seismic Structurd Systems:PRESSS Report No.01/03-09, UW Report No.SM02-02[R]. Seatle, WA, USA:Department of Civil Engineering University of Washington, 2002.
[12] FEMA-P695.Quantification of Building Seismic Performance Factors [R]. Washington, DC: Federal Emergency Management Agency, 2009.
[13] American Society of Civil Engineering(ASCE). Minimum Design Loads for Building and Other Structures: ASCE 7-2010[S]. Resfon, VA, USA: ASCE, 2010.
[14] 宋良龙,郭彤. 腹板摩擦式自定心预应力混凝土框架的抗震性能研究[J]. 工程力学, 2014, 31(12): 47-55.
[15] 谢钦,周臻,卢璐,等. 自复位摩擦耗能支撑的套管长度误差对多层结构地震响应的影响[J].土木工程学报, 2014 (增刊1): 96-101.
[16] FEMA. HAZUS-MH: Advanced Engineering Building Module (AEBM) Technical and User’s Manual[S]. Washington, D.C:Federal Emergency Management Agency,2010.
[17] MANIATAKIS C A, PSYCHARIS I N, SPYRAKOS C C. Effect of Higher Modes on the Seismic Response and Design of Moment-Resisting RC Frame Structures [J]. Engineering Structures, 2013, 56(6):417-43.
[18] 中华人民共和国住房和城乡建设部.建筑抗震设计规范:GB 50011—2010[S].北京:中国建筑工业出版社,2010.
[19] HUANG L, ZHOU Z, ZHANG Z, et al. Seismic Performance and Fragility Analyses of Self-Centering Prestressed Concrete Frames with Infill Walls[J]. Journal of Earthquake Engineering, 2018. DOI:org/10.1080/13632469.2018.1526142.