预制装配式混凝土框架(PCF)与传统现浇框架相比,具有生产效率高、建设周期短、产品质量好及耗费人工少等优点,近年来受到了众多学者的关注[1-2]。柳炳康等对一榀两层两跨预应力装配式混凝土框架进行了拟动力和拟静力试验,试件可实现理想的破坏模式,具有良好的变形能力和抗倒塌能力[3]。高向玲等对提出的一种预制装配式混凝土梁柱节点进行了低周反复试验,并对采用该节点形式的预制装配式框架进行推覆分析,结果表明该节点具有饱满的滞回曲线,且预制装配式框架的承载力和刚度与现浇框架相比还有所提高[4]。
由于节点设计合理的装配式混凝土框架具有与现浇框架相似的抗震性能,地震时会产生剪切型变形模式,下部楼层的构件易出现较大损伤。而屈曲约束支撑(BRB)是一种有效的控震技术,具有拉压承载力对称和饱满的滞回特征[5]。将BRB与装配式混凝土框架组合形成BRB-PCF双重体系,不仅能有效减小结构变形集中效应,而且通过BRB的塑性耗能可以降低梁柱的损伤程度。王静峰等通过对3榀BRB-PCF框架试件进行低周反复荷载试验,验证了BRB可以有效提高装配式混凝土框架的抗震性能[6]。
BRB的布置原则对BRB-抗弯框架双重体系抗震性能的改善效果会产生较大影响。贾明明等对9层BRB-钢框架双重体系采用三种不同的支撑布置原则,结果表明基于支撑与框架抗侧刚度比设计的结构延性较好且层间位移角分布最均匀[7]。Aukeman等对抗弯框架分别承担15%、25%、40%设计基底剪力的3个BRB-钢框架双重体系模型进行时程分析后,认为三个结构的抗震性能差异并不明显[8]。冯玉龙等通过对单层BRB-钢框架双重体系进行抗震性能参数化分析,给出BRB-钢框架的建议刚度比为2[9]。由于装配式混凝土框架的力学性能与钢框架存在较大的差异,BRB-钢框架的分析结果并不完全适用于BRB-PCF双重体系,因此还需要进一步研究支撑布置原则对BRB-PCF双重体系抗震性能的影响。
本文基于支撑与框架抗侧刚度比的支撑布置原则,分别建立了不同刚度比的3、6和9层BRB-PCF双重体系分析模型,通过非线性动力时程分析,研究了刚度比的变化对结构抗震性能的影响及其合理取值范围。
1 BRB-PCF双重体系的工作机理
BRB-PCF双重体系是由装配式混凝土框架和BRB支撑体系共同提供抗侧刚度和承载力。地震时,BRB-PCF双重体系中的PCF体系和BRB体系受各层楼板的约束,通过变形协调共同抵抗地震作用。由于BRB体系在地震作用下表现为弯曲型变形模式,使得结构的变形会集中于上部楼层,而PCF体系由于其剪切型变形模式,能有效控制结构上部楼层的变形,使得BRB-PCF双重体系的变形沿竖向分布更加均匀(图1)。通过合理分配PCF体系和BRB体系承担的层剪力,能有效减小结构的变形集中效应[10]。

图1 BRB-PCF双重体系变形特点
Fig.1 Deformation characteristics of the BRB-PCF dual system
图2通过叠加BRB体系和PCF体系的荷载-位移曲线,得到BRB-PCF双重体系的推覆曲线。由于BRB体系和PCF体系的荷载-位移曲线均可理想化为具有明显屈服点的双折线,使得BRB-PCF的推覆曲线表现出三折线特征。在加载初期,BRB和框架部分均处于弹性状态,结构整体具有较大的初始刚度;当位移增大到BRB的屈服位移时,由于BRB部分的承载力不再随位移增大而提高,结构的刚度下降为PCF体系的刚度;随着位移的进一步增大,PCF体系也发生屈服并进入塑性阶段,结构整体刚度减小到0,承载力不再随位移的增大而提高。
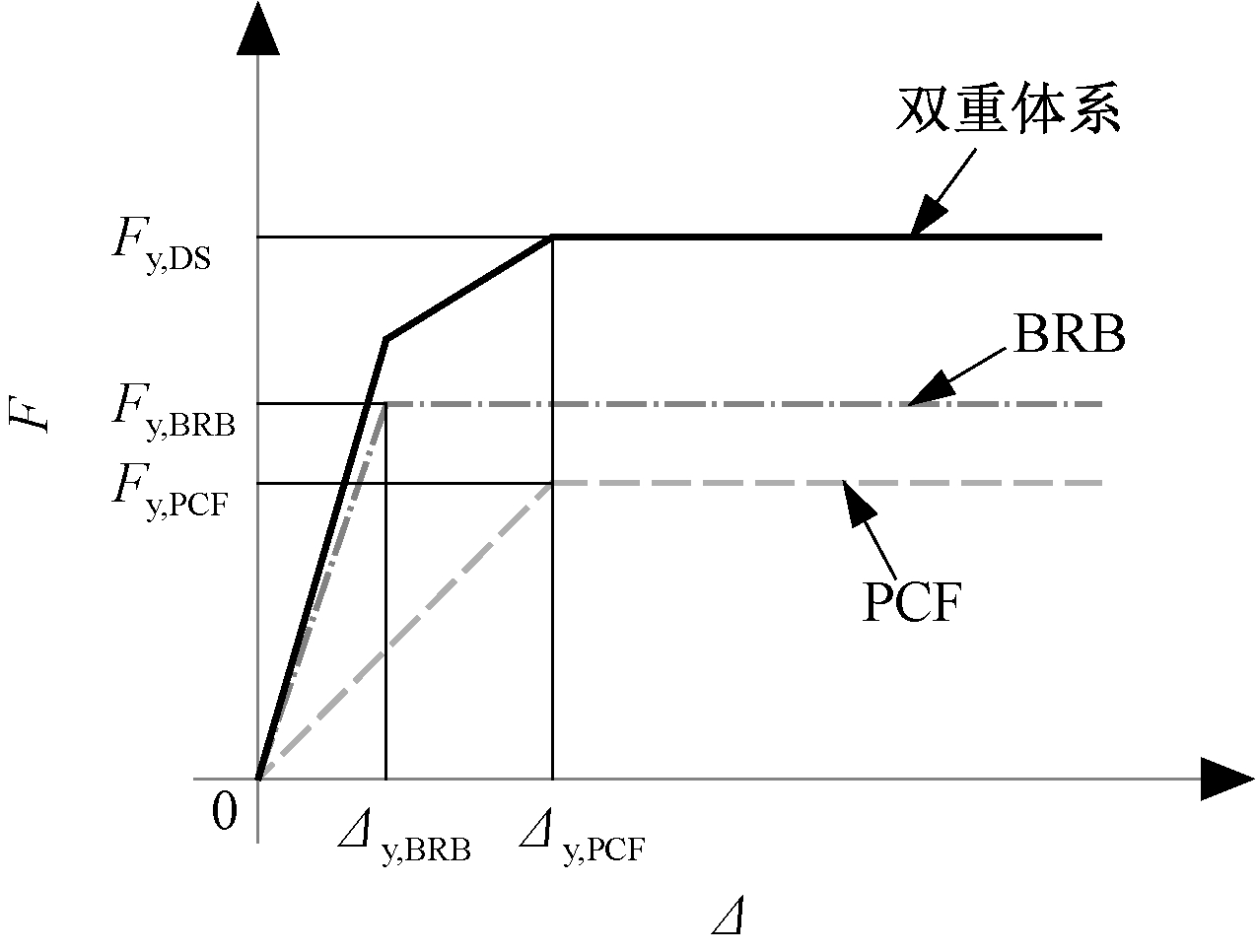
图2 BRB-PCF双重体系推覆曲线
Fig.2 Pushover curves of the BRB-PCF dual system
BRB-PCF双重体系的结构水平作用力由式(1)计算:
Fy,DS=Fy,BRB+Fy,PCF
(1)
式中:Fy,DS、Fy,BRB和Fy,PCF分别为BRB-PCF双重体系、BRB和PCF的结构水平作用力。
BRB-PCF双重体系的整体抗侧刚度为:
KDS=KBRB+KPCF
(2)
式中:KDS、KBRB和KPCF分别为BRB-PCF双重体系、BRB和PCF的抗侧刚度。
而BRB与PCF的抗侧刚度之比k为:
k=KBRB/KPCF
(3)
2 BRB与PCF抗侧刚度计算
BRB体系的抗侧刚度可以通过改变支撑安装倾角和几何尺寸进行调整。图3为BBR的基本构造,支撑整体由无约束非屈服段、约束非屈服段和约束屈服段组成,图中Aj、At和Ac分别表示三个区段的截面面积,Lj、Lt和Lc分别表示三个区段的总长度。

图3 BRB构造
Fig.3 Configuration of the BRB
BRB提供的抗侧刚度可以表示为:
(4)
式中:E为钢材的弹性模量;α为支撑与水平面的夹角。
PCF的抗侧刚度可按照D值法计算:
(5)
式中:β为修正系数,可由梁柱的线刚度比计算得到;E、I和h分别为各层柱子的弹性模量、惯性矩和高度。
3 分析模型的建立
图4为本文建立的3,6,9层BRB-PCF双重体系分析模型,柱间距为8.0 m,结构首层层高为4.5 m,其余各层层高均为4.0 m。结构的楼面恒载和活载分别为5 kN/m2和2 kN/m2。结构所在地区的场地类别为II类,地震分组为第二组。结构设计选用C40混凝土和HRB400级钢筋,BRB支撑选用Q235级钢材。
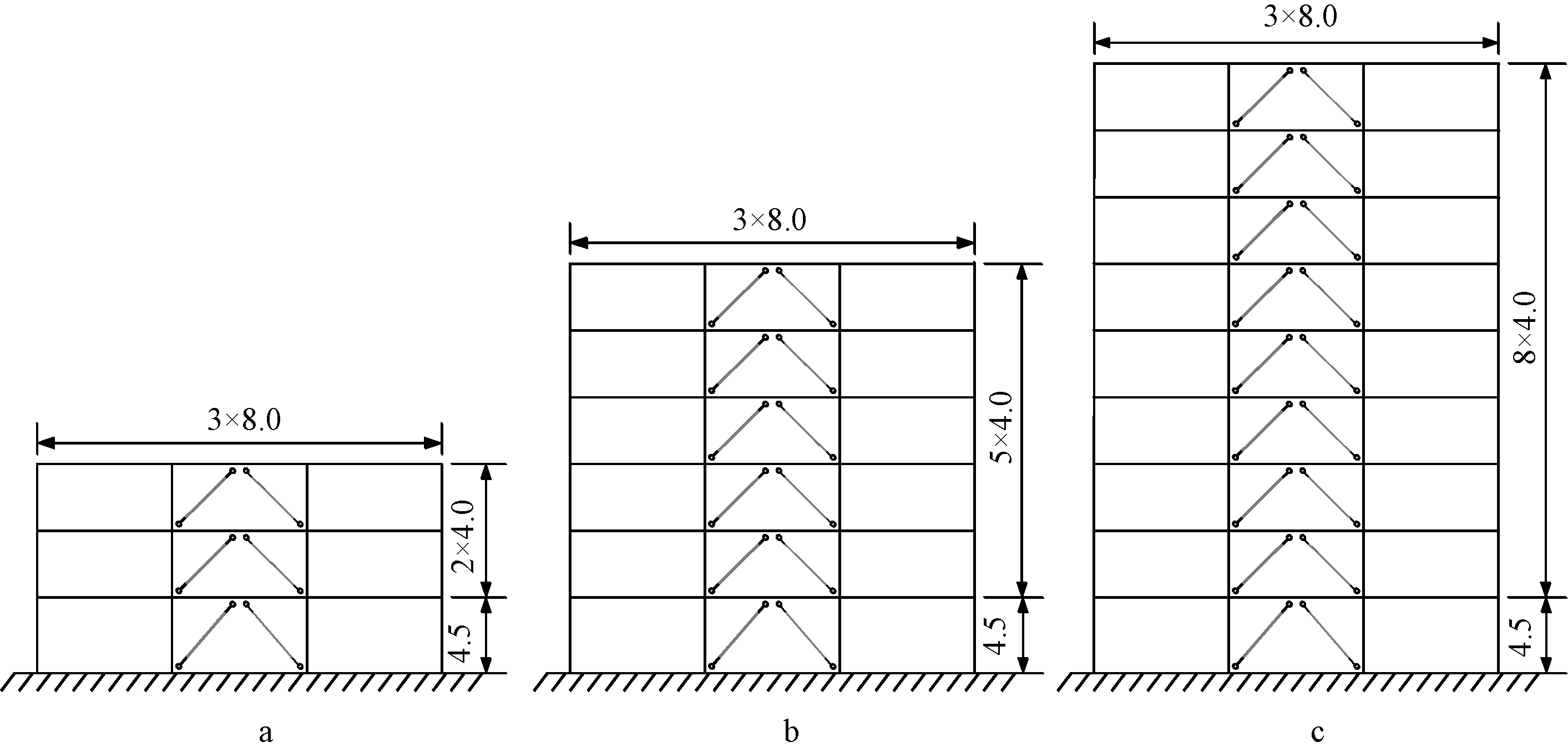
a—3层模型; b—6层模型; c—9层模型。
图4 BRB-PCF双重体系模型立面 m
Fig.4 Elevation view of the models of BRB-PCF dual system
为研究刚度比k对BRB-PCF双重体系抗震性能的影响,首先按GB 50010—2010《混凝土结构设计规范》和GB 50011—2010《建筑抗震设计规范》设计了3层、6层、9层的装配式混凝土框架,然后基于各层框架的层刚度按照k=0,0.2,0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0设计各层的BRB支撑。BRB支撑的基本构造为:Aj=4Ac,At=2Ac,Lj=0.2L,Lt=0.05L和Lc=0.75L,其中L为支撑的总长。配置的支撑信息见表1,PCF的设计结果见表2。
表1 BRB-PCF双重体系模型支撑布置信息
Table 1 Brace layout information of the models of BRB-PCF dual system
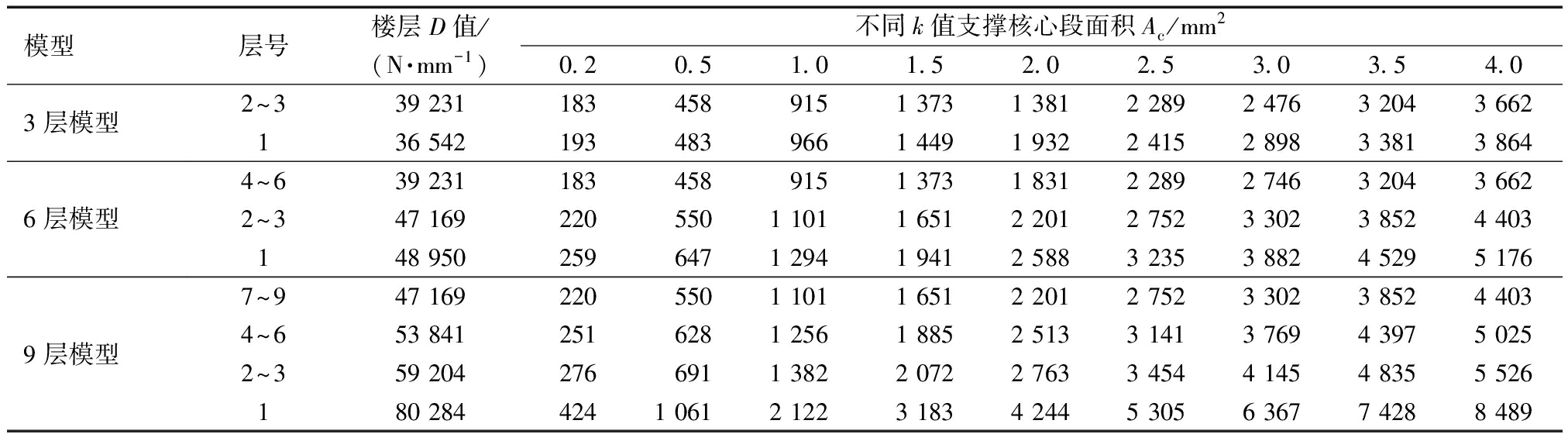
模型层号楼层D值/(N·mm-1)不同k值支撑核心段面积Ac/mm20.20.51.01.52.02.53.03.54.03层模型6层模型9层模型2~339 231183 4589151 3731 3812 2892 4763 2043 662136 542193 4839661 4491 9322 4152 8983 3813 8644~639 2311834589151 3731 8312 2892 7463 2043 6622~347 1692205501 1011 6512 2012 7523 3023 8524 403148 9502596471 2941 9412 5883 2353 8824 5295 1767~947 1692205501 1011 6512 2012 7523 3023 8524 4034~653 8412516281 2561 8852 5133 1413 7694 3975 0252~359 2042766911 3822 0722 7633 4544 1454 8355 526180 2844241 0612 1223 1834 2445 3056 3677 4288 489
本文采用Perform-3D软件建立BRB-PCF双重体系的有限元分析模型并进行抗震性能分析。框架梁和柱选用基于柔度法的梁柱纤维单元,而支撑则选用Perform-3D软件中的BRB单元来模拟,并基于YULRX五折线本构模型[11]模拟梁、柱和BRB的材料特性。
采用Perform-3D软件对相应文献中的混凝土试件和BRB支撑的滞回性能进行模拟,并通过与试验结果的对比验证本文建模的可靠性。陆新征等采用拟静力水平加载方式对混凝土柱试件的滞回性能进行了研究[12],本文选取其边柱A试件进行有限元模型验证。通过对比可知模拟滞回曲线与试验滞回曲线吻合较好(图5),表明纤维柱单元能有效实现混凝土柱刚度退化和捏缩效应的滞回特征,从而较为准确地模拟试件各加载阶段的刚度和强度。BRB的模型验证则基于黄波等的国标Q235钢屈曲约束支撑拟静力试验[13]。选取其中的试件BRB-W-V1进行有限元建模,通过对比BRB的试验曲线和模拟曲线(图6)可知两组曲线吻合较好,表明有限元模型能够实现对BRB弹塑性刚度转换、等向强化和随动强化等滞回特性的模拟。
表2 PCF结构设计信息
Table 2 Design information of the PCF structures
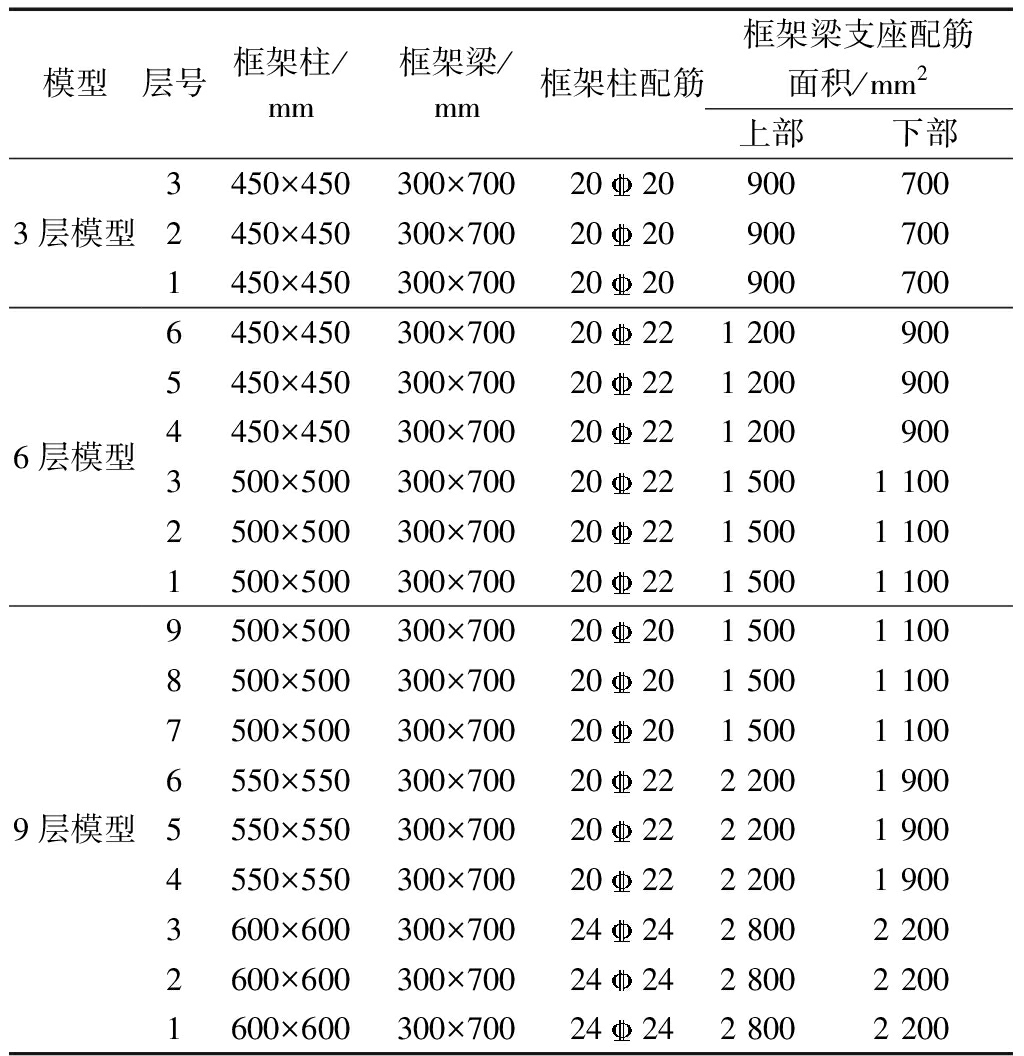
模型层号框架柱/mm框架梁/mm框架柱配筋框架梁支座配筋面积/mm2上部下部3层模型6层模型9层模型3450×450300×70020209007002450×450300×70020209007001450×450300×70020209007006450×450300×70020221 2009005450×450300×70020221 2009004450×450300×70020221 2009003500×500300×70020221 5001 1002500×500300×70020221 5001 1001500×500300×70020221 5001 1009500×500300×70020201 5001 1008500×500300×70020201 5001 1007500×500300×70020201 5001 1006550×550300×70020222 2001 9005550×550300×70020222 2001 9004550×550300×70020222 2001 9003600×600300×70024242 8002 2002600×600300×70024242 8002 2001600×600300×70024242 8002 200
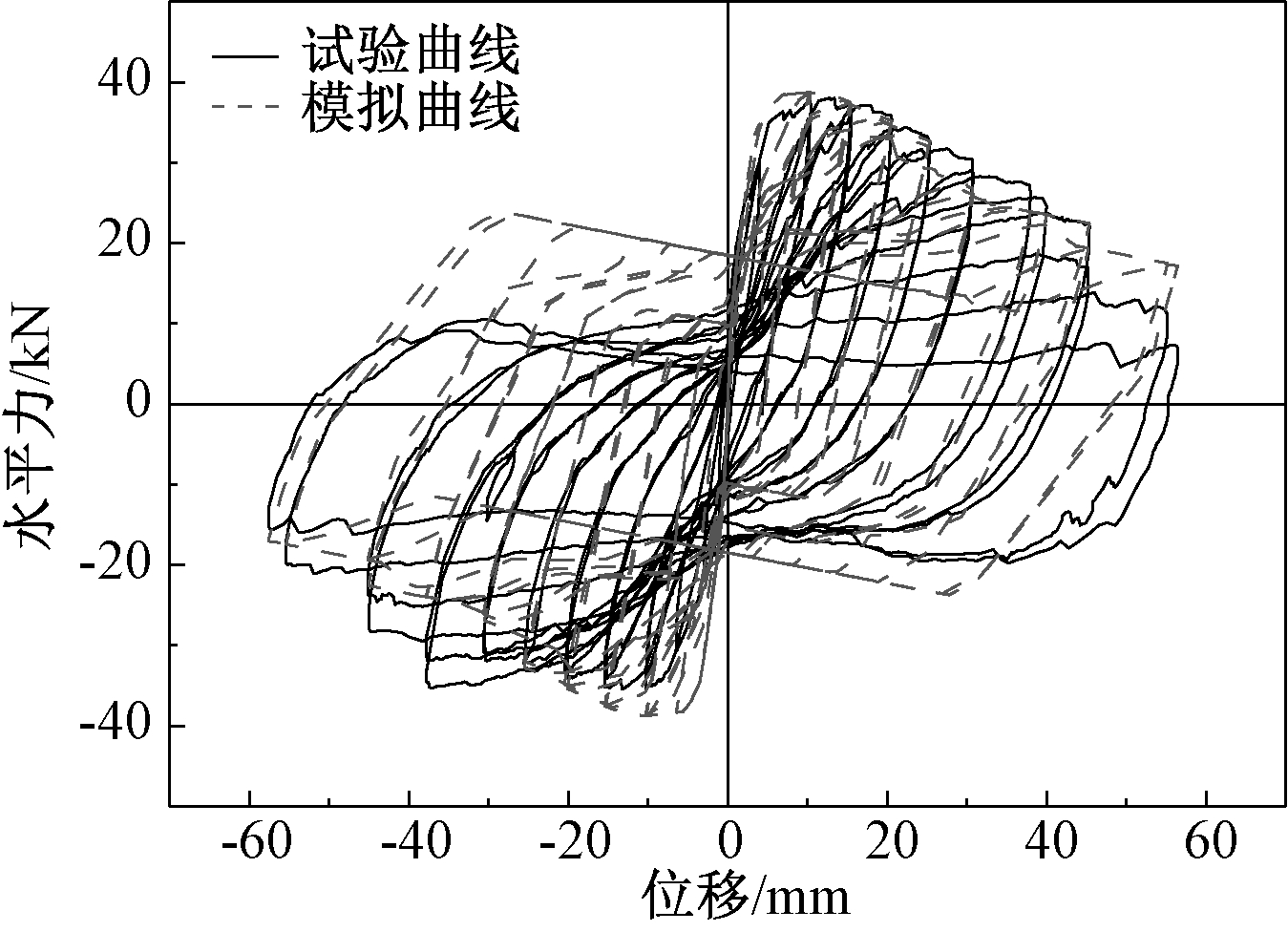
图5 混凝土柱试验曲线与模拟曲线对比
Fig.5 Comparison between test curves and simulation
curves of concrete column
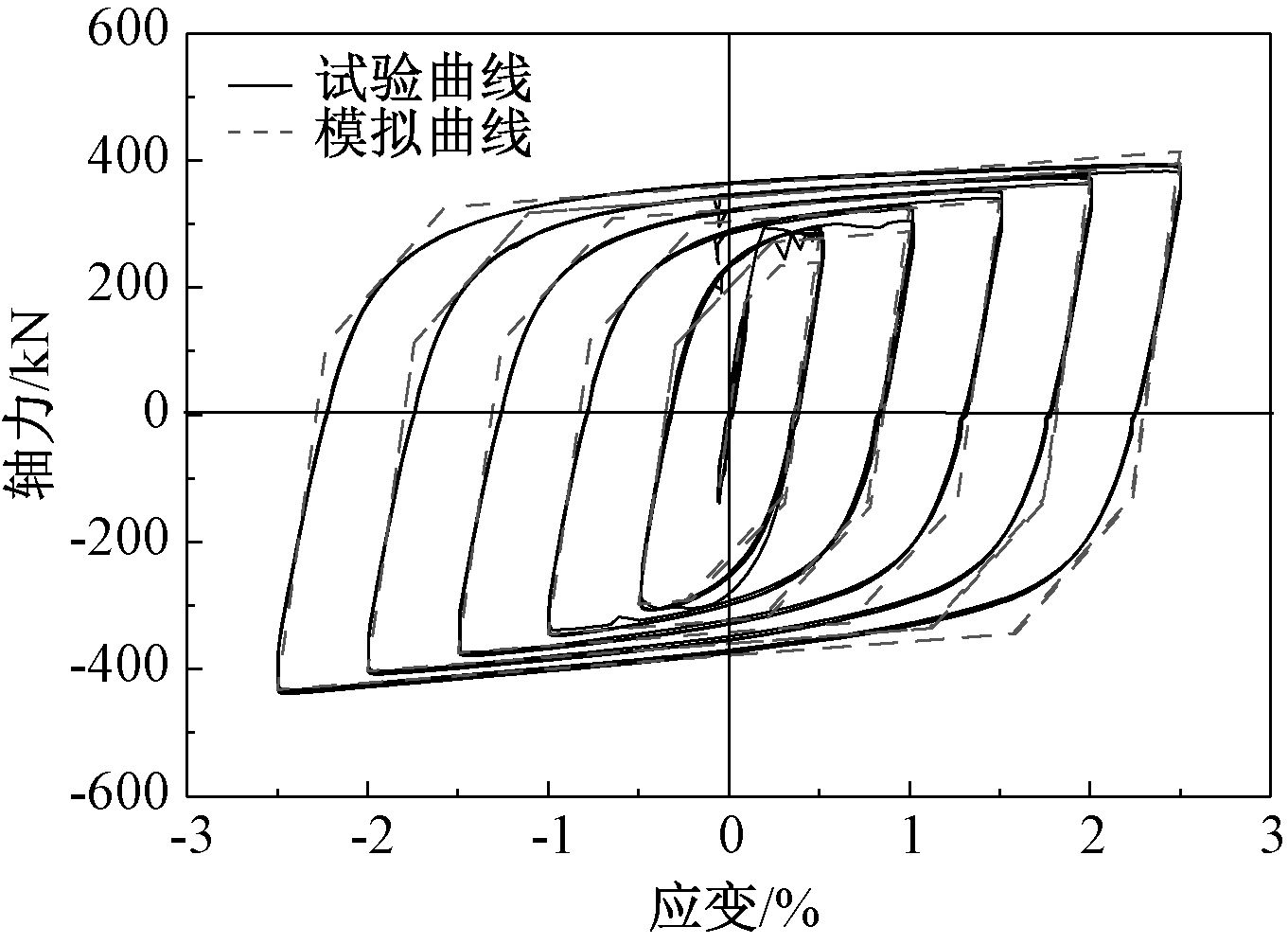
图6 BRB试验曲线与模拟曲线对比
Fig.6 Comparison between test curves and simulation curves of BRB
4 动力时程分析
4.1 地震波选取
地震动记录的选取关系到分析结果的准确性。由于本文三个结构模型的周期跨度比较大,为保证选取地震波的反应谱与GB 50011—2010的设计谱在结构特征周期段内具有较高吻合度,参考文献[14]中的选波方法,运用Quakemanager软件共选取10条远场地震波记录(表3),地震波反应谱如图7所示。
表3 地震波记录
Table 3 Ground motion records

ID地震记录台站震级峰值加速度/g放大系数GM1ParkfieldCholame-Shandon Array #126.190.06 7.5 GM2Imperial Valley-06Calipatria Fire Station6.530.13 4.0 GM3Imperial Valley-06Delta6.530.24 1.6 GM4Imperial Valley-06Niland Fire Station6.530.11 4.0 GM5Loma PrietaAgnews State Hospital6.930.17 3.0 GM6LandersAmboy7.280.11 3.0 GM7LandersFeatherly Park-Maint7.280.05 6.5 GM8Northridge-01El Monte - Fairview Av6.690.13 4.0 GM9Northridge-01 LA - Baldwin Hills6.690.23 2.6 GM10El MayorEl Centro Array #47.200.25 2.1
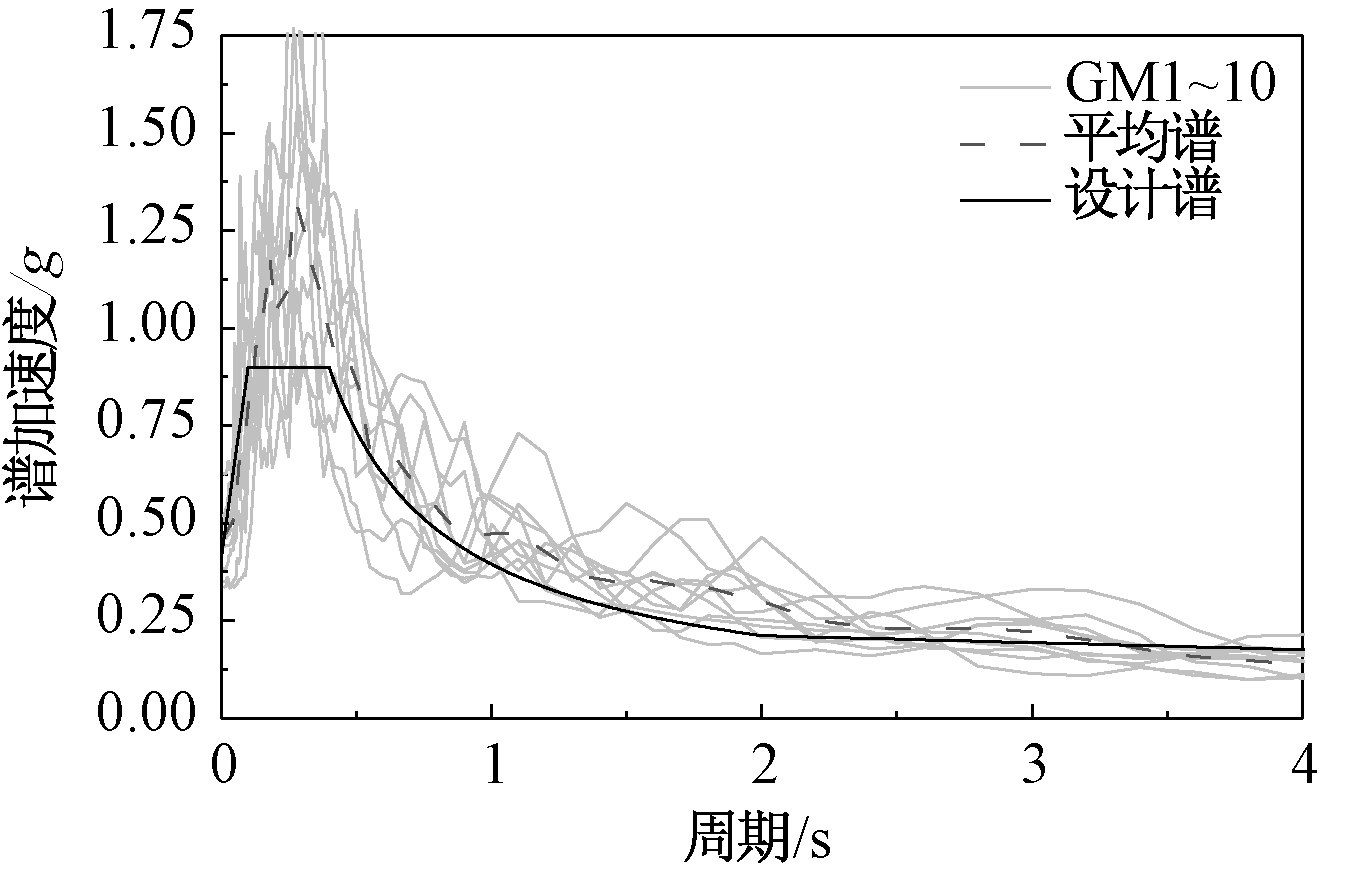
图7 地震波反应谱
Fig.7 Response spectra of the ground motion records
4.2 结构动力响应
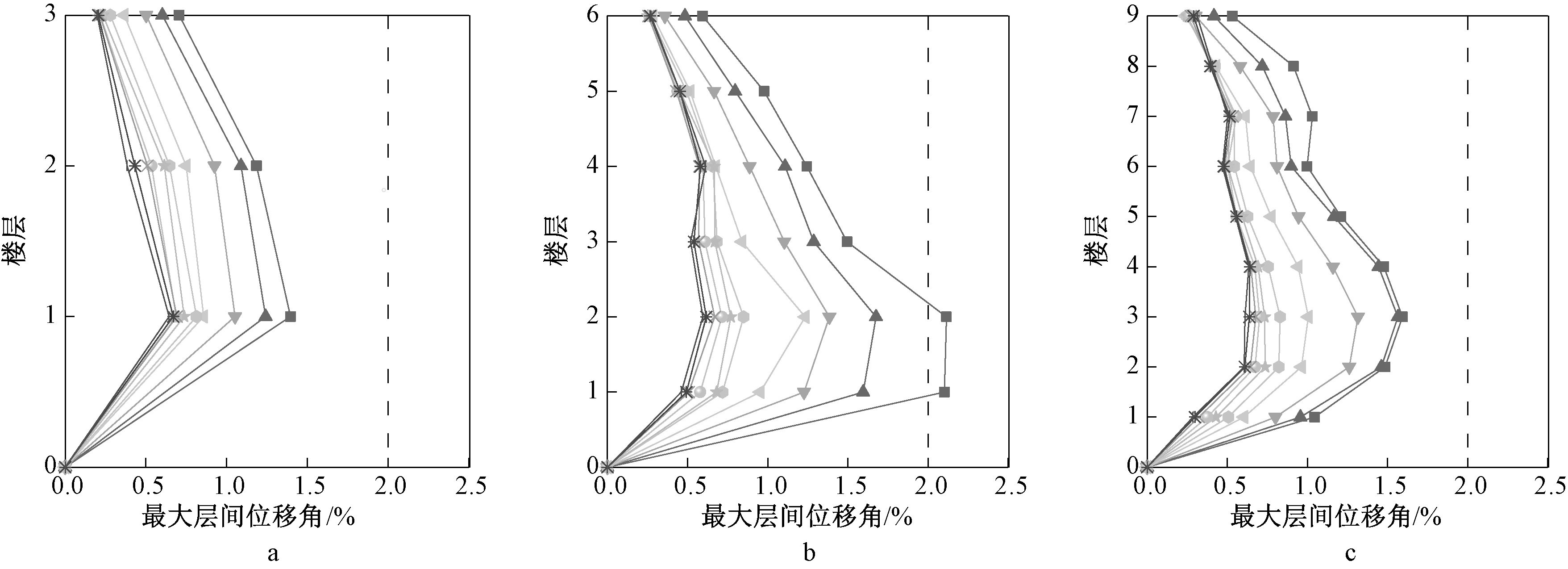
a—3层结构; b—6层结构; c—9层结构。![]() —k=0;
—k=0; ![]() —k=0.2;
—k=0.2; ![]() —k=0.5;
—k=0.5; ![]() —k=1.0;
—k=1.0; ![]() —k=1.5;
—k=1.5; ![]() —k=2.0;
—k=2.0; ![]() —k=2.5; ……k=3.0;
—k=2.5; ……k=3.0; ![]() —k=3.5
—k=3.5 ![]() —k=4.0。
—k=4.0。
图8 不同k值的BRB-PCF双重体系的最大层间位移角(均值+标准差)沿结构高度分布
Fig.8 Peak story drifts (mean plus standard deviation) along the height for BRB-PCF dual systems with different k
对不同刚度比k的BRB-PCF双重体系进行非线性动力时程分析。图8为各结构的最大层间位移角均值+标准差的分析结果沿高度分布。对于不同层数的PCF体系(即k=0),最大层间位移角基本满足罕遇地震下层间位移角不超过0.02的要求,但结构的层间位移角分布比较不均匀,结构变形明显集中于下部楼层。在PCF体系中设置BRB后,结构的各层变形均得到有效的控制。随着刚度比k的增大,结构各层的层间位移角均减小,特别是变形较为明显的下部楼层减小幅度最大,这使得结构的层间位移角分布更加均匀,变形集中效应得到改善。但当k达到1.0后,继续增大刚度比对结构位移角的控制作用在减弱,并在k≥1.5以后不再产生明显影响。
在BRB-PCF双重体系中,BRB支撑、耗能梁段和底层柱底塑性铰是为结构提供耗能能力的主要构件。其中BRB支撑作为结构的抗震保险装置,起到提高结构抗震性能和降低震后修复难度的重要作用,具体实现方式为:1) 为结构提供附加刚度和承载力,降低结构多遇地震时的弹性变形;2)通过BRB支撑的塑性耗能提高结构阻尼,降低罕遇地震时的动力响应,在将损伤主要集中于BRB的同时,保证主体结构的基本完整,实现震后快速修复的目的。因此可将BRB塑性耗能占比(即BRB消耗的能量与结构的总耗能之比)作为体现BRB对主体结构保护程度的重要参数。
图9为10条地震波作用下,BRB-PCF双重体系的BRB塑性耗能以及BRB塑性耗能占比与刚度比k的关系曲线。当k≤1.0时,BRB塑性耗能以及BRB塑性耗能占比均随着k的增大同步增加;当刚度比k≥1.0时,随着刚度比增加,BRB塑性耗能占比的增量减小,并在k=1.0~1.5之间BRB塑性耗能出现拐点,BRB消耗的能量陆续下降,BRB的耗能效率明显降低。
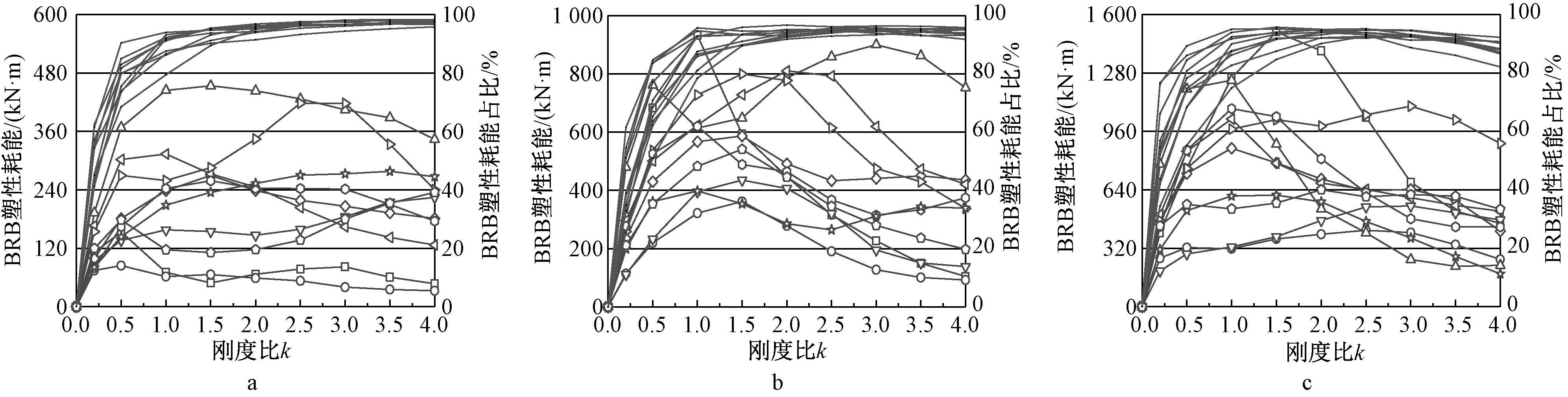
a—3层结构; b—6层结构; c—9层结构。
注:带标记点曲线为GM1~10塑性耗能;其余为GM1~10 BRB塑性耗能占比。
图9 地震下BRB-PCF双重体系的BRB塑性耗能及BRB塑性耗能占比与刚度比的关系曲线
Fig.9 The relationship of BRB plastic energy dissipation, BRB plastic energy dissipation ratio and
stiffness ratio of BRB-PCF dual system under earthquake
图10和图11分别为GM3和GM8地震作用下,各结构的PCF体系塑性耗能和BRB支撑塑性耗能的统计结果。增大刚度比k能有效提高BRB的耗能,而PCF体系的塑性耗能则显著降低,说明结构主体的损伤程度在下降。当刚度比k≥1.5后,BRB已承担结构绝大部分的耗能,而PCF体系的塑性耗能很小并趋于稳定,继续增大刚度比的作用并不显著。

a—3层结构; b—6层结构; c—9层结构。
图10 GM3作用下BRB-PCF双重体系的PCF塑性耗能和BRB塑性耗能的统计
Fig.10 Statistics of PCF plastic energy dissipation and BRB plastic energy dissipation in BRB-PCF dual system under GM3
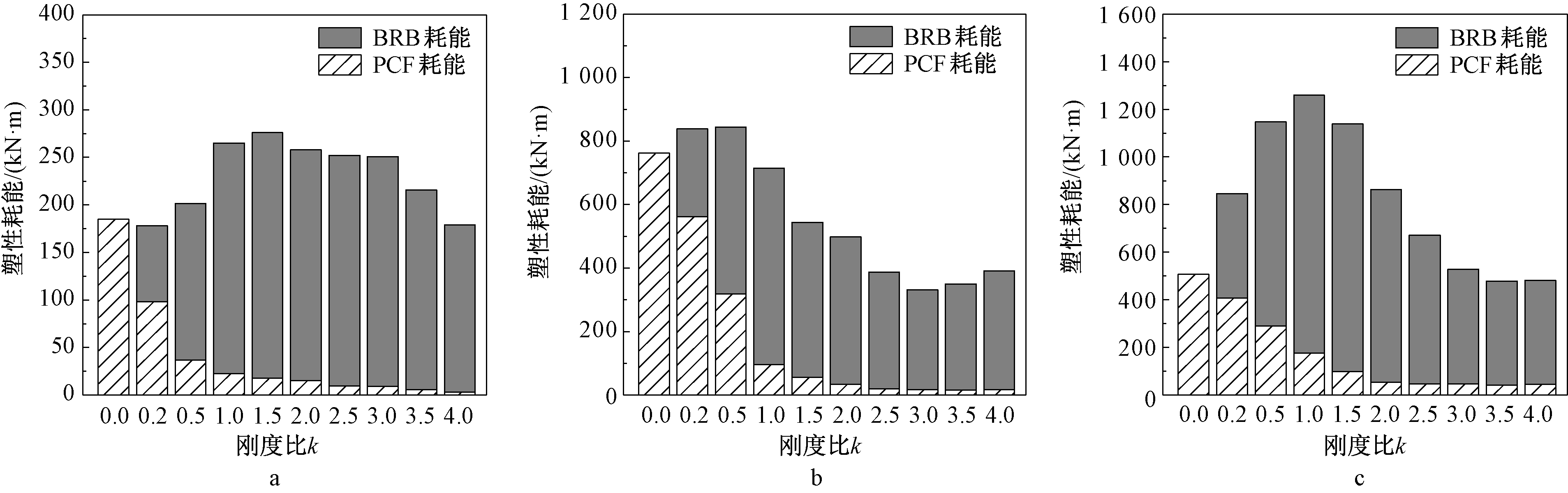
a—3层结构; b—6层结构; c—9层结构。
图11 GM8作用下BRB-PCF双重体系的PCF塑性耗能和BRB塑性耗能的统计
Fig.11 Statistics of PCF plastic energy dissipation and BRB plastic energy dissipation in BRB-PCF dual system under GM8
5 结束语
本文为研究刚度比k对BRB-PCF双重体系抗震性能的影响,对不同层数的分析模型进行了非线性动力时程分析。结论如下:
1)在PCF体系中适当地布置BRB能够有效提高结构的抗震性能,并使结构损伤主要集中于BRB,而结构其他主要构件基本完好,震后仅需更换BRB支撑,提高了结构的修复效率。
2)刚度比的增大能提升结构抗震性能,但当k≥1.5时,继续增大k对层间位移角的控制作用减弱,结构抗震性能的提升较小,建议合理的刚度比范围为k≤1.5。
[1] 吴刚, 冯德成. 装配式混凝土框架节点基本性能研究进展[J]. 建筑结构学报, 2018, 39(2): 1-16.
[2] 吴从晓, 赖伟山, 周云, 等. 新型预制装配式消能减震混凝土框架节点抗震性能试验研究[J]. 土木工程学报, 2015,48(9): 23-30.
[3] 柳炳康, 宋满荣, 蒋亚琼, 等. 预制预应力混凝土装配整体式框架抗震性能试验研究[J]. 建筑结构学报, 2011, 32(2): 24-32.
[4] 高向玲, 徐龙标, 李杰, 等. 预制混凝土梁柱节点试验及框架受力性能分析[J]. 湖南大学学报(自然科学版), 2017, 44(7): 97-103.
[5] 赵俊贤, 吴斌, 欧进萍. 新型全钢防屈曲支撑的拟静力滞回性能试验[J]. 土木工程学报, 2011, 44(4): 60-70.
[6] 王静峰, 王新乐, 李贝贝, 等. 屈曲约束支撑装配式混凝土框架结构抗震性能试验研究[J]. 土木工程学报, 2018, 51(12): 72-82.
[7] 贾明明,张素梅,吕大刚,等. 抑制屈曲支撑布置原则对钢框架抗震性能的影响[J]. 工程力学,2009,26(7): 140-146.
[8] AUKEMAN L J, LAURSEN P. Evaluation of the ASCE 7-05 Standard for Dual Systems: Response History Analysis of a Tall Buckling-Restrained Braced Frame Dual System[C]//Structures Congress 2011. ASCE, 2011: 2707-2717.
[9] 冯玉龙, 吴京, 孟少平, 等. 单层屈曲约束支撑框架的抗震参数[J]. 东南大学学报(自然科学版), 2015, 45(3): 544-549.
[10] 谢钦, 周臻, 孔祥羽, 等. 梁柱退化和剪力比对自定心BRB双重体系抗震性能的影响[J]. 振动与冲击, 2018(8): 9-16.
[11] Computers & Structure Inc(CSI). Components and Elements for Perform-3DTM and Perform-Collapse[M].Berkely, CA: CSI,2011.
[12] 陆新征, 叶列平, 潘鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅱ: 关键构件试验[J]. 建筑结构, 2012, 42(11): 23-26.
[13] 黄波, 陈泉, 李涛, 等. 国标Q235钢屈曲约束支撑低周疲劳试验研究[J]. 土木工程学报, 2013, 46(6): 29-34.
[14] 杨溥, 赖明. 结构时程分析法输入地震波的选择控制指标[J]. 土木工程学报, 2000, 33(6): 33-37.