1 预应力预制混凝土框架节点形式
预制装配结构是实现建筑工业化的必由之路。连接方式是预制装配结构的核心技术。根据节点受力特性的不同,连接方式分为刚性连接和延性连接两大类,刚性连接是传统的预制混凝土结构的连接方式,通过节点区的现浇混凝土及构造措施模拟现浇混凝土结构,并要求节点的承载力及延性不低于现浇结构。此类节点需要现场湿作业,施工程序复杂,在地震作用下吸收地震能量较多,震后残余变形较大,修复成本较高甚至无法修复。
通过预应力筋将预制构件连接在一起是一种延性连接方式,其受力性能与现浇框架结构不同:在地震作用下弹塑性变形集中在梁柱连接节点处,梁、柱构件基本保持弹性;节点具有较强的自复位能力,震后残余变形很小,易修复。
预应力预制混凝土结构中耗能元件是研究的热点之一。顶底角钢作为连接件在钢结构中应用较为广泛,同时在预应力自复位钢框架结构以及预应力自复位联肢墙结构中作为耗能元件使用[1-2]。为了发展我国的预制装配结构体系,在国内外已有研究成果的基础上[1-5],采用顶底角钢作为耗能元件,提出一种新型预应力预制混凝土框架节点,称为PTED节点[6](图1),该节点的梁、柱构件通过预应力筋、顶底角钢以及高强螺栓拼接在一起。预应力筋采取跨内通长无黏结形式以保证在罕遇地震下不屈服,且节点具有良好的自复位功能,同时也便于施工。角钢的作用是在施工阶段、预应力筋尚未张拉时作为预制梁的临时支撑,结构形成整体后为梁端截面提供部分抗弯、抗剪承载力,更重要的是在地震中可通过角钢的弹塑性变形耗能。
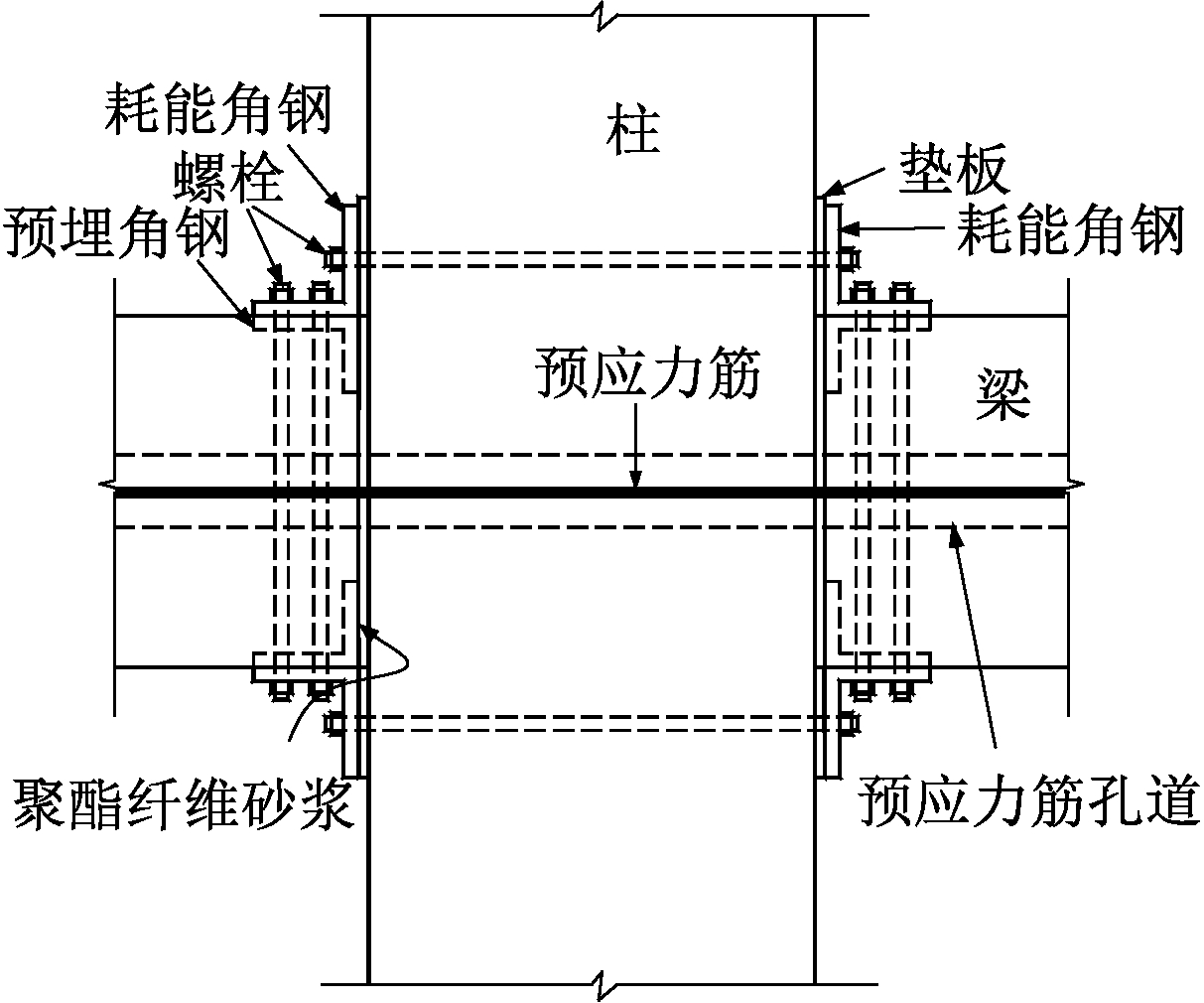
图1 PTED节点
Fig.1 PTED joints
为了验证PTED节点装配方式的可行性和节点具有优越的抗震性能,对PTED边节点进行了拟静力试验研究[6],节点试验装置见图2,其中节点T3-4S0.5-1的M-Δ(M为节点梁端弯矩,Δ为节点层间位移角)滞回曲线见图3,由图3可知:PTED节点的滞回曲线具有明显的捏拢效应,节点残余变形较小,具有良好的可恢复性,同时由于角钢的耗能,节点还具备一定的耗能能力,节点的总体滞回曲线呈旗形。

图2 PTED节点试验照片
Fig.2 Photo of PTED joints in test
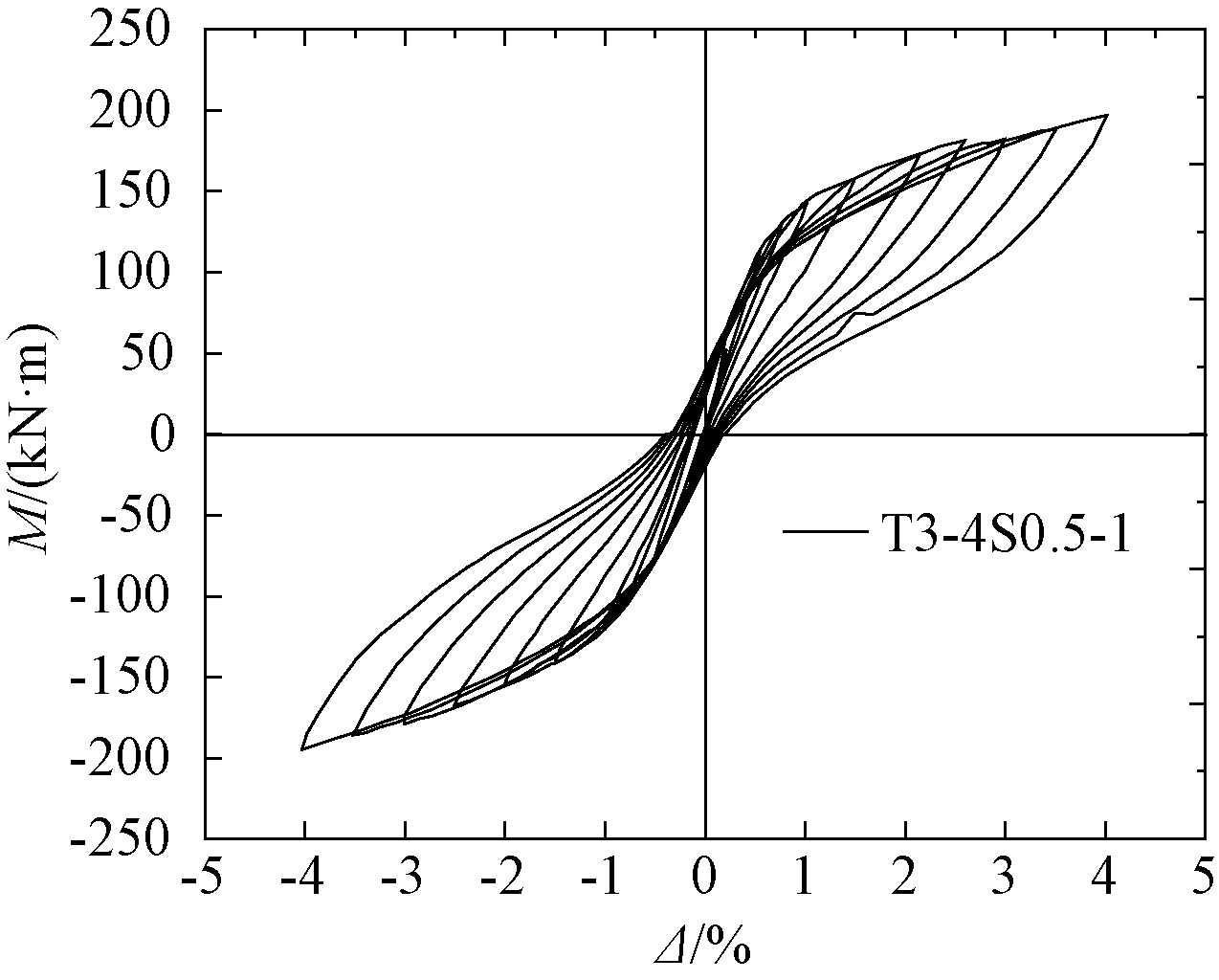
图3 节点试验滞回曲线
Fig.3 Hysteresis curves of the joint
2 节点梁端承载能力极限状态设计
2.1 节点梁端抗弯设计
通过梁柱连接处受力性能分析可知,当计算节点梁端受弯承载力时,可采用如下基本假定[7]:1)梁端受拉角钢处于屈服状态,且梁端顶底角钢的拉力Tayx与压力Cayx相等;2) 忽略预应力筋合力的变化,预应力筋合力近似等于初始预应力筋有效应力的合力Pbi;3) 梁柱接合面处梁端受压区混凝土压应力按等效矩形应力图形均匀分布,应力大小为fc。
2.1.1 预应力筋面积的确定
PTED框架节点梁端受弯承载力Mbd由预应力筋、受压区混凝土以及梁端顶、底角钢共同提供,可得下式:
Mbd=Mbp+Mba
(1)
式中:Mbp为预应力筋、受压区混凝土提供的受弯承载力;Mba为梁端顶、底角钢提供的受弯承载力。
为了验证上述式(1)的可靠性,对节点进行了系列组件试验[8]:包括PTED节点T3-4S0.5-1、PT节点T3-4S0.5(仅靠预应力筋、无角钢连接的节点)及ED节点T3-1(仅靠角钢、无预应力筋连接的节点)的拟静力荷载试验,图4给出了各试件的M-Δ关系的骨架曲线,其中,曲线T3-4S0.5+T3-1为T3-4S0.5与T3-1的骨架曲线数值叠加。由图可知:T3-4S0.5-1的骨架曲线与T3-4S0.5+T3-1基本重合,说明T3-4S0.5-1的梁端弯矩Mb可由T3-4S0.5的梁端弯矩Mbp和T3-1的梁端弯矩Mba叠加得到,即验证式(1)的正确性。

![]() —T3-4S0.5-1;
—T3-4S0.5-1; ![]() —T3-4S0.5+T3-1;
—T3-4S0.5+T3-1;![]() —T3-4S0.5;
—T3-4S0.5; ![]() —T3-1。
—T3-1。
图4 各试件的骨架曲线
Fig.4 Skeleton curves of the specimens
预应力筋的设计参数包括预应力筋面积、预应力筋有效应力。预应力筋有效应力若取值过大,则框架结构在侧向荷载作用下引起预应力筋的伸长导致预应力筋的应力增大,可能会引起预应力筋的屈服,从而导致结构自复位功能的下降,若取值过小,则会导致预应力筋面积的增大,建议预应力筋有效应力fpi可取(0.45~0.55)fptk。
为了确定预应力筋的面积和角钢的相关设计参数,引入预应力度的概念[9],即预应力度λ为由预应力筋提供的抗弯承载力占总的梁端抗弯承载力的比例:
λ=Mbp/Mbd
(2)
λ作为PTED框架节点重要的设计参数,对节点的受力性能影响很大,保持梁端受弯承载力大小不变,调整预应力度的大小,当λ较小时,角钢提供的抗弯承载力较大,则节点的滞回曲线饱满,节点耗能能力较好,但残余变形较大,节点的自复位能力较差;λ取值较大,则自复位能力较好,但耗能能力较差。综合考虑节点的耗能能力以及自复位能力的大小,建议λ取值为0.5~0.6。
PTED节点梁端受弯承载力的计算简图见图5。图中Pbi为预应力筋有效应力的合力,hb为梁高,cb为梁端受压区混凝土高度,Cayx为受压角钢水平肢的轴向压力,Tayx为受拉角钢水平肢的轴向拉力,ta为角钢厚度。
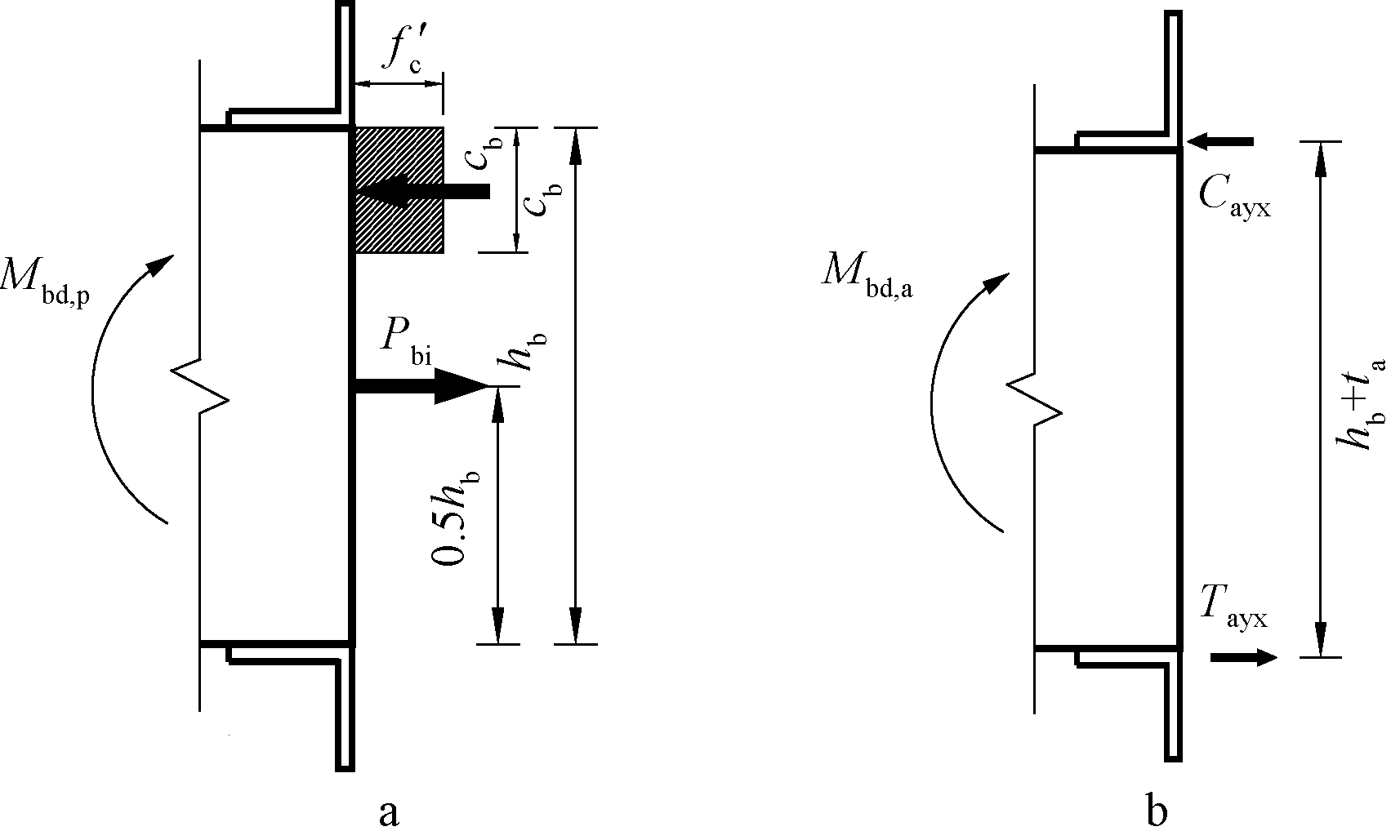
a—预应力筋对梁端受弯承载力的贡献;
b—角钢对梁端受弯承载力的贡献。
图5 梁端受弯承载力的示意简图
Fig.5 Schematic diagram of bending moment at beam end
由图5可知:预应力筋有效应力的合力可由下式确定:
(3)
式中:Mb为梁端弯矩设计值,根据实际情况取非抗震组合和抗震组合的较大值,如式(4)所示:
Mb=max{γG MG+γQ MQ+M次,
γRE(γG MGE+γEh MEhk+M次)}
(4)
式中:MG、MQ分别为恒载和活载弯矩标准值;M次为预应力产生次弯矩;γG、γQ分别为恒载、活载分项系数;MGE、MEh分别为重力荷载和地震作用下弯矩标准值;γGE、γEh分别为其分项系数;γRE为承载力抗震调整系数。
则预应力筋的合力Pbi为:

(5)
则由Pbi=fpi Ap可确定预应力筋的面积Ap。
2.1.2 角钢尺寸的确定
角钢的主要作用为在PTED框架结构使用阶段提供梁端受弯、受剪承载力以及耗能能力,同时可在施工阶段作为预制梁的支撑,因此角钢的设计需同时考虑使用阶段和施工阶段的要求。
在使用阶段,角钢与预应力筋共同承担梁端弯矩,角钢承担的梁端弯矩为(1-λ)Mb,由图6可知,角钢的水平屈服荷载Tayx可由式(6)确定[6]:
(1-λ)Mb≤Mba=Tayx(hb+ta)
(6)
由角钢的水平屈服荷载Tayx可确定角钢的主要设计参数如角钢的屈服强度fay、角钢厚度ta、角钢与柱连接的螺栓中心至角钢水平边的距离lgv等,各主要设计参数可由式(7)确定。
(7a)
Va0=fay la ta/2
(7b)
式中:la为角钢的长度,一般与梁宽相同;wa为螺栓帽的宽度;Ka为角钢圆弧端点至角钢水平边的距离;Va0为不考虑剪切-弯曲相互作用的角钢塑性剪切力。各主要设计参数的意义见图6。

图6 角钢屈服力计算参数
Fig.6 Calculation parameters of yield force of angle steel
根据角钢的主要设计参数,选择角钢规格,确定角钢与梁、柱连接螺栓的位置,建议所选用角钢的水平屈服力略大于Tayx即可,若角钢的水平屈服力过大,会导致罕遇地震作用下角钢未屈服,耗散地震能量较少,同时造成角钢材料的浪费。
2.2 节点连接处抗剪设计
由于PTED节点梁柱接合面非连续,传统的梁端抗剪承载力计算理论无法应用于PTED节点连接处的抗剪设计。PTED节点梁柱连接处的抗剪承载力主要由两部分构成:梁柱接合面间的摩擦力以及柱与角钢之间的摩擦力。PTED节点连接处的抗剪设计要求保证在梁端剪力作用下梁柱接合面不产生相对的剪切滑移,即:
Vbd=Vba+Vbp≥Qb
(8)
式中:Vbd为梁端抗剪承载力;Qb为梁端剪力设计值,需考虑梁端强剪弱弯的调整系数;Vba、Vbp分别为角钢与柱之间摩擦抗剪承载力以及梁柱接合面间的摩擦抗剪承载力,计算需考虑梁端顶底角钢并且考虑抗力分项系数,两者表达式如下:
式中:Pn为单个角钢上所有与柱相连的螺栓预紧力之和;Pp为梁端受压区压应力的合力,为了简化计算,可取预应力筋的初始合力。角钢与混凝土接触面之间的摩擦系数μa可取0.33[10],梁柱端混凝土接触面间的摩擦系数μp可取0.6。
3 节点梁端正常使用极限状态设计
PTED节点梁柱连接处纵筋不贯通,仅靠预应力筋和角钢连接,梁柱接合面不是连续的截面,不符合平截面假定。在缺乏试验研究基础的情况下,现浇预应力混凝土受弯构件裂缝控制通常采用的名义拉应力法无法借鉴[11]。本文给出PTED框架结构较为简单的梁端裂缝控制方法。
对于抗裂等级为一级的构件,要求荷载标准组合下截面不出现拉应力,则:
Mk≤fci W0
(10)
式中:Mk为按荷载标准组合的梁端弯矩值;fci为扣除全部预应力损失后在抗裂验算边缘混凝土的预压应力;W0为换算截面抵抗矩。
对于抗裂等级为二级的构件,应使构件在荷载标准组合下拉应力不超过砂浆与混凝土间的黏结强度,在荷载准永久组合下截面不出现拉应力,即:
式中:Mk,Ml分别为荷载标准组合和准永久组合下对应的梁端弯矩值;ftk为砂浆与混凝土间的黏结抗拉强度。
对于抗裂等级为三级的构件,限制其裂缝宽度不超过0.2 mm。正常使用极限状态时,角钢仍处于弹性阶段,受拉角钢的拉力Tax为:
Tax=K0g
(12)
式中:K0为受拉角钢的弹性刚度;g为裂缝宽度,取0.2 mm。
预应力筋此时伸长量较小,可忽略不计,应力仍取初始有效应力值fpi,则预应力筋的合力为:
Pbi=Ap fpi
(13)
由文献[6]分析可知顶底角钢的拉、压力近似相等,由截面的静力平衡条件,可得:
Pbi=Cb
(14)
式中:Cb为受压区混凝土压应力的合力。
截面此时处于弹性状态,受压区混凝土应力分布呈现三角形分布,截面受力示意见图7,由试验可知,裂缝延伸的截面高度不超过1/3,即梁端混凝土受压区高度为2hb/3时,梁端裂缝宽度的限值不超过0.2 mm,故梁端弯矩标准值满足式(15)时,即可满足裂缝宽度的要求:
Mk≤Mw,lim=fpi Ap(0.5hb-cb/3)+
Tax(hb+ta)=0.278fpi Ap hb+Tax(hb+ta)
(15)
式中:cb为混凝土受压区高度;hb为梁端截面高度。
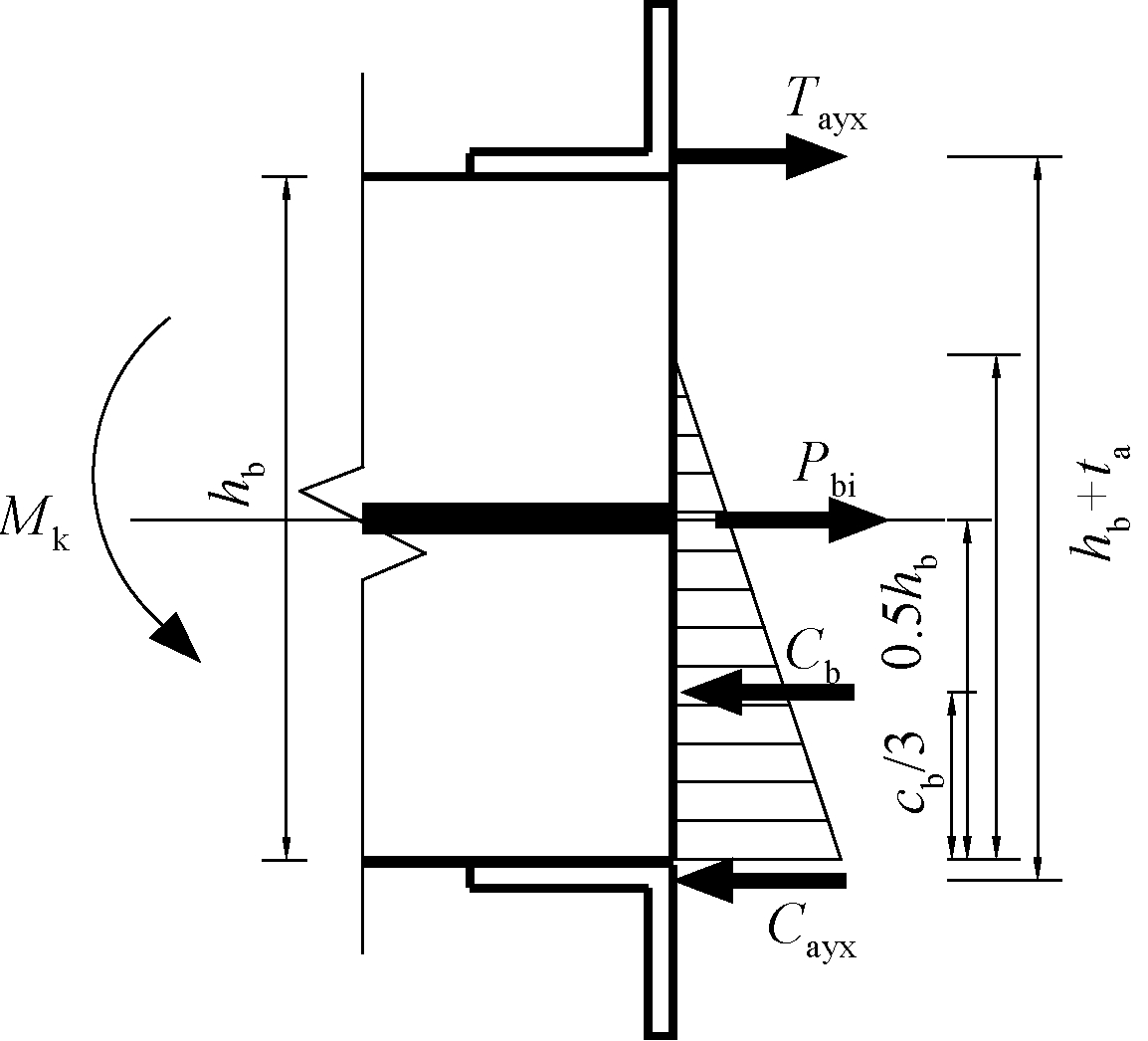
图7 截面受力示意
Fig.7 Force diagram of the section
4 节点施工阶段的验算
在施工阶段角钢可作为预制梁端支承,受力状态如图8所示[12]。角钢的支承面主要集中在距柱约1.5~2.5倍的角钢厚度范围内,等效集中力距柱端位置约为角钢厚度的2倍。PTED框架通常作为纵向抗震框架,预制梁施工阶段只承受自重和部分施工活载,因此梁端支承反力在角钢竖肢上产生的弯曲应力很小。角钢的设计主要考虑梁端的受弯、受剪承载力以及耗能能力的大小。
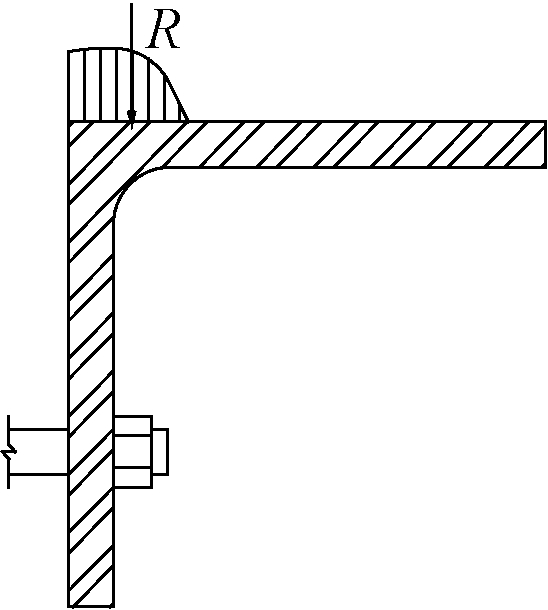
图8 施工阶段角钢受力情况
Fig.8 Force state of angle steel in the construction stage
施工阶段需考虑角钢与柱之间的抗滑移能力,为保证预应力筋和螺栓在节点上的准确定位与安装,施工阶段预制梁在竖向荷载作用下不应产生滑移,即预制梁搁置在角钢上产生的竖向反力不超过柱与角钢竖肢之间的抗滑移力,该抗滑移力为通过张拉高强螺栓在角钢与柱之间产生的静摩擦力,计算式如下:
R≤Vlu=μa Pn
(16)
式中:R为施工阶段简支梁作用在角钢上的竖向力;Vlu为底部角钢与柱之间的静摩擦力;μa为角钢竖肢与柱之间的摩擦系数,取μa=0.33;Pn为底部角钢所有螺栓的设计预拉力的合力。
5 节点核心区抗剪承载力计算
5.1 节点核心区受剪承载力
由节点拟静力试验可知[6],节点核心区基本处于弹性工作阶段,且节点的剪力基本由混凝土承担,箍筋应力很小,采用斜压杆机制[6],见图9,可得节点核心区受剪承载力为:
Vc=0.8fcc bj scos2α
(17)
式中:0.8为混凝土强度降低系数(考虑交叉斜裂缝的影响);fcc为约束混凝土的极限强度;bj为节点核心区宽度;α为斜压杆倾斜角;s为节点核心区受压高度。
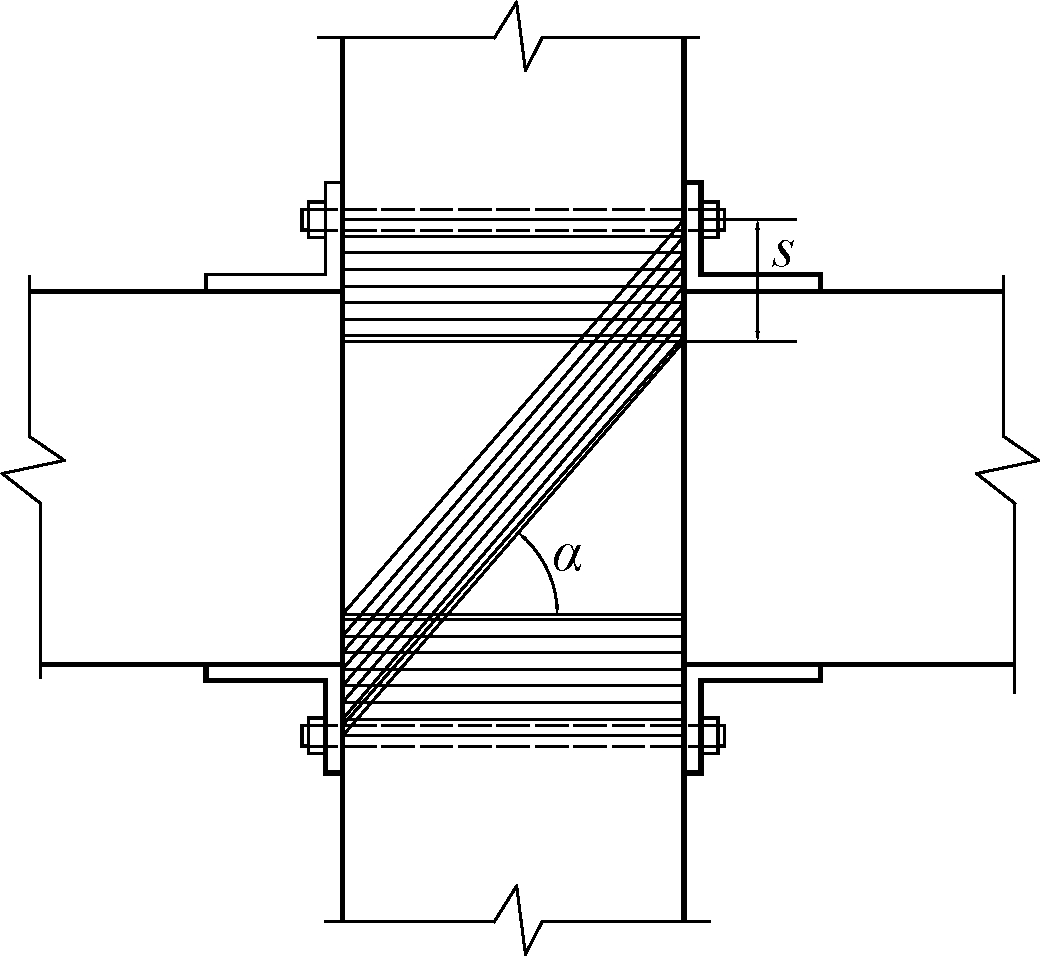
图9 PTED节点斜压杆模型
Fig.9 Diagonal compression strut model of PTED joints
5.2 节点核心区抗裂承载力
考虑到节点部位的重要性及裂缝出现后修复的困难,对严格控制其不出现裂缝者,必须对节点进行抗裂分析和验算,否则会影响建筑物的美观和使用者的安全感,降低结构的承载能力、刚度和耐久性,因此对于地震区的一般工业与民用建筑,除了应计算节点承载力外,尚应按众值烈度进行框架节点的抗裂验算,以保证在较多几率遇到的多遇地震的情况下,框架无需修复或只需稍加修复仍能连续正常工作。
混凝土开裂时的剪应力vcr[13]:
(18)
式中:fxc为梁端预压力在节点核心区轴线上引起的水平均布压应力;fyc为柱端轴压力在节点核心区轴线上引起的竖向均布压应力;ftk为混凝土抗拉强度标准值。
将节点核心区的剪应力用节点名义剪应力表示vj=Vj/(bj cj)。其中Vj为裂缝出现时节点所受的剪力[6],bj、cj分别为节点核心区的有效宽度和高度。
(19)
其中 zp=hp-cb/2
式中:λ为预应力度;zp为预应力筋合力内力臂长度;cb为等效矩形截面的受压区高度;hp为预应力筋合力点至截面受压边缘的距离;hax为顶底角钢水平肢的中心距离。
则节点抗裂验算式为:
Vj≤ηψbj cj vcr
(20)
式中:ψ为节点约束系数,无直交梁时取1.0,有直交梁时取1.0~1.5;η为综合影响系数,考虑节点剪应力分布的不均匀,以及箍筋、垂直钢筋等对核心区初裂的影响,η偏保守可取0.67[14]。
6 结束语
针对基于角钢-高强螺栓连接的预应力预制混凝土框架节点的梁柱连接处,提出具体的设计方法,包括使用阶段的承载能力极限状态和正常使用极限状态并考虑施工阶段节点的工作状态,确定预应力筋的面积、初始张拉力、角钢尺寸及螺栓连接位置等设计参数的方法,本文所提设计方法可供设计参考。
[1] RICLES J, SAUSE R, GARLOCK M, et al. Posttensioned Seismic-Resistant Connections for Steel Frames[J]. Journal of Structural Engineering, 2001, 127(2):113-121.
[2] SHEN Q, KURAMA Y C. Nonlinear Behavior of Posttensioned Hybrid Coupled Wall Subassemblages [J]. Journal of Structural Engineering, 2002, 128(10): 1290-1300.
[3] 周颖,吕西林. 摇摆结构及自复位结构研究综述[J]. 建筑结构学报,2011,32(9):1-10.
[4] 吕西林,陈云,毛苑君. 结构抗震设计的新概念-可恢复功能结构[J]. 同济大学学报,2011,39(7): 941-948.
[5] 潘振华,潘鹏,叶列平. 自复位钢框架节点有限元模拟及参数分析[J]. 建筑结构学报,2011,32(3):35-42.
[6] 蔡小宁. 新型预应力预制混凝土框架结构抗震能力及设计方法研究[D].南京: 东南大学, 2012.
[7] BRAD D W, KURAMA Y C. Nonlinear Behavior of Precast Concrete Coupling Beams Under Lateral Loads [J].Journal of Structural Engineering, 2007, 133(11):1571-1581.
[8] 蔡小宁,孟少平,孙巍巍.自复位预制框架边节点组件受力性能试验研究[J]. 工程力学,2014,31(3):160-167.
[9] 王俊,刘立新,尚世宇.预应力度对预应力混凝土梁徐变曲率影响试验研究[J].土木工程学报,2010,43(8):37-43.
[10] SHEN Q, KURAMA Y C.Seismic Design and Analytical Modelling of Posttensioned Hybrid Coupled Wall Subassembladges [J].Journal of Structural Engineering, 2006, 132(7): 1030-1040.
[11] 种迅. 后张预应力预制混凝土框架结构抗震能力和设计方法的研究[D].南京:东南大学,2007.
[12] 周波.干性连接预制预应力混凝土框架设计方法研究[D]. 南京:东南大学,2014.
[13] EL-SHEIKH M. Seismic Analysis,Behavior, and Design of Unbonded Post-Tensioned Precast Concrete Frames[D].Bethlehem:Lehigh University,1997.
[14] 邢国华,吴涛,刘伯权.钢筋混凝土框架节点抗裂承载力研究[J].工程力学,2011,28(3):163-169.